Abstract
The Ibragimov–Khasminskii theory established a scheme that gives asymptotic properties of the likelihood estimators through the convergence of the likelihood ratio random field. This scheme is extending to various nonlinear stochastic processes, combined with a polynomial type large deviation inequality proved for a general locally asymptotically quadratic quasi-likelihood random field. We give an overview of the quasi-likelihood analysis and its applications to ergodic/non-ergodic statistics for stochastic processes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider an \(\textsf {m}\)-dimensional semimartingale \(Y=(Y_t)_{t\in [0,T]}\) having a decomposition
on a stochastic basis \((\Omega ,\mathcal{F},\mathbf{F},P)\) with a filtration \(\mathbf{F}=(\mathcal{F}_t)_{t\in [0,T]}\). The time horizon T is fixed. The process \(w=(w_t)_{t\in [0,T]}\) is an \(\textsf {r}\)-dimensional Wiener process with respect to \(\mathbf{F}\), and  is a given function. The process \(b=(b_t)_{t\in [0,T]}\) and \(X=(X_t)_{t\in [0,T]}\) are respectively \(\textsf {m}\)-dimensional and \(\textsf {d}\)-dimensional progressively measurable processes. The process b is unobservable but we observe the data \((X_{t_{j}},Y_{t_{j}})_{j=0,1,...,n}\) for \({t_{j}}=t_j^n=jT/n\). We aim at estimation of the unknown parameter \(\theta \in \Theta \), a \(\textsf {p}\)-dimensional bounded open set. The model (1.1) includes diffusion processes on the time interval [0, T]. The model (1.1) is called a stochastic regression model.
is a given function. The process \(b=(b_t)_{t\in [0,T]}\) and \(X=(X_t)_{t\in [0,T]}\) are respectively \(\textsf {m}\)-dimensional and \(\textsf {d}\)-dimensional progressively measurable processes. The process b is unobservable but we observe the data \((X_{t_{j}},Y_{t_{j}})_{j=0,1,...,n}\) for \({t_{j}}=t_j^n=jT/n\). We aim at estimation of the unknown parameter \(\theta \in \Theta \), a \(\textsf {p}\)-dimensional bounded open set. The model (1.1) includes diffusion processes on the time interval [0, T]. The model (1.1) is called a stochastic regression model.
When \(Y=X\) and \(b_t=b^o(X_t)\) for some function  , the likelihood function is
, the likelihood function is
if the distribution of the initial value \(X_0\) does not depend on \(\theta \), where \(p_h(x,y,\theta )\) is the transition density of the diffusion process. However, we do not know about the function \(b^o\) by assumption, so we cannot use the function \(L_n\) for estimation. Even if we know the function \(b^o\), it is not in general easy to compute \(p_h(X_{t_{j-1}},X_{t_{j}},\theta )\) since it is a solution to a partial differential equation, besides, optimization is necessary after getting \(L_n(\theta )\). The situation is more severe when \(Y\not =X\) since no information about the structure of X is given. In any case, it is more realistic to replace the likelihood function \(L_n\) by some other easily handled utility function.
A candidate of the utility function is the quasi-log likelihood function  defined by
defined by

where
\(S=\sigma \sigma ^\star \), \(\star \) denoting the matrix transpose, and \(\Delta _jY=Y_{t_{j}}-Y_{t_{j-1}}\). The brackets \([\cdots ]\) stand for the inner product. For example, \(M[v^{\otimes }]=\sum _{i,j}M_{i,j}v^iv^j\) for a square matrix \(M=(M_{i,j})\) and a vector \(v=(v^i)\). A quasi-maximum likelihood estimator \(\widehat{\theta }_n\) is obtained by maximizing  with respect to \(\theta \). Then \(\widehat{\theta }_n\) is asymptotically mixed normal and asymptotically efficient in Hájek’s sense. To establish this property, we need to show that the risk function, e.g., the \(L^p\)-risk \(E_\theta \big [\vert \sqrt{n}(\widehat{\theta }_n-\theta )\vert ^p\big ]\) (locally) asymptotically attains the lower bound of risks, in particular, that the \(L^p\)-norm of (the scaled error of) \(\widehat{\theta }_n\) is bounded.
with respect to \(\theta \). Then \(\widehat{\theta }_n\) is asymptotically mixed normal and asymptotically efficient in Hájek’s sense. To establish this property, we need to show that the risk function, e.g., the \(L^p\)-risk \(E_\theta \big [\vert \sqrt{n}(\widehat{\theta }_n-\theta )\vert ^p\big ]\) (locally) asymptotically attains the lower bound of risks, in particular, that the \(L^p\)-norm of (the scaled error of) \(\widehat{\theta }_n\) is bounded.
By using differentiability in \(\theta \) of  , we can derive a stochastic expansion of \(\widehat{\theta }_n\), namely,
, we can derive a stochastic expansion of \(\widehat{\theta }_n\), namely,
where \(\theta ^*\) is the true value of \(\theta \) and \(\Gamma \) is the random Fisher information matrix define by (5.1). The variable \(M_n\) is given by
where \(I_\textsf {r}\) is the \(\textsf {r}\)-dimensional identity matrix and \(\Delta _jw=w_{t_{j}}-w_{t_{j-1}}\), and the variable \(N_n\) is of \(O_p(1)\) having a complicated expression involving multiple stochastic integrals. Asymptotic expansion of the distribution of \(\widehat{u}_n\) can be obtained if we apply the martingale expansion by Yoshida (2013) (updated by arXiv:1210.3680v3 (2012)). More precisely, we can derive asymptotic expansion of the joint distribution of \((Z_n,\Gamma )\) for \(Z_n=M_n+n^{-1/2}N_n\) and next obtain the expansion for \(\widehat{u}_n\) by transforming \((Z_n,\Gamma )\) into it. In this procedure, the Malliavin calculus is applied and then we need \(L^p\)-boundedness of \(\widehat{u}_n\). As a matter of fact, boundedness of a smooth deformation of \(\widehat{u}_n\) in the Sobolev space  can be shown with the aid of the \(L^p\)-boundedness of \(\widehat{u}_n\). Relatively high order of integrability (i.e., a large p) is necessary to carry out this plot because the integration-by-parts formula in the Malliavin calculus requires algebras of variables. Asymptotic expansion of Skorokhod integrals recently presented by Nualart and Yoshida (2019), combined with Yoshida (2020), is also applicable to this problem in place of the martingale expansion.
can be shown with the aid of the \(L^p\)-boundedness of \(\widehat{u}_n\). Relatively high order of integrability (i.e., a large p) is necessary to carry out this plot because the integration-by-parts formula in the Malliavin calculus requires algebras of variables. Asymptotic expansion of Skorokhod integrals recently presented by Nualart and Yoshida (2019), combined with Yoshida (2020), is also applicable to this problem in place of the martingale expansion.
The \(L^p\)-boundedness of an estimator is a key to develop the asymptotic theory. The celebrated Ibragimov–Khasminskii theory (Ibragimov and Khas’minskii 1973a, b; Ibragimov and Has’minskiĭ 1981) answered this important question. Epoch-making was their introduction of the notion of weak convergence of the likelihood ratio random filed, from which the asymptotic properties of the likelihood estimators (i.e., the maximum likelihood estimator and the Bayesian estimator) are induced in a unified way. The likelihood ratio random field  is defined by
is defined by  with the likelihood function \(L_n\) and a scaling matrix \(a_n\). They proved the convergence
with the likelihood function \(L_n\) and a scaling matrix \(a_n\). They proved the convergence

in a certain space of continuous functions on  for suitably extended
for suitably extended  . When
. When  is locally asymptotically normal (Le Cam 1960), the limit becomes
is locally asymptotically normal (Le Cam 1960), the limit becomes

with the Fisher information matrix \(I(\theta ^*)\) at \(\theta ^*\) and a random vector \(\Delta \sim N_\textsf {p}(0,I(\theta ^*))\). Thanks to the functional convergence (1.3), roughly speaking, we can apply the \(\text {argmax}_\theta \) operator to the both sides of (1.3) to obtain the convergence \({\hat{u}}_n=a_n^{-1}\big (\widehat{\theta }_n-\theta ^*\big )\rightarrow ^d I(\theta ^*)^{-1}\Delta \). For the Bayesian estimator
with respect to the quadratic loss function and a prior density \(\varpi \), the error of \(\widetilde{\theta }_n\) has the expression

Then the convergence (1.3) suggests the joint convergence

and hence

if (1.4) holds. One crucial point we should pay attention to is that the integrals appearing in (1.5) are essentially integrals over non-compact space since the domain tends to  as \(n\rightarrow \infty \) even if \(\Theta \) is bounded. To control these integrals, we need fast decay of the random field
as \(n\rightarrow \infty \) even if \(\Theta \) is bounded. To control these integrals, we need fast decay of the random field  .
.
The Ibragimov–Khasminskii theory features the large deviation inequality

for the likelihood ratio random field  , where \(\alpha \) is a positive constant and \({{\mathfrak {e}}}(r)\) is a function of the form \(c_0e^{-c_1r^{c_2}}\) or \(c_0r^{-L}\). Then the \(L^p\)-boundedness of \(\widehat{u}_n\) is a consequence of (1.6). The inequality (1.6) is extremely important since it quantitatively estimates the tail of
, where \(\alpha \) is a positive constant and \({{\mathfrak {e}}}(r)\) is a function of the form \(c_0e^{-c_1r^{c_2}}\) or \(c_0r^{-L}\). Then the \(L^p\)-boundedness of \(\widehat{u}_n\) is a consequence of (1.6). The inequality (1.6) is extremely important since it quantitatively estimates the tail of  . As well as the maximum likelihood estimator, the \(L^p\)-boundedness of \(\widetilde{u}_n\) also follows from (1.6).
. As well as the maximum likelihood estimator, the \(L^p\)-boundedness of \(\widetilde{u}_n\) also follows from (1.6).
Kutoyants (1984, 1994, 2004, 2012) successfully applied the Ibragimov–Khasminskii theory to semimartingales. Motivated by his pioneering works, the author tried to approach inference for stochastic processes by means of a quasi-likelihood (Yoshida 1990, 2011, 2021). In the applications of this article, the statistical models are differentiable and the used limit theorems are standard. So our interest is in the large deviation inequality (1.6). The aim of this paper is to give an overview of the quasi-likelihood analysisFootnote 1 and its applications.
2 Quasi-likelihood analysis
In this section, we will recall a simplified version of the quasi-likelihood analysis. We refer the interested reader to Yoshida (2021, 2011) for details.
2.1 Polynomial type large deviation inequality
We will work with a sequence of random fields 
 for a probability space \((\Omega ,\mathcal{F},P)\) and a bounded open set \(\Theta \) in
for a probability space \((\Omega ,\mathcal{F},P)\) and a bounded open set \(\Theta \) in  . The set
. The set  is driving the asymptotic theory, supposed to satisfy
is driving the asymptotic theory, supposed to satisfy  and
and  . As for the regularity of the random field
. As for the regularity of the random field  , since most basic is the case where the map
, since most basic is the case where the map  is of class \(C^2(\Theta )\) for a.s \(\omega \), we suppose this regularity and also that the map
is of class \(C^2(\Theta )\) for a.s \(\omega \), we suppose this regularity and also that the map  is continuous for a.s \(\omega \). Though this smoothness assumption is much stronger than that assumed in the Ibragimov–Khasminskii theory and Le Cam’s LAN theory, it simplifies our theory and still applies to many applications in practice.
is continuous for a.s \(\omega \). Though this smoothness assumption is much stronger than that assumed in the Ibragimov–Khasminskii theory and Le Cam’s LAN theory, it simplifies our theory and still applies to many applications in practice.
The targeted value of \(\theta \) is denoted by \(\theta ^*\in \Theta \). The limit of the observed information is denoted by a \(\textsf {p}\times \textsf {p}\) random symmetric matrix \(\Gamma \). The minimum eigenvalues of a symmetric matrix M is denoted by \(\lambda _{\text {min}}(M)\). We need identifiability of \(\theta ^*\) expressed in terms of a random field  , that will be related with
, that will be related with  at (2.4), and non-degeneracy of \(\Gamma \) as follows.
at (2.4), and non-degeneracy of \(\Gamma \) as follows.
- [T1]:
-
- (i):
-
There exists a positive random variable \(\chi _0\) and the following conditions are fulfilled.
- (i-1):
-
 for all \(\theta \in \Theta \).
for all \(\theta \in \Theta \). - (i-2):
-
For every \(L>0\), there exists a constant C such that
$$\begin{aligned} P\big [\chi _0\le r^{-1}\big ]\le & {} \frac{C}{r^L}\quad (r>0). \end{aligned}$$(2.1)
- (ii):
-
For every \(L>0\), there exists a constant C such that
$$\begin{aligned} P\big [\lambda _{min}(\Gamma )< r^{-1}\big ]\le \frac{C}{r^L}\quad (r>0) \end{aligned}$$
Condition [T1] is almost trivial in ergodic statistics because \(\chi _0\) is a constant and \(\Gamma \) is a deterministic matrix. We remark that \(\chi _0^{-1}\in L^{\infty {-}}=\cap _{p>1}L^p\) under [T1] (i-2). Moreover, \(\vert \Gamma ^{-1}\vert \in L^{\infty {-}}\) under [T1] (ii) since \(\big (\lambda _{min}(\Gamma )\big )^{-1}\in L^{\infty {-}}\) and \(\vert \Gamma ^{-1}\vert \le C_\textsf {p}\big (\lambda _{min}(\Gamma )\big )^{-1}\) for a constant only depending on \(\textsf {p}\).
Let \(a_T\) be a \(\textsf {p}\times \textsf {p}\) regular matrix such that \(\vert a_T\vert \rightarrow 0\) as \(T\rightarrow \infty \). The matrix \(a_T\) will specify the rate of convergence of the QLA estimators. Define \(b_T\) by \(b_T=\big \{\lambda _{\text {min}}(a_T^\star a_T)\}^{-1}\). Obviously, \(b_T\rightarrow \infty \) as \(T\rightarrow \infty \). It is assumed that
for all  , for some constant \(C_0\in [1,\infty )\). A typical example is n for \(b_T\) and \(n^{-1/2}I_\textsf {p}\) for \(a_T\), \(I_\textsf {p}\) being the identity matrix. Define a \(\textsf {p}\)-dimensional random variable \(\Delta _T\) and a \(\textsf {p}\times \textsf {p}\) random matrix \(\Gamma _T(\theta )\) by
, for some constant \(C_0\in [1,\infty )\). A typical example is n for \(b_T\) and \(n^{-1/2}I_\textsf {p}\) for \(a_T\), \(I_\textsf {p}\) being the identity matrix. Define a \(\textsf {p}\)-dimensional random variable \(\Delta _T\) and a \(\textsf {p}\times \textsf {p}\) random matrix \(\Gamma _T(\theta )\) by

respectively. Consistency of an estimator based on the random field  is established when
is established when  is associated with the random field
is associated with the random field

We assume the following set of conditions.
- [T2]:
-
There exist positive numbers \(\epsilon _1\) and \(\epsilon _2\) such that the following conditions are satisfied for all \(p>1\):
- (i):
-

- (ii):
-

- (iii):
-

- (iv):
-

To verify Conditions [T2] (ii) and (iii), one can apply Sobolev’s embedding inequality, the Garsia-Rodemich-Rumsey inequality, or Kolmogorov’s continuity theorem.
Let  . We define the random field
. We define the random field  on
on  by
by

for  . When
. When  is a log likelihood function, the random field
is a log likelihood function, the random field  is the likelihood ratio between \(\theta =\theta ^*+a_Tu\) and \(\theta ^*\).
is the likelihood ratio between \(\theta =\theta ^*+a_Tu\) and \(\theta ^*\).
For \(r_T(u)\) defined by

under [T2], the random field  admits the representation
admits the representation

with \(r_T(u)\rightarrow ^p0\) as \(T\rightarrow \infty \) for every  , i.e., the random field
, i.e., the random field  is locally asymptotically quadratic (LAQ) at \(\theta ^*\). The property (2.6) suggests that the tail of the random field
is locally asymptotically quadratic (LAQ) at \(\theta ^*\). The property (2.6) suggests that the tail of the random field  is light like a Gaussian kernel. This fact is stated as a polynomial type large deviation inequality. Write
is light like a Gaussian kernel. This fact is stated as a polynomial type large deviation inequality. Write  for \(r>0\).
for \(r>0\).
Theorem 2.1
Suppose that [T1] and [T2] are fulfilled. Let \(\xi \in (1,2)\). Then, for any \(L>0\), there exists a constant C such that

for all \(r>0\) and  . The supremum of the empty set should read \(-\infty \).
. The supremum of the empty set should read \(-\infty \).
The polynomial type large deviation inequality (2.7) ensures the \(L^p\)-boundedness of the scaled error of the QLA estimators. Usually, a common \(L^p\)-inequality based on some kind of orthogonality such as a martingale or mixing property can veirfy Condition [T2], combined with an uniform estimate like Sobolev’s inequality. This enables flexible applications of the scheme to nonlinear stochastic processes, as we will see in various applications later.
2.2 Quasi-maximum likelihood estimator
Suppose that \(\mathcal{G}\) is a \(\sigma \)-field satisfying \(\sigma [\Gamma ]\subset \mathcal{G}\subset \mathcal{F}\). For a sequence  of random elements on \((\Omega ,\mathcal{F},P)\), we say that \(V_T\) converges \(\mathcal{G}\)-stably to a random element \(V_\infty \) defined on an extension of \((\Omega ,\mathcal{F},P)\) if \((V_T,\Psi )\rightarrow ^d(V_\infty ,\Psi )\) as \(T\rightarrow \infty \) for any \(\mathcal{G}\)-measurable random variable \(\Psi \). The \(\mathcal{G}\)-stable convergence is denoted by \(\rightarrow ^{d_s(\mathcal{G})}\). We assume the \(\mathcal{G}\)-stable convergence
of random elements on \((\Omega ,\mathcal{F},P)\), we say that \(V_T\) converges \(\mathcal{G}\)-stably to a random element \(V_\infty \) defined on an extension of \((\Omega ,\mathcal{F},P)\) if \((V_T,\Psi )\rightarrow ^d(V_\infty ,\Psi )\) as \(T\rightarrow \infty \) for any \(\mathcal{G}\)-measurable random variable \(\Psi \). The \(\mathcal{G}\)-stable convergence is denoted by \(\rightarrow ^{d_s(\mathcal{G})}\). We assume the \(\mathcal{G}\)-stable convergence
as \(T\rightarrow \infty \), for some \(\textsf {p}\)-dimensional random vector \(\Delta \) on some extension of \((\Omega ,\mathcal{F},P)\).
Any measurable mapping \({\hat{\theta }}_T^M:\Omega \rightarrow {\overline{\Theta }}\) is called a quasi-maximum likelihood estimator (QMLE) for  if
if

Such a measurable function always exists, which is ensured by the measurable selection theorem applied to  , a continuous random filed on the compact \({\overline{\Theta }}\). We do not assume uniqueness of \({\hat{\theta }}_T^M\). Let \({\hat{u}}_T^M=a_T^{-1}({\hat{\theta }}_T^M-\theta ^*)\) for the QMLE \({\hat{\theta }}_T^M\). Let \({\hat{u}}=\Gamma ^{-1}\Delta \).
, a continuous random filed on the compact \({\overline{\Theta }}\). We do not assume uniqueness of \({\hat{\theta }}_T^M\). Let \({\hat{u}}_T^M=a_T^{-1}({\hat{\theta }}_T^M-\theta ^*)\) for the QMLE \({\hat{\theta }}_T^M\). Let \({\hat{u}}=\Gamma ^{-1}\Delta \).
Theorem 2.2
Suppose that Conditions [T1] and [T2] are satisfied and that the convergence (2.8) holds as \(T\rightarrow \infty \). Then
-
(a)
\(\displaystyle {\hat{u}}_T^M-\Gamma ^{-1}\Delta _T \rightarrow ^p 0 \) as \(T\rightarrow \infty \).
-
(b)
 as \(T\rightarrow \infty \) for any
as \(T\rightarrow \infty \) for any  and any \(\mathcal{G}\)-measurable random variable \(\Phi \in \cup _{p>1}L^p\).
and any \(\mathcal{G}\)-measurable random variable \(\Phi \in \cup _{p>1}L^p\).
Remark 2.3
Define a random field  on
on  by
by

for  . From (2.7) and (2.8), we obtain the convergence
. From (2.7) and (2.8), we obtain the convergence

if  is adequately, measurably extended as a random variable taking values in
is adequately, measurably extended as a random variable taking values in  , where
, where  is the space of continuous functions f on
is the space of continuous functions f on  satisfying \(\lim _{\vert u\vert \rightarrow \infty }f(u)=0\). The space
satisfying \(\lim _{\vert u\vert \rightarrow \infty }f(u)=0\). The space  is equipped with the supremum norm. Roughly speaking, by applying the argmax-operator to the both sides of (2.11), we obtain the convergence \(\widehat{u}_T^M\rightarrow ^{d_s(\mathcal{G})}\widehat{u}=\Gamma ^{-1}\Delta \). This is a smart way but one can bypass the discussion on the space
is equipped with the supremum norm. Roughly speaking, by applying the argmax-operator to the both sides of (2.11), we obtain the convergence \(\widehat{u}_T^M\rightarrow ^{d_s(\mathcal{G})}\widehat{u}=\Gamma ^{-1}\Delta \). This is a smart way but one can bypass the discussion on the space  . See e.g. Yoshida (2021).
. See e.g. Yoshida (2021).
2.3 Quasi-Bayesian estimator
The mapping

is called a quasi-Bayesian estimator (QBE) with respect to the prior density \(\varpi \). The QBE \({\hat{\theta }}_T^B\) is the Bayesian estimator with respect to the quadratic loss function when  is the log likelihood function. The QBE \({\hat{\theta }}_T^B\) takes values in the convex-hull of \(\Theta \), therefore the values are bounded but may be outside of \(\Theta \). It is assumed that \(\varpi \) is continuous and \(0<\inf _{\theta \in \Theta }\varpi (\theta )\le \sup _{\theta \in \Theta }\varpi (\theta )<\infty \).
is the log likelihood function. The QBE \({\hat{\theta }}_T^B\) takes values in the convex-hull of \(\Theta \), therefore the values are bounded but may be outside of \(\Theta \). It is assumed that \(\varpi \) is continuous and \(0<\inf _{\theta \in \Theta }\varpi (\theta )\le \sup _{\theta \in \Theta }\varpi (\theta )<\infty \).
Theorem 2.4
Suppose that Conditions [T1] and [T2] are satisfied and that the convergence (2.8) holds as \(T\rightarrow \infty \). Moreover, suppose that \(\vert \Gamma \vert \in L^q\) for some \(q>\textsf {p}\). Then
-
(a)
\( {\hat{u}}_T^B-\Gamma ^{-1}\Delta _T \rightarrow ^p 0 \) as \(T\rightarrow \infty \).
-
(b)
 as \(T\rightarrow \infty \) for any
as \(T\rightarrow \infty \) for any 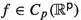 and any \(\mathcal{G}\)-measurable random variable \(\Phi \in \cup _{p>1}L^p\).
and any \(\mathcal{G}\)-measurable random variable \(\Phi \in \cup _{p>1}L^p\).
As seen above, the QLA is constructed in an abstract way, and Conditions [T1] and [T2] are easy to verify. By this reason, the QLA theory has been widely applied, in particular, to nonlinear stochastic processes. We will discuss several applications in the following sections.
3 Diffusion process
3.1 Quasi-likelihood analysis for ergodic diffusion processes
Suppose that a \(\textsf {d}\)-dimensional stationary mixing diffusion process  satisfies the stochastic differential equation
satisfies the stochastic differential equation
on a stochastic basis \((\Omega ,\mathcal{F},\mathbf{F},P)\) with a filtration  . Here
. Here  is an \(\textsf {r}\)-dimensional \(\mathbf{F}\)-Wiener process,
is an \(\textsf {r}\)-dimensional \(\mathbf{F}\)-Wiener process,  and
and  are given functions. The parameter space \(\Theta _i\) of \(\theta _i\) is a bounded open set in
are given functions. The parameter space \(\Theta _i\) of \(\theta _i\) is a bounded open set in  for \(i=1,2\). A standard Sobolev embedding inequality \(W^{1,p_i}(\Theta _i)\hookrightarrow C(\Theta _i)\) is assumed for \(p_i>\textsf {p}_i\), for each \(i=1,2\). We also assume that the functions a and b are continuously extended to the boundaries
for \(i=1,2\). A standard Sobolev embedding inequality \(W^{1,p_i}(\Theta _i)\hookrightarrow C(\Theta _i)\) is assumed for \(p_i>\textsf {p}_i\), for each \(i=1,2\). We also assume that the functions a and b are continuously extended to the boundaries  , respectively, and that b is uniformly non-degenerate.
, respectively, and that b is uniformly non-degenerate.
The process X is observed at discrete times \(t_j=jh\) (\(j\in \{0,1,...,n\}\)) for a positive value \(h=h_n\) depending on n. We assume that \(h\rightarrow 0\), \(nh\rightarrow \infty \) and \(nh^2\rightarrow 0\) as \(n\rightarrow \infty \), that is, we have high frequency and long-run data. For estimation of the parameter \(\theta =(\theta _1,\theta _2)\), we consider a random field \(\mathcal{H}_n\) given by
for \(B=bb^\star \).
The asymptotic properties of the QMLE \(\widehat{\theta }_n^M=(\widehat{\theta }_{n,1}^M,\widehat{\theta }_{n,2}^M)\) with respect to \(\mathcal{H}_n\) of (3.2) can be shown by the QLA approach recalled in Sect. 2.2, as was done in Yoshida (2011). Denote by \(\theta ^*=(\theta _1^*,\theta _2^*)\) the true value of \(\theta \). To obtain the asymptotic properties for \(\widehat{\theta }_{1,n}^M\) for \(\theta _1\), we can use the random field

in the proof, for  in the general theory. In the second step, the random field
in the general theory. In the second step, the random field

is used for  in the proof of the asymptotic properties of \(\widehat{\theta }_{2,n}\). Since the relation (a) of Theorem 2.2 has been obtained for each component \(\widehat{\theta }_{i,n}\), we have the joint convergence of these components. As a matter of fact, Yoshida (2011) gave the convergence
in the proof of the asymptotic properties of \(\widehat{\theta }_{2,n}\). Since the relation (a) of Theorem 2.2 has been obtained for each component \(\widehat{\theta }_{i,n}\), we have the joint convergence of these components. As a matter of fact, Yoshida (2011) gave the convergence

as \(n\rightarrow \infty \) for any continuous function f of at most polynomial growth, where \(\xi _i\) is a \(\textsf {p}_i\)-dimensional centered Gaussian random vector with covariance matrix \(\Gamma _i^{-1}\) for each \(i=1,2\), and \(\xi _1\) and \(\xi _2\) are independent. More precisely,

where \(\nu \) is the stationary probability measure of X, and

The condition (2.2) is not restrictive since one can choose a suitable random field  with a single scale at each step of the proof of asymptotic properties, although there are two different scales of estimators. Condition [T1] is trivial in the present situation, and Condition [T2] can be checked with the help of Sobolev’s inequality and a Rosenthal type inequality. This task is easy.
with a single scale at each step of the proof of asymptotic properties, although there are two different scales of estimators. Condition [T1] is trivial in the present situation, and Condition [T2] can be checked with the help of Sobolev’s inequality and a Rosenthal type inequality. This task is easy.
For quasi-Bayesian inference, Yoshida (2011) proposed the adaptive Bayesian method (adaBayes). Though the adaptive Bayesian estimator was defined for the general  having k scales, it becomes in the present situation as follows. For an arbitrarily fixed value \(\theta _2^0\) of \(\theta _2\), we define the quasi-Bayesian estimator \(\widehat{\theta }_{1,n}^B\) for \(\theta _1\) by
having k scales, it becomes in the present situation as follows. For an arbitrarily fixed value \(\theta _2^0\) of \(\theta _2\), we define the quasi-Bayesian estimator \(\widehat{\theta }_{1,n}^B\) for \(\theta _1\) by
for a prior density \(\varpi _1\) for \(\theta _1\), and next define the quasi-Bayesian estimator \(\widehat{\theta }_{2,n}^B\) for \(\theta _2\) by
for a prior density \(\varpi _2\) for \(\theta _2\). Then, for the adaptive Bayesian estimator \(\widehat{\theta }_n^B=\big (\widehat{\theta }_{1,n}^B,\widehat{\theta }_{2,n}^B\big )\), we can apply the scheme in Sect. 2.3 twice to obtain the convergence

as \(n\rightarrow \infty \) for f and \(\xi _i\) (\(i=1,2\)) described at (3.3).
The YUIMA is an R package for simulation and statistical analysis for stochastic processes. It constructs a yuima object from the user’s data of a stochastic differential equation. The YUIMA function “qmle” implemented the QMLE, and the function “adaBaye” the adaptive Bayesian estimator. For example, the “qmle” applied to a yuima object returns the estimated value and the standard error of the QMLE. See Brouste et al. (2014) and Iacus and Yoshida (2018).
3.2 Adaptive methods
An advantage of the adaptive method is that it can suppress the dimension of the integral in computation of the Bayesian estimate. The maximum likelihood type estimator also enjoys this merit by the idea of adaptive estimation. Adaptive methods for diffusion models were studied by Yoshida (1992) and Kessler (1995). The condition \(nh^2\rightarrow 0\) is called the condition for rapidly increasing experimental design (Prakasa Rao 1983; Prakasa Rao 1988). The relaxation of this condition to \(nh^3\rightarrow 0\) was by Yoshida (1992) with a higher-order expansion of the transition probability of the diffusion process, and this was extended by Kessler (1997) to achieve \(nh^p\rightarrow 0\) for any \(p>0\).
Uchida and Yoshida (2012) proposed various adaptive methods of the maximum likelihood type for the stochastic differential equation (3.1). They introduced a ladder of annealed random fields for  , and applied the QLA to prove that their adaptive schemes gave the same convergence as (3.3) at the last stage of the algorithm under the assumption \(nh^p\rightarrow 0\), as explained below. Consider a sequence of estimating functions \(U_{p,n}\) (\(p=1,2,...\)) as follows. Let
, and applied the QLA to prove that their adaptive schemes gave the same convergence as (3.3) at the last stage of the algorithm under the assumption \(nh^p\rightarrow 0\), as explained below. Consider a sequence of estimating functions \(U_{p,n}\) (\(p=1,2,...\)) as follows. Let
Denote by \(\widehat{\theta }_{1,n}^{(0)}\) a maximum likelihood (ML) type estimator for \(\theta _1\):
For \(p\ge 2\), let \(k_0=\lfloor p/2 \rfloor \) and \(l_0=\lfloor (p-1)/2\rfloor \). Then the function \(U_{p,n}\) for \(p\ge 2\) is defined by
where the functions \(r^{(k_0)}(h,x,\theta )\), \(D^{(k)}(x,\theta )\) and \(E^{(k)}(x,\theta )\) are coming from an expansion of the semigroup of the diffusion process satisfying (3.1). The adaptive ML type estimators \(\widehat{\theta }_{1,p,n}^{(l_0)}\) for \(\theta _1\) and \(\widehat{\theta }_{2,p,n}^{(k_0)}\) are characterized by \(\widehat{\theta }_{1,p,n}^{(0)}=\widehat{\theta }_{1,n}^{(0)}\) and
for \(k=1,2,...,k_0\). Remark that \(l_0\le k_0\le l_0+1\). In Uchida and Yoshida (2012), the QLA provided \(L^{\infty {-}}=\cap _{q>1}L^q\)-boundedness of \((nh)^{k/(p-1)}\big (\widehat{\theta }_{2,p,n}^{(k)}-\theta _2^*\big )\) when \(p\ge 2k+1\), and of \(n^{(k+1)/p}\big (\widehat{\theta }_{1,p,n}^{(k)}-\theta _1^*\big )\) when \(p\ge 2(k+1)\). Climbing up the ladder, under the balance condition \(nh^p\rightarrow 0\), they proved the convergence

as \(n\rightarrow \infty \) for any continuous function f of at most polynomial growth, where \(\xi _1\) and \(\xi _2\) are given in Sect. 3.1.
Uchida and Yoshida (2014) provided three types of algorithms for adaptive quasi-Bayesian estimation. The QLA worked effectively to show that the spiral of the estimators based on the annealed quasi-likelihood functions attains the convergence (3.3). To reduce computational load for the adaptive estimators, Kamatani and Uchida (2014) proposed hybrid multi-step estimators for diffusion processes. According to their numerical studies, the hybrid multi-step estimator with an initial QBE gives stable estimates.
Recently, Kutoyants (2017) proposed a multi-step MLE for ergodic diffusion, and Kutoyants (2014) presented approximation of the solution of the backward stochastic differential equation with a multi-step method. Dabye et al. (2018) gave moments estimators and multi–step MLE for Poisson Processes.
4 Stochastic differential equation with jumps
4.1 Jump diffusion process
Let us consider a \(\textsf {d}\)-dimensional ergodic process  satisfying the stochastic differential equation
satisfying the stochastic differential equation
 , on a stochastic basis \((\Omega ,\mathcal{F},\mathbf{F},P)\) with filtration
, on a stochastic basis \((\Omega ,\mathcal{F},\mathbf{F},P)\) with filtration  . For each \(i\in \{1,2\}\), the unknown parameter \(\theta _i\) is in a bounded open set \(\Theta _i\) of
. For each \(i\in \{1,2\}\), the unknown parameter \(\theta _i\) is in a bounded open set \(\Theta _i\) of  . The coefficients
. The coefficients  ,
,  and
and  are supposed to satisfy some mild regularity conditions. In (4.1),
are supposed to satisfy some mild regularity conditions. In (4.1),  is an \(\textsf {r}\)-dimensional \(\mathbf{F}\)-Wiener process, and p(dt, dz) is a Poinsson random measure on
is an \(\textsf {r}\)-dimensional \(\mathbf{F}\)-Wiener process, and p(dt, dz) is a Poinsson random measure on  with the deterministic \(\mathbf{F}\)-compensator \(q^{\theta _2}(dt,dz)\). We want to estimate the true value \(\theta ^*=(\theta _1^*,\theta _2^*)\) of the unknown parameter \(\theta =(\theta _1,\theta _2)\) by observing the data \((X_{t_{j}})_{j=0,1,...,n}\) with \({t_{j}}=jh\).
with the deterministic \(\mathbf{F}\)-compensator \(q^{\theta _2}(dt,dz)\). We want to estimate the true value \(\theta ^*=(\theta _1^*,\theta _2^*)\) of the unknown parameter \(\theta =(\theta _1,\theta _2)\) by observing the data \((X_{t_{j}})_{j=0,1,...,n}\) with \({t_{j}}=jh\).
Estimation of a semimartingale with jumps has a different technical aspect than that of a continuous semimartingale. A natural idea for constructing an estimator is to apply a Gaussian type likelihood to the continuous part of X and a Poissonian likelihood to the jump component of X. However, this idea is naive. It is impossible to tell whether an increment \(\Delta _jX=X_{t_{j}}-X_{t_{j-1}}\) of X has jumps since only temporally discrete observations are available. We need some filter that detects jumps from the increments \((\Delta _jX)_{j=1,...,n}\). Shimizu and Yoshida (2006) proposed an estimator for \(\theta \) by a threshold method and showed its asymptotic normality. Threshold method is a standard technique going back to studies of Lévy processes at latest.
The QLA was presented by Ogihara and Yoshida (2011) for the jump-diffusion process (4.1) satisfying a mixing condition. They considered the time-discretization step-size \(h=h_n\) satisfying \(n^{-3/5}\lesssim h\lesssim n^{-4/7}\), where \(a_n\lesssim b_n\) means \(s_n\le Cb_n\) for all  , for some constant C, for sequences \((a_n)\) and \((b_n)\) of numbers. This balance condition is equivalent to \(n^{2/5}\lesssim nh\lesssim n^{3/7}\) and \(n^{-1/5}\lesssim nh^2\lesssim n^{-1/7}\). Suppose that for each \((\theta _2,x)\), the mapping \(z\mapsto y=c(x,z,\theta _2)\) is an injection from \(\textsf {E}\) into \(\textsf {E}\) and has an inverse \(z=c^{-1}(x,y,\theta _2)\) from the image of c onto \(\textsf {E}\). We assume that \(q^{\theta _2}(dt,dz)=f_{\theta _2}(z)dzdt\) with a density \(f_{\theta _2}(z)\) (possibly \(\int f_{\theta _2}(z)dz\not =1\)). Let
, for some constant C, for sequences \((a_n)\) and \((b_n)\) of numbers. This balance condition is equivalent to \(n^{2/5}\lesssim nh\lesssim n^{3/7}\) and \(n^{-1/5}\lesssim nh^2\lesssim n^{-1/7}\). Suppose that for each \((\theta _2,x)\), the mapping \(z\mapsto y=c(x,z,\theta _2)\) is an injection from \(\textsf {E}\) into \(\textsf {E}\) and has an inverse \(z=c^{-1}(x,y,\theta _2)\) from the image of c onto \(\textsf {E}\). We assume that \(q^{\theta _2}(dt,dz)=f_{\theta _2}(z)dzdt\) with a density \(f_{\theta _2}(z)\) (possibly \(\int f_{\theta _2}(z)dz\not =1\)). Let
We suppose that \(B(x)=\text {Im}\big (c(x,\cdot ,\theta _2)\big )\) is independent of \(\theta _2\in \Theta _2\). With \(B=bb^\star \), a positive constant \(\rho \) less than 1/2 and a positive constant D, Ogihara and Yoshida (2011) defined the random field \(\mathcal{H}_n(\theta )\) by
where \(\overline{\Delta _jX}=\Delta _jX-ha(X_{t_{j-1}},\theta _2)\) and \(\varphi _n\) is a truncation function that removes extremely small or extremely large increments. Denote by \(\nu \) the invariant probability measure of the jump diffusion process X. By applying the QLA theory, Ogihara and Yoshida (2011) obtained the convergence (3.3) of the QMLE \(\widehat{\theta }_n^M=\big (\widehat{\theta }_{1,n}^M,\widehat{\theta }_{2,n}^M\big )\) with respect to \(\mathcal{H}_n\) of (4.2), \(\Gamma _1\) given by (3.4) and \(\Gamma _2\) by

instead of (3.5), where \(A(x):=\{y\in B(x);\>\Psi _{\theta _2}(y,x)\not =0\}\) is supposed to be independent of \(\theta _2\in \Theta _2\). The adaptive QBE \(\widehat{\theta }_n^B=\big (\widehat{\theta }_{1,n}^B, \widehat{\theta }_{2,n}^B\big )\) is defined by (3.6) and (3.7) with \(\mathcal{H}_n\) of (4.2). The QLA ensures the convergence (3.8) with \(\Gamma _1\) of (3.4) and \(\Gamma _2\) of (4.3).
4.2 Gaussian quasi-likelihood to Lévy driven stochastic differential equation
Given a stochastic basis \((\Omega ,\mathcal{F},\mathbf{F},P)\) with a filtration  , we consider an \(\mathbf{F}\)-adapted process
, we consider an \(\mathbf{F}\)-adapted process  satisfying the stochastic differential equation
satisfying the stochastic differential equation
where  is an \(\textsf {r}\)-dimensional Wiener process, and
is an \(\textsf {r}\)-dimensional Wiener process, and  is an \(\textsf {r}_1\)-dimensional pure-jump Lévy process with Lévy measure \(\lambda \). The functions
is an \(\textsf {r}_1\)-dimensional pure-jump Lévy process with Lévy measure \(\lambda \). The functions  ,
,  and
and  are supposed to satisfy certain regularity conditions. The parameter spaces \(\Theta _1\) and \(\Theta _2\) are bounded open sets in
are supposed to satisfy certain regularity conditions. The parameter spaces \(\Theta _1\) and \(\Theta _2\) are bounded open sets in  and
and  , respectively, each having a nice boundary.
, respectively, each having a nice boundary.
In this section, our interest is in the phenomena when the Gaussian quasi-likelihood is applied to the Lévy driven stochastic differential equation. Nothing to say, this is a quasi-likelihood approach. This problem is of practical importance because implementation is easy with the Gaussian quasi-likelihood, as YUIMA (Brouste et al. 2014, Iacus and Yoshida 2018).
We assume that \(\vert J_1\vert \in L^{\infty {-}}\), \(E[J_1]=0\) and \(E[J_1^{\otimes 2}]=I_{\textsf {r}_1}\), the \(\textsf {r}_1\)-dimensional identity matrix. Let \(V=bb^\star +cc^\star \) and assume the non-degeneracy of V. The fact that b and c share a common parameter \(\theta _1\) and the use of the function V suggest that only the variance structure of the increments will be paid attention in what follows.
We assume high frequency long-run data, that is, the data consists of \((X_{t_{j}})_{j=0,1,...,n}\) with \({t_{j}}=jh\), \(h=h_n\), and \(nh\rightarrow \infty \) and \(nh^2\rightarrow 0\) as \(n\rightarrow \infty \). Let \(\Theta =\Theta _1\times \Theta _2\), \(\theta =(\theta _1,\theta _2)\in \overline{\Theta }\) and \(\textsf {p}=\textsf {p}_1+\textsf {p}_2\). For estimation of \(\theta \), we will work with the Gaussian quasi-likelihood

A measurable mapping \(\widehat{\theta }_n=(\widehat{\theta }_{1,n},\widehat{\theta }_{2,n})\) is called a Gaussian quasi-maximum likelihood estimator (GQMLE) if  . By a not straightforward application of the QLA theory, under ergodicity, Masuda (2013) showed the convergence
. By a not straightforward application of the QLA theory, under ergodicity, Masuda (2013) showed the convergence

as \(n\rightarrow \infty \) for any continuous function  of at most polynomial growth, where \(\theta ^*\) denotes the true value of \(\theta \), \(\xi ^*\sim N_{\textsf {p}}(0,\Sigma )\), and \(\Sigma \) is a \(\textsf {p}\times \textsf {p}\) positive-definite matrix. Matrix \(\Sigma \) is not necessarily a block diagonal matrix, in other words, \(\theta _1\) and \(\theta _2\) are not necessarily orthogonal.
of at most polynomial growth, where \(\theta ^*\) denotes the true value of \(\theta \), \(\xi ^*\sim N_{\textsf {p}}(0,\Sigma )\), and \(\Sigma \) is a \(\textsf {p}\times \textsf {p}\) positive-definite matrix. Matrix \(\Sigma \) is not necessarily a block diagonal matrix, in other words, \(\theta _1\) and \(\theta _2\) are not necessarily orthogonal.
5 Quasi-likelihood analysis for volatility
5.1 Estimation of volatility
We treated inference for ergodic processes in Sects. 3 and 4 . If the time horizon is finite, two probability measures for different values of the drift parameter can be absolutely continuous, and this means the drift parameter cannot be estimated consistently. Therefore, the diffusion parameter is only targeted by asymptotic statistics. Let us go back to the estimation problem for the unknown parameter \(\theta \) in the \(\textsf {m}\)-dimensional semimartingale \(Y=(Y_t)_{t\in [0,T]}\) having the decomposition (1.1). We observe the data \((X_{t_{j}},Y_{t_{j}})_{j=0,1,...,n}\) for \({t_{j}}=t_j^n=jT/n\) with fixed T, while the process b is unobservable. The parameter space \(\Theta \) is supposed to be a \(\textsf {p}\)-dimensional bounded open set having a good boundary to admit Sobolev’s embedding inequality.
Uchida and Yoshida (2013) constructed the QLA for the model (1.1). The quasi-log likelihood function  is defined by (1.2). Based on
is defined by (1.2). Based on  of (1.2), the QMLE \(\widehat{\theta }_n^M\) is characterized by (2.9) with n in place of T, and the QBE \(\widehat{\theta }_n^B\)is defined by (2.12) with n for T. The true value of \(\theta \) is denoted by \(\theta ^*\). The information matrix at \(\theta ^*\) is defined by
of (1.2), the QMLE \(\widehat{\theta }_n^M\) is characterized by (2.9) with n in place of T, and the QBE \(\widehat{\theta }_n^B\)is defined by (2.12) with n for T. The true value of \(\theta \) is denoted by \(\theta ^*\). The information matrix at \(\theta ^*\) is defined by
for  . The matrix \(\Gamma \) is symmetric and random because it involves the process X. We prepare the random field
. The matrix \(\Gamma \) is symmetric and random because it involves the process X. We prepare the random field  as
as

where \(I_\textsf {m}\) is the \(\textsf {m}\)-dimensional identity matrix. The key index to estimation is

If the key index \(\chi _0\) satisfies the non-degeneracy (2.1), i.e. [T1] (i-2), then under mild regularity conditions,

as \(n\rightarrow \infty \) for any continuous function  of at most polynomial growth and any \(\mathcal{F}\)-measurable random variable \(\Phi \in \cup _{p>1}L^p\), where \(\zeta \) is a \(\textsf {p}\)-dimensional standard Gaussian random vector independent of \(\mathcal{F}\). This statistics is non-ergodic. Handy criteria for Condition (2.1) are available. See Uchida and Yoshida (2013) for details. The asymptotic mixed normality of the QMLE was presented by Genon-Catalot and Jacod (1993).
of at most polynomial growth and any \(\mathcal{F}\)-measurable random variable \(\Phi \in \cup _{p>1}L^p\), where \(\zeta \) is a \(\textsf {p}\)-dimensional standard Gaussian random vector independent of \(\mathcal{F}\). This statistics is non-ergodic. Handy criteria for Condition (2.1) are available. See Uchida and Yoshida (2013) for details. The asymptotic mixed normality of the QMLE was presented by Genon-Catalot and Jacod (1993).
5.2 Jump filters
It is necessary to modify the estimating function (1.2) when the process Y has a jump component. Instead of (1.1), we will consider a semmartingale Y having the decomposition
and estimate \(\theta \) from the data \((X_{t_{j}},Y_{t_{j}})_{j=0,1,...,n}\). The jump component \(J=(J_t)_{t\in [0,T]}\) is a random step process. As discussed in Sect. 4.1, we need some jump filter. The classical filter \(\vert \Delta _jY\vert >Dh^\rho \) is a possibility. However, it is known that the performance of the classical filter strongly depends on the tuning parameters; see e.g. Iacus and Yoshida (2018). Recently, Inatsugu and Yoshida (2021a) (updated by arXiv:1806.10706 (2018)) proposed global jump filters to enable stable and precise estimation of the volatility parameter \(\theta \). The global filter uses the order statistics of the increments. Let \(V_j=\vert (\overline{S}_{n,j-1})^{-1/2}\Delta _jY\vert \) with an initial estimator \(\overline{S}_{n,j-1}\) for the spot volatility \(S(X_{t_{j-1}},\theta ^*)\) up to a possibly unknown scaling constant. The r-th order statistic of \(\{V_j\}_{j=1,...,n}\) is denoted by \(V_{(r)}\). For a preset constant \(\alpha \in (0,1)\), the global jump filter is specified by the index set
with \(s_n(\alpha )=\lfloor n(1-\alpha )\rfloor \). Then the \(\alpha \)-quasi-log likelihood function is given by

In Formula (5.4), \(p(\alpha )=1-\alpha \), and the constant \(q(\alpha )\) is determined by \(q(\alpha )=\textsf {m}^{-1}E[V1_{\{V\le c(\alpha )\}}]\), where the constant \(c(\alpha )\) is the upper \(\alpha \)-quantile of the chi-square distribution of degree \(\textsf {m}\), i.e., \(P[V\le c(\alpha )]=1-\alpha \) for a random variable \(V\sim \chi ^2(\textsf {m})\). The cap function \(K_{n,j}=1_{\{\vert \Delta _jY\vert <C_*n^{-1/4}\}}\) with positive constant \(C_*\). This function is a very loose filter only for removing technical assumptions on the distribution of the jumps \(\Delta J_t\). Practically \(K_{n,j}\) will be almost always 1. A measurable mapping \(\widehat{\theta }^{M,\alpha }_n\) maximizing  in \(\theta \in \overline{\Theta }\) is called an \(\alpha \)-quasi-maximum likelihood estimator (\(\alpha \)-QMLE). Inatsugu and Yoshida (2021a) (updated by arXiv:1806.10706 (2018)) gave a rate of convergence in \(L^p\)-norm of the \(\alpha \)-QMLE \(\widehat{\theta }^{M,\alpha }_n\) with the help of an annealed quasi-likelihood ratio process and a resulting polynomial type large deviation inequality. A quasi-Bayesian estimator is also treated there. Morevoer, they introduced the QMLE \(\widehat{\theta }_n^{M,\alpha _n}\) and the QBE \(\widehat{\theta }_n^{B,\alpha _n}\) with a shrinking \(\alpha _n\) to obtain the same convergence as (5.2), that is,
in \(\theta \in \overline{\Theta }\) is called an \(\alpha \)-quasi-maximum likelihood estimator (\(\alpha \)-QMLE). Inatsugu and Yoshida (2021a) (updated by arXiv:1806.10706 (2018)) gave a rate of convergence in \(L^p\)-norm of the \(\alpha \)-QMLE \(\widehat{\theta }^{M,\alpha }_n\) with the help of an annealed quasi-likelihood ratio process and a resulting polynomial type large deviation inequality. A quasi-Bayesian estimator is also treated there. Morevoer, they introduced the QMLE \(\widehat{\theta }_n^{M,\alpha _n}\) and the QBE \(\widehat{\theta }_n^{B,\alpha _n}\) with a shrinking \(\alpha _n\) to obtain the same convergence as (5.2), that is,

as \(n\rightarrow \infty \) for any continuous function  of at most polynomial growth and any \(\mathcal{F}\)-measurable random variable \(\Phi \in \cup _{p>1}L^p\), where \(\zeta \) is a \(\textsf {p}\)-dimensional standard Gaussian random vector independent of \(\mathcal{F}\). The global filter is applied to the realized volatility by Inatsugu and Yoshida (2021b). The realized volatility with a global jump filter outperforms the bipower variation and the minimum realized volatility, that were regarded as estimators robust against jumps.
of at most polynomial growth and any \(\mathcal{F}\)-measurable random variable \(\Phi \in \cup _{p>1}L^p\), where \(\zeta \) is a \(\textsf {p}\)-dimensional standard Gaussian random vector independent of \(\mathcal{F}\). The global filter is applied to the realized volatility by Inatsugu and Yoshida (2021b). The realized volatility with a global jump filter outperforms the bipower variation and the minimum realized volatility, that were regarded as estimators robust against jumps.
5.3 Non-synchronous observations
Different components of high frequency data often have asynchronous timestamps. A seemingly natural idea for estimation of the covariance between two components is to use the ordinary realized co-volatility after synchronizing the data by some interpolation method. However, it is known as the Epps effect (Epps 1979) that any such interpolation causes a severe bias and the estimated correlation disappears when the frequency of the observations diverges. This problem of measurement of multivariate volatilities was solved by Malliavin and Mancino (2002) with a Fourier series method and by Hayashi and Yoshida (2005) with an association kernel. These estimators are nonparametric.
Ogihara and Yoshida (2014) studied parametric estimation of volatility with non-synchronous data. Consider the model (1.1). Suppose that Y is two-dimensional, X is possibly multi-dimensional and different components in (Y, X) are observed in a non-synchronous manner. The quasi-likelihood function is based on local Gaussian approximation but a global quadratic form having many off-diagonal nonzero elements appears due to non-synchronicity. Though theoretical treatment is fairly complicated, it is possible to construct a QLA, and consequently to prove asymptotic mixed normality and moments convergence of QMLE and QBE. The nonsynchronous covariance estimator (H-Y estimator) has a central limit theorem (Hayashi and Yoshida 2008, 2011). It is said that the H-Y estimator attains the minimum asymptotic variance among nonparametric estimators. If we consider a simple model having a constant diffusion matrix, then we can compare the two estimates of covariance between the two components of Y, one is obtained as a product of estimates by the QMLE and another one from the H-Y estimator. It is shown that the parametric estimator achieves better precision, as expected since it uses information about the structure of the model. Ogihara (2015) proved the local asymptotic mixed normality for a non-synchronously observed diffusion process, and concluded that the QMLE and QBE are asymptotically optimal.
6 Model selection
Eguchi and Masuda (2018) applied the QLA to a Schwarz type model selection criterion for stochastic processes. In short, they considered the integral

for a quasi-log likelihood random field  ,
,  , given a probability space \((\Omega ,\mathcal{F},P)\). The parameter space \(\Theta \) is a bounded open set in
, given a probability space \((\Omega ,\mathcal{F},P)\). The parameter space \(\Theta \) is a bounded open set in  , and \(\varpi _n\) is a prior density on \(\Theta \). The technical essence of the quasi-Bayesian information criterion (QBIC) is to validate an \(L^1\)-approximation of \(F_n=-2\log I_n\) by the statistic \(\text {QBIC}^\natural _n\) given by
, and \(\varpi _n\) is a prior density on \(\Theta \). The technical essence of the quasi-Bayesian information criterion (QBIC) is to validate an \(L^1\)-approximation of \(F_n=-2\log I_n\) by the statistic \(\text {QBIC}^\natural _n\) given by

where \(\widehat{\theta }_n\) is a QMLE for \(\theta \). The expression (6.1) of \(I_n\) is useful for the estimate since

Then it is possible to estimate the \(L^1\)-norm of \(F_n-\text {QBIC}^\natural _n\) by using a polynomial type large deviation inequality for  . Finally, they reached the \(\text {QBIC}_n\) defined by
. Finally, they reached the \(\text {QBIC}_n\) defined by

The QBIC is valid for non-ergodic models, not only for ergodic models. Eguchi and Masuda (2018) showed that QBIC performs well for volatility model selection and selection of ergodic diffusion models. The results are practically promising as well as showing effectiveness of the QLA theory. Further considerations may be possible in some philosophical and technical aspects.
In the context of information criteria for semimartingales, the QLA was first applied in Uchida (2010) by Uchida, who treated the exact likelihood of a sampled diffusion process by means of the Malliavin calculus to derive the contrast based information criterion (CIC).
The QLA found another application in Umezu et al. (2019) to AIC for the non-concave penalized likelihood method. Sparse estimation is a new direction of the QLA theory. The polynomial type large deviation (PLD) inequality for a random field  having the LAQ property can be transferred to a PLD inequality for the penalized random field
having the LAQ property can be transferred to a PLD inequality for the penalized random field  (Kinoshita and Yoshida 2019). Therefore, the PLD inequality is basic even in the theory of sparse estimation for stochastic processes. Related papers are Masuda and Shimizu (2017) and Suzuki and Yoshida (2020). Partial quasi-likelihood analysis is another direction of extension of the theory (Yoshida 2018).
(Kinoshita and Yoshida 2019). Therefore, the PLD inequality is basic even in the theory of sparse estimation for stochastic processes. Related papers are Masuda and Shimizu (2017) and Suzuki and Yoshida (2020). Partial quasi-likelihood analysis is another direction of extension of the theory (Yoshida 2018).
7 Point processes
Recently, modeling with point processes is attracting attention in applications of ultra-high frequency financial data (cf. Abergel and Jedidi 2015). Multi-dimensional point processes are used to model the limit order book.
On a stochastic basis \((\Omega ,\mathcal{F},\mathbf{F},P)\),  , we consider a \(\textsf {d}\)-dimensional point process
, we consider a \(\textsf {d}\)-dimensional point process  ,
,  . More precisely, \(N_0=0\) and each
. More precisely, \(N_0=0\) and each  is a simple counting process. We will assume that the components \(N^\alpha \) (
is a simple counting process. We will assume that the components \(N^\alpha \) ( ) have not common jump. Further, we assume the \(\mathbf{F}\)-compensator of N has an intensity process
) have not common jump. Further, we assume the \(\mathbf{F}\)-compensator of N has an intensity process  . That is, \(\lambda ^*\) is a nonnegative locally integrable predictable process such that \(N-\int _0^\cdot \lambda _s^*ds\) is a \(\textsf {d}\)-dimensional local martingale with respect to \(\mathbf{F}\).
. That is, \(\lambda ^*\) is a nonnegative locally integrable predictable process such that \(N-\int _0^\cdot \lambda _s^*ds\) is a \(\textsf {d}\)-dimensional local martingale with respect to \(\mathbf{F}\).
For statistical modeling of this point process, we consider a random field  . The set \(\Theta \) is a bounded open set in
. The set \(\Theta \) is a bounded open set in  as usual. Suppose that the map
as usual. Suppose that the map  is an
is an  -valued left-continuous adapted process for every \(\theta \in \overline{\Theta }\), and the map \(\Theta \ni \theta \mapsto \lambda (s,\theta )\) is of class \(C^3(\Theta )\) for every
-valued left-continuous adapted process for every \(\theta \in \overline{\Theta }\), and the map \(\Theta \ni \theta \mapsto \lambda (s,\theta )\) is of class \(C^3(\Theta )\) for every  . We refer the reader to Clinet and Yoshida (2017) for other regularity conditions and details of this section. We assume that the \(\lambda _t^*=\lambda (t,\theta ^*)\) for some \(\theta ^*\in \Theta \). Statistically, the value \(\theta ^*\) is unknown and to be estimated from the data \((X_t)_{t\in [0,T]}\). The quasi-log likelihood function for estimation of \(\theta \) is
. We refer the reader to Clinet and Yoshida (2017) for other regularity conditions and details of this section. We assume that the \(\lambda _t^*=\lambda (t,\theta ^*)\) for some \(\theta ^*\in \Theta \). Statistically, the value \(\theta ^*\) is unknown and to be estimated from the data \((X_t)_{t\in [0,T]}\). The quasi-log likelihood function for estimation of \(\theta \) is

Let  . For ergodicity, we assume that for each
. For ergodicity, we assume that for each  , there exists a mapping
, there exists a mapping  such that
such that
for every \((\psi ,\theta )\in C_b(\textsf {E})\times \overline{\Theta }\). Then, under an identifiability condition, Clinet and Yoshida (2017) showed asymptotic normality and moments convergence for QMLE and QBE with respect to \(\ell _T\). These results were applied to a multivariate Hawkes process, for which ergodicity can be verified. Today the Hawkes process is one of standard models in analysis of limit order books.
Muni Toke and Yoshida discussed about modeling intensities of order flows in a limit order book in Muni Toke and Yoshida (2017), analysis of order flows in limit order books with ratios of Cox-type intensities in Muni Toke and Yoshida (2019), and marked point processes and intensity ratios for limit order book modeling in Muni Toke and Yoshida (2020). QLA and information criteria for stochastic processes were applied. Flexible modeling is possible thanks to the formulation of the QLA . The resulting models incorporate various effective covariates. This approach enables us to predict the next market order more precisely than the traditional models.
Notes
The quasi-likelihood is not in the sense of the GLM. This term comes from statistics for stochastic processes, where one inevitably needs to resort to a quasi-likelihood method since the exact likelihood is not available for nonlinear discretely sampled processes.
References
Abergel F, Jedidi A (2015) Long-time behavior of a Hawkes process-based limit order book. SIAM J Financ Math 6(1):1026–1043
Brouste A, Fukasawa M, Hino H, Iacus S, Kamatani K, Koike Y, Masuda H, Nomura R, Ogihara T, Shimuzu Y, Uchida M, Yoshida N (2014) Statistical inference for stochastic processes: overview and prospects. J Stat Softw 57(4):1–51
Clinet S, Yoshida N (2017) Statistical inference for ergodic point processes and application to limit order book. Stoch Process Their Appl 127(6):1800–1839
Dabye AS, Gounoung AA, Kutoyants YA (2018) Method of moments estimators and multi-step MLE for Poisson processes. J Contemp Math Anal (Armenian Acad Sci) 53(4):237–246
Eguchi S, Masuda H (2018) Schwarz type model comparison for LAQ models. Bernoulli 24(3):2278–2327
Epps T (1979) Comovements in stock prices in the very short run. JASA 74:291–298
Genon-Catalot V, Jacod J (1993) On the estimation of the diffusion coefficient for multi-dimensional diffusion processes. Ann Inst H Poincaré Probab Statist 29(1):119–151
Hayashi T, Yoshida N (2005) On covariance estimation of non-synchronously observed diffusion processes. Bernoulli 11(2):359–379
Hayashi T, Yoshida N (2008) Asymptotic normality of a covariance estimator for nonsynchronously observed diffusion processes. Ann Inst Stat Math 60(2):367–406. https://doi.org/10.1007/s10463-007-0138-0
Hayashi T, Yoshida N (2011) Nonsynchronous covariation process and limit theorems. Stoch Process Appl 121(10):2416–2454. https://doi.org/10.1016/j.spa.2010.12.005
Iacus SM, Yoshida N (2018) Simulation and inference for stochastic processes with YUIMA. Springer, Berlin
Ibragimov I, Khas’minskii R (1973) Asymptotic behavior of statistical estimators in the smooth case. I. Study of the likelihood ratio. Theory Probab Appl 17(3):445–462
Ibragimov I, Khas’minskii R (1973) Asymptotic behavior of some statistical estimators II. limit theorems for the a posteriori density and Bayes’ estimators. Theory Probab Appl 18(1):76–91
Ibragimov IA, Has’minskiĭ RZ (1981) Statistical estimation, Applications of Mathematics, vol. 16. Springer-Verlag, New York. Asymptotic theory, Translated from the Russian by Samuel Kotz
Inatsugu H, Yoshida N (2021a) Global jump filters and quasi likelihood analysis for volatility. Annals of the Institute of Statistical Mathematics, on-line
Inatsugu H, Yoshida N (2021b) Global jump filters and realized volatility. arXiv:2102.05307
Kamatani K, Uchida M (2014) Hybrid multi-step estimators for stochastic differential equations based on sampled data. Stat Inference Stoch Process 18(2):177–204
Kessler M (1995) Estimation des paramètres d’une diffusion par des contrastes corrigés. C R Acad Sci Paris Sér I Math 320(3):359–362
Kessler M (1997) Estimation of an ergodic diffusion from discrete observations. Scand J Statist 24(2):211–229
Kinoshita Y, Yoshida N (2019) Penalized quasi likelihood estimation for variable selection. arXiv preprint arXiv:1910.12871
Kutoyants YA (1984) Parameter estimation for stochastic processes.vol. 6. Heldermann. Translated from the Russian and edited by B. L.S. Prakasa Rao
Kutoyants YA (1994) Identification of dynamical systems with small noise, Mathematics and its Applications, vol 300. Kluwer Academic Publishers Group, Dordrecht
Kutoyants YA (2004) Statistical inference for ergodic diffusion processes. Springer Series in Statistics. Springer-Verlag London Ltd., London
Kutoyants YA (2012) Statistical inference for spatial Poisson processes, vol 134. Springer Science & Business Media, Berlin
Kutoyants YA (2014) Approximation of the solution of the backward stochastic differential equation. Small noise, large sample and high frequency cases. Proc Steklov Inst Math 287(1):133–154
Kutoyants YA (2017) On the multi-step MLE-process for ergodic diffusion. Stoch Process Their Appl 127(7):2243–2261
Le Cam L (1960) Locally asymptotically normal families of distributions. Univ California Publ Statist 3:37–98
Malliavin P, Mancino ME (2002) Fourier series method for measurement of multivariate volatilities. Finance Stoch 6(1):49–61
Masuda H (2013) Convergence of Gaussian quasi-likelihood random fields for ergodic Lévy driven sde observed at high frequency. Ann Stat 41(3):1593–1641
Masuda H, Shimizu Y (2017) Moment convergence in regularized estimation under multiple and mixed-rates asymptotics. Math Methods Stat 26(2):81–110
Muni Toke I, Yoshida N (2017) Modelling intensities of order flows in a limit order book. Quant Finance 17(5):683–701
Muni Toke I, Yoshida N (2019) Analyzing order flows in limit order books with ratios of Cox-type intensities. Quantitative Finance pp 1–18
Muni Toke I, Yoshida N (2020) Marked point processes and intensity ratios for limit order book modeling. arXiv:2001.08442
Nualart D, Yoshida N (2019) Asymptotic expansion of Skorohod integrals. Electron J Probab 24:1–64
Ogihara T (2015) Local asymptotic mixed normality property for nonsynchronously observed diffusion processes. Bernoulli 21(4):2024–2072
Ogihara T, Yoshida N (2011) Quasi-likelihood analysis for the stochastic differential equation with jumps. Stat Inference Stoch Process 14(3):189–229. https://doi.org/10.1007/s11203-011-9057-z
Ogihara T, Yoshida N (2014) Quasi-likelihood analysis for nonsynchronously observed diffusion processes. Stoch Process Their Appl 124(9):2954–3008
Prakasa Rao B (1988) Statistical inference from sampled data for stochastic processes. Statistical inference from stochastic processes (Ithaca, NY, 1987) 80, 249–284
Prakasa Rao BLS (1983) Asymptotic theory for nonlinear least squares estimator for diffusion processes. Math Operationsforsch Stat Ser Stat 14(2):195–209
Shimizu Y, Yoshida N (2006) Estimation of parameters for diffusion processes with jumps from discrete observations. Stat Inference Stoch Process 9(3):227–277. https://doi.org/10.1007/s11203-005-8114-x
Suzuki T, Yoshida N (2020) Penalized least squares approximation methods and their applications to stochastic processes. Japanese J Stat Data Sci 3(2):513–541
Uchida M (2010) Contrast-based information criterion for ergodic diffusion processes from discrete observations. Ann Inst Stat Math 62(1):161–187
Uchida M, Yoshida N (2012) Adaptive estimation of an ergodic diffusion process based on sampled data. Stoch Process Their Appl 122(8):2885–2924
Uchida M, Yoshida N (2013) Quasi likelihood analysis of volatility and nondegeneracy of statistical random field. Stoch Process Appl 123(7):2851–2876. https://doi.org/10.1016/j.spa.2013.04.008
Uchida M, Yoshida N (2014) Adaptive Bayes type estimators of ergodic diffusion processes from discrete observations. Stat Inference Stoch Process 17(2):181–219
Umezu Y, Shimizu Y, Masuda H, Ninomiya Y (2019) AIC for the non-concave penalized likelihood method. Ann Inst Stat Math 71(2):247–274
Yoshida N (1990) Asymptotic behavior of M-estimator and related random field for diffusion process. Ann Inst Stat Math 42(2):221–251
Yoshida N (1992) Estimation for diffusion processes from discrete observation. J Multivariate Anal 41(2):220–242
Yoshida N (2011) Polynomial type large deviation inequalities and quasi-likelihood analysis for stochastic differential equations. Ann Inst Stat Math 63(3):431–479
Yoshida N (2013) Martingale expansion in mixed normal limit. Stoch Process Their Appl 123(3):887–933
Yoshida N (2018) Partial quasi-likelihood analysis. Japanese J Stat Data Sci 1(1):157–189
Yoshida N (2020) Asymptotic expansion of a variation with anticipative weights. arXiv:2101.00089
Yoshida N (2021) Simplified quasi-likelihood analysis for a locally asymptotically quadratic random field. arXiv:2102.12460
Acknowledgements
The author thanks Professor Yury Kutoyants for the invitation to the special issue and his valuable comments. This work was in part supported by Japan Science and Technology Agency CREST JPMJCR14D7, JPMJCR2115; Japan Society for the Promotion of Science Grants-in-Aid for Scientific Research No. 17H01702 (Scientific Research); and by a Cooperative Research Program of the Institute of Statistical Mathematics.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Professor Rafail Z. Khasminskii on the occasion of his 90th anniversary
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yoshida, N. Quasi-likelihood analysis and its applications. Stat Inference Stoch Process 25, 43–60 (2022). https://doi.org/10.1007/s11203-021-09266-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11203-021-09266-0
Keywords
- Ibragimov–Khasminskii theory
- Quasi-likelihood
- Locally asymptotically quadratic random field
- Polynomial type large deviation
- Quasi-maximum likelihood estimator
- Quasi-Bayesian estimator
- Diffusion process
- Adaptive estimator
- Jump-diffusion process
- Lévy process
- Volatility
- Jump filter
- Point process
- Non-synchronous observations
- Information criterion
- Sparse estimation





 for all
for all 



 as
as  and any
and any  as
as 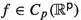 and any
and any