1 Introduction

Belomestny and Schoenmakers (2015) considered the problem of recovering the distribution of an independent random time T based on iid samples from a one-dimensional Brownian motion B at time T. Comte and Genon-Catalot (2015) already considered this problem for Poisson processes. Here we use the method of Belomestny and Schoenmakers (2015) and derive corresponding results for self-similar processes. We particularly focus on Bessel processes. As a consequence, we extend results from Belomestny and Schoenmakers (2015) to multi-dimensional Brownian motion. This is accomplished by considering the two-norm of the multi-dimensional Brownian motion, thus reducing the problem to the case of a Bessel process which is a one-dimensional process and can be treated similarly to the case of one-dimensional Brownian motion. More specifically, we give a non-parametric estimator for the density \(f_T\) of T. We show consistency of this estimator with respect to the \(L^2\) risk and derive a polynomial convergence rate for sufficiently smooth densities \(f_T\). Moreover, we show that this rate is optimal in the minimax sense. The constructed estimator is also shown to be asymptotically normal.

The paper is organized as follows: In Sect. 2 we recapitulate the Mellin transform which is our main tool throughout this paper. Using this transform we construct our estimator in Sect. 3 by solving a multiplicative deconvolution problem which is related to the original problem through self-similarity of the underlying process. The use of the Mellin transform in multiplicative deconvolution problems proposed by Belomestny and Schoenmakers (2015) is different to the standard approach which consists in applying a log-transformation and thus reducing the problem to an additive deconvolution problem which is usually addressed by the kernel density deconvolution technique. In Sect. 4 we give bounds on bias and variance of the estimator in the general self-similar case. In the following two sections we lay our focus on Bessel processes and give the convergence rates of our estimator for this case (Sect. 5) and show its asymptotic normality (Sect. 6). Section 7 is devoted to two further examples of self-similar processes where our method yields consistent estimators. Their convergence rates are provided there. In the following Sect. 8 we show optimality in the minimax sense of all previously obtained rates. Some numerical examples are given in Sect. 9. Finally, we collect some of the longer proofs in Sect. 10.

2 Mellin transform

In this section we recapitulate some properties of the Mellin transform from Butzer and Jansche (1997). This integral transform will be our main tool in estimation procedures of the next sections. For an interval I define the space

$$\begin{aligned} {\mathfrak {M}}_{I} := \bigcap \limits _{c\in I} \left\{ f:\mathbb {R_+}\rightarrow {\mathbb {C}} \Bigg | \int _0^\infty |f(x)|x^{c-1}dx<\infty \right\} . \end{aligned}$$

If f is the density function of an \({\mathbb {R}}_+\)-valued random variable, then we have at least \(f\in {\mathfrak {M}}_{[1,1]}\). Moreover, if \(f:\mathbb {R_+}\rightarrow {\mathbb {R}}\) is locally integrable on \({\mathbb {R}}_+\) with

$$\begin{aligned} f(x)=\left\{ \begin{array}{l@{\quad }l} {\mathcal {O}}(x^{-a}), &{} \text {for}~~ x\rightarrow 0\\ {\mathcal {O}}(x^{-b}), &{} \text {for}~~ x\rightarrow \infty \end{array}\right. , \end{aligned}$$

then \(f\in {\mathfrak {M}}_{(a,b)}\) holds.

Definition 1

For a densitiy function \(f\in {\mathfrak {M}}_{(a,b)}\) of a random variable X define

$$\begin{aligned} {\mathcal {M}}[f](s) := {\mathcal {M}}[X](s):= \int _0^\infty f(x)x^{s-1}dx \end{aligned}$$

as the Mellin transform of f (or of X) in \(s\in {\mathbb {C}}\) with \({\text {Re}}(s)\in (a,b)\).

If \(f\in {\mathfrak {M}}_{(a,b)}\) holds, then \({\mathcal {M}}[f](s)\) is well defined and holomorphic on the strip \({\{s\in {\mathbb {C}}|{\text {Re}}(s)\in (a,b) \}}\) according to Butzer and Jansche (1997).

Example 2

  1. (i)

    Consider gamma densities

    $$\begin{aligned} f(x)=\frac{r^{\sigma }}{\varGamma (\sigma )}x^{\sigma -1}e^{-rx} \end{aligned}$$
    (1)

    for \(x,\sigma ,r>0\). For all \(s\in {\mathbb {C}}\) with \({\text {Re}}(s-\sigma +1)> 0\) we have

    $$\begin{aligned} {\mathcal {M}}[f](s)=\frac{r^{1-s}}{\varGamma (\sigma )}\varGamma (s+\sigma -1). \end{aligned}$$
  2. (ii)

    Consider for \(t>0\), \(d\ge 1\) the densities

    $$\begin{aligned} f_t(x) = \frac{2^{1-\frac{d}{2}}t^{-\frac{d}{2}}}{\varGamma \left( {d}/{2}\right) } x^{d-1} e^{-\frac{x^2}{2t}} ,\quad x> 0. \end{aligned}$$
    (2)

    For \({\text {Re}}({s})> 1-d\) elementary calculus shows that

    $$\begin{aligned} {\mathcal {M}}[f_1](s) = \frac{1}{\varGamma \left( {d}/{2}\right) }\varGamma \left( \frac{s+d-1}{2}\right) 2^{\frac{s-1}{2}}. \end{aligned}$$
    (3)

Similar to the well-known relation of the classical Fourier transform to sums of independent random variables, the Mellin transform behaves multiplicatively with respect to products of independent random variables:

Theorem 3

Let X and Y be independent \({\mathbb {R}}_+\)-valued random variables with densities \(f_X\in {\mathfrak {M}}_{(a,b)}\) and \(f_Y\in {\mathfrak {M}}_{(c,d)}\), and Mellin transforms \({\mathcal {M}}[X]\) and \({\mathcal {M}}[Y]\) for \(a<b,~c<d,~(a,b)\cap (c,d)\ne \emptyset \). Then XY has a density \(f_{XY}\in {\mathfrak {M}}_{(a,b)\cap (c,d)}\), and

$$\begin{aligned} {\mathcal {M}}[XY](s) ={\mathcal {M}}[X](s){\mathcal {M}}[Y](s) \end{aligned}$$

for all \({s \in {\mathbb {C}}}\) with \({\text {Re}}(s)\in (a,b)\cap (c,d)\).

In the setting of Theorem 3 it is easy to see that \(f_{XY}\) is identical to

$$\begin{aligned} (f_X \odot f_Y)(s) :=\int _0^\infty f_X\left( \frac{s}{x}\right) f_Y(x) \frac{1}{x} dx \end{aligned}$$
(4)

for all \({s \in {\mathbb {C}}}\) with \({\text {Re}}(s)\in (a,b)\cap (c,d)\). The function \(f_X \odot f_Y\) is called Mellin convolution of \(f_X\) and \(f_Y\).

For \(a<b\) denote the space of holomorphic functions on \(\{s\in {\mathbb {C}}|{\text {Re}}(s)\in (a,b) \}\) by \({\mathcal {H}} (a,b)\). The mapping \({\mathcal {M}}:{\mathfrak {M}}_{(a,b)}\rightarrow {\mathcal {H}} (a,b)\), \(f\mapsto {\mathcal {M}}[f]\) is injective. Given the Mellin transform of a function f we can reconstruct f:

Theorem 4

For \(a<\gamma <b\) let \(f\in {\mathfrak {M}}_{(a,b)}\). If

$$\begin{aligned} \int _{-\infty }^\infty |{\mathcal {M}}[f](\gamma +iv)| dv<\infty , \end{aligned}$$

then the inversion formula

$$\begin{aligned} f(x)= \frac{1}{2\pi } \int _{-\infty }^{\infty } {\mathcal {M}}[f](\gamma +iv)x^{-\gamma -iv} dv \end{aligned}$$

holds almost everywhere for \(x\in {\mathbb {R}}_+\).

Another important result in the theory of Mellin transforms is the Parseval formula for Mellin tranforms (see (Bleistein and Handelsman 1986, page 108) for the proof):

Theorem 5

Let \(f,g:{\mathbb {R}}_+\rightarrow {\mathbb {R}}\) be measurable functions such that

$$\begin{aligned} \int _0^\infty f(x)g(x)dx \end{aligned}$$

exists. Suppose that \({\mathcal {M}}[f](1-\cdot )\) and \({\mathcal {M}}[g](\cdot )\) are holomorphic on some vertical strip \({\mathcal {S}}:=\{z\in {\mathbb {C}}|a<{\text {Re}}(z)<b\}\) for \(a,b\in {\mathbb {R}}\). If there is a \(\gamma \in (a,b)\) with

$$\begin{aligned} \int _{-\infty }^\infty |{\mathcal {M}}[f](1-\gamma -is)|ds<\infty \quad \text {and} \quad \int _{0}^\infty x^{\gamma -1} |g(x)|dx<\infty , \end{aligned}$$

then

$$\begin{aligned} \int _0^\infty f(x)g(x)dx=\frac{1}{2\pi i}\int _{\gamma -i\infty }^{\gamma +i\infty } {\mathcal {M}}[f](1-s){\mathcal {M}}[g](s)ds. \end{aligned}$$

3 Construction of the estimator

We consider a real-valued stochastic process \((Y_t)_{t\ge 0}\) with càdlàg paths which is self-similar with scaling parameter H (for short, H-ss), that is

$$\begin{aligned} (Y_{at})_{t\ge 0}{\mathop {=}\limits ^{d}}(a^H Y_t)_{t\ge 0} \quad \text {for all}~ a>0. \end{aligned}$$
(5)

Here, \({\mathop {=}\limits ^{d}}\) denotes identity of all finite dimensional distributions. Let \(T\ge 0\) be a stopping time with density \(f_T\) independent of Y. Let \(X_1,\dots ,X_n\) be iid samples of \(Y_T\). In order to construct a non-parametric estimator for \(f_T\) we use the simple consequence of (5) that

$$\begin{aligned} {T}^H Y_1 {\mathop {=}\limits ^{d}}Y_{T}. \end{aligned}$$
(6)

We take the absolute value on both sides and assume that \(f_T\in {\mathfrak {M}}_{(a,b)}\) with \({0\le a<b}\) and that the density of \(Y_1\) is in \({\mathfrak {M}}_{(0,\infty )}\), so we can apply the Mellin transform on both sides of (6) and obtain

$$\begin{aligned} {\mathcal {M}}[|Y_T|](s) = {\mathcal {M}}[{T}^H](s) {\mathcal {M}}[|Y_1|](s) = {\mathcal {M}}[{T}]\left( Hs-H+1\right) {\mathcal {M}}[|Y_1|](s) \end{aligned}$$

for \({\max \{0,\frac{a+H-1}{H}\}< {\text {Re}}(s) < \frac{b+H-1}{H}}\). Setting \(z:=Hs-H+1\) we conclude that

$$\begin{aligned} {\mathcal {M}}[T](z) = \frac{{\mathcal {M}}[|Y_T|]\left( \frac{z+H-1}{H}\right) }{{\mathcal {M}}[|Y_1|]\left( \frac{z+H-1}{H}\right) }, \quad {\max \{1-H,a\}< {\text {Re}}(z) < b}. \end{aligned}$$
(7)

If the Mellin inversion formula (Lemma 4) is applicable to T, we may write

$$\begin{aligned} f_{T}(x) = \frac{1}{2\pi i} \int _{\gamma -i\infty }^{\gamma +i\infty } {\mathcal {M}}[T](z)x^{-z} dz = \frac{1}{2\pi } \int _{-\infty }^{\infty } {\mathcal {M}}[T](\gamma +iv)x^{-\gamma -iv} dv \end{aligned}$$
(8)

for \(a< \gamma < b\). Combining (7) and (8) we obtain the representation

$$\begin{aligned} f_{T}(x) = \frac{1}{2\pi } \int _{-\infty }^{ \infty } \frac{{\mathcal {M}}[|Y_T|]\left( \frac{\gamma +H-1+iv}{H}\right) }{{\mathcal {M}}[|Y_1|] \left( \frac{\gamma +H-1+iv}{H}\right) } x^{-\gamma -iv}dv \end{aligned}$$
(9)

for \(\max \{1-H,a\}< \gamma < b\). In order to obtain an estimator of \(f_T\) based on (9) we would like to replace \({\mathcal {M}}[|Y_T|]\) by its empirical counterpart

$$\begin{aligned}{\mathcal {M}}_n [|Y_{T}|](s):= \frac{1}{n}\sum \limits _{k=1}^{n} |X_k|^{s-1}.\end{aligned}$$

However, this substitution may prevent the integral in (9) from converging. Thus, we introduce a sequence \((g_n)_{n\in {\mathbb {N}}}\) with \(g_n\rightarrow \infty \) (chosen later) in order to regularize our estimator. In view of (9) define

$$\begin{aligned} \hat{f_n}(x):= \frac{1}{2\pi } \int _{-g_n}^{g_n} \frac{{\mathcal {M}}_n[|Y_T|]\left( \frac{\gamma +H-1+iv}{H}\right) }{{\mathcal {M}}[|Y_1|] \left( \frac{\gamma +H-1+iv}{H}\right) } x^{-\gamma -iv} ~dv \end{aligned}$$
(10)

for \(x>0\) and \(\max \{1-H,a\}< \gamma < b\) as an estimator for \(f_T\).

4 Convergence analysis

For the sake of brevity we introduce the notation \(f(x)\lesssim g(x)\) for \(x\rightarrow a\), if \(f={\mathcal {O}}(g)\) in the Landau notation. We write \(f(x)\sim g(x)\) for \(x\rightarrow a\), if \(f(x)\lesssim g(x)\) and \(g(x)\lesssim f(x)\) for \(x\rightarrow a\). For \(0\le a<b\) and \(\beta \in (0,\pi )\) consider the class of densities

$$\begin{aligned} {\mathcal {C}}(\beta ,a,b):= \left\{ f\in {\mathfrak {M}}_{(a,b)}\Bigg | {\begin{array}{c} \exists {{\tilde{f}}}:S_\beta \rightarrow {\mathbb {C}}\text { holomorphic with } {{\tilde{f}}}|_{{\mathbb {R}}_+}=f, \\ \tilde{f}(z)\lesssim z^{-a} \text { as }z\rightarrow 0, f(z)\lesssim z^{-b} \text { as }|z|\rightarrow \infty \end{array}} \right\} , \end{aligned}$$

where

$$\begin{aligned} S_\beta := \{z\in {\mathbb {C}}: |\arg (z)|\le \beta \} \quad \text {and} \quad {\mathcal {C}}(\beta ,a,\infty ):=\bigcap \limits _{b\ge 0} {\mathcal {C}}(\beta ,a,b), \end{aligned}$$

For the bias of the estimator (10) we have:

Theorem 6

Let \((Y_t)_{t\ge 0}\) be H-ss with càdlàg paths. Let \(T\ge 0\) be a stopping time independent of Y with density \(f_T\). If \(f_T\in {\mathcal {C}}(\beta ,a,b)\) with \(\beta \in (0,\pi )\) and \(0\le a<b\), then

$$\begin{aligned} {\text {E}}[f_T(x)- \hat{f_n}(x)] \lesssim x^{-\gamma } e^{-\beta g_n} \end{aligned}$$
(11)

for all \(x>0\), \(\gamma \in (\max \{a,1-H\},b)\).

Proof

Let \(x> 0\). By Fubini’s theorem and (7),

$$\begin{aligned} {\text {E}}[\hat{f_n}(x)]&= {\text {E}}\left[ \frac{1}{2\pi } \int _{-g_n}^{g_n}\frac{{\mathcal {M}}_n[|Y_T|]\left( \frac{\gamma +H-1+iv}{H}\right) }{{\mathcal {M}}[|Y_1|]\left( \frac{\gamma +H-1+iv}{H}\right) } x^{-\gamma -iv}~dv \right] \nonumber \\&= \frac{1}{2\pi } \int _{-g_n}^{g_n} \frac{{\text {E}}\left[ {\mathcal {M}}_n[|Y_T|]\left( \frac{\gamma +H-1+iv}{H}\right) \right] }{{\mathcal {M}}[|Y_1|]\left( \frac{\gamma +H-1+iv}{H}\right) } x^{-\gamma -iv} ~dv .\nonumber \\&= \frac{1}{2\pi } \int _{-g_n}^{g_n} \frac{{\mathcal {M}}[|Y_T|]\left( \frac{\gamma +H-1+iv}{H}\right) }{{\mathcal {M}}[|Y_1|] \left( \frac{\gamma +H-1+iv}{H}\right) } x^{-\gamma -iv} ~dv \nonumber \\&= \frac{1}{2\pi } \int _{-g_n}^{g_n} {\mathcal {M}}[T](\gamma +iv) x^{-\gamma -iv} dv. \end{aligned}$$
(12)

We combine Theorem 4 with (12) to get

$$\begin{aligned} |f_T(x)-{\text {E}}[\hat{f_n}(x)] |\le \frac{x^{-\gamma }}{2\pi } \int _{\{|v|>g_n\} } \left| {\mathcal {M}}[T](\gamma +iv) \right| dv. \end{aligned}$$
(13)

Since \(f_T\in {\mathcal {C}}(\beta ,a,b)\) implies \(|{\mathcal {M}}[T](\gamma +iv)| \lesssim e^{-\beta |v|}\) for \(v\rightarrow \pm \infty \), \(\gamma \in (a,b)\) (see Proposition 5 in Flajolet et al. (1995)), we have

$$\begin{aligned} L:= \int _{\{|v|>g_n\} } e^{\beta |v|}\left| {\mathcal {M}}[T](\gamma +iv) \right| dv<\infty . \end{aligned}$$
(14)

Moreover, (13) gives

$$\begin{aligned} |f_T(x)- {\text {E}}[\hat{f_n}(x)]|&\le e^{-\beta g_n} \frac{x^{-\gamma }}{2\pi } \int _{\{|v|>g_n\} } e^{\beta |v|}\left| {\mathcal {M}}[T](\gamma +iv) \right| dv \le e^{-\beta g_n} x^{-\gamma }\frac{L}{2\pi } \end{aligned}$$

for all \(x>0\), which is our claim. \(\square \)

Having established an upper bound on the bias of \({\hat{f}}_n\), we now shall do the same for the variance of our estimator.

Theorem 7

Let \((Y_t)_{t\ge 0}\) be H-ss with càdlàg paths. Let \(T\ge 0\) be a stopping time independent of Y with density \(f_T\). If \(f_T\in {\mathfrak {M}}_{(a,b)}\) with \({0\le a< b}\) and the density of \(|Y_1|\) is in \({\mathfrak {M}}_{(0,\infty )}\), then

$$\begin{aligned} {\text {Var}}[ {{\hat{f}}}_n(x) ]&\le \frac{{\mathcal {M}}[|Y_1|]\left( \frac{2\gamma -2}{H}+1\right) {\mathcal {M}}[T](2\gamma -1)}{4\pi ^2 x^{-2\gamma } n} \\&\quad \times \left( \int _{-g_n}^{g_n} \frac{1}{|{\mathcal {M}}[|Y_1|]\left( \frac{\gamma +H-1+iv}{H}\right) |} dv \right) ^2 \end{aligned}$$

for all \(n\in {\mathbb {N}}\) and all \(x>0\).

Proof

Let \(x> 0\), \(n\in {\mathbb {N}}\). As

$$\begin{aligned} {\text {Var}}\left[ \int _a^b f_v dv\right] \le \left( \int _a^b \sqrt{{\text {Var}}[f_v]}dv\right) ^2, \end{aligned}$$

for any bounded random function \(f_v\) (continuous in v), we obtain

$$\begin{aligned} {\text {Var}}[ \hat{f_n}(x)]&\le \frac{1}{4\pi ^2 x^{-2\gamma }} \left( \int _{-g_n}^{g_n} \frac{\sqrt{{\text {Var}}[{\mathcal {M}}_n[|Y_T|]\left( \frac{\gamma +H-1+iv}{H}\right) ]}}{|{\mathcal {M}}[|Y_1|]\left( \frac{\gamma +H-1+iv}{H}\right) |} dv \right) ^2\nonumber \\&= \frac{1}{4\pi ^2 x^{-2\gamma } n} \left( \int _{-g_n}^{g_n} \frac{\sqrt{{\text {Var}}[|Y_T|^\frac{\gamma -1+iv}{H}]} }{|{\mathcal {M}}[|Y_1|]\left( \frac{\gamma +H-1+iv}{H}\right) |} dv \right) ^2. \end{aligned}$$
(15)

In order to get a bound on \({\text {Var}}[|Y_T|^\frac{\gamma -1+iv}{H}]\) we use the self-similarity of Y to get

$$\begin{aligned} {\text {Var}}[|Y_T|^\frac{\gamma -1+iv}{H}]&\le {\text {E}}[(|Y_T|)^{(2\gamma -2)/H}]\\&= \int _0^\infty {\text {E}}[(|Y_t|)^{(2\gamma -2)/H}] f_T(t) dt \\&= {\text {E}}[(|Y_1|)^{(2\gamma -2)/H}] \int _0^\infty t^{2\gamma -2} f_T(t) dt, \end{aligned}$$

which (together with (15)) gives the desired bound on \({\text {Var}}[\hat{f_n}(x)]\). \(\square \)

5 Application to Bessel processes

In this section we choose Y to be a Bessel process \(BES=(BES_t)_{t\ge 0}\) starting in 0 with dimension \(d\in [1,\infty )\). Note that the case \(d=1\) leads to the absolute value of the one-dimensional Brownian motion and was already considered in Belomestny and Schoenmakers (2015). We refer to Revuz and Yor (1999) for detailed information about Bessel processes. It is well-known, that Bessel processes are \(\frac{1}{2}\)-ss and have continuous paths. Marginal densities are given by:

$$\begin{aligned} f_t(y)= \frac{2^{1-\frac{d}{2}}t^{-\frac{d}{2}}}{\varGamma \left( {d}/{2}\right) } y^{d-1} e^{-\frac{y^2}{2t}} ,\quad y\ge 0. \end{aligned}$$

In Example 2(ii) we calculated \({\mathcal {M}}[BES_1](s) = \frac{1}{\varGamma \left( {d}/{2}\right) }\varGamma \left( \frac{s+d-1}{2}\right) 2^{\frac{s-1}{2}}\). Looking at (10) we obtain

$$\begin{aligned} \hat{f_n}(x)= \frac{1}{2\pi } \int _{-g_n}^{g_n} \frac{ \varGamma \left( \frac{d}{2}\right) \frac{1}{n}\sum _{k=1}^{n}X_k^{2(\gamma -1+iv)}}{\varGamma \left( \gamma +\frac{d}{2}-1+iv\right) 2^{\gamma -1+iv}} x^{-\gamma -iv} ~dv \end{aligned}$$
(16)

as an estimator for the density \(f_T(x)\) of a stopping time \(T\ge 0\) for \(x>0\) and \(\max \{1/2,a\}< \gamma < b\), where a, b are such that \(f_T\in {\mathfrak {M}}_{(a,b)}\) and \(X_1, \ldots ,X_n\) are independent samples of \(BES_T\). With our major result Theorem 8 we shall derive the convergence rates for (16).

Theorem 8

If \(f_T\in {\mathcal {C}}(\beta ,a,b)\) for some \(0\le a<b\), \(\beta \in (0,\pi )\) and if there is a \(\gamma \in (a,b)\) with \(2\gamma -1\in (a,b)\) and \(\gamma > (4-d)/4\), then

$$\begin{aligned} x^{2\gamma }{\text {E}}[ |f_T(x)- \hat{f_n}(x)|^2 ] \le C_{L,d,\gamma } \left( \frac{1}{n}e^{\pi g_n} + e^{-2\beta g_n}\right) ,\quad x> 0 \end{aligned}$$
(17)

for some \(C_{L,d,\gamma }>0\) depending only on \(L,\gamma ,d\) as well as T. Moreover, taking

$$\begin{aligned} {g_n= \frac{\log n}{\pi +2\beta }} \end{aligned}$$
(18)

in (17), one has for all \(x>0\) the polynomial convergence rate

$$\begin{aligned} \sqrt{{\text {E}}[ |f_T(x)- \hat{f_n}(x)|^2 ]} \lesssim x^{-\gamma } n^\frac{-\beta }{\pi +2\beta } ,\quad n\rightarrow \infty . \end{aligned}$$
(19)

Proof

Let \(x> 0\). We use the upper bound on variance obtained in Lemma 7 with \(H=1/2\) to get

$$\begin{aligned} {\text {Var}}[ x^\gamma {{\hat{f}}}_n(x) ]&\le \frac{C_0(\gamma ,d)}{4\pi ^2 n} \left( \int _{-g_n}^{g_n} \frac{1}{|{\mathcal {M}}[BES_1]({2\gamma -1+2iv})|} dv \right) ^2 \end{aligned}$$
(20)

for some \(C_0(\gamma ,d)>0\). By Example 2(ii) and Lemma 21(ii) we have

$$\begin{aligned} {\text {Var}}[ x^\gamma {{\hat{f}}}_n(x) ]&\le \frac{C_0(\gamma ,d)\varGamma \left( \frac{d}{2}\right) ^2 }{\pi ^2 2^{2\gamma }n} \left( \int _{-g_n}^{g_n} \frac{1}{|\varGamma \left( \gamma -1+\frac{d}{2}+iv\right) |} dv\right) ^2 \nonumber \\&\le \frac{C_0(\gamma ,d)\varGamma \left( \frac{d}{2}\right) ^2 }{\pi ^2 2^{2\gamma }n} (C_1(d,\gamma )+C_2e^{\pi g_n/2})^2 \end{aligned}$$
(21)

for some constants \(C_1(d,\gamma )\) and \(C_2\). Adding (21) and (11) gives

$$\begin{aligned} x^{2\gamma }{\text {E}}[ |f_T(x)- \hat{f_n}(x)|^2 ]&\le \frac{C_0(\gamma ,d)\varGamma \left( \frac{d}{2}\right) ^2 }{\pi ^2 2^{2\gamma }n} (C_1(d,\gamma )+C_2e^{\pi g_n/2})^2 + C^2 e^{-2\beta g_n} \nonumber \\&\le C_{L,d,\gamma } \left( \frac{1}{n}e^{\pi g_n} + e^{-2\beta g_n}\right) \end{aligned}$$
(22)

for some \(C_{L,d,\gamma }>0\). The choice (18) yields the rate (19). \(\square \)

The class \({\mathcal {C}}(\beta ,a,b)\) is fairly large. In particular, \({\mathcal {C}}(\beta ,0,\infty )\) includes for all \(\beta \in (0,\pi /2)\) such well-known families of distributions as Gamma, Weibull, Beta, log-normal and inverse Gaussian. So, if T belongs to one of those families, Theorem 8 is true for any \(\gamma >\max \{1/2,(4-d)/4 \}\). If \(d\ge 2\), then we only require \(\gamma >1/2\).

6 Asymptotic normality for Bessel processes

Note that the estimator (16) can be written as

$$\begin{aligned} \hat{f_n}(x)= \frac{1}{n}\sum _{k=1}^{n} Z_{n,k} \end{aligned}$$
(23)

with

$$\begin{aligned} Z_{n,k}:= \frac{\varGamma \left( \frac{d}{2}\right) }{\pi } \int _{-g_n}^{g_n} \frac{X_k^{2(\gamma -1+iv)}}{\varGamma \left( \gamma +\frac{d}{2}-1+iv\right) 2^{\gamma +iv}} x^{-\gamma -iv} ~dv. \end{aligned}$$
(24)

Since \(\hat{f_n}\) is a sum of iid variables, we can show that (under mild assumptions on \(f_T\)) \(\hat{f_n}\) is asymptotically normal. In fact, we have:

Theorem 9

Let \(f_T\in {\mathfrak {M}}_{(a,b)}\) for some \(0\le a<b\). Suppose there is a \(\gamma \in (a,b)\) such that \(2\gamma -1\in (a,b)\), \(\gamma >(4-d)/4\) and \((\delta +2)\gamma -\delta -1\in (a,b)\) for some \(\delta >0\) and

$$\begin{aligned} \int _{-\infty }^\infty |{\mathcal {M}}[T](2\gamma -1+iv)|dv<\infty . \end{aligned}$$
(25)

If we choose \(g_n \sim \log (n)\) in (16) then we have

$$\begin{aligned} \sqrt{n}\nu _n^{-1/2}(\hat{f_n}(x)-{\text {E}}[\hat{f_n}(x)]) {\mathop {\rightarrow }\limits ^{d}} {\mathcal {N}}(0,1) \end{aligned}$$
(26)

for all \(x>0\), where

$$\begin{aligned} \nu _n:={\text {Var}}[Z_{n,1}]=\frac{c\varGamma \left( \frac{d}{2}\right) }{2\pi ^3 x^{2\gamma }} g_n^{-2\gamma +d-3} e^{\pi g_n} \log ^{-2}(g_n) (1+o(1)) \end{aligned}$$
(27)

with some \(c>0\) given by (47).

We present the proof in Sect. 10.1. As we mentioned in the end of Sect. 5, we can often assume \((a,b)=(0,\infty )\), so that the choice of \(\gamma \) is only restricted by \(\gamma >\max \{1/2,(4-d)/4 \}\). In this case a suitable \(\delta \) can always be found: For \(\gamma \in (1/2,1)\) choose \(\delta <(1-2\gamma )/(1-\gamma )\), for \(\gamma >1\) choose \(\delta >(1-2\gamma )/(1-\gamma )\) and for \(\gamma =1\) any \(\delta >0\). If in addition to \((a,b)=(0,\infty )\) we have \(d\ge 2\), then the statement is true for all \(\gamma >1/2\).

It is possible to give a Berry-Esseen type error estimate for the convergence in (26). This is a new result even for dimension \(d=1\).

Theorem 10

Let \(f_T\in {\mathfrak {M}}_{(a,b)}\) for some \(0\le a<b\). Suppose there is a \(\gamma \in (a,b)\) such that \(2\gamma -1\in (a,b)\), \(\gamma >(4-d)/4\), \(3\gamma -2\in (a,b)\) and (25) holds. Fix some \(x>0\). Denote by \(F_n\) the distribution function of

$$\begin{aligned} \sqrt{n}\nu _n^{-1/2}(\hat{f_n}(x)-{\text {E}}[\hat{f_n}(x)]) \end{aligned}$$

(where \(\hat{f}_n(x)\) is defined by (16) and \(\nu _n=n{\text {Var}}[\hat{f}_n(x)]\) is given by (27)) and by \(\varPhi \) the distribution function of the standard normal distribution. If we choose \(g_n \sim \log (n)\) in (16) then we have

$$\begin{aligned} \rho _n :=\sup \limits _{y\in {\mathbb {R}}} |F_n(y)-\varPhi (y)|\lesssim {\left\{ \begin{array}{ll} n^{-\frac{1}{2}} (\log n)^{4\gamma -d+3} \log ^{3}(\log (n)) , &{}\text {~if~}\quad \gamma <\frac{3-d}{2}\\ n^{-\frac{1}{2}} (\log n)^{3(2\gamma -d+3)/2} \log ^{3}(\log (n)) , &{}\text {~if~}\quad \gamma \ge \frac{3-d}{2} \end{array}\right. } \end{aligned}$$
(28)

for \(n\rightarrow \infty \).

Proof

Let \(x>0\) and \(n\in {\mathbb {N}}\). Consider the representation (23) of \({{\hat{f}}}_n(x)\). Berry-Esseen Theorem (see Gänssler and Stute 1977) states

$$\begin{aligned} \rho _n \le \frac{6 {\text {E}}[|Z_{n,1}-{\text {E}}[Z_{n,1}]|^3]}{({\text {Var}}[Z_{n,1}])^{3/2} n^{1/2}}. \end{aligned}$$
(29)

We choose \(j=3\) in Lemma 11 to get

$$\begin{aligned} {\text {E}}[|Z_{n,1}-{\text {E}}[Z_{n,1}]|^3]\lesssim {\text {E}}[|Z_{n,1}|^3]\lesssim {\left\{ \begin{array}{ll} g_n^{-\gamma -d/2+3/2} e^{3\pi g_n/2}, &{}\text {~if~}\gamma +d/2-3/2 < 0\\ e^{3\pi g_n/2}, &{}\text {~if~}\gamma +d/2-3/2 \ge 0 \end{array}\right. } \end{aligned}$$
(30)

for \(n\rightarrow \infty \). By Theorem 9 we have (27). Choose \({g_n\sim \log (n)}\). Plugging (30) and (27) into (29) concludes the proof. \(\square \)

Note that the signs of the powers \({4\gamma -d+3}\) and \({3(2\gamma -d+3)/2}\) in (28) are ambiguous and depend on the relative positions of \(\gamma \) and d. However, if \(d\ge 2\) then we only have the case \(\gamma +d/2-3/2\ge 0\) and the power of the logarithm is positive.

The following observation about the absolute moments of \(Z_{n,1}\) is useful in the proof of Theorem 9 but also holds some insights in itself.

Lemma 11

Let \(f_T\in {\mathfrak {M}}_{(a,b)}\) for some \(0\le a<b\) and \((g_n)_{n\in {\mathbb {N}}}\subset {\mathbb {R}}_+\) with \(g_n\rightarrow \infty \) as \(n\rightarrow \infty \). If there is a \(\gamma \in (a,b)\) such that \(2\gamma -1\in (a,b)\), \(\gamma >(4-d)/4\) and \((\gamma -1)j+1\in (a,b)\), then

$$\begin{aligned} {\text {E}}[|Z_{n,1}|^{j}] \lesssim {\left\{ \begin{array}{ll} g_n^{-\gamma -d/2+3/2} e^{\pi g_n j/2}, &{}\text { if }\gamma +d/2-3/2 < 0\\ e^{\pi g_n j/2}, &{}\text { if }\gamma +d/2-3/2 \ge 0 \end{array}\right. } \end{aligned}$$
(31)

as \(n\rightarrow \infty \) for all \(j\in {\mathbb {R}}_+\). In particular, all absolute moments of \(Z_{n,1}\) exist for all \(n\in {\mathbb {N}}\) greater than some \(n_0\in {\mathbb {N}}\).

Proof

Case \(\gamma +d/2-3/2 \ge 0\): By Jensen inequality, Lemma 21(ii) and (7) (with \(H=1/2,~Y=BES\) there) we have

$$\begin{aligned} {\text {E}}[|Z_{n,1}|^{j}]&\le c {\text {E}}[X_1^{2(\gamma -1)j}] \int _{-g_n}^{g_n} \frac{1}{\left| \varGamma \left( \gamma +d/2-1+iv\right) \right| ^{j}} ~dv \\&\le c {\mathcal {M}}[X_1](2(\gamma -1)j+1) (C_{\gamma ,d,j}+C_j e^{\pi g_n j/2} )\\&= c {\mathcal {M}}[T]((\gamma -1)j+1) {\mathcal {M}}[BES_1](2(\gamma -1)j+1) (C_{\gamma ,d,j}+C_j e^{\pi g_n j/2} ), \end{aligned}$$

where \(c:=\varGamma \left( \frac{d}{2}\right) ^{j}(2^\gamma \pi x^\gamma )^{-j} \) and \(C_{\gamma ,d,j},C_j>0\). The case \(\gamma +d/2-3/2 < 0\) follows similarly applying Lemma 21(i) instead of (ii). \(\square \)

For the special case \((a,b)=(0,1)\) and \(d=j=1\) this result is mentioned in Belomestny and Schoenmakers (2015) but without an extensive proof which we provide here. Note that for \(d\ge 2\) the assumption \(\gamma >(4-d)/4\) is redundant. Moreover, we always have the smaller bound of the second case in (31).

7 Some other self-similar processes

7.1 Normally distributed processes

Let \(Y=(Y_t)_{t\ge 0}\) be H-ss with càdlàg paths and \(Y_1\) standard normally distributed. As example consider a fractional Brownian motion. This setting is easily generalized to the case where \(Y_1\sim {\mathcal {N}}(0,\sigma ^2)\) with \(\sigma ^2>0\) by considering the process \(({{\tilde{Y}}}_t)_{t\ge 0} := (Y_t/\sigma )_{t\ge 0}\) and modifying our observations to \(\tilde{X}_i :=X_i/\sigma \). Taking \(d=1\) in Example 2(ii) we see that estimator (10) assumes the form

$$\begin{aligned} \hat{f_n}(x)= \frac{1}{2\sqrt{\pi }} \int _{-g_n}^{g_n} \frac{ \frac{1}{n}\sum _{k=1}^{n}X_k^{(\gamma -1+iv)/H}}{\varGamma \left( \frac{\gamma +H-1+iv}{2H}\right) 2^{\frac{\gamma +2H-1+iv}{2H}}} x^{-\gamma -iv} ~dv \end{aligned}$$
(32)

for \(x>0\) and \(\max \{1-H,a\}< \gamma < b\). We can prove a convergence result for this estimator, similar to Theorem 8.

Theorem 12

Let \(0\le a<b\). Suppose \(f_T\in {\mathcal {C}}(\beta ,a,b)\) for some \(\beta \in (0,\pi )\). If there is some \(\gamma \in (\max \{a,1-H,3/4\},b)\), then

$$\begin{aligned} x^{2\gamma } {\text {E}}[ |f_T(x)- \hat{f_n}(x)|^2 ] \lesssim {\left\{ \begin{array}{ll} \frac{1}{n}e^{\pi g_n/(2H)} + e^{-2\beta g_n}, &{}\text {if} \quad \gamma \ge 1\\ \frac{1}{n} g_n^{(1-\gamma )/H}e^{\pi g_n/(2H)}+ e^{-2\beta g_n}, &{}\text {if} \quad \gamma < 1 \end{array}\right. } \end{aligned}$$
(33)

for \(n\rightarrow \infty \) and all \(x>0\). Taking

$$\begin{aligned} g_n= {\left\{ \begin{array}{ll} \frac{2H\log n}{\pi +4H\beta }, &{}\text {if} ~~\gamma \ge 1\\ \frac{2H\log n - 2(\gamma -1)\log \log n}{\pi +4H\beta }, &{}\text {if} ~~\gamma < 1 \end{array}\right. }, \end{aligned}$$
(34)

we obtain for all \(x>0\) the polynomial convergence rate

$$\begin{aligned} x^{\gamma }\sqrt{{\text {E}}[ |f_T(x)- \hat{f_n}(x)|^2 ]} \lesssim {\left\{ \begin{array}{ll} n^{-\frac{2H\beta }{\pi +4H\beta }}, &{}\text {if} \quad \gamma \ge 1\\ n^{-\frac{2H\beta }{\pi +4H\beta }} (\log n)^{\frac{(1-\gamma )2\beta }{\pi +4H\beta }}, &{}\text {if} \quad \gamma < 1 \end{array}\right. } \end{aligned}$$
(35)

for \(n\rightarrow \infty \).

Proof

The proof is analogous to the one of Theorem 8 except for the upper bound on variance which is in this case

$$\begin{aligned} {\text {Var}}[ x^\gamma {{\hat{f}}}_n(x) ]&\le \frac{C_0(\gamma ,H) H^2 }{\pi 2^{\frac{\gamma +2H-1}{2H}}n} \times {\left\{ \begin{array}{ll} \left( C_1(\gamma ,H)+C_2e^{\frac{\pi g_n}{4H}}\right) ^2, &{}\text {if} \quad \gamma \ge 1\\ C_1^2\left( 2H/g_n\right) ^{\frac{\gamma -1}{H}}e^{\frac{\pi g_n}{2H}}, &{}\text {if} \quad \gamma < 1 \end{array}\right. } \end{aligned}$$

for some \(C_0(\gamma ,H)>0\). Combining this with the bound on the bias from Lemma 6(i) we obtain (33). Plugging (34) into (33) gives the rate (35). \(\square \)

Taking \(H=1/2\) in Theorem 12 we obtain the same rates as for Bessel processes (see Theorem 8). For smaller H the rate is worse and for greater H it is better. Note that we work with observations of \(|Y_T|\) rather than \(Y_T\).

7.2 Gamma distributed processes

Let \(Y=(Y_t)_{t\ge 0}\) be H-ss with càdlàg paths such that \(Y_1\) has Gamma density (1) with \(r=1\). We can easily generalize to the case \(r>0\), by considering the process \({({{\tilde{Y}}}_t)_{t\ge 0} := (r Y_t)_{t\ge 0}}\) and modifying our observations to \({{\tilde{X}}}_i :=r X_i\). As an example consider the so-called square of a Bessel process with dimension d starting at 0 (see Revuz and Yor 1999, Chapter XI, §1). Considering Example 2(i) estimator (10) takes the form

$$\begin{aligned} \hat{f_n}(x)= \frac{\varGamma (\sigma )}{2{\pi }} \int \limits _{-g_n}^{g_n} \frac{ \frac{1}{n}\sum _{k=1}^{n}X_k^{(\gamma -1+iv)/H}}{\varGamma \left( \frac{\sigma H+\gamma -1+iv}{H} \right) } x^{-\gamma -iv} ~dv \end{aligned}$$
(36)

for \(x>0\) and \(\max \{1-\sigma H ,a\}< \gamma < b\). We can prove a convergence result for this estimator, that is similar to Theorems 8 and 12.

Theorem 13

Let \(0\le a<b\). Suppose \(f_T\in {\mathcal {C}}(\beta ,a,b)\) for some \(\beta \in (0,\pi )\). If there is some \(\gamma \in (\max \{a,1-\sigma H, 1-\sigma /4 \},b)\) with \(2\gamma -1\in (a,b)\), then

$$\begin{aligned} x^{2\gamma } {\text {E}}[ |f_T(x)- \hat{f_n}(x)|^2 ] \lesssim {\left\{ \begin{array}{ll} \frac{1}{n} e^{\frac{\pi g_n}{H}}+ e^{-2\beta g_n}, &{}\text {if} \quad \gamma \ge 1-\sigma H+\frac{H}{2}\\ \frac{1}{n} g_n^{1-\frac{2(\gamma +\sigma H-1)}{H}}e^{\frac{\pi g_n}{H}}+ e^{-2\beta g_n},&{}\text {if} \quad \gamma < 1-\sigma H+\frac{H}{2} \end{array}\right. } \end{aligned}$$
(37)

for \(n\rightarrow \infty \) and all \(x > 0\). If

$$\begin{aligned} g_n= {\left\{ \begin{array}{ll} \frac{\log n}{\frac{\pi }{H}+2\beta }, &{}\text {if} \quad \gamma \ge 1-\sigma H+\frac{H}{2}\\ \frac{\log n - \left( 1-\frac{2(\gamma +\sigma H-1)}{H}\right) \log \log n}{\frac{\pi }{H}+2\beta }, &{}\text {if} \quad \gamma < 1-\sigma H+\frac{H}{2} \end{array}\right. }, \end{aligned}$$
(38)

then for all \(x>0\) we have

$$\begin{aligned} x^{\gamma } \sqrt{{\text {E}}[ |f_T(x)- \hat{f_n}(x)|^2 ]} \lesssim {\left\{ \begin{array}{ll} n^{-\frac{\beta }{\frac{\pi }{H}+2\beta }}, &{}\text {if}\quad \gamma \ge 1-\sigma H+\frac{H}{2}\\ n^{-\frac{\beta }{\frac{\pi }{H}+2\beta }} (\log n)^{-k}, &{}\text {if} \quad \gamma < 1-\sigma H+\frac{H}{2} \end{array}\right. } \end{aligned}$$
(39)

for \(n\rightarrow \infty \), where \(k=\frac{\beta }{\frac{\pi }{H}+2\beta } \left( \frac{2(\gamma +\sigma H-1)}{H}-1\right) \).

Proof

In this case he upper bound on variance becomes

$$\begin{aligned} {\text {Var}}[ x^\gamma {{\hat{f}}}_n(x) ]&\lesssim {\left\{ \begin{array}{ll} \frac{1}{n} e^{\frac{\pi g_n}{H}}, &{}\text {if} ~~\gamma \ge 1-\sigma H+\frac{H}{2}\\ \frac{1}{n} g_n^{1-\frac{2(\gamma +\sigma H-1)}{H}}e^{\frac{\pi g_n}{H}}, &{}\text {if} ~~\gamma < 1-\sigma H+\frac{H}{2} \end{array}\right. }, \end{aligned}$$

Rest is again analogue to the proof of Theorem 8. \(\square \)

8 Optimality

The rates from Theorems 8, 12 and 13 are optimal in the minimax sense.

Theorem 14

For all \(\beta \in (0,\pi )\) and \(0<a<b<\pi /\beta \) there is \(x>0\) such that

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty } \psi _n^{-2} \inf \limits _{{{\hat{f}}}_n} \sup \limits _{f\in {\mathcal {C}}(\beta ,a,b)} {\text {E}}[|{{\hat{f}}}_n(x)-f(x)|^2] \ge c \end{aligned}$$
(40)

for some \(c>0\), where infimum is over all estimators based on samples of \(Y_T\) with

  1. (i)

    a Bessel process Y with dimension \(d\in [1,\infty )\) and \(\psi _n=n^{-\frac{\beta }{\pi +2\beta }}\);

  2. (ii)

    a H-ss. Gaussian process Y (\(H\in (0,2)\)) and \(\psi _n=n^{-\frac{\beta }{\frac{\pi }{2H}+2\beta }}\);

  3. (iii)

    a H-ss. Gamma distributed process Y (\(H\in (0,2)\)) and \(\psi _n=n^{-\frac{\beta }{\frac{\pi }{H}+2\beta }}\).

See Sect. 10.2 for the proof of this theorem. A similar optimality result was obtained in Belomestny and Schoenmakers (2015) for the case where the absolute value of a one-dimensional Brownian motion is observed. (40) means that for each estimator \({{\hat{f}}}_n\), that we may construct with our observations, there is a true density \(f\in {\mathcal {C}}(\beta ,a,b)\) such that

$$\begin{aligned} \sqrt{{\text {E}}[|{{\hat{f}}}_n(x)-f(x)|^2]}\gtrsim \psi _n,\quad n\rightarrow \infty \end{aligned}$$

for some \(x>0\), i.e. it is impossible to construct an estimator with a convergence rate (w.r.t. \(L^2\)-distance) faster than \(\psi _n\) for all \(f\in {\mathcal {C}}(\beta ,a,b)\) and all \(x>0\).

9 Simulation study

In this Section we test our estimator (16) with some simulated data. Consider a Bessel process with dimension \(d=5\) and a Gamma(2, 1) distributed stopping time T, i.e. T has the density

$$\begin{aligned} f(x)=xe^{-x}, \quad x\ge 0. \end{aligned}$$

In order to evaluate the estimator (16) we choose \(\gamma =0.7\). Take the cut-off parameter \(g_n=\frac{\log (n)}{(\pi +2\beta )}\) (in accordance with (18)) and \(\beta =0\). To choose \(\beta \) small appears counterintuitive at first because we showed in Theorem 8 that the convergence rate is better for large \(\beta \). However, in our examples the choice \(\beta =0\) delivers the best results. This can be explained as follows: Our bound on the bias of estimator \({{\hat{f}}}_n\) contains the constant L (see (14)) as a factor. This constant is growing in \(\beta \) and seems to make a crucial contribution to the overall error. We refer to Belomestny and Schoenmakers (2015) and Schulmann (2019) for an alternative choice of \(g_n\) based purely on the data.

In order to test the performance of \({{\hat{f}}}_n\) we compute it based on 100 independent samples of \(BES_T\) of size \(n\in \{1000,5000,10{,}000,50{,}000\}\). In Fig. 1 we see the resulting box-plots of the loss.

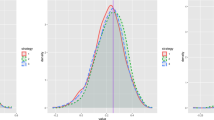
Let us demonstrate the performance of our estimator for different distributions of T. As examples we consider Exponential, Gamma, Inverse-Gaussian and Weibull distributions. To construct the estimate (16) we choose \(d=5\), \(\gamma =0.8\), \(n=1000\) and \(g_n\) as before. Figure 2 shows the densities of the four distributions and their 50 respective estimates based on 50 independent samples of \(BES_T\).

We can see that the error is particularly large in the neighborhood of 0. That is because our estimator is not defined in 0 and \(\lim \limits _{x\rightarrow 0} {\hat{f}}_n(x)\) does not exist for fixed n. Note also that the variance of our estimator is large for small x (see (27)). Conversely, we obtain better results for large x.

Fig. 1
figure 1

Box plot of the loss \(\sup _{x\in [0,10]} \{|\hat{f}_n(x)-f_T(x)| \}\) for different sample sizes

Full size image
Fig. 2
figure 2

Estimated densities (red) and their 50 respective estimates (grey). (Color figure online)

Full size image

10 Proofs

10.1 Proof of Theorem 9

We roughly imitate the proof of an analogous result for the special case \({d=1}\), \((a,b)=(0,1)\) found in Belomestny and Schoenmakers (2015). In distinction from Belomestny and Schoenmakers (2015) we do not restrict ourselves to the case \(x=1\) in the proof and provide the specific form of \(\nu _n\) for all \(x>0\).

Let \(x>0\). It suffices to show the Lyapunov condition, i.e. for a \(\delta >0\):

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } \frac{{\text {E}}[|Z_{n,1}-{\text {E}}[ Z_{n,1}]|^{2+\delta }]}{n^{\delta /2}({\text {Var}}[Z_{n,1}])^{1+\delta /2}} =0. \end{aligned}$$
(41)

The claim (26) follows from (41) with \(\nu _n={\text {Var}}[Z_{n,1}]\). Note that \({\text {E}}[Z_{n,1}]\rightarrow f_T(x)\) for \(n\rightarrow \infty \) by monotone convergence and (9) (if we choose \(Y=BES\) there). So, (41) holds if we can prove, that \({\text {Var}}[Z_{n,1}]\rightarrow \infty \) and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } \frac{{\text {E}}[|Z_{n,1}|^{2+\delta }]}{n^{\delta /2}({\text {Var}}[Z_{n,1}])^{1+\delta /2}} = 0. \end{aligned}$$
(42)

In any case of Lemma 11 (for \(j=\delta +2\)) we have

$$\begin{aligned} {\text {E}}[|Z_{n,1}|^{2+\delta }] \lesssim g_n^{c} e^{\pi (2+\delta )g_n/2}, \quad n\rightarrow \infty \end{aligned}$$
(43)

for all \(\delta \in {\mathbb {R}}_+\) and some \(c>0\). Now we investigate the asymptotic behavior of \({\text {Var}}[Z_{n,1}]\). Looking at (24) we use Fubini’s theorem to obtain

$$\begin{aligned}&{\text {Var}}[Z_{n,1}]\\&\quad = \frac{\varGamma \left( \frac{d}{2}\right) ^2}{\pi ^2} \int _{-g_n}^{g_n}\int _{-g_n}^{g_n} \frac{{\text {Cov}}[X_1^{2\gamma -1+iv},X_1^{2\gamma -1+iu}]dvdu}{(2x)^{2\gamma +i(v-u)} \varGamma \left( \gamma +\frac{d}{2}-1+iv\right) \varGamma \left( \gamma +\frac{d}{2}-1-iu\right) } \\&\quad = \frac{\varGamma \left( \frac{d}{2}\right) ^2}{\pi ^2} \int _{-g_n}^{g_n}\int _{-g_n}^{g_n} \frac{{\text {E}}[X_1^{4\gamma -4+2i(v-u)}]dvdu}{(2x)^{2\gamma +i(v-u)}\varGamma \left( \gamma +\frac{d}{2}-1+iv\right) \varGamma \left( \gamma +\frac{d}{2}-1-iu\right) } \\&\qquad - \frac{\varGamma \left( \frac{d}{2}\right) ^2}{\pi ^2} \int _{-g_n}^{g_n}\int _{-g_n}^{g_n} \frac{ (2x)^{-2\gamma -i(v-u)}{\text {E}}[X_1^{2\gamma -2+ 2iv}]{\text {E}}[X_1^{2\gamma -2 - 2iu}]dvdu }{\varGamma \left( \gamma +\frac{d}{2}-1+iv\right) \varGamma \left( \gamma +\frac{d}{2}-1-iu\right) } \\&\quad = \frac{\varGamma \left( \frac{d}{2}\right) ^2}{\pi ^2} \int _{-g_n}^{g_n}\int _{-g_n}^{g_n} \frac{{\mathcal {M}}[X_1](4\gamma +2i(v-u)-3)dvdu}{(2x)^{2\gamma +i(v-u)}\varGamma \left( \gamma +\frac{d}{2}-1+iv\right) \varGamma \left( \gamma +\frac{d}{2}-1-iu\right) } \\&\qquad -\frac{\varGamma \left( \frac{d}{2}\right) ^2}{\pi ^2} \left| \int _{-g_n}^{g_n} \frac{{\mathcal {M}}[X_1](2\gamma -1+ 2iv) }{(2x)^{\gamma +iv}\varGamma \left( \gamma +\frac{d}{2}-1+iv\right) } dv \right| ^2~=:R_1-R_2. \end{aligned}$$

By Example 2(ii) we can estimate

$$\begin{aligned} R_2&\le \frac{1}{\pi ^2 x^{2\gamma }} \left( \int _{-g_n}^{g_n} \left| {\mathcal {M}}[T](\gamma + iv) \right| dv \right) ^2<C< \infty \end{aligned}$$

for some \(C>0\) and further

$$\begin{aligned} R_1&= \frac{\varGamma \left( \frac{d}{2}\right) }{2\pi ^2 x^{2\gamma }} \int _{-g_n}^{g_n}\int _{-g_n}^{g_n} \frac{{\mathcal {M}}[T](2\gamma -1+i(v-u)) \varGamma \left( 2\gamma -2+\frac{d}{2}+i(v-u)\right) }{x^{i(v-u)}\varGamma \left( \gamma +\frac{d}{2}-1+iv\right) \varGamma \left( \gamma +\frac{d}{2}-1-iu\right) } dvdu. \end{aligned}$$

Our strategy now is to decompose the double integral defining \(R_1\) into pieces that are easy to estimate. To that end let \(\rho _n:=g_n^{\alpha }\), where \(0<\alpha <1/2\) and define

$$\begin{aligned} I^1_{n}:= \int _{-g_n}^{g_n}\int _{-g_n}^{g_n} {\mathbb {1}}_{|v-u|\ge \rho _n} \frac{{\mathcal {M}}[T](2\gamma -1+i(v-u)) \varGamma \left( 2\gamma -2+\frac{d}{2}+i(v-u)\right) }{x^{i(v-u)}\varGamma \left( \gamma +\frac{d-2}{2}+iv\right) \varGamma \left( \gamma +\frac{d-2}{2}-iu\right) } dvdu. \end{aligned}$$

By Lemma 20 there are \(C_1,C_2>0\) such that

$$\begin{aligned} \left| \varGamma \left( \gamma +(d/2)-1+iv\right) \right|&\ge C_1 {\mathbb {1}}_{|v|\le 2 }+ C_2 {\mathbb {1}}_{|v|>2 } |v|^{\gamma -1+\frac{d-1}{2}} e^{-\pi |v|/2}\\ \left| \varGamma \left( \gamma +(d/2)-1-iu\right) \right|&\ge C_1 {\mathbb {1}}_{|u|\le 2 }+ C_2 {\mathbb {1}}_{|u|>2 } |u|^{\gamma -1+\frac{d-1}{2}} e^{-\pi |u|/2} \end{aligned}$$

and \(K_1,K_2>0\) such that

$$\begin{aligned}&\varGamma \left( 2\gamma -2+(d/2)+i(v-u)\right) \le K_1 {\mathbb {1}}_{|v-u|\le 2}\\&\quad + K_2 {\mathbb {1}}_{|v-u|>2 } |v-u|^{2(\gamma -1)+\frac{d-1}{2}} e^{-\pi |v-u|/2}. \end{aligned}$$

With the help of these inequalities we deduce

$$\begin{aligned} |I^1_{n}|&\lesssim g_n^{3|\gamma -1|+d-2} e^{\pi (g_n-\rho _n)/2} +g_n^{4|\gamma -1|+(3d-5)/2} e^{\pi (g_n-\frac{\rho _n}{2})}, \\&\quad n\rightarrow \infty . \end{aligned}$$

Similarly,

$$\begin{aligned}&\int _{-g_n}^{g_n}\int _{-g_n}^{g_n} {\mathbb {1}}_{|u|\le g_n-\rho _n} {\mathbb {1}}_{|v-u|\ge \rho _n} \nonumber \\&\qquad \frac{{\mathcal {M}}[T](2\gamma -1+i(v-u)) \varGamma \left( 2\gamma +\frac{d-4}{2}+i(v-u)\right) }{x^{i(v-u)}\varGamma \left( \gamma +\frac{d-2}{2}+iv\right) \varGamma \left( \gamma +\frac{d-2}{2}-iu\right) } dvdu \nonumber \\&\quad \lesssim g_n^{l} e^{\pi (g_n-\rho _n)} , \quad n\rightarrow \infty \end{aligned}$$
(44)

and

$$\begin{aligned} \int _{-g_n}^{g_n}&\int _{-g_n}^{g_n} {\mathbb {1}}_{|v|\le g_n-\rho _n} {\mathbb {1}}_{|v-u|\ge \rho _n} \frac{{\mathcal {M}}[T](2\gamma -1+i(v-u)) \varGamma \left( 2\gamma +\frac{d-4}{2}+i(v-u)\right) }{x^{i(v-u)}\varGamma \left( \gamma +\frac{d-2}{2}+iv\right) \varGamma \left( \gamma +\frac{d-2}{2}-iu\right) } dvdu\nonumber \\&\lesssim g_n^{l} e^{\pi (g_n-\rho _n)} , \quad n\rightarrow \infty . \end{aligned}$$
(45)

for some \(l\ge 0\). Combine (44) and (45) to obtain

$$\begin{aligned} I^2_{n}&:= \int _{-g_n}^{g_n}\int _{-g_n}^{g_n} {\mathbb {1}}_{|v-u|\le \rho _n} \frac{{\mathcal {M}}[T](2\gamma -1+i(v-u)) \varGamma \left( 2\gamma +\frac{d-4}{2}+i(v-u)\right) }{x^{i(v-u)}\varGamma \left( \gamma +\frac{d-2}{2}+iv\right) \varGamma \left( \gamma +\frac{d-2}{2}-iu\right) } dvdu \\&\lesssim \int _{-g_n}^{g_n}\int _{-g_n}^{g_n} {\mathbb {1}}_{|v|\ge g_n-\rho _n}{\mathbb {1}}_{|u|\ge g_n-\rho _n} {\mathbb {1}}_{|v-u|\le \rho _n}\\&\quad \times \frac{{\mathcal {M}}[T](2\gamma -1+i(v-u)) \varGamma \left( 2\gamma +\frac{d-4}{2}+i(v-u)\right) }{x^{i(v-u)}\varGamma \left( \gamma +\frac{d-2}{2}+iv\right) \varGamma \left( \gamma + \frac{d-2}{2}-iu\right) } dvdu +{\mathcal {O}}( g_n^{l} e^{\pi (g_n-\rho _n)})\\&=:I^3_{n}+{\mathcal {O}}( g_n^{l} e^{\pi (g_n-\rho _n)}). \end{aligned}$$

Next, we examine the asymptotic behavior of the integral \(I^3_{n}\). To this end, we take advantage of Stirling’s formula (Lemma 19)

$$\begin{aligned} \varGamma \left( \gamma +\frac{d-2}{2}+iv\right)&= \left( \gamma +\frac{d-2}{2}+iv\right) ^{\gamma +\frac{d-3}{2}+iv} e^{-\gamma -\frac{d-2}{2}-iv}\sqrt{2\pi }(1+{\mathcal {O}}(v^{-1})) \end{aligned}$$

for \(v\rightarrow \infty \). Consider the integrand of \(I^3_{n}\). In the denominator it holds by means of the identity \({\log (iv)=\log (v)+\frac{i\pi }{2}}\) that

$$\begin{aligned}&\varGamma (\gamma +(d/2)-1+iv)\varGamma (\gamma +(d/2)-1-iu)\\&\quad = 2\pi e^{iv\log v - iu\log u - i(v-u)} e^{-\frac{\pi }{2}(u+v)} (vu)^{\frac{2\gamma +d-3}{2}} (1+{\mathcal {O}}(v^{-1})+{\mathcal {O}}(u^{-1})) \end{aligned}$$

for \(u,v\rightarrow \infty \). On the set

$$\begin{aligned} \left\{ |u|\ge g_n-\rho _n \right\} \cap \left\{ |v|\ge g_n-\rho _n \right\} \cap \{ |v-u|\le \rho _n \} \cap \{ v\ge 0, u\ge 0 \} \end{aligned}$$

we define \(u=g_n -r\), \(v=g_n -s\) with \(0<r,s<\rho _n\), \(|r-s|<\rho _n\) to obtain

$$\begin{aligned}&\varGamma (\gamma +(d/2)-1+iv)\varGamma (\gamma +(d/2)-1-iu)\\&\quad = 2\pi \exp [i(g_n-s)\log (g_n-s)- i(g_n-r)\log (g_n-r) -i(r-s)]\\&\qquad \times g_n^{2\gamma +d-3} e^{-\pi g_n} e^{\pi (r+s)/2} (1+{\mathcal {O}}(g_n^{-1}))(1+{\mathcal {O}}(\rho _n g_n^{-1})\\&\qquad +{\mathcal {O}}(\rho _n^2 g_n^{-1}))^{\gamma +(d-3)/2}. \end{aligned}$$

Note that due to the choice of \(\rho _n\), we have \(\rho _n g_n^{-1}\rightarrow 0\) and \(\rho ^2_n g_n^{-1}\rightarrow 0\). We use the asymptotic decomposition

$$\begin{aligned} (g_n -s)\log (g_n-s)- (g_n -r)\log (g_n-r)-(r-s)=(r-s)\log (g_n)+{\mathcal {O}}(\rho _n^2/g_n) \end{aligned}$$

to obtain

$$\begin{aligned}&\varGamma \left( \gamma +(d/2)-1+iv\right) \varGamma \left( \gamma +(d/2)-1-iu\right) \\&\quad =2\pi g_n^{2\gamma +d-3}\exp (i(r-s)\log (g_n))\\&\qquad \times e^{-\pi g_n} e^{\pi (r+s)/2} (1+ O(\rho _n^2 g_n^{-1})). \end{aligned}$$

Analogously, on the set

$$\begin{aligned} \left\{ |u|\ge g_n-\rho _n \right\} \cap \left\{ |v|\ge g_n-\rho _n \right\} \cap \{ |v-u|\le \rho _n \} \cap \{ v\le 0, u\le 0 \} \end{aligned}$$

we define \(u=-g_n +r\), \(v=-g_n +s\) with \(0<r,s<\rho _n\), \(|r-s|<\rho _n\) to obtain

$$\begin{aligned}&\varGamma \left( \gamma +(d/2)-1+iv\right) \varGamma \left( \gamma +(d/2)-1-iu\right) \\&\quad = 2\pi g_n^{2\gamma +d-3}\exp (-i(r-s)\log (g_n))\\&\qquad \times e^{-\pi g_n} e^{\pi (r+s)/2} (1+ O(\rho _n^2 g_n^{-1})). \end{aligned}$$

Hence, \(I^3_{n}\) can be decomposed as follows:

$$\begin{aligned} I^3_{n}&= \frac{1}{2\pi }\frac{\exp (\pi g_n)}{g_n^{2\gamma +d-3}} \int _{0}^{\rho _n} \int _{0}^{\rho _n} {\mathbb {1}}_{|r-s|\le \rho _n} x^{i(s-r)} e^{-\frac{\pi }{2}(r+s)} \varGamma (2\gamma +\frac{d-4}{2}+i(r-s)) \\&\quad \times {\mathcal {M}}[T](2\gamma -1+i(r-s)) \exp (i(s-r)\log (g_n)) (1+O(\rho _n^2 g_n^{-1}))^{-1}drds \\&= \frac{1}{2\pi }\frac{\exp (\pi g_n)}{g_n^{2\gamma +d-3}} \{{\text {Re}}[I^4_{n}]+O(\rho _n^2 g_n^{-1})] \}, \end{aligned}$$

where

$$\begin{aligned} I^4_{n}&:= \int _{0}^{\rho _n} \int _{0}^{\rho _n} {\mathbb {1}}_{|r-s|\le \rho _n} e^{-\frac{\pi }{2}(r+s)} \varGamma (2\gamma +\frac{d-4}{2}+i(r-s)) \\&\quad \times {\mathcal {M}}[T](2\gamma -1+i(r-s)) \exp (i(s-r)\log (g_n)) x^{i(r-s)} drds \\&= \int _{0}^{\rho _n} e^{-\pi v}R_n(v)dv \end{aligned}$$

with

$$\begin{aligned} R_n(v) := \int _0^{\rho _n-v} e^{-\frac{\pi }{2} u}x^{iu} \varGamma (2\gamma +\frac{d-4}{2}+iu) {\mathcal {M}}[T](2\gamma -1+iu) e^{iu\log (g_n)}du. \end{aligned}$$
(46)

The integral in (46) allows a series representation via Lemma 22. In fact,

$$\begin{aligned} R_n(v)&= i \varGamma \left( 2\gamma +\frac{d-4}{2}\right) {\mathcal {M}}[T](2\gamma -1) \log ^{-1}(g_n) \\&\quad -\frac{d}{du} [e^{-\frac{\pi }{2} u}x^{iu} \varGamma \left( 2\gamma +\frac{d-4}{2}+iu\right) {\mathcal {M}}[T](2\gamma -1+iu)]\bigg |_{u=0}\log ^{-2}(g_n) \\&\quad +{\mathcal {O}}(\log ^{-3}(g_n)) \end{aligned}$$

uniformly in v. Thus,

$$\begin{aligned} {\text {Re}}[I^4_{n}]= \frac{c}{\pi }\log ^{-2}(g_n)+{\mathcal {O}}(\log ^{-3}(g_n)) \end{aligned}$$

holds with

$$\begin{aligned} c&:= {\text {Re}}\left[ \frac{d}{du} e^{-\frac{\pi }{2} u}x^{iu} \varGamma \left( 2\gamma +\frac{d-4}{2}+iu\right) {\mathcal {M}}[T] (2\gamma -1+iu)\bigg |_{u=0}\right] \nonumber \\&= \frac{\pi }{2} \varGamma \left( 2\gamma +\frac{d-4}{2}\right) {\mathcal {M}}[T](2\gamma -1). \end{aligned}$$
(47)

Summing up the auxiliary quantities introduced above we get

$$\begin{aligned} {\text {Var}}[Z_{n,1}]&= \frac{\varGamma \left( \frac{d}{2}\right) }{2\pi ^2 x^{2\gamma }} \left[ g_n^{-2\gamma +d-3} e^{\pi g_n} \left\{ \frac{c}{\pi }\log ^{-2}(g_n)+{\mathcal {O}}(\log ^{-3}(g_n))+{\mathcal {O}}(\rho _n^2 g_n^{-1}) \right\} \right. \\&\quad + \left. {\mathcal {O}}(g_n^{l}e^{\pi (g_n-\rho _n)})\right] +{\mathcal {O}}(1) \end{aligned}$$

and thus (27). If \(g_n\sim \log (n)\), then (27) and (43) imply (42) and hence the claim.

10.2 Proof of Theorem 14

The basic construction used in this proof is due to Belomestny and Schoenmakers (2016), where it is used in the context of an observed Brownian motion. Define the \(\chi ^2\)-divergence

$$\begin{aligned} \chi ^2(P_{1}|P_{0}):=\chi ^2(q_{1}|q_{0}):=\int \frac{(q_{0}(x)-q_{1}(x))^2}{q_{0}(x)}dx \end{aligned}$$
(48)

between two probability measures \(P_0\) and \(P_1\) with densities \(q_0\) and \(q_1\). The following general result forms the basis for the subsequent steps (see Tsybakov 2008 for a proof).

Theorem 15

Let \(\{P_f|f\in \varTheta \}\) be family of probability measures indexed by a non-parametrical class of densities \(\varTheta \). Suppose that \(X_1, \ldots ,X_n\) are iid observations in model n with \({\mathcal {L}}(X_1)\in \{P_f|f\in \varTheta \}\). If there are \(f_{n,0},f_{n,1}\in \varTheta \) such that

$$\begin{aligned} |f_{0,n}(x)-f_{1,n}(x)| \gtrsim \psi _n, \quad n\rightarrow \infty \end{aligned}$$
(49)

and if

$$\begin{aligned} (1+\chi ^2(P_{f_{1,n}}|P_{f_{0,n}}))^n \le \alpha \end{aligned}$$
(50)

holds for some \(\alpha >0\) independent of n, then

$$\begin{aligned} \liminf \limits _{n\rightarrow \infty } \psi _n^{-2} \inf \limits _{{{\hat{f}}}_n} \sup \limits _{f\in \varTheta } {\text {E}}[|{{\hat{f}}}_n(x)-f(x)|^2] \ge c \end{aligned}$$
(51)

holds for some \(c>0\), where the infimum is over all estimators.

Let \(\beta \in (0,\pi )\) and \(0<a<b<\pi /\beta \). Define for \(M>0\)

$$\begin{aligned} q(x):=\frac{ \sin (\beta )}{\beta } \frac{1}{1+x^{\pi /\beta }} \quad \text {and} \quad \rho _M(x):=\frac{1}{\sqrt{2\pi }} e^{-\log ^2(x)/2}\frac{\sin (M\log (x))}{x}, \quad x\ge 0. \end{aligned}$$

The following lemma provides some properties of the functions q and \(\rho _M\).

Lemma 16

The function q is a probability density on \({\mathbb {R}}_+\) with Mellin transform

$$\begin{aligned} {\mathcal {M}}[q](z)=\frac{\sin (\beta )}{\sin (\beta z)},\quad 0<{\text {Re}}(z)<\pi /\beta . \end{aligned}$$
(52)

The Mellin transform of the function \(\rho _M\) is given by

$$\begin{aligned} {\mathcal {M}}[\rho _M](z)=\frac{e^{(z-1+iM)^2/2} - e^{(z-1-iM)^2/2}}{2i}, \quad z\in {\mathbb {C}}. \end{aligned}$$
(53)

Proof

Formula (52) can be found in Oberhettinger (2012) and (53) is shown in (Belomestny and Schoenmakers 2016, Lemma 6.2). \(\square \)

Set now for any \(M >0\) and some \(\delta >0\),

$$\begin{aligned} f_{0,M}(x):=q(x)\quad \text {and} \quad f_{1,M}(x):=q(x)+ \delta (q\odot \rho _M)(x) \end{aligned}$$
(54)

for \(x\ge 0\), where \(q\odot \rho _M\) is defined by (4). The following lemma will help us verify condition (49).

Lemma 17

For any \(M>0\) and some \(\delta >0\) not depending on M the function \(f_{1,M}\) is a probability density satisfying

$$\begin{aligned} \sup \limits _{x\ge 0} |f_{0,M}(x)-f_{1,M}(x)|\gtrsim \exp (-M\beta ),\quad M\rightarrow \infty . \end{aligned}$$
(55)

Moreover, \(f_{0,M}\) and \(f_{1,M}\) are in \({\mathcal {C}}(\beta ,a,b)\) for all \(\beta \in (0,\pi )\) and \(0<a<b<\pi /\beta \).

Proof

For (55) see (Belomestny and Schoenmakers 2016, Lemma 6.3) where it is also shown that for \(\delta \) small enough:

$$\begin{aligned} \delta |(q\odot \rho _M)(x)| \le \delta \int _0^\infty \left| \frac{q(t)\rho _M(x/t)}{t} \right| dt \le f_{0,M}(x), \quad x\ge 0. \end{aligned}$$
(56)

It is easy to see that \(f_{0,M}\in {\mathcal {C}}(\beta ,a,b)\) for all \(\beta \in (0,\pi ),~0<a<b<\pi /\beta \) and (56) implies the same for \(f_{1,M}\). \(\square \)

Looking further towards applying Theorem 15 let us consider the densities \(p_{M,0}\) and \(p_{M,1}\) of an observation associated with the hypotheses \(f_{0,M}\) and \(f_{1,M}\), respectively. At this point we have to differentiate between the models we discussed so far. We will only present the proof for the Bessel case, parts (ii) and (iii) of Theorem 14 can be showed along the same lines.

Let \(T_{0,M}\) and \(T_{1,M}\) be two random variables with respective densities \(f_{0,M}\) and \(f_{1,M}\). The density of the random variable \(BES_{T_{i,M}}\), \(i=0,1\) is obtained via (4):

$$\begin{aligned} p_{i,M}(x)=\frac{2^{1-\frac{d}{2}}}{\varGamma \left( {d}/{2}\right) } x^{d-1} \int _0^\infty \lambda ^{-d/2} e^{-\frac{x^2}{2\lambda }} f_{i,M}(\lambda ) d\lambda ,\quad x>0,d\ge 1,i=0,1. \end{aligned}$$

For the Mellin transform of \(p_{i,M}\) we use self-similarity of BES and (3) to get

$$\begin{aligned} {\mathcal {M}}[p_{i,M}](s)&={\mathcal {M}}[BES_1](s){\mathcal {M}}[T_{i,M}]((s+1)/2) \nonumber \\&= \frac{1}{\varGamma \left( {d}/{2}\right) }\varGamma \left( \frac{s+d-1}{2}\right) 2^{\frac{s+1}{2}}{\mathcal {M}}[f_{i,M}]((s+1)/2), \quad i=0,1 \end{aligned}$$
(57)

for \({\text {Re}}(s)>1-d\) and \({\text {Re}}(s)\in (-1,\frac{2\pi }{\beta }+1)\).

Lemma 18

For all \(d\ge 1\) and \(\beta \in (0,\pi )\) we have

$$\begin{aligned} \chi ^2(p_{1,M}|p_{0,M})\lesssim M^{(\pi /\beta )+d-2} e^{-M(\pi +2\beta )},\quad M\rightarrow \infty \end{aligned}$$

Proof

Define \(c_{\beta ,d}:=\frac{2^{1-\frac{d}{2}}}{\varGamma \left( {d}/{2}\right) }\frac{ \sin (\beta )}{\beta }\). By the change of variables \(y=\frac{1}{\lambda }\),

$$\begin{aligned} p_{0,M}(x)&= c_{\beta ,d} x^{d-1} \int _0^\infty \lambda ^{-d/2} e^{-\frac{x^2}{2\lambda }} \frac{1}{1+\lambda ^{\pi /\beta }} d\lambda \nonumber \\&= c_{\beta ,d} x^{d-1}\int _0^\infty e^{-y\frac{x^2}{2}} y^{\frac{\pi }{\beta }+\frac{d}{2}-2} \left( 1-\frac{y^{\pi /\beta }}{y^{\pi /\beta }+1}\right) dy\nonumber \\&= c_{\beta ,d} x^{d-1}\left( \int _0^\infty e^{-y\frac{x^2}{2}} y^{\frac{\pi }{\beta }+\frac{d}{2}-2} dy -R\right) \nonumber \\&= c_{\beta ,d} \left( \varGamma \left( \frac{\pi }{\beta }+\frac{d}{2}-1\right) 2^{\frac{\pi }{\beta }+\frac{d}{2}-1} x^{-\frac{2\pi }{\beta }+1} -x^{d-1} R\right) \nonumber \\&\gtrsim x^{-\frac{2\pi }{\beta }+1}, \quad x\rightarrow \infty \end{aligned}$$
(58)

with

$$\begin{aligned} R:= \int _0^\infty e^{-y\frac{x^2}{2}} \frac{y^{2\pi /\beta +d/2-2}}{y^{\pi /\beta }+1} dy&\le \int _0^\infty e^{-y\frac{x^2}{2}} y^{\frac{\pi }{\beta }+\frac{d}{2}-\frac{3}{2}} dy\lesssim x^{-\frac{2\pi }{\beta }-d+1},\quad x\rightarrow \infty . \end{aligned}$$

For the next step let \(a\in \{0,(2\pi /\beta )-1\}\). We apply Theorem 5 and the rule \({\mathcal {M}}[(\cdot )^a f(\cdot )](z)={\mathcal {M}}[f(\cdot )](z+a)\) and obtain

$$\begin{aligned}&\int _0^\infty x^{a} (p_{0,M}(x)-p_{1,M}(x))^2 dx \nonumber \\&\quad = \frac{\delta ^2 2^\frac{3+a}{2}}{\pi i\varGamma \left( {d}/{2}\right) ^2} \int _{\gamma -i\infty }^{\gamma +i\infty } \varGamma \left( \frac{z+d-1}{2}\right) {\mathcal {M}}[q\odot \rho _M]\left( \frac{z+1}{2}\right) \\&\qquad \times \varGamma \left( \frac{a+d-z}{2}\right) {\mathcal {M}}[q\odot \rho _M]\left( \frac{2+a-z}{2}\right) dz \nonumber \end{aligned}$$
(59)

for suitable \(\gamma \), where \({\mathcal {M}}[q\odot \rho _M]={\mathcal {M}}[q] {\mathcal {M}}[\rho _M]\). Due to (53), we can estimate

$$\begin{aligned} |{\mathcal {M}}[\rho _M](u+iv)| \le e^{\frac{(u-1)^2}{2}}\frac{\varphi (v+M) +\varphi (v-M)}{2} \end{aligned}$$
(60)

with \(\varphi (v)=e^{-\frac{v^2}{2}}\). Next, we use Lemma 20 in (59) to estimate the gamma terms, then plug in (60) and \(|{\mathcal {M}}[q](u+iv)| \le ce^{-\beta |v|}\) for some \(c>0\) to obtain

$$\begin{aligned} \int _0^\infty x^{a} (p_{1,M}(x)-p_{0,M}(x))^2 dx \lesssim M^\frac{2d+a-3}{2} e^{-M\pi (1+2\beta /\pi )} , \quad M\rightarrow \infty \end{aligned}$$
(61)

for \(a\in \{0,(2\pi /\beta )-1\}\). By (58) and (61),

$$\begin{aligned} \chi ^2(p_{1,M}|p_{0,M})&= \int _0^\infty \frac{(p_{M,1}(x)-p_{M,0}(x))^2}{p_{M,0}(x)}dx \\&\lesssim \int _{0}^{\infty } (p_{M,1}(x)-p_{M,0}(x))^2 dx\\&\quad + \int _{0}^\infty x^{-\frac{2\pi }{\beta }+1} (p_{M,1}(x)-p_{M,0}(x))^2 dx\\&\lesssim M^{(2d-3)/2} e^{-M(\pi +2\beta )} +M^{(\pi /\beta )+d-2} e^{-M(\pi +2\beta )}, \quad M\rightarrow \infty , \end{aligned}$$

where \(M^{(\pi /\beta )+d-2} e^{-M(\pi +2\beta )}\) is the dominating term. This proves the lemma. \(\square \)

Lemma 18 implies (50). With the choice

$$\begin{aligned} M= \frac{\log (n)}{\pi +2\beta } \end{aligned}$$

Lemma 17 implies (49). Claim of Theorem 14(i) follows with Theorem 15.