In the United States, women have long surpassed men in tertiary education attendance and completion (DiPrete & Buchmann, 2013; De Brey et al., 2021). Nonetheless, women are still less likely than men to major in the STEM fields; i.e., in the fields of science, technology, engineering, and math (Charles & Bradley, 2009; National Science Foundation & National Center for Science and Engineering Statistics, 2015). Using data from the Educational Longitudinal Survey (ELS), Weeden et al. (2020) recently showed that among ELS students who graduated from high school in 2004 and entered college the following year, men were more than twice as likely as women to complete bachelor’s degrees in STEM, including in premed fields (18% and 8%, respectively), and were more likely to continue in these fields after entering these majors by their sophomore year (58.2% and 42.5%, respectively; Weeden et al., 2020). Consequently, despite making up nearly half of the U.S. workforce, women hold less than 25% of STEM-type jobs (Beede et al., 2011), which tend to be higher paying than the helping and service occupations in which female college graduates are overrepresented (Beede et al., 2011; Charles & Grusky, 2004).

In seeking to explain the under-representation of female students in STEM careers, the literature has cited several factors, including sex-role expectations, self-assessed math ability, occupational plans, parental and peer influence, and the climate within STEM majors and organizations (Casad et al., 2019; Ceci et al., 2009; Muenks et al., 2020; O’Brien et al., 2016; Weeden et al., 2020). The family has been identified as an important socializing environment that affects whether girls and young women develop an interest in STEM (Sáinz & Müller, 2018; Torche, 2011). Factors such as the presence of the father in the household, parental education, occupation, and household income have been shown to contribute to gender differences in educational and career choices (Dabney et al., 2013; Jacobs & Bleeker, 2004; Leppel et al., 2001; Plasman et al., 2021; Sigle-Rushton & McLanahan, 2004). However, while the influence of parents on their children’s decisions to seek out training and careers in STEM has been extensively examined, much less is known about the role of siblings and sibling group composition in these decisions (but see Barclay et al., 2017 for an exception). Our study helps to close this research gap by focusing on the compositional characteristics of siblings as contextual factors that encourage female students to take (or that discourage them from taking) the STEM path in college.

Theoretical Frameworks

Previous research has provided extensive evidence that the size, birth order, birth spacing, and gender composition of sibling groups are potential sources of (dis)advantage that influence people’s educational outcomes, including their years of completed schooling and grade point average (see Steelman et al., 2002 for a review). However, there is relatively little previous research on the question of whether and, if so, how sibling group features and dynamics may influence gender differences in college major preferences and outcomes. The literature on the configuration and educational attainment of siblings has mostly framed this link using the parental resource dilution hypothesis (Blake, 1981; Coleman, 1988; Conley, 2004). However, parents are not the only resourceful and influential family members, as developmental psychology has shown that siblings also influence on each other while growing up, particularly via social and attitudinal learning (McHale et al., 2001; Whiteman et al., 2009). In addition to the parental resource dilution model, we draw from social learning aspects embedded in role modeling perspectives (Brim, 1958; Dunn, 1983) and the same-sex competitive stimulation approach (Conley, 2000) to derive hypotheses on how sibling group compositional characteristics may be linked to young adults’ decisions to pursue a STEM major in college.

The differential filtration of females into STEM careers appears to be an outcome of gender role socialization during childhood, which is partially mediated by the family. From early age, parents expose their children to and provide them with insights and lessons about gender roles and encourage their sons and daughters to perform and engage in specific behaviors and activities (Bussey & Bandura, 1999; Fouad et al., 2010). These social experiences differ for boys and girls, as parents are more likely to support, expect, and encourage their sons rather than their daughters to be interested in and to pursue STEM activities (e.g., Crouter et al., 2007; Fouad et al., 2010; Gabay-Egozi et al., 2015; McHale et al., 2003; Muenks et al., 2020). Exploring early gender differences, recent studies provide evidence that boys outperform girls in spatial tasks at rather early ages (Levine et al., 1999 for preschool years; and Levine et al., 2005 for second and third graders). Focusing on mathematical achievement, Penner and Paret (2008) reported on an advantage of boys at the top of the distribution early on at kindergarten (ages 5–6), whereas by the third grade this male dominance spreads to the rest of the distribution.

Along with parents, siblings are another influential source of socialization. Even though siblings share genes and often grow up in a similar environment by living in the same home, the outcomes of siblings can vary greatly (Björklund & Jäntti, 2012), possibly because each individual experiences the social environment within the family differently depending on the siblings’ compositional characteristics. Theoretically, a younger sibling is born into a family after the rules and roles have already been established with the first-born child and is likely to be influenced by the behaviors that were already adopted by their older siblings (Zajonc & Markus, 1975). Thus, sibling socialization is at least in part a top-down process in which older siblings serve as role models for younger siblings to look up to and imitate, whereas a bottom-up process is less likely to occur (Whiteman et al., 2014). In this article, we focus on the relationship between each of our respondents (henceforth the focal child) and the sibling born immediately before them (henceforth the older sibling) in terms of gender composition, spacing, and math ability, while also modeling the presence of other siblings through, for instance, the sibling group size and the respondent’s birth order. To anticipate our analytic strategy, we also tested our models using parallel measurements referring to the relationship between the respondent and the first-born sibling – i.e., the eldest sibling in a sibling group – instead of the sibling born immediately before the respondent. We show and discuss the results for both measurement approaches, which provide the same findings and conclusions. We present a three-fold theoretical framework of the potential pathways through which these sibling group compositional characteristics may be linked to the decision of a young woman or man to pursue a STEM major in college.

Resource Dilution Hypothesis: Sibling Group Size

According to the resource dilution hypothesis, siblings from smaller families and older siblings tend to have an advantage over siblings from larger families and their younger counterparts in terms of their access to parental financial resources (De Haan, 2010); time investments (Price, 2008); and energy, monitoring, and supervision efforts (Hotz & Pantano, 2015). These differences in access to resources between siblings appear to result in lower educational attainment for children from larger families and for later-born siblings (Björklund & Jäntti, 2012; Black et al., 2005; Downey, 1995; Price, 2008). In addition, wider spacing between siblings allows for greater parental investments in older children, and thus contributes to their academic outcomes (Buckles & Munnich, 2012; Powell & Steelman, 1990, 1995; Price, 2010). However, recent studies have found that spacing has no significant effects on educational attainment (Barclay & Kolk, 2017; Grätz, 2018). Finally, using Swedish register data, Barclay et al. (2017) found that first-born children are more likely than their later-born siblings to have college majors with higher expected earnings and occupational prestige, such as engineering, medicine, and life sciences (Barclay et al., 2017). Since tertiary education is free in Sweden, these results should not be primarily driven by the exhaustion of family financial resources, which is more likely to occur in countries where tuition fees are high, such as in the US. These findings underscore that when testing whether sibs-group size is linked to majoring in STEM via resource dilution, it is important to control for family socioeconomic characteristics, ideally measured during the respondent’s childhood. Following the resource dilution argument, we first expect to find that net of the respondents’ demographic and family background characteristics, math ability, birth order, and birth spacing,

Hypothesis 1: Individuals from larger sibling groups are less likely to choose a STEM major in college than individuals from smaller families [H1].

Competition Hypothesis: Same-Gender Stimulation

In addition to its size, order, and spacing, a sibling group is characterized by its gender composition. Studies have shown that gender composition matters within educational environments. There is, for instance, evidence that male-dominated student groups, which are common in STEM fields, may create a threatening intellectual environment for females (Casad et al., 2019), and elicit performance-impinging stereotypes (Inzlicht & Ben-Zeev, 2000). Thus, the gender composition of an environment can play a critical role in people’s appraisal of it as safe or threatening (Inzlicht & Ben-Zeev, 2000). Unlike for women in female-dominated fields, for women in male-dominated fields, the relationships between experiencing threats, activating gender stereotypes, and academic disengagement are often strong (Casad et al., 2019; Inzlicht & Ben-Zeev, 2000). Therefore, the gender composition of a sibling group is likely to play an important role in the gendered educational outcomes of sisters and brothers. However, whether this is the case has not previously been examined in the context of college major choice. Moreover, studies that have investigated gender differences in educational attainment have generally assumed that the effects of the sibling group compositional characteristics are the same for sisters and brothers (see Breen & Gabay-Egozi, 2013). In the few studies we know of that have explicitly tested how sibling group gender composition relates to educational attainment, none accounted for the possibility that group-level gender composition is experienced differently by girls and boys or offered theoretical explanations for their results (Butcher & Case, 1994; Kaestner, 1997; Kuo & Hauser, 1997; Powell & Steelman, 1989, 1990).

One exception is Conley’s (2000) finding that children raised with siblings of the opposite gender have a lower level of educational attainment than their same-gender peers with same-gender siblings. Conley (2000) suggested that it is relatively advantageous to have same-gender siblings, as their presence creates a competitive environment that pushes children to perform better. This propensity for siblings of the same gender to compete with one another in similar tasks leads individuals in these families to have better outcomes than individuals who have opposite-gender siblings. Focusing on advanced math and science courses in high school, Joensen and Nielsen (2018) showed that having older siblings causally affects the educational choices of the younger siblings, with the strongest spillover effects occurring among closely spaced male siblings.

Following Conley’s (2000) interpretation we expect to find that net of the respondents’ demographic and family background characteristics, math ability, sibling group size, birth order, and birth spacing,

Hypothesis 2a: For girls, having an older sister (and more sisters), rather than an older brother (and more brothers), is positively associated with the likelihood of pursuing a STEM major in college [H2a].

Hypothesis 2b: For boys, having an older brother (and more brothers), rather than an older sister (and more sisters), is positively associated with the likelihood of pursuing a STEM major in college [H2b].

Role Modeling Perspective: Older Siblings’ Math Ability

In addition, older siblings might directly affect their younger siblings’ educational development by serving as social partners and role models during everyday interactions (McHale et al., 2001; Whiteman et al., 2009). As older siblings usually possess the characteristics of effective socialization agents, such as status, nurturance, and similarity, they are particularly influential models for their younger siblings (Bandura, 1977). This strong social attachment can produce a downstream positive role modeling process (Brim, 1958) in which younger siblings imitate their older siblings’ constructive social behaviors (Dunn, 1983), and learn and develop social-cognitive skills (Dunn, 2007; Howe et al., 2002). This asymmetric relationship between older and younger siblings is also affected by the organization of schooling by age (Oettinger, 2000). Older siblings contribute to their younger siblings’ academic engagement (Bouchey et al., 2010), offer social support and information transmission, and provide them with a clear perception of what the educational journey looks like (Davies, 2019). Given that social learning can occur via sibling modeling, we expect to observe that younger siblings learn from and imitate their older siblings.

In this article, we use the math ability of the older siblings as a proxy for role modeling. Research has shown that math achievement is positively linked to pursuing a STEM career (Wang & Degol, 2017; Wang et al., 2015), although some scholars have pointed out that the relationship between having cognitive mathematical abilities and majoring in STEM is complex, and is likely contingent on an individual’s other cognitive abilities and field-specific ability beliefs, or may even be insignificant when the person’s occupational plans are taken into account (Daker et al., 2021; Wang & Degol, 2017; Weeden et al., 2020). Nonetheless, high achievement in math is generally considered a predictor of pursuing a STEM career (Wang & Degol, 2017). Moreover, it has been shown that math anxiety prevents students from taking STEM courses, net of their math ability (Daker et al., 2021). There is also evidence that later-born siblings acquire sports skills from their older siblings, and that young children learn block building skills more effectively from their older siblings than from their peers (Azmitia & Hesser, 1993; Hopwood et al., 2015). We therefore expect to find that older siblings with high ability in math will encourage their younger siblings to cultivate similar skills both through role modeling and active teaching, and through preventing their younger siblings from developing math-related anxieties by actively modeling that high math performance is achievable. Thus, through their observations of and interactions with their older siblings, the math achievements of their older siblings may shape the younger siblings’ orientation, interest, motivation, and anxiety in relation to pursuing a STEM career (Legewie & DiPrete, 2014). Therefore, we hypothesize that net of the respondents’ demographic and family background characteristics, math ability, sibling group size, birth order, birth spacing, and siblings’ gender composition,

Hypothesis 3: Younger siblings with an older sibling with strong math skills are more likely to choose a STEM major in college [H3].

Role Modeling via Same-Gender Competitive Stimulation

The same-gender stimulation hypothesis and the role modeling approach, which we presented above, likely operate simultaneously. Social psychology research has suggested that the impact of older sibling role modeling is enhanced when same-gender siblings perform “gender-typed” behaviors (Brim, 1958; Koch, 1960; McHale et al., 2003, 2012). In addition, math and sciences have been represented historically and culturally as competitive masculine disciplines that mostly appeal to boys. By contrast, girls have been socialized to avoid mixed-gender competition, and tend do worse in high-stakes, mixed-gender domains (Niederle & Vesterlund, 2007). Thus, the positive effect of role modeling on the probability of pursuing a STEM field may operate primarily among same-gender siblings. Hence, we hypothesize that the positive association between the math ability of the older sibling and the younger sibling’s likelihood of choosing a STEM major in college is moderated by the gender of the older sibling. Specifically, we expect that net of the respondents’ demographic and family background characteristics, math ability, sibling group size, birth order, birth spacing, and siblings’ gender-composition,

Hypothesis 4a: For girls, having an older sister who is a high achiever in math , rather than an older brother who is good at math, might stimulate a girl’s interest in and motivation to pursue a STEM major in college [H4a].

Hypothesis 4b: For boys, having an older brother who is a high achiever in math, rather than an older sister who is good at math, is positively associated with the likelihood of pursuing a STEM major in college [H4b].

Method

Participants

At the core of our study is the question of how and, if so, to what extent the compositional characteristics of sibling groups are associated with gender differences in the likelihood of choosing a STEM major later in life. Since we are interested in the spillover effects of the sibling group features, we focused our attention on the college major preferences of respondents who were non-first-born siblings. First-born children spend at least some portion of the beginning of their life without other siblings, and some never have other siblings; whereas non-first-born children have older siblings as role models to look up to and imitate from birth (Whiteman et al., 2014; Zajonc & Markus, 1975). To investigate our research question, we used data from the Child and Young Adult (CY-NLSY79) module of the National Longitudinal Survey of Youth 1979 cohort (NLSY79). The NLSY79 is a nationally representative sample of the U.S. population consisting of 12,686 individuals (6,403 male and 6,283 female respondents) who were between the ages of 14–22 on December 31, 1978 (age mean = 17.9), and out of three ethnic subsamples; Hispanic or Latino (2,002), Black (3,174), and non-Black/non-Hispanic (7,510). The NLSY79 respondents were re-interviewed annually until 1994, and biennially thereafter. In follow-up waves starting in 1986, the NLSY79 female sample members with children were asked to complete a module for their own children. Due to this multigenerational design, which was not applied to the younger cohorts of the NLSY, comprehensive information was collected about all of the siblings in the family throughout the childhood of each respondent. The children of the NLSY79 mothers have been interviewed and assessed biennially to follow their cognitive, physical, and socio-emotional development, as well as about each child’s later life outcomes, including their academic history (Center for Human Resource Research, 2001). In addition, the NLSY collected rich information on parental characteristics, which were measured reliably during the childhood of each of the target individuals in our sample. In 1986 of the 5,842 NLSY79 female respondents who were eligible to take part in a first child interview, more than 2,900 mothers and 4,971 children were interviewed. From this sample of eligible children, assessment data were collected for 4,786 individuals (CY-NLSY79 child module). Starting in 1994, children who had reached the age of 15 by the end of the survey year were no longer assessed, but were instead asked to participate in personal interviews similar to those their mothers took part in during late adolescence and into adulthood (CY-NLSY79 young adult module). The Children of the NLSY79 survey is sponsored and directed by the U.S. Bureau of Labor Statistics and the National Institute for Child Health and Human Development. The survey is managed by the Center for Human Resource Research (CHRR) at The Ohio State University and interviews are conducted by the National Opinion Research Center (NORC) at the University of Chicago (Bureau of Labor Statistics, U.S. Department of Labor, and National Institute for Child Health and Human Development, 2019).

This data collection approach is a unique strength of the data set, as it enabled us to control for the family’s socioeconomic characteristics as they occurred during the respondent’s childhood, instead of having to rely on retrospective information. The participants in these CY-NLSY79 modules (1986–2012) served as the basis target sample for our analysis. As of 2012, a total of 11,512 children have been identified as having been born to the original 6,283 NLSY79 female respondents. The CY-NLSY79 module, which is administered annually to the children of all of the original female NLSY79 respondents, is representative of approximately 70%-75% of all children who are born to a typical cohort of American women (Center for Human Resource Research, 2009).

We followed a sample selection strategy to target our data based on sibling group size, birth order, and birth cohort. Because we focused our attention on non-first-born siblings, only-child families (n = 1,176) were dropped, and first-born siblings were also excluded (n = 3,754). Of the remaining respondents, we excluded respondents who were too young to have graduated from college, which reduced our analytic sample to 4,498 children born prior to 1991 who were not the first-born child in their family. Next, the sample was further restricted to the 3,130 respondents who attended college. All further sample reductions were due to listwise deletion. In this stage, most sample attrition was attributable to missing values for college attendance information, and for mathematic ability during early adolescence for the older sibling and the respondent. To review the full progression of the elimination of the respondents, see Appendix A in the supplementary section. The listwise deletion yielded an analytic sample of 1,545 non-first-born children – 888 females and 657 males –from 1,202 households.

Analytic Strategy

To model the respondents’ preference for a STEM rather than a non-STEM college major, we chose to use the linear probability model (LPM) rather than nonlinear models, because the LPM allowed us to make direct comparisons of coefficients across models and groups (Mood, 2010). To test our hypotheses, we estimated six nested models. Model I analyzed the gross effect of the respondent’s gender on their college major choice. In Model II, we added the respondent’s birth cohort and race, and the characteristics of their parental household, including whether it was a two-parent household, the mother’s education and occupation, and the total net family income. To test our first hypothesis – i.e., the resource dilution hypothesis – in Model III, we added the sibling characteristics related to resource dilution accounting for the sibling group size, net of birth order, birth spacing and the respondent’s math ability (Model III, testing H1). Next, to test the same gender competitive stimulation premise cited in Hypotheses 2a and 2b, we included in Model IV the older sibling’s gender and the proportion of boys in the sibling group (Model IV, testing H2a and H2b). In Model V, we accounted for the older sibling’s math ability to test our third hypothesis related to the role-modeling perspective (Model V, testing H3). In our final model, Model VI, we explored the possibility that the role modeling effect was more likely to occur among same-gender than opposite-gender siblings by adding an interaction term for the older sibling’s math ability and gender (Model V, testing H4a and H4b). In addition, all of the siblings’ covariates in Models III-V were interacted with the gender of the respondent. To facilitate the comparison of the effects of the continuous independent variables within the models, we standardized them to a mean of zero and a unit standard deviation. The dummy variables retained their original metric.

Finally, all of the models were estimated using the appropriate sample weights, as provided by the NLSY79, with standard errors clustered on household ID to account for dependence between co-residential siblings. To correct the initial NLSY79 minority oversamples we used the weight parameter provided by the NLSY79 to adjust these unweighted cases. Also, most of the initial NLSY79 women have had more than one child, including a rather large sample of women who have had three or more children, as they approach the end of their childbearing years. When analyzing our linear probability models, thus, we corrected for dependence between co-residential siblings using clustering on household ID.

Measures

Preference for STEM Fields in College

Following other studies, we classified science, technology, engineering, mathematics, and doctoral-track medicine programs as STEM majors, while courses of study that focused on the humanities, social sciences, and clinical or health sciences (non-doctoral-track) were considered non-STEM majors (Weeden et al., 2020). To be considered a STEM major, the respondent’s first declared field of study for their bachelor’s degree must have been in one of the identified STEM fields. All other non-STEM fields or an undeclared major were considered non-STEM. Of the respondents in our sample, 895 declared a non-STEM major and 307 did not declare a major. The two groups were collapsed into the non-STEM preference category. Utilizing the first declared major enabled us to eliminate college-related contextual factors that may be associated with persistence within a major. Although about 28% of bachelor’s degree students and 20% of associate’s degree students enter a STEM field (Chen, 2013), more than half of those who declare a STEM major upon entering college leave these fields before graduation (Chen, 2009; Higher Education Research Institute, 2010). Type of tertiary institution, college STEM course-taking, and relative performance in STEM in college have been found to increase the likelihood that students will change their major to a non-STEM field (Chen, 2013). To avoid these possible effects of STEM degree completion, we have chosen to use each respondent’s first declared major. Among our 1,545 sample members who attended college, 343 of them (22%) declared a major in a STEM field.

Sibling Group Size, Order, Spacing, Gender Composition, and the Older Sibling’s Math Ability

To account for the sibling group compositional characteristics, we used five key independent variables: sibling group size, the proportion of boys in a sibling group, the respondent’s birth order, and the older sibling’s gender and math ability. With the older sibling’s characteristics, we captured the relationship between the respondent and the sibling born immediately before them (henceforth the older sibling) in terms of sex, spacing, and the math ability of the older sibling. In a robustness check, we tested our models using alternative parallel measurements that refer to the relationship between the respondent and the first-born sibling; i.e., the eldest sibling in a sibling group, instead of the sibling born immediately before the respondent. Our findings did not change when this alternative definition was used (models are presented in supplementary Appendix B).

We considered three measurements for sibling group compositional characteristics related to resource dilution: the sibling group size, which measured the number of children; the birth order, measured as a dummy variable indicating the second-born (coded 1) compared to the third-born and higher-order births (coded 0); and birth spacing, which measured the age distance (in months) between the respondent and the sibling born immediately before them. Testing the birth order as a continuous variable and using birth spacing as a dummy variable yielded similar results (models not shown, but available upon request). To test the same-gender competition stimulation hypothesis, we constructed two measurements of the sibling group gender composition: the gender of the older sibling born just before the respondent (male coded as 1) and the proportion of boys in the sibling group.

The older sibling’s math ability, our measurement of role modeling, was based on scores from the math subtest of the Peabody Individual Achievement Test (PIAT). The PIAT is a widely used and highly reliable measure of academic achievement for children aged 5–15 (Center for Human Resource Research, 2009) that is composed of multiple-choice questions that increase in difficulty, ranging from identifying numbers to performing trigonometry. The PIAT was administered in each survey wave for children aged 5–15, and our measure relied on the siblings’ most recent available standardized test scores when they were aged 10–14. As controlling for the math ability of the siblings other than the older sibling born immediately before the respondent substantially diminished our sample size, we decided to exclude these indicators from our analysis. We also tested the effect of the older sibling’s STEM major (not shown), which yielded no significant results net of the older sibling’s math ability, the sibling group, and individual and family characteristics.

Control Variables: Individual and Parental Household Characteristics

As we noted in the theoretical section, previous research has shown that children’s parental family background and household characteristics are associated with their gendered interest in and motivation to pursue a STEM career. Information about the parents measured when the respondent was aged 6–10 was used to construct controls for the mother’s education, the number of parents in the household, and the total net family income (logged and adjusted to constant dollars), which provides a composite income figure from a number of income values for the household members related to the mother by marriage or blood. We also constructed a measure of the mother’s occupation that captures her employment status and occupational gender orientation when the focal child was aged 6–14 using the mother’s self-reported work history data. We classified the mother’s work status information into five categories: male-type occupation, female-type occupation, unemployed, out of the labor force, and missing. The classification of occupations as male type or female type was based on Weeden's (2004) classification scheme, which relies on saturated scale values of female and male participation in U.S. occupations in 1970 and 1990 (Weeden, 2004, Appendix Table A5.1. pp 162-176). Weekly employment information was obtained from each NLSY79 mother, yielding up to 416 observations per mother. The modal value across all 416 records was used to determine the mother’s overall employment status and occupation when she was in the labor force. Controlling for the mother’s occupation enabled us to differentiate between the parental influences and the effects of the compositional characteristics of the sibling groups on our outcome of interest.

Finally, we created measures for the respondent’s birth cohort, race/ethnicity, and math ability, as high math achievement is generally considered a predictor of pursuing a STEM career. The measure for the respondent’s math ability was similar to the measure for the older sibling’s math ability described above.

Results

Descriptive Analysis

Table 1 contains descriptive statistics for our dependent and independent variables, separately by respondent's gender. As expected, young men were found to be more likely than young women to prefer a STEM field as their major in college (30% and 17%, respectively). Male respondents also displayed higher average math ability in young adolescence than female respondents (13.35 and 12.55, respectively). The distribution of the sibling group compositional characteristics largely followed the same patterns for female and male respondents. About 35%-41% respondents were raised in a 3-child family, about 30% came from a 2-child family, 19% came from a 4-child family, and the remaining 12%-16% were raised in a family with five or more children. Most of the respondents (66%-67%) were the second-born sibling, 23%-26% were the third-born sibling, and 11%-7% were the fourth-born child or a higher birth order. The female and the male respondents had an equal likelihood of having a brother or a sister as their older sibling who was born immediately before them. However, compared with the female respondents, the males were more likely to be raised in a sibling group with a higher proportion of male siblings and with an older sibling who had a high level of math achievement. It is also worth noting that the young men in our sample were more likely than the female respondents to be raised in a two-parent family.

Table 1 Means (standard deviations) and proportions of respondents’ educational choices, sibling group compositional characteristics, and other individual and family characteristics by gender
Full size table

LPM Analysis: Hypotheses Testing

Table 2 contains the standardized estimates from six LPMs that predict the respondent’s preference for a STEM versus a non-STEM major by the sibling’s compositional characteristics, net of demographic and family background variables. Starting with the gross effect of gender, Model I, our null model, indicated that the male respondents were, on average, 12% more likely than the female respondents to choose a STEM major in college rather than a non-STEM major. This gender gap in the likelihood of preferring a STEM major was similar when we controlled in Model II for the respondent’s birth cohort, race/ethnicity, and family background characteristics, including the mother’s occupation. Moving on to test the resource dilution hypothesis (H1) in Model III, we added three measurements of the siblings’ characteristics: the sibling group size, and the respondent’s birth order and birth spacing relative to the older sibling. We also controlled for the respondent’s math ability. These four variables were interacted with the gender of the respondent. The results showed that for both young men and women in our sample, the sibling group size was negatively associated with preferring a STEM field in college. With each additional sibling in a sibling group, a respondent’s preference for a STEM major decreased by about 4%. In terms of birth order, females and males who were the second born in a sibling group (most of our sample, Table 1) were 8% less likely to prefer a STEM major than the respondents of higher birth orders. As birth spacing did not reach the statistical significance threshold, we concluded that it was not related to the preference for a STEM major in college.

Table 2 LPM standardized coefficients predicting college STEM major preference by sibling compositional characteristics, older sibling measurements refer to the sibling born just before the respondent (N = 1,545)
Full size table

In addition, Model III showed that higher math achievers were more likely to choose a STEM field, and that this inclination was similar among the young men and women in our sample. With each additional standard deviation point in a respondent’s math ability score (respondents’ math ability (std. = 13, Table 1), their probability of preferring a STEM major increased by 5.7%. That is, increases of about 6.5–13 points in a respondent’s math ability score raised their chances of pursuing a STEM major by 3%-6%.

Next, in Model IV, we addressed H2a and H2b by adding two variables: the gender of the older sibling and the percentage of boys in a sibling group. The results suggested that for the male respondents, having an older brother, rather than having an older sister, increased their preference for a STEM major by 12%; whereas for the female respondents, the gender of their older sibling had a non-significant effect on their chances of preferring a STEM major. However, the effect of the older sibling’s gender lost its statistical significance power once we controlled for the older sibling’s math ability in Model V. This may suggest that the effect of the gender of the older sibling on the younger sibling’s college major preference may be channeled via the older sibling’s math ability, as suggested by Hypotheses 4a and 4b. To anticipate later findings, this observation was indeed supported by the results of our final Model (Model VI).

The effect of having a higher proportion of brothers in a sibling group, as shown in Model IV, was positively associated with preferring a STEM field for both genders. In other words, with each additional 15%-30% of brothers in a sibling group (proportion of brothers in a sibling group (std. = .28, Table 1), both the young men and women in our sample increased their preference for a STEM field by about 3%-6%. From yet another perspective, being raised in a sibling group consisting of 66% brothers was associated with a 6% increase in the likelihood of majoring in a STEM field compared to being raised in a sibling group with 33% brothers. These results imply that, thus far, our findings do not support the same-gender siblings’ competition stimulation hypothesis (H2a and H2b) suggested by Conley (2000). For both the male and the female respondents, having a male-dominated sibling group (based on the proportion of brothers) increased their chances of preferring a STEM field; whereas for young men, being raised with an older brother further enhanced their chances of pursuing a STEM college major.

In Model V, we examined the likelihood that the male and the female respondents with an older sibling with strong math skills opted for a STEM major in college, as suggested by H3. Despite a positive coefficient, no statistically significant association was found between the older sibling’s math ability and preferring a STEM major when not interacted with the gender of the older sibling, which contradicted H3. However, the estimates from our final model (Model VI), in which we tested for H4, indicated that the effect of the older sibling’s math ability on the younger sibling differed by the gender of the respondent and of the older sibling. For the young women in our sample, the preference for a STEM field increased by 2.5%-5% with every 7–14 points in the older sister’s math score (older sibling’s math ability std. = 13.77, Table 1). By contrast, having an older brother with strong math skills was negatively associated with the likelihood of preferring a STEM major for the female respondents. An increase of 7–14 points in the older brother’s math score resulted in the female respondents being 1%-2% less likely to prefer a STEM field in college. Among the young men in our sample, we found a similar negative pattern for opposite-gender sibling pairs, i.e., having an older sister with high math ability reduced the male respondents’ likelihood of preferring a STEM major by 2.5%-5% with every additional 7–14 points in the older sister’s math score. However, having an older brother with strong math skills also had a small negative effect on the male respondents’ preferences for a STEM major. With every additional 7–14 points in the older brother’s math score, the young men’s likelihood of preferring a STEM major was reduced slightly, by about 1%-2%.

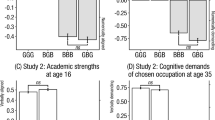
To further illustrate the interaction between the older sibling’s math ability and their gender in our final model (Model VI), Fig. 1 shows the predicted probabilities of choosing a major in a STEM field for young men and women from selected sibling group configurations, while holding the covariates at their mean values. The bottom panes in Fig. 1 show the predicted probabilities of preferring a STEM major conditional on the older sibling’s math ability for the female respondents (left figure) and the male respondents (right figure). Here, two findings stand out. First, the variation in the math ability of an older brother or sister did not predict any relevant differences in the likelihood of choosing a major in a STEM field for the male or the female respondents, which refutes H3. Second, the mix of the siblings’ genders did affect whether the older sibling’s high (but not low) math ability predicted the younger sibling’s preference for a STEM major, which supported H4a and H4b. For the young women in our sample, having an older sister, rather than an older brother, in the 75th percentile of the math score distribution significantly boosted their probability of choosing a major in a STEM field, from 18 to 26%. This difference between having a highly math skilled older sister versus highly math skilled older brother was found to be statistically significant when tested via an additional model that categorized the continuous measurement of the older sibling’s math ability into three math score tertile-dummy variables: low (0–33%), medium (34–66%), and high (66–100%) math score tertile (models not shown, but available upon request). Here, the female respondents with an older sister with strong math skills were significantly more likely to pursue a STEM major than those with an older brother with a high level of math achievement (p = .0149). Young men also showed a same-gender dyad advantage with respect to having an math skilled older sibling (21% STEM choice for an older sister with strong math skills and 33% for an older brother with strong math skills) in the predicted values from our main model. However, in the additional model, which categorized the older siblings’ math ability into the three tertile-dummies, the difference in STEM choice among young men with an older brother versus an older sister in the highest math skilled tertile did not reach statistical significance (p > .05). We therefore concluded that the gender of the older sibling with high math ability influenced the likelihood of choosing a STEM major for the young women in our sample, but not for the young men. In addition, the upper panes of Fig. 1 show the negative effect of the sibling group size and the positive effect of the proportion of brothers on the probability of preferring a STEM major. Again, however, the effects were larger among the female respondents, and the confidence intervals of the predictions for males overlapped for both measures. Hence, as we stated above, the resource dilution argument (H1) was supported, but only for young women (from 26% STEM major preference in 2-child family to 7% in a 7-child family; whereas it was around 28% for young men of all  sibling group sizes); and being in a male-dominated subgroup was found to increase the likelihood of preferring a STEM field for female respondents (from 12% having no male siblings to 32% for male siblings only), but not for male respondents (here, the increase from 26 to 30% was not statistically significant).

Fig. 1
figure 1

Predicted probability of preferring a STEM college major by the main sibling group compositional characteristics (based on LPM Table 2 Model IV)

Full size image

Finally, to further assess the relevance of our sibling group compositional measures for explaining the gender gap in the likelihood of choosing a major in a STEM field, we estimated how much variance in the gender gap these measures explained compared to the demographic and family background control variables. We did this by graphing the predicted probabilities of choosing a major in a STEM field for males and females in each of the Models I-VI, while holding all the covariates at their mean values (Fig. 2). As we described above, in the descriptive null model without any covariates (model I), the probability of preferring a STEM major in college was about 30% for the male respondents and 18% for the female respondents (i.e., a 12% gender gap). Controlling for demographic and family background variables (model II) and accounting for the sibling group size and the respondent’s birth order, birth spacing, and math ability (model III) did not change the predicted gender gap in the likelihood of choosing a STEM major. The gap remained at 10%-12% and stayed highly statistically significant, as indicated by the non-overlapping confidence intervals of the predictions in Fig. 2. However, the gender difference in the probability of choosing a STEM major was reduced to 7% (28% for males and 21% for females), and the confidence intervals started to overlap once we accounted for the older sibling’s gender and the proportion of boys in the sibling group (model IV). Adding the older sibling’s math ability (model IV) and interacting the older sibling’s math ability and gender with the respondent’s gender (model VI) further reduced the gap to 6%.

Fig. 2
figure 2

Predicted probability of preferring a STEM college major among young men and women (based on LPM Table 2 Models I-VI)

Full size image

Robustness Checks

We conducted a variety of robustness checks for our findings. First, we assessed our analytical strategy by testing nonlinear models (probit or logistic regression), which yielded the same conclusions (See Supplement B in the online supplement for these results). Next, we evaluated the robustness of our findings on role modeling by testing whether downstream influences remained present when we replaced the measurements of the older sibling born immediately before the respondent (math ability, gender, birth spacing) with measurements of the first-born sibling. The results of these models bolstered our findings (See the last two columns in Supplement B in the online supplement). We also considered potential bias due to the operationalization of the sibling group size, excluding children from families with 5 or more children, as is commonly done in the literature to eliminate potential outliers. The results remained the same (models not shown, but available upon request).

Further, we assessed whether our sampling selective processes or loss of cases may have led to bias in our results. To assess this, we first examined differences in the basic demographic variables of the respondents with missing data due to attrition (1,585 cases) and of the respondents who had complete information (1,545 focal respondents who were included in the analysis). Those who were excluded from the analysis were more likely to be i) a white male, who was ii) born between the mid-1970s and the mid-1980s, iii) was an additional two months younger than their older sibling, iv) was raised in a less affluent family, v) came from a one-parent households, and vi) had an uneducated mother. Nonetheless, and important to the matter, no differences were found between these two groups on sibling group size, birth order, or older sibling gender. Next, we assessed potential biases due to sample selection stemming from a) selection into college attendance and b) selective panel attrition due to missing values on educational outcomes in young adulthood. To this end, we created a dependent variable with four categories (STEM major, non-STEM major, no college attendance, missing college education information), and re-estimated all the models using multinomial logit analysis. Our intent was to a) assess whether our findings on the differences between college students who did and did not pursue a STEM major held when the presence of non-college goers and respondents lost to panel attrition were accounted for, and b) to assess whether non-college goers and respondents lost to panel attrition varied significantly in terms of our predictors of interest, that is sibling group configuration. Even when accounting for omitted cases, our main conclusions did not change (models not shown, but available from the authors upon request). Equally important, our results showed that the sibling group configuration did not predict either non-college attendance or panel attrition. This finding alleviates potential concerns and increases our confidence that the analysis was not significantly biased due to panel attrition or the exclusion of non-college goers, because it indicates those who left the panel did not differ in terms of their family configuration from the other groups.

A further remarkable finding to notice was that respondents lost to panel attrition were much more similar in their math ability to the group of those who remain in the panel and do not attend college, than the college attendees. Hence, it seems likely that those who dropped out due to panel attrition may not have attended college anyway, and therefore would not be included in our analysis even if they had remained in the panel. As a final step, we estimated our models separately for focal male and female respondents (See Supplement C in the online supplement for these results). The results reinforced our conclusions, i.e., that the sibling group compositional characteristics affected the likelihood of choosing a major in a STEM field for the female respondents, whereas for the male respondents, the probability of preferring a STEM field was driven by their own math ability. Our pooled models (Table 2) were more parsimonious than the separate models, because they did not interact the control variables with the respondent’s gender. It is, therefore, possible that the low statistical confidence in the sibling group configuration measures among male respondents was due to sample size limitations.

Discussion

Although educational expansion has created unprecedented opportunities for women, there is persistent horizontal gender inequality in the field of study that still translates into men and women having unequal access to resources in the labor market and beyond. Previous research on how the family influences children's educational outcomes in general and STEM career choices mainly focused on the interactions between parents and children. However, there has been much less research on how sibling group features influence children’s gendered substantive educational preferences in general, and their likelihood of taking STEM courses or majoring in a STEM field. Our study sought to close this research gap by examining whether a young adult’s decision to major in a STEM field in college was associated with the compositional characteristics of their sibling group, including the math ability of their older sibling, net of demographic and family background features. Specifically, we offered a three-fold theoretical framework of four not mutually exclusive hypotheses on how the siblings’ compositional characteristics as contextual factors may be linked to their likelihood of pursuing a STEM major in college as a young adult. Our results showed that the sibling group compositional characteristics influenced whether the respondents chose a STEM field in college, but only for the young women. In the following, we briefly list our research hypotheses, and indicate whether they were supported (or refuted) in our analysis.

Following the resource dilution argument, we first hypothesized that net of the respondent’s demographic and family background characteristics, math ability, birth order, and spacing, individuals from larger sibling groups were less likely to choose a STEM major in college than those from smaller families [H1]. We found that net of other compositional features, women were less likely to prefer a STEM major if they were raised in a larger sibling group. This finding provided descriptive evidence for H1, the resource dilution hypothesis, which was previously supported by research on years of schooling but had not been investigated with respect to the choice of a major, which can be seen as a “qualitative” educational outcome. Thus, for girls to excel in math and other STEM subjects – which are still gender-atypical subjects for girls – they may need more support from their parents or other adults in the private realm, as it appears that in school, girls are receiving less support than boys (Sansone, 2019). This may help to explain our finding that a large sibling group size had a detrimental effect on the likelihood of preferring a STEM major for women, but not men.

Building on Conley's (2000) same-sex competitive positive stimulation approach, we expected to find that for girls, net of demographic and family background characteristics, the respondent’s math ability, sibling group size, birth order, and birth spacing, having an older sister (and more sisters) rather than having an older brother (and more brothers) was positively associated with the likelihood of pursuing a STEM major in college [H2a]. Similarly, for boys, we expected to observe that having an older brother (and more brothers) rather than having an older sister (and more sisters) was positively associated with the likelihood of pursuing a STEM field in college [H2b]. Based on our data set, H2a and H2b were refuted. Instead, we found that the proportion of boys in a sibling group was positively associated with preferring a STEM career, and mainly for the female respondents. Male sibling group dominance, as indicated by a higher proportion of brothers in a family, may suggest the formation of a normative male-role sibling group climate, as suggested by Powell and Steelman (1990). This could affect the interest in STEM of the sisters of the boys in several ways, such as through repeated exposure to and familiarization with more “male” interests and activities. Thus, a family with more male children may include more children who are socialized to adhere to male role expectations, which may expose the girls in the family to these expectations as well, regardless of their individual sex.

Drawing on role modeling perspectives (Brim, 1958; Dunn, 1983), we suggested in H3 that the math achievement levels of older siblings may shape the younger siblings’ interest in and anxiety about pursuing a STEM career, and that a younger sibling with an older sibling with strong math skills is therefore more likely to choose a STEM major in college. However, we found a more complex pattern suggesting that the positive association between having an older sibling with high math ability and the respondent’s likelihood of choosing a STEM major in college was moderated by the older sibling’s sex, but mainly for girls. These findings refuted H3 but supported H4a. Accordingly, it appears that having an older sister who is good at math stimulates the younger girl’s interest in and motivation to pursue a STEM career. For male respondents, the results were much weaker, which we interpret as suggesting that males did not gain (nor lose) much from having a same-gender or an opposite-gender older sibling with strong math skills. These findings indicate that role modeling and the influence of an older sibling by channeling the younger sibling’s educational preferences for a STEM field were stronger and were mostly relevant for females. This finding is, again, intuitive, given that choosing a STEM major is still atypical for women, and may occur mainly when women have extra exposure to or support in STEM during childhood and adolescence. Being exposed to counter-stereotypical views and experiences can promote women’s interest in STEM majors (Dunlap & Barth, 2019). Hence, having an older sister who is a high achiever in math may serve as a mechanism to reduce the gendered nature of implicitly held beliefs related to STEM careers. Moreover, an older sister with strong math skills may create a competitive yet positive environment that pushes her younger sister to excel in similar domains; alternatively, there may be increased cooperation and support among sisters who both excel in gender-atypical school subjects. Similarly, an older brother with high math achievement may push his younger sister to seek alternative and atypical pathways for her own career, perhaps by engaging in atypical gendered behavior.

Our results yielded a further insight. Very generally, the siblings’ compositional characteristics appeared to matter for the educational development of girls but not of boys, which spilled over into the decision to pursue, or not to pursue, a STEM major in college. Controlling for the sibling group compositional factors used in our study reduced the gender gap in the likelihood of choosing a STEM major to 6%, and thus rendered it statistically nonsignificant. It therefore appears that sibling group composition represents an important yet largely overlooked source of gender socialization that shapes the college major choices of girls. While the question of whether the sibling group composition predicts gender differences in educational attainment measured “quantitatively” – i.e., based on the time spent in the educational system – has been studied extensively, prior to our analysis, little was known about the linkage between sibling group configurations and gendered outcomes with respect to more “qualitative” educational outcomes within the same level of education. Thus, this article’s main contribution is that it broadens our understanding of the possible down streaming influences of an older sibling’s gender and role modeling, while also accounting for the presence of other siblings.

Future research is needed to further explore the specific mechanisms by which siblings influence each other in the development of their substantive educational interests and preferences, particularly as they pertain to persistently gendered subjects, such as STEM. One potentially promising avenue is to examine to what extent the association between the sibling group composition and girls’ interest in STEM is rooted in the psychological realm. A growing body of literature has indicated that the underrepresentation of girls in STEM fields is due in part to psychological elements, such as their lower levels of confidence in their STEM specific competencies (Tellhed et al., 2017); their greater gender stigma consciousness and their gender-based rejection sensitivity, which leads them to perceive STEM academic environments as threatening (Casad et al., 2019); and their significantly higher levels of math anxiety, which directly affects their avoidance of STEM fields, regardless of their math abilities (Daker et al., 2021; Maloney et al., 2012). Our results suggest that girls from specific sibling group compositional backgrounds may be more prepared to thrive in STEM learning environments because of their early exposure to male-dominated group climates, or because they believe more strongly that girls can be competent in math, as modeled by an older sister with high math ability. This would also explain why we found no sibling group compositional effects on the likelihood of boys entering STEM fields: i.e., because STEM subjects are socially constructed as male, boys may not, on average, need extra encouragement from their family of origin to feel drawn toward and to succeed in STEM educational settings.

Limitations and Future Directions

This study is not without limitations. Our sample was drawn from a population of the children born to the NLSY79 women who were aged 14 to 21 on December 31, 1978 (Center for Human Resource Research, 2009). Due to the study design, of the 11,512 children who were born to the female respondents of the NLSY79 by 2012, only 3,130 were found to be eligible for inclusion in our sample due to their family positioning (having siblings, not the first-born child, born after 1990, and attended college). Of those remaining 3,130 children, 1,585 were excluded from the analysis, due to listwise deletion for missing information on college attendance (78%), birth spacing (< .001%), the math ability of the older sibling (13%), the math ability of the respondent (7%), and family income (.01%) (See Supplement A in the online supplement for these details.). The missing values of most concern are those on college attendance. Missing data is an unfortunate yet common occurrence in higher education research. Thus, the number of individuals with missing information was not ideal and warrants acknowledgment. As we mentioned above, we took specific steps to assess whether our sampling selective processes or the loss of respondents may lead to bias in our results and found that the rate of panel attrition was not a major source of bias for our results. Nonetheless, future research that uses larger samples with less missing information, such as register data from the Scandinavian countries, should put our findings to the replication test. In addition, the sample examined respondents born in the 1970s and the 1980s. Whether the association between the sibling group composition and the likelihood of majoring in STEM fields we found still holds for later-born girls, or for the generation of girls who were born at the turn of the millennium and are currently attending college, should be investigated by future research.

Moreover, the data were correlational, which limited our ability to make causal claims; and which, relatedly, did not allow us to directly test the mechanisms driving the demonstrated patterns. Although our results strongly supported for girls our expectation that there would be a role-modeling effect via competitive stimulation, the underlying specific mechanisms of this effect remain unclear. One potential pathway may be that parents tend to prepare their home environment and adapt their parenting practices based on the gender of their first child or the majority of their children, especially if both their first and their second child were of the same sex. The ways in which this pattern could be meaningful for subsequent children are myriad: gendered toys, clothes, child-geared equipment like furniture or sports equipment, games, family activity routines, and parenting styles established in the family, and the interactions with same-gender friends of the older child, all form a “parenting infrastructure” that is established after the first child is born, and that could have downstream spillover effects that set a “gendered tone” for subsequent children. This gendered tone logic is not exclusive to the first-born sibling and can also operate via the overall sibling group gender ratio, as is suggested by Powell and Steelman (1990) normative climate hypothesis and is also shown in our findings. Hence, regardless of the gender of the first-born child, having more male siblings in a household may make male role expectations more common, which could affect all children regardless of their sex. Future work must build on what we know about sibling compositional characteristics by combining this knowledge with more qualitative measures of the home environment and the gendered nature of sibling dynamics and interactions. In this vein, another limitation of our study was that we were unable to differentiate between the true influence of siblings and the effects of the parental or the broader family environment. As the sex of fetuses is random, the sibling group configurations and the gender mixes cannot be affected by parental values and preferences. Nonetheless, as we noted above, parents may play an active and direct role in shaping the family environment based the gender of the first child or the first two children, which may, in turn, influence a (later born) child’s eventual choice of a college major. In this case, the association between the sibling group composition and the choice of a college major would be spurious and mediated by parental guidance.

Another potential limitation of our study that was related to our inability to directly test the mechanisms was our inability to reconcile theoretical reasonings into one straightforward narrative. Most research, including our own, assumes that there are positive asymmetrical associations in which older brothers and sisters promote and evoke similarities between themselves and their younger siblings. Recently, however, several studies have reported other dynamics (e.g., Whiteman et al., 2014). We acknowledge that it is possible for competition between siblings to be non-collaborative and even adversarial, which could lead to less positive or to opposite outcomes, as implied by Sulloway’s work (1996). Thus, relying on Conley’s sex-minority competition hypothesis (Conley, 2000) to interpret our findings could be understood as reflecting an opposite gendered role modeling process (Sulloway, 1996; Whiteman et al., 2014). When competing for and seeking parental investment, later-born children are forced to become more original in order to attract that investment (Sulloway, 1996). It has been argued that when young people are choosing different niches and developing distinct personal qualities, they are protecting themselves from the rivalry and resentment of their siblings, and are, in turn, seeking to receive their share of parental love and attention (Casad et al., 2019; Feinberg & Hetherington, 2000). These differentiation processes appear to be more prevalent when siblings are of the same gender (Whiteman et al., 2014). Thus, it is possible that the sibling dynamics we observed may have led to different effects if we had focused on other gendered niches, such as occupational domains or risk-taking spheres, such as extreme sports. Since we have no direct mechanisms to test this potential explanation, we need to be cautious and modest in our interpretations.

Following this line of logic, another limitation comes to mind. Our analyses controlled for a variety of socioeconomic factors of the siblings’ family of origin, measured during childhood, including the mother’s employment status, her occupation, and its gendered context. Although this eliminated the effect of some parental influences, specifically of the mother’s occupational role modeling and knowledge, future research should investigate whether the parental gender ideology mediates the relationship between an older sister’s math ability and a younger sister’s STEM major preference by directly modeling parental gender ideology, rather than indirectly deriving it from the mother’s occupation. As the parents’ beliefs about a child’s abilities and the degree to which they encourage their child to pursue a STEM career are influenced by gender stereotypes (Muenks et al., 2020), it is possible that parents with strong gender egalitarian values may invest heavily in their daughter’s math and science education in order to provide her with equal life chances. In this scenario, parental gender ideology would affect both the older sister’s high math score and the younger daughter’s preference for a STEM major. Indeed, gender equality has increased in recent decades, and there has been a corresponding increase in adults with gender-egalitarian attitudes (Blakemore & Hill, 2008; Marks et al., 2009). Either way, we suggest that future research on persisting gender differences in educational and career preferences and choices should look more deeply into the role modeling effects of siblings in families, and to what extent they are mediated by or are independent of parental features.

In addition, some may argue that our analyses excluded several key variables that are known to be related to gender differences in college major preferences and choices. Traditional theories connect the gender segregation in a field of study to males being relatively advantaged compared to females in terms of math and verbal abilities (Jonsson, 1999), general life goals, gender roles attitudes (Jacobs, 1989), expectations about work–family compatibility (Eccles, 2011a, b), and gendered desires for extrinsic or intrinsic occupational preferences (Marini et al., 1996). Unfortunately, all these measurements are absent from our analysis, largely due to a lack of available data. Although our results provide preliminary support for some theories over others, future work is needed to determine the mechanisms through which older siblings affect younger siblings, and how parental influences shape these dynamics. Nonetheless, as life goals, gendered beliefs, and occupational preferences are typically measured during adolescence or early adulthood, they may be influenced by sibling group compositional factors themselves. Thus, future research should test whether, and, if so, to what extent, these more established predictors of STEM educational choices may be affected by the sibling group compositions themselves.

Despite these limitations, a descriptive study such as ours is an important first step in developing a deeper understanding of how gendered family environments influence the educational and other outcomes of young people. Our results suggest that a key aspect of educational stratification by gender is overlooked without considering sibling group compositional characteristics and the gender differences in the social dynamics between siblings, with the effects being especially large for girls. Future research should open the “black box” of parental investments and interactions among siblings to reveal the mechanisms that underlie these patterns, starting with those we put forward in our discussion.

Practice Implications

The compositional characteristics of siblings have, up to now, been overlooked as a factor that contributes to horizontal gender segregation in education. Our study has helped to close this research gap. Assuming the sex of each child is random, our research provides a unique opportunity of using a “quasi-experimental” setting to study how the pre-gendered sibling environment affected the educational preferences and choices of later-born children. Although it is impossible to intervene in the compositional characteristics of the siblings in a family, early childhood social policies could help to counterbalance fewer positive effects rooted in sibling group structures and could be a powerful tool in providing experiences not available at home. Educators and policymakers can draw on our findings to develop interventions aimed at creating a safe and encouraging climate for young girls to engage in gender-atypical activities. Social policy practitioners may want to design programs for preschools to heighten awareness among caregivers of the sibling constellations in the homes of children, and their relevance for the development of gender-(a)typical self-concepts. Experimental studies have tested intervention programs, which intend to help parents promote their adolescent children's STEM utility-value and motivate them to take mathematics and science courses in high school (Harackiewicz et al., 2012; Rozek et al., 2015). Focusing on parents’ utility-value beliefs and the possibility to communicate them to their kids, these experiment interventions showed an increase in children's interest and performance in STEM topics (Harackiewicz et al., 2012; Rozek et al., 2015). Rozek et al. (2015), moreover, found that these interventions worked best for girls with high past performance in STEM courses, and for boys with low past performance record in these fields. Contrary, the intervention did not increase course-taking for low achiever girls, and it had no effect for boys with high past performance.

Furthermore, specific interventions, such as providing girls with targeted exposure to games, toys, and concepts gendered as “male” may help to enrich the future educational and career opportunities of these girls. Moreover, for school-age girls, providing them with repeated substantial exposures to gender-atypical female role models through, for example, mentoring programs may encourage them to engage in gender-atypical activities in adolescence, and, later, to major in a STEM field in college. Our results indicate that girls without brothers, girls from families with many children, and later-born girls could benefit from such support. Perhaps even more importantly, our findings underscore those interactions among children play a role in the development of young people’s educational interests in STEM subjects more generally. While our study focused solely on sibling group composition in the family realm, our findings may be extended to preschool and school settings. Future studies are needed to measure and analyze how peer interactions shape the development of children’s educational interests, preferences, and self-beliefs. Nonetheless, our findings suggest that improving educators’ awareness of the interactions among the children themselves, and whether they help girls to engage in activities and concepts socially constructed as male or provide girls with exposure to positive role modeling by older girls with an interest in STEM, is a promising avenue for empowering girls to access advanced STEM education.

Conclusion

This study shows that the composition of a girl’s sibling group – in its size, gender composition, and the math ability of her elder sibling(s) – likely matters for whether she will choose a STEM major in college. No such statistically significant sibling group effects for boys’ STEM college major preference were found. Taken together, these results extend the literature in two important ways. First, they empirically indicate that sibling group composition itself likely plays an important socializing role for girls, predicting their gendered educational choices, whatever the reasons. The predicted gender-gap in STEM major choice was reduced to 6% (from 13%) and rendered statistically insignificant when sibling group size, gender composition, the gender of the oldest sibling, and the oldest child’s math ability were controlled for. Future research is needed to examine the underlying mechanisms, as well as to investigate whether sibling group compositions may affect STEM major choices via shaping occupation aspirations and other attitudinal and psycho-social aspects, such as math-anxiety, or self-efficacy, which have been shown to be important predictors of choosing STEM educational pathways.

Second, our findings enrich our understanding of how sibling group compositions may influence substantive educational preferences in general, and STEM major choices specifically. We find support for the resource dilution theory, which underscores those girls from larger families may be disadvantaged not only in terms of the amount of schooling they receive, but also in terms of their chances of majoring in a STEM field. In addition, we find support for the presence of role modeling, but only under specific circumstances – namely, among female same-gender siblings when the older sister was good at math – which lends support to the hypothesis that role modeling occurs in contexts characterized by same-gender competitive stimulation. Most importantly, these theorized effects, when present, were found to apply to girls only, and not to boys, across all the theoretical concepts we considered. These findings underscore the need to differentiate these theoretical approaches by gender, particularly when applied to gendered outcomes such as STEM career trajectories. They also suggest that socialization experiences that operate on the sibling (or peer) level play a crucial role in whether girls become interested in and pursue “gender-atypical” educational choices, and thus deserve more attention in future research.