Introduction

Increased social and economic requirements forced universities to broaden their traditional functions. Innovative research and the transfering these findings to society became necessary since providing high-quality education is no longer a sufficient factor. From first to third-generation universities, innovation, transfer, and implementation have been added to traditional university functions (Skribans et al., 2013). Today, the entrepreneurial and value-creating structures of 3rd generation universities make them stand out from the competition.

According to the 11th Development Plan of Türkiye for 2019–2023, the need to transform R&D results into economic and social benefits and to develop entrepreneurship and commercialization activities are still important. In this scope, there is a mandatory transition period for 3rd generation universities in which universities take an active role in transforming the knowledge produced into value and in close cooperation with industry and the public. Entrepreneur and Innovative University Index (EIUI) is used to objectively measure and rank the transformation journeys of universities into 3rd generation universities. In addition, it gives valuable information to all stakeholders of the entrepreneurship ecosystem, such as governments/policy makers and current/potential entrepreneurs.

The Entrepreneur and Innovative University Index (EIUI) ranks the first 50 universities among 208 universities in Türkiye based on their “scientific and technological research capabilities”, “intellectual property pool”, “cooperation and interaction” and “economic and social contribution” since 2012. Prepared by the Scientific and Technological Research Council of Türkiye (TUBITAK), it aims to increase the entrepreneurship and innovation-oriented competition between universities and to contribute to the development of the entrepreneurial and innovation ecosystem. The index, initially evaluated under five dimensions before 2018, was reduced to 4 with the revision. The composite indicator of weighted four dimensions and 23 indicators is calculated from data gathered from public records, universities, and technoparks. Thus, the scientific activities of universities and industry collaborations are simultaneously considered.

There are various studies in the literature about EIUI to disseminate entrepreneurship and innovation among universities. İskender and Batı (2015) compared the EIUI results with the ranking obtained by sentiment analysis on 13,007 tweets containing the “entrepreneur” keyword and 14,579 tweets that contained the “innovation” keyword. Karagöz et al. (2020) calculated the efficiency scores of the top 50 universities for 2011–2016 EIUI data by Data Envelopment Analysis, identifying 35 universities that do not use resources efficiently and provide periodic systematic improvement. Selamzade and Özdemir (2021) analyzed the efficiencies of the entrepreneurial and innovative universities using constant return to scale (CRS) and variable return to scale methods (VRS) of Data Envelopment Analysis based on 2020 EIUI data. Regarding the Entrepreneurship and Innovation Dimensions of EIUI, they found that only 18% of universities are efficient in CRS analysis and 26% in VRS analysis.

The evaluation of entrepreneurship and innovation performance involves multiple criteria with different priorities (weights), which can be modeled as a multiple-criteria decision-making (MCDM) problem. Table 1 summarizes some studies on ranking universities in Türkiye according to their entrepreneurship and innovation performance using different multi-criteria decision-making methods (MCDM). According to Table 1, 50 universities were ranked using different MCDM methods in three studies. Oğuz (2022) used four dimensions according to the revision made in 2018. Ömürbek and Karataş (2018) and Oğuz (2022) used two MCDM methods for comparison purposes. In addition, criterion weighting methods (Entropy and CRITIC) were only used in two of the studies.

Table 1 Literature summary
Full size table

In the literature, a limited number of studies focus on ranking universities, countries, or organizations based on entrepreneurship and innovation performance using MCDM. Rostamzadeh et al. (2014) prioritized the entrepreneurial intensity among small and medium-sized enterprises using the Fuzzy Analytic Hierarchy Process (F-AHP) based VIKOR and TOPSIS techniques. Quan and Zhou (2018) employed Entropy TOPSIS to rank the innovation and entrepreneurship education capacity of 9 colleges and universities in Jiangsu Province in 2016. Karimi et al. (2019) utilized the Analytical Network Process (ANP) and the Decision Making Trial and Assessment Laboratory (DEMATEL) to rank the innovation and entrepreneurship indices of international companies. Özkan et al. (2019) ranked 81 cities in Türkiye according to the R&D performance using a hybrid MCDM model including DEMATEL and ANP for assigning importance to the indicators and VIKOR for ranking performance. Altıntaş (2020) conducted a comparative analysis of the Global Innovation Index of G7 countries using Entropy-based Grey Relational Analysis. Ishizaka et al. (2020) applied PROMETHEE to rank 162 UK universities based on their portfolio of knowledge transfer activity from the 2015–2016 Higher Education Business and Community Interaction Survey dataset. Zhu et al. (2022) evaluated the entrepreneurial environment of 48 countries according to World Development Indicators by using Grey Relational Analysis.

EIUI ranking involving the weight of the jth criterion (j = 1,2,…,n) and the performance of ith university (i = 1,2,…,m) with respect to jth criterion is a multi-criteria decision-making problem in nature. This paper aims to emphasize that using different multi-criteria decision-making methods with varying criteria weights may lead to different university rankings and to highlight the causes contributing to different results. To the best of the authors’ knowledge, comparative analysis of Grey Relational Analysis and PROMETHEE for different criteria weights (Equal, TUBITAK, and Data Based-Entropy Weights) has not been conducted for university ranking before. The reasons for choosing these methods are listed below.

  1. 1.

    EIUI is based on the subjective weight of each dimension. Given that judgments specific to a particular time period are based on the experience or knowledge of decision-makers, it is necessary to review and evaluate the weighting system for reliable and robust decision-making. This study employed the Entropy Method, an objective weighting method using currently available data, to determine the criterion weights instead of relying on a past cross-sectional perspective based on expert judgments.

  2. 2.

    IEUI includes 23 size-dependent criteria, such as the number of Ph.D. graduates favoring large and/or old-founded universities. The absence of size-independent criteria results in rankings against small but productive universities. GRA was employed to rank universities in this study, as grey system theory deals with uncertain systems with partially known information, mirroring the uncertainty in the EIUI calculation.

  3. 3.

    As another MCDM method for comparison, PROMETHEE was used because of its visual support in exploring the structure of the decision problem and better interpreting the results.

In summary, this study proposes an approach for ranking universities in terms of the Entrepreneur and Innovative University Index by leveraging the strengths of each MCDM method used. Using GRA and PROMETHEE with varying criteria weights provides comprehensive evaluation. To the best of the authors’ knowledge, there is no study in which 50 universities are ranked on the basis of 4 dimensions of EIUI using GRA and MCDM methods with different criterion weights. In this scope, the rest of this paper is organized as follows: “Method” Section briefly explains the weighting and MCDM methods used in this study. “Data” Section presents the data used, and “Analysis” Section displays the results of ranking studies. The last section is a discussion and conclusions.

Method

Multi-Criteria Decision Making (MCDM) is a scientific discipline that addresses various decision-making problems. Considering multiple conflicting criteria, these methods evaluate alternatives to rank or select the optimal solution. Numerous MCDM methods are available in the literature, including AHP, ELECTRE, TOPSIS, PROMETHEE, and Grey Theory, as highlighted by Aruldoss et al. (2013). Due to their different aggregation procedures, normalization methods, and treatment for the cost/benefit criteria, there is no clear guideline on selecting which method to solve a specific decision problem. The choice depends only on the nature of the problem to be solved. Aruldoss et al. (2013) provide a detailed discussion of the advantages and disadvantages of some MCDMs. Selmi et al. (2013) proposed a comparative study to identify similarities and divergences between six MCDM methods: ELECTRE III, PROMETHEE I and II, TOPSIS, AHP, and PEG-MCDM. They used the Gini Index to measure dispersion of ranks obtained from the mentioned methods. A case study noted a good similarity between PROMETHEE-AHP and TOPSIS-PEG and a larger dispersion between ELECTRE III-TOPSIS and ELECTRE III-PEG.

Since the final decision in MCDM is influenced by the criteria weights, several methods, objective and subjective in nature, are utilized (Paramanik et al., 2022). Objective methods calculate the criteria weights based on available data by mathematical algorithms neglecting the experience of the decision-makers. Conversely, subjective methods rely on decision-makers judgments based on expertise, experience, and cognitive efforts in calculating criteria weights. However, it is essential to note that the lack of experience or knowledge of the decision-maker can potentially lead to incorrect decisions when using subjective methods.

The following sections summarize the Entropy Method as an objective criteria weighting method and MCDM methods (GRA and PROMETHEE) used in ranking universities.

Entropy method

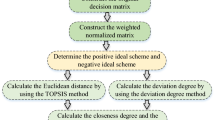
Entropy, introduced by Shannon (1948) into information theory, is a measure of how disordered a system is. A higher entropy value indicates a higher degree of disorder and a lower utility value of information. As an uncertainty measurement of a system, entropy is considered a reliable method for objectively calculating the criteria weightings of multi-criteria decision-making problems by avoiding the effect of human judgment in calculating criteria weighting (Guoliang & Qiang, 2007). The original procedure of Shannon’s entropy involves the following steps (Guoliang & Qiang, 2007; Quan & Zhou, 2018; Safari et al., 2012):

Step 1 A decision matrix is created. The performance of alternative-i for criteria-j is denoted by \({X}_{ij}\) in Eq. (1).

$$X_{ij} = \left[ {\begin{array}{*{20}c} {x_{11} x_{12} \ldots .x_{1n} } \\ {x_{11} x_{12} \ldots .x_{2n} } \\ { \ldots \ldots \ldots \ldots \ldots ..} \\ {x_{m1} x_{12} \ldots .x_{mn} } \\ \end{array} } \right]$$
(1)
$$i = 1,2, \ldots ,m\,\left( {{\text{Alternatives}}} \right)$$
$$j = 1,2, \ldots ,n\,\left( {{\text{Criteria}}} \right)$$

Step 2 The decision matrix is normalized to transform different scales and units into common measurable units.

$$P_{ij} = \frac{{x_{ij} }}{{\mathop \sum \nolimits_{i = 1}^{m} x_{ij} }}$$
(2)

where \({P}_{ij}\) is the normalized value.

Step 3 Entropy value (\({e}_{j}\)) is calculated.

$$e_{j} = - \frac{{\mathop \sum \nolimits_{i = 1}^{m} P_{ij} \ln \left( {P_{ij} } \right)}}{\ln \left( m \right)}$$
(3)
$$d_{j} = 1 - e_{j}$$
(4)

where dj is the redundancy index as diversification degree.

Step 4 Entropy weight (\({W}_{j})\) for each criterion is calculated.

$$W_{j} = \frac{{d_{j} }}{{\mathop \sum \nolimits_{j = 1}^{d} d_{j} }}$$
(5)
$$\mathop {\sum\nolimits_{i = 1}^{n} {w_{j} = 1} }\limits_{{}}^{{}}$$
(6)

Grey relational analysis

Developed by Deng (1982), the grey theory provides relational analysis, prediction, decision-making, programming, and control in a grey system consisting of imprecise and incomplete information. The distinctions between grey systems and the other uncertain systems (stochastics, fuzzy, and rough) are discussed in Liu et al. (2012). GRA solves multi-criteria decision-making problems by aggregating all performance attribute values for each alternative into a single value (Zhu et al., 2022). In order to analyze the similarity between the reference series and alternative series in a grey system, GRA involves the following steps (Hu, 2009; Lin et al., 2004; Wu, 2017).

Step 1 The data set is prepared, and the decision matrix (X) is created.

$$X = \left[ {\begin{array}{*{20}c} {X_{1} \left( 1 \right)X_{1} \left( 2 \right) \ldots X_{1} \left( n \right)} \\ {x_{2} \left( 1 \right)x_{2} \left( 2 \right) \ldots x_{2} \left( n \right)} \\ { \ldots \ldots \ldots \ldots . \ldots \ldots \ldots \ldots ..} \\ {x_{m} \left( 1 \right)x_{m} \left( 2 \right) \ldots x_{m} \left( n \right)} \\ \end{array} } \right]$$
(7)
$$X_{i} = \left( {X_{i} \left( j \right), \ldots \ldots ,X_{i} \left( n \right)} \right)$$
$$i = 1,2, \ldots ,m\,\left( {{\text{Alternatives}}} \right)$$
$$j = 1,2, \ldots ,n\,\left( {{\text{Criteria}}} \right)$$

where \(X_{i} \left( j \right)\) is the value of ith alternative for jth criteria.

Step 2 Data values that have different measurement units are transformed into 0–1 intervals for comparison using one of the following formulas to normalize the data.

If the expectancy is “the larger- the better”, then the data is normalized using the following formula.

$$X_{i}^{*} = \frac{{X_{i} \left( j \right) - minX_{i} \left( j \right)}}{{maxX_{i} \left( j \right) - minX_{i} \left( j \right)}}$$
(8)

If the expectancy is “the smaller- the better”, then the data is normalized using the following formula.

$$X_{i}^{*} = \frac{{maxX_{i} \left( j \right) - X_{i} \left( j \right)}}{{maxX_{i} \left( j \right) - minX_{i} \left( j \right)}}$$
(9)

where \({X}_{i}\) is the original sequence, \({X}_{i}^{*}\) is the sequence after the data preprocessing, \(max{X}_{i}\left(j\right)\) is the largest value of \({X}_{i}\left(j\right)\), and \(min{X}_{i}\left(j\right)\) is the smallest value of \({X}_{i}\left(j\right)\). The standardized decision matrix is as follows.

$$X^{*} = \left[ {\begin{array}{*{20}c} {X_{1}^{*} \left( 1 \right)X_{1}^{*} \left( 2 \right) \ldots X_{1}^{*} \left( n \right)} \\ {X_{2}^{*} \left( 1 \right)X_{2}^{*} \left( 2 \right) \ldots X_{2}^{*} \left( n \right)} \\ { \ldots \ldots \ldots \ldots . \ldots \ldots \ldots \ldots ..} \\ {X_{m}^{*} \left( 1 \right)X_{m}^{*} \left( 2 \right) \ldots X_{m}^{*} \left( n \right)} \\ \end{array} } \right]$$
(10)

Step 3 Reference series is determined.

$$X_{0} = \left( {X_{0} \left( 1 \right), \ldots \ldots ,X_{0} \left( n \right)} \right)$$

where \({X}_{0}\left(j\right)\) is the standardized and largest value in the jth factor.

Step 4 Absolute Differences (Distances) between the reference series and compared series are calculated.

$$\Delta_{0i} \left( j \right) = \left| {X_{0}^{*} \left( j \right) - X_{i}^{*} \left( j \right)} \right|$$
(11)
$$\Delta_{0i} = \left| {\begin{array}{*{20}c} {\Delta_{01} \left( 1 \right)\Delta_{01} \left( 2 \right) \ldots \Delta_{01} \left( n \right)} \\ {\Delta_{02} \left( 1 \right)\Delta_{02} \left( 2 \right) \ldots \Delta_{02} \left( n \right)} \\ { \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots .} \\ {\Delta_{0m} \left( 1 \right)\Delta_{0m} \left( 2 \right) \ldots \Delta_{0m} \left( n \right)} \\ \end{array} } \right|$$
(12)

where \(\Delta_{0i} \left( j \right)\) is the deviation sequence.

Step 5 Grey relational coefficient is calculated.

$$\gamma_{0i} \left( j \right) = \frac{{\mathop {\min }\limits_{i} \mathop {\min }\limits_{j} \Delta_{0i} \left( j \right) + \xi \mathop {\max }\limits_{i} \mathop {\max }\limits_{j} \Delta_{0i} \left( j \right)}}{{\Delta_{0i} \left( j \right) + \delta \mathop {\max }\limits_{i} \mathop {\max }\limits_{j} \Delta_{0i} \left( j \right)}}$$
(13)

where \(\xi\) is an identification (distinguished) coefficient between 0–1, generally, it is set to 0.5 for good stability(Wu, 2017).

Step 6 Grey relational degree (grade) indicating the degree of similarity between the reference and comparable sequences is calculated. If the two series are identical, grey relational grade equals to 1.

$$\Gamma_{0i} = \mathop {\sum\nolimits_{j = 1}^{n} {w_{j} .\gamma_{0i} \left( j \right)} }\limits_{{}}^{{}}$$
(14)

where \({w}_{j}\) is the criteria weight and \(\mathop {\sum\nolimits_{i = 1}^{n} {w_{j} = 1} }\limits_{{}}^{{}}\).

Step 7 Alternatives are ranked according to \(\Gamma_{0i}\).

PROMETHEE

PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation) was developed as a reliable multi-criteria decision-making method in the early 1980s by Brans et al. (1986). PROMETHEE methods are based on mutual comparisons of each alternative pair with respect to each of the selected criteria. Two notable variants include PROMETHEE I for partial ranking and PROMETHEE II for complete ranking. The application of the PROMETHEE method to decision-making problems involves the following steps (Ishizaka et al., 2020; Karahan & Peşmen, 2021; Safari et al., 2012):

Step 1 Create a decision matrix. The basis of the PROMETHEE method is to compare alternatives \(A = \left\{ {a_{1} ,a_{2} , \ldots .,a_{n} } \right\}\) in pairs for defined criteria \(C = \left\{ {c_{1} ,c_{2} , \ldots .,c_{m} } \right\}\). The PROMETHEE method, therefore, starts by creating a Decision Matrix (DM) containing the values of the alternatives for each criterion. This matrix is given below:

$$DM = \left[ {\begin{array}{*{20}c} {c_{1} \left( {a_{1} } \right)} & \cdots & {c_{1} \left( {a_{n} } \right)} \\ \vdots & \ddots & \vdots \\ {c_{m} \left( {a_{1} } \right)} & \cdots & {c_{m} \left( {a_{n} } \right)} \\ \end{array} } \right]$$
(15)

where.

cj (ai) = value of i alternative according to criteria j,

$$i = 1,2, \ldots ,m\,\left( {m{\text{ denotes the number of alternatives}}} \right)$$
$$j = 1,2, \ldots ,n\,\left( {n{\text{ denotes the number of criteria}}} \right)$$

Step 2 Define preference functions. The preference level for an alternative ai over alternative aj is defined by the preference function as given below:

$$P_{{\text{k}}} \left( {d_{{\text{k}}} } \right) = c_{{\text{k}}} \left( {a_{{\text{i}}} } \right) - c_{{\text{k}}} \left( {a_{{\text{j}}} } \right)$$
(16)
$$0 \le P_{{\text{k}}} \left( {d_{{\text{k}}} } \right) \le 1$$
$$P_{{\text{k}}} \left( {d_{{\text{k}}} } \right) \, = 0 \, - {\text{ no preference between }}a{\text{ and }}b;$$
$$P_{k} \left( {d_{k} } \right)0 \, \sim a{\text{ is preferable weakly over }}b$$
$$P_{{\text{k}}} \left( {d_{{\text{k}}} } \right) 1 \, - \, a{\text{ is preferable strongly over }}b$$
$$P_{{\text{k}}} \left( {d_{{\text{k}}} } \right) = \, 1 \, - \, a{\text{ is definitely preferable over }}b$$

Step 3 Calculate the preference index.

$$\Pi \left( {a_{i} ,a_{j} } \right) = \mathop {\sum\nolimits_{j = 1}^{n} {P_{j} \left( {a_{i} ,a_{j} } \right)w_{j} } }\limits_{{}}^{{}}$$
(17)

where ∏ (ai,aj) represents the strength of alternative ai over alternative aj.

Step 4 Calculate negative and positive outranking flows (PROMETHEE I).

$$\phi^{ - } \left( {a_{i} } \right) = \frac{1}{n - 1}\mathop {\sum\nolimits_{j = 1, j \ne i}^{n} {\Pi \left( {a_{j} ,a_{i} } \right)} }\limits_{{}}^{{}}$$
(18)
$$\phi^{ + } \left( {a_{i} } \right) = \frac{1}{n - 1}\mathop {\sum\nolimits_{j = 1, j \ne i}^{n} {\Pi \left( {a_{i} ,a_{j} } \right)} }\limits_{{}}^{{}}$$
(19)

where ϕ+(ai) positive outflow of alternative ai and, ϕ−(ai) negative outflow of alternative ai.

Step 5 Calculate the complete ranking (PROMETHEE II). The net outranking flow of each alternative is calculated using the following equation.

$$\phi^{net} \left( {a_{i} } \right) = \phi^{ + } \left( {a_{i} } \right) - \phi^{ - } \left( {a_{i} } \right)$$
(20)

Alternatives are ranked according to \(\phi^{net} \left( {a_{i} } \right)\).

The results provided by PROMETHEE II can be better understood by using a geometrical tool known as the “Geometrical Analysis for Interactive Aid (GAIA) Plane”, which was developed by Marechal and Brans (1988). The fundamental approach for GAIA involves performing a principal component analysis (PCA) on the uni-criterion net flows of each alternative. The GAIA plane is defined by the corresponding unit Eigenvectors u and v, resulting from a covariance matrix of the uni-criterion net flows obtained using PCA. In the GAIA plane, each point represents an alternative, and the axes indicate criteria. The net flow of an alternative is the vector of its single criterion net flows for weight w. The orientation of the axes indicates compatible criteria and conflicting criteria. The length of the axis will indicate the parsing of the criteria. The decision axis (∏) is the projection of the weight vector. The best alternative and the decision axis are in the same direction. The length of the decision axis is a strong indicator of selecting alternatives in the same direction. Criteria expressing similar preferences over alternatives are located on the same side of the GAIA plane while conflicting criteria for alternatives are located on the opposite side of the GAIA plane.

Data

In the calculation of IEUI, 23 criteria are evaluated under four dimensions (Table 2). As per TUBITAK scoring, the highest achievable value for a dimension is limited to its weight. The dimensions’ scores are obtained by the weighted average of the criteria evaluated in the range of 0–100. Subsequently, universities are ranked according to the sum of the scores of the four dimensions.

Table 2 Dimensions used in IEUI
Full size table

The codes of 50 universities among 208 universities ranked from highest to lowest EIUI in 2022 are shown in Table 3.

Table 3 Codes of the top 50 universities in 2022 EIUI
Full size table

In this study, four dimensions of EIUI were used to rank universities. Since the original data’s largest dimension value is limited to that dimension’s weight value, TUBITAK weights were used to transform the data so that the score of the relevant dimension falls within the 0–100 scale. Table 7 in the Appendix presents only the scores for dimensions, as it is impractical to display values for 50 universities across 23 criteria.

Analysis

TUBITAK provides the subjective weights for all dimensions based on the decision maker’s expertise and judgment (Table 2). In this study, Shannon’s entropy method as an objective method without considering the decision maker’s preferences was employed to determine reasonable dimension weights for proper ranking of universities. Table 4 shows entropy weights by using the scores given in Table 7. The closer the entropy of a dimension to 1, the less important the dimension is deemed to be. “Intellectual property pool” was identified to be the most important dimension. In addition to Entropy weights, equal weights for dimensions were also used for comparison purposes.

Table 4 Dimension weights
Full size table

For GRA, data in Table 7 was normalized using Eq. (8) since high values of dimensions provide better performance. Difference/Distance values and Grey Relational Coefficients were then calculated based on normalized data (Table 8 in the Appendix).

The decision matrix given in Table 7 was also used for PROMETHEE analysis. The preference parameters, including three different weight sets, are given in Table 5.

Table 5 Preference parameters for PROMETHEE
Full size table

PROMETHEE analysis was carried out using Visual PROMETHEE Academic Edition software. Obtained outranking values for each university are given in Table 9 (see Appendix). The positive flow expresses how much a university dominates the others, and the negative flow how much the others dominate it.

Results

Table 6 illustrates the overall evaluation of universities using GRA and PROMETHEE methods with different dimension weights from Table 4. Notably, the ranks of U1 (Orta Dogu Teknik Univ) and U2 (Sabanci Univ) remained the same across all calculations, including the EIUI rank in the first column. The main reason is that all the dimension values of U1 and U2 surpass those of other universities. Clearly, the combined effects of dimensions, some high and some low, affect the ranking. Estimating this combined effect of dimensions for each university is based on the mathematical framework of the MCDM method and the weight assigned to each dimension.

Table 6 Comparative rankings based on GRA and PROMETHEE for different weights
Full size table

The rankings of the top 10 universities varied little according to different methods. These universities are located in Ankara, Istanbul, Kocaeli, and Izmir, which are attractive cities in terms of employment, infrastructure, and transportation opportunities. Four of the universities in these cities are state-owned technical universities (Orta Dogu Teknik Univ, Istanbul Teknik Univ, Yildiz Teknik Univ, Gebze Teknik Univ.), and they have a sizeable academic staff with developed industrial relations. Others (Koc Univ., Sabanci Univ., Ozyegin Univ, Ihsan Dog. Bilkent Univ.) are private foundation universities with high R&D budgets.

The graphs created to show the differences between the university rankings obtained through the methods (GRA and PROMETHEE) and the IEUI rankings in Table 6 are presented in Fig. 1. According to Fig. 1a, which shows differences in rankings according to TUBITAK weight, it is understood that the rankings align closely with minor variances, except for a few universities (18, 25, 44, and 50). Notably, the differences are more significant in the ranking based on the PROMETHEE method, owing to distinct mathematical perspectives in calculations. Another reason for this is the relatively high variation in the values of dimension D2 (Intellectual Property Pool), as highlighted in Fig. 2.

Fig. 1
figure 1figure 1

Ranking differences between EIUI and Each method according to different weights of dimensions

Full size image
Fig. 2
figure 2

Dimension values for each university

Full size image

Figures 1b and 1c show the differences between the MCDM (GRA and PROMETHEE) rankings and EIUI rankings based on entropy weights and equal weights, respectively. Notably, the differences are particularly evident after the top 10 universities. The minor differences between the rankings obtained by the different MCDM methods can be attributed to differences in the mathematical formulations and computations of the method used to solve the decision problem. According to Fig. 1a–c, which show the difference between the EIUI ranking declared according to the total score given in Table 7 and the GRA and PROMETHEE rankings, although MCDM methods give similar results, it is observed that the deviations increase for different dimension weights.

The Visual PROMETHEE software provides GAIA planes in Figs. 3, 4 and 5, indicating the relative position of the dimensions, universities, and decision (π) axis for more in-depth analysis and understanding of ranking. In the GAIA plane, criteria are shown with axes originating from the center, while universities are represented by dots. The decision axis (thick line) is a visual representation of the weights of the dimensions in the GAIA plane, indicating the importance of each dimension to the decision maker. Dimensions positioned closely reflect similar preferences. The position of the decision axis is closer to the dimension with a higher weight. For the entropy weight, since the total weight of D2 (Intellectual Property Pool) and D3 (Cooperation and Interaction) is 0.715 (see Table 4), the decision axis is close to them (Fig. 3). Likewise, the decision axis in Fig. 5 is close to D1 and D4 for the TUBITAK weight because the total weight of D1 (Scientific and Technological Research Capabilities) and D4 (Economic and Social Contribution) equals 0.55.

Fig. 3
figure 3

GAIA plane for entropy weight

Full size image
Fig. 4
figure 4

GAIA plane for equal weight

Full size image
Fig. 5
figure 5

GAIA plane for TUBITAK weight

Full size image

Figure 3 represents GAIA planes based on entropy weight, with a quality level of 90,9%, indicating a reliable and informative analysis. The position of universities relative to the decision axis reflects their ranking, with those aligned with the decision axis being ranked higher. As shown in Fig. 3, universities (U1-Orta Dogu Teknik Univ, U2-Sabanci Univ, U3-Istanbul Teknik Univ, U4-Yildiz Teknik Univ, U5-Ihsan Dog Bilkent Univ, and U6-Koc Univ) located in the direction of the decision axis have similar and high performance for all dimensions. Conversely, universities located opposite to the decision axis have lower performance. The farther a university is from the direction of the decision axis, the lower its ranking.

The position of universities according to the dimensions is another important evaluation issue. For instance, U9-Ozyegin Univ has high performance for dimensions (D2 and D3) but exhibits low performance in the other dimensions (D1-Scientific and Technological Research Capabilities and D4-Economic and Social Contribution). Improving its performance value in terms of D1 and D4 would consequently enhance U9’s ranking.As illustrated in Fig. 4, representing the GAIA plane for equal weight of criteria, the decision axis aligns with the u-axis, indicating that all criteria are equal. Figure 5 represents the GAIA plane for the entropy weight of criteria. As can be seen in Fig. 5, the decision axis is closer to D1 and D4. The primary distinction among Figs. 3, 4 and  5 lies in the positioning of the decision axis. As the location of the decision axis changes, the ranking of universities correspondingly shifts.

The length of the criterion axes indicates the discriminative power of that criterion among universities. Longer axes imply a higher discriminative power. Dimensions D2 and D4 in Fig. 3, 4 and 5 exhibit nearly the same length, and both are longer than D1 and D3. It can be concluded that these two dimensions differentiate universities from each other.

The direction of the criteria axes is also essential in demonstrating how closely the criteria are related. As shown in Figs. 3, 4 and 5, the axes of D2 and D3 are close to each other, meaning that Universities with a high “intellectual property” also tend to have a “Cooperation and interaction capacity”. Similarly, the axes of D1 and D4 are close to each other. That is, a university with high “Scientific and technological research capabilities” also has high “economic and social contribution”. This insight highlights the interrelationships between dimensions.

Conclusion

Today, universities are not considered only for education and research but also for their active role in the country’s economy through entrepreneurship. With the recognition that new enterprises can create relatively more new jobs, universities have increased their focus on their role in entrepreneurial ecosystem in addition to their core roles of research and teaching. Universities need to develop and strengthen their entrepreneurial and innovative aspects in order to serve the country by ensuring economic development and building an innovative country. Therefore, it is very necessary for the universities to become the entrepreneurial university.

This study conducted a literature review on the theoretical information and methods used to investigate the primary factors and causes that form and define the entrepreneurial university model. TUBITAK has been publishing the Entrepreneurial and Innovative University Index (EIUI) annually since 2012, utilizing four dimensions and ranking universities based on subjective weight to each dimension. Based on EIUI data, the study focused on assessing the impact of different MCDM methods with different dimension weights on ranking order. The dimensions and sub-criteria of EIUI were accepted as they were developed by TUBITAK, and the study is limited to EIUI ranking in its current form.

In order to eliminate the subjectivity in dimension weighting, the entropy method as an objective weighting method was also used. Subsequently, the universities were ranked using MCDM methods (GRA and PROMETHEE), which have their own characteristics and advantages. According to the results, the ranking of some universities has changed significantly (U18, U25, U44, U50), some slightly (U11, U12, U32). Notably, the ranking of the top 10 universities remained essentially unchanged. The results obtained depend not only on the MCDM method chosen but also on the criteria weights. This study revealed that criterion weights were the most influential factor in ranking, leading to different results with the support of graphs. However, in this inference, the effect of normalization methods on the ranking was not considered. Future studies could benefit from examining the effects of different normalization methods on the ranking outcomes.

GAIA plane added visual richness to the results that help decision makers for a comprehensive assessment considering various dimensions. The position of each university, represented by a point in the GAIA plane, is related to its evaluations on dimensions in such a way that universities with similar performance will be closer to each other. The universities (U1 to U6) close to the optimal line in the GAIA plane (Figs. 3, 4, 5) perform well for all criteria. Universities below the optimal line and around dimensions D2 and D3 are good at these dimensions but have low values for other dimensions. Similar comments can be made for universities above the optimal line. Thus, this plane shows which dimension or dimensions universities need to improve to rise to the top in the EIUE rankings.