Introduction

The scientific productivity has a strong impact on the opportunities to enhance the academic career of scholars. Thus, a fair evaluation of scholars’ research activities should always take into account the peculiarities of the scientific area in which they do research.

Since the last decade of the twentieth Century, the dissemination of new technologies has fostered the communication among scholars from different universities and countries, has made a huge amount of data easily available and a lot of scientific works have become increasingly accessible. At the same time, the knowledge of scholars has become more and more specialized. For these reasons, the collaboration among scholars is nowadays a key element for the advance of knowledge in many scientific fields. This is especially true for statisticians, because Statistics is, by its very nature, a multidisciplinary science that provides support to many different fields of knowledge (e.g., social and economic sciences, agricultural sciences, medicine, pharmaceutical sciences, psychology. biology, engineering, etc.). This peculiarity is well synthesized by an aphorism of John Wilder Tukey, a well known famous statistician: “The best thing about being a statistician is that you get to play in everyone’s backyard”.

In Italy, scholars employed in the universities (i.e., researchers, associate and full professors) are clustered in groups (named Scientific Disciplinary Sectors, SDSs) that identify the prominent orientation of the research profile of each scholar. We expect a different style of work and collaboration among scholars belonging to different SDSs that, in turn, is expected to affect the scientific productivity of scholars (e.g., in terms of quantity of scientific works, editorial classification, number of co-authors, scientific field of the co-authors). Moreover, the access to public competitions for the recruitment or for the advancement in the academic role of professor is subordinated to the achievement of a national scientific qualification that takes into account the scientific productivity related to the SDS in which the scholar does research. However, in many cases current legislation groups two or more SDSs in a same Competition Sector (CS) for academic recruitment and advancement purposes.

The research question that arises from the context at issue concerns whether grouping scholars belonging to different SDSs in a same CS truly reflects similar research interests, styles of work and collaboration so as to guarantee a fair comparison among scholars. Aim of this contribution is to propose a methodological approach based on network analysis (Scott, 2000; Kolaczyk, 2009; Newman, 2010) and quantile regression models (Koenker & Bassett, 1978; Koenker, 2005; Davino et al., 2013) to assess the differences among scholars belonging to different SDSs. In particular, we test our approach focusing on the work and collaborative style of Italian academic statisticians. As before mentioned, such class of scholars has, by its nature, an intrinsic propensity to multidisciplinarity. Moreover, being Statistics the disciplinary field to which the authors of this paper belong, awareness of its dynamics can help in understanding the results obtained. However, it is worth noting that the proposed analysis can be applied to any other subset of Italian SDSs and it can also be generalized to all (not Italian) situations in which scholars are grouped by research fields or by any other type of pre-established aggregation.

According to the current legislation, Italian statisticians are grouped in five SDSs and three CSs. For our aim, in the following we define the co-authorship network of Italian statisticians from the entries recorded in the SCOPUS web information system, one of the largest multi-disciplinary database of peer-reviewed journal articles and other scientific contribution. We detect and compute descriptive measures of such network and estimate quantile regression models to assess the effect of the SDS on the network measures, after controlling for individual and university characteristics.

Our contribution fits the international literature about network analysis applied to bibliographic data source and scientific collaborations. Recently, Baccini et al. (2022) implemented a multi-layer network analysis to identify homogeneous clusters of scientific journals where Italian statisticians usually publish: differences among SDS specializations are reflected in clusters they found (i.e., probability theory, theoretical statistics, applied statistics, economics). As concerns the scientific collaboration context in Italy, in the last years numerous scientific contributions (see, among others, Baccini and De Nicolao, 2016; Franceschini and Maisano, 2017; Demetrescu et al, 2020; De Stefano et al, 2022; Akbaritabar et al, 2021) focused on the effects and biases induced by regulations adopted by the Italian Ministry of University and Research (MUR) to promote the research assessment exercises, whereas, at least to our knowledge, consequences of aggregation of SDSs for purposes of recruitment and career advancements have not yet been studied from a scientific point of view. In this contribution we focus on this latter aspect.

We ideally prosecute the work by De Stefano et al. (2013), De Stefano and Zaccarin (2016), and De Stefano et al. (2019). De Stefano et al. (2013) analyzed the co-authorship networks of Italian academic statisticians in the time 1990-2009 resulting from three different databases (Web of Science, Current Index of Statistics, and a database retrieved from the MUR) and, among other things, investigated the collaborative styles of statisticians finding that statisticians from different SDSs have different styles. Focusing on the same databases, De Stefano and Zaccarin (2016) investigated the relation between scholars’ h-index and some descriptive network measures at node level and De Stefano et al. (2019) analyzed the tendency of scholars to cluster in communities. Both these studies corroborated the differences among scientific sectors. Differently from these works, our interest lies in how descriptive measures of the network at the node (i.e., scholar) level are affected by the SDS membership, having a special attention for those sectors that are aggregated by law for recruitment and career advancement purposes.

The remaining part of this contribution is organized as follows. In Sect. “The Italian structure of academic scientific fields” the actual Italian regulation that established SDSs and CSs is illustrated. In Sect. “Data collection and network characterization” details are provided on the collection from web of data concerning the scientific publications of scholars in the field of Statistics. In Sect. “Network description” the collaborative network of Italian statisticians is described. In Sect. “Quantile regression models” theoretical fundamentals about quantile regression models are illustrated and in Sect. “Results and discussion” evidence on the network of statisticians from a quantile regression analysis is provided and discussed. In Sect. “Conclusions” some final remarks conclude the contribution.

The Italian structure of academic scientific fields

The scientific collocation of scholars working in the Italian university system plays an important role, because it drives several organizational aspects of the academic life, such as the definition of bachelor and master degree programs, the constitution of university departments, and the recruitment of scholar staff (i.e., researchers and professors). To date, the scientific collocation of scholars is articulated on three main levels: 86 macro-fields, 190 fields (i.e., the Competition Sectors—acronym CSs), and 383 sub-fields (i.e., the Scientific Disciplinary Sectors—acronym SDSs), as stated by the Ministerial Decree DM 855/2015. The legislative milestones that led to the current organizational set-up are provided at the web page of the MURFootnote 1.

The current grouping scheme originates from an antecedent streamlined structure established by the Ministerial Decree DM 4/10/2000 that defined (annex AFootnote 2) the 14 research areas and related SDSs in which academic scholars are still framed, and stated (annex BFootnote 3) the typology of research activity characterizing each SDS. Framing academic scholars in SDSs has a practical utility, as the classification in SDSs is applied to the comparative assessment procedures, as stated at article 2 of the Ministerial Decree at issue.

In 2010 a radical reform of the Italian academic system has been released with the Law 240 of 30/12/2010. Among other things, this reform introduced a national scientific qualification as a necessary (but not sufficient) preliminary condition for career advancement in the Italian academy (i.e., to progress from researcher to associate professor or from associate professor to full professor). In this regard, Law 240/2010 (article 15, paragraph 1) introduced the CSs, that are a hierarchical aggregation of SDSs (each CS is articulated in one or more SDSs and each SDS belongs to just one CS) and that must be linked to the procedures for the recognition of the national scientific qualification. The detailed list of CSs, with the related SDSs nested within them, is defined in the Ministry Decree DM 855/2015 (annex AFootnote 4) together with the description of the typology of research activity characterizing each CS (annex BFootnote 5).

In summary, Italian academic scholars are currently classified both in CSs and in SDSs according to their research activity. Regarding the career progression, the national scientific qualification is the first requirement, and those who attained this qualification may compete in a public comparative examination. The procedure for the national scientific qualification relies on the grouping in CSs, whereas the public comparative examinations rely on the grouping in SDSs.

The aggregation of SDSs in CSs was carried out following criteria essentially linked to the areas of research activity characterizing a certain SDS and the relative number of scholars belonging to it. Therefore, with rare exceptions, the SDSs nested in a same CS are usually those with a low number of scholars and/or with similar or quite overlapped research topics as it can be deduced from the descriptive declaration of each SDS (see the above cited Annex B of the Ministerial Decree DM 4/10/2000).

As anticipated in the previous Section, Italian academic statisticians are classified in three CSs that include five SDSs:

  • CS 13-D1: Statistics

    • SDS S01: Methodological Statistics

    • SDS S02: Statistics for Experimental and Technological Research

  • CS 13-D2: Economic Statistics

    • SDS S03: Economic Statistics

  • CS 13-D3: Demography and social statistics

    • SDS S04: Demography

    • SDS S05: Social Statistics

The aggregation of sectors S01 and S02 in the same CS is mainly due to the very low number of scholars belonging to the SDS S02. Differently, the overlapping of most of the research topics is the main reason that justified the aggregation of sectors S04 and S05 in the same CS.

However, the reasons above mentioned do not guarantee that scholars belonging to different SDSs and aggregated in a same CS have the same working style in terms of, among others, propensity to collaborate with (few or numerous) other scholars of the same or different SDSs. In turn, these elements affect the scientific productivity of a scholar, such as the quantity of published papers and the typology of scientific journals (e.g., national journal, international journals, journals with or without impact factor, monographs), on which the national scientific qualification is based. Therefore, to avoid the aggregation of scholars coming from SDSs characterized by substantially different styles of work, a quantitative analysis of these differences proves to be an additional useful instrument to support decision makers for a possible critical review of the composition of the CSs.

Data collection and network characterization

In developing this work we had to gather and manipulate information from different sources. The starting point was the list of the 783 statisticians employed as tenured teaching staff in an Italian (public or private) university institution at the end of February 2021. This list can be publicly downloaded from the MUR websiteFootnote 6. All the scholars in this list are classified in one of the five SDSs cited in Sect. “The Italian structure of academic scientific fields”, that is, S01, S02, S03, S04, and S05. Statisticians working within the Italian university system but without tenure, such as research fellows and PhD students in Statistics, as well as statisticians working outside of the Italian university system are excluded from the list.

As well known, SCOPUS is one of the largest multidisciplinary registry of peer-reviewed journal articles. It covers more than 30 million publications from 1996 to the present. Authors with publications referenced in SCOPUS are automatically assigned a unique Author Identifier (named SCOPUSId) to avoid disambiguation problems when querying the registry. Unfortunately, the SCOPUSId is missing in the set of information downloadable from the MUR website. We were able to retrieve the SCOPUSId of 758 out of 783 statisticians thanks the features of the Scival (by Elsevier) web serviceFootnote 7.

SciVal is an analytical insights tool based (and weekly updated) on data collected by SCOPUS, designed for research performance evaluation. Inside Scival, the SCOPUSId is obtainable in a semiautomatic way: the association is performed directly by the system if no ambiguity is detected. Otherwise, possible ambiguities are highlighted and a manual intervention is required to resolve such cases. The need to resolve ambiguities arises in the rare cases where multiple SCOPUS profiles have been generated for the same scholar, since the SCOPUS registry is updated through the information gathered from published papers that may contain incomplete authors’ surname and/or given-names (respectively in the case of multiple surnames or first names) or old affiliations. Obviously, the richer the scholar information passed to Scival, the better the chances of identifying the right SCOPUS profile. In querying Scival, we used the full set of information released by the MUR website, and the manual intervention to resolve ambiguities was only necessary for about fifty scholars (whose SCOPUSId was retrieved browsing manually the SCOPUS website or from their curriculum published on his/her academic institution website).

In the literature, some authors involved with the analysis of similar sources of information (describing scientific collaboration between scholars) approached the disambiguation problem in different ways. De Stefano et al. (2013) compared the network of collaborations between Italian statisticians recurring to three different bibliographic archives (one general, one thematic and one national), each of them using specific key identifiers. The authors’ information gathered from the MUR list about the tenured Italian academic statisticians was used to directly query each registry. However, this strategy has resulted in the need for manual interventions in the querying phase and final data cleaning procedures were required to eliminate possible errors (duplication of records or wrong attributions). Fuccella et al. (2016) tried to derive a unified archive merging different sources of bibliographic data relative to a bounded scientific community. In exploiting this task they faced two main challenges: the implementation of a records linkage procedure to avoid (or minimize) duplication of data referring to the same paper, and the need to disambiguate authors that was resolved recurring to an unsupervised technique due to the lack of training data. Carchiolo et al. (2022) designed a special algorithm generating a list of queries to be directly submitted in SCOPUS on the basis of the information gathered by the MUR website (shuffling the given name, if more than one, together with the initials of the first name and the affiliation; in case of failure, the condition about affiliation was discarded and queries repeated). Differently from the two works above mentioned that analyzed different sources of information, Carchiolo et al. (2022) used only SCOPUS as source of bibliometric data, but, differently from our proposal, they omitted the preliminary step of retrieving the authors’ identifiers, which has proved to be extremely useful in reducing disambiguation issues.

As anticipated above, the SCOPUSId was missing for 25 statisticians out of 783 from our initial list. They were scholars without scientific contributions indexed in SCOPUS when the list of statisticians was extracted (generally because they were very young researchers recently employed).

The SCOPUSId of the 758 statisticians was then used to download the list of their research products from the SCOPUS website. The download was performed using the SCOPUS “advanced search” functionality and returned a dataset made up of 14,838 records, each of them identified by a unique alphanumeric code (labeled EId) assigned by the SCOPUS bibliographic information system. A lot of additional information is also available for download from the SCOPUS registry: authorship information, bibliographical information, abstract and keywords, citation information, funding details, and others of minor importance (e.g., the eventual conference in which the paper was presented). To keep our database manageable and to avoid computational efforts in the later phases of the analysis, we limited the query extension to the authorship information, the entire citation information set and some bibliographical data like the serial identifier of the scientific journal that published the paper and the language in which it was written.

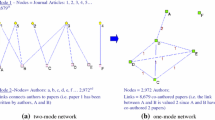
It is worth noting that the two datasets (the authors list and the related works list) are interrelated sources of information in a specific domain of knowledge, that is, the scientific collaboration among scholars where at least one of the authors is a tenured Italian academic statistician. Such a framework can conveniently be represented by the notation of the Entity-Relationship model (firstly proposed by Chen, 1976), with the relationship between authors and related works belonging to the so called “many to many” relationships class: each scholar collaborates on at least one work and each work can be co-authored by more than one scholar. The strength of the last relation is expected to be particularly high among statisticians because of the various fields of applications that characterize Statistics. To confirm this hypothesis, the SCOPUS product list revealed that about 90% of the downloaded articles were written by two or more authors. Unfortunately, such list was released with the information about the authorship merged in a single field (a unique sequence of all the author identifiers separated by semicolons). To overcome this inconvenience, we developed a special Visual Basic for Application (VBA) routine to parse and decompose each authorship string. This routine resulted in a dataset of 65,797 distinct combinations of the two unique identifiers previously described (EId and SCOPUSId); among these, only 18,813 pairs of key identifiers have a SCOPUSId corresponding to one of the 758 Italian statisticians registered in the MUR registry. The very high number of pairs not referable to scholars referenced in the MUR list is another element supporting the multidisciplinary nature of Statistics, although part of them could be attributable to statisticians working abroad or (in a vary minimal part) to PhD students or other non-tenured statisticians working within the Italian university system. This dataset was passed in input to a specially devised algorithm, developed inside the R environment, aimed at building the matrix describing the number of products co-authored by each pair of authors. The Entity-Relationship model describing the relations between the various sources of information used to describe the network of collaborations among Italian statisticians is depicted in Fig. 1.

Fig. 1
figure 1

Entity-relationship model of the available data

Full size image

Obviously, starting from the MUR list of the tenured Italian academic statisticians, the final number of scholars identified is much greater the initial one: the resulting scientific collaboration network is composed of 23,339 nodes, corresponding to the 758 Italian academic statisticians and their co-authors (non-statisticians as well as statisticians not belonging to the tenured staff of the Italian academy), and 159,250 edges, where each edge connects a pair of nodes representing two scholars co-authored at least one of the 14,838 papers referenced on SCOPUS. It must be emphasized that the distinction between statisticians and non-statisticians cannot be retrieved from the SCOPUS database: indeed, the lists of “topics” and “subject areas” provided for each author embrace a wide range of objects and, thus, it is not possible to univocally attribute a scholar to a specific matter (i.e., statistics or other subjects).

Each edge of the network is weighted inversely according to the number of co-authors for each paper, following the proposal of Newman (2001). Assuming that the reciprocal knowledge between co-authors i and j is as smaller as higher is the overall number of scholars that collaborated on the same paper p, weight \(w_{ij}\) of the edge connecting nodes i and j is defined as

$$\begin{aligned} w_{ij} = \sum _p\frac{1}{N_{p(ij)}-1}, \end{aligned}$$
(1)

where \(N_{p(ij)}\) is the total number of co-authors of paper p co-authored by i and j. The assumption underlying this formulation is that scientist shares his/her time equally between the other \(N_{p(ij)}-1\) co-authors. We are aware that in presence of at least three co-authors, a scientist generally spends more time with some co-authors than with others. However, due to the absence of such information (the time spent) we believe this is a good approximation to make.

For the aims of the present study, in what follows we focus on the sub-network composed of the 758 nodes, which correspond to the Italian academic statisticians distributed among the five SDSs (as mentioned in Sect. “The Italian structure of academic scientific fields”), and the related 1730 edges, with each edge connecting a pair of Italian academic statistician scholars that co-authored at least one work. Edges are weighted as above described, thus they account for the total number of co-authors of each author.

Relying on some specific network indices detailed in the next section that summarize the scholars’ work style, the present contribution will investigate the following two main research questions:

Q1::

Does belonging to a certain SDS have a significant impact on a scholar’s work style?

Q2::

Do SDSs aggregated in a same CS differ significantly from one other?

Network description

Some descriptive statistics about the set of scholars involved in the analysis are reported in Table 1 (marginal distributions) and in Table 2 (conditioned distributions per SDS).

Table 1 Distribution of Italian academic statisticians, by SDS, gender, academic role, geographical area, university size, university management type, type of delivered academic curricula (absolute and relative frequencies)
Full size table
Table 2 Distribution of Italian academic statisticians per SDS, by gender, academic role, geographical area, university management type, type of delivered academic curricula, and university size (conditioned relative frequencies, given the SDS)
Full size table

The major part of the statisticians (almost 60%) belongs to the S01 SDS, followed by S03 (almost 20%); S04 and S05 collect about the 9% of statisticians (S04: 8.6%; S05: 9.9%), whereas the remaining 2.8% belongs to S02. Genders are equally represented in sectors S01, S02, and S05, while a preponderance of males is in S02 and S03 (57.1 and 59.2%, respectively) and a preponderance of females in S04 (61.5%). The role of associate professor is the one with the highest frequency (41.6%), followed by the full professor (29.6%); researchers as a whole (i.e., fixed-term and permanent) represent a total of 28.9% reaching one-third in S05 and exceeding the 40% in S02. Other statistics reflect the territorial distribution of academic institutions and related characteristics within the nation. Universities are generally equally distributed over the national territory, with a predominant presence of state institutions delivering a wide range of academic curricula. This situation is reflected in the distribution of statisticians belonging to S01, while several differences emerge for scholars in the other SDSs. Scholars of S02 and S05 are mainly concentrated in universities located in the South and islands (61.9 and 44.0%, respectively), whereas universities located in the Centre collect one third of statisticians of S03 (32.9%) and S04 (32.3%). Moreover, the percentage of scholars employed in private universities is marginal for SDSs S02 (4.8%) and S03 (6.6%) and, on the opposite, is more consistent for S04 (12.3%) and S05 (10.7%). The major part of statisticians belongs to mega (44%) and large (31%) universities; only a residual part works in a small university. This is especially true for scholars of S04 and S05, of whom 80% are employed in large and mega universities; on the opposite, medium size universities collect a high percentage of scholars of S03 (30.3% vs an average of 17.4%) and small size universities are most attractive for scholars of S02 (14.3% vs an average of 7.7%).

The network of scholars is represented in Fig. 2, in which each scholar is represented by a node with a size proportional to the number of his/her publications, the edge size proportional to the weight \(w_{ij}\), and the node color that identifies the SDS the scholar belongs to. Some global network measures are also provided in the Table 3, for the entire network and separately by SDS.

Fig. 2
figure 2

Graph of the network, with one node for each scholar and one edge for each pair of scholars that co-authored at least one work (node size proportional to the number of publications; edge size proportional to the edge weight; color specific for each SDS)

Full size image
Table 3 Network cohesion measures: density, average clustering, and average path length coefficients, by SDS
Full size table

Looking at Table 3, the network of Italian academic statisticians presents low values both for density (proportion of observed edges relative to potential edges equal to 0.006), for average clustering (proportion of triples that close to form triangles equal to 0.272), and for average path length (average number of steps required to connect any pair of nodes along the shortest path equal to 3.51). A certain variability can be observed at level of SDS, with a higher density for sectors S02 and S04, a higher tendency to form clusters for sectors S03 and S05, and a substantial inefficiency of flows across the network for sector S03 (average path length higher than the logarithm of the nodes of the sub-graph; Kolaczyk, 2009).

As displayed in Fig. 2, the network of Italian academic statisticians is quite complex. For this reason, the analysis of the network requires to compute specific indices that allow us to evaluate the work style of scholars from multiple perspectives. First, a global quantification of the scientific production of a scholar is provided counting the number of papers referenced on SCOPUS, including single-author papers. Second, the propensity to collaborate with other scholars may be measured through certain indices developed in the literature about network analysis (Scott, 2000; Kolaczyk, 2009; Newman, 2010; Luke, 2015): node degree, node degree strength, node centrality indices, and index of propensity to collaborate with other members of the network.

The node degree is the number of edges incident upon a certain node (i.e., coming in or going out), thus accounting only for the presence or absence of an edge and not for its weight. In our context, the node degree corresponds to the number of Italian academic statisticians’ co-authors.

Differently from the node degree, the node degree strength is obtained by summing up the weights of edges incident to a certain node, thus providing a scholar’s weighted number of papers in co-authorship with other scholars.

The tendency of a node to play a central role with respect to the other nodes may be measured through centrality indices: among others, we consider the betweenness centrality index, the harmonic centrality index, and the eigenvector (eigenvalue) centrality index. All these indices are computed on the weighted network.

In detail, the betweenness centrality index denotes the extent to which a node is located between other pairs of nodes. In more detail, nodes with high betweenness lie on a large number of non-redundant shortest paths between other nodes. Scholars with high betweenness centrality can be conceived as bridges among other scholars and control the flow of collaborations in the network.

The harmonic centrality index (also known as valued centrality; Rochat, 2009) measures how much a node is close to many other nodes and it is defined as the mean inverse distance of a node to all the other nodes. Hence, high values of the harmonic centrality index reveal scholars holding a central position in the network. The inverse distance to an unreachable node is considered to be zero. This index is a generalization of the closeness centrality index for unconnected graphs.

The eigenvector centrality index measures the extent to which a node is connected with other well-connected nodes; it resembles the authority score. Note that a scholar can have few connections with other scholars, but a high eigenvector centrality whenever the few connections are with nodes that, in turn, are well connected.

Another interesting measure to evaluate the working style of a scholar is the transitivity index (also known as clustering coefficient). It measures the probability that the adjacent nodes of a node are connected and is calculated by the ratio between the observed number of closed triplets and the maximum possible number of closed triplets in the graph. Briefly, the transitivity index denotes the propensity to collaborate with co-authors of the node’s co-authors.

As a further measure to characterize the propensity to collaborate, we define an index to disentangle the propensity of each Italian academic statistician to collaborate with other members of the group of Italian academic statisticians and with other scholars that, as above pointed, include both non-statisticians and statisticians not belonging to the tenured staff of the Italian academy. For this aim, we rely on a modified version of the Goodman and Kruskal’s \(\gamma\) coefficient (Goodman & Kruskal, 1954), which is used in the context of contingency tables to measure the association between ordered variables and based on the comparison between concordant and discordant pairs of units. Goodman and Kruskal’s \(\gamma\) coefficient was originally applied in the context of collaborative networks by Krackhardt and Stern (1988), with the name of External-Internal (EI) index: it was based on the comparison of the number of internal links (i.e., in our context the number of edges among Italian academic statisticians) and external links (i.e., in our context the edges between Italian academic statisticians and other co-authors). We propose to modify the original EI index to account for the weights of the edges, that is,

$$\begin{aligned} EI_i = \frac{\sum _j w_{ij} \mathcal {I}\{s_j = 0\} - \sum _j w_{ij} \mathcal {I}\{s_j = 1\}}{\sum _j w_{ij} \mathcal {I}\{s_j = 0\} + \sum _j w_{ij} \mathcal {I}\{s_j = 1\}}, \end{aligned}$$

with \(w_{ij}\) weight of the edge linking node i and node j, computed as in Eq. (1); \(\mathcal {I}\{\cdot \}\) indicator function equal to 1 if its argument is true; \(s_j\) dummy equals 1 if co-author j is an Italian academic statistician (internal link), 0 otherwise (external link). In synthesis, the denominator of \(EI_i\) denotes the total number of weighted edges that accounts for the number of co-authors, whereas the numerator is the difference between the number of external and internal weighted edges. Note that the definition of EI index relies on the general network composed of 23,339 nodes and 159,250 related weighted edges, defined in Sect. “Data collection and network characterization”. Thus, index i ranges from 1 to 758, being specific of each Italian academic statistician, whereas index j ranges from 1 to 23,339, being specific of all the nodes (i.e., Italian academic statisticians with tenure and their co-authors) of the general network, from which the sub-network in Fig. 2 derives. In virtue of its definition, the EI index takes values in the range \([-1, +1]\), being equal to \(-1\) when scholar i collaborates only with other Italian academic statisticians and equal to \(+1\) when scholar i collaborates only with scholars external to the sub-network of Italian academic statisticians; value 0 denotes no particular propensity to work with scholars internal or external to the sub-network.

In Table 4 descriptive indices are displayed that synthetize the distribution of the network nodes’ measures; graphical representations are reported in the Appendix A (Figs 3, 4, 5, 6, 7, 8, 9, 10).

Table 4 Distribution of total number of publications, node degree, node degree strength, betweenness centrality index, harmonic centrality index, eigenvalue centrality index, transitivity index, and EI index, by SDS
Full size table

In summary, descriptive analyses display distributions with a strong skewness, positive for total number of publications, degree, degree strength, betweenness centrality, eigenvector centrality, and (but at a lower extent) transitivity, and negative for the EI index; only harmonic centrality distribution appears substantially symmetric, but with excess of zeros. This implies a network characterized by many scholars with similar characteristics and just a few of them with extreme levels. Moreover, the distributions of the descriptive indices differ among SDS. Scholars of S02, followed by colleagues of S01, distinguish for the high number of publications (mean = 31.2, 26.9 and median = 25.0, 21.0, respectively) and, on the opposite, scholars of S05 characterize for the lowest number of publications (mean = 19.5; median = 15.0); all sectors show high variability and outliers, with the exception of S02 (coefficient of variation = 66.2). The highest number of co-authors is observed for scholars of S04 (mean = 6.0; median = 5.0) and the smallest one for scholars belonging to S03 and S04 (mean = 3.7, 3.8, respectively; median = 3.0). As far as the number of papers co-authored with other statisticians (node degree strength), the highest values are observed in sector S01 (mean = 9.0; median = 6.5), followed by S04 (mean = 7.9; median = 5.0), whereas the smallest values concern sectors S05 (mean = 4.7; median = 4.0) and S02 (mean = 5.3; median = 3.7). This last result is coherent with a higher tendency for scholars in S02 to collaborate with scholars external to the sub-network of Italian academic statisticians (first quartile of EI index = 0.4) with respect to scholars in S04 and S01 (first quartile of EI index = − 0.3 and − 0.2, respectively). Furthermore, the presence of researchers with a relatively high centrality position tends to be the highest in S04 and the lowest in S05 and S03, as outlined by the comparison of percentiles and mean values of betweenness centrality and harmonic centrality indices; no relevant information can be retrieved by the eigenvector centrality, whose values are around 0. Finally, as concerns the propensity to collaborate with co-authors of their own co-authors, transitivity index tends to be distributed along the entire range 0–1 with an average value around 0.40 (median equal to 0.333); there is a substantial homogeneity among the SDSs.

The skewed shape of these distributions suggests to perform inferential analyses based on models, such as the Quantile Regression (QR) models, that provide a characterization of this type of data richer than ordinary linear regression models. Details on these models are provided in the next section.

Quantile regression models

QR was originally proposed by Koenker and Bassett (1978) (for recent references see, among others, Koenker, 2005; Davino et al., 2013). Authors introduced their proposal observing that in the Ordinary Least Square (OLS) method, the only information obtained modelling the relationship between a certain response variable Y and the vector of covariates \({\varvec{X}}\) is the way in which the mean of Y varies as \({\varvec{X}}\) varies. Modelling the expected value of Y conditionally on covariates can be restrictive, mainly when the basic assumptions of the OLS model (e.g., the normality of the response variable) are violated. Moreover, OLS linear models often fail in describing heteroscedastic data and in presence of outliers. QR overcomes this limits, as it focuses on assessing the effect of covariates on the quantiles (other than the mean) of the response variables, which are robust to the presence of outliers and other leverage points. Moreover, QR does not make assumptions about the distribution of the model’s residuals as it happens for OLS linear models. The unique drawback of such methodology is its lower efficiency compared with OLS linear model; thus, a higher sample size is required to achieve the same power (Geraci & Bottai, 2014).

The estimates of the coefficients of a QR model generally rely on the hypothesis that the conditioned quantile can be expressed as a linear combination of the set of covariates; such setting is referenced as “regular” QR modeling. Sometimes, this assumption might be too restrictive leading to a non-parametric estimation of parameters. In our case the linearity assumption is suitable because the covariates in the model are of qualitative nature (measured on a nominal scale) and the estimation of their effect requires the preliminary dichotomization of their categories: namely, we do not consider relevant to hypothesize a nonlinear approach in a context of binary covariates.

The QR model is formulated defining the generic quantile \(\omega _{\tau }\) of order \(\tau\) (with \(\tau \in \{0, \ldots , 1\}\)) for the distribution of variable Y as the value satisfying the following condition:

$$\begin{aligned} \hat{Q}_{\tau }(Y) = \text {argmin}_{\omega _{\tau }} \left\{ \sum _{i: \, Y_i \ge \omega _{\tau }} \tau \cdot \mid Y_i - \omega _{\tau }\mid + \sum _{i: \, Y_i < \omega _{\tau }} (1-\tau ) \cdot \mid Y_i - \omega _{\tau }\mid \right\} \end{aligned}$$
(2)

Note that, when \(\tau = 0.5\), the above formula simplifies as

$$\begin{aligned} \hat{Q}_{0.5}(Y) = \text {argmin}_{\omega _{0.5}} \left\{ \sum _{i} \mid Y_i - \omega _{0.5}\mid \right\} , \end{aligned}$$

thus obtaining \(\omega _{0.5}\) equal to the median, namely the value that minimizes the sum of the absolute deviations.

The QR model for a response variable Y regressed on a vector of covariates \({\varvec{X}}\) is formulated as

$$\begin{aligned} y_i = {\varvec{x}}_i'{\varvec{\beta }}_{\tau } + e_{i\tau } \quad i = 1, \ldots , n, \end{aligned}$$
(3)

with \(y_i\) response variable observed on individual i, \({\varvec{x}}_i = (x_{i1}, x_{i2}, \ldots , x_{ij}, \ldots , x_{iJ})'\) vector of J covariates observed on individual i, \({\varvec{\beta }}_{\tau } = (\beta _{1\tau }, \beta _{2\tau }, \ldots , \beta _{j\tau }, \ldots , \beta _{J\tau })'\) vector of regression coefficients, and \(e_{i\tau }\) error component. Assuming that \(\hat{Q}_{\tau }(e_{i\tau }\mid {\varvec{x}}_i) = 0\), the quantile of Y of level \(\tau\) conditionally on \({\varvec{X}}\) is given by \({\varvec{x}}_i'{\varvec{\beta }}_{\tau }\), and the estimation of the parameters vector \({\varvec{\beta }}_{\tau }\) can be obtained solving a linear programming problem (Buchinsky, 1998).

It is worth to be noted that the OLS regression model \(y_i = {\varvec{x}}_i'{\varvec{\beta }}+ e_i\) is obtained along a similar reasoning, by assuming \(E(e_{i}\mid {\varvec{x}}_i) = 0\): in such a case, \({\varvec{x}}_i'{\varvec{\beta }}\) represents the expected value (instead of a quantile of order \(\tau\)) of Y conditionally on \({\varvec{X}}\). However, differently from the OLS regression where only a vector of regression coefficients \({\varvec{\beta }}\) is given, in the QR the vector of regression coefficients \({\varvec{\beta }}_{\tau }\) changes according to \(\tau\): given \(\tau\), coefficient \(\beta _{j\tau }\) denotes how the \(\tau\) quantile of Y changes for each unit increase of covariate \(X_j\) (\(j = 1, \ldots , J\)), conditionally on the levels of the other covariates. Thus, the QR allows to analyze the impact of covariates on the various points of the distribution of the response variable Y, not merely on its conditional mean (as in the OLS regression). Under the hypothesis of normality of the errors terms OLS has optimal properties, but when the hypothesis of normality does not hold the QR estimators can be more efficient than the OLS one (and the L-estimator based on a linar combination of the various \(\beta _{\tau }\) is always more efficient than the OLS one). For this reason QR represents an useful instrument when a variable has a skewed shape, because in this case its conditional mean is not an interesting outcome to investigate. Furthermore, the estimates of the parameters vector are not affected by the possible presence of outliers in the distribution of the response variable.

QR models suitably specified allow us to answer the research questions established at the end of Sect. “Data collection and network characterization”, which can be restated with specific reference to the QR modelling approach as:

Q1::

Does the SDS represent a significant determinant of the responses’ quantiles? And, conditionally on an affirmative answer to this question, is the effect of the SDSs constant across the quantiles?

Q2::

Do SDSs aggregated in a same CS have regression coefficients that are significantly different from each other?

To answer the above questions we specify a QR model as in Eq. (3) for each of the node’s descriptive measures defined in Sect. “Network description”. The covariate of main interest is represented by the SDS, with S01 as reference level (vs. S02, S03, S04, and S05). We also control for the observed individual and university characteristics displayed in Table 1. In particular, we consider gender (reference: female) and academic role (reference: associate professor) at individual level, whereas at university level we take into account geographical area where the university is located (reference: centre), type of management (reference: state), type of degree programs delivered by the university (reference: generic curricula), and university size (reference: mega).

Given the substantial positive skewness of the responses’ distributions, we focus on the orders \(\tau = 0.25, 0.50, 0.75, 0.90, 0.95\); only for the EI index we focus on \(\tau = 0.05, 0.10, 0.25, 0.50, 0.75\) to account for the negative skewness.

Results and discussion

In this section results related with the QR models are illustrated and discussed. We first focus on the effect of the SDS on the response variables and, then, we provide details of the effects of the control variables.

We outline that QR models for eigenvector centrality index and transitivity index do not return any significant effect of independent variables, thus these two response variables will not be further discussed below.

Evidence about the effects of SDS

To make easier the readability of the results, we disentangle the output in order to answer research questions Q1–Q2. Note that all results shown in this section refer to models controlled for the individual and university characteristics, but, for the sake of space, only coefficients related to variable SDS are displayed, whereas coefficients related to the control variables and the interaction effects are shown in the Appendix B.

Q1: does belonging to a certain SDS have a significant impact on a scholar’s work style?

First, to answer question Q1 about the global effect of SDS on the response variables’ quantiles, for each value of \(\tau\) we compare a QR model without covariate SDS with a QR model with covariate SDS through an ANOVA test, being constant all the other covariates. Table 5 displays the resulting p-values.

Table 5 Global effect of SDS on response variables’ quantiles: p-values of ANOVA tests that compare models with and without SDS, by \(\tau\)
Full size table

Looking at Table 5, there is a clear evidence of a significant effect of SDS on the quantiles of number of publications, degree, degree strength, and, mostly, harmonic centrality and EI index, whereas the effect of SDS on the betweenness centrality is definitely weaker, being significant only for \(\tau = 0.75\) and \(\tau = 0.90\). Details about the differences between SDSs are provided in Table 6 that shows the estimated regression coefficients of variables S02, S03, S04, and S05 (versus S01), together with the corresponding standard errors and significance levels.

Table 6 Effect of SDS on the response quantiles: regression coefficients, standard errors (in parenthesis) and statistical significance (.: \(\alpha = 0.10\); *: \(\alpha = 0.05\); **: \(\alpha = 0.01\); ***: \(\alpha = 0.001\)), by SDS (ref. S01) and \(\tau\)
Full size table

Taking as reference sector S01, scholars from sector S02 tend to have a number of publications 4–11 units higher with respect to colleagues from sector S01, whereas scholars from the remaining sectors show an often significant lower number of publications (range of regression coefficients: \(-2\) to \(-13\)). On the other hand, focusing on the weighted number of papers in coautorship (node degree strength) all sectors show values significantly lower than S01, with a peak of a difference of more than 6-7 units (\(\tau = 0.90, 0.95\)) for scholars in S02 and S05; only sector S04 does not present significant differences with respect to S01. Moreover, the number of co-authors (node degree) is 1-2 units lower for scholars in sectors S03 and S05; a similar evidence holds for sector S02 for extreme quantiles \(\tau = 0.90, 0.95\). As far as the betweenness centrality generally not significant or, at most, weak (\(\alpha = 0.10\)) differences rise. Differently, significant differences are observed for the harmonic centrality: with respect to scholars of S01, colleagues of sectors S03 and S05 tend to be more distant from the other nodes, whereas scholars of S02 do not present significant differences. Finally, the propensity to collaborate with scholars others than Italian academic statisticians (EI index) is generally higher for scholars from sectors S02 and S05 and lower (but not significant) for scholars from sector S04 in comparison with scholars from S01.

ANOVA tests comparing models with different quantile levels are performed to verify the assumption that the effect of SDS is constant across the quantiles. Resulting p-values are displayed in Table 7.

Table 7 Effect of SDS on the response quantiles: p-values of ANOVA tests that compare models with different values of \(\tau\) (and same covariates)
Full size table

Results are different according to both the response variable and the SDS. For instance, the effect of S02 (with respect to S01) is quantile-dependent for the degree strength (p-value = 0.008) and the EI index (p-value = 0.012). In detail (Table 6), the negative difference in the weighted number of papers in coautorship ranges from less than 1 (\(\tau = 0.25\); not significant coefficient) to around 7 (\(\tau = 0.90, 0.95\)); the EI index presents no significant difference for \(\tau = 0.05\) and \(\tau = 0.10\), while it significantly increases for higher quantiles (0.53 for \(\tau = 0.25\) to 0.22 for \(\tau = 0.95\)). In addition to the degree strength and the EI index, the effect of S03 is quantile-dependent (p-value = 0.010) also for the node degree (difference of the regression coefficients ranging from around 0 to -2, Table 6). Differently, sector S04 presents differential effects only on the quantiles of the harmonic centrality index (p-value = 0.002), with differences in the regression coefficients that range from positive values for \(\tau = 0.25, 0.50, 0.75\) to negative values for \(\tau = 0.90, 0.95\) (Table 6). Finally, sector S05 distinguishes for significantly different effects on the quantiles of node degree (p-value = 0.007) and node degree strength (p-value < 0.0001): indeed, the difference (with respect to S01) in the number of co-authors ranges from around 0 (for \(\tau = 0.25\)) to -2 (for \(\tau = 0.75, 0.90\)) and the difference in the weighted number of co-authored papers ranges from -1 (for \(\tau = 0.25\)) to over -6 (for \(\tau = 0.90, 0.95\)).

In summary, the results above discussed are consistent with the assumption (research question Q1) that the aggregation of Italian academic statisticians in different disciplinary sectors reflects different styles of work, mainly with reference to the scientific productivity measured through the total number of publications and the weighted number of co-authored papers (node degree strength), and the propensity to collaborate with other scholars in general (node degree) and with scholars outside the sub-network of Italian academic statisticians (EI index). No difference or just weak and sporadic differences are observed with respect to the tendency to play a central role in the network.

Q2: do SDSs aggregated in a same CS differ significantly from one other?

To favor the comparison between pairs of SDSs clustered in a same CS, that is, S01 vs. S02 and S04 vs. S05, Table 8 reports the quantile levels for which the estimated regression coefficients are statistically significantly different.

Table 8 Effect of SDS: statistically significant differences between S01 vs. S02 and S04 vs. S05 (if not indicated: \(\alpha = 0.05\); \(.: \alpha = 0.10\))
Full size table

As far as sectors S01 and S02, significant differences involve all the investigated response variables with respect to several quantiles, with the only exception of the harmonic centrality index. Scholars belonging to S01 and S02 positioned in the centre of the distributions (i.e., median) present significant differences with respect to the total number of publications, the weighted number of co-authored publications, and the propensity to collaborate outside the network of Italian academic statisticians (EI index). Moreover, scholars positioned in the extreme tails of the distributions (i.e., 90% and 95% quantiles) differ also for the degree and the betweenness centrality, other than for the degree strength.

A different situation is depicted for S04 and S05. On one hand, there is no significant difference in the number of publications between scholars from the two sectors. On the other hand, scholars positioned in the centre of the distribution and in the extreme quantiles show significant differences with respect to the other variables.

To summarize, these results allow us to positively answering our second research question (Q2) concerning the presence of significant differences between those disciplinary sectors that have been aggregated by law in a same group for competitions (a same CS), that is, S02 grouped with S01 in the CS Statistics and S05 grouped with S04 in the CS Demography and social statistics. In both cases, the network analysis provides evidence in favor of different styles of work, thus advising against a tout-court aggregation of the two pairs of SDSs.

Effects of control variables

In this section we briefly summarize the effect of control variables used in the QR models (estimates of regression coefficients together with standard errors are displayed in the Appendix B, Tables 9, 10, 11, 12, 13, 14).

Among the variables considered in the estimated models, the academic role presents the most relevant effects. Indeed, full professors have both a total and a weighted number of publications (node degree strength), a number of collaboration with other Italian academic statisticians (node degree), and a propensity to control the flow of collaborations in the network (betweenness centrality) significantly higher than associate professors; the opposite holds for fixed-term and permanent researchers. Moreover, permanent researchers have a tendency to play a central position (harmonic centrality) significantly lower than associate professors and a propensity to work outside the sub-network of Italian academic statisticians (EI index) higher than associate professors (statistically significant for \(\tau = 0.50, 0.75\)). These results reflect the differences that are inherent the various academic roles. Namely, full professor represents the highest level of the academic career, thus a full professor is expected to have a rich history of publications and collaborations and playing a central role in the academic network. On the opposite, fixed-term researchers are usually young scholars, newcomers in the tenured academic system and their academic relations are often limited to the PhD thesis supervisor. A different remark applies to permanent researchers, whose academic position is in exhaustion since the year 2010 when it was substituted with the fixed-term researcher (Law 240 of 30/12/2010). More than ten years after the abolition of the role, permanent researcher represents a residual category of academic scholars.

Scholar gender impacts in a significant way on the total number of publications and on the EI index for \(\tau = 0.50, 0.75\), with males having a higher total productivity and a higher propensity to collaborate with scholars outside the sub-network than females.

As concerns the university characteristics, the university size has a significant effect on the degree strength and the EI index: scholars working in small academic institutions compared to colleagues working in mega institutions tend to have a lower weighted number of co-authored papers and a higher propensity to work with scholars outside the sub-network. Besides, the geographical area where the university is located has a significant impact on several of the response variables considered in the QR models: scholars working at the South and Islands distinguish from colleagues working at the North or the Centre of Italy for a lower number of publications and a lower tendency to work with scholars outside the sub-network and, on the opposite, for higher values of node degree, node degree strength, and harmonic centrality index (for \(\tau = 0.25, 0.50\)). These differences between scholars from the South and Islands and colleagues from the Centre-North are, at least in part, the effect of national policies aimed at providing ad hoc funding for the South of Italy, which, among the various sectors, also involve the academic sector.

Finally, working in a polytechnic university (vs. other type of university) strongly affects the total number of publications (definitely higher than those of colleagues working in generic universities). We also observe a positive effect on the degree strength (statistically significant for \(\tau = 0.90, 0.95\)), a negative effect on the harmonic centrality index (statistically significant for \(\tau = 0.90, 0.95\)), and a positive tendency to work outside the sub-network of Italian academic statisticians (statistically significant for \(\tau = 0.10, 0.50, 0.75\)). These results reflect the specific profile characterizing scholars employed in polytechnic universities, where the competitiveness is high and there is a predominance of engineers that naturally drive scholars from the other subjects (e.g., statistics) to collaborate with them.

In virtue of the statistical relevance of the academic role, interaction effects between this variable and the SDS have been added to the QR models. The estimation results (see Appendix B, Table 15) show statistically significant interaction effects for the total number of publications (on quantiles \(\tau = 0.25, 0.50, 0.75, 0.90\)), the degree strength (on quantiles \(\tau = 0.50, 0.75, 0.90\)), the harmonic centrality (on quantiles \(\tau = 0.90, 0.95\)), and the EI index (on quantiles \(\tau = 0.05, 0.10, 0.25\)). In more detail, the role of full professor generates a decrease in the number of publications for sector S05 and in the node degree strength for sectors S03 and S05. Differently, the role of researcher generates an increase in the quantiles of the number of publications and of the EI index for sectors S02 (permanent researcher) and S04 (both fixed-term and permanent researcher).

These results reflect changes that have taken place in the last 10-20 years in the modalities of recruitment in the Italian Universities that, in turn, have strongly affected the approach to the research activity, leading to differences between researchers (usually younger) and full professors (usually older). In the past, mainly in certain fields (i.e., humanities and social sciences), there was a general tendency to publish fewer scientific papers (monographs in Italian language were often the most appreciated outcome to evaluate the quality of a scholar) and to collaborate less with other scholars with respect to the nowadays orientation, which is characterized by a strong push to publish a lot in brief time that leads to expand the circle of collaborations. The change of perspective has interested all the academic fields with different intensity: statistics stays in an intermediate position between the “pure” scientific fields (e.g., mathematics, physics, chemistry) and medicine, where the current orientation has been common practice for several decades, and humanistic and social sciences fields, where the change of perspective proceeds slowly. Besides, differences rise also within statistical sectors, as displayed by our analysis.

Conclusions

The present contribution was motivated by the recent Italian regulation that aggregates some academic scientific sectors (Scientific Disciplinary Sectors, SDS) in a same Competition Sector (CS) for purposes of recruitment and career advancement. We aimed at investigating the differences among academic scholars belonging to different scientific sub-fields, in terms of work and collaborative style, in order to understand if the aggregations set by law are justifiable on a scientific basis.

The analysis was carried out on the Italian academic statisticians’ network obtained merging the list of scholars employed with tenure in an Italian university and framed in one of the five SDSs referred to statisticians with the SCOPUS database. The resulting network consists of a node for each scholar and an edge for each pair of co-authors, weighted by the number of co-authored works. The scholars’ work and collaborative style was assessed through descriptive network measures at node level: number of publications, node degree, node degree strength, centrality indices (betweenness, harmonic, and eigenvector), transitivity, and weighted External-Internal index.

The relation between the node’s network measures and the SDS was investigated through quantile regression models, controlling for individual and university characteristics. In particular, analyses showed a clear evidence of a significant effect of the SDS on the work and collaborative style, especially pronounced on the distribution of the number of publications and the degree strength. Furthermore, analyses revealed quite evident differences between sectors S01 (Statistics) and S02 (Statistics for Experimental and Technological Research) as well as between S04 (Demography) and S05 (Social Statistics). These results provide useful suggestions for the decision maker: indeed, the aggregation of S04 and S05 on one side and S01 and S02 on the other side in the same competitive sectors appears questionable. It is worth to outline that the approach here proposed has been applied to the Statistics area for illustrative purposes, but it may be applied to any other scientific research area of the Italian academy. Indeed, the website of the Italian Ministry of University and Research allows us to freely download the list of the entire tenured academic body (see, for instance, Akbaritabar et al., 2021, for a study on Italian academic sociologists that relies on the same data source), thus the procedure illustrated to link the SCOPUS database may be applied on any list of authors and the analyses performed in this contribution may be replicated for the other scientific disciplinary sectors and competition sectors. More in general, the proposed statistical analysis can be generalized to all those situations in which scholars are grouped by research fields.

We note that a legislative decree entered into effect on June 30th 2022Footnote 8 recognized the need to reform the current system based on CSs and SDSs. In the light of this last regulatory act (not yet implemented while the final drafting of the present contribution was nearing conclusion), the importance of a scientifically-based approach to drive the choices of the legislator is more and more evident.

The analysis presented in this contribution can be improved along multiple lines that will be object of future research. First, being available further information from bibliographic data sources and from administrative databases, the edge weights could be defined distinguishing the number of co-authors that are statisticians from the number of co-authors that are not statisticians, and also distinguishing compatriots from foreign co-authors. Second, the analysis could be extended to combine the SCOPUS database with further sources of bibliographic data (e.g., Web of Sciences) as well as to integrate with typologies of scientific products not covered by these databases, such as books and book chapters; details about problems and solutions related with combination of different bibliographic databases are provided in Fuccella et al. (2016), whereas the integration with individual scientific curricula is treated in De Stefano et al. (2023). Furthermore, integrating the list of Italian academic tenured statisticians of the MUR website used in the present contribution with information from additional administrative databases would make it possible to enlarge the study to the non-tenured academic scholars (i.e., research fellows and PhD students) as well as to statisticians working outside the university system (e.g., national institute of statistics). Finally, the hierarchical structure of data, with scholars nested within universities, could be taken into account to control for the unobserved heterogeneity through the formulation and estimation of quantile mixed models (Geraci & Bottai, 2014).