Abstract
The field of science mapping has shown the power of citation-based clusters for literature analysis, yet this technique has barely been used for information retrieval tasks. This work evaluates the performance of citation-based clusters for information retrieval tasks. We simulated a search process with a tree hierarchy of clusters and a cluster selection algorithm. We evaluated the task of finding the relevant documents for 25 systematic reviews. Our evaluation considered several trade-offs between recall and precision for the cluster selection. We also replicated the Boolean queries self-reported by the systematic reviews to serve as a reference. We found that citation-based clusters’ search performance is highly variable and unpredictable, that the clusters work best for users that prefer recall over precision at a ratio between 2 and 8, and that the clusters are able to complement query-based search by finding additional relevant documents.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Researchers and other knowledge workers need special information retrieval (IR) tools because their IR tasks and practices differ from the general public and from each other (Ellis, 1993; Kuhlthau, 1991; Russell-Rose et al., 2018). Academic literature search is an essential part of any research project, and the most commonly used IR method is query-based retrieval: search using keyword queries to retrieve a ranked list of documents. However, some users complement this method with citation-based IR methods that follow the citations of the documents (Hemminger et al., 2007; Ortuño et al., 2013). These methods have two major advantages over query-based retrieval: (1) They are independent of the keywords, helping with lack of vocabulary knowledge or semantic ambiguity, and (2) they use the intellectual information of the citations, helping find documents that other researchers already connected. However, these methods can be timewise inefficient for users (Wright et al., 2014).
Given the prominence of citation clusters in scientometric research (Waltman & van Eck, 2012), it is remarkable that citation cluster-based IR (CCIR) is largely absent from the toolset of users (Wolfram, 2015). CCIR combines citation-based IR and cluster-based IR by making use of clusters of documents identified based on citation links. CCIR could allow users to also use approaches developed in scientometric research, such as science maps (Chen, 2017), cluster labeling (Sjögårde et al., 2021), and visualization software (van Eck & Waltman, 2010). CCIR offers two potential benefits over other citation-based IR methods: (1) it is less hindered by documents that cite the relevant literature poorly (Robinson et al., 2014) and (2) it communicates the topic structure of a document corpus, including the relative size of different topics and the relations between topics (Pirolli et al., 1996).
Effective cluster-based IR requires the clusters to group together the documents that are relevant for the IR task of the user (i.e., the cluster hypothesis (van Rijsbergen, 1979)). The extent to which this condition is fulfilled by CCIR is an open question. The answer may be different for different types of IR tasks (Hearst & Pedersen, 1996) and for different CCIR implementations. We consider one specific IR task, namely performing a literature search to write a systematic review (SR), and one specific CCIR implementation, namely a tree hierarchy of citation-based clusters of MEDLINE documents. As discussed below, we believe this to be a sensible use of CCIR. Moreover, data for experimentation was relatively easily available for this task. To determine the extent to which CCIR groups together relevant documents, we address the following research questions:
-
What types of users are best served by CCIR?
-
What types of SRs are best served by CCIR?
-
What are the strengths and weaknesses of CCIR?
We answer these questions by simulating a CCIR search process, evaluating its performance and analyzing its results. We simulated the CCIR search process in the tree hierarchy with an algorithm that aims to simulate the behavior of a human user. The idea of a CCIR hierarchy is based on classical cluster-based IR strategies (Cutting et al., 1992; Jardine & van Rijsbergen, 1971) and on a frequently used scientometric approach for creating classification systems of science (Waltman & van Eck, 2012). We evaluated the performance of CCIR for the task of finding the relevant documents for 25 SRs from a benchmark dataset (Scells et al., 2017), using as performance reference the SRs’ self-reported Boolean query search retrieved documents, obtained through intensive manual annotation. This task is well-suited for cluster-based IR because all relevant documents are considered equally important; the task is considered a Boolean retrieval task, so there is no ranking of documents. From these results we analyzed the different preferences of hypothetical users regarding the trade-off between precision and recall, the overlap between documents retrieved by CCIR and by a Boolean query, and how the topic of a SR affects its task performance.
To our knowledge, our work is the first study that evaluates the performance of CCIR. We additionally provide two outputs that can be reused by other researchers: (1) an evaluation protocol for clusters-based IR methods that uses SRs, and (2) an extension of the original SR dataset with the annotated Boolean queries.
This paper is organized as follows. We discuss related work in Sect. “Related work”, explain out methodology in Sect. “Method”, show our results in Sect. Reults, discuss our results in Sect. “Discussion”, and conclude our work in Sect. “Conclusion”.
Related work
Science mapping
Our research on CCIR is part of a bigger trend of research that attempts to connect the fields of scientometrics and information retrieval. Experts agree that these fields have much to gain from each other (Frommholz et al., 2021; Mayr & Scharnhorst, 2015). While research on CCIR seems to have slowed down in recent years, research on clustering methods in the field of scientometrics continues to move forward.
Closest to our research are the citation clusters used for science mapping and field delineation studies (Chen, 2017; Cobo et al., 2011). It has been shown that these clusters create communities of documents with semantic similarity (i.e., a common topic) (Klavans & Boyack, 2006) and that they provide insights for analyzing these documents (Small & Garfield, 1985). Citation clusters are also used to represent communities of documents in the visualization of a citation network (which is a network of documents and their citations to each other) (Chen, 2006; van Eck & Waltman, 2017). Text similarity-based clusters, both on their own (Callon et al., 1983) and enriched with citations (Ahlgren et al., 2020; Janssens et al., 2008), have also been used to map science. Waltman et al. (2020) compare citation-based similarity clusters with text similarity-based clusters. We decided not to include the use of text similarity in our research because text similarity-based cluster IR is already a well-studied method (see Sect. “Results”).
Citation-based IR
Citation-based IR methods are frequently used in academic search. The most common method is to retrieve the documents that cite or are cited by a given document (a.k.a. citation tracking). A further step of this method is to track the citations of these retrieved documents (a.k.a. snowballing). Some of the developments in citation-based IR are tools to track citations (Chandra et al., 2021; Inciteful, 2022; Janssens et al., 2020; Liang et al., 2011; Madeira & Vot, 2018; Pitt et al., 2022; van Eck & Waltman, 2014), protocols to find relevant documents to write a SR by tracking citations (Belter, 2016; Horsley et al., 2011), tools that delineate fields by tracking citations (Zitt, 2015), methods to rank search results by tracking citations (Belter, 2017; Mutschke & Mayr, 2015), and methods to find the seminal documents of a topic by tracking citations (Haunschild & Marx, 2020). Additionally, citation-based IR is addressed by the communities around the workshop series Bibliometric-enhanced Information Retrieval (BIR) (Frommholz et al., 2021) and the related workshop series Bibliometric-enhanced Information Retrieval and Natural Language Processing for Digital Libraries (BIRNDL) (Cabanac et al., 2017).
The most significant difference between CCIR and citation tracking is that CCIR creates clusters and retrieves documents using the structure of the whole citation network, while citation tracking retrieves documents using only the structure of the documents closest to the initially selected document in the citation network. Both methods focus on different aspects of the citation network, so both can be valuable to the academic IR toolset.
Cluster-based IR
Cluster-based IR methods retrieve one or more clusters of documents, and these clusters are usually based on text similarity. These methods have been used for academic search both in commercial (Iris.Ai, 2019) context and academic (Open Knowledge Maps: A Visual Interface to the World’s Scientific Knowledge., 2019) contexts, and have also included the text from cited documents in their similarity score (Abbasi & Frommholz, 2015). Non-academic IR has also been used to cluster web search results (Stefanowski & Weiss, 2003). Additionally, the seminal Scatter/Gather browsing model (Cutting et al., 1992) (on which we draw inspiration for our evaluation) proposes a user interaction protocol where the user removes irrelevant documents over several iterations by creating new sets of documents using the clusters from the previous iteration. Bascur et al. (2019) proposed specifications for a CCIR tool that uses the Scatter/Gather model.
Cluster-based IR works have a wide methodological variety, reflected in the following methodological choices:
-
Relatedness attribute between documents: Connections (e.g. citations, as we did) or shared elements (e.g. text, authors, keywords);
-
Which set of documents to cluster: Either the whole corpus (as we did) or a subset of the corpus that is retrieved by a query;
-
What is the structure of the clustering solution: Either hierarchical (as we did) or flat (a.k.a. independent clusters);
-
How to select clusters during the evaluation: Either select clusters using knowledge of the document relevance (as we did) or select clusters using a query match;
-
How to retrieve documents during the evaluation: Either retrieve all documents within a cluster (as we did) or retrieve only some.
Our purpose is not to compare the pros and cons of each of these methodological choices. Instead, our focus is on evaluating the specific methodological choices considered in our work. Similar to our work is the work of He et al. (2019), who visualize academic search results using, among other elements, citation-based clusters. The difference between their approach and ours is that we use the clusters as a means to retrieve documents, while they use the clusters for visualization of search results. In their work, they showed that their visualization can increase the efficiency (i.e., completion time) and user satisfaction for complex tasks, but not for simple tasks. This result suggests that the effectiveness of CCIR may depend on the task. Therefore, we look at individual SR tasks to see how the effectiveness differs between them.
Measuring the effectiveness of clustering, both for IR and for other purposes, is not trivial, as no clustering solution can satisfy every possible search task (Yuan et al., 2022). Our approach is to measure clustering effectiveness without the participation of real users (a.k.a. offline evaluation). Many other studies have adopted the same approach. For instance, Abdelhaq et al. (2013) created a metric for evaluating Twitter data clustering based on the stability and coverage of the most common keywords in a cluster. In a bioinformatics example, Atkinson et al. (2009) evaluated the effectiveness of a gene similarity network clustering by observing to what extent each cluster had a single gene function. Yuan et al. (2022) created novel metrics that consider the number of clusters necessary to retrieve a given percentage of the relevant documents. De Vries et al. (2012) created an evaluation framework where the relevant documents are known and the clustering solution is compared with a random baseline. Abbasi and Frommholz (2015) evaluated clustering with a simulation where a virtual user already knows which are the relevant documents. Our evaluation is most similar to the latter two studies because our cluster selection algorithm already knows which are the relevant documents, which is a common assumption in evaluation of retrieval methods (Manning et al., 2008).
Method
Task design and data collection
The task we address is to find the documents necessary to write a given SR. The data that we use for this task comes from the dataset published by Scells et al. (2017) (from now on referred to as the Scells dataset). This dataset contains:
-
177 SRs published by the Cochrane library between 2014 and 2016.
-
The references of each SR that belong to the included studies or excluded studies category of that SR. We consider both categories necessary for the task of writing a SR, so we included documents from both categories in the set of relevant documents of the task (see below for an explanation).
-
The self-reported Boolean query that the authors of each SR used when they searched using the OVID search platform with the MEDLINE database, hereafter referred to as the Boolean query.
We intend to retrieve the documents that the authors of the SR found in their search, thus we use the authors’ Boolean queries to retrieve documents. We retrieved these documents following these steps:
-
1.
We manually confirmed that the Boolean queries in the Scells dataset were the same as the ones self-reported by the SRs, and when this was not the case, we used the self-reported one.
-
2.
We translated the Boolean queries from the OVID format into the PubMed format because the OVID search platform does not have an API service, while the PubMed search platform does (PubMed API, 2018) and it also includes the MEDLINE database. We translated the formats using the TRANSMUTE software (Scells et al., 2018) and then we manually checked that the translation was correct (i.e., that both formats would retrieve the same documents). Some translations were not possible because the OVID search platform provides functionalities that the PubMed search platform does not (e.g., word distance-based arguments). A full report on the translations and how we handled difficult cases can be found in the supplementary material, Tables S1 and S2.
-
3.
For each SR, we performed a search using the PubMed API based on the PubMed Boolean query, and we included the retrieved documents in the document set retrieved by the Boolean query.
-
4.
We removed from the retrieved document set the documents that were not in the citation network (which is described in Sect. “Citation network”). We also removed from the relevant document set (see below) the documents that were absent from the document set retrieved by the Boolean query in order to maintain consistency between both sets (i.e., so that the relevant document set is a subset of the document set retrieved by the Boolean query).
To improve the quality of our evaluation, we selected a subset of the SRs in the Scells dataset to be used in our evaluation. Our selection criteria were:
-
The relevant document set contains at least 10 documents. We chose this value because with fewer relevant documents, the increase in recall for each retrieved document would be more than 0.1 and we wish a more fine-grained increase to facilitate interpretation of the results.
-
The number of retrieved documents self-reported by the authors (i.e., from all their search sources) is of a similar order of magnitude (i.e., between 10 times less and 10 times more) as the size of the document set retrieved by us with the Boolean query. This condition excludes SRs whose self-reported number of retrieved documents is vastly different from ours.
This selection resulted in 25 SRs (see Fig. 4A in Sect. Results for the number of relevant documents per SR), of which 7 were published in 2014, 10 in 2015 and 8 in 2016. The number of SRs may seem small, for instance in comparison with the work by Janssens et al. (2020), who used 250 SRs. However, we manually annotated the Boolean queries, which is very labor intensive. Additionally, while the number of SRs is modest, the number of document in our citation networks is very large (~ 7 million per network, see below).
Cochrane library SRs have, for our purposes, three categories of documents in their references:
-
Included studies: Studies that provide information that advances the objective of the SR.
-
Excluded studies: Studies that were considered for the included studies category but were discarded because they did not match the selection criteria of the SR.
-
Additional references: Documents that were not considered for the included studies category.
The Cochrane library has a clear rule for which documents should go into the excluded studies category: When a user discards a document, after they have read the document full text to any extent, the document is an excluded study, else it is not (e.g., discarded after reading the abstract).
We decided to regard the excluded studies as relevant documents for the retrieval task because, by the above rule, the user needs to find and read these documents in order to exclude them. Additionally, the selection criteria that discard an excluded study can be so particular (e.g., number of participants in the study) that we believe it is not reasonable to expect an IR tool to be able to discard these documents.
Citation network
We needed to create a citation network for the tree hierarchy of clusters. We used the in-house Dimensions database, which contains all the documents included in MEDLINE and also their citation links. We created the citation network following these steps:
-
1.
We retrieved all the documents contained in the Dimensions database.
-
2.
We removed all the documents published the same year or later than the SRs to make sure we do not provide unfair advantageous information to the clustering (see below). Therefore, we created a different citation network for each publication year in the Scells dataset: One until 2013, another until 2014 and another until 2015.
-
3.
We limited the documents of the citation networks to the ones available in the MEDLINE database, because the self-reported Boolean queries were performed exclusively within the MEDLINE database. We identified the MEDLINE documents using the PubMed database available at Leiden University’s Centre for Science and Technology Studies (CWTS).
-
4.
Because of the computing resources needed to handle large citation networks, we limited the publishing years of each network to 11 years (2003-2013, 2004-2014, and 2005–2015).
The sizes of the citation networks were:
-
Citation network 2003-2013: 6,549,426 documents, 81,284,099 citation links.
-
Citation network 2004-2014: 6,879,646 documents, 86,001,142 citation links.
-
Citation network 2005-2015: 7,194,514 documents, 90,164,417 citation links.
Documents that are in the reference lists of a given SR are connected to the SR by a citation link. These connections help the clustering algorithm to put all these documents in the same cluster, which would artificially increase the performance of CCIR. This is not fair because in a real scenario these connections could not exist because the SR has not been published yet. We removed not only these connections, but all the documents published in the same year and in later years because they could be influenced by these connections. Because we remove the documents published in the same year, we may also remove some documents that existed before the publication of the SR. However, none of the relevant documents were removed in this process.
Simulation of CCIR
In this section we explain how we simulated the CCIR search process so we can evaluate the performance of CCIR.
Clustering
We created a tree hierarchy of clusters for each citation network. We started by clustering the documents into at most 10 clusters, based on the idea that in practice it may be difficult for users to handle more than 10 clusters. Then, the documents of each cluster were again clustered into at most 10 smaller clusters, and so on. As discussed below, the documents that could not be included in these clusters were excluded from the tree. This process created a nested tree of clusters with a depth of 13 levels (not counting the root level). We only clustered into smaller clusters the clusters that contained relevant documents because otherwise they were irrelevant for the evaluation.
We performed the clustering using a methodology built on the work of Waltman and van Eck (2012). This methodology is used in combination with the Leiden algorithm (Traag et al., 2019). This combination provides a state-of-the-art approach for document clustering in the field of scientometrics. This approach has been used in a large number of research articles (e.g. Boyack et al., 2020; Held & Velden, 2022; Sjögårde & Ahlgren, 2020). It is also used in products of the analytics companies Elsevier (Elsevier, n.d.) and Clarivate (Potter, 2020). We therefore consider it the state-of-the-art approach for citation-based clustering.
In the methodology of Waltman and van Eck (2012), the tree hierarchy is built in a bottom-up manner while we take a top-down approach. We made this change because it reflects how a real user would create a tree, going from the general to the specific. It also saves computer resources by not creating sub-clusters for clusters that are of no interest. Another change is that Waltman and van Eck merged small clusters based on a cluster size threshold, while we merged small clusters based on a number of clusters threshold (at most 10 clusters, as mentioned before). We made this change because for a real user it is more intuitive to control the maximum number of clusters than the minimum number of documents per cluster.
The purpose of the Leiden algorithm is to assign documents to clusters based on the connections between the documents. The algorithm rewards pairs of documents in the same cluster that are connected by a citation link and penalizes pairs of documents in the same cluster that are not connected. The magnitude of the penalty is determined by the resolution parameter of the algorithm, which must be provided externally. A higher resolution leads to more and smaller clusters.
Mathematically, the clustering algorithm maximizes the following quality function:
In this quality function, i and j are documents, xi is the cluster of document i, and r is the resolution parameter. aij equals 1 if there is a citation link between documents i and j. Otherwise aij equals 0. δ equals 1 if xi and xj are equal (i.e., documents i and j are in the same cluster). Otherwise δ equals 0.
The Leiden algorithm returns the clustering solution that maximizes Eq. 1. To limit the number of clusters per clustering (i.e., children clusters per parent cluster) to at most 10, we merged the smaller clusters following these steps:
-
1.
If there are more than 10 clusters in the clustering solution, select the smallest cluster. If there is a tie in the size, randomly select one of the smallest clusters. If the number of clusters is 10 or fewer, stop.
-
2.
If there are no citation links between the documents in the selected cluster and documents outside the selected cluster, remove the selected cluster from the clustering solution and then go back to step 1.
-
3.
For each cluster other than the selected cluster, calculate the highest resolution under which this cluster would merge with the selected cluster (method from Waltman and van Eck (2012)). This resolution is always lower than the current resolution because otherwise the clustering algorithm would have already merged these clusters.
-
4.
Merge the selected cluster with the cluster for which the highest resolution was obtained in step 3, and then go back to step 1.
The resolution parameter must be provided externally, but the literature has not yet established a rule of thumb for selecting a suitable value (although the work of Sjögårde and Ahlgren (2018, 2020) goes in that direction). We therefore used our own heuristic. Using a trial-and-error approach, we tried to find resolution values for each level so that the following conditions were satisfied as much as possible:
-
The size of the 10 largest clusters after merging was similar to the size of these clusters before merging. This condition aims to minimize the effect of cluster merging.
-
The 10 largest clusters after merging were of similar size. This condition aims to avoid creating one or a few clusters with a disproportionally large number of documents.
Our heuristic resulted in a resolution of 2 × 10−5 for the first level of the tree hierarchy. For each subsequent level we multiplied the resolution by 3. At level 13 the resolution is greater than 1 (2 * 10−5 * 312 = 1.06) which is why we have 13 levels (a resolution greater than 1 yields only singleton clusters).
Cluster selection
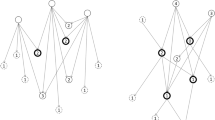
We use a greedy algorithm to select the clusters, starting from the root of the tree hierarchy. The algorithm goes down the tree hierarchy selecting child clusters based on their score, until none of the child clusters has a score higher than the currently selected cluster (see Fig. 1). We use a greedy algorithm because this reflects how a real user would navigate a tree hierarchy. The score function is the F-score of retrieving the documents in a cluster, determined based on the relevant documents of a given SR:
Cluster selection algorithm. The bubbles represent clusters of documents. The text in a bubble shows the label and the score of a cluster. The lines are the connections between the parent and the child clusters in the tree hierarchy. The arrows point toward the child clusters. Only the child clusters of the selected clusters are shown. The orange bubbles represent the clusters selected by the algorithm. The orange lines indicate the path followed by the algorithm. The pointer finger shows the selection of the algorithm. A Calculate the score of each cluster at the highest level of the tree hierarchy (Clusters 1, 2, and 3). B Select the cluster with the highest score (Cluster 2). C: Calculate the score of each child cluster of the selected cluster (Clusters 2.1, 2.2, and 2.3). D Retrieve the cluster that was already selected (Cluster 2) because it has a higher score than any of the child clusters
The precision and recall of each cluster are calculated based on the number of documents in the cluster (i.e., number of positives), the number of relevant documents in the cluster (i.e., number of true positives), and the number of relevant documents not in the cluster (i.e., number of false negatives). A real user does not have access to these numbers. The greedy algorithm therefore simulates an optimistic scenario in which a user is able to accurately assess the quality of different clusters.
The parameter β of the F-score function (Eq. 2) reflects how a hypothetical user balances recall against precision (van Rijsbergen, 1979): Lower values of β favor precision, while higher values favor recall. If β = 1, precision and recall have equal weight. For each SR we retrieve several clusters, each one using different values of β to cover a wide range of precision-recall trade-offs: β ∈ {0.125, 0.25, 0.5, 1, 2, 4, 8, 16, 32, 64, 128}. The idea of using a greedy algorithm and different values of β to reflect real users is inspired by the “what-if” experiments methodology (Azzopardi et al., 2011).
Quantitative analysis
For our quantitative evaluation, we group the results of the SRs according to value of β used by the cluster selection algorithm. In this way, we can compare the aggregated results for different values of β. We report the number of retrieved documents, the tree-level of the retrieved cluster, precision, recall, and F-score (β = β used by the cluster selection algorithm).
We report four more metrics that are generated by comparing the cluster selection algorithm results with the Boolean query retrieved documents:
-
Intersection proportion of the cluster selection algorithm: Proportion of the documents retrieved by the cluster selection algorithm that are also retrieved by the Boolean query.
-
Intersection proportion of the Boolean query: Proportion of the documents retrieved by the Boolean query that are also retrieved by the cluster selection algorithm.
-
Ratio of retrieved documents: Number of documents retrieved by the cluster selection algorithm divided by the number documents retrieved by the Boolean query.
-
F-score difference: F-score of the cluster selection algorithm minus the F-score of the Boolean query (β = β used by the cluster selection algorithm).
The purpose of the F-score difference is to evaluate the performance of CCIR while also taking into consideration the difficulty of the task for the authors of the SR. We refrain from using the F-score difference to make claims about the relative performance of CCIR compared to the Boolean query. We do not consider such claims to be justified, because there are too many issues that we are not able to take into account in our analyses. For instance, we assume that the Boolean query retrieves all relevant documents, but we are unable to assess the accuracy of this assumption. Also, in practice, a Boolean query is written over several iterations of trial and error. We are unable to analyze the impact of this iterative process, since we have access only to the final version of a Boolean query.
Instead of directly comparing the performance of a CCIR approach with a Boolean query approach, our quantitative analysis focuses on answering the following questions:
-
To what extent does the performance of CCIR varies between individual SRs? We answer this by analyzing the dispersion of the F-score difference grouped by of β.
-
How similar are the sets of documents retrieved by CCIR and the Boolean query? We answer this by analyzing the intersection proportion of both CCIR and the Boolean query
-
For which values of β is CCIR more effective? We answer this by analyzing most of the quantitative metrics, and how their values change when the value of β increases or decreases.
Qualitative analysis
In our qualitative analysis we address the following questions:
-
How does the nature of a SR affect the performance of CCIR and a Boolean query?
-
What type of documents does CCIR or a Boolean query retrieve or miss?
We address these questions by an expert reading of the SRs performed by the first author of our paper (Juan Pablo Bascur), who is trained in the biomedical field, and supported by an expert in Boolean query searches for biomedical purposes (Jan W. Schoones).
We performed the qualitative analysis on the retrieved documents of three SRs. We selected the SRs based on their F-score difference for β = 4 (we used β = 4 because it had the highest recall dispersion, which helps highlight the differences between SRs; see Sect. Results). We selected the SRs with the lowest, highest and third highest F-score difference, which in the Scells dataset correspond to the ids SR59 (Peinemann et al., 2013), SR47 (Cousins et al., 2016) and SR80 (Ma, 2015), respectively.
For each SR, we characterized:
-
Goal: The question that the authors of the SR want to answer.
-
Needs: The nature of the documents that the authors need to retrieve to achieve the goal.
-
Boolean query components: The components of which the Boolean query consist. A component is a group of Boolean terms that belong to the same topic.
For each SR we also selected one of the clusters that CCIR retrieved for this SR, that we subjectively found it had good precision and recall (hereafter known as the optimal cluster). We also selected from the clusters that CCIR retrieved the parent and the child of the optimal cluster to expand the range of our analysis, but we discarded the child clusters because they were so small that they did not provide qualitative information. Therefore, we selected the parent of the optimal cluster, hereafter known as the parent cluster.
We inferred the topic of each set of documents (these are, the clusters and the document retrieved by the Boolean query) from the titles of the documents. For the bigger document sets, we facilitated this process by inferring the topics from the most common noun-phrases in the titles of the documents. We extracted noun phrases from titles using the spaCy Python library (Honnibal et al., 2020).
To guide our analysis, we use Venn diagrams of the overlap between the relevant documents, the selected clusters of CCIR and the documents retrieved by the Boolean query. We also look for documents retrieved by CCIR but not by the Boolean query that, given their nature, could have been relevant documents if the authors of the SR had found them.
Results
Quantitative results
In this section we describe the quantitative analysis of the 25 SRs evaluation results. Figure 2 shows the precision, recall, F-score and F-score difference, Fig. 3 shows the intersection proportions, Fig. 4 shows the number and ratio of retrieved documents, and Fig. 5 shows the level of the selected clusters.
Precision, Recall and F-Score. A Precision of the Boolean query. Each data point is a SR, and the X axis is the precision. B–E Each data point is a SR, the X axis is the β group, and the Y axis is the respective metric of that β group for that SR. B Precision of CCIR. C Recall of CCIR. D F-Score of CCIR. E F-score difference between CCIR and the Boolean query (CCIR minus Boolean query). F Precision and recall of β = 8. Each data point is a SR, the X axis is the precision of CCIR, the Y axis is the recall of CCIR, and the red lines are the isocurves of the F-score (β = 8)
Documents sets sizes. A Relevant documents sets sizes. Each data point is a SR, and the X axis is the size of the relevant documents set. B Boolean query retrieved documents sets sizes. Each data point is a SR, and the X axis is the size of the Boolean query retrieved documents set. C and D Each data point is a SR, the X axis is the β group, and the Y axis is the respective metric of that β group for that SR. C CCIR retrieved documents sets sizes. D Ratio of retrieved documents. Calculated as the CCIR retrieved documents set size divided by the Boolean query retrieved documents set size
To what extent does the performance of CCIR vary between individual SRs?
Figure 2E shows that the F-score difference values have a large dispersion: within β groups the interquartile range is 0.2 or higher, and the highest range (at β = 4) is 0.5. This result shows that the performance varies between SRs, and it highlights the importance of analyzing individual SRs in the qualitative analysis presented in Sect. “Qualitative results”.
How similar are the sets of documents retrieved by CCIR and the Boolean query?
Figure 3 shows that these two sets of documents are very different because their intersection proportion is very low. We analyzed Fig. 3 focusing on three β groups, which we selected based on Fig. 4D: when both document sets are of the same size (β = 16), when the CCIR set is 10 times bigger than the Boolean query set (β = 128), and when the CCIR set is 10 times smaller than the Boolean query set (β = 2). When both sets are the same size and when the CCIR set is 10 times bigger, the intersection proportion is surprisingly low: 0.1 for the former (Figs. 3A and B) and 0.5 for the latter (Fig. 3B). When the CCIR set is 10 times smaller, the proportion is also low (0.6), but additionally this value starts to fall dramatically on the subsequent groups of β (Fig. 3A).
For which values of β is CCIR more effective?
Figure 5 shows that the tree-level of the selected clusters is linearly correlated with the value of β (using our powers of 2 scale), or in other words, the median level goes up by 1 level for each sequential β value.
Figure 4D shows that, for β between 2 and 128, the CCIR retrieved document set was between 10 times smaller and 10 times bigger than the Boolean query document set. Figure 2B shows that the β groups after β = 8 have less precision than the Boolean query (0.025, Fig. 2A). Figure 2C shows that recall improves little after β = 8. Therefore, we think that the results of groups β = 2, β = 4 and β = 8 balance size, precision and recall the best. Also, outside these groups the balance decreases much faster from β = 1 to the lower values of β than from β = 16 to the higher values of β.
Qualitative results
In this section we describe the qualitative analysis of three selected SRs and their evaluation results. Figure 6 shows their Venn diagram of the intersection between the Boolean query, the CCIR and the relevant documents. Table 1 shows their quantitative data, Table 2 shows their characterization and Table 3 shows the topic of their sets of documents. The details on the construction of their Boolean query components can be found in supplementary material Figures S1, S2 and S3, and their topics in supplementary material Tables S3, S4 and S5.
SR59: Retinoic acid post consolidation therapy for high‐risk neuroblastoma patients treated with autologous hematopoietic stem cell transplantation
This SR had the lowest F-score difference and also a high Boolean query precision (Table 1). Its goal was to determine if patients with the condition Neuroblastoma recuperate better from the treatments Chemotherapy and Bone Marrow Transplant if they are treated with the medication Retinoic Acid (Table 2).
The document set of Boolean query and the two clusters had similar topics, but the cluster topics were missing the component Retinoic Acid (Table 3), which is one of the needs of SR59 (Table 2). This suggests that CCIR did not create a cluster with Retinoic Acid, and we wonder why. All the relevant documents of SR59 clearly share a common topic (we read their titles) so it would seem that they should be mostly in the same CCIR cluster. An explanation for this mystery seems to be given by the topic of the parent cluster. Here, we found that the topic fulfills the needs of SR59, except that instead of Retinoic Acid it has the component 131L-MIBG, which is a medication with similar uses to Retinoic Acid. It seems then that the existence of a cluster with the needs of SR59 and Retinoic Acid was mutually exclusive with the existence of a cluster with the needs of SR59 and 131L-MIBG, and CCIR created the latter instead of the former because of its higher fitness. This likely resulted in CCIR spreading the relevant documents of SR59 among other clusters, decreasing the F-score difference value.
The Boolean query of SR59 is missing the component Bone Marrow Transplant from the needs of SR59 (Table 2), yet the Boolean query achieves a high precision (Table 1). This is because the combination of the components Neuroblastoma and Retinoic Acid was so infrequent in the literature that it was enough for Boolean query. This shows that the Boolean query can give high precision for highly specific needs.
SR47: Surgery for the resolution of symptoms in malignant bowel obstruction in advanced gynaecological and gastrointestinal cancer
This SR had the highest F-score difference (Table 1). Its goal was to determine how effective the treatment Surgery is to treat the condition Intestinal Obstruction when caused by the conditions Gynecological Cancer or Gastrointestinal Cancer (Table 2).
We could not identify the topic of the Boolean query document set because the most common noun-phrases were present in only a minor portion of the documents. This could be either because the set of documents was big and therefore has too much diversity, or because it has several disconnected topics, and we believe the latter explanation is the correct one. On the other hand, the topics of the two clusters (Table 3) were similar to the needs of SR47 (Table 2).
We believe that the Boolean query has several disconnected topics because the needs SR47 were hard to express in a Boolean query format, which ends up retrieving a noisy set of documents. The needs are documents on Surgery to treat Intestinal Obstruction due to Gynaecological and Gastrointestinal Cancer (Table 2). However, the Boolean query cannot specify if Surgery treats Intestinal Obstruction or treats Gynaecological and Gastrointestinal Cancer. This case shows that CCIR can help with searches where the relation between the Boolean query terms is ambiguous.
Additionally, we saw an interesting phenomenon happening with the topics of the clusters. Among their documents, there were three synonym noun-phrases that refer to intestinal obstruction: Malignant Bowel Obstruction, Malignant Colorectal Obstruction and Malignant Colonic Obstruction. The optimal cluster only had the first form, while the parent cluster had all three of them. This implies that the documents with the first form cite each much more intensely than the documents with the other two forms. We see no science-related reason for this to be the case, so we imagine that this citation pattern arises from a community of researchers with the same writing conventions that cite each other. This citation pattern shows one of the risks of CCIR and of citation-based clustering in general: The citations may not only represent an intellectual relationship between two documents, but also other non-scientific relationships that are of no use for IR purposes.
We saw another interesting phenomenon happening with the topics of the clusters. Two of the most common noun-phrases of the optimal cluster were Inoperable Bowel Obstruction and Octreotide (which is a medication for inoperable tumors). Both noun-phrases imply that their documents lack surgery, but Surgery is a need of SR47. This shows that, even when the F-score difference value is high, CCIR may still not have created a cluster with the topic that the user needs.
SR80: Rituximab for rheumatoid arthritis (Review)
This SR had the third highest F-score difference (Table 1). Its goal was to evaluate the medication Rituximab to treat the condition Rheumatoid Arthritis. There are two things we must mention for our analysis of SR80: First, that the medication Rituximab belongs to a group of medications called DMARDs (which means Disease-Modifying Antirheumatic Drugs), and second, that the needs of SR80 include comparing Rituximab treatments with either no treatment (a.k.a. placebo) or other DMARDs treatments (Table 2).
The topic of the Boolean query and the clusters is the same and fits the needs of SR80. This shows that CCIR created a cluster for the right topic. However, CCIR still missed several relevant documents, which shows that creating a cluster for the right topic can be insufficient. We believe that the reason these relevant documents were not in the clusters is that, even if two documents are about the same topic, they may be poorly connected to each other by direct or indirect citations due to the citing practices of their research community. This result challenges one of the core assumptions of CCIR: That two given documents that share a topic will be directly or indirectly well connected by citations.
It seems that the authors of the SR made the conscious decision of building the Boolean query in such a way that it sacrifices precision in favor of recall. This is suggested by the following difference between the required needs of SR80 and the Boolean query components of SR80 (Table 2): SR80 requires comparisons between treatments with Rituximab (itself a DMRAD) and treatments with placebo or other DMRADs, but the Boolean query components do not require a document to mention Rituximab, resulting in several retrieved documents that do not serve the needs. We believe that the authors made this decision because they expected many documents that use Rituximab to mention it in their metadata under the more general term DMRADs. This case shows that CCIR can help with searches where the Boolean query cannot be sufficiently specific.
An interesting observation is that, among the most common noun-phrases, the Boolean query mentions the same DMRADs as the parent cluster, but the latter also mentions one extra DMRAD (Certolizumab Pegol). This is interesting because the component DMRADs of the Boolean query searched for all the available DMARDs, so it should also have found Certolizumab Pegol. We found that this happens because of the MeSH term that the component DMARDs uses (“Antibodies, Monoclonal”[Mesh Terms:noexp]) does not retrieve Certolizumab Pegol (which goes under “Antibodies, Monoclonal, Humanized” [Mesh Terms:noexp]). Biologically speaking, DRMADs is better described by the latter MeSH term than by the former, but it seems that the convention of the National Library of Medicine is to use the former MeSH term for all DRMADs except for Certolizumab Pegol. The authors may not have been aware of this because otherwise they presumably would have incorporated the second MeSH term in the Boolean query. We believe that this case shows that CCIR can help Boolean query users to ensure they include all necessary vocabulary in their Boolean query.
We wondered if any of the documents of the parent cluster with Certolizumab Pegol in their title may have been a relevant document if the authors of SR80 had seen the document during their literature search. We tested this hypothesis by comparing these documents with the needs SR80. We found one document (Weinblatt et al., 2012) which cannot be discarded based only on the title or the abstract, and therefore is a relevant document. This case shows that CCIR can find relevant documents that the Boolean query does not.
Discussion
In this section we discuss our findings in relation to our research questions and then discuss the limitations of our work.
What types of users are best served by CCIR?
We can answer questions about users by connecting user preferences for recall and precision with the β value (user prefer recall β times as much as precision). We saw that β = 2, β = 4 and β = 8 had the best balance, and that outside these β values the balance decreases faster for lower β values than for higher β values. Therefore, we can say that CCIR serves best users that prefer recall over precision with a ratio between 2 and 8 times, and for users outside that range it serves higher ratios better than lower ratios.
We wondered if users that perform a literature search for a SR are within this range of ratios, and we used the Boolean queries values as a proxy to answer this. Figure 2A shows that the precision of the Boolean queries is between 0.01 and 0.06, and by definition the Boolean queries have a recall 1.0, so the ratio of recall over precision is 1 over 0.01–0.06, or 17–100, very far from our prior range of 2–8. While it is true that the recall of the Boolean query is unrealistically high, the recall would have to be 10 times lower for the ratio to be within the range, which, given that SR literature searches aim for maximum recall, is unlikely. Therefore, we believe that the users that are best served by CCIR are not users that do a literature search for SR. It is beyond our knowledge which type of user might prefer the range 2–8.
We saw that the median tree-level is sensitive to the β value. While we do not have a standard to evaluate which levels are better for users, we know that the more a user prefers recall, the closer to the root, the less effort the user needs to make to reach that level.
We also saw that the Boolean query and CCIR retrieve different documents (Fig. 3), and these documents could be relevant (analysis of SR80). Therefore, CCIR could serve users willing to use more than one IR method by finding more relevant documents.
What types of SRs are best served by CCIR?
We saw that there is a substantial variance among the F-score difference values of the SRs (Fig. 2E), meaning that for some SRs, CCIR performs much worse than for others. We would imagine that, for CCIR, a SR with general needs (e.g. a disease) would perform better than a SR with specific needs (e.g. interaction between two medications), while the opposite would be true for Boolean queries (Carmel et al. (2006) analyzed how the needs affect query difficulty). However, the three SRs that we analyzed had specific needs (Table 2) yet one had bad performance and two had good performance. The only clue that we can use to infer the performance of a SR is in SR47: its need is hard to write as a Boolean query, so we can infer that IR methods not based on a Boolean query are likely to have an advantage. However, this inference is more about the bad performance of the Boolean query than the good performance of the CCIR.
What are the strengths and weaknesses of CCIR?
Strengths
CCIR may find documents that the Boolean query does not. We know this from the results of intersection proportions (Fig. 3), where it shows that CCIR and the Boolean query retrieve different documents. We also know this from the newly discovered relevant document of SR80.
CCIR may reduce the noise of searches that are hard to write as a Boolean query. We know this from how CCIR performs well for SR47 and SR80: The former’s Boolean query could not be sufficiently specific because the Boolean query format does not allow to specify subject-object relations between terms. The latter’s Boolean query could not be specific because of the risk of missing documents with poorly annotated metadata.
CCIR may help expand the vocabulary used in a Boolean query. We know this from our experience with SR80. By looking at the difference between the noun-phrases of the parent cluster and the Boolean query of SR80, we realized that the Boolean query was missing a relevant search term which was likely not considered by the authors of the Boolean query.
Weaknesses
CCIR may not create a cluster with the exact topic that the user needs. We know this because in SR47 and SR59 there was a divergence between the user needs and the topic of the CCIR sets of retrieved documents. The tree hierarchy did not had a cluster with the same topic as the user needs, which may happen because documents may relate to multiple topics.
The performance for a given SR can be unpredictable. We know this because of the high dispersion of the F-score difference values (Fig. 2E) and because the characteristics of SR59, SR47 and SR80 did not give a clue about their performance.
Documents that share the same topic may be poorly directly or indirectly connected in a citation network. We know this from our experience with SR80. While a cluster with the relevant topic was retrieved, several relevant documents were missing. Also, the noun-phrases differences between the retrieved documents of the optimal cluster and the parent cluster of SR47 suggest that the optimal cluster was created based on the citation practices of the authors instead of the topic of the documents. Potentially, this issue could be diminished by combining citation-based and semantic-based clustering.
The clusters at the highest levels have too many documents, which makes the topic of the clusters hard to interpret for a real user because the documents are so diverse. This is a serious problem because selecting the wrong cluster at this level is a critical mistake (Willett, 1988). Our evaluation did not suffer from this issue because CCIR already knows in which clusters the relevant documents can be found. In a real situation, a user may be able to handle this issue if they know at least some of the relevant documents, and then they could even select clusters bottom-up instead of top-down (Van Rijsbergen & Croft, 1975). Alternatively, the user can create the tree hierarchy with fewer documents.
Limitations of this work
We identified four potential limitations to our work.
First, we did not cover all the possible clustering solutions. We used a single clustering solution, instead of using several clustering solutions or letting a user create clustering solutions on the run. Some of the characteristics of the tree hierarchy could have been different, like the clustering algorithm that we used, the clustering resolution parameters, the number of child clusters, the number of levels and the fact that we created the tree hierarchy by a top-down division of clusters instead of a bottom-up agglomeration of clusters.
Second, we did not cover all the possible citation networks. We used a citation network of direct citations, and not a more densely connected citation network using co-citations (Small, 1973) or bibliographic coupling (Martyn, 1964), which when combined with direct citation improve the representation of the structure of science (Waltman et al., 2020). We made the citation network using the full corpus, but we could also have used for example the documents retrieved from a query, which some studies reported to be more effective for cluster-based IR (Tombros et al., 2002).
Third, the cluster selection algorithm does not reflect fully realistic (and noisy) user behavior. The cluster selection algorithm knows the relevant documents—an assumption commonly made in information retrieval evaluation –, which a real user would not. A real user would have to select the clusters based on their own personal evaluation of which cluster is more likely to contain the relevant documents, and also they would have to evaluate when to stop going down the tree hierarchy. This process would take cognitive effort, which our evaluation does not consider. A less cognitively heavy alternative for a user could be to eliminate a cluster that does not contain relevant documents and then create a new clustering solution, as there is likely to be an obvious candidate for elimination. This is the same process as selecting more than one cluster, as we discussed in the weaknesses (Sect. “Weaknesses”), and we decided against implementing it in the evaluation because it would create too many steps and the clustering would take too much computational resources. Another unrealistic behavior is that the cluster selection algorithm never chooses the wrong cluster, unlike a real user. We could have implemented mistakes by giving imperfect information to the cluster selection algorithm, but we decided not to so to have less variables that could affect the interpretation of our results. Finally, it is not realistic to allow the cluster selection algorithm to choose very small clusters (size between 1 and 10 documents) because this size of clusters does not appear in real situations (as discussed by Willet (Willett, 1988)). Future work could address more noisy user behavior, similar to user behavior modeling in information retrieval (Hofmann et al., 2013).
The final limitation is that it could be argued that the Boolean queries we used are not realistic. A real Boolean query is created over several iterations, where the creators of the query keep refining the query until they are satisfied with the search results. Our evaluation does not consider this. Also, our Boolean queries had a recall of 1.0 (i.e., they found all the relevant documents), which is unlikely for a real IR method. Additionally, we only considered the documents retrieved by the Boolean query on MEDLINE, while the authors of the SRs usually used more than one database or method to search for documents, including the expert knowledge of their colleagues. We did not include more sources because it would be too much effort to retrieve the documents of each method and to harmonize the results between SRs that used different methods. Finally, the translation from OVID format to PubMed format is likely to have modified the set of retrieved documents, especially if the Boolean query used OVID-specific features (like distance between words). We tried to remove the cases with the biggest modification of the set of retrieved documents by removing the SRs with Boolean queries that retrieved a number of documents too different from the number documents self-reported by the authors (see Sect. “Task design and data collection”).
Conclusion
In this work we have shown some of the advantages and limitations of using CCIR for academic search, both for generic CCIR and for our specific tree hierarchy implementation. We have also introduced an evaluation protocol for cluster-based IR methods with the task of finding relevant documents for SRs. This protocol can be used and modified by other researchers. We release our data for use by other researchers in the form of the three tree hierarchies, the set of relevant documents and the set of documents retrieved by the Boolean query, the latter one created through intensive manual annotation. The current CCIR implementation can be used as a straightforward CCIR tool of value for real users.
Our research shows that the best served users are those who prefer recall over precision 2 to 8 times. Users that prefer even more recall, like SR users, are less well served, and users that prefer more precision are the worst served. CCIR may complement Boolean query searches in various ways: it may help SR users that have problems to state their requirements as Boolean queries, it may suggest terms for Boolean queries, and it may retrieve relevant documents not retrieved by a Boolean query.
A problematic aspect of CCIR is that performance varies significantly because there sometimes is no cluster that contains the topic of the SR. This may happen because documents may relate to multiple topics, leading to clusters that do not match with the topic of the SR. It may also happen because of a lack of citation connections between the documents related to the topic of interest. Another problematic aspect is that the current implementation of CCIR demands a high cognitive effort from a user.
For future work related to CCIR, interesting research directions are how to improve its performance (how to create better clusters, re-clustering based on the selection of multiple clusters by a user, mixing with semantic-based clustering), how it compares to other IR methods (especially citation-based or cluster-based methods) and how real users interact with it (how to select clusters, how to complement with other IR tools).
Data availability
The code used to run the experiments in this paper is available in GitHub (https://github.com/jpbascur/citation_clusters_evaluation) and the data is available in Zenodo (Bascur, 2022).
References
Abbasi, M. K., & Frommholz, I. (2015). Cluster-based polyrepresentation as science modelling approach for information retrieval. Scientometrics, 102(3), 2301–2322. https://doi.org/10.1007/s11192-014-1478-1
Abdelhaq, H., Sengstock, C., & Gertz, M. (2013). EvenTweet: Online localized event detection from twitter. Proceedings of the VLDB Endowment, 6(12), 1326–1329. https://doi.org/10.14778/2536274.2536307
Ahlgren, P., Chen, Y., Colliander, C., & van Eck, N. J. (2020). Enhancing direct citations: A comparison of relatedness measures for community detection in a large set of PubMed publications. Quantitative Science Studies, 1(2), 714–729. https://doi.org/10.1162/qss_a_00027
Atkinson, H. J., Morris, J. H., Ferrin, T. E., & Babbitt, P. C. (2009). Using sequence similarity networks for visualization of relationships Across diverse protein superfamilies. PLoS ONE, 4(2), e4345. https://doi.org/10.1371/journal.pone.0004345
Azzopardi, L., Järvelin, K., Kamps, J., & Smucker, M. D. (2011). Report on the SIGIR 2010 workshop on the simulation of interaction. ACM SIGIR Forum, 44(2), 35. https://doi.org/10.1145/1924475.1924484
Bascur, J. P., van Eck, N. J., & Waltman, L. (2019). An interactive visual tool for scientific literature search: Proposal and algorithmic specification. Proceedings of the 8th International Workshop on Bibliometric-Enhanced Information Retrieval (BIR) Co-Located with the 41st European Conference on Information Retrieval (ECIR 2019), 76–87.
Bascur, J. P. (2022). Academic information retrieval using citation clusters: In-depth evaluation based on systematic reviews (Data) (1.0). Zenodo. https://doi.org/10.5281/zenodo.6702252
Belter, C. W. (2016). Citation analysis as a literature search method for systematic reviews. Journal of the Association for Information Science and Technology, 67(11), 2766–2777. https://doi.org/10.1002/asi.23605
Belter, C. W. (2017). A relevance ranking method for citation-based search results. Scientometrics, 112(2), 731–746. https://doi.org/10.1007/s11192-017-2406-y
Boyack, K. W., Smith, C., & Klavans, R. (2020). A detailed open access model of the PubMed literature. Scientific Data, 7(1), 408. https://doi.org/10.1038/s41597-020-00749-y
Cabanac, G., Chandrasekaran, M. K., Frommholz, I., Jaidka, K., Kan, M.-Y., Mayr, P., & Wolfram, D. (2017). Report on the joint workshop on bibliometric-enhanced information retrieval and natural language processing for digital libraries (BIRNDL 2016). ACM SIGIR Forum, 50(2), 36–43. https://doi.org/10.1145/3053408.3053417
Callon, M., Courtial, J.-P., Turner, W. A., & Bauin, S. (1983). From translations to problematic networks: An introduction to co-word analysis. Social Science Information, 22(2), 191–235. https://doi.org/10.1177/053901883022002003
Carmel, D., Yom-Tov, E., Darlow, A., & Pelleg, D. (2006). What makes a query difficult? Proceedings of the 29th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval - SIGIR ’06, 390. https://doi.org/10.1145/1148170.1148238
Chandra, K., Slater, B., & Ma, M. (2021). Research Rabbit. https://www.researchrabbit.ai/
Chen, C. (2006). CiteSpace II: Detecting and visualizing emerging trends and transient patterns in scientific literature. Journal of the American Society for Information Science and Technology, 57(3), 359–377. https://doi.org/10.1002/asi.20317
Chen, C. (2017). Science Mapping: A Systematic Review of the Literature. Journal of Data and Information Science, 2(2), 1–40. https://doi.org/10.1515/jdis-2017-0006
Cobo, M. J., López-Herrera, A. G., Herrera-Viedma, E., & Herrera, F. (2011). Science mapping software tools: Review, analysis, and cooperative study among tools. Journal of the American Society for Information Science and Technology, 62(7), 1382–1402. https://doi.org/10.1002/asi.21525
Cousins, S. E., Tempest, E., & Feuer, D. J. (2016). Surgery for the resolution of symptoms in malignant bowel obstruction in advanced gynaecological and gastrointestinal cancer. Cochrane Database of Systematic Reviews. https://doi.org/10.1002/14651858.CD002764.pub2
Cutting, D. R., Karger, D. R., Pedersen, J. O., & Tukey, J. W. (1992). Scatter/Gather: A Cluster-based Approach to Browsing Large Document Collections. Proceedings of the 15th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval., 12. https://doi.org/10.1145/133160.133214
De Vries, C. M., Geva, S., & Trotman, A. (2012). Document Clustering Evaluation: Divergence from a Random Baseline. ArXiv:1208.5654 [Cs]. https://doi.org/10.48550/arXiv.1208.5654
Ellis, D. (1993). Modeling the information-seeking patterns of academic researchers: A grounded theory approach. The Library Quarterly, 63(4), 469–486. https://doi.org/10.1086/602622
Elsevier. (n.d.). Topic Prominence in Science—Scival. Elsevier.Com. Retrieved January 25, 2023, from https://www.elsevier.com/solutions/scival/features/topic-prominence-in-science
Frommholz, I., Mayr, P., Cabanac, G., & Verberne, S. (2021). Bibliometric-Enhanced Information Retrieval: 11th International BIR Workshop. In: D. Hiemstra, M.-F. Moens, J. Mothe, R. Perego, M. Potthast, & F. Sebastiani (Eds.), Advances in Information Retrieval (Vol. 12657, pp. 705–709). Springer International Publishing. https://doi.org/10.1007/978-3-030-72240-1_85
Haunschild, R., & Marx, W. (2020). Discovering seminal works with marker papers. Scientometrics, 125(3), 2955–2969. https://doi.org/10.1007/s11192-020-03358-z
He, J., Ping, Q., Lou, W., & Chen, C. (2019). PaperPoles: Facilitating adaptive visual exploration of scientific publications by citation links. Journal of the Association for Information Science and Technology, 70(8), 843–857. https://doi.org/10.1002/asi.24171
Hearst, M. A., & Pedersen, J. O. (1996). Reexamining the Cluster Hypothesis: Scatter/Gather on Retrieval Results. Proceedings of the 19th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM. https://doi.org/10.1145/243199.243216
Held, M., & Velden, T. (2022). How to interpret algorithmically constructed topical structures of scientific fields? A case study of citationbased mappings of the research specialty of invasion biology. Quantitative Science Studies, 3(3), 651–671.
Hemminger, B. M., Lu, D., Vaughan, K. T. L., & Adams, S. J. (2007). Information seeking behavior of academic scientists. Journal of the American Society for Information Science and Technology, 58(14), 2205–2225. https://doi.org/10.1002/asi.20686
Hofmann, K., Whiteson, S., & de Rijke, M. (2013). Balancing exploration and exploitation in listwise and pairwise online learning to rank for information retrieval. Information Retrieval, 16(1), 63–90. https://doi.org/10.1007/s10791-012-9197-9
Honnibal, M., Montani, I., Van Landeghem, S., & Boyd, A. (2020). spaCy: Industrial-strength Natural Language Processing in Python.
Horsley, T., Dingwall, O., & Sampson, M. (2011). Checking reference lists to find additional studies for systematic reviews. Cochrane Database of Systematic Reviews. https://doi.org/10.1002/14651858.MR000026.pub2
Inciteful. (2022). https://inciteful.xyz/
Iris.ai. (2019, September 30). https://iris.ai/
Janssens, F., Glänzel, W., & De Moor, B. (2008). A hybrid mapping of information science. Scientometrics, 75(3), 607–631. https://doi.org/10.1007/s11192-007-2002-7
Janssens, A. C. J. W., Gwinn, M., Brockman, J. E., Powell, K., & Goodman, M. (2020). Novel citation-based search method for scientific literature: A validation study. BMC Medical Research Methodology. https://doi.org/10.1186/s12874-020-0907-5
Jardine, N., & van Rijsbergen, C. J. (1971). The use of hierarchic clustering in information retrieval. Information Storage and Retrieval, 7(5), 217–240. https://doi.org/10.1016/0020-0271(71)90051-9
Klavans, R., & Boyack, K. W. (2006). Quantitative evaluation of large maps of science. Scientometrics, 68(3), 475–499. https://doi.org/10.1007/s11192-006-0125-x
Kuhlthau, C. C. (1991). Inside the search process: Information seeking from the user’s perspective. Journal of the American Society for Information Science, 42(5), 361–371. https://doi.org/10.1002/(SICI)1097-4571(199106)42:5%3c361::AID-ASI6%3e3.0.CO;2-#
Liang, Y., Li, Q., & Qian, T. (2011). Finding Relevant Papers Based on Citation Relations. In H. Wang, S. Li, S. Oyama, X. Hu, & T. Qian (Eds.), Web-Age Information Management. Springer. https://doi.org/10.1007/978-3-642-23535-1_35
Ma, L.-O. (2015). Rituximab for rheumatoid arthritis (Review). Cochrane Database of Systematic Reviews, 253.
Madeira, F., & Vot. (2018). Citation Gecko. https://github.com/CitationGecko/gecko-client
Manning, C. D., Raghavan, P., & Schütze, H. (2008). Introduction to Information Retrieval. Cambridge University Press.
Martyn, J. (1964). Bibliographic coupling. Journal of Documentation, 20(4), 236–236. https://doi.org/10.1108/eb026352
Mayr, P., & Scharnhorst, A. (2015). Scientometrics and information retrieval: Weak-links revitalized. Scientometrics, 102(3), 2193–2199. https://doi.org/10.1007/s11192-014-1484-3
Mutschke, P., & Mayr, P. (2015). Science models for search: A study on combining scholarly information retrieval and scientometrics. Scientometrics, 102, 2323–2345. https://doi.org/10.1007/s11192-014-1485-2
Open Knowledge Maps: A Visual Interface to the World’s Scientific Knowledge. (2019). Open Knowledge Maps. https://openknowledgemaps.org
Ortuño, F. M., Rojas, I., Andrade-Navarro, M. A., & Fontaine, J.-F. (2013). Using cited references to improve the retrieval of related biomedical documents. BMC Bioinformatics, 14(1), 113. https://doi.org/10.1186/1471-2105-14-113
Peinemann, F., Bartel, C., Grouven, U., & Berthold, F. (2013). Retinoic acid post consolidation therapy for high-risk neuroblastoma patients treated with autologous hematopoietic stem cell transplantation. Cochrane Database of Systematic Reviews. Wiley.
Pirolli, P., Schank, P., Hearst, M., & Diehl, C. (1996). Scatter/gather browsing communicates the topic structure of a very large text collection. Proceedings of the SIGCHI Conference on Human Factors in Computing Systems Common Ground - CHI ’96, 213–220. https://doi.org/10.1145/238386.238489
Pitt, A., Dixon, D., & Webster, K. (2022). Litmaps. https://www.litmaps.com/
Potter, I. (2020). Introducing Citation Topics in InCites. Clarivate Blog. https://clarivate.com/blog/introducing-citation-topics/
PubMed API. (2018). https://www.ncbi.nlm.nih.gov/books/NBK25500/
Robinson, K. A., Dunn, A. G., Tsafnat, G., & Glasziou, P. (2014). Citation networks of related trials are often disconnected: Implications for bidirectional citation searches. Journal of Clinical Epidemiology, 67(7), 793–799. https://doi.org/10.1016/j.jclinepi.2013.11.015
Russell-Rose, T., Chamberlain, J., & Azzopardi, L. (2018). Information retrieval in the workplace: A comparison of professional search practices. Information Processing & Management, 54(6), 1042–1057. https://doi.org/10.1016/j.ipm.2018.07.003
Scells, H., Zuccon, G., Koopman, B., Deacon, A., Azzopardi, L., & Geva, S. (2017). A Test Collection for Evaluating Retrieval of Studies for Inclusion in Systematic Reviews. Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval - SIGIR ’17, 1237–1240. https://doi.org/10.1145/3077136.3080707
Scells, H., Locke, D., & Zuccon, G. (2018). An Information Retrieval Experiment Framework for Domain Specific Applications. The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, 1281–1284. https://doi.org/10.1145/3209978.3210167
Sjögårde, P., & Ahlgren, P. (2018). Granularity of algorithmically constructed publication-level classifications of research publications: Identification of topics. Journal of Informetrics, 12(1), 133–152. https://doi.org/10.1016/j.joi.2017.12.006
Sjögårde, P., & Ahlgren, P. (2020). Granularity of algorithmically constructed publication-level classifications of research publications: Identification of specialties. Quantitative Science Studies, 1(1), 207–238. https://doi.org/10.1162/qss_a_00004
Sjögårde, P., Ahlgren, P., & Waltman, L. (2021). Algorithmic labeling in hierarchical classifications of publications: Evaluation of bibliographic fields and term weighting approaches. Journal of the Association for Information Science and Technology, 72(7), 853–869. https://doi.org/10.1002/asi.24452
Small, H. (1973). Co-citation in the scientific literature: A new measure of the relationship between two documents. Journal of the American Society for Information Science, 24(4), 265–269. https://doi.org/10.1002/asi.4630240406
Small, H., & Garfield, E. (1985). The geography of science: Disciplinary and national mappings. Journal of Information Science, 11(4), 147–159. https://doi.org/10.1177/016555158501100402
Stefanowski, J., & Weiss, D. (2003). Carrot2 and Language Properties in Web Search Results Clustering. In E. Menasalvas, J. Segovia, & P. S. Szczepaniak (Eds.), Advances in Web Intelligence. Springer.
Tombros, A., Villa, R., & Van Rijsbergen, C. J. (2002). The effectiveness of query-specific hierarchic clustering in information retrieval. Information Processing & Management, 38(4), 559–582. https://doi.org/10.1016/S0306-4573(01)00048-6
Traag, V. A., Waltman, L., & van Eck, N. J. (2019). From Louvain to Leiden: Guaranteeing well-connected communities. Scientific Reports. https://doi.org/10.1038/s41598-019-41695-z
van Rijsbergen, C. J. (1979). Information Retrieval (2nd ed.). Butterworths.
van Eck, N. J., & Waltman, L. (2010). Software survey: VOSviewer, a computer program for bibliometric mapping. Scientometrics, 84(2), 523–538. https://doi.org/10.1007/s11192-009-0146-3
van Eck, N. J., & Waltman, L. (2014). CitNetExplorer: A new software tool for analyzing and visualizing citation networks. Journal of Informetrics, 8(4), 802–823. https://doi.org/10.1016/j.joi.2014.07.006
van Eck, N. J., & Waltman, L. (2017). Citation-based clustering of publications using CitNetExplorer and VOSviewer. Scientometrics, 111(2), 1053–1070. https://doi.org/10.1007/s11192-017-2300-7
Van Rijsbergen, C. J., & Croft, W. B. (1975). Document clustering: An evaluation of some experiments with the cranfield 1400 collection. Information Processing & Management, 11(5–7), 171–182. https://doi.org/10.1016/0306-4573(75)90006-0
Waltman, L., & van Eck, N. J. (2012). A new methodology for constructing a publication-level classification system of science. Journal of the American Society for Information Science and Technology, 63(12), 2378–2392. https://doi.org/10.1002/asi.22748
Waltman, L., Boyack, K. W., Colavizza, G., & van Eck, N. J. (2020). A principled methodology for comparing relatedness measures for clustering publications. Quantitative Science Studies. https://doi.org/10.1162/qss_a_00035
Weinblatt, M. E., Fleischmann, R., Huizinga, T. W. J., Emery, P., Pope, J., Massarotti, E. M., van Vollenhoven, R. F., Wollenhaupt, J., Bingham, C. O., Duncan, B., Goel, N., Davies, O. R., & Dougados, M. (2012). Efficacy and safety of certolizumab pegol in a broad population of patients with active rheumatoid arthritis: Results from the REALISTIC phase IIIb study. Rheumatology, 51(12), 2204–2214. https://doi.org/10.1093/rheumatology/kes150
Willett, P. (1988). Recent trends in hierarchic document clustering: A critical review. Information Processing & Management, 24(5), 577–597. https://doi.org/10.1016/0306-4573(88)90027-1
Wolfram, D. (2015). The symbiotic relationship between information retrieval and informetrics. Scientometrics, 102(3), 2201–2214. https://doi.org/10.1007/s11192-014-1479-0
Wright, K., Golder, S., & Rodriguez-Lopez, R. (2014). Citation searching: A systematic review case study of multiple risk behaviour interventions. BMC Medical Research Methodology, 14(1), 73. https://doi.org/10.1186/1471-2288-14-73
Yuan, M., Zobel, J., & Lin, P. (2022). Measurement of clustering effectiveness for document collections. Information Retrieval Journal. https://doi.org/10.1007/s10791-021-09401-8
Zitt, M. (2015). Meso-level retrieval: IR-bibliometrics interplay and hybrid citation-words methods in scientific fields delineation. Scientometrics, 102(3), 2223–2245. https://doi.org/10.1007/s11192-014-1482-5
Acknowledgements
We would like to thank Jan W. Schoones for his expert support in biomedical Boolean queries, and Vincent Traag and Roel van der Ploeg for their invaluable feedback. We are also grateful to an anonymous reviewer for their comments on our work.
Funding
We did not receive any funding for the research presented in this paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
We have no competing interests to declare.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bascur, J.P., Verberne, S., van Eck, N.J. et al. Academic information retrieval using citation clusters: in-depth evaluation based on systematic reviews. Scientometrics 128, 2895–2921 (2023). https://doi.org/10.1007/s11192-023-04681-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11192-023-04681-x