Ockham’s index of citation impact

Abstract

We demonstrate that by using a triple of simple numerical summaries: an author’s productivity, their overall impact, and a single other bibliometric index that aims to capture the shape of the citation distribution, we can reconstruct other popular metrics of bibliometric impact with a sufficient degree of precision. We thus conclude that the use of many indices may be unnecessary – entities should not be multiplied beyond necessity. Such a study was possible thanks to our new agent-based model (Siudem et al. in Proc Natl Acad Sci 117:13896–13900, 2020, https://doi.org/10.1073/pnas.2001064117), which not only assumes that citations are distributed according to a mixture of the rich-get-richer rule and sheer chance, but also fits real bibliometric data quite well. We investigate which bibliometric indices have good discriminative power, which measures can be easily predicted as functions of other ones, and what implications to the research evaluation practice our findings have.

Introduction

The way we quantify the reality behind the generation of scientific output has important consequences for, amongst others, the practice of grant competitions and applying for tenure or academic promotion. The popular tools for aggregating citation records at an individual level, including the h- (Hirsch, 2005), and the g-index (Egghe, 2006) became part of scientific jargon. The number of available bibliometric impact measures is overwhelming, and new indices are still being proposed, see, e.g., (Bihari et al., 2021;  Wildgaard et al., 2014) for example reviews. In this paper we are interested in tackling the question whether introducing new measures can contribute to a more informative description of this complex system.

Bibliometric indices are often deemed to combine both the quality of a scientist’s output (the impact of an individual paper measured by the number of citations it has received) and its quantity (or productivity, measured by the number of published papers). Over the years, numerous theoretical studies were conducted in order to investigate their properties in various settings, e.g., (Egghe and Rousseau, 2021; Gagolewski, 2013; Woeginger, 2008). There is also a growing body of research devoted to experimental comparisons of selected indices using real-life data in the search for the best metric, or at least the best in a context at hand.

Many papers analysed the interdependencies between the values of indices on selected datasets and, as a result, suggested that many measures are actually redundant, because they seem to behave quite similarly. For example, the investigation carried out by Bornmann et al. (2008) is focused on the h-index and its variants. Based on data from biomedicine, the authors determined that the indices can be clustered into two groups: those which measure the impact of a few most cited papers and those that quantify how many papers are impactful. Further, Ain et al. (2019) and Ghani et al. (2019) ask which indices can indicate the most prominent authors best. A benchmark set describing the award-winning mathematicians revealed that the orderings established by the most popular bibliometric measures were not consistent with the evaluations made by experts. Moreover, correlations between some pairs of considered indices were found to be very high, which might indicate that there is no added value in defining new metrics. Similar conclusions were reached by Ayaz and Masood (2020) for a sample of computer science works and by Bornmann et al. (2011) who present a meta-analysis of a few older studies.

Also, Wildgaard et al. (2014) recollect 108 author-level indicators, compares their properties in a theoretical setting, and groups them into a few classes. The authors conclude that using just one indicator is inadequate and cannot capture the nature of a citation vector, thus many of them should be used at the same time and the selection of the appropriate index should always be based on its properties that are desired in a particular use case. Other authors were interested in measuring the agreement between the rankings of researchers obtained by various bibliometric measures (Blagus et al., 2019) and whether they can predict the future success of an author (Wang et al., 2019).

In this paper, we take a much different approach to studying the relationships between the bibliometric indices. We formulate a framework that allows us to reproduce the values of bibliometric measures based on only three parameters: the total number of citations (a measure of impact), the number of publications (a measure of productivity), and the value of some other carefully chosen index (a measure of the shape/inequality/skewness of the citation distribution).

Our analysis can be considered an extension of the idea presented by Bertoli-Barsotti and Lando in (2017a) and (2017b), where the h-index has been expressed (analytically) by means of 4 other sample statistics for a few models known from the literature. In this paper, however, we utilise a new model that we have recently derived in (Siudem et al., 2020). Due to the complexity of our enterprise, we shall present the results of a numerical study. This way, we can also consider those indices that do not yield an analytic solution.

The structure of this contribution is as follows. In “Data” section we describe the employed sample from the DBLPv12 database of computer science papers, in “Methods” section we detail the utilised methodology, in “Results section we present and discuss the key findings, and in “Conclusion” section we give the concluding remarks.

Data

The analysis shall be conducted on the DBLP-Citation-network v12 database¹ [see (Tang et al., 2008) for more details] which features 45,564,149 citation relationships between 4,894,081 papers in major computer science outlets. We have grouped all authors by their identifiers (IDs) as assigned by the data source itself. Note that it may happen that one author is represented by two or more IDs. It can also be the case that some authors will appear under the same IDs. However, the problem of author name disambiguation is difficult in general and is not the subject of this work.

In the preprocessing stage of the analysis, we have removed all papers with zero citations (because they are problematic on the log-scale; moreover, many bibliometric indices ignore their presence anyway). Further, all authors with the h-index less than 5 were omitted, as any inference based on small samples cannot be deemed statistically reliable. This resulted in $M=243{,}873$ citation vectors in total, which is still a very large data sample.

Methods

3DSI model

In the recent paper (Siudem et al., 2020) we have introduced the so-called 3DSI model (3 dimensions of scientific impact). It is an agent-based model inspired by (Ionescu and Chopard, 2013; Żogała-Siudem et al., 2016) that captures the evolution of an author’s citation record which we represent with

$$\begin{aligned} \mathbf {X} = (X_1, X_2, \ldots , X_N), \quad \mathrm {such\ that} \quad X_1 \ge X_2 \ge \cdots \ge X_N, \end{aligned}$$

where $X_k$ denotes the number of citations received by the k-th most referenced paper. The 3DSI model has the following intuitive underlying assumptions: in each time step one new paper is added into the author’s track record. Then, the existing publications are cited based on a mixture of sheer chance and the preferential attachment mechanism [the rich-get-richer rule, see, e.g., Merton, 1968; Perc, 2014)].

Each author is described by 3 parameters:

• their number of papers, N,

• the total number of citations distributed, $C=X_1+X_2+\dots +X_N$,

• the ratio of citations distributed according to the preferential attachment rule, $\rho$, where $\rho \simeq 0$ means that all the papers are referenced completely at random and $\rho \simeq 1$ denotes the dominance of the rich-get-richer rule.

In Siudem et al. (2020) we have shown that, for given N, C, and $\rho \in (0,1)$, the k-th most cited paper is expected to receive

$$\begin{aligned} \hat{X}_k(N,C,\rho ) =\frac{1-\rho }{\rho }\frac{C}{N}\left( \frac{\Gamma (N+1)}{\Gamma (k)} \frac{\Gamma (k-\rho )}{\Gamma (N+1-\rho )} - 1\right) \end{aligned}$$

(1)

citations, where $\Gamma$ is the gamma function. Note that for any $\alpha \in [0,1)$ it holds that $\Gamma (N+1-\alpha )/\Gamma (k-\alpha )=(N-\alpha )\cdot (N-1-\alpha )\cdots (k+1-\alpha )\cdot (k-\alpha )$, hence

$$\begin{aligned} \hat{X}_k(N,C,\rho ) =\frac{1-\rho }{\rho }\frac{C}{N}\left( \frac{N\cdot (N-1)\cdots k}{(N-\rho )\cdot (N-1-\rho )\cdots (k-\rho )}- 1\right) . \end{aligned}$$

Further, in (Cena et al., 2022) we noted that for $\rho =0$ our model reduces to the harmonic one:

$$\begin{aligned} \hat{X}_k(N,C,0)= \frac{C}{N}\sum \limits _{i=k}^N\frac{1}{i}. \end{aligned}$$

What is more, recently we have noted (Gagolewski et al., 2022) that the case $\rho <0$ is possible as well and that it also yields Eq. (1), which corresponds to inverse preferential attachment in our agent-based model. Note that the interpretation of $\rho = 0$ denoting a completely random citation distribution in the model (Siudem et al., 2020) still holds, because it relates to what happens in each individual iteration. Overall, for $\rho =0$, the final citation distribution is not uniform, because of the inherent “old-get-richer” component.

Fig. 1

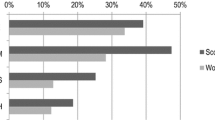
Example citation vectors demonstrating the effects of altering the $\rho$ parameter in the 3DSI model (Siudem et al., 2020) given by Eq. (1) for a fixed N and C. Note that despite the average number of citations’ being retained, the higher the $\rho$, the higher the inequality of the citation distribution. Small $\rho$s result in flatter vectors

Figure 1 shows three example vectors that are generated by the model when $\rho$ varies but N and C are fixed. We see that $\rho$ is an independent dimension in our feature space and is crucial for identifying the citation distribution. In particular, for $\rho \simeq 1$ almost all load is allocated to the most cited paper. Moreover, the smaller the $\rho$, the flatter the vector. Hence, $\rho$ can be considered a measure of shape of the citation distribution.

Model fitting

Fitting $N, C, \rho$ to a true (empirical) citation vector $\mathbf {X}=(X_1,\dots ,X_N)$ can be done in many ways. In (Siudem et al., 2020) we have employed a procedure that takes N (the length of the citation vector) and C (the sum of elements in the citation vector, $\sum _{i=1}^N X_i$) from the sample and then numerically minimises the least squared error with respect to the log-Cauchy loss, i.e.,

$$\begin{aligned} \min _{\rho \in (-\infty ,1)} \sum _{k=1}^N \log \left( 1 + \left( \log \hat{X}_k(N,C,\rho )-\log X_k\right) ^2\right) . \end{aligned}$$

(2)

Such a loss function is robust in the presence of outliers and yields a good fit in the tail of the citation distribution, i.e., is suitable for the modelling of the most cited papers (Cena et al., 2022). From now on, we shall denote with $\rho _C$ the parameter estimated with this very method, i.e., the solution to Eq. (2) for a given vector $\mathbf {X}$ (using scipy.optimize.least_squares from SciPy 1.6.2 for Python 3.9.5 which is based on a trust region reflective-type algorithm with 5 restarts from random initial guesses).

Also note that, in practice, many other loss functions can be considered, such as the log-linear one, yielding $\sum _{k=1}^N \left( \log \hat{X}_k(N,C,\rho )-\log X_k\right) ^2$, or the log-soft-$l_1$ loss, corresponding to the problem of minimising the objective $\sum _{k=1}^N \left( \sqrt{1+\left( \log \hat{X}_k(N,C,\rho )-\log X_k\right) ^2}-1\right)$. Each of them induces a distinctive estimator of the $\rho$ parameter, having possibly different statistical properties (bias, mean squared error, etc.). From the perspective of our analysis, the Cauchy loss gave slightly better results than the other two, hence its choice herein.

Reparametrisation by means of citation indices

It is worth stressing that by fitting the 3DSI model to empirical data, the whole citation vector, regardless of its size N, is being “compressed” into merely 3 well-interpretable parameters.

However, some practitioners might find the fitting based on the above optimisation procedure not necessarily straightforward. It would hence be much more convenient to have some other ways to estimate the $\rho$ parameter from data.

Here we propose that $\rho$ be determined by the means of a proxy bibliometric index $j$, e.g., the Hirsch h-index. For a single author and their citation record $(X_1,\dots ,X_N)$ we determine their:

• number of papers (productivity), N,

• number of citations (total impact), $C=\sum _{i=1}^N X_i$,

• citation index (usually a summary of the top cited papers), $J= j (X_1,\dots ,X_N)$.

Given N, C, and J, the $\rho$ parameter can be computed by solving:

$$\begin{aligned} j \!\left( \hat{X}_1(N,C,{\rho }), \dots , \hat{X}_N(N,C,{\rho })\right) = j (X_1,\dots ,X_N), \end{aligned}$$

(3)

i.e., recreating the theoretical citation vector (based on the 3DSI model, Eq. (1)) that yields the same citation index as the observed one. This somewhat resembles the method of moments/quantiles estimators in statistics. For brevity, we will denote the above as

$$\begin{aligned} j \!\left( \hat{\mathbf {X}}(N,C,{\rho })\right) =J \end{aligned}$$

(4)

with respect to $\rho$.

Ideally, if the data exactly followed the assumed model, for given N and C we would be expecting a one-to-one correspondence between J and $\rho$. In practice, however, there will be deviations from the theoretical distribution; after all, any model is merely an approximation to the complex reality described thereby.

Unfortunately, it might be difficult to solve the above analytically (see below for a derivation for the csr-index). Therefore, we will be relying upon equivalent solutions obtained numerically.

Also, for some indices it might happen that the solution to the above does not exist at all or is ambiguous. In particular, h, g, w, and i10 are not only integer-valued, but also bounded from above by N. Therefore, in general we shall rather be seeking the closest approximation by minimising

$$\begin{aligned} \min _\rho \left( j \!\left( \hat{\mathbf {X}}(N,C,{\rho })\right) -J\right) ^2. \end{aligned}$$

(5)

which of course reduces to Eq. (3) if $j$ is well-behaving. In case of the objective function’s being minimised not at a single point, but at a whole interval $[\rho ^L, \rho ^U]$, we have tested a number of approaches and found that choosing the minimiser closest to 0 yields the best results overall. This is the one that we shall be using below.

Indices studied

Not all indices are created equal. It is frequently the case in statistical practice that there might be many different estimators of the underlying parameters—they will differ in bias, variance, robustness in presence of contaminated data, etc. After all, even for such basic statistical models as independent random variables following a normal distribution, the expected value $\mu$ can be estimated using a variety of aggregates, including the arithmetic mean, median, or other winsorised or trimmed means.

In what follows we shall thus consider a wide range of popular bibliometric measures as listed in Table 1—including the famous h- and g-indices (Hirsch, 2005; Egghe, 2006). Moreover, we have included some measures not used in the bibliometric context before. They all have quite different characteristics and focus on different aspects of the citation vectors they aim to summarise. Some are even chiefly of theoretical interest, e.g., w was developed in the axiomatic analysis context of (Woeginger, 2008).

We also indicate which index is normalised, $j (N, N, \dots , N)=N$ (N items of impact N each—a square-shaped citation distribution) for all integer $N\ge 1$. Also, let us consider the dominance relation $\preceq$ such that $(X_1,\dots ,X_N)\preceq (X_1',\dots ,X_{N'}')$ if and only if $N\le N'$ and $X_i\le X_i'$ for all i [see (Woeginger, 2008) and (Gagolewski, 2013; Wu and Zhang, 2017) for further discussion]. Then we say that an index $j$ is monotone with respect to $\preceq$, whenever for all $(X_1,\dots ,X_N)\preceq (X_1',\dots ,X_{N'}')$ it holds that $j (X_1,\dots ,X_N)\le j (X_1',\dots ,X_{N'}')$. Some indices may be transformed so that they are monotone or normalised, but we wanted to retain a degree of variability with regards to this matter.

Table 1 Bibliometric impact indices considered in our study, assuming a citation vector $\mathbf {X}=(X_1,\dots ,X_N)$ meets $X_1 \ge \dots \ge X_N$

In particular, the rmp-index is the square root of the MAXPROD-index (Kosmulski, 2007). The hg- (Alonso et al., 2010), o- (Dorogovtsev & Mendes, 2015), and r- (Jin et al., 2007) indices are defined as geometric means of other measures. The a-index (Alonso et al., 2009) is the average number of citations in the so-called h-core of a vector.

The slg-index, being the sum of logarithms of citations, is often used as an estimator in the context of the Pareto distribution [e.g., (Arnold, 2015)], to which our model is related, see (Siudem et al., 2022).

The cube root-sum-square (css) is a measure highly sensitive to outliers as it is based on second moments (again, commonly considered in statistics). Further, the cube root-sum-rank, csr, is a function of the average rank, $\sum _{i=1}^N i x_i/C$ (proposed by one of the reviewers of this manuscript, see below for discussion). They both have been normalised and made monotone with respect to the dominance relation.

Entropy (ent) is often used in information theory. The p20-index is the proportion of citations allocated to the top 20% cited papers stems from economics (compare the Pareto 80-20 principle). Both can be considered measures of data distribution’s inequality.

Finally, the i10-index is the number of papers with at least 10 citations, and is being reported by some commercial bibliographic databases.

Analytic solution

Furthermore, one of the reviewers of this manuscript pointed out that the expected rank in the 3DSI model,

$$\begin{aligned} \hat{R}=\sum _{i=1}^N i \frac{\hat{X}_i}{C}, \end{aligned}$$

can be expressed analytically as

$$\begin{aligned} \hat{R}=\frac{N (\rho -1)+\rho -3}{2 (\rho -2)}. \end{aligned}$$

Computing the corresponding statistic from the empirical citation vector, $er (\mathbf {X})=\sum _{i=1}^N i \frac{X_i}{C}$, solving the above for $\rho$, and noting that $er (\mathbf {X})= ( csr ^3(\mathbf {X})+C)/2C$ gives us the rank-size domain method of moments estimator of our parameter

$$\begin{aligned} \rho _{R}= \frac{N-4 { er (\mathbf {X})}+3}{N-2 { er (\mathbf {X})}+1} = \frac{N-2 { csr ^3(\mathbf {X})}/C+1}{N- { csr ^3(\mathbf {X})}/C} . \end{aligned}$$

(6)

Note that this is exactly the solution to Eq. (3) with $j = csr$, but this time having an explicit open-form solution.

Results

Fig. 2

Spearman’s rank correlation coefficients between each pair of bibliometric indices considered in this study as well as the number of papers N, total number of citations C, and $\rho$ estimated by solving Eq. (2). Note that high correlation (values close to 1.00) means that one index can be expressed as a monotonic function of another one from the corresponding pair, with high precision. In our case, however, we are using the 3DSI model to predict all citation indices by means of a triple: N, C, and some other proxy index. Also note the occurrence of natural clusters: indices highly correlated with $\rho$, C, and N

Pairwise correlations

For all the 243, 873 citation vectors that we have extracted from the DBLP database, we have determined the corresponding N (the number of papers with at least 1 citation), C (citation count), $\rho _C$ (the $\rho$ parameter minimising the Cauchy loss; Eq. (2); unlike in (Siudem et al., 2020), we now also allow $\rho <0$), and all the 15 bibliometric indices listed in Table 1.

Figure 2 gives Spearman’s $r_S$ rank correlation coefficients between each pair of indices. Interestingly, overall, the Spearman’s rank coefficient is quite close to the Pearson’s coefficient computed for the logarithms of index pairs (more precisely, transforming $J\mapsto \log (J+1)$; e.g., when $r_S \ge 0.9$, then the maximal absolute difference in these two coefficients is 0.035). Hence, a simple linear model on the double log scale could be sufficient to describe some indexes as a function of other ones.

Recall that we are interested in describing an author using three “sufficient” parameters in such a way that most other indices can be reproduced by the 3DSI model sufficiently well. Hence, it would be best for the proxy index not to be overly correlated with N and C so that it can constitute a less “dependent” dimension. In particular, we note that N, C, and $\rho _C$ are only quite weakly tied with each other. On the other hand, C, g, r, and rmp are all very similar.

We can distinguish three natural clusters of indices. Namely, those that are quite highly correlated with:

• C: a-, max-, o-, css-, rmp-, g-, hg-, and r-index;

• N: csr-, i10-, slg-, h-, w-, ent-index;

• $\rho _C$: p20-index.

However, there is some natural overlap between these groups, e.g., csr and i10 are also somewhat related to C and hg is correlated with N.

Fig. 3

Predicted (from the 3DSI model) vs observed (true) indices when the h-index is used as a proxy. The scatter plots are ordered with respect to the mean relative prediction error (when read rowwisely). The dotted line represents $y=x$, whereas the dashed one gives the fitted regression lines with no intercept, $y=cx$ for some c in order to indicate which estimators are more biased than others. Overall, many indices can be reproduced quite well, despite the fact that h takes only integer values between 1 and N

How well can the h-index reconstruct other indices?

Let us first take a close look at how well the h-index, one of the most commonly used bibliometric tools, can serve as the proxy measure.

Figure 3 gives the scatter plots of the observed indices (true, i.e., applied on the original sample $X_1,\dots ,X_N$) vs those predicted by means of the 3DSI model (based on the approximated citation vector $\hat{X}_1(N,C,{\rho _H}), \dots , \hat{X}_N(N,C,{\rho _H})$ with $\rho _H$ computed via Eq. (5) and $j$ being the h-index).

We see that our model can reconstruct some of the indices fairly well: h itself, hg, g, r, a, csr, slg, and w. Thus, given N, C, and the value of h, other indices might be deemed somewhat redundant, as they do not bring much new information to the general picture.

This is despite the fact that h only takes values in the set $\{1, 2, \dots , N\}$, which is problematic from the perspective of Eq. (5). Also, recall the index ignores all information outside the h-core, i.e., if it is equal to H we only know that there are H papers with H or more citations each.

On the other hand, it seems that our model overestimates the sample maximum, and hence the related indices such as o and rmp will be affected too.

Which is the best proxy index?

Of course, we do not expect the h-index to be an optimal choice for the proxy measure. Let us thus employ every other index in the context of estimating $\rho$ by means of Eq. (5).

Fig. 4

Mean relative prediction errors. The css-, ent-, max-, p20-, csr-, and slg-indices (first rows) are good proxies for predicting many other indices, whereas the w-, g-, rmp-, r-, and o-indices (last rows) should not be used for this purpose. On the other hand, the g- and r-indices (the 13th and the 15th column, respectively) are very easy to reproduce regardless of the reference index used, whereas max and i10 (the 2nd and the 9th column) are not. The boxplots summarise data in each row, i.e., how well does each proxy index predict the other ones

Figure 4 gives the mean relative prediction errors. For instance, the value in the 8th row and the 8th column (4%) corresponds to the h-index being the proxy measure and the a-index being the one we are trying to replicate. This is hence a numerical summary of what we see in the 5th subplot in Fig. 3 (counted rowwisely). It is computed via the formula

$$\begin{aligned} \frac{1}{M}\sum _{m=1}^{M} \frac{\left| a \!\left( \hat{\mathbf {X}}(N,C,{\rho _H}^{(m)})\right) - A^{(m)}\right| }{|A^{(m)}|}. \end{aligned}$$

(7)

where $M=243{,}873$, $A^{(m)}= a (\mathbf {X}^{(m)})$ is the true (observed) a-index of the m-th vector in the database, and $a \!\left( \hat{\mathbf {X}}(N,C,{\rho _H}^{(m)})\right)$ is the a-index predicted by the 3DSI model with $\rho _H^{(m)}$ determined by solving Eq. (5) with the proxy index being $j = h$.

Also, the boxplots summarise the results in each row of the error matrix. Additionally, we have marked the arithmetic means (which give the ordering of rows) with red crosses.

Similarly, Fig. 5 gives the mean relative bias given by

$$\begin{aligned} \frac{1}{M}\sum _{m=1}^{M} \frac{ a \!\left( \hat{\mathbf {X}}(N,C,{\rho _H}^{(m)})\right) - A^{(m)}}{|A^{(m)}|}. \end{aligned}$$

(8)

thanks to which we can determine which indices are under- or overestimated when specific proxies are used.

Fig. 5

Relative bias. The o-index serving as a proxy is the least biased estimator, whereas g, rmp, and r are the most biased. Note that most estimators tend to overestimate max, i10, and w and underestimate rmp

In terms of how the indices are defined, we can group them as follows:

• max, o, and to a great extent rmp are defined in such a way that they require $X_1$ to be reproduced accurately, which our model tends to overestimate. This may be the reason for rmp being underestimated—empirically, it is more highly correlated with C than with max. Also, taking into account that the coverage of bibliographic databases is limited, they are perhaps amongst the least reliable measures anyway.

• slg, css, csr, and ent take all elements (information) in a vector directly into account (sums of transformed items). Therefore it is not surprising that they work well as proxy indices.

• p20, r, a rely on the sum of a few top cited items, but only in the first case their number is fixed (and hence not subject to additional error). Despite r’s being similarly defined to a, it is very highly correlated with C.

• h, g, w, i10 but also hg take only a number of possible different values (which is problematic in terms of solving our optimisation task) and ignore a lot of information in the citation vector (e.g., the h-index does not care about anything beyond the h-core, rmp has a similar limitation)—therefore, one should be sceptical about their performance as estimators (proxies). However, they have an appealing interpretation.

The r- and g-indices are extremely easy to reconstruct with all the other measures as a proxy. This is most likely due to their being very strongly correlated with C (compare Fig. 2). On the other hand, high correlation between C (and r and g) does not help the rmp-index, whose some degree of reliance on max we have pointed out above.

As far as the quality of the proxy measures is concerned, overall, css, ent, max, p20, csr, and slg recreate the other ones reasonably well. We note that for each such index $j$, $j\, \!\left( \hat{\mathbf {X}}(N,C,{\rho })\right)$ is a continuous and monotone function of $\rho$, which makes Eq. (3) have a well-defined solution (recall that csr leads to an analytic one).

The high average performance of max (despite its being hard to predict by other indices) can partially be explained by its much better predictive power when predicting itself and the o-index. This indicates that our model can fit well either to the top-cited paper or to the rest of the citation curve—there is an inherent tension between these two.

We also tried fixing $\rho$ at different values, but the reconstruction performance dropped significantly. The results in Figs. 4 and 5 additionally feature the case $\bar{\rho }=0.1417$, being the average $\rho _C$ over the whole sample, which locates itself amongst the weakest estimators: rmp, r, and g (unsurprisingly, as they are highly correlated with C). It seems that the 3rd independent model parameter indeed makes a significant difference.

For the sake of comparison, we have included the case of the $\rho _C$ estimator (see Eq. (2)). Interestingly, estimating $\rho$ through proxy indices turned out better than based on the whole citation record. The performance of $\rho _C$ is similar to the one of the slg-index which itself emerges in the context of maximum likelihood estimation of the shape parameter in the Pareto-type 2 distribution [e.g., (Arnold, 2015)], to which our model is related, see (Siudem et al., 2022). However, still, we should keep in mind that $\rho _C$ was fit based on the rank-size (i.e., quantile) distribution and not the probability density or cumulative distribution function, which would be more typical in statistics.

The above conclusions are summarised in Table 1.

Note that we also tested a number of other measures, but these fell somewhere in-between the presented ones and thus did not bring much more information to the overall picture. In other words, the indices we have selected for the purpose of this study were quite representative.

Fig. 6

Predicted (from the 3DSI model) vs observed (true) indices when the csr-index is used as a proxy (note that the index not only fulfils the desirable properties listed in Table 1, but also enjoys the analytic solution for $\rho$). Most indices are reproduced quite well. Unless a high quality estimate for the most cited papers is required (and indices heavily influenced thereby: o and rmp), we may conclude that the use of multiple indices is not necessary, as they can easily be derived from the base index

Conclusion

What we have exercised in this paper is similar to the quest for identifying (minimal) sufficient statistics in probability theory: finding data aggregates that enable us to pinpoint the underlying data distribution without loss in the information carried over.

We have indicated that thanks to the 3DSI model, a number of citation indices can be reproduced quite well by using the measure of an author’s productivity, their overall impact, and one other citation index, e.g., the h, p20-, or csr-index. We thus conclude that the use of many indices may be unnecessary—entities should not be multiplied beyond necessity. The said “Ockham’s index” is a parameter triple, giving a broad picture of the modelled entities.

The h- or any other index alone (as a standalone measure, i.e., not complemented by N and C) can of course still be somewhat informative when quantifying the scientific impact. In particular, the csr-index seems a noteworthy choice as it is normalised, fulfils the dominance relation, enjoys an analytic solution for $\rho$, and yields small overall prediction error (see Fig. 6 for the scatter plots). However, from the perspective of our model, this statement comes with an asterisk: a bibliometric index is a one-dimensional projection of a much more complex (in our case: three-dimensional) reality and many combinations of other parameters can yield the same h-index value.

Undoubtedly, the higher the N, C, and H altogether, the “better”. However, such a parameter triple can only be ordered partially. Whether $N_1=20$ papers with $C_1=100$ citations and $H_1=7$ is more (or less) desirable than $N_2=25$ papers with $C_1=64$ citations and $H_1=8$ cannot be determined without making further explicit assumptions (e.g., with regards to the weighting of each component), which should always be made carefully, see (Gagolewski, 2013) for discussion.

From this viewpoint, e.g., the p20-index seems an interesting addition to N and C, because it aims to capture the shape or inequality of the citation distribution and it definitely should not be taken for granted whether high or low citation distribution inequality is a welcome state or not.

Note that we have refrained from analysing citation vectors with small N and C in order to avoid making guesses and predictions from data that is mostly noise—that any inference based upon small samples is inherently subject to high variability is a well known phenomenon in statistics. Due to this, we believe that young (but not only) scientists’ outputs should rather be evaluated qualitatively and not quantitatively.

If empirical data followed the model exactly, we could re-express one index as a function of another one, and they all would work equally well. Instead, we have observed that not every measure can serve as a valuable proxy—some of them do not have the same discriminative power or are too easy to reproduce, hence do not constitute a meaningful complement to other measures. Also, what is interesting, the log-Cauchy loss-based estimator, $\rho _C$, turned out slightly worse than the best performing bibliometric index. Hence, from now on, we recommend the use of the $\rho _R$ index as given by Eq. (6) instead of $\rho _C$. Still, we are aware that with a different choice of indicators, the aggregated results might shift towards slightly different final rankings.

As a future research idea, we shall verify whether some more indices as well as generalisations thereof can be expressed by means of closed-form equations and solved analytically for $\rho$ [(just like the sum-rank based csr-index yielding $\rho _R$ given by Eq. (6)]. Nevertheless, if this is the case, they will still yield the same results as the ones that we obtained here (although, of course, with less computational effort), hence the conclusion from our analysis will still hold.

Also note that the 3DSI model is not the only one that fits informetric and other types of data well (although contrary to many of its more complex counterparts, it has an appealingly interpretable parametrisation). In particular, in Cena et al. (2022) we have studied other tools such as the log-normal or discretised generalised beta distributions. As another topic for further research, it would be interesting to verify whether the popular bibliometric indices can be effectively employed as estimators of their underlying parameters as well and if any data-driven corrections for bias can be applied to compensate for the fact that they might not always be flexible enough to handle atypical cases (e.g., vectors with small N and very large C).