Abstract
Evaluating the impact of papers, researchers and venues objectively is of great significance to academia and beyond. This may help researchers, research organizations, and government agencies in various ways, such as helping researchers find valuable papers and authoritative venues and helping research organizations identify good researchers. A few studies find that rather than treating citations equally, differentiating them is a promising way for impact evaluation of academic entities. However, most of those methods are metadata-based only and do not consider contents of cited and citing papers; while a few content-based methods are not sophisticated, and further improvement is possible. In this paper, we study the citation relationships between entities by content-based approaches. Especially, an ensemble learning method is used to classify citations into different strength types, and a word-embedding based method is used to estimate topical similarity of the citing and cited papers. A heterogeneous network is constructed with the weighted citation links and several other features. Based on the heterogeneous network that consists of three types of entities, we apply an iterative PageRank-like method to rank the impact of papers, authors and venues at the same time through mutual reinforcement. Experiments are conducted on an ACL dataset, and the results demonstrate that our method greatly outperforms state-of-the art competitors in improving ranking effectiveness of papers, authors and venues, as well as in being robust against malicious manipulation of citations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Due to the rapid development of science and technology, the total number of papers published in recent years has increased significantly. According to an STM report (Johnson et al., 2018), there were 33,100 peer-reviewed English journals in mid-2018, and over 3 million articles were published per year. The total number of publications and the number of journals have both grown steadily for over two centuries, at the rates of 3% and 3.5% per year, respectively. Facing such a huge number of publications, academia and other sectors of the society have become keen to find answers to the following questions: How can the importance of a research paper be measured? How can the performance of a researcher or a research organization be evaluated? It is necessary to have an objective evaluation system to measure the performance of papers, authors and venues.
For a long time, many researchers have tried various ways to evaluate the academic impact effectively. Citation count plays an important role in evaluating papers and authors. Based on citation count, many metrics, such as the h-index (Hirsch, 2005), the g-index (Egghe, 2006), the journal impact factor (Garfield, 2006), and others, have been proposed. These metrics are straightforward, but some factors, such as citation sources and co-authorship, are not considered. Heterogeneous academic networks, which include multiple types of entities including papers, authors, and venues, are very good a platform for academic performance evaluation, because all related information is available for us to exploit. Based on such networks, graph-based methods can be used (Jiang et al., 2016; Simkin & Roychowdhury, 2003; Zhang & Wu, 2020). For example, both SCImago Journal Rank (SJR) (González-Pereira et al., 2010, 2012) and the Eigenfactor score (Bergstrom, 2007) use PageRank-like algorithms (Brin & Page, 1998) to evaluate journals. MutualRank (Jiang et al., 2016) and Tri-Rank (Liu et al., 2014) rank papers, authors and venues simultaneously based on heterogeneous academic networks. These graph-based methods have some advantages for ranking academic entities due to their ability of leveraging structural information in academic networks and the mutual reinforcement relationship among papers, authors and venues.
Many existing graph-based ranking algorithms treat all citations as equally influential (Chakraborty & Narayanam, 2016; Zhu et al., 2015), without distinguishing that some of them may be more important than others. Such an approach may be questionable. Typically, for many papers, a small number of references play an important role (Chakraborty & Narayanam, 2016; Simkin & Roychowdhury, 2003; Wan & Liu, 2014), while most of the others do not have much impact (Teufel et al., 2006). In order to deal with such a problem, various aspects have been considered to weight citation links. For a given paper, we may consider many different aspects such as who cites the paper, where the citing paper is published, the time gap between two papers’ publication, if it is a self-citation, and so on. We may also consider the topical similarity of the two papers or how the cited paper is related to the citing paper (referred to as citation strength in this paper). Different rationales are behind those aspects. For example, considering the venue that the citing paper is published, the citation is more valued if it is cited by a paper published in a prestigious venue than in an average venue. If it is a self-citation, it will get less credit than the others.
The primary goal of this paper is to investigate the middle to long-term impact of academic entities through a comprehensive framework (Kanellos et al., 2021). Especially we exploit some content-based features such as citation strength and topical similarity between the cited and citing papers, which are used to define weighted citation links. A heterogeneous network of papers, authors, and venues is built to reflect the relationships among them. Three types of entities are ranked at the same time through a PageRank-like algorithm with mutual reinforcement.
One possible problem with PageRank is it favors older papers than newer papers. This is referred to as the ranking bias (Jiang et al., 2016; Zhang et al., 2019a). It always takes time for a paper to be recognized in the community; a similar situation may also happen to authors. Therefore, a good evaluation system should be able to balance papers published at different time. In the same vein, we apply time-aware weights for all the papers involved.
Moreover, our framework includes a number of good features. In the heterogeneous network generated, seven types of relations are defined and supported. They are paper citation, author citation, venue citation, co-authorship, paper-author, paper-venue, and author-venue relations. For both authors and venues, their performance is evaluated on a yearly basis. Such a fine granularity enables us to catch the dynamics of the entities involved more precisely.
Citation manipulation (e.g., padded, swapped, and coerced citations) usually occurs in citations that do not contribute to the content of an article.Footnote 1 Because some government agencies rely heavily on impact factors to evaluate the performance of researchers and research organizations, there is evidence that various types of citation manipulation exist. For example, some scholars add authors to their research papers even those individuals contribute nothing to the research effort (Fong & Wilhite, 2017). Some journal editors suggest or request that authors cite papers in designated journals to inflate their citation counts (Fong & Wilhite, 2017; Foo, 2011). Peer reviewers may deliberately manipulate the peer-review process to boost their own citation counts (Chawla, 2019). Some scientists may self-citing extremely (Noorden & Chawla, 2019). Therefore, it is desirable to take this problem seriously into consideration when ranking academic entities. Citation manipulation (Bai et al., 2016; Chakraborty & Narayanam, 2016; Wan & Liu, 2014) is a problem that needs to be considered for academic entity ranking. As an extra benefit to the measures we apply, we believe that the proposed approach is robust and able to mitigate various kinds of citation manipulation problems (Bai et al., 2016; Chakraborty & Narayanam, 2016; Wan & Liu, 2014).
By consolidating all the measures above-mentioned, in this paper we propose a framework, WCCMR (Weighted Citation Count-based Multi-entity Ranking), to evaluate the impact of multiple entities. There are a number of contributions in this piece of work:
-
1
An ensemble learning method is used with three base classifiers to classify citations into five different categories. The fused results are better than that of all base classifiers, which represent the up-to-date technologies.
-
2
A word embedding-based method is used to measure topical similarity between the citing paper and the cited paper.
-
3
The above two content-based features are combined to define weighted citation links. To the best of our knowledge, we have not seen such a weighing scheme for citation before.
-
4
Apart from the weighted citation scheme, our framework has a number of good features: time-aware weighting, fine granularity for authors and venues, and seven types of relations among the same or different types of entities.
-
5
Experiments with the ACL (Association for Computational Linguistics Anthology Network) dataset (Radev et al., 2013) show that the proposed method outperforms other state-of-the-art methods in evaluating the effectiveness of papers, authors and venues, as well as in robustness against malicious manipulations.
The remainder of this paper is organized as follows: Sect. 2 presents related work on performance evaluation of academic entities, mainly by using various types of academic networks. Section 3 describes the framework proposed in this study. Section 4 presents the detailed experimental settings, procedures, and results. Some analysis of the experimental results is also given. Section 5 concludes the paper.
Related work
As an important task to the research community and beyond, evaluating scientific papers, authors and venues has been studied by many researchers for a long time. Citation count has been widely used and many citation-based metrics have been proposed (Jiang et al., 2016; Wang et al., 2016). For example, h-index (Hirsch, 2005) and g-index (Egghe, 2006) are used to measure researchers, the Impact Factor (IF) (Garfield, 1972), 5 year Impact Factor (5 year IF) (Pajić, 2015), and Source Normalized Impact per Paper (SNIP) (Moed, 2010; Waltman et al., 2013) are used to measure venues. These citation-based metrics are easy to understand and calculate. However, they have some crucial shortcomings. Firstly, many related metadata about any paper, such as its author(s) and venue, are ignored. This may have a negative effect on accuracy of the evaluation; Secondly, simple citation count lacks immunity to manipulation of citations. This is also an important issue that needs to be addressed.
As a remedy to some of the problems of using simple citation count, applying PageRank-like algorithms into academic networks has been investigated by quite a few researchers in recent years. For instance, the Eigenfactor score (Bergstrom, 2007) and SJR (González-Pereira et al., 2010, 2012) are used to evaluate journals. According to what type of information is used, we may divide those methods into two categories: metadata-based approach (time-aware weighting is a popular sub-category) and content-based approach.
Metadata-based approach has been investigated in (Yan & Ding, 2010; Zhang & Wu, 2018; Zhang et al., 2019a, b; Zhou et al., 2016) among others. To improve paper ranking performance and robustness against malicious manipulation, Zhou et al. (2016) proposed a weight assignment method for citation based on the ratio of common references between the citing and cited papers. Similar to Zhou et al. (2016), Zhang et al. (2019b) considered the reference similarity between the citing and cited papers. They also considered the topical similarity (calculated using titles and abstracts) between the two papers and combined them for weighting. Believing that immediate citations after publication is an indicator of good quality, some researchers allocated heavy weights to those papers that are cited shortly after publication (Yan & Ding, 2010; Zhang & Wu, 2018; Zhang et al., 2019a). For alleviating the ranking bias towards newly published papers, Walker et al. (2006) and Dunaiski et al. (2016) allocated heavier weights to newer papers, while Wang et al. (2019) considered the citations in the first 10 years of any paper since its publication and ignored the later ones. Self-citation, which is given a lighter weight than a “normal” citation, is investigated in (Bai et al., 2016).
Content-based approach has been investigated in (Chakraborty & Narayanam, 2016; Wan & Liu, 2014; Xu et al., 2014). Wan and Liu (2014) and Chakraborty and Narayanam (2016) classified citations into five categories of strength based on content analysis of the citing papers, and then assigned different weights for those citations accordingly. In Wan and Liu (2014), Support Vector Regression is used to estimate the strength of each citation. While in Chakraborty and Narayanam (2016), a graph-based semi-supervised model, GraLap, is used to estimate citation strength. In both cases, dozens of features, either metadata-based or content-based, are used in their model. Xu et al. (2014) proposed a variant of PageRank in which a dynamic damping factor is used instead. At each paper node, its damping factor is decided by the topic freshness and publication age of the paper in question. Topic freshness per year is obtained by analyzing contents of all the papers in the dataset investigated.
To make full use of the information in academic networks and/or evaluate multiple entities at the same time, some researchers have proposed some PageRank variants by using various heterogeneous networks (Bai et al., 2020; Jiang et al., 2016; Liu et al., 2014; Meng & Kennedy, 2013; Yan et al., 2011; Yang et al., 2020; Yang et al., 2020; Zhang & Wu, 2018, 2020; Zhang et al., 2018, 2019a; Zhao et al., 2019; Zhou et al., 2021). Yan et al. (2011) proposed an indicator, P-Rank, to score papers. For each citation, the impact of the citing paper, the citing authors and the citing journal are considered at the same time. Differentiating each venue year by year, Zhang and Wu (2018) proposed a ranking method, MR-Rank, to evaluate papers and venues simultaneously. Meng and Kennedy (2013) proposed a method, Co-Ranking, for ranking papers and authors. Tri-Rank, proposed by Liu et al. (2014), can rank authors, papers, and journals simultaneously. Especially, Tri-Rank considers the ordering of authors and self-citation problems. Jiang et al. (2016) proposed a ranking model MutualRank, which is a modified version of randomized HITS for ranking papers, authors and venues simultaneously. Zhang et al. (2018) proposed a classification-based method to predict authors’ influence. They firstly classified authors into different types according to their citation dynamics and then applied the modified random walk algorithms in a heterogeneous temporal academic network for prediction. Based on a heterogeneous network that includes both paper citation and paper-author relations, Zhao et al. (2019) measured the influence of authors on two large data sets, and one of which included 500 million citation links. By assigning weight to the links of citation network and authorship network according to the citation relevance and author contribution, Zhang et al. (2019a) ranked scientific papers by integrating the impact of papers, authors, venues and time awareness. By differentiating each venue and researcher on a yearly basis, Zhang and Wu (2020) proposed a framework, WMR-Rank, to predict the future influence of entities including papers, authors, and venues simultaneously. For balanced treatment of old and new papers, they considered both the publication age and recent citations of all the papers involved at the same time. Bai et al. (2020) measured the impact of institutes and papers simultaneously based on the heterogeneous institution-citation network. Based on a heterogeneous network that including co-authorship, author-paper and paper citation relation, Zhou et al. (2021) proposed an improved random walk algorithm to recommend research collaborators. Especially, they considered both time awareness and topic similarity. Similar to Zhou et al. (2021), Yang et al. (2020) recommend researcher collaborators by using an improved walking algorithm. A heterogeneous network by combing co-author network and institution network is used.
It is likely that the work in Wan and Liu (2014) and Chakraborty and Narayanam (2016) are the most relevant to our work in this paper, however, there are considerable differences between our work in this paper and either of them. First, we use an ensemble learning method for citation strength estimation and the results show that it is more effective than the methods used in those two papers. Besides, topic similarity is also included for determining the weighting of citation link. This is not included in either Wan and Liu (2014) and Chakraborty and Narayanam (2016). Lastly, a sophisticated network with multiple types of entities is built and used in this paper to evaluate their impact at the same. As we will see later in the experimental part, it works with other components to achieve very good results.
The proposed method
In this section, we introduce all the components required and then present the multi-entity ranking algorithm. The Symbols used in this paper and their meanings are summarized in Table 1.
Citation strength and topical similarity
When researchers write papers, they usually need to cite other papers for various reasons, such as pointing to a baseline method for comparison, applying a proposed method or making some improvement of it, referring to the definition of an evaluation metric, as evidence of supporting a point of view, and so on. Considering all those different purposes of citation, some of which may be more important than some others. Therefore, in line with the work of Liu (2014) and Chakraborty and Narayanam (2016), we define five levels of citation strength as follows.
-
1.
Level 1 The cited reference has the lowest importance to the citing paper. It is related to the citing paper casually. It usually follows words like “such as”, “for example”, “note” in the text, and can be removed or replaced without hurting the competence of the references.
-
2.
Level 2 The cited reference is related to the citing paper to some extent. For example, it is cited to support a point of view or to introduce the development of research fields related to the citing paper. It is usually mentioned together with other references and appears in parts such as “introduction”, “related work”, or “conclusion and future work”.
-
3.
Level 3 The cited reference is important and related to the citing paper. For example, it may serve as a baseline method. It is usually mentioned several times in the paper with long citation sentences and may appear in more than one part of the paper.
-
4.
Level 4 The cited reference is very important to the citing paper. It is usually mentioned separately in one or more sentences and appears in the methodology section, such as algorithms or models used in the citing paper. It can be an integral part of the model proposed in the paper.
-
5.
Level 5 The cited reference is extremely important and highly related to the citing paper. For example, the citing paper makes an improvement based on the cited reference or borrows its main idea from the cited reference. It is usually mentioned multiple times, sometimes following “this method is influenced by”, “we extend”, etc., and very likely appears in multiple parts of the paper such as “introduction”, “related work”, “method”, “experiment”, “discussion”, or “conclusion”.
Citation topical similarity refers to the topical similarity between the cited paper and the citing paper. It is independent from citation strength. A word-embedding based approach is used for this. It is also a good indicator of proper citation. The higher the similarity is between the citing paper and the cited paper, the lower the likelihood that the cited paper is artificially manipulated. A linear combination of them is set to be the weight of the citation. See Eq. (1) later in this paper. Based on that, a heterogeneous network can be built with the desirable properties. We consider that differentiating citations instead of taking simple citation counts may produce more reliable evaluation results.
A heterogeneous academic network
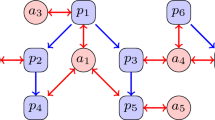
A heterogeneous academic network is composed of nodes and edges. Each node represents an entity and each edge between two nodes represents the relation between the two entities. There are three types of nodes: papers, authors, and venues, and seven types of relations: paper citation, paper-author relation, paper-venue relation, coauthor relation, author citation, author-venue relation and venue citation. A suitable weight needs to be assigned to each of the edges involved. In the following we discuss these seven types of relations one by one, in which weight assignment for each type of edges is the key issue.
Paper citation relation
A paper citation relation exists when one paper cites another paper. If paper \({p}_{j}\) cites paper \(p_{i}\), the weight is defined as
where \(\mathrm{strength}\left({p}_{i},{p}_{j}\right)\) and \(\mathrm{sim}\left({p}_{i},{p}_{j}\right)\) are the citation strength and topical similarity between \({p}_{i}\) and \({p}_{j}\), respectively. \({p}_{i}\leftarrow {p}_{j}\) denotes that paper \({p}_{i}\) is cited by paper \({p}_{j}\). It is required that both \(\mathrm{strength}\left({p}_{i},{p}_{j}\right)\) and \(\mathrm{sim}\left({p}_{i},{p}_{j}\right)\) are defined in the same range. Otherwise, normalization may be required to make them comparable.
Author citation relation
Through paper citation, we can set up an indirect relation of author citation. paper \({p}_{i}\) is cited by paper \({p}_{j}\), \({\overline{a} }_{m}\) is the only author or one of the authors of \({p}_{i}\), and \({\overline{a} }_{n}\) is the only author or one of the authors of \({p}_{j}\), then \({\overline{a} }_{m}\) is cited by \({\overline{a} }_{n}\) \(({\overline{a} }_{m}\leftarrow {\overline{a} }_{n})\). The same as in Zhang and Wu (2020), we differentiate each author year by year and allocate the credit that author \({\overline{a} }_{m}\) who published paper \({p}_{i}\) in year \({t}_{{\overline{a} }_{m}}\), obtains from \({\overline{a} }_{n}\) who published paper \({p}_{j}\) in year \({t}_{{\overline{a} }_{n}}\), through paper citation \({p}_{i}\leftarrow {p}_{j}\) as
where \(\mathrm{order}(a,p)\) is the position of author \(a\) in paper \(p\). Normalization is required for all the authors involved.
where \({S}_{A}\left(p\right)\) is the set of all the authors of paper \(p\).
An author \({\overline{a} }_{n}\) may cite another author \({\overline{a} }_{m}\) multiple times. The total credit that \({\overline{a} }_{m}\) in year \({t}_{{\overline{a} }_{m}}\) obtains from \({\overline{a} }_{n}\) in year \({t}_{{\overline{a} }_{n}}\) is the summation of all the papers involved.
where \({S}_{P}\left(a\right)\) is the set of papers written by author \(a\).
Coauthorship relation
A coauthorship relation exists in the network if two or more author nodes connect to the same paper node. Any author obtains certain credit from all other authors if they write a paper together. The credit that \({\overline{a} }_{i}\) who has published papers in year \({t}_{{\overline{a} }_{i}}\) obtains from her coauthor \({\overline{a} }_{j}\) through paper \(p\) is defined as
which needs to be normalized. We have
Two authors may co-write more than one paper. Hence, the credit that \({\overline{a} }_{i}\) in year \({t}_{{\overline{a} }_{i}}\) obtains from \({\overline{a} }_{j}\) over all co-authored papers is
where \({S}_{P}\left({\overline{a} }_{i}\right)\) denotes all the papers written by \({\overline{a} }_{i}\).
Venue citation relation
Similar to author citation, we may define venue citation. For venues \({v}_{i}\) and \({v}_{j}\), if \({v}_{i}\leftarrow {v}_{j}\), the weight between \({v}_{i}\) and \({v}_{j}\) can be denoted as
Paper-author relation
Paper coauthorship happens very often. However, for one paper written by a group of coauthors, their contributions to the paper are differentiated by their ordered positions (Abbas, 2011; Du & Tang, 2013; Egghe et al., 2000; Stallings et al., 2013). More specifically, we adopt a geometric counting approach (Egghe et al., 2000) for the paper-author relation. Suppose author \({a}_{i}\) is in the Rth position among all T coauthors in paper \({p}_{j}\); then, the amount of credit that author \({a}_{i}\) and paper \({p}_{j}\) obtain from each other is as follows:
Paper-venue relation
If paper \({p}_{i}\) is published in venue \({v}_{j}\), then there is an edge between paper \({p}_{i}\) and venue \({v}_{j}\); thus, paper \({p}_{i}\) and venue \({v}_{j}\) get credit from each other. We let
Author-venue relation
If author \({a}_{i}\) publishes more than one paper in venue \({v}_{j}\), then the credit that \({a}_{i}\) obtains from \({v}_{j}\) is the sum of the credit she obtains from all the papers published in \({v}_{j}\). The same is true for the credit \({v}_{j}\) obtains from \({a}_{i}\).
Recent citation bonus
An entity (paper or author) obtains a score from a citation and its final score is the sum of these individual scores. In order to mitigate the ranking bias toward old papers (Jiang et al., 2016) and treat all the papers in a balanced way, it is necessary to consider the recent citations of entities including papers and authors. Therefore, besides the normal scores, an entity obtains an extra bonus if the citation is very close to the evaluation year.
For an entity \({e}_{i}\), assume that \({e}_{i}\) has been cited in the most recent N years (including the evaluation year), and the evaluation year is \({t}_{evaluate}\). A bonus is given to entity \({e}_{i}\) as
where \(score\left({e}_{j}\right)\) is the score of \({e}_{j}\) that is calculated based on some other aspects of the entity, \(W({e}_{i},{e}_{j})\) is the weight between \({\mathrm{e}}_{i}\) and \({e}_{j}\), \(f({t}_{j})\) is a time-related function.
where \(\theta \) is a parameter. In this paper, we set \(\theta \hspace{0.17em}\)= 0.8 and N = 5. \(W({e}_{i},{e}_{j})\times f({t}_{j})\) is the bonus weight of entities.
For papers, the bonus weight \({W}_{RP}\) is defined as
For authors, the bonus weight \({W}_{R\overline{A} }\) is defined as
Self-connections between same type of entities
In this framework, both authors and venues may be considered as a whole or on a yearly basis. Therefore, we need to connect them in some situations. For example, for an author \({a}_{j}\in A\), there are a group of \({\overline{a} }_{i}\in \overline{A }\) (for 1 ≤ i ≤ n), both \({a}_{j}\) and \({\overline{a} }_{i}\) refer to the same author. Each \({\overline{a} }_{i}\) refers to \({a}_{j}\) in a specific year. \({W}_{\overline{A}A }\left({\overline{a} }_{i},{a}_{j}\right)\) is defined as
The second one is to set different weights for papers published in different years.
where \(\mu \) is a parameter, \({t}_{{\overline{a} }_{j}}\) is the year at which \({\overline{a} }_{j}\) is published.
Venues are considered on a yearly basis. However, there is a need to consider its previous performance for \({t}_{v}\) years. Suppose \({v}_{i}\) and \({v}_{j}\) are the same conference but held in different years, \({v}_{i}\) is held later than \({v}_{j}\) but within \({t}_{v}\) years, the corresponding weight is defined as
The WCCMR method
The proposed method, WCCMR, works with the abovementioned heterogeneous academic network. After setting initial values for all the entities, an iterative process is applied to them, and at each step every entity obtains an updated score. Note that all the entities involved affect each other and all the scores converge after enough iterations. The algorithm stops when a threshold \(\upvarepsilon \) for the difference between two consecutive iterations is satisfied. Algorithm 1 gives the details of the proposed method.
Initially, the rank vector of papers P, authors A (without considering the time), and venues V are set to \({I}_{P}/|{V}_{P}|\), \({I}_{A}/|{V}_{A}|\), and \({I}_{V}/|{V}_{P}|\). \({I}_{P}\), \({I}_{A}\) and \({I}_{V}\) are unit vectors, and \(\left|{V}_{P}\right|\), \(|{V}_{A}|\) and \(|{V}_{V}|\) are the number of papers, authors and venues.
The main part of the algorithm is included in a while loop. Inside the loop (lines 1–13), the scores for all the nodes involved are updated. All papers’ new scores are calculated in lines 3–4. Four factors are considered: authors (line 3), venues (line 3), citations (line 4), and recent citation bonus (line 4). All authors’ new scores are calculated in lines 5–7. Five factors are considered: published papers (line 5), coauthors to the published papers (line 5), the venues in which the papers are published (line 5), author citations (line 6), and recent citation bonus (line 6). Finally, we sum up all the yearly scores by using a time function to obtain the total score for each author (line 7). All venues’ new scores are calculated in line 8–9. Three factors are considered: published papers (line 8), authors (line 8), and venue citations (line 9). Although multiple types of entities are involved in the algorithm, it still converges quite quickly. For example, with the dataset used in this study and \(\upvarepsilon \) set to 1e-6., the algorithm stops after 13 iterations.

Experimental setting
Dataset
In this experiment, we use the ACL Anthology Network datasetFootnote 2 (AAN) (Radev et al., 2013), which is constructed from papers published in natural language processing venues (including journals, conferences and workshops from 1965 to 2011).Footnote 3 We choose AAN because it provides both citations and full text for almost all the papers involved.
In order to make it suitable for the experiment, the dataset is pre-processed as follows. First, those papers that neither cite any other papers nor are cited by any other papers are removed, because they have no impact to the investigation in this paper. Those papers that have no full text are also removed, because we need full text for citation strength analysis and estimation. Second, any joint conferences are considered to have dual identity. For example, COLING-ACL’2006 is a joint conference of COLING and ACL. Third, in addition to regular papers, many conferences publish short papers, student papers, demos, posters, tutorials, etc. Usually, the quality of non-regular papers is not as good as that of regular papers. Therefore, we let all regular papers remain in the main conference while putting all non-regular papers into its companion, a separate venue. Finally, for those papers with more than 5 authors, we retained the first five authors and ignored the rest. After above-mentioned pre-processing, 13,591 papers remain with an average of 5.26 references for each of them, 10,140 authors and 248 venues without considering time, or 437 venues if taking each venue per year as a separate entity. Table 2 shows the general statistics of the dataset.
Calculating citation strength and topical similarity
Machine learning methods are good options for estimating citation strength because they have been very successful in many such applications. Stacking technique can combine classifiers via a meta-classifier to achieve better performance. In this study, we classify the citation strength by using the stacking technique with the features used in Chakraborty and Narayanam (2016). Random Forest (RF), Support Vector Classifier (SVC) and GraLap (Chakraborty & Narayanam, 2016) are selected as base classifiers because they are very good and represent up-to-date technology. Figure 1 shows the major steps involved in a meta-classifier. First a training data set is required to training base models and the meta-model as well. Then the trained model can be used to classify instances in the test set.
First, we select a group of 96 papers from the whole data set randomly. From them we get 2735 valid references whose full texts are available in the data set. By using the Parscit package (Councill et al., 2008) plus a few hand-coded rules, we extracted 4993 citation sentences and sections in which the sentences locate. Such information along with the original papers are provided to a group of 15 annotators, all of which are graduate research students in computer science in our school. Among all 2735 papers, 215 are annotated at level 1, 2046 are at level 2, 287 are at level 3142 are at level 4, and 45 are at level 5.
Then as in Chakraborty and Narayanam (2016) and Wan and Liu (2014), we extracted citation features such as the number of occurrences, sections in which it appears, similarity between the citing paper and cited paper, and others for all 2735 citing papers. They are divided into five groups, each of which includes one fifth of the papers at each individual level. This was done by running a random selection process to the papers at each level separately.
A five-fold cross-validation is carried out to validate the performance of the stacking approach. We find that classification of the instances at level 5 are the least accurate, while level 2 instances reaches the highest classification accuracy of more than 0.8. Note that level 2 has the largest number of instances while level 5 has the least number of instances. One possible explanation is: for level 2 instances, we have enough instances for the base classifiers and the stacking method to learn a good model. In contrast for level 5 instances, they are not enough. Table 3 shows its performance with two other approaches, SVR (Support Vector Regression) (Wan & Liu, 2014), and GraLap (Chakraborty & Narayanam, 2016). Note that SVR is slightly different from SVC. Both use support vector machine but treat the same problem as either a classification problem or a regression problem. We can see that the stacking classifier is slightly better than the two other methods when any of the three measures are used for evaluation.
For topical similarity, we extract the title and abstract of each paper and calculate the topic similarity based on word2vec after performing stemming. In the experiment, the dimension of the word vector is set to 200, and the context window is set to 5.
Ranking benchmarks
For papers, rather than calculating citation count of each paper, we consider that experts’ opinion is a more authoritative measure to decide the impact of papers in the scientific community. Therefore, in this article, we use the gold standard papers provided in Jiang et al. (2016). A collection of gold standard papers, named GoldP, is assembled as recommended papers from the reading lists of graduate-level courses in natural language processing or computational linguistics and the reference lists of two best-selling natural language processing textbooks. Only those papers taken from the AAN dataset with at least two recommendations are selected. In total, 93 papers are selected in GoldP. The statistical information of those selected papers is shown in Table 4.
In the same vein as gold standard papers, we use WRT (weighted recommendation times) to measure the influence of authors. The influence score of author \({a}_{i}\) is defined as
where \(RT({p}_{j})\) is the number of recommendations that paper \({p}_{j}\) receives and \({W}_{AP}\left({a}_{i},{p}_{j}\right)\) is related to the ordering position of the author in question. See Eq. (12) in the “Paper-author relation” section for its definition of \({W}_{AP}\left({a}_{i},{p}_{j}\right)\). The final score that \({a}_{i}\) obtains, \(WRT({a}_{i})\), is the sum of the scores of all the papers in GoldP written by \({a}_{i}\). We consider this measure to be better than the citation count for authors because the inflationary effect can be mitigated. All the authors are regarded as influential authors (GoldA) if he/she wrote one or more gold standard papers. In this way, we obtain 149 authors in total.
For any venue, if it has two or more recommended papers in GoldP, then we set it as a recommended venue, GoldV. It includes 55 venues in total. The statistical information of GoldV is shown in Table 5.
The influence score of venue \({v}_{i}\) is defined as
It summarizes the recommendations received by all the papers in the venue.
Evaluation metrics
We use two evaluation metrics: precision at a given ranking level and a modified version of NDCG (Jiang et al., 2016). They are used to evaluate the effectiveness of a ranked list of entities E = {\({e}_{1}\), \({e}_{2}\),…,\({e}_{n}\)}.
Precision \(P@K\) is defined as
where \({inf(e}_{i})\) takes binary values of 0 or 1. If \({e}_{i}\) is an influential entity, then \({inf(e}_{i})\) is 1, otherwise, \({inf(e}_{i})\) is 0.
For a number of entities, the best ranking must exist, and it ranks all the entities in descending order of a given metric values. A group of papers can be ranked according to the times of recommendation received. WRT scores and number of recommended papers can be used for author and venue ranking, respectively. For a ranked list of entities \(E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{K} } \right\}\), assume that its corresponding best ranking list is \(E^{\prime} = \left\{ {e^{\prime}_{1} ,e^{\prime}_{2} , \ldots ,e^{\prime}_{K} } \right\}\) , we let \(credit()\) denote the metric value of entity \(e_{k}\) obtain, and \(best\_credit()\) the metric value of entity \(e^{\prime}_{k}\) obtain. \(\mathrm{NDCG}@\mathrm{K}\) is defined as
In Eq. (22), the top-ranked entities are given a weight of 1, then the weights decrease with rank by a factor \({1/log}_{2}(k+1)\).
Methods for comparison
The ranking algorithms used for comparison are as follows:
-
1.
Citation Count (CC). It is widely used to assess the influence of papers because it is single-valued and easy to understand (Zhu et al., 2015).
-
2.
SVR-based Weighted Citation Count (WCC-SVR). It provides each citation with a citation strength value calculated by SVR (Wan & Liu, 2014).
-
3.
GraLap-based Weighted Citation Count (WCC-GraLap). It provides each citation with a citation strength value calculated by GraLap (Chakraborty & Narayanam, 2016).
-
4.
MutualRank (MR). A state-of-the-art method that ranks papers, authors and venues simultaneously in heterogeneous networks (Jiang et al., 2016).
-
5.
Tri-Rank (Tri). Similar to MutualRank, Tri-Rank also ranks papers, authors and venues simultaneously in heterogeneous networks (Liu et al., 2014).
-
6.
PageRank with SVR_based network (PR-SVR). The PageRank algorithm runs over a modified citation network in which each citation has a specific weight calculated by SVR (Wan & Liu, 2014).
-
7.
PageRank with GraLap-based network (PR-GraLap). The PageRank algorithm runs over a modified citation network in which each citation has a specific weight calculated by GraLap (Chakraborty & Narayanam, 2016).
-
8.
WCCMR. The method proposed in this paper (see Algorithm 1).
Parameter setting
There are five parameters in the proposed ranking model: \({\alpha }_{1}\), \({\alpha }_{2}\), \({\alpha }_{3}\), \({\alpha }_{4}\) and \(\upvarepsilon \). We set \(\upvarepsilon \) to 1e-6. For \({\alpha }_{1}\), \({\alpha }_{2}\), \({\alpha }_{3}\) and \({\alpha }_{4}\), we first set an intuitively reasonable value for each parameter: \({\alpha }_{1}\hspace{0.17em}\)= 0.50, \({\alpha }_{2}={\alpha }_{4}\hspace{0.17em}\)= 0.33, and \({\alpha }_{4}\hspace{0.17em}\)= 0.50. Then, fix three of them and let the remaining one vary to see its effect, and Fig. 2 shows the results (P@100 is used for performance evaluation).
From Fig. 2a, one can see that paper evaluation performance is quite stable when \({\alpha }_{1}\) is in the range of 0.00 and 1.00. The best performance is achieved when \({\alpha }_{1}\hspace{0.17em}\)= 0.90. Similarly, from Fig. 2b, c we can see that \({\alpha }_{2}\hspace{0.17em}\)= 0.35, \({\alpha }_{3}\hspace{0.17em}\)= 0.35, and \({\alpha }_{4}\hspace{0.17em}\)= 0.5 are also good for these parameters.
Note that the parameters of \({\alpha }_{1}\) and (1 − \({\alpha }_{1}\)) are used to adjust the relative weights of authors and venues. A larger \(\alpha \) value does not necessarily mean that authors are more important than venues because these two components are not directly comparable. \({\alpha }_{1}\) partially serves as a normalization measure. We find the same conclusion for the other parameters \({\alpha }_{2}\), \({\alpha }_{3}\) and \({\alpha }_{4}\).
Ranking performance
In this section, we present the evaluation results of the proposed algorithm, along with those of a group of state-of-the-art baseline methods.
Ranking effectiveness for papers
We first study paper ranking effectiveness of the proposed algorithm. Figure 3 shows the effectiveness curves of the different algorithms for ranking papers measured by P@K and NDCG@K. We can see that the proposed method, WCCMR, constantly outperforms all the other methods when either P@K or NDCG@K is used. Tri and CC are close. They are not as good as WCCMR but better than the others. It is also noticeable that the curves of PR-SVR and PR-GraLap are always very close. This is not surprising because both run PageRank. The difference between them is the way of setting citation weights in the heterogeneous network.
To investigate the properties of all the methods involved for top-ranked papers, we list the top 20 papers returned by WCCMR and its competitors in Table 6. We can see that 18 of the top 20 WCCMR papers are influential papers, while the numbers for Citation Count, MutualRank, Tri-Rank, PR-SVR, and PR-GraLap are 16, 15, 16, 7, and 8, respectively. All the methods fail to identify the most influential paper, but all of them successfully identify the second most influential paper in top 20.
Ranking effectiveness for authors
We use both GoldA and WRC for influence evaluation of authors (see Eq. 19 in “Ranking benchmarks” section for its definition). Figure 4 shows the effectiveness curves of the different algorithms for ranking authors measured by precision and NDCG. From Fig. 4, we can see that the proposed method, WCCMR, is better than all the other methods when NDCG is used, MutualRank is the worst, while the other four are very close. However, when P@K is used, the performances of all the methods are closer. When K is 50 or more, WCCMR is a little better than the others. MutualRank is the worst in most of the cases, although the difference between it and the others is small.
To have a close look at the top 20 ranked authors by all the methods involved, we list them in Table 7 their corresponding ranking position in GoldA by their WRT scores. MutualRank identifies 17 influential authors, while all other methods reach 19. The results show that all the algorithms are very good on identifying influential authors. Therefore, P@20 is very good for all the methods involved.
Ranking effectiveness for venues
Figure 5 shows the effectiveness curves of different algorithms for ranking venues measured by precision and NDCG. From Fig. 5, we can see that WCCMR performs better than the other algorithms when either the precision or NDCG is used. However, the difference between and WCCMR and four others besides MutualRank is small. MutualRank is the worst and it is much worse than all the others.
For the top 20 venues returned by WCCMR and all other algorithms, we also list their corresponding ranking positions by the number of recommended papers in Table 8. It shows that all five algorithms besides MutualRank are equally good by identifying the same number of 16 influential venues, while MutualRank is not as good as the others and it secures 12 of them.
Average and median ranking positions of all influential entities
It is generally accepted that a good ranking algorithm should be effective in identifying all the influential entities in a comprehensive style (Wang et al., 2019). For the ranked list from a given ranking method, we find out the ranking positions of all those influential entities (e.g., all the papers in GoldP) and calculate the average rank and median rank of them. In this way, we are able to evaluate the general performance of the algorithm by using a single metric. Figure 6 shows the results.
From Fig. 6, we can see that the average rank and the median rank for WCCMR are the smallest in all the cases. In five out of six cases, the difference between it and the others are significant. However, the difference is very small in the case of average rank for venues. On the other hand, considering performance variance of all the algorithms involved, paper ranking is the highest, venue ranking is the lowest, while author ranking is in the middle. Especially when average rank is considered for author ranking, all the algorithms are very close.
Evaluation of several variants of WCCMR
WCCMR incorporates a few factors such as variable citation weights and bonus for recent citations. It is interesting to find how these two factors impact ranking performance. To achieve this goal, we define some variants that implement none or one of the features of WCCMR.
-
1.
WCCMR-R. It is a variant of WCCMR that sets equal weight to all the citations.
-
2.
WCCMR-S. It is a variant of WCCMR that does not implement bonus for recent citations.
-
3.
WCCMR-N. It is a variant of WCCMR. It sets all citation weights equally and does not implement bonus for recent citations.
Now let us have a look at how these variants perform compared with the original algorithm. See Fig. 7 for the results. It is not surprising that WCCMR performs better than all three variants of WCCMR, while the variant with none of the two components performs the worst in ranking all three types of academic entities. Such a phenomenon demonstrates that both components are useful for entity ranking, either used separately or in combination. However, the usefulness of these two components is not the same. In most cases, WCCMR-S performs better than WCCMR-R, which means that variable citation weights have larger impact than bonus for recent citations.
Robustness
Some types of abnormality may happen in citation networks. it can be caused by citation manipulation. Such a phenomenon certainly impacts the ranking of scientific entities, especially for PageRank-like algorithms. Therefore, robustness is a desirable property for ranking algorithms to fight against inappropriate citations. Of course, if there is no way to distinguish important citations from trivial ones, then we cannot do much to mitigate this problem. Therefore, we assume that it is more likely that citation manipulation happens to those with low to moderate citation strength and/or topical similarity and to those recently published papers.
To investigate the robustness of WCCMR when working with an abnormous network, we need a proper data set. AAN may not be good for this without any moderation. Instead of using some other data sets, we decide to make AAN more suitable for this purpose by adding some fake citations into it. Let us look at the situation for paper, author, and venue ranking separately.
-
For paper ranking, we select a target paper pt from the data set, then generate up to 50 fake papers, and each of which cites pt and a number of others chosen randomly.
-
For author ranking, we select a target author at from the data set, then generate up to 50 fake papers, and each of which cites a randomly chosen paper written by at and a number of others not written by at.
-
For venue ranking, we select a target venue vt from the data set, then generate up to 50 fake papers, and each of which cites a randomly selected paper published in vt and a number of other papers not published in vt.
For a target entity, we observe its ranking position change when more fake citations are added into the network. It is obvious that if an entity already has relatively a large number of citations, then adding a few more may not affect much its ranking position, while those entities with very few citations are more sensitive to such changes. In order to investigate the robustness of our algorithm, we choose those entities with very few citations (0 citation for a paper or an author and up to 10 citations for a venue). For all added fake citations, both citation strength and topical similarity are set to small to moderate values. We use rank difference to measure the robustness of any algorithm \({\Delta R}_{h}={R}_{0}-{R}_{h}\). Here \({R}_{0}\) is the initial rank of the entity and Rh is the rank position of the entity after h citations are added. Naturally, smaller rank difference indicates better robustness (Zhou et al., 2016).
Figure 8 shows the results of a group of algorithms, which is the average of 50 trials. The curves of WCC-SVR, WCC-GraLap always overlap with each other, because they are implemented in a very similar way with small difference. Not surprisingly, Citation Count is the most sensitive to added citations and WCCMR is the most insensitive, while WCC-SVR, WCC-GraLap, and Tri-Rank are in the middle.
Conclusions
In this paper, we have presented a ranking method for the impact of papers, authors, and venues in a heterogeneous academic network. Its main characteristic is rather than assigning equal weights to all the citations, we assign variable weight to each of them based on its strength and topical similarity between the citing paper and the cited paper. Both of these two values are determined through content analysis of the papers involved. Especially the ensemble learning technique has been used to decide citation strength of two papers. Experiments carried out with a publicly available data set AAN show that the proposed ranking algorithm, WCCMR, outperforms other baseline algorithms including MutualRank, Tri-rank, and GraLap.
Based on the AAN data set with some fake citations added, we demonstrate that WCCMR is more robust than the others. Although the data set used for this purpose is not completely real, the assumptions behind the artificial citations is reasonable.
As our future work, we would go further in a few directions. The first is to study appropriate approaches to deal with the missed citation information in the data set used. For example, for many papers in the AAN data set, their citation information is not complete. Some external resources such as Google scholar and Microsoft Academic may be used to enhance it. How to include such extra information into the academic network and the ranking framework in an efficiently and effectively style is a challenging issue. The second is how to evaluate academic entities across disciplines. For example, Biology and Mathematics are very different. One can expect that on average a Biology research paper can attract more citations than a Mathematics research paper. Even inside one discipline different research areas may have different properties. For example, in computer science, one can expect that on average a machine learning paper may attract more citations than an information retrieval paper. How to balance disparity among different disciplines or areas is also a challenging research problem. The third is to further study machine learning methods for content-based citation strength estimation. Two major subtasks includes detecting useful features and effective machine learning models.
Notes
https://publicationethics.org/files/COPE_DD_A4_Citation_Manipulation_Jul19_SCREEN_AW2.pdf. Accessed 30 July 2020.
Note that the dataset we use does not include papers published in 2011, just as in Jiang et al. (2016).
References
Abbas, A. M. (2011). Weighted indices for evaluating the quality of research with multiple authorship. Scientometrics, 88(1), 107–131.
Bai, X., Xia, F., & Lee, I. (2016). Identifying anomalous citations for objective evaluation of scholarly article impact. PLoS ONE, 11(9), e0162364.
Bai, X., Zhang, F., Ni, J., Shi, L., & Lee, I. (2020). Measure the impact of institution and paper via institution-citation network. IEEE Access, 8, 17548–17555.
Bergstrom, C. (2007). Eigenfactor: Measuring the value and prestige of scholarly journals. College and Research Libraries News, 68(5), 314–316.
Brin, S., & Page, L. (1998). The anatomy of a large-scale hypertextual web search engine. Computer Networks and ISDN Systems, 30(1–7), 107–117.
Chakraborty, T. & Narayanam, R. (2016). All Fingers are not Equal: Intensity of References in Scientific Articles. In Conference on empirical methods in natural language processing (Pp. 1348–1358).
Chawla, D. S. (2019). Elsevier investigates hundreds of peer reviewers for manipulating citations. Nature, 573, 174.
Councill I. G., Giles C. L. & Kan M. -Y. (2008). Parscit: an open-source CRF reference string parsing package. In Proceeding of the Language Resources and Evaluation Conference (Pp. 661–667).
Du, J., & Tang, X. (2013). Potential of harmonic counts for encouraging ethical co-authorship practices. Scientometrics, 96(1), 277–295.
Dunaiski, M., Visser, W., & Geldenhuys, J. (2016). Evaluating paper and author ranking algorithms using impact and contribution awards. Journal of Informetrics, 10(2), 392–407.
Egghe, L. (2006). Theory and practise of the g-index. Scientometrics, 69(1), 131–152.
Egghe, L., Rousseau, R., & Hooydonk, G. V. (2000). Methods for accrediting publications to authors or countries: Consequences for evaluation studies. Journal of the American Society for Information Science, 51(2), 145–157.
Fong, E. A., & Wilhite, A. W. (2017). Authorship and citation manipulation in academic research. PLoS One. https://doi.org/10.1371/journal.pone.0187394
Foo, J. (2011). Impact of excessive journal self-citations: A case study on the Folia Phoniatrica et Logopaedica journal. Science and Engineering Ethics, 17(1), 65–73.
Garfield, E. (1972). Citation analysis as a tool in journal evaluation. Science, 178(4060), 471–479.
Garfield, E. (2006). The history and meaning of the journal impact factor. JAMA, 295(1), 90–93.
González-Pereira, B., Guerrero-Bote, V. P., & Moya-Anegón, F. (2010). A new approach to the metric of journals scientific prestige: The SJR indicator. Journal of Informetrics, 4(3), 379–391.
González-Pereira, B., Guerrero-Bote, V. P., & Moya-Anegón, F. (2012). A further step forward in measuring journals scientific prestige: The SJR2 indicator. Journal of Informetrics, 6(4), 674–688.
Hirsch, J. E. (2005). An index to quantify an individual’s scientific research output. Proceedings of the National Academy of Sciences of the United States of America, 102(46), 16569–16572.
Jiang, X. R., Sun, X. P., Yang, Z., Zhuge, H., & Yao, J. M. (2016). Exploiting heterogeneous scientific literature networks to combat ranking bias: Evidence from the computational linguistics area. Journal of the Association for Information Science and Technology, 67(7), 1679–1702.
Johnson, R., Watkinson, A. & Mabe, M. (2018). The STM report: an overview of scientific and scholarly publishing. https://www.stm-assoc.org/2018_10_04_STM_Report_2018.pdf. Accessed June 2019.
Kanellos, I., Vergoulis, T., Sacharidis, D., Dalamagas, T., & Vassiliou, Y. (2021). Impact-based ranking of scientific publications: A survey and experimental evaluation. IEEE Transactions on Knowledge and Data Engineering, 33(4), 1567–1584.
Liu, Z. R., Huang, H. Y., Wei, X. C. & Mao, X. L. (2014). Tri-Rank: An Authority Ranking Framework in Heterogeneous Academic Networks by Mutual Reinforce. In 26th IEEE international conference on TOOLS with artificial intelligence (ICTAI2014) (Pp. 493–500).
Meng, Q. & Kennedy, P. J. (2013). Discovering influential authors in heterogeneous academic networks by a co-ranking method. In Proceedings of the 22nd ACM international conference on information & knowledge management (Pp. 1029–1036).
Moed, H. F. (2010). Measuring contextual citation impact of scientific journals. Journal of Informetrics, 4(3), 265–277.
Noorden, R. V., & Chawla, D. S. (2019). Hundreds of extreme self-citing scientists revealed in new database. Nature, 572, 578–579.
Pajić, D. (2015). On the stability of citation-based journal rankings. Journal of Informetrics, 9(4), 990–1006.
Radev, D. R., Muthukrishnan, P., Qazvinian, V., & Abu-Jbara, A. (2013). The ACL anthology network corpus. Language Resources and Evaluation, 47(4), 919–944.
Simkin, M. V., & Roychowdhury, V. P. (2003). Read before you cite! Complex System, 14(2003), 269–274.
Stallings, J., Vance, E., Yang, J., Vannier, M., Liang, J., Pang, L., Dai, L., Ye, I., & Wang, G. (2013). Determining scientific impact using a collaboration index. Proceedings of the National Academy of Sciences of the United States of America, 110(24), 9680–9685.
Teufel, S., Siddharthan, A. & Tidhar, D. (2006). Automatic classification of citation function. In Conference on empirical methods in natural language processing (Pp.103–110).
Walker, D., Xie, H., Yan, K., & Maslov, S. (2006). Ranking scientific publications using a simple model of network traffic. Journal of Statistical Mechanics-Theory and Experiment, 6(6), P06010–P06015.
Waltman, L., Eck, N. J. V., Leeuwen, T. N. V., & Visser, M. S. (2013). Some modifications to the snip journal impact indicator. Journal of Informetrics, 7(2), 272–285.
Wan, X. J., & Liu, F. (2014). Are all literature citations equally important? Automatic citation strength estimation and its applications. Journal of the Association for Information Science and Technology, 65(9), 1929–1938.
Wang, S. Z., Xie, S. H., Zhang, X. M., Li, Z. J., Yu, P. S., & He, Y. Y. (2016). Coranking the future influence of multi-objects in bibliographic network through mutual reinforcement. ACM Transactions on Intelligent Systems and Technology, 7(4), 1–28.
Wang, Y., Zeng, A., Fan, Y., & Di, Z. (2019). Ranking scientific publications considering the aging characteristics of citations. Scientometrics, 120(3), 155–166.
Xu, H., Martin, E., & Mahidadia, A. (2014). Contents and time sensitive document ranking of scientific literature. Journal of Informatics, 8(3), 546–561.
Yang, C., Liu, T., Chen, X., Bian, Y., & Liu, Y. (2020). HNRWalker: Recommending academic collaborators with dynamic transition probabilities in heterogeneous networks. Scientometrics, 123(1), 429–449.
Yan, E., & Ding, Y. (2010). Weighted citation: An indicator of an article’s prestige. Journal of the American Society for Information Science and Technology, 61(8), 1635–1643.
Yan, E., Ding, Y., & Sugimoto, C. R. (2011). P-Rank: An indicator measuring prestige in heterogeneous scholarly networks. Journal of the American Society for Information Science and Technology, 62(3), 467–477.
Zhang, F. & Wu, S. (2018). Ranking scientific papers and venues in heterogeneous academic networks by mutual reinforcement. In: ACM/IEEE joint conference on digital libraries (JCDL) (Pp.127–130).
Zhang, F., & Wu, S. (2020). Predicting future influence of papers, researchers, and venues in a dynamic academic network. Journal of Informatics, 14(2), 101035.
Zhang, J., Xu, B., Liu, J., Tobla, A., Al-Makhadmeh, Z., & Xia, F. (2018). PePSI: Personalized prediction of scholars’ impact in heterogeneous temporal academic networks. IEEE Access, 6, 55661–55672.
Zhang, L., Fan, Y., Zhang, W., Zhang, S., Yu, D., & Zhang, S. (2019a). Measuring scientific prestige of papers with time-aware mutual reinforcement ranking model. Journal of Intelligent and Fuzzy Systems, 36, 1505–1519.
Zhang, Y., Wang, M., Gottwalt, F., Saberi, M., & Chang, E. (2019b). Ranking scientific articles based on bibliometric networks with a weighting scheme. Journal of Informetrics, 13(2), 616–634.
Zhao, F., Zhang, Y., Lu, J., & Shai, O. (2019). Measuring academic influence using heterogeneous author-citation networks. Scientometrics, 118(3), 1119–1140.
Zhou, J., Zeng, A., Fan, Y., & Di, Z. (2016). Ranking scientific publications with similarity-preferential mechanism. Scientometrics, 106(2), 805–816.
Zhou, X., Liang, W., Wang, K., Huang, R., & Jin, Q. (2021). Academic influence aware and multidimensional network analysis for research collaboration navigation based on scholarly big data. IEEE Transactions on Emerging Topics in Computing, 9(1), 246–257.
Zhu, X. D., Turney, P., Lemire, D., & Vellino, A. (2015). Measuring academic influence: Not all citations are equal. Journal of the American Society for Information Science and Technology, 66(2), 408–427.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, F., Wu, S. Measuring academic entities’ impact by content-based citation analysis in a heterogeneous academic network. Scientometrics 126, 7197–7222 (2021). https://doi.org/10.1007/s11192-021-04063-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11192-021-04063-1