(E-) Valuative Metrics as a Contested Field: A Comparative Analysis of the Altmetrics- and the Leiden Manifesto

Abstract

This article comparatively analyzes two manifestos in the field of quantitative science evaluation, the Altmetrics Manifesto (AM) and the Leiden Manifesto (LM). It employs perspectives from the Sociology of (E-) Valuation to make sense of highly visible critiques that organize the current discourse. Four motifs can be reconstructed from the manifestos’ valuation strategies. The AM criticizes the confinedness of established evaluation practices and pledges for an expansion of quantitative research evaluation. The LM denounces the proliferation of ill-applied research metrics and calls for an enclosure of metric research assessment. It can be shown that these motifs are organized diametrically: The two manifestos represent opposed positions in a critical discourse on (e-) valuative metrics. They manifest quantitative science evaluation as a contested field.

Introduction: why manifestos?

Metric assessments of scientific practices have been the subject of recurrent critiques. Social scientific studies into the effects of quantifying scientific performance (Butler, 2003b, 2004; Espeland & Sauder, 2007; Sauder & Espeland, 2009) are increasingly joined by publications of a more political intention (DORA, 2012). More and more such critiques become part of reflexivity and critical self-scrutinization (Wilsdon et al., 2015) both in bibliometrics and in quantitative science evaluation more general. Two much-noticed examples stand out from these debates. On the one hand, the Altmetrics Manifesto (AM) advocates the quantification of science-related online events as an alternative to established forms of research evaluation (Priem et al., 2010). On the other hand, the Leiden Manifesto (LM) criticizes the misapplication of quantitative indicators more general and suggests ten best practice principles to guide research evaluation (Hicks et al., 2015). This article presents the results of a comparative analysis of these manifestos. It is part of a larger GT study of reflexivity in (e-) valuative metrics. The project applies perspectives of Valuation and Evaluation (Lamont, 2012) to the study of Quantification (Espeland & Stevens, 2008). On the one hand, this allows to understand evaluation as practices of valuation that not only assess value but necessarily ascribe value to the thus (e-) valuated objects. On the other hand, this perspective permits to scrutinize the means of evaluation as (e-) valuative objects. From this stance, quantitative indicators not only value the counted objects (e.g. citations) and evaluate others (e.g. articles) but become themselves objects that are valued and evaluated. The present analysis scrutinizes two particularly salient positions in the discourse around such (e-) valuative metrics. This enables us to take on a reflexive stance toward our practices of negotiating the value of these objects.

In how far do manifestos represent significant data material? To answer this question, one could go into great length regarding the implications of the text genre and its historic development (e.g. Malsch, 1997). The most crucial point is, however, that manifestos are manifestations of crisis as their justifying potential depends on diagnoses of deficiency. As Klatt and Lorenz (2011) find, “manifestos seem to occur especially in phases of societal change, political conflict, [and] unstable conditions” (p. 7).¹ This makes manifestos highly relevant from a pragmatist point of view. In the philosophy and social theory of John Dewey (1938, 1939) reflexive action takes place in problematic or indeterminate situations. Only when routine behavior is inhibited do persons need to reflect upon the situation, identify problematic conditions, and actively try to reinstall their ability to act. This reflexivity is the reason why indeterminate situations – manifestations of crisis, contestation, and debate – are of empirical interest: Where the conditions that allow people to act are irritated, we can observe what matters to the situations, practices, or fields that we scrutinize. Similarly, Boltanski and Thévenot’s neo-pragmatist theory of “Justification” (Boltanski & Thévenot, 2006) emphasizes the empirical importance of critique. In their view, social reality is organized according to a number of worlds, whose respective principles of justice are incompatible with one another. These principles are conventions of equivalence that arrange relevant objects, humans and things, in orders of worth and hence allow for social coordination. This more structural aspect of sociality, however, is necessarily unstable. Coordination fails and tests are required to identify deficiency and reestablish order. Conflicts arise between different worlds and where no temporary compromise can be found the dispute needs to be settled within one single world. Manifestos are manifestations of critique and as such offer us the opportunity to understand what matters in a certain field or community.

My approach shares common ground with other scrutinizations of reflexivity in the sciences. Kaltenbrunner (2015), for instance, argues that the methodological stance of infrastructural inversion (Bowker & Star, 1999) can be understood as a specific form of articulation work (Strauss, 1985, 1988). This allows him to understand researchers’ critiques of scientific conventions of work as inversions of infrastructure, which offer insights into otherwise invisible work procedures as well as their challenge by alternative visions. However, many forms of critique lack the necessary detail and analytical rigor to understand them as inversions in the sense of Bowker and Star (1999). Below, I offer a conceptualization of the manifesto that accounts for the specific critical potentials of this genre.

The relevance of manifestos has been recognized by several research fields: The text genre has been subdivided into literary (e.g. Schultz, 1981), artistic (e.g. Malsch, 1997) and political manifestos (cf. Klatt & Lorenz, 2011, p. 8). The present contribution may give an impulse to think of scientific manifestos as a further subtype of the genre. Difficulties persist in arriving at a comprehensive definition, which is mainly due to the historical changes of the manifesto’s use (Klatt & Lorenz, 2011, pp. 8, 18). An overview of the manifesto’s history is provided by Malsch (Malsch, 1997, pp. 49–84). Here I will focus on the manifesto’s most consequential transformation, which took place in the course of the French Revolution. Formerly serving the proclamation of a sovereign’s decisions the manifesto now became a medium of the opposition and other groups that were not in power. Originally legitimized by the authority of a sovereign ruler and utilized as a means of official propaganda it now took on the function of subversive mass communication. Ironically it was the king himself who heralded this change, being the first who deployed the manifesto from a marginalized position. The dethroned Loius XVI. made use of the manifesto in order to demand his reinstatement as sovereign ruler, which had the opposite effect of further spurring the revolution. This change became also visible in the manifesto’s layout. The ruler’s manifesto declared its official author in the title, while the authors’ of the subversive manifesto signed below the text (Malsch, 1997, p. 60; cf. Klatt & Lorenz, 2011, p. 9). As this work will show, both more subversive and more authoritative versions of the manifesto exist to the present day – what they have in common is their connection to conflictual situations with uncertain outcomes.

The following outline of a pragmatist conception of manifestos will allow to analyze these texts as manifestations of crisis. Due to the political origin of the genre, I will build upon a characterization of political manifestos provided by Klatt and Lorenz (2011).² My conceptualization consists of seven characteristics: The manifesto’s first and perhaps most important property is its public character. Whether it is a ruler who proclaims her decisions to her subjects, the Communist League addressing the “Working Men of ALL Countries” (Marx & Engels, 1975 [1848]), or a group of scientometricians and research administrators speaking to the field of research evaluation, the purpose of all these manifestos depends on the particular public audience they are directed at. How this audience is addressed at the same time constitutes the speaking position of the text. The manifesto’s public orientation is directly connected to a second characteristic, its aim to bring about change of some sort. The ruler’s manifesto proclaimed change brought about by the sovereign’s decision, the subversive manifesto makes public the objectives of its issuers. Without envisioned change there is no need for a manifesto. Because reaching the proclaimed goals requires the choice of definite actions, it seems reasonable to differentiate change from a third characteristic that is the suggested course of action. There is more than one way to reach a particular goal and not always does the end in itself justify the means. Thus, a manifesto must prove the relevance and legitimacy of both its envisioned change and the suggested course of action in the eyes of its public audience. This need for justification can be regarded as the manifesto’s fourth and central feature because it provides the hinge between the former three characteristics. This interconnection calls attention to a fifth characteristic, the critique of a current state of things. A suggested course of action that brings about change logically depends on a previously existing state that, in order for the change to be justified, needs to be criticized for one reason or the other. Critique is the counterpart of justification; where justification defends a particular order of things, critique challenges another. This is why critique can be mobilized as an (e-) valuative resource for justification. The tension that arises between the critique of a current state of things and the aspired change is the sixth characteristic of the manifesto: The necessary difference between what is and what ought to be is the problem that defines the situation outlined by the manifesto as indeterminate. The problem is constituted, one could also say manifested, by the manifesto. Neither is it necessarily preexistent to the text nor does it need to be explicitly stated in the text. It may be the analyst’s task to reconstruct the particular problem from the manifesto’s strategies of justification and critique. The seventh and last characteristic of the manifesto consists in the enrolement of relevant beings. Enrolement refers both to enroll relevant participants in a course of action and to enrole these participants, as in ascribing them a role to play within this course. The concept is borrowed from ANT³ where it depicts the “definition and distribution of roles”, whereas “roles are not fixed and pre-established, and neither are they necessarily successfully imposed upon others” (Callon et al., 1986, pp. xvi). The manifesto must convince the public audience that the aspired change is not only justified but also feasible. Hence, central participants must be enrolled in the suggested course of action in such a way that their resistance to the projected process is unlikely. In this respect, the speaking position that the authors assume in addressing their public audience (cf. above) is central to enrolement. In summary, a manifesto is directed at a specific public, promotes change, suggests a course of action, and justifies such change and action on the basis of critique leveled against a current state of things. It thus addresses a problem that consists in the difference between what is and what ought to be and enrolls relevant objects in the suggested course of action. These characteristics should not be thought of in numerical succession. As elements co-constituting the text their relations should be studied empirically. This conceptualization does not claim to reflect all forms of manifestos at all times. It provides a framework for the application of different pragmatist theories to the analysis of manifestos as manifestations of crisis. In the next section, I will outline the heuristics of the present analysis by applying the model to the works of Dewey (1938, 1939).

Some will argue that a manifesto is but one of many text forms and that critique is an inevitable part of scientific discourse. While this is partly true, there is a decisive difference between critique in manifestos and critique in other scientific texts. Take as an example the two articles providing the basis of the present work (Espeland & Stevens, 2008; Lamont, 2012). Both give an overview of a broad range of research which they bind together with regard to a common thematic. And both make the lack of a joint research program the basis of their respective calls for a Sociology of Quantification or (E-) Valuation. Hence, critique in both academic manifestos and other forms of scientific texts can serve the alignment of scientific communities. Yet, common forms of academic communication lack the specific political dimension of the manifesto. Scientific articles are usually not concerned with problems that put into question the conventions of scientific conduct. They may re-arrange academic knowledge and can thus be argued to organize the epistemic space of a scientific community. Contrarily, manifestos are engaged precisely with conditions that challenge the coordination of social activity. Scientific manifestos are not only concerned with what is being researched but with the very premises under which researchers do their work – they aim to re-organize the conventional space of a scientific community.

Material and methods

Two manifestos provide the data material of this contribution. In the following I will give a short introduction to either text. Subsequently, I will explain the heuristics that led to the results presented in the next section.

The AM was openly published online in 2010 under the title “altmetrics: a manifesto” (Priem et al., 2010). It was authored by Jason Priem, Dario Taraborelli, Paul Groth, and Cameron Neylon. The authors are listed in the end of the text with links to their personal web pages and twitter accounts. On these profiles, all four state their interest in or advocacy for Open Access (OA), Open Data, or Open Science more general. The publication of the manifesto followed the introduction of the Altmetrics⁴ term via Jason Priem’s Twitter account earlier that year.⁵ The AM defines Altmetrics as countable data traces produced in the course of scholarly work in online environments. It promotes the collection and use of Altmetrics as ‘new filters’ of impact measurement. Its claims are supported by various critiques leveled against established methods of science (e-) valuation, so called ‘traditional filters’. In a nutshell, the AM calls for investment in Altmetrics because existing measures were unfit to the present pace of scholarly communication.

“The Leiden Manifesto for research metrics” (Hicks et al., 2015) was published in 2015 as a comment in Nature. Despite its publication in this renowned, subscription-based venue the text is freely available as PDF. There is also a webpage, leidenmanifesto.org, which links to the Nature article page. It includes 23 translations (as from June 12, 2020) of the manifesto’s text, a video version, and an active blog. Both the webpage and the article page prominently feature the authors’ names before presenting the text. The full list of authors includes Diana Hicks, Paul Wouters, Ludo Waltman, Sarah de Rijcke, and Ismael Rafols. Three of the five authors are affiliated to the Centre for Science and Technology Studies (CWTS) located in Leiden, the Netherlands. According to the LM, the ‘Leiden’ label stems from the conference at which it was formed, the STI 2014 hosted in Leiden by the CWTS. The manifesto argues that a proliferation of metric indicators had superseded expert judgement in research evaluation. As a result, such metrics were largely ill-applied to the evaluation of scientific performance, leading to misguiding incentives and unintended effects. The LM then presents ten principles of best practice in metric research evaluation. Using these principles would prevent damaging effects and redirect research evaluation to its original purpose of improving science.

The two manifestos were analyzed according to GT coding techniques (Corbin & Strauss, 2008; Strauss, 1987). They offer empirical access to the debate around the value of (e-) valuative metrics. Following Clarke (2005), the larger research project directs special attention to both discursive elements and non-human objects as important constituents of this situation. Along these lines, the two texts make manifest important discourse positions regarding the role of non-human objects (metric indicators) in science (e-) valuation. The present analysis thus provides an entry point into a larger situation, but at the same time offers valuable insights into current disputes that organize the community. Coding the material according to the constant comparative method, first, confirmed the value of pragmatist theory. Both manifestos instantiate crises of metric research evaluation and both employ strategies of valuation and critique to resolve the situation and return to a transformed routine. Second, the problem-centered structure of the texts suggested the value of applying the pragmatist conception of the manifesto to the theories of Dewey. In the following I will explain the heuristics that resulted from this conceptualization.

From the viewpoint of classical pragmatism (Dewey, 1938, 1939) the manifesto becomes a manifestation of an indeterminate situation. The first step of reflexive problem solving, which defines the situation as indeterminate, is the institution of the problem. The problem consists in an irritation of object-relations that allow routine activity to proceed. Solving the problem requires the re-ordering of objects, which allows practices to transition back from reflexive problem-solving to routine action (Dewey, 1938; Strübing, 2017).⁶ In the “Theory of Valuation” (Dewey, 1939) reflexive re-ordering takes on the form of means-end valuations. On the one hand, such valuation involves the prizing of ends that will solve the problem. On the other hand, the value of ends cannot be assessed without the appraisal of means toward these ends. While prizing relates to the attribution of value based on personal emotions, appraisal depicts the comparative evaluation of objects as an intellectual activity (Krüger & Reinhart, 2016, pp. 492). Only in conjunction can persons value particular means-end relations over others and thus come to a solution that restores their ability to act. We can hence understand manifestos’ strategies of justification as means-end valuations, while critique takes the form of means-end de-valuations. The distinction between prizing and appraisal allows us, first, to ask what change is regarded as valuable and, second, to reconstruct motifs of appraisal that help us understand in what ways this change is worthwhile. Dewey refers to reflexive action only in-situ; the problematic situation is resolved by re-ordering its objects. The peculiar nature of the manifesto is that the volatile moment of irritation is made durable, stretched out in time, so to say. The manifesto cannot resolve the situation by itself but needs to propagate a course of action that will eventually solve its problem. In order for this course of action to be realized, the manifesto must enroll key actors from its intended audience. Theoretically, this enrolement does not differ much from the (e-) valuation of other objects. But because actors such as individuals, groups, or organizations can be particularly resistant to such ordering activity, the manifesto must be as persuasive as possible. The analytic task is to show how the text tries to convince relevant audiences to become part of the outlined project. The manifesto must try to become manifest evidence of a problem as well as its solution in order to constitute an enduring position in the process that follows.

This conceptualization of the manifesto allows us to compare the two texts with regard to their respective motifs of appraisal. These motifs or themes correspond to the manifestos’ respective strategies of valuation and de-valuation and thus allow us to mould out similarities and differences between the two texts. Resulting from theoretically informed GT coding, this heuristics identifies relevant motifs insofar as they organize cohesive complexes of means-end (de-) valuations. Put differently, two or more means-end relations belong to the same complex inasmuch as they refer to a common motif. These motifs do not comprise the respective texts in their entirety: Because they are reconstructed by comparing the two manifestos along the lines of the above conceptualization, they reflect similarities and differences of these texts’ (e-) valuative positionings. This allows the analyst to identify dimensions of contention and agreement that organize the common discourse.

The decision to base the heuristics on classical pragmatism does not mean that I refrain from neo-pragmatist positions. Both theoretical strands build on similar premises and can thus supplement each other in the interpretation of results. Indeed, because Dewey’s perspective focuses on in-situ valuations, analysis will benefit from a recourse to the more inter-situational aspects of neo-pragmatism. The next section will commence by presenting the results of the outlined heuristics and shift towards more neo-pragmatist perspectives in the later, more synthetical parts of analysis.

Analysis: the central motifs of valuation and critique

The analytical section reconstructs the two manifestos according to the central motifs organizing their strategies of critique and valuation. Analysis will commence with the AM to then proceed with the motifs of the LM. Subsequently, the relation of the four motifs will be discussed with regard to what they say about the organization of a larger critical discourse.

The Altmetrics Manifesto

The AM institutes a problem that is argued to concern each and every scientist, the question how to choose relevant literature from the fast-increasing volume of published texts. This problem is made manifest by a categorial distinction between ‘traditional’ and ‘new filters’ and the comparative (de-) valuation of these objects. The manifesto’s first paragraph, which summarizes the key assertions of the text reads as follows:

“NO ONE CAN READ EVERYTHING. We rely on filters to make sense of the scholarly literature, but the narrow, traditional filters are being swamped. However, the growth of new, online scholarly tools allows us to make new filters; these altmetrics reflect the broad, rapid impact of scholarship in this burgeoning ecosystem. We call for more tools and research based on altmetrics.” (Priem et al., 2010, e.i.o.⁷)

The problem of the text, how to decide what to read, is addressed right at the beginning in capital letters. It is related to the scientific community as the manifesto’s public audience. The use of inclusive identifiers such as “We” and “us” positions the authors as part of those to whom they speak. This unites authors and readers with respect to their common problem: Each and every one of ‘us’ scientists must be empowered to make sense of the incomprehensible magnitude of literature. This problem is made manifest by the tension arising between the critique of ‘traditional filters’ and the justification of using ‘new filters’ or Altmetrics. Traditional filters are de-valuated as an insufficient means toward the end of identifying the most important literature. By contrast, Altmetrics are valued as the means best fit to filter out the most impactful sources. The critique of what is justifies what ought to be, i.e. “more tools and research based on altmetrics” (ibid.) as the AM’s envisioned change.

The motif of confinedness

The critique of ‘traditional filters’ follows a motif of confinedness. Traditional filters’ insufficiency is connected to the growth of the problem: “As the volume of academic literature explodes, scholars rely on filters to select the most relevant and significant sources from the rest. Unfortunately scholarship’s three main filters of importance are failing” (Priem et al., 2010, o.e.⁸). These three filters are peer review, citation counting, and the Journal Impact Factor (JIF). They are criticized for being too slow, narrow, and closed and hence unable to adapt to the fast pace of scholarly communication. Altmetrics, by contrast, are valued for the timeliness of their calculation, the diversity of the reflected impact, and the openness of their underlying processes. The critiques of traditional filters’ slowness, closedness, and narrowness all relate to these objects’ inability to adapt to the rapid expansion of scientific literature. We can thus find these critiques to follow an overall motif of confinedness.

In the following, I will reconstruct the three critiques by showing how they apply to each of the ‘traditional filters’. Peer review, to start with, is presented as being both slow and closed: “Peer-review has served scholarship well, but is beginning to show its age. It is slow, encourages conventionality, and fails to hold reviewers accountable” (Priem et al., 2010). First, this (e-) valuative object is directly criticized for being slow. The reference to its age, too, depicts the inability to adapt to the increasing speed of scholarly communication, as does the general designation as ‘traditional’. Its slowness confines this filter with respect to both present and future requirements. Second, peer review is incapable of holding liable the reviewers, which relates to the closedness of a procedure held opaque in order to prevent bias. This critique tackles both a lack of transparency and insufficient participation in a process judging the quality of research by means of only two opinions. Both the age of the process and the lack of external control invite ‘conventionality’, which again relates to peer review’s confinedness or inability to innovate. In contrast, “[w]ith altmetrics we can crowdsource peer-review. Instead of waiting months for two opinions, an article’s impact might be assessed by thousands of conversations and bookmarks in a week” (ibid.). Not only are Altmetrics faster than traditional filters, their speed derives from open participation by many different assessors. The tension arising between peer review and Altmetrics consists in both the timeliness and openness of filters. Similarly, citation counting is criticized for being both slow and narrow:

“Metrics like the h-index are even slower than peer-review: a work’s first citation can take years. Citation measures are narrow; influential work may remain uncited. These metrics are narrow; they neglect impact outside the academy, and also ignore the context and reasons for citation.” (Priem et al., 2010).

Regarding their slowness, citation measures are de-valuated as even worse a means to filter important literature than peer review. The assertion that citations can take years to occur is linked to a preprint by Brody and Harnad,⁹ which scrutinizes article downloads as a predictor of later citation counts, provided that articles are published OA. Thereby, the critique of citation counts’ slowness implicitly refers the reader to their closedness too. The preprint concludes that correlation between download variance and citation counts indicates later citation impact, while the uncorrelated share of download variance indicated a different form of impact (Brody et al., 2006). This is mirrored by the AM’s critique of narrowness: Citation metrics are denounced for ignoring the academic impact of non-cited work but also for overlooking impact outside the scientific community. Furthermore, their narrowness is related to the long-standing critique that it is unclear what citation counts indicate. On the contrary, “altmetrics will track impact outside the academy, impact of influential but uncited work, and impact from sources that aren’t peer-reviewed” (Priem et al., 2010). What is more, “Altmetrics are fast […] open […] and emphasize semantic content” (ibid.). Again, traditional filters’ confinedness in time, space, and accessibility is contrasted with Altmetrics timeliness, broadness, and openness.

Finally, being based on citation counting, the aforementioned critiques apply to the JIF as well. It is further criticized for being narrow, and closed. The JIF “is often incorrectly used to assess the impact of individual articles” (Priem et al., 2010). This tackles the narrowness of a measure that is confined to indicating the importance of a venue instead of single articles. Moreover, “It’s troubling that the exact details of the JIF are a trade secret, and that significant gaming is relatively easy” (ibid.). Again, these assertions are linked to OA-articles, that criticize opaqueness regarding what type of citing articles are included in the denominator, whether a particular JIF is skewed by few highly cited papers, and whether authors are encouraged to cite other articles published in the same journal (Arnold & Fowler, 2010; Rossner et al., 2007; The PLoS Medicine Editors, 2006). These critiques once more denounce the closedness of a measure whose calculation is in private hands and negotiated behind closed doors. Hence, “The JIF is appallingly open to manipulation”, whereas “mature altmetrics systems could […] algorithmically detect and correct for fraudulent activity” (Priem et al., 2010). Traditional filters’ narrowness, slowness, and closedness all relate to a common motif of confinedness: They are confined with respect to the forms of ‘impact’ they can reflect, the time they need to measure impact, and the level of transparency and participation they allow for. Taken together their confinedness represents traditional filters’ stagnation – the incapacity to adapt to changes of what they measure.

The AM presents ‘traditional filters’ as equally unable to reflect impact. But how is it possible that such disparate objects – peer review, citation counting, and the JIF¹⁰ – are conceived of as instances of one and the same category? What is the common element that makes them equal objects of critique? All three are based on the same conventions of scholarly communication. In a simplified manner, we can reduce these to two basic conventions. First, ‘traditional filters’ relate to objects worth of being published in – predominantly commercial – journals. Second, such objects must adhere to conventions of referring to previously published objects, which again is regarded as valuable. ‘Traditional filters’ are connected by conventions that establish equivalence between heterogeneous objects (Desrosières, 1998): Only once we perceive human beings on the basis of their gender does the enumeration of men and women stand to reason. And likewise, only if academic works are regarded as comparable on the basis of being cited can anyone consider to count citations. Conventions of equivalence form what Desrosières (1998) calls an equivalence space: In order to systematically describe heterogeneous observations, they must be classified in systems of categories that reduce their singularity for the sake of making them comparable (324). Traditional filters are connected by an equivalence space that I will refer to as the publication-citation nexus: The mutual attribution of value realized by the indexing of peer reviewed, commercially published journals in proprietary citation databases that becomes most apparent in the JIF. First, being published in any one indexed journal establishes equivalence between articles: They are equal with regard to being published in journals that are valuable by virtue of being indexed. Second, counting how often indexed articles are cited commensurates articles in the sense that they are comparable on a dimension of quantity (Espeland & Stevens, 2008, pp. 408): Articles are equal regarding their quality of being citable, yet different with respect to the quantity of citations they accumulate. The various critiques that tackle the confinedness of ‘traditional filters’ also challenge this nexus as their conventional basis. It is the (e-) valuation of conventionally published articles that is too narrow, slow and closed to capture the change of scholarly communication.

The motif of expansion

While the AM’s critique of ‘traditional filters’ follows a motif of confinedness, the valuation of Altmetrics follows a motif of expansion. On the one hand, this motif consists in expanding the speed, diversity and openness of hitherto established evaluation methods. On the other hand, what is accomplished by this (e-) valuative strategy requires further analysis. I will reconstruct this accomplishment by subdividing the expansion motif into seven aspects.

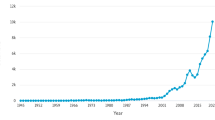
The first aspect consists in the institution of an expanding problem: The AM needs to make manifest the ‘explosive growth’ (cf. above) of scientific literature, which provides the basis for both the motifs of confinedness and expansion. The manifesto prominently features a graph that depicts “MEDLINE-indexed articles published per year” (cf. Fig. 1) between 1950 and 2010. The AM’s running text does not refer to the graph. The figure stands on its own just as if the depicted numbers were speaking for themselves. And in a way they do exactly that. The sharp increase of the last decade implicitly corresponds with the asserted ‘explosion’ of scientific literature. Numerical pictures such as this graph are “visual manifestations” of numbers’ capacity to present complex phenomena in intelligible ways (Espeland & Stevens, 2008, p. 423). By both making an argument and providing evidence for that argument (p. 428), they allow recipients to literally “see” (p. 426) the asserted phenomenon. As communication media numerical pictures are based on manipulation: The encoding of numerical information needs to foresee the decoding process that accomplishes communication (ibid. p. 425; WRT Cleveland, 1994). Understanding this process allows us to analyze both the doings and non-doings of its realization: The depicted graph indeed makes an argument and provides evidence for that argument. It makes manifest and thus allows us to see the explosive growth of literature. However, forgoing an explicit interpretation¹¹ of the depicted numbers, is to mold their perception as self-explaining, non-questionable truth. This is consequential for the AM’s valuation strategy: A substantial problem requires substantial solutions and a problem of large numbers seems well fit to be solved by tangible numbers of impact measurement.

Fig. 1

Manifestation of the problem (Reprinted from Priem et al., 2010) with permission under CC BY-SA

The second aspect consists in an expansion of the problem. The AM performs a shift in perspective away from filtering ‘just literature’ and toward the assessment of science more general. Was the purpose of ‘traditional filters’ merely to make sense of the literature, “altmetrics reflect the broad, rapid impact of scholarship” at large (Priem et al., 2010, o.e.). This challenges both the journal article as the dominant form of scientific text and the singular worth attributed to authorship. It is no longer just the published literature that counts, i.e. the end product of the research process, but a whole range of scholarly activities: “In growing numbers, scholars are moving their everyday work to the web. Online reference managers Zotero and Mendeley each claim to store over 40 million articles […]; as many as a third of scholars are on Twitter, and a growing number tend scholarly blogs” (Priem et al., 2010, o.e.). The focus is on ‘everyday work’ as opposed to the rather seldom event of publication. Managing literature, communicating findings, curating scientific knowledge; expanding the problem of research (e-) valuation comes along with an increased pervasion of academic work processes. This broadening of perspective is directly addressed where Altmerics are said to “help in measuring the aggregate impact of the research enterprise itself.” (ibid.).

Third, the redefinition of the problem is accompanied by an expansion of the reference space. This expansion is connected to the critique of ‘traditional filters’ and the confinedness of the publication-citation nexus as their common basis. The AM not only challenges traditional filters’ reference space and its underlying conventions but expands it to the “burgeoning ecosystem” of “new, online scholarly tools”. Breaking up the equivalence space of hitherto measurement re-establishes congruence between the problem and that which provides the reference for its solution: “Because altmetrics are themselves diverse, they’re great for measuring impact in this diverse scholarly ecosystem. In fact, altmetrics will be essential to sift these new forms, since they’re outside the scope of traditional filters.” (Priem et al., 2010).

Fourth, the congruence of the problem and its solution means that Altmetrics refer to a constantly expanding reference space. It is the “growth” of the new tools and services that defines the respective online environments as “burgeoning”, flourishing or in short expanding which lends credibility to the metaphor of the “ecosystem” (Priem et al., 2010). New online services and their related practices arise at fast pace, which further broadens the range of assessable activity. Because Altmetrics result from the very same online activities, they are meant to assess, the reference space grows in congruence with scholarly online activity: “These new forms reflect and transmit scholarly impact: […] This diverse group of activities forms a composite trace of impact far richer than any available before. We call the elements of this trace altmetrics” (ibid.). The fifth and sixth aspect of the expansion motif directly result from this congruent development.

The fifth aspect lies in expanding what counts as impact. As the AM puts it, “Altmetrics expand our view of what impact looks like, but also of what’s making the impact” (Priem et al., 2010, o.e.). This broadening of view follows a logic of exploration. The newly acquired land of interactive virtual spaces allows ‘us’ to discover formerly unknown forms of impact:

“that dog-eared (but uncited) article that used to live on a shelf now lives in Mendeley, CiteULike, or Zotero–where we can see and count it. That hallway conversation about a recent finding has moved to blogs and social networks–now, we can listen in. The local genomics dataset has moved to an online repository–now, we can track it.” (ibid.)

These examples correspond with the aforementioned potential of Altmetrics to track the impact of both uncited and non-peer reviewed sources and, with respect to social media, impact outside academia. Potentially every online event that relates to a scientific object becomes a valuable reference point for evaluation. Sixth, the expansion motif consists in expanding the range of assessable outputs: The focus is on the second part of the above quote, the expansion of “what’s making the impact” (ibid., o.e.). This, too, relates to Altmetrics’ diversity vis-à-vis ‘traditional filters’ narrowness:

“This matters because expressions of scholarship are becoming more diverse. Articles are increasingly joined by:

• The sharing of “raw science” like datasets, code, and experimental designs

• Semantic publishing or “nanopublication,” where the citeable unit is an argument or passage rather than entire article.

• Widespread self-publishing via blogging, microblogging, and comments or annotations on existing work.” (Priem et al., 2010)

This expansion of assessable outputs breaks down the scientific publication into its many constitutive acts: The initial design of a research project is made an object of metric impact assessment all the same as its data collection methods, the resulting datasets, code written for their analysis, and single arguments, which in a publication would build up to the line of argument. On the one hand, this attributes value to previously un(der)appreciated content or invisible work: With Altmetrics the outputs of work tasks other than publication become valuable. On the other hand, this means that more and more aspects of scientific work are made object of evaluation: The commensuration of more and more parts of the research process by Altmetrics makes it increasingly difficult to evade assessment. The notion of (e-) valuation comprises exactly these meanings of valuation/evaluation as two sides of the same coin. In correspondence with the second aspect of the AM, the fifth and sixth aspect thus stand for a pervasive expansion of (e-) valuative measurement.

The seventh and last aspect of the expansion motif consists in expanding participation in metric evaluation. Not only do Altmetrics emphasize partaking in assessable online activities, their openness puts weight on participation in measurement itself: Altmetrics use “public APIs to gather data in days or weeks. They’re open–not just the data, but the scripts and algorithms that collect and interpret it” (Priem et al., 2010, o.e.). Interfaces are public, codes and data are open; everyone is able to participate. Both the public accessibility of interfaces and the openness of commonly re-usable algorithms suggest that everybody can and indeed should participate in the collaborative Altmetric endeavor. The fraternizing use of the personal pronoun ‘we’ has a similar effect. Indeed, participation is presented as key to Altmetrics’ success: “In the future, greater participation and better systems for identifying expert contributors may allow peer review to be performed entirely from altmetrics” (ibid.). Expanding the participation in metric filtering practices entails an empowerment of the individual researcher, the qualification of each and every one of ‘us’ scientists to take part in impact assessment hitherto closed and limited to few, mainly commercial players and those who can afford their services.

This last aspect of the expansion motif also best illustrates the AM as a subversive manifesto. As the beginning of this section illustrates, the authors position themselves as part of those to whom they speak. They argue from outside an established power position and challenge existing procedures of research (e-) valuation. Most importantly, however, they advocate larger participation of the generality of researchers and question the elevated position of the privileged few who practice (e-) valuation behind closed doors. The call for openness, which emphasizes both transparency and participation, tackles allegedly closed processes that obscure how results are brought about. Corresponding to this historically younger type of manifesto the authors ‘sign’ at the end of the text, putting emphasis on the argument rather than the authority embodied in their speaking position. The same applies to the manifesto’s publication outside an established journal. The seven aspects of expansion build on the critique of the publication-citation nexus in an attempt to burst open the conventional confines of science evaluation. Breaking down both scholarly activities and scientific outputs into ever smaller (e-) valuable entities envisions a pervasive expansion of metric (e-) valuation as the suggested course of action. It should be mentioned that the manifesto’s subversiveness and attack against established infrastructures go hand in hand with the valuation of new platform infrastructures (Gillespie, 2010; Plantin et al., 2018) – Twitter, Mendeley, Zotero etc. – and a call to capitalize on “the statistical power of big data” (Priem et al., 2010). We know this modelling of revolutionary rhetoric on a market context from the “Californian Ideology” (Barbrook & Cameron, 1996): A strong belief in the democratizing potential of new virtual technologies is fused with liberal economics’ ideal of unrestricted entrepreneurship. The AM’s valuation strategy replaces the old infrastructures of the publication-citation nexus with web infrastructures that largely depend on platform capitalism (Mirowski, 2018). The idealistic vision of open participation blinds this view for the new economic divides produced in these novel markets.

The Leiden Manifesto

The LM addresses the problem that expert judgement in research evaluation was superseded by the pervasive misuse of metric indicators: “Research evaluations that were once bespoke and performed by peers are now routine and reliant on metrics. The problem is that evaluation is now led by the data rather than by judgement.” (Hicks et al., 2015, p. 429, o.e.). The basic tension of the LM is between the proliferation of research metrics on the one hand and the enclosure of indicator use on the other. It is based on a categorial distinction between “qualitative” and “quantitative evaluation” (p. 430). The notion of judgement refers to the relation of these two categories. One telling section puts it like this: “Quantitative metrics can challenge bias tendencies in peer review […] However, assessors must not be tempted to cede decision-making to the numbers. Indicators must not substitute for informed judgement” (p. 430). This produces a paradox situation: The manifesto as a whole aims to safeguard a specific notion of expert practice, the ‘craft’ of metrification in evaluation. Yet, this is attained by limiting metrical dominance over evaluation processes. In order for metrics to maintain their value, they need to be devaluated. The LM argues from the position of expert evaluators, addressing the field of science evaluation as its public audience. Its title reads: “The Leiden Manifesto for research metrics: Use these ten principles to guide research evaluation, urge Diana Hicks, Paul Wouters and colleagues.” (Hicks et al., 2015, p. 429, e.i.o.). As mentioned earlier, the ‘Leiden’ label stems from a conference hosted by the CWTS. On the one hand, the label draws on the expert authority of this internationally renowned institution. On the other hand, its conference origin lends the LM a more international character, allowing it to speak for the field of science evaluation as a whole. Its global claim and expert position are emphasized by naming the LM’s highest-ranking authors in the subtitle, underlining the contribution of experts from both sides of the Atlantic. Similarly, being published in the comments section of Nature not only promises a high visibility but also comes with the journal’s prestige. Finally, expertise is crucial for understanding the problem: “As scientometricians, social scientists and research administrators, we have watched with increasing alarm the pervasive misapplication of indicators to the evaluation of scientific performance” (p. 430). This problem is addressed by a “codification” (p. 430) of ten best practice principles. The overall (e-) valuation strategy consists in the valuation of this ‘code of conduct’ vis-à-vis the critique of proliferating research metrics.

The motif of proliferation

The LM’s critique of the current state of things follows a motif of proliferation: “Metrics have proliferated: usually well intentioned, not always well informed, often ill applied” (Hicks et al., 2015, p. 429, o.e.). The proliferation of research metrics consists in the gradual replacement of peer discussion (qualitative evaluation) by metrical data (quantitative evaluation) leading to an absence of judgement in research evaluation. As such, proliferation is the cause of the problem; the “pervasive misapplication of indicators” (p. 430) is the reverse of the medal. We can reconstruct the proliferation and pervasive misapplication of (e-) valuative metrics in three steps. First, the genesis or growth of the field. Second, the fall of man or the replication of long-standing criticisms against bibliometric indicators. Third, the manifestation of an obsession with indicators or the cardinal sin at the root of the problem. Indeed, the LM comprises a number of surprisingly biblical elements, most apparently the ‘revelation of the ten commandments’ of research evaluation. This corresponds with the speaker’s position of the text; the LM exhibits several features of a ruler’s manifesto (cf. Section 1). First, as was the case with the manifesto of a sovereign, the authors (at least those of highest rank) are named in the title. Second, just as the ruler’s manifesto was legitimized by the God-given sovereignty of its issuer, the LM’s claims are legitimized by the authority of professional experts. This is bolstered by falling back on eminent authorities: “Luminaries in the field, such as Eugene Garfield (founder of the ISI), are on record stating some of these principles” (Hicks et al., 2015, p. 430). The authors do not argue from a marginalized position but from the center of professional power. Third, the LM shares the programmatic character and propagandistic function of the ruler’s manifesto in 17th cen. France (Klatt & Lorenz, 2011, pp. 8). It is neither concerned with putting forth subversive demands nor with proclaiming singular decisions but with the dissemination of rules to be followed on a long-term basis.

Following the introductory paragraph, the LM presents the genesis of the field, i.e. the development of metric research evaluation. ‘In the beginning God created …’ here takes the form “Before 2000, there was the Science Citation Index [SCI] on CD-ROM from the Institute for Scientific Information (ISI), used by experts for specialist analyses” (Hicks et al., 2015, p. 429). Above, I have shown how the LM refers to Eugene Garfield as the luminous creator of this pristine Eden. The importance of expertise in this original state is underlined by the tautologic use of “experts” conducting “specialist analyses”. Beginning with the SCI, the LM tells a story of exceptional growth in both metric providers and the dissemination of indicator use: The establishment of the Web of Science (WoS) in 2002, Scopus in 2004, and Google Scholar in that same year, the development of related services such as InCites (WoS), SciVal (Scopus) and Publish or Perish (Google Scholar), the quick spread of the h-index after 2005 and the JIF’s constant growth in importance all culminate in an account of companies providing “metrics related to social usage and online comment” (Hicks et al., 2015, pp. 429), namely F1000Prime, Mendeley, and Altmetric.com. This tellingly represents Altmetrics as the provisional endpoint of a development conceived of as problematic. The reference to Altmetrics is directly followed by the expression of “alarm regarding the pervasive misapplication of indicators” (p. 430). The misuse of (e-) valuative metrics results from the genesis of the field that entails the proliferation of metric indicators.

What I call the fall of man refers to the manifestation of critique regarding the (mis-) use of metric indicators. Criticisms include the prevalence of “global rankings (such as the Shanghai Ranking and Times higher Education’s List), even when such lists are based on what are, in our view, inaccurate data and arbitrary indicators” (p. 430),¹² the application of the h-index in recruitment and promotion decisions, the obligation “to publish in high-impact journals” (ibid.), and the allocation of funding and bonuses on the basis of impact factors or even individual impact scores. In later paragraphs, the LM seizes further critiques like the misrepresentation of non-English journals in the WoS, the non-consideration of field-dependent publication patterns, or funding based on publication counts, as described by Linda Butler for the case of Australia (Butler, 2003a, 2003b). This assemblage of criticism commonly leveled against bibliometrics makes manifest a “crisis in research evaluation” (Hicks et al., 2015: cf. figure p. 431), which provides an ideal contrast for the justification of envisioned change. Neo-pragmatism offers a perspective to better understand the nature of such a crisis: A crisis is best illustrated by contrasting it to a “natural situation” (Boltanski & Thévenot, 2006, p. 35), in which everybody agrees upon the just associations among beings. In such an “Eden-like world” (p. 36) all things and people express a high level of generality with respect to a common principle of justice. One could imagine for instance a highly efficient evaluation regime justly reflecting each performed task and everyone involved. Or, indeed, a database such as the SCI used ‘by experts for specialist analyses’ only. We have seen how the development away from this original state, the invasion of a sacred realm by the profane, so to say, has resulted in misery and vice: “[w]e risk damaging the system with the very tools designed to improve it, as evaluation is increasingly implemented by organizations without knowledge of, or advice on, good practice and interpretation” (Hicks et al., 2015, p. 429). In Boltanski and Thévenot’s (2006) words, the crisis or “Fall from Eden” (p. 36) – a borrowing from the biblical ‘fall of man’ – entails objects that deviate from the general principle and thus have to be addressed in particular terms, lowering their value in relation to the general worth of the situation. On the one side this explains why the LM replicates well known critiques of particular bibliometric objects, on the other side it resolves the paradox that the value of quantitative evaluation is maintained by de-valuing metric indicators. Showing in what ways metric indicators are misused emphasizes the value of expertise in indicator use. The LM’s best practice advice tries to reverse the original sin of letting the profane enter the professional field of science evaluation.¹³

Apart from the genesis and fall of quantitative science evaluation the LM makes manifest the proliferation of metrics by denouncing the cardinal sin of “obsession” (Hicks et al., 2015, pp. 429, 431). I use this metaphor in order to underline how the alleged ‘irrational preoccupation’ with metric indicators gives rise to a long list of potential misuses. Because an obsession with numbers is the opposite of rational, expert judgement, it lies at the core of the problem. As the LM states, “Universities around the world have become obsessed with their position in global rankings” (p. 430). Rising interest in the JIF is labeled “Impact-factor obsession” (p. 429). The reader is then referred to a figure titled with precisely that expression (cf. Fig.  2, Hicks et al., 2015, p. 431). The sub-title states, “Soaring interest in one crude measure […] illustrates the crisis in research evaluation” (ibid.). In a manner quite similar to the AM, the graph and diagram of this figure make manifest the problem that defines the situation as critical. The upper graph depicts “Articles mentioning ‘impact factor’ in title” (p. 431) per 100.000 papers indexed in the WoS, published per year between 1984 and 2014. It distinguishes the development of editorial texts from that of research articles. Both show a marked increase from 1994 onwards and peak in 2012. The depicted development suggests a long-term rise of interest in the measure. However, the numerators of the illustrated fractions are strikingly low with the peak of the graphs depicting 8/100,000 (or 0.00008%) and 4/100,000 (or 0.00004%) respectively. To speak of an obsession in the face of such modest, if increasing numbers is more than questionable.¹⁴ Nevertheless, the depicted increase and its valuation as obsessive allows the reader to ‘see’ the asserted crisis. In this respect the strategy of substantializing the addressed problem is very similar to that of the AM. Both manifestos use numerical pictures to illustrate a rapid increase and both refrain from further discussing the depicted phenomena.

Fig. 2

“Impact-Factor Obsession” Reprinted from Hicks et al., (2015, p. 431). Copyright 2015 by Nature Publishing Group. Reprinted with permission, p. 431

The LM instantiates the problem that expert evaluation was increasingly superseded by the ill-application of metric indicators. This problem is made manifest by de-valuating a number of indicator uses. This critique follows a motif of proliferation: Metrics’ unchecked rise in importance is demonstrated by recapitulating the fast growth of the field, by replicating well-known critiques of (e-) valuative measurements, and by substantializing an obsession with metric indicators. This overall theme of the LM’s criticism serves as a contrast for the valuation of its best practice advice.

The motif of enclosure

The LM’s answer to the proliferation of indicator misuse follows a motif of enclosure. This motif consists of four aspects that can be reconstructed from the manifesto’s ten best practice principles. All four relate to limiting the legitimate use of metric indicators to particular contexts. First, qualitative evaluation encloses quantitative assessment. The first of the ten principles states, “Quantitative evaluation should support qualitative, expert assessment” (Hicks et al., 2015, p. 430). Quality is installed as a kind of resistor, superior to metric assessment and hence confining it in its applicability. In contrast, quantitative information is enrolled in a mere supporting function. The LM addresses quality in a variety of ways, all of which point to assuring the adequacy of quantitative information in the respective evaluation context. Accordingly, the seventh principle states evaluators should “base assessment of individual researchers on a qualitative judgement of their portfolio” (p. 431). This is combined with a critique of the h-index for its age- and data base dependency. In conclusion, “Reading and judging a researcher’s work is much more appropriate than relying on one number” (ibid.).

Second, the LM stresses the context- and goal dependency of metric indicators. Principle two advises the reader to „Measure performance against the research missions” of the evaluated project (Hicks et al., 2015, p. 430). Indicators had to be chosen in concert with the “goals” of these projects and according to their “wider socio-economic and cultural contexts” (ibid.). Metrics should reflect the “merits” relevant to the wider research framework. Briefly put, “No single evaluation model applies to all contexts” (ibid.). Research specific ‘missions’, ‘goals’, ‘merits’, and ‘contexts’ all enclose the legitimate use of metric indicators in particular evaluation situations. Similarly, the third principle calls on the readers to “Protect excellence in locally relevant research” (p. 430). Regionally engaged projects could only be evaluated adequately with “metrics built on high-quality non-English literature” (ibid.). By contrast, generalized indicators based upon “the mostly English-language Web of Science” would misrepresent local relevance. Such emphasis on both goal-dependent merits and local relevancies enclose the (qualitative) meaning reflected by metric indicators in particular contexts. This narrows down the general worth of quantitative assessment by virtue of indicators’ restricted generalizability.

Third, research metrics are enclosed with regard to their field dependent variation and verification. Principle six states “Account for variation by field in publication and citation practices” (Hicks et al., 2015, p. 430). The reader is referred to the case of a research group rated low in peer-review due to the publication of books instead of articles in WoS-indexed journals. The example is meant to illustrate how quantitative indicators can supersede the qualitative information, which the reviewers should have assessed. In order to avoid such fallacies, evaluators ought to be careful in choosing the right indicators to reflect field specific quality: “Best practice is to select a suite of possible indicators and allow fields to choose among them” (ibid). It becomes clear that not only should quantitative methods be adjusted with regard to the evaluated discipline but that quantitative indicators do not allow for comparison across fields of research. What is more, enclosing the adequacy of indicator use in particular fields is to be ensured by including these very fields into the choice of suitable metrics. This latter aspect is specified in principle five: “Allow those evaluated to verify data and analysis” (p. 430). The evaluated researchers are enrolled as the evaluators of the evaluators: “Data quality” should be ensured by “self-verification or third-party audit”. In a way, such enrolement can be read as an immunization against critique. In a first step, well-known criticism against both scientometric indicators and quantitative research evaluation is replicated within the motif of proliferation. As part of the second step of enclosure, the potential critics – “those evaluated” – are ascribed the role of controlling their just evaluation. The legitimate use of metric indicators is enclosed in disciplinary contexts by virtue of the evaluated researchers’ expertise in these disciplines. The valuation of such contextual expertise in turn helps maintaining the expert status of professional evaluators who dictate the rules of the process at large.

Fourth, metric indicator use is enclosed by the requirement to recognize the reactivity and regular adjustment of evaluative measures. The ninth principle invites readers to “Recognize the systemic effects of assessment and indicators” (Hicks et al., 2015, p. 431). The various critiques replicated by the motif of proliferation, are here translated into expert advice on the proper use of these metrics. As is the case with the aspect of variation and verification (cf. above), critique is made an integral part of expertise in quantitative evaluation: “Indicators change the system through the incentives they establish. These effects should be anticipated. This means that a suite of indicators is always preferable — a single one will invite gaming and goal displacement” (ibid.). Linda Butler’s (2003a) popular study of funding effects is cited as an example for such reactive measurement. Again, this sheds light on the seeming paradox that metrics are weakened in order to maintain their value: Critique becomes a resource for the appraisal of expertise. In order to henceforth avoid unintended effects of metric assessment, expert judgement has to be reintroduced into evaluation processes. This ninth principle serves as a basis for principle number ten: “Scrutinize indicators regularly and update them” (Hicks et al., 2015, p. 431). The need for ongoing scrutinization of indicators yet again emphasizes the value of professional knowledge and procedures: Metric evaluation itself is in constant need of (e-) valuation. Moreover, the tenth principle is related back to the context- and goal dependency of research metrics: “Research missions and the goals of assessment shift and the research system itself co-evolves. […] Indicator systems have to be reviewed and perhaps modified” (ibid.). This emphasizes a temporal dimension in the enclosure of (e-) valuative metrics: Not only are they confined to specific contexts, enclosed by fields and research missions, the change of these contextual conditions over time makes expert judgement indispensable to the functioning of research assessment. This also shows quite plainly that the ten best practice principles do not in themselves solve the problem of indicator misuse. They rather reflect upon a number of problems resulting from a lack of insight into metric research assessment, thereby underlining the general worth of expert knowledge to science evaluation.

The four aspects of enclosure confine the legitimate use of metric indicators to specific contexts. This is based on a comparative valuation of quality over quantity: Quantitative indicators are only helpful insofar as they indicate context-, goal-, field-, system- and time-dependent qualities. Such enclosure values expertise in metric research evaluation as the means to justly relate quality and quantity. Table 1 summarizes the four motifs’ key aspects. This will serve as a reminder for the next section, which discusses the inter-textual relation of these themes.

Table 1 Four motifs of (de-) valuation

The diametrical organization of motifs

Until now, I have discussed only the intra-textual relation of the two manifestos’ (de-) valuation motifs. In this section, I will show that the motifs of either text can be related to one another and that these inter-textual relations are organized diametrically. Figure 3 illustrates this opposition of positions. The discussion will follow the relations indicated by the blue arrows. It will show that the means-end relation appraised as the solution in one text is the object of critique in the other and vice versa.

Fig. 3

The diametrical organization of motifs

Confinedness versus enclosure

Both, the motifs of confinedness and enclosure relate to the limitation of established means of science (e-) valuation but arrive at diametrical conclusions. The AM envisions a problem of rapidly growing scientific literature and hence criticizes various aspects of ‘traditional filters’ confinedness. Contrarily, the LM opts for the very enclosure of metric indicators in order to get the proliferation of metrics under control. Both motifs are justified against the backdrop of an alleged (in-) congruence of the means and the objects of (e-) valuation: To the AM, traditional filters’ confinedness makes them unable to adapt to the change of scholarly communication; they are too narrow, slow, and closed to reflect the real impact of scientific work. To the LM, only limiting the use of metric indicators to specific contexts, fields, localities, time frames and goals makes them conform to the ends of (e-) valuation; the uncontrolled application of metrics would unleash their reactive potentials resulting in unintended effects.

Taking the AM as a reference point, we can explore this diametrical organization on the dimensions slow/fast, narrow/diverse, and closed/open. Whereas the AM denounces the narrowness of citation measures, the LM understands narrowing down the meaning of indicators to particular evaluation goals as a virtue: “Simplicity is a virtue in an indicator because it enhances transparency” (Hicks et al., 2015, p. 430). The risks implied in such simplicity are balanced out by peer review, by “[r]eading and judging a researcher’s work”. As we have seen, to the AM both peer review and citation counting are procedures far too slow to reflect the fast impact of scholarship. Again, the LM holds a contrary view: “Accurate, high-quality data take time and money to collate and process. Budget for it.” (ibid.). The last of the AM’s critiques, the closedness of traditional filters is the only one without a clear opposition of the two manifestos. With respect to enhanced participation in (e-) valuation the frontiers are still clear-cut: The AM intends to replace peer review with crowdsourced opinions and actively promotes participation in Altmetrics. To the LM, increased participation represents part of the problem, with more and more non-experts implementing (e-) valuation procedures. When it comes to transparency, however, both manifestos seem to be on the same page. Both appraise transparency of methods as a condition of successful (e-) valuation and both criticize (e-) valuation procedures for their opacity. The AM denounces both peer review and the JIF for their opaqueness and underscores Altmetrics’ transparency qua openness. As can be seen from the above quote, also the LM upholds transparency, but claims it to be provided by the enclosure of indicators. Its fourth principle calls on readers to “Keep data collection and analytical processes open, transparent and simple” (Hicks et al., 2015, p. 430). It appears that one cannot argue about the virtue of transparency. However, the two manifestos’ means to achieve it are again quite contrary in nature.

This quarrel over the right means to achieve transparency provides insight into what is at stake in the larger dispute over legitimate (e-) valuation practices. We have seen that the critiques of confinedness tackle the underlying conventions of the publication-citation nexus. Peer review as the gatekeeper of journal quality is even criticized for the very reason of inviting “conventionality” (Priem et al., 2010). As the opposite of innovation, such conventionality is part of traditional filters’ stagnation and incongruence with what they measure. The LM, to the contrary, makes the existence of long-established conventions the basis of transparency:

“The construction of the databases required for evaluation should follow clearly stated rules, set before the research has been completed. This was common practice among the academic and commercial groups that built bibliometric evaluation methodology over several decades. Those groups referenced protocols published in the peer-reviewed literature. This transparency enabled scrutiny.” (Hicks et al., 2015, p. 430)

Many of the previously discussed themes are assembled in this quote: Evaluation should be a rule-governed process, reliant on curated reference spaces. Such common practices, or conventions (Boltanski & Thévenot, 2006; Desrosières, 1998), were established by experts building the methodology over a long time period. Transparency in this respect means to transparently communicate the application of professional conventions to an expert audience. The fall from this Eden-like professionalism prompts critique: “Recent commercial entrants should be held to the same standards; no one should accept a black-box evaluation machine.” (Hicks et al., 2015, p. 430). Considering that the genesis of the field culminates in an account of companies such as “Altmetric.com” (ibid.) one gets an idea whom this critique is directed at. The LM values the very convention-based tradition, which the AM criticizes as the conventionality of overcome, traditional filters. To one position, proven conventions are the only means to restore balanced judgement, to the other they cause the insufficient measurement of changing scientific practices. This opposition corresponds with the text type of the respective manifestos: As a subversive manifesto the AM argues from outside an established power position, trying to undermine the rigid rules that govern professional practice. Arguing from the ruling position of established experts, the LM resembles a ruler’s manifesto, which attempts to consolidate the value of professional expertise. The LM’s ten principles can best be understood as an answer to a field that more and more escapes the control of established experts. They express the expert authority to ‘say what’s right’ and thus restore a conventional basis for judgement. This claim to power, to ‘dictate the law’ of science evaluation, demonstrates what is at stake in the dispute unfolding between the seemingly unconnected manifestos: Ultimately, the opposing positions represent a struggle over the jurisdiction (Abbott, 1988) of the field.

To Abbot (1988), jurisdiction denotes professional control over certain work tasks. He puts emphasis on ligation, the process that defines actors (professions) and their locations (work) by establishing a relation (jurisdiction) between them (Abbott, 2005, p. 248). Because professions compete over work tasks, jurisdictions always remain vulnerable to attacks. The two manifestos are manifest evidence of such a struggle over legitimate forms of work. The established experts have become subject to the “imperative to justify” (Boltanski & Thévenot, 2006, p. 23): The LM’s proclamation of best practice principles represents a jurisdictional claim that bears witness to an actual loss of control. In the academic ecology locations “lack the strongly exclusive character of professional jurisdictions”, which is why Abbott (2005) refers to them as “settlements”¹⁵ (p. 250). Boundaries between different actor groups – disciplines, professions, sub- and inter-disciplines etc. – are more blurred, which makes exclusive control over particular settlements a difficult matter. This is precisely why expert control of metric (e-) valuation is so easily put into question by the AM. As an academic field it is settled by many different actors, which is illustrated quite clearly by the different disciplinary backgrounds of the LM’s authors. What holds together this interdisciplinary settlement is “an esemble of research practices, evidentiary conventions, rhetorical strategies” (Abbott, 2001, p. 140) and such like that is all too easily challenged by newcomers developing new work tasks in the same area of work.

As a strategy of ligation, the LM tries to defend the conventions of the established settlement against external attacks. Thèvenot’s (1984) concept of form investments will help us better understand this focus on conventions. An investment in form can be defined “as a costly operation to establish a stable relation with a certain lifespan” (p. 11, e.i.o.). For both Boltanski and Thévenot (2006) and Desrosières (1998) conventions represent forms of social coordination. What differentiates these forms from one another are investments into their lifespan, their area of validity, and their material objectification (Thévenot, 1984). Such form investments result in diverging degrees of “rigidness or inflexibility (the ability to resist efforts to distort, adjust or negotiate them)” (ibid., p. 10). The LM represents an investment into the rigidness of established, yet challenged work forms: The “ten principles are not news to scientometricians, although none of us would be able to recite them in their entirety because codification has been lacking until now.” (Hicks et al., 2015: p. 430, o.e.). The resulting code of conduct makes manifest an increasingly challenged order of worth, which allows to ‘justly distinguish’ appropriate from inappropriate forms of the craft. A law code may be the best-known example of such a codified, i.e. manifest order of worth.¹⁶ The LM’s notion of judgement does not merely relate to judging the quality of scientific work but also to judging the (il-) legitimacy of work forms. In its academic surroundings, however, the LM cannot claim any rights to jurisdictional exclusiveness. Its code of conduct objectifies relations between experts, (e-) valuation methods, and the (e-) valuated beings – including their temporal organization – in order to justify the validity of these forms before its public audience.

The LM is in fact directed at several different public audiences and it is here that the concept of enrolement comes into play. Abbott (2001) describes several different audiences of academic disciplines but the most important are clients, providers, and other scientists (p. 141). I have already discussed how the LM enrolls the evaluated – the clients of research (e-) valuation – in a way that supports the expert authority of evaluators. Furthermore, in order to allow transparency, other scientists as well as “recent commercial entrants” should act in accordance with established conventions (Hicks et al., 2015, p. 430, cf. above). Finally, this should be guaranteed by those allocating the resources necessary for science (e-) valuation – administrators and funders – who are directly addressed by the call to “budget” for “high-quality data” and the time needed to assemble it (ibid., cf. above). Enrolement operates via the attribution of competence and responsibility: Only when the newcomers take responsibility by acting in accordance with transparent principles can they be judged as competent actors. Likewise, the transparent advice of the LM enables funders to make competent decisions in allocating resources, which comes with the responsibility to spend money wisely. Drawing on established conventions, the LM’s code of conduct represents an investment in form that not only represents a strategy of ligation but also enrolls relevant audiences in such a way that their ascribed roles add to the legitimacy of the established expert-work relation. The alleged crisis of research (e-) valuation is resolved in a suggested course of action that relates relevant beings – experts, newcomers, quality, quantity, funders, and the evaluated – in an order of worth that assures the efficiency of metric (e-) valuation (Boltanski & Thévenot, 2006 pp. 203).

Expansion versus proliferation

Both the motif of expansion and the motif of proliferation describe the growth of (e-) valuative metrics but value this increase quite contrarily. To the AM an expansion in metric measurement is necessary to adequately reflect expanding scholarly activities in the web. This includes a pervasive expansion in both counted activities and outputs that count. Expanding the development and use of (e-) valuative metrics accounts for the expanding problem of fast and vast amounts of academic communication. Altmetrics are the answer to a task that more and more escapes the capacity of established (e-) valuation measures. Because Altmetrics expand with the practices they reflect, they restore congruence between the objects and means of measurement. Conversely, the LM judges the very expansion of metric filtering practices as a proliferation that escapes the control of expert conduct. The increase in metrics and their providers makes the field increasingly hard to oversee and those who implement evaluation lack expert advice on good practice. The proliferation of research metrics thus leads to the pervasive ill-application and misuse of these indicators, which has potentially harmful effects on the research system. In the view of the LM, the uninformed application of metric indicators to whatever (e-) valuation context results in a misfit or incongruence of metrics and what they’re meant to measure. Again, the diametrical organization of motifs depicts a dispute over the (in-) congruence of measures and the objects of measurement. To the AM a pervasive expansion of metric measurement is the solution of the problem, to the LM this leads to the pervasive misapplication of metric indicators.

This opposition is connected to the different ends, which the two manifestos prize as the solution to their respective problems. To the LM the proliferation of metric measurement supersedes balanced judgement. What matters to the AM is the measurement of the broadest possible impact in the fastest possible ways. What do we make of these different notions, judgement and impact measurement, that cause such dissimilar valuations of one and the same development? With respect to judgement, which relates to the right balance between qualitative and quantitative evaluation, a recourse to the neo-pragmatist view “On Justification” (Boltanski & Thévenot, 2006) stands to reason.

According to Boltanski & Thévenot, beings become valuable when they are qualified within an order of worth. “Qualification” (2006, p. 1, p. 130, p. 359) categorizes persons and things in equivalence classes. This by no means leads to unidimensional quality: On the one hand, the meaning of a qualified being depends on its relation of equivalence to other beings of the same class. On the other hand, it is defined by the relation of this class to all other equivalence classes within the same order. Qualification is performative in the sense that beings are qualified to co-ordinate action by virtue of their relations to one another. Parents become parents by virtue of their relation to their children, the school or nursery, the grandparents, their home, the things they provide, etc. Put differently, subjects and objects are qualified as worthy beings by virtue of their relations to all other beings within the order. I will refer to the sum of a being’s relational qualities as its meaning. Qualification connects beings to a common principle of justice, a convention of equivalence that makes them (e-) valuable in the light of a specific order (p. 140). For example, in the industrial world, beings are of general worth if they function efficiently (p. 204). Because “each order of worth corresponds to a scale going from the general to the particular (and not simply from higher to lower, as in physical measurements)” (p. 141), qualification can be regarded as a reciprocal process: Qualification delineates both what general worth means in a particular situation and how particular beings matter in a more general sense. If beings can’t “rise to the occasion” (134), if their qualities can’t be generalized in the light of a higher common principle, their meaning is particularized, that is, their qualities are diminished in worth. This is what the LM does by reproducing the critiques leveled against bibliometric indicators. Yet, particular meanings are not to be confused with particularized deficiencies, which can be regarded as irrelevant to the general worth of the order. I will use the term relevance to delineate beings’ ability to rise to the occasion, to be generalized in the light of a higher common principle. The distinction between meaning and relevance¹⁷ emphasizes beings’ multidimensional meanings vis-à-vis their state of worth, which tends to dominate Boltanski and Thévenot’s (2006) line of argument. It will allow us, first, to abstract from the LM’s terminology of ‘quality’ vs. ‘quantity’ and, second, to compare the divergent instantiations of meaning and relevance by the manifestos’ respective concepts of impact and judgement.

The relation of meaning and relevance is of central concern to both the AM and LM because both are concerned with commensuration (Espeland & Stevens, 2008). In the terminology I have just outlined, commensuration ascribes amounts of relevance to objects by counting one particular quality – of all qualities making up their meaning – as an indicator of their general worth. If, then, metric indicators express the comparative relevance of the commensurated objects, the question rises, what these numbers mean, i.e. what it is that they indicate. This question is by no means new to quantitative science (e-) valuation. Moed (2005) dedicates a whole chapter (p. 193) to how different scholars and disciplinary traditions ascribe meaning to both references and citation measures. As we have seen, the AM makes use of this ambiguity, criticizing that citation counting was ignoring the reasons for citation. Being aware of this problem, the LM relates the meaning and relevance of metric indicators as follows: In general, quantitative indicators should reflect quality, which will allow for balanced judgement: The original state of evaluation is peer discussion and where metrics are employed they should support qualitative assessment. Quality is thus of highest relevance to the LM. However, what quality means in a specific context has to be answered in particular. The general notion of quality encompasses all particular qualities and therefore also the metrics that indicate these qualities in particular evaluation contexts. Meaning is contextualized and thus cannot be answered on the LM’s high level of generality. This is why those evaluated within the respective contexts are enrolled as the guarantors of contextual qualities. In order for indicators to adequately reflect worth, the contextual experts have to choose which metrics indicate qualities that matter to their field. This competence of the evaluated, to signify the meaning of metric indicators, goes along with the competence of expert evaluators to ensure the general worth of these numbers. The meaning of (e-) valuative metrics is externalized, so to say, which enables their qualification as indicators of relevance. Accordingly, the critique of proliferation denounces situations in which indicators express relevance without delineating their meaning. The potential damage of proliferating metrics resides in signaling the relevance of counted qualities without binding these qualities to a contextual meaning. The result are unintended effects and false incentives.

I have argued, that the LM at least indirectly criticizes Altmetrics for adding to the pervasive misapplication of metric indicators. And indeed, the AM’s notion of impact instantiates a completely different relation of meaning and relevance. The notion of impact lends credence to the metaphor of the filter: The dissimilar objects contained in the categories of ‘traditional’ and ‘new filters’ are judged with respect to their ability to reflect Impact. Impact establishes equivalence within each class and thus provides the hinge between both these categories: The two equivalence classes are differentiated by the degree to which they reflect impact. Within the situation depicted by the AM, impact is thus of highest worth. Traditional filters are denounced because they do not adequately reflect impact. This represents a particularization of established (e-) valuative beings – citation counts, the JIF, peer reviewers – and the publication-citation nexus as their common basis. The expansion motif broadens the situation to include impact in a more general sense than these particularities do. This is exactly what is addressed by “broader impact” visible through ‘diverse expressions of scholarship’ within a “diverse scholarly ecosystem” and measurable “[b]ecause altmetrics are themselves diverse” (Priem et al., 2010). Diversity refers to the many different forms of impact, which add up to the “composite trace of impact” visible within expanding online environments. By the means of Altmetrics, all particular forms of impact are generalized to reflect impact at large. This is also reflected in a figure that features under the AM’s sub-heading “How can altmetrics improve existent filters?” (ibid., e.i.o.). It is reproduced in Fig. 4. Here, Altmetrics are represented as one of many possible ways to measure impact. The category includes things like “storage”, “links”, “bookmarks”, and “conversations” (Priem et al., 2010). Although based on web behavior, “downloads” and “views” are not listed as Altmetrics but categorized as “usage”.¹⁸ The “citations” category does not feature any examples or explanations, which corresponds with the critique of their unclear meaning (cf. above). Peer review, however, is qualified as “expert opinion”¹⁹ and in this respect assumes the same meaning as in the LM: Peer review reflects relevance (quality in the LM, impact in the AM) by virtue of its meaning to express expert opinion. Both, the contrast to the shorter, if existent, lists under the other three categories and the emphasis on “alt- “ for ‘alternative’ underscore Altmetrics as the more diverse measures, able to reflect impact in a more general sense. Accordingly, the AM presents Altmetrics as measures of relevance: “scholars rely on filters to select the most relevant and significant sources from the rest. Unfortunately, scholarship’s three main filters for importance are failing” (Priem et al., 2010, o.e.). ‘Relevance’, ‘significance’, and ‘importance’ are used as synonyms for impact. But if impact delineates the relevance of these alternative measures, what do Altmetrics mean? In what ways are they qualified to be of relevance, i.e. to express impact? Do Altmetrics simply mean that scientific content has been ‘stored’, ‘hyperlinked’, ‘bookmarked’, or ‘conversed on’? And if so, how is this relevant to the (e-) valuation of scientific activity? These questions are left open. The AM does not answer how Altmetrics reflect meaning in any other way than citation measures reflect the reasons for citation. Instead, the choice inherent in any process of quantification is obscured by a naturalization of Altmetrics. Counted objects are not referred to as (raw) data but as Altmetrics in their own right. This corresponds to the notion of the “filter” that allows to “sift” (ibid.) online activities for impact as if it was a material thing, preexistent to measurement. The manifesto’s problem of ever-expanding scientific information is believed to be solved by algorithmically sifting the continuous streams of online data for numerical relevance. What these numbers mean, in what ways they matter to science, is left open. It seems then, that Altmetrics equal significance with meaning, that the mere existence of numbers justifies their relevance. Their reiterated potential to measure impact comes along with Altmetrics’ ambiguity of meaning.

Fig. 4

Four ways to measure impact Reprinted from Priem et al., (2010) with permission under CC BY-SA

This is not meant as a critique. In fact, there is a particular reason for the AM’s relation of meaning and relevance; Altmetrics’ ambiguity of meaning is connected to the potentiality of their possible uses. Although refraining from the explication of any particular meaning, the AM names a whole range of Altmetrics’ possible uses: “With Altmetrics, we can crowdsource peer-review.”, “altmetrics will track impact outside the academy, impact of influential but uncited work, and impact from sources that aren’t peer reviewed.”, “mature altmetrics systems could […] algorithmically detect and correct for fraudulent activity.”, “The speed of altmetrics presents the opportunity to create real-time recommendation and collaborative filtering systems”, “Faster, broader impact metrics could also play a role in funding and promotion decisions.”, and “can also help in measuring the aggregate impact of the research enterprise itself.” (Priem et al., 2010). These various potential uses represent what I address as Altmetrics’ potentiality. This potentiality is enabled by Altmetrics’ ambiguity of meaning that corresponds to their alleged diversity. Diverse measures can have diverse meanings, which allows to remain vague about Altmetrics’ particular qualifications. This in turn enables the attribution of altmetrics with all of the above potentials. What in synopsis may almost seem like the praising of panacea is not unknown to us. Indeed, it may resemble a pitch seeking to attract investors. Altmetrics’ potential value lies in the potentiality of their possible uses, which in turn represent valuable opportunities for investment. I have argued that the LM draws on invested forms in order to substantiate the authority of established experts. Altmetrics, by contrast, are new, largely formless things, and while the AM represents a form investment itself, its main goal is to mobilize further investment by others: “Altmetrics are in their early stages; many questions are unanswered. But given the crisis facing existing filters and the rapid evolution of scholarly communication, the speed, richness, and breadth of altmetrics make them worth investing in.” (Priem et al., 2010, o.e.). As I have shown above, the AM’s authors position themselves as part of those to whom they speak. In this way, the AM can enrole a broad scientific public to openly participate in Altmetrics. However, in a manner similar to the LM, the AM needs to address multiple audiences so as to enroll potential investors in its suggested course of action:

“Researchers must ask if altmetrics really reflect impact, or just empty buzz. Work should correlate between altmetrics and existing measures, predict citations from altmetrics, and compare altmetrics with expert evaluation. Application designers should continue to build systems to display altmetrics, develop methods to detect and repair gaming, and create metrics for use and reuse of data. Ultimately, our tools should use the rich semantic data from altmetrics to ask ‘how and why?’ as well as ‘how many?’” (Priem et al., 2010, o.e.)

First and maybe less surprising, application designers are called upon to realize the various technical possibilities ascribed to Altmetrics. Work must be invested to write the algorithms and build the systems that enable the above potentials. The AM opens a new field of work for information experts to engage in. At the same time Altmetrics potentiality attracts the attention of organizations interested in these potentials and willing to fund the necessary work. On the one hand, this may include those who capitalized on the academic settlement before and whose position is challenged by the AM’s critique and the rise of new (e-) valuative objects: Publishers and providers of citation databases who form large parts of the publication-citation-nexus. On the other hand, the manifesto’s borrowings from the Californian ideology open up market niches for both digital artisans and established players of the platform economy. Second, the call for researchers to invest themselves to Altmetrics – their time, resources, and conceptual work – aims to give substance and form to yet a vague idea. The curious thing is, that the enrolled audience, those expert in the existing methodology are in part the very experts whose conventions are so sharply criticized by the AM. Addressing someone as competent in a particular area of work leaves one with two options: Either to turn down the offer, which means to deny one’s competence and, even worse, leave the task to others. Or to accept the competence to handle the issue, which goes along with the responsibility to really do that work. It is not surprising then, that the harshest critics of Altmetrics are at the same time adding substance to this matter by the very means of their scrutiny (e.g. Haustein et al., 2016a, b; Haustein, 2016, 2016a; Robinson-Garcia et al., 2017). The last sentence of the quote relates precisely to Altmetrics’ future relation of meaning and relevance. The form investments by both app designers and researchers is believed to answer the question what altmetrics mean in due time. For the AM it is enough to maintain Altmetrics’ ability to measure impact. The potentiality and investment opportunity resulting from this ambiguity of meaning will eventually add substance to the matter.

Synthesis: holding numbers to account

After having explored the main motifs of the two manifestos’ (e-) valuation strategies, I have demonstrated the diametrical organization of these strategies. The AM and the LM contradict each other on two dimensions of contention. This section first reviews these issues and subsequently explains their interrelation from the perspective of accountability: Ultimately both manifestos relate to the question of who is competent to responsively (e-) valuate science.

A first dimension of contention could be reconstructed from the diametrical motifs of confinedness and enclosure. This dispute is about who legitimately (e-) valuates science and in what ways. The critiques put forth in the AM challenge the established academic settlement of this field by questioning the adequacy of conventions defining its reference spaces. By firstly developing new work tasks in the same area of work and secondly drawing on long-standing critiques of (e-) valuative practices, the AM alleges the incongruence of science (e-) valuation with what it is supposed to measure. Contrarily, by enclosing the legitimate use of metric indicators in particular contexts, the LM justifies the very conventions questioned by the accusation of confinedness. Only such enclosure could guarantee the congruence of measures with what is to be measured. Its ten principles represent an investment in form that makes manifest the just relation of evaluators and evaluated, established experts and newcomers, funders and justifiably fundable work. As conventions of equivalence the ten principles allow the numerical (quantity) and the narrative (quality) to co-exist and thus attempt to re-stabilize control over a contested field of work. This strategy of ligation, on the one hand, allows to distinguish adequate from inadequate forms of the craft. On the other hand, because this is based on criticism commonly directed toward bibliometrics, it enables immunization against critique from outside the established settlement.

The second dimension of contention is between the motifs of proliferation and expansion. Here, the dispute concerns the justness of metric indicators, more precisely the relation between their meaning and relevance. The AM equals the value of Altmetrics with their ability to reflect impact, i.e. the relevance of (e-) valuated objects. Yet, while impact is equaled with relevance, the AM does not address Altmetrics’ meaning. This ambiguity of meaning allows to ascribe Altmetrics with a whole range of different potentials. The potentiality of Altmetrics’ possible uses, in turn, goes hand in hand with opportunities of investment. Leaving open the question of meaning allows the AM to enrole different investors with the competence and responsibility to provide Altmetrics with substance and form. In the LM, by contrast, quality is of highest relevance and metrics should thus indicate quality. However, the question what quality means in particular contexts is externalized by enrolling contextual experts – those evaluated – as the guarantors of quality in their respective fields. This relation of quality, quantity, and the evaluated assures the position of expert evaluators who in turn ensure the general worth of metric indicators.

If contextual proficiency signifies meaning, the competence of expert evaluators is the reverse of the medal. As conventions of equivalence the ten principles of the LM guarantee that indicators generally reflect quality – as long as one accepts the value of expertise in research evaluation. Again, such competences come along with responsibility: Accepting the competence to justly delineate what matters to one’s field, makes one responsible to rightly guide evaluators in their tasks. In the LM, this nexus is used for an immunization against critique; external criticism is integrated into the worth order by making potential critics part of the process. The conceptual pair of competence and responsibility is addressed as accountability: “We offer this distillation of best practice in metrics-based research assessment so that researchers can hold evaluators to account, and evaluators can hold their indicators to account.“ (Hicks et al., 2015, p. 430). As can be seen from the discussion of transparency (cf. Section 3.3), accountability is of similar importance to the AM: Neither peer reviewers nor the corporate players of the publication-citation-nexus are held accountable for their actions. By contrast, open participation in Altmetrics promises the transparency to prevent gaming and to clearly show who is responsible for which expression.

Accountability, the nexus of competence and responsibility, provides the conceptual hinge between the manifestos’ two dimensions of contention: On the one hand the LM’s manifestation of conventions represents a claim to power. The ten principles are an attempt to consolidate the established conventions of expert research evaluation in order to regain control over the interdisciplinary settlement of that field. Enrolement, as in ascribing others a role in a certain course of action, makes the enrolled accountable within a resulting hierarchy of power. The evaluated can hold evaluators to account on the basis of manifest conventions. Yet, the former then have to accept the latter’s competence to evaluate them. Accountability qua enrolement here follows the principle divide et impera. On the other hand, this distribution of roles stabilizes the value of quantitative indicators by relating their meaning and relevance in an accountable way. Externalizing the meaning of indicators as the responsibility of contextual experts endows the general experts of research evaluation with the competence to ensure the general worth of research metrics as indicators of relevance. Accountability of both evaluators and their indicators justifies established forms of commensuration.

As for the AM, on the one side it challenges the conventions of research (e-) valuation by undermining the established distribution of competences and responsibilities. Broadening practices of metrification and (e-) valuation, involves the expansion of reference spaces, the expansion of both valued activities and evaluated objects, and the expansion of participation in Altmetric production and measurement. The misfit between existing means of science (e-) valuation and that, which is to be (e-) valuated, causes the unaccountability of the established settlement. The enrolement of a basically open number of non-experts represents an even further diffusion of expert research evaluation (as compared to its consolidation by established conventions). The expansion of both the measures and the personnel of metric (e-) valuation blurs the conventional boundaries of the field and thus threatens the cohesion of its settlement. On the other side, the AM enrolls particular audiences with particular competences. Application designers should develop the envisioned tools and researchers “must” ask, what kind of impact Altmetrics measure, i.e. what they mean. Accepting these competences assures these groups to take part in new work tasks that could potentially transform the academic field and its settlement. This potentiality that is enabled by Altmetrics’ ambiguity of meaning thus functions as a self-fulfilling prophecy. By being responsible for research on the subject, researchers put the weight of their names behind the object, moulding its form in the process. By virtue of scientific objectification, Altmetrics become things of relevance. By means of their conceptualization (e.g. Haustein et al., 2016a, b), they assume meaning. The established community has accepted the challenge; their form investments have added weight to Altmetrics. Thus, the settlement is in part accountable for its own transformation that is so forcefully criticized by the LM.

Conclusion

This article analyzed two manifestos in the field of metric science (e-) valuation. Manifestos matter because they are indications of crisis. They reliably occur in times of conflict and dispute. Manifestos both constitute a problem and provide a solution for that problem. The authors make every possible effort to demonstrate the gravity of the situation and convince their audience of the suggested change. Manifestos are expressions of too great a challenge to remain silent. In this sense they are not merely indications for but manifestations of crisis. The field of Bibliometrics and Scientometrics has recently experienced two such instances of critical discourse. The Altmetrics Manifesto (AM) challenges established means of science (e-) valuation, While the Leiden Manifesto (LM) argues for a return to established forms of the craft. As contrasting positions in a debate on the right means to evaluate science, they are worth a closer look. The two manifestos could be reconstructed along four motifs of critique and justification. These motifs are organized diametrically. The AM denounces the confinedness of the conventional forms of science evaluation. By contrast, the LM advocates the return to established conventions arguing for a rule-guided enclosure of metric indicators in particular contexts. To the LM the problem consists in the proliferation and pervasive misuse of research metrics. Conversely, the AM promotes a pervasive expansion in such metrics as the only means to make sense of the sheer volume of scholarly communication. This diametrality alone provides sufficient food for thought regarding the future orientation of the field. At best, it invites for reflexivity in the discourse on how we should (e-) valuate scientific practice.

In this contribution I have tried to make a first step in this direction: In an effort to make sense of the manifestos’ opposing (e-) valuation strategies, I have offered one possible interpretation of this dispute. Understanding the four motifs as lying on two dimensions of contention I argued, first, that the quarrel over the adequacy of conventions represented a competition over an academic area of work. The established field of Bibliometrics and Scientometrics represents an interdisciplinary settlement held together by agreed upon ways of doing the respective work (Abbott, 2001). As a ruler’s manifesto, the LM tries to justify these conventions by giving them the form of expert rules of conduct (Thévenot, 1984). By contrast, the AM as a subversive manifesto tries to destabilize the settlement by undermining the conventionalized space it rests upon (Desrosières, 1998). This dispute over who has the right to do (e-) valuative work and thus to control the field is connected to a second dimension of contention, the question what (e-) valuative metrics should measure. I have addressed this question by discussing how the two manifestos relate the meaning and relevance of numbers. To the LM, metrics are of relevance in so far as they indicate quality. However, the question what quality means in particular contexts, is given to the responsibility of those expert in the evaluated fields. In this way, all beings relevant – numbers, humans, abstract concepts, etc. – are integrated into an order of worth, that grants highest relevance to the experts of metric research (e-) valuation (Boltanski & Thévenot, 2006). As for the AM, the relevance of metrics is equaled to the measured relevance, i.e. impact, of the (e-) valuated objects. Here, the question of meaning remains unaddressed, which is linked to the manifesto’s aim of mobilizing form investments: Altmetrics’ ambiguity of meaning allows to ascribe them a variety of potential uses and this potentiality represents opportunities of investment. In a manner quite similar to the LM, the AM enrolls relevant audiences in its investment pitch, ascribing researchers the competence to delineate what Altmetrics could possibly mean. The manifestos’ dimensions of contention can be summarized as a dispute over the right means to establish accountability, the transparent distribution of competences and responsibilities. The LM tries to consolidate existing forms of (e-) valuation and to integrate evaluators and evaluated, the numerical (quantity) and the narrative (quality), in a worth order that sustains the elevated position of experts. The AM denounces this position and tries to replace it with the open participation of non-experts. It tries to diffuse established forms of science evaluation and to mobilize form investments that give substance to the concept of Altmetrics.

I have not touched on every single argument of the two manifestos. Analysis focused on topics, which are addressed in both texts and hence matter to their respective positioning. The goal of this article was to show that these positions exist and thus to reconstruct important aspects of a larger debate. These are not mere ratchet effects. As usual in science, the earlier is material for the latter. But the LM is not an open reply to the AM. Although sequence matters, the addressed discourses – transparency, quality, reactivity etc. – are not baked from scratch. It rather seems that the mirrored issues have been part of a conflict for some time before becoming part of a manifest crisis. The manifesto is of course only one type of text. The bulk of academic communication, including critical discourse, takes place in other formats. However, as extraordinary events referring to a crisis too large to be addressed in common form, manifestos reflect the weight of the expressed critique. Critique is an essential part of science. Yet, manifestos create addressability of position. It makes a difference whether to simply argue over a certain thing, even when arguing fiercely, or to provide potential followers with a reference point that subsumes their individual positions. This raises the question whether the two manifestos are nothing but power play without any meaning to the substantial discourse. While power certainly matters, it matters no less, what people argue about in order to maintain power. The dispute isn’t about a particular matter. It concerns the adequacy of fundamental practices. The academic field is held together by practice – and practices regarded as either vulnerable or worthy of protection provide insight into the condition of that field. Of course, the manifestos do not mirror actual practice, everyday business differs from idealized rules or prophetic visions. Yet, as reference points, they offer valuable resources for both levelling and defending against critique: It is unclear what Altmetrics indicate – yet, citations have the same problem, and Altmetrics are both faster and more diverse. Bibliometric measures have reactive effects – yet, sticking to the LM, such effects can be avoided. However, the manifestos are not merely intended for an external audience. The outside could ask, why the experts do not keep their promises. As manifestations of position, manifestos represent a commitment. In this sense, they may open up potentials (AM) or have disciplining effects (LM). The alternative would be to de-qualify the manifesto’s relevance. The opposite is the case: Both manifestos are at a premium; they are frequently referenced positions in the discourse on (e-) valuative metrics.

Practices of (e-) valuation stand both at the beginning and end of the two manifestos. On the one hand, they are causing the crisis: The current modus operandi is no longer sustainable. On the other hand, the manifesto outlines a transformed course of action. It provides a vantage point that connects what is and what ought to be and therefore provides empirical access to conceptions of the valuable. One position insists on discipline, the other puts weight on trial and experimentation. This opposition opens up a political dimension. Yet, the antagonism is in part an exaggeration. The established need to experiment too. Of course, the innovators try to establish conventions of their own. Both understand that established conventions are needed just as much as new forms of evaluation. Discipline is no less important than innovation. All four are needed, the point of contention lies in how to restrict them respectively. The established and the newcomers are bound together by objects and practices, both are part of the same field. What does this mean for the development of the academic settlement? Will the dispute result in a schism defined by a long-term crisis? Will the factions ignore each other or try to discredit the opponent? Or will the settlement be transformed by integrating the new practices? These questions cannot be answered by the present analysis. One future task is to study both the reception of the two positions and reactions to their respective arguments. Another task is to take a closer look at how the dispute transforms the practices of non-experts. How do scientists and organizations handle new metric indicators and how does this relate to existing forms of (e-) valuation? Both these approaches must ask how meaning and relevance are related to one another and thus constitute the value of metrics.

In this analysis, we have seen two ways of producing such a relation. This enables reflexivity on what the Scientometric community understands as quality in its own field. To the LM this quality depicts that which must necessarily be followed in order to avoid repercussions. Yet, the AM is not interested in such technical quality at all. Here the focus is on the utility of measures to reach certain ends – on pragmatism in the common sense of the word. This provides insight into how different perceptions of quality collide and how quality may be modified: By challenging established conventions and attracting investment for the establishment of new forms.