Abstract
In this paper a methodology for identifying and delineating spatial technology clusters based on patenting concentration is developed. The methodology involves the automated geocoding of patent inventor addresses, the application of a home bias correction factor and a sensitivity analysis to determine the optimal parameters of the kernel density estimation interpolation distance and the minimum concentration threshold to identify clusters. The methodology’s performance is compared to a number of other cluster identification methods and it is validated across 18 individual sectors, including mature broad-based high-technology sectors and emerging niche sustainable energy technology sectors. The results suggest that the performance of the methodology exceed that of alternative cluster identification methods, although there is some variation in performance between different sectors. This demonstrates that the methodology provides researchers, practitioners and policy makers with a useful tool to gain insight into the spatial distribution of sectoral innovation activity at a global scale and sub-national regional level and to monitor changes over time, thereby supplementing more readily available global statistical data which is available at the national level.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The innovation literature attaches significant importance to the sub-national regional scale, as well as global connections and competition between clusters (Fujita et al. 2001; Gertler and Wolfe 2006; Porter 2000; Simmie 2004). However global data sets at the sub-national level such as clusters are typically lacking. Even if sub-national administrative divisions are available, these may show a poor overlap with actual inventive activity (Alcácer and Zhao 2016; Van Egeraat et al. 2018). Furthermore, the spatial scale of sub-divisions can vary greatly from country to country, making international sub-national comparisons difficult. This creates a significant knowledge gap for researchers aiming to study cluster-based phenomena on a global scale.
The concept of a cluster is well defined in the literature (Marshall 1920; Nooteboom 2006; Porter 1998). Marshall (1920) defined industrial districts (clusters) as “concentration of specialized industries in particular localities”, which offer a number of specialization advantages to firms located there. Porter (1998) defines industry clusters as “geographic concentrations of interconnected companies and institutions in a particular field”. Other authors all emphasize spatial concentration as the key characteristic of technology clusters (Feldman and Kogler 2010; Malecki 2014; Malmberg and Maskell 2002; Nooteboom 2006; Spencer et al. 2010).
Patenting plays an important role in the innovation process because patents grant monopoly rights to inventors over a particular idea or design for a fixed period of time. Patent output is closely correlated to other measures of innovation activity such as R&D expenditure or the number of active researchers (Hagedoorn and Cloodt 2003; Lanjouw and Schankerman 2004; Squicciarini et al. 2013). Alcácer and Zhao (2016) therefore suggest that the spatial concentration of patenting is a clear indicator of a technology cluster’s existence.
This paper describes a new ‘organic’ (Alcácer and Zhao 2016) cluster identification methodology that uses heat maps (kernel density estimation) to identify ‘hot spots’ of innovation activity which are detected as cluster once they exceed a particular threshold. Heat maps are widely used in spatial analysis in fields as diverse as epidemiology, archaeology and transportation safety (Anderson 2009; Baxter et al. 1997; Bithell 1990), but they appear to be absent from scientific studies of innovation activity. This paper demonstrates that using heat maps is an effective way of identifying technology clusters and that the methodology’s performance exceeds that of alternative approaches.
The paper begins with a review of earlier studies in which patent data is used to identify technology clusters (“Cluster identification from patent data” section). This is followed by a detailed description of the methodology, including the process of geocoding patents (“Data and methodology” section). Thereafter a sensitivity analysis is carried out to discover suitable parameter values (“Calibration and sensitivity analysis” section). The methodology is then applied to eight emerging sustainable energy sectors and ten mature high-technology sectors to compare its effectiveness across different sector types (“Validation with multiple sectors” section). The paper ends with a discussion of the key findings, including sectoral differences in the methodology’s effectiveness (“Discussion and conclusion” section).
Cluster identification from patent data
Researchers of technology and innovation seeking to understand the spatial dynamics of innovation activity at a global scale on the sub-national regional level face significant challenges. While there is significant sub-national regional statistical data available for Organisation of Economic Cooperation and Development (OECD) member countries, this data typically excludes emerging sectors such as renewable energy technologies and fast-developing non-OECD countries in Asia and elsewhere. Furthermore, detailed statistics on technology and innovation for OECD countries tend to only be available at the national level and not at the sub-national regional level.
Databases from the World Bank and United Nations Education, Scientific and Cultural Organisation (UNESCO) tend to cover a greater number of countries, but do not provide sub-national data and often have more limited statistics on technology and innovation. This data deficit makes it difficult, if not impossible, to explore a sector’s true global spatial distribution.
Patents are frequently used as a proxy for innovation output, including at the sub-national level of regions or cities (Bergquist et al. 2017; Crescenzi and Jaax 2017). Patent data offers an opportunity to overcome the limitations of statistical data because patent data is global in scale and patents often contain geographical information such as an inventor address, which allows for the identification of a city or other sub-national spatial unit (Alcácer and Zhao 2016; Bergquist et al. 2017). Patents are the ‘paper trail’ of innovation activity (Jaffe et al. 1993) and patent data has been widely used in spatial studies of innovation since the 1990s, whereby patent counts typically serve as a proxy for innovation activity in a particular area or region (Acs et al. 2002; Crescenzi and Jaax 2017; De Rassenfosse and van de la Potterie 2009, p. @charlot2014; Ó hUallacháin and Leslie 2007). This makes patents a highly suitable data source to map global innovation activity at a sub-national scale.
One concern with the use of patent count data are the differences in patenting propensity between industry sectors (Arundel and Kabla 1998; Hall et al. 2005; Kleinknecht et al. 2002). Another concern is that there are also significant differences in patenting propensity between countries due to economic and governance factors (Bacchiocchi and Montobbio 2010; De Rassenfosse and van de la Potterie 2009; Yang and Kuo 2008). However these concerns have not stopped the wide use of patent data in technology and innovation research, including for the identification of spatial concentrations of innovation activity,
In the economic geography literature there are essentially two approaches to identifying the spatial concentration of innovation activity: (i) by measuring relative concentration within predefined spatial boundaries, and (ii) using the actual spatial concentration of specific points within a data set (e.g. plant locations, inventor locations, etc.) to define new boundaries of high spatial concentration (Clark and Wójcik 2018). This last methodology is also described as ‘organic’ cluster identification (Alcácer and Zhao 2016).
The first approach is to identify clusters using pre-existing statistical boundaries such as: states, Metropolitan Statistical Areas (MSA, United States), Nomenclature of Territorial Units for Statistics (NUTS, European Union), statistical divisions and subdivisions (Australia), prefectures (Japan), departments (France), etc. The use of pre-existing boundaries has advantages and disadvantages. The advantage of pre-existing boundaries is that scientometric data can be coupled to other statistical data such as R&D expenditure, labor market information, income levels, etc. For that reason Ó hUallacháin and Leslie (2007), Spencer et al. (2010) and Charlot et al. (2014) all utilize pre-existing regional boundaries to identify concentrations of industry or innovation activity.
The disadvantage of using pre-existing boundaries is that the scales of the statistical boundaries can vary significantly, especially when international comparisons are attempted (a ‘province’ in China is many times larger than a ‘province’ in the Netherlands or South Korea). Furthermore, a concentration of R&D activity may spill over into multiple pre-existing boundaries, or occupy just a small part of a pre-existing boundary, which can dilute the concentration of innovation activity for the area(s) within the pre-existing boundary.
An alternative to using pre-existing statistical or administrative boundaries is to use an organic cluster identification methodology that delineates cluster boundaries based on the actual concentration of patenting. The organic approach is especially advantageous in international research because it overcomes the challenge of using differing statistical boundary sizes for different countries. The approach also avoids potential dilution or distortions due to the use of inappropriate boundaries (Alcácer and Zhao 2016; Van Egeraat et al. 2018).
Assuming the organic clustering approach is based on patent data, the use of patent data in a global cluster identification exercise suffers from its own set of complications: (i) patent data carries a home bias effect, whereby patents and patent citations of patents invented in the home country are inflated in the home country patent database (Bacchiocchi and Montobbio 2010; van de la Potterie and De Rassenfosse 2008). Thus patents by American inventors occur more frequently and are cited more highly on average in the United States Patent and Trademark Office (USPTO) database than patents from foreign inventors. Second, R&D activity tends to follow patterns of urbanization which can yield very large urban corridors, such as from Boston to Philadelphia via New York (United States), Tokyo-Nagoya (Japan) and even Cologne-Frankfurt-Zurich (Europe) (Stek 2019), which stretch the definition of ‘spatial proximity’ and thus what constitutes a cluster.
To test the performance of their organic clustering algorithm, Alcácer and Zhao (2016) propose a useful benchmark. They observe which percentage of co-inventors who are located within 10–20 mi (16–32 km) from each other are classified as being within the same cluster and which percentage of co-inventors located more than 20 mi (32 km) apart, are classified as being in different clusters. While the 16 and 32 km distances are somewhat arbitrary, it does provide a common benchmark for comparing the performance of different clustering methodologies, including both pre-existing boundaries and organic cluster boundaries. Therefore this cluster performance benchmark is used in the sensitivity analysis (“Calibration and sensitivity analysis” section) and in evaluating the performance of the clustering methodology across different sectors (“Validation with multiple sectors” section).
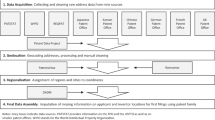
Data and methodology
In this study patent data is obtained from the PatentsView database which is published by the Office of Chief Economist in the United States Patent and Trademark Office (USPTO) and contains data on 6,647,699 patent grants from the USPTO (May 2018 edition).Footnote 1 Because of the delay between patent application and grant, the most recent year for which full patent grant data is available is 2011 (as at time of writing). As the United States is a large and open economy, many foreign entities also apply for patent protection at the USPTO, and therefore the PatentsView database provides the most extensive global coverage of patents among national (incl. European) patent databases (Kim and Lee 2015). The choice of a single patent database means that some form of home bias adjustment needs to be made. On the other hand, the advantage of using a single source of patents means that all patents are granted in accordance to a single standard, improving the validity of making international comparisons (Toivanen and Suominen 2015).
An alternative to using a single-country database like the USPTO is to use ‘triadic patents’. Triadic patents appear in all three major patent databases and have been granted by the USPTO, European Patent Office (EPO) and the Japan Patent Office (JPO). This approach appears to eliminate any home-bias effect, but the number of patents that are triadic is very small, as only the most valuable patents are filed at all three patent offices (Criscuolo 2006). Therefore significant patenting activity can go undetected, especially innovation activity from emerging countries where patent quality is often lower (Frietsch and Schmoch 2009). As an example, an emerging economy such as India had 2669 patent grants at the USPTO (2016) but only 359 triadic patents (13%) in the same year (source: OECD).
Other multi-country patent databases such as the Patent Cooperation Treaty (PCT) database also carry a degree of bias, notably the higher presence of South Korean, Japanese and Chinese patents due to different rules for patent approval in those countries (Boeing et al. 2016; Laurens et al. 2015). This is problematic for the purposes of identifying and quantifying technology clusters because it overstates the cluster size in some countries. The PCT database also appears to exclude Taiwan, which is not a signatory to the PCT (Bergquist et al. 2017).
For the purposes of identifying clusters worldwide, the increased coverage of the USPTO database makes it the preferred choice.
The USPTO PatentsView database contains basic bibliographic information of patent documents such as patent identification numbers, application dates, inventors and assignees, the city, state and country of inventors and assignees, and patent citations, along with technological classifications. The patent inventor and assignee addresses and technological classifications are essential for the cluster identification process. The technological classifications link a patent to a particular industry based on a concordance table (discussed in “Sectoral delineation” section). The address enables the identification of a geographic location of where the inventive activity took place that led to the patent application.
All data processing, calculations and spatial analysis are performed using a combination of R statistical software (R Core Team 2019), MySQL database software (Widenius et al. 2002) and QGIS spatial analysis software (QGIS Development Team 2019).
Patent geocoding
In deciding which address to use to identify clusters, the choice of inventors (individuals who carried out the R&D) rather than assignees (typically firms that financed the R&D) is not trivial. Inventors’ location provides information about where the R&D took place whereas the assignee location provides information about who owns the inventions. Given the globalization of R&D activity, assignees and inventors are frequently found in different countries. Assignees may be based in tax havens such as the British Virgin Islands or Cayman Islands, which have very small economic and R&D activity (Sung et al. 2014). Inventor locations are commonly used to locate innovation activity (Acs et al. 2002; Crescenzi and Jaax 2017; De Rassenfosse and van de la Potterie 2009, p. @charlot2014).
To identify areas of high R&D activity, inventor address information is converted into coordinates through a geocoding process. For example, the address ‘Delft, The Netherlands’ is converted into the coordinates 51.9995142, 4.2938295.
Although the PatentsView database does provide coordinates for patent addresses, upon closer examination a number of these appear to be inaccurate because the coordinates are located in a different country than the address or the coordinates are only geolocated at the country or state level, and not at that of a town or city. This is a problem in larger countries where the state or country can cover a very large area. For this reason approximately 6.5% of PatentsView addresses are geocoded again, a process carried out in three steps, described in Table 1.
The combination of geocoding techniques described in Table 2 raises the number of addresses that can be accurately located from 93 to 96%.
As an added screening, clusters identified in areas with no significant population center are subject to additional scrutiny and often lead to the identification of miscoded locations (false positives). This problem seems to occur primarily in South Korea and Japan where 11 miscoded locations are identified, including Daejeon, Yokkaichi, Kurashiki, Nara, Sendai, Kanagawa and Tochigi. These miscoded locations are manually corrected in the geolocation database.
After geolocating inventors, each identified location \(i\) receives a weighting (\(PTW_{i}\)) based on the number of inventors with an address in a location (\(INV_{ij}\)) divided by the number of inventors of the patent (\(INVT_{j}\)), which is then summed for all patents \(k\) at location \(i\). Thus:
An example of the calculation: a patent with 3 inventors, 2 of whom have an address in ‘Delft, The Netherlands’ would therefore add a weighting of \(2/3 = 0.67\) to the location of ‘Delft, Netherlands’ (51.9995142, 4.2938295).
Home bias correction
When calculating location-based weightings, it is important to address the home bias inherent in the USPTO patent data. The home bias of the USPTO data means patents with inventors located in the United States are over represented in terms of the number appearing in the database and the number of citations per patent (Bacchiocchi and Montobbio 2010; van de la Potterie and De Rassenfosse 2008).
The home bias is addressed by correcting the patenting frequency of non-United States invented patents which appear underrepresented in the USPTO database. Therefore a patent output correction factor is applied, \(COR_{PAT}\).
The correction factor is calculated by comparing United States-invented patents to Japan-invented patents in the USPTO database. Japan is chosen because its qualitative patenting profile is the most similar to the United States compared to all other countries (Mancusi 2008; Toivanen and Suominen 2015). Therefore differences between Japan and United States-invented patents can be attributed primarily to the home bias effect, rather than to other technological or economic factors. If another country were used in the comparison with the United States, differences in patenting behavior because of technological or economic factors could be wrongly attributed to home bias, thus reducing the accuracy of the correction factor.
The correction factor is calculated based on national averages to increase robustness and avoid potential sectoral distortions. Although Japan and the United States have a relatively similar national technological profile, basing the correction factor on a single sector can potentially distort the correction factor if a significant innovation gap exists between the two countries in that particular sector.
The patent output correction factor (\(COR_{PAT}\)) is based on a comparison of the ratio of researchers to patent output for Japan and the United States. If there is no home bias effect, advanced economies with a comparable qualitative patenting profile should have a very similar ratio of patent output to researchers because the same inputs (researchers) should lead to similar outputs (patents). \(COR_{PAT}\) is calculated as follows:
whereby \(PAT_{US}\) is total number of United States-invented patents, \(RES_{US}\) is the total number of researchers in the United States, \(PAT_{Japan}\) is the total number of Japan-invented patents and \(RES_{Japan}\) is the total number of researchers in Japan. The number of researchers and USPTO patent count data (by inventor residence) are obtained from the UNESCO Institute of StatisticsFootnote 2 and the USPTO PatentView database, respectively.
Calculated values of the correction factor are given for four periods, as shown in Table 2. The values show a discernible trend of falling home bias in the patent output correction factor (\(COR_{PAT}\)). This trend is also visible when the coefficients are calculated on an annual basis, or when using data for other countries (Germany, South Korea, Taiwan) and therefore these changes appears to be systematic, although the causes are unknown.
Because of this trend, different correction factor values should be used for different periods. The correction is made by multiplying non-United States patent counts by the correction factor.
Sectoral delineation
The ability to spatially identify and delineate technology clusters from patent data can be combined with a sectoral delineation, providing insight into where technology clusters are located. Industry sectors typically incorporate multiple technologies (Pavitt 1984), and therefore industry inventive activity can be mapped based on a selection of patents covering a particular set of technological fields. There are a number of different ways in which sector patents can be delineated.
First, it is possible to identify sectors based on a patent technological classifications. For example the OECD has identified biotechnology and nanotechnology as important emerging technologies whose development it monitors using patent data with a specific International Patent Classification (IPC) code (OECD 2013).
Second, in some cases it is possible to use special sectoral-technological patent classifications. The PatentsView database contains various technological classifications, including the IPC and the relatively new Collaborative Patent Classification (CPC, Leydesdorff et al. 2014). The CPC is a joint initiative of the USPTO and EPO and includes additional technology classes for renewable energy technologies and other green house gas reducing inventions (Y-classes) that are not included in the IPC. Technological classes are assigned by patent examiners at the respective patent office at which the patent is filed.
Third, patents that belong to a particular industry can be identified using concordance tables that link industry classes to technological classes such as the CPC. Using a probabilistic methodology based on text mining, Lybbert and Zolas (2014) have developed technology-industry concordance tables that incorporate multiple levels of industry and technological classifications, including for the CPC with the International Standard Industry Classification (ISIC). ISIC is a classification maintained by the United Nations Department of Economic and Social Affairs Statistics Division (UNSD) in New York and is used by countries to classify economic activity and collect economic statistics. The ISIC system consists of multiple industry groups and (sub)divisions, including a number of mature high technology sectors such as electronics, computers, chemicals, aerospace, etc. (Galindo-Rueda and Verger 2016). The advantage of the ISIC classification is that it allows patents to be linked to economic statistics which also follow the ISIC classification.
The high-technology ISIC sectors, biotechnology, nanotechnology and emerging sustainable energy technologies and their respective identification classes are listed in Table 3.
Calibration and sensitivity analysis
Once patent counts for specific locations are known (see “Patent geocoding” section), and the patent output correction factor has been applied (see “Home bias correction” section), clusters can be identified using the heatmap approach. Formally known as Kernel Density Estimation (KDE) (Parzen 1962; Rosenblatt 1956), heat maps are a spatial interpolation technique that assigns areas with frequent and high occurrences of a phenomenon (e.g. high prices, high temperatures, high crime rates, high occurrence of a particular disease) with high values, so-called ‘hotspots’. In this study the heatmap KDE is carried out on a raster with squares of 5 km by 5 km covering the entire world.
The heatmap method appears to offer some important advantages over the cluster identification method used by Alcácer and Zhao (2016). Firstly, Alcácer and Zhao (2016) appear to have gone through a process of assigning patent addresses to particular cities and then combining cities that are in close proximity (less than 40 mi or 64.4 km) into the same cluster. The KDE method skips the need to assign an address to a city as the weightings of nearby locations are combined, thus neighborhoods, neighboring cities, adjacent villages or a university campus are automatically interpolated into one ‘hotspot’. The KDE method is also less rigid than a fixed 64.4 km boundary, using interpolations instead.
When applying the KDE method decisions must be made about two important variables: the interpolation range (\(R\)) and the concentration threshold (\(T\)) for recognizing an area as being of ‘high concentration’ and thus part of a technology cluster. The interpolation range can be decided based on several criteria, for example Van Egeraat et al. (2018) uses commuting distance while Alcácer and Zhao (2016) uses 20 mi (32 km, without any justification given). Acs et al. (2002) notes that within a 50 mi (80.5 km) distance from the boundaries of a metropolitan statistical area, there is still some positive innovation effect. The distance cited by Acs et al. (2002) is about four times the largest average daily commuting distance of a US city (Atlanta, GA, average commuting distance of 20.6 km) (Kneebone and Holmes 2015). There is thus no clear guidance from the literature about the ‘correct’ interpolation range.
To classify an area as part of a cluster, the intensity of inventive activity must be within the upper percentiles of global R&D activity. However determining where to set this limit is subjective: should it be at the 90th, 95th or 97.5th or at an even higher percentile threshold? Once again, the literature offers no strong clues.
Therefore, to determine a suitable interpolation distance (\(R\)) and threshold value (\(T\)) a sensitivity analysis is carried out. The cluster spatial distributions that come out of this sensitivity analysis are evaluated based on three criteria.
-
(i)
the maximum cluster size (\(A_{max}\)) should not exceed the size of a large urban area. Very large clusters suggest that the interpolation distance is too great or the threshold value is too low ‘sticking’ multiple urban areas together. This situation can occur in urbanized and R&D intensive parts of the world such as Western Europe, New England, South Korea and Japan where giant ‘clusters’ that encompass whole or even multiple countries can appear (Stek 2019). To gain an idea of a ‘reasonable’ urban area size, see the areas of selected large urban areas in Table 4.
Table 4 Selected major urban areas -
(ii)
to measure the performance of the cluster identification methodology, patent co-inventors close together should be identified as being in the same cluster whereas those located further apart should be identified as being in different clusters. In their paper on identifying clusters from patent data, Alcácer and Zhao (2016) calculate the share of patents with co-inventors located 16–32 km apart within the same cluster (\(D_{same}\)) and the share of patents with co-inventors located more than 32 km and located in different clusters (\(D_{dif}\)). A high value for both indicators suggests the cluster spatial distribution in question is of high quality. The values for \(D_{same}\) and \(D_{dif}\) calculated by Alcácer and Zhao (2016) are listed in Table 5. The best-performing cluster boundaries are those for Organic Clustering (world).
Table 5 Performance measures of cluster identification methods, selected (Alcácer and Zhao 2016) -
(iii)
the number of clusters (\(n\)) identified is an important criterion to evaluate the cluster spatial distribution because a method that identifies only a small number of clusters is likely blind to many smaller or emerging clusters, rendering the cluster identification process incomplete.
The sensitivity analysis is carried out using patent data for all sectors for the 2008–2011 period with the patent output correction factor (\(COR_{PAT}\)) applied to all patent inventor locations outside the United States. The results of the sensitivity analysis are provided in Table 6.
Assessing the sensitivity analysis results based on the first criterion, the largest cluster area (\(A_{max}\)), shows that when \(T\) = 90% or \(R\) = 50 km very large cluster areas are identified which exceed the size of typical large urban areas (Table 7). The smallest value for \(A_{max}\) = 45,413 km2 (\(R\) = 50 km, \(T\) = 99%) is larger than the urban areas centered on New York and Guangzhou. Other distance-threshold combinations also show \(A_{max}\) values that seem excessively large, including \(R\) = 25 km with \(T\) = 95%, and \(R\) = 32 km and \(T\) = 97.5%. At these combinations of interpolation distance and concentration thresholds unrealistically large technology clusters are identified.
Assessing the sensitivity analysis results based on the second criterion, the performance of the cluster identification algorithm, reveals an interesting trend: results where \(R\) = 25 or 15 km have a less than 100% value for \(D_{same}\), suggesting that some of the identified clusters are ‘too small’ as inventors located nearby fall outside of the cluster boundaries. The combinations with the highest cumulative cluster performance value (\(D_{same} + D_{dif}\)) and a \(D_{same}\) value of at least 99% are \(R\) = 25 km and \(T\) = 97.5% or 99%, with a cumulative cluster performance value of 165% and 166%, respectively.
When comparing the two aforementioned cluster distributions, \(T\) = 97.5% yields a significantly larger number of clusters (\(n\) = 355) than the \(T\) = 99% alternative (\(n\) = 169). Therefore the former (\(R\) = 25 km, \(T\) = 97.5%) is considered as the optimum heatmap cluster identification parameters.
Compared to the organic clustering method by Alcácer and Zhao (2016), the heatmap method with optimum parameters compares favorably in terms of \(D_{dif}\), where \(D_{dif}\) = 66% for the heatmap method, compared to \(D_{dif}\) = 59% for the organic method by Alcácer and Zhao (2016). However \(D_{same}\) = 99% for the heatmap method, compared to \(D_{dif}\) = 100% for the organic method. Although it is important to note that Alcácer and Zhao (2016) use semiconductor patents for a different time period, whereas the heatmap cluster identification methodology is applied to patents from all sectors.
The smallest technology clusters identified using the optimum heatmap method (\(R\) = 25 km, \(T\) = 97.5%) are 50 km2. The largest clusters are centered on New York City (32,972 km2), Tokyo (15,941 km2), Los Angeles (12,723 km2) and San Francisco (11,733 km2). Although this large range in sizes might challenge the traditional conception of how a cluster should be defined, when the cluster areas are placed on a logarithmic scale, they are normally distributed.
Some sample heatmaps with cluster boundaries are provided in the “Appendix”.
Validation with multiple sectors
Having calibrated the heatmap cluster identification method with the most promising interpolation distance and threshold parameters, the same methodology (with the same parameters) is now applied to 18 different sectors. Because the cluster identification method is largely automated, producing data on the global distribution of sectoral clusters is relatively fast. An overview of the key cluster indicators for each sector are provided in Table 7. In addition to the maximum cluster area (\(A_{max}\)), share of co-inventors located 16–32 km apart within the same cluster (\(D_{same}\)) and the share of patents with co-inventors located more than 32 km and located in different clusters (\(D_{dif}\)), the total number of patents from the sector (\(P_{total}\)), the share of patents located in clusters (\(PS_{cluster}\)) and the average collaboration distance (\(CD\)) are also shown.
The cluster identification performance results show considerable variation between sectors. While most sectors perform well in terms of \(D_{same}\), there is a group of sectors (Defense, Biotechnology, Hydrogen technology, Photovoltaics, Smart grids and Wind turbines) which have a value of \(D_{same}\) < 98% and a clustering share of \(PS_{cluster}\) < 50%. However some of these sectors have high \(D_{dif}\) values, typically above 80% (Biotechnology, Hydrogen Technology and Wind Turbines), while others do not (Defense, Photovoltaics and Smart Grids).
The mature high technology sectors typically have a high clustering share (\(PS_{cluster}\) > 60%), \(D_{same}\) > 98% and \(D_{dif}\) > 60%, with the exception of some of Machinery and equipment and Motor vehicles, which show a lower figure for \(D_{dif}\).
A lower value for \(D_{same}\) implies a greater number of false negatives, whereby a nearby inventor was excluded from a cluster. A lower value for \(D_{dif}\) implies a greater number of false positives, whereby an inventor at more than 32 km away is nevertheless included in the cluster. In theory both indicators would have values of close to 100% if the collaboration distance between inventors is well below 32 km or many times greater than 32 km so that false positives and false negatives are unlikely to occur (a high spatial concentration linked to long-distance networks). One would expect a higher value for \(D_{same}\) if the sector is spatially concentrated (coinciding with a high \(PS_{cluster}\) value) and a high value for \(D_{dif}\) if the average collaboration distance (\(CD\)) is high.
Based on the above considerations the sectors can be classified based on their spatial distribution and collaboration typologies and the performance of the cluster identification method.
The first typology are sectors which have a high spatial concentration (\(PS_{cluster}\) > 50%) and which collaborate over long distances (\(CD\) > 900 km), thus yielding few false negatives (\(D_{same}\) > 98%) and few false positives (\(D_{d} if\) > 60%). Type 1 sectors include mostly mature high-technology sectors including Aerospace, Chemicals, Computers, Electrical equipment and Pharmaceuticals, and the emerging Nanotechnology and Fuel cells sectors.
The second typology are sectors which have a high spatial concentration (\(PS_{cluster}\) > 50%) but which collaborate over shorter distances (\(CD\) < 1000 km), thus yielding few false negatives (\(D_{same}\) > 98%) but relatively many false positives (\(D_{d} if\) < 60%). Type 2 sectors include Machinery, Motor vehicles and Electric vehicles.
The third typology are sectors which are spatially distributed (\(PS_{cluster}\) < 50%) and which collaborate over very long distances (\(CD\) > 1100 km). This spatial configuration yields an increase in false negatives (\(D_{same}\) < 99%) but a much lower than average rate of false positives (\(D_{dif}\) > 85%). Type 3 sectors include Biotechnology, Hydrogen technology and Wind turbines.
The fourth typology are sectors which are spatially distributed (\(PS_{cluster}\) < 50%) and which collaborate over relatively shorter distances (\(CD\) < 1100 km), a pattern that produces both high false negatives (\(D_{same}\) < 98%) and high false positives (\(D_{dif}\) < 98%). Type 4 sectors include Defense, Energy storage, Photovoltaics and Smart grids.
The sector typologies are summarized in Table 8.
The sector typologies summarized in Table 8 show that there are different degrees of spatial concentration and long-distance collaboration depending on the sector. This adds nuance to the observation that innovation activity, like other high value-added economic activities, has a high degree of spatial concentration and is globally inter-connected (Fujita et al. 2001; Malecki 2014). The results show that there is considerable variation between sectors.
A second implication of the observed sectoral differences is that the parameters of the heatmap cluster identification methodology could be re-calibrated for different sector typologies to improve the performance of the methodology, which is especially low for type 4 sectors. On the other hand, the use of different heatmap cluster identification parameters may complicate cross-sectoral comparisons.
On a final note regarding the sectoral results, it is important to highlight that the work of Alcácer and Zhao (2016) is based on the semiconductor sector, which is a significant part of the Computer, electronic and optical products sector (Table 8). For this sector the heatmap methodology performs slightly better than the results for semiconductors from Alcácer and Zhao (2016), showing the same values for \(D_{same}\) and a slightly higher value for \(D_{dif}\) of 62% (compared to 59%, see Table 6). Based on this comparison the heatmap methodology appears to slightly out-perform the organic clustering methodology.
Discussion and conclusion
Although the focus of this paper is primarily methodological, some theoretical questions concerning differences in sectoral spatial distribution and collaboration have inadvertently been raised. These sectoral differences can be attributed to differences in the innovation process, which in turn can be linked to underlying differences in a sector’s knowledge base, institutions and market structure (Asheim and Coenen 2005; Binz and Truffer 2017; Breschi and Malerba 1997).
This demonstrates the value of the methodology, as it allows the spatial distribution of different sectors to be mapped and compared at the sub-national regional level and on a global scale. The richness of patent data also means that the identified clusters can be characterized in terms of the actors involved in the innovation activity (Bhattacharya 2004), collaboration relations (Kwon et al. 2012; Zheng et al. 2014), their longitudinal development (Dong et al. 2012), innovation capabilities (Wu 2014), etc. This creates a rich source of data for future research.
The main advantages of the methodology are that basing cluster delineation on real innovation activity offers a more accurate delineation of innovation activity as compared to using pre-defined boundaries and that the methodology can be applied across multiple countries. Although the heatmap methodology shows slightly better results than the organic method of Alcácer and Zhao (2016), the studies use somewhat different data, and therefore the earlier result primarily serves as a useful benchmark, against which the results of this study compare quite favorably.
The method presented here is also highly automated. No adjustments are made for commuting distances in densely populated areas nor are significant manual interventions undertaken to locate patents. The geocoding process is automated, a single patent frequency correction factor is calculated and the generation of heatmaps and calculation of concentration thresholds is all standardized. Nevertheless the methodology’s performance seems to approach or even exceed that of Alcácer and Zhao (2016). While there may be some inaccuracies due to automation, the benefits of automation is that 18 sectors (or many more) can be analysed quickly, and the method is therefore also very suitable for longitudinal studies. To illustrate the difference in scale between the two studies: Alcácer and Zhao (2016) used 23,675 unique patents, whereas in the present study for the Computer, electronics and optical products sector alone, 326,316 patents were included.
The relative ease with which technology clusters from different sectors can be identified allows the global monitoring of technology clusters over time. In fact patent applications (instead of patent grants) could be used to monitor the most recent development of technology clusters. Such monitoring could help practitioners and policy makers identify where innovation is taking place, compare different clusters, observe changes over time and use other patent indicators to identify key innovation actors and observe research collaborations. This information could be used for benchmarking purposes, to identify potential markets for high technology products, to identify potential locations for R&D investment, to identify prospective research partners, etc.
Despite these possibilities some questions concerning cluster identification from patent data still remain. First, the heatmap interpolation range and cluster concentration threshold parameters can be re-calculated for each sector to account for differences in their spatial distribution and collaboration distances. Whether such sector-based calibrations are appropriate would depend on the research aims.
Second, there could be differences in outcomes if another patent database is used: the size of certain clusters might be estimated differently and the correction factor that is applied can be implemented based on the number of researchers, research expenditure, or another indicator. Stated differently: USPTO patenting may not tell a complete picture of innovation activity for all sectors and countries and a single correction factor may be too broad.
Third, different kinds of interpolation techniques could be explored in addition to the standard KDE applied in this research and the performance of the cluster identification methodology could be evaluated based on different parameters.
Notes
The PatentsView database tables can be downloaded at: http://www.patentsview.org/download/ (accessed 24 March 2019).
Database titled ‘Science, technology and innovation: Gross domestic expenditure on R&D (GERD), GERD as a percentage of GDP, GERD per capita and GERD per researcher’ is available from: http://data.uis.unesco.org/ (last accessed 1 October 2019).
References
Acs, Z. J., Anselin, L., & Varga, A. (2002). Patents and innovation counts as measures of regional production of new knowledge. Research Policy, 31(7), 1069–1085.
Alcácer, J., & Zhao, M. (2016). Zooming in: A practical manual for identifying geographic clusters. Strategic Managment Journal, 37(1), 10–21.
Anderson, T. K. (2009). Kernel density estimation and k-means clustering to profile road accident hotspots. Accident Analysis and Prevention, 41(3), 359–364.
Arundel, A., & Kabla, I. (1998). What percentage of innovations are patented? Empirical estimates for european firms. Research Policy, 27(2), 127–141.
Asheim, B. T., & Coenen, L. (2005). Knowledge bases and regional innovation systems: Comparing nordic clusters. Research Policy, 34(8), 1173–1190.
Bacchiocchi, E., & Montobbio, F. (2010). International knowledge diffusion and home-bias effect: Do uspto and epo patent citations tell the same story? Scandinavian Journal of Economics, 112(3), 441–470.
Baxter, M. J., Beardah, C. C., & Wright, R. V. (1997). Some archaeological applications of kernel density estimates. Journal of Archaeological Science, 24(4), 347–354.
Bergquist, K., Fink, C., & Raffo, J. (2017). Identifying and ranking the world’s largest clusters of inventive activity’. In The Global Innovation Index 2017: Innovation Feeding the World, pp. 161–176.
Bhattacharya, S. (2004). Mapping inventive activity and technological change through patent analysis: A case study of India and China. Scientometrics, 61(3), 361–381.
Binz, C., & Truffer, B. (2017). Global innovation systems: A conceptual framework for innovation dynamics in transnational contexts. Research Policy, 46(7), 1284–1298.
Bithell, J. F. (1990). An application of density estimation to geographical epidemiology. Statistics in Medicine, 9(6), 691–701.
Boeing, P., Mueller, E., & Sandner, P. (2016). China’s r&D explosion—Analyzing productivity effects across ownership types and over time. Research Policy, 45(1), 159–176.
Breschi, S., & Malerba, F. (1997). Sectoral innovation systems: Technological regimes, schumpeterian dynamics, and spatial boundaries. In C. Edquist (Ed.), Systems of innovation: Technologies, institutions and organizations (pp. 130–156). London: Pinter.
Charlot, S., Crescenzi, R., & Musolesi, A. (2014). Econometric modelling of the regional knowledge production function in europe. Journal of Economic Geography, 15(6), 1227–1259.
Clark, G. L., & Wójcik, D. (2018). The new Oxford handbook of economic geography. Oxford: Oxford University Press.
Crescenzi, R., & Jaax, A. (2017). Innovation in Russia: The territorial dimension. Economic Geography, 93(1), 66–88.
Criscuolo, P. (2006). The ‘home advantage’ effect and patent families. A comparison of OECD triadic patents, the USPTO and the EPO. Scientometrics, 66(1), 23–41.
De Rassenfosse, G., & van de la Potterie, B. P. (2009). A policy insight into the R&D–patent relationship. Research Policy, 38(5), 779–792.
Dong, B., Xu, G., Luo, X., Cai, Y., & Gao, W. (2012). A bibliometric analysis of solar power research from 1991 to 2010. Scientometrics, 93(3), 1101–1117.
Feldman, M. P., & Kogler, D. F. (2010). Stylized facts in the geography of innovation. In Handbook of the economics of innovation (Vol. 1, pp. 381–410). Elsevier.
Frietsch, R., & Schmoch, U. (2009). Transnational patents and international markets. Scientometrics, 82(1), 185–200.
Fujita, M., Krugman, P. R., & Venables, A. J. (2001). The spatial economy: Cities, regions, and international trade. Cambridge: MIT Press.
Galindo-Rueda, F., & Verger, F. (2016). OECD taxonomy of economic activities based on r&D intensity (OECD science, technology and industry working papers No. 4) (Vol. 2016). Paris: OECD Publishing.
Gertler, M. S., & Wolfe, D. A. (2006). Spaces of knowledge flows: Clusters in a global context. In B. Asheim, P. Cooke, & R. Martin (Eds.), Clusters and regional development (pp. 218–235). London: Routledge.
Hagedoorn, J., & Cloodt, M. (2003). Measuring innovative performance: Is there an advantage in using multiple indicators? Research Policy, 32(8), 1365–1379.
Hall, B. H., Jaffe, A., & Trajtenberg, M. (2005). Market value and patent citations. RAND Journal of Economics, 36, 16–38.
Hamstead, Z. A., Fisher, D., Ilieva, R. T., Wood, S. A., McPhearson, T., & Kremer, P. (2018). Geolocated social media as a rapid indicator of park visitation and equitable park access. Environment and Urban Systems: Computers.
Jaffe, A. B., Trajtenberg, M., & Henderson, R. (1993). Geographic localization of knowledge spillovers as evidenced by patent citations. The Quarterly Journal of Economics, 108(3), 577–598.
Kim, J., & Lee, S. (2015). Patent databases for innovation studies: A comparative analysis of USPTO, EPO, JPO and KIPO. Technological Forecasting and Social Change, 92, 332–345.
Kleinknecht, A., Van Montfort, K., & Brouwer, E. (2002). The non-trivial choice between innovation indicators. Economics of Innovation and New Technology, 11(2), 109–121.
Kneebone, E., & Holmes, N. (2015). The growing distance between people and jobs in metropolitan America. Washington, DC: The Brookings Institution.
Kwon, K.-S., Park, H. W., So, M., & Leydesdorff, L. (2012). Has globalization strengthened South Korea’s national research system? National and international dynamics of the triple helix of scientific co-authorship relationships in South Korea. Scientometrics, 90(1), 163–176.
Lanjouw, J. O., & Schankerman, M. (2004). Patent quality and research productivity: Measuring innovation with multiple indicators. The Economic Journal, 114(495), 441–465.
Laurens, P., Le Bas, C., Schoen, A., Villard, L., & Larédo, P. (2015). The rate and motives of the internationalisation of large firm R&D (1994–2005): Towards a turning point? Research Policy, 44(3), 765–776.
Leydesdorff, L., Alkemade, F., Heimeriks, G., & Hoekstra, R. (2014). Geographic and technological perspectives on “photovoltaic cells:” Patents as instruments for exploring innovation dynamics. Internetquelle: http://arxiv.org/abs/1401.2778 (03.08. 2014).
Lybbert, T. J., & Zolas, N. J. (2014). Getting patents and economic data to speak to each other: An “algorithmic links with probabilities” approach for joint analyses of patenting and economic activity. Research Policy, 43(3), 530–542.
Malecki, E. J. (2014). The geography of innovation. In M. Fischer & P. Nijkamp (Eds.), Handbook of regional science (pp. 375–389). Berlin: Springer.
Malmberg, A., & Maskell, P. (2002). The elusive concept of localization economies: Towards a knowledge-based theory of spatial clustering. Environment and Planning A: Economy and Space, 34(3), 429–449.
Mancusi, M. L. (2008). International spillovers and absorptive capacity: A cross-country cross-sector analysis based on patents and citations. Journal of International Economics, 76(2), 155–165.
Marshall, A. (1920). Principles of economics (8th ed.). London: Macmillan; Co.
Nooteboom, B. (2006). Innovation, learning and cluster dynamics. In B. Asheim, P. Cooke, & R. Martin (Eds.), Clusters and regional development (pp. 155–181). London: Routledge.
Ó hUallacháin, B., & Leslie, T. F. (2007). Rethinking the regional knowledge production function. Journal of Economic Geography, 7(6), 737–752.
OECD. (2013). OECD science, technology and industry scoreboard 2013. Paris: Organisation for Economic Co-operation; Development (OECD).
Parzen, E. (1962). On estimation of a probability density function and mode. The Annals of Mathematical Statistics, 33(3), 1065–1076.
Pavitt, K. (1984). Sectoral patterns of technical change: Towards a taxonomy and a theory. Research Policy, 13(6), 343–373.
Porter, M. E. (1998). Clusters and the new economics of competition. Harvard Business Review, 76(6), 77–90.
Porter, M. E. (2000). Location, competition, and economic development: Local clusters in a global economy. Economic Development Quarterly, 14(1), 15–34.
QGIS Development Team. (2019). QGIS geographic information system. Beaverton: Open Source Geospatial Foundation Project. Retrieved from http://qgis.osgeo.org.
R Core Team. (2019). R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing. Retrieved from https://www.R-project.org/.
Rosenblatt, M. (1956). Remarks on some nonparametric estimates of a density function. The Annals of Mathematical Statistics, 27, 832–837.
Sessions, C., Wood, S. A., Rabotyagov, S., & Fisher, D. M. (2016). Measuring recreational visitation at us national parks with crowd-sourced photographs. Journal of Environmental Management, 183, 703–711.
Simmie, J. (2004). Innovation and clustering in the globalised international economy. Urban Studies, 41(5–6), 1095–1112.
Sloan, L., & Quan-Haase, A. (2017). The Sage handbook of social media research methods. London: Sage.
Spencer, G. M., Vinodrai, T., Gertler, M. S., & Wolfe, D. A. (2010). Do clusters make a difference? Defining and assessing their economic performance. Regional Studies, 44(6), 697–715.
Squicciarini, M., Dernis, H., & Criscuolo, C. (2013). Measuring patent quality: Indicators of technological and economic value. Paris: Organisation for Economic Cooperation; Development (OECD).
Stek, P. E. (2019). Mapping high R&D city-regions worldwide: A patent heat map approach. Quality & Quantity, 54, 279–296.
Sung, H.-Y., Wang, C.-C., Chen, D.-Z., & Huang, M.-H. (2014). A comparative study of patent counts by the inventor country and the assignee country. Scientometrics, 100(2), 577–593.
Toivanen, H., & Suominen, A. (2015). The global inventor gap: Distribution and equality of world-wide inventive effort, 1990–2010. PLoS ONE, 10(4), e0122098.
van de la Potterie, B. P., & De Rassenfosse, G. (2008). Policymakers and the R&D-patent relationship. Intereconomics, 43(6), 377–380.
Van Egeraat, C., Morgenroth, E., Kroes, R., Curran, D., & Gleeson, J. (2018). A measure for identifying substantial geographic concentrations. Papers in Regional Science, 97(2), 281–300.
Widenius, M., Axmark, D., & Arno, K. (2002). MySQL reference manual: Documentation from the source. Sebastopol: O’Reilly Media.
Wu, C.-Y. (2014). Comparisons of technological innovation capabilities in the solar photovoltaic industries of Taiwan, China, and Korea. Scientometrics, 98(1), 429–446.
Yang, C.-H., & Kuo, N.-F. (2008). Trade-related influences, foreign intellectual property rights and outbound international patenting. Research Policy, 37(3), 446–459.
Zheng, J., Zhao, Z.-Y., Zhang, X., Chen, D.-Z., & Huang, M.-H. (2014). International collaboration development in nanotechnology: A perspective of patent network analysis. Scientometrics, 98(1), 683–702.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stek, P.E. Identifying spatial technology clusters from patenting concentrations using heat map kernel density estimation. Scientometrics 126, 911–930 (2021). https://doi.org/10.1007/s11192-020-03751-8
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11192-020-03751-8