Abstract
The purpose of this paper is to analyze the causes and effects of arbitrariness in the peer review process. This paper focuses on two main reasons for the arbitrariness in peer review. The first is that referees are not homogenous and display homophily in their taste and perception of innovative ideas. The second element is that reviewers are different in the time they allocate for peer review. Our model replicates the NIPS experiment of 2014, showing that the ratings of peer review are not robust, and that altering reviewers leads to a dramatic impact on the ranking of the papers. This paper also shows that innovative works are not highly ranked in the existing peer review process, and in consequence are often rejected.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The process of peer review is one of the main underlying practice used for the publication of research. The quality of the published articles is influenced by the efficiency and the competence of the peer process. Lately, many studies have emphasized the problems inherent to the process of peer review (for a summary, see Squazzoni et al. 2017). Moreover, Ragone et al. (2013) have shown that there is a low correlation between peer review outcome and the future impact measured by citations.Footnote 1
One of the most severe problems of the peer review process is emphasized by the results of the NIPS experiment. The NIPS experiment, which took place in 2014, consisted of altering the reviewers of papers, since a fraction of submissions went through the review process twice. This experiment has shown that the ratings are not robust, e.g., changing reviewers had dramatic impact on the review results. Indeed, the papers accepted differed significantly among the two group of reviewers.Footnote 2
The purpose of this paper is to analyze the causes and effects of arbitrariness in the peer review process. We first develop a small model, and then, we perform simulations, which can replicate the results of the NIPS experiment.
In this paper, we focus on two main elements which affect the bias in the peer process. The first element is that referees display homophily in their taste and perception of innovative ideas. Homophily is the notion that similarity breeds connections, so that individuals with same taste will connect more easily (see Hirshman et al. 2008; McPherson et al. 2001). We refer to cultural traits, which are characteristics of human societies, and which are potentially transmitted by non-genetic means and can be owned by an agent (see Birukou et al. 2013). Similar notions have also been introduced in Boudreau et al. (2016) as “intellectual distance” and in Travis and Collins (1991) as “cognitive particularism”.
Adapting this notion to reviewers, we assume that reviewers are more likely to appreciate level of innovations similar to their own research tendency, and give grades according to how these projects are close to their own taste.
So reviewers who are developing conventional ideas will tend to give low grades to innovative projects, while reviewers who have developed innovative ideas tend, by homophily, to give higher grades to innovative projects.
The second element leading to a high variance in the peer review process is that reviewers are not investing the same amount of time to analyze the projects (or equivalently are not with the same abilities). We show that this heterogeneity among referees will lead to seriously affect the whole peer review process, and will lead to main arbitrariness in the results of the process.
After having developed a model in the first part of the paper, then, in the second part, we present simulations, which describe the peer review process of grant proposals, and acceptance to conferences.
The paper leads to two main results. The first one is that there is arbitrariness in the papers and projects accepted. We show that the variance between the grades given by two reviewers is high. Moreover, we replicate the results of the NIPS experiment.
Our Proposition 2 emphasizes that the peer review process leads to the rejection of papers and projects with higher degrees of novelty. This paper stresses that homophily in the taste for innovation may explain the rejection of innovative projects. This result confirms the conclusion of some early research which has shown that grant-review committees are hesitant to risk funds on innovative proposals (see Garfield 1987; Luukkonen 2012), often because of the high variance in the review scores (Linton 2016).Footnote 3
These two elements, homophily and heterogeneity of reviewers, are among the main elements that have to be taken into account if we aim at improving the peer review process.
The paper is divided in four parts. In the next section, we present some facts related to the peer review process. In Sect. 3, we present the model. In Sect. 4, we present the results and simulations, and part V concludes.
Facts related to peer review
The Peer review process is used in three different channels of science. First, it is used by journals for deciding which papers to publish. Second, governments and NGOs who provide grants chose the projects through peer review process. And third, conference organizers also use peer review process to choose the papers to be presented in conferences. There are some differences between these three channels, but our model is general enough to be appropriate for all of them. In these three channels, the criteria for ranking are quite similar. This is the topic of the next section.
Criteria of peer review and acceptance rates
In each peer review process, the committee publishes the criteria by which the reviewers should judge the papers or projects. The criteria in the process of ranking grants are very similar to these in the process of ranking papers for conferences. More specifically, we have focused on the criteria chosen in computer science conferences, and have chosen sub-fields as artificial intelligence, cryptology and computer vision.
We have found that funding committees and conference organizers propose many criteria such as ‘presentation quality’, ‘clarity’, ‘reproducibility’, ‘correctness’, ‘novelty’ and ‘value added’.Footnote 4 The criteria such as ‘presentation quality’ and ‘clarity’ are very often chosen.
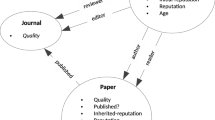
We have found a total of 12 criteria used for ranking papers. These 12 criteria can be regrouped in three main categories of criteria: (1) soundness, dealing with the presentational and scientific validity aspects; (2) contribution, responsible for the importance of the results; and (3) innovation, showing how novel the results or ideas are. The criteria are presented in Table 1.
These three categories of criteria affect the ranking of papers and projects. The weight given to these criteria is also an important element of the peer review process. In consequence, in the model we develop in the next section, we take into account these three categories of criteria.Footnote 5
Related to acceptance rates, they vary for conferences as well as for projects to be financed. For conferences, the acceptance rate for computer science conferences, has a median acceptance rate of 37% (see Malicki et al. 2017). In the case of NIPS (see below), it is of 22%.
For projects, the acceptance rates are small and are between 1 and 20%, with an average of 10%. In the European H2020 calls, the acceptance rate is of 1.8%.Footnote 6
The NIPS experiment
In December 2014, in a conference on Neural Information Processing Systems (NIPS) which took place in Montreal, for 10% of the papers, the main committee of the conference split the program committee in two, forming two independent committees. The two committees have received the same papers.
The acceptance rate was pre-defined at 22%. There were 166 papers submitted, which underwent a “duplicate” peer review, and 37 papers had to be accepted.
Of the 37 papers to be accepted by both committees, only 16 papers were accepted by both committees (43%), while they disagreed on 21 (57%), and recall that these results were for a 22% acceptance rate.
There are some main conclusions to be drawn from this ex-post experiment. The conclusions are: (1) there is arbitrariness in the peer review process, since the two committees have chosen a very different set of papers to be presented in their conference (the solution was to accept all papers and to add more sessions in this conference). (2) The arbitrariness was for more than 50% of the papers.
These conclusions necessitate a thorough analysis of the underlying reason for these facts. The following model analyzes the reasons for this arbitrariness, and tries to simulate the results of the NIPS experiment.
The model
Introduction
The purpose of this paper is to underline possible channels for arbitrariness in the peer review process. The paper focuses on two main elements for getting this effect; and these two elements are crucial for obtaining our results.
The first one is the concept of homophily implying that reviewers have personal bias. More specifically, we assume that reviewers are different in their taste for innovation, and in consequence, they give grades according to how the projects assessed to them are close to their own taste for innovation. The second element incorporated in this model is that reviewers are different in the time they allocate for peer review.Footnote 7
Another element included in this model is the correlation between homophily and time devoted to peer review. Are reviewers with less innovation taste, the ones to devote more or less time to peer review? In this paper we assume that the decisions about innovative tastes and time devoted to reviewing are independent. It could be that some more innovative people will devote more time for referring, but it could also be the opposite.
We now turn to present our model. Our model will allow us to explain the results of the NIPS experiment. Moreover, it shows that good but innovative projects are often rejected.
Criteria for papers and projects valuation
Let us assume that we have k projects from which only h can be funded, or equivalently k papers from which only h can be published. Since our model is pertinent for peer review of papers to be presented in conference, and to peer review for projects to be funded, we will use the terminology of “papers” also for projects in order to make sentences shorter, and not use “projects/papers”.
We first describe the criteria by which we define the true value of a paper. As shown in Sect. 2, we can group all these criteria under three main categories—‘soundness’, ‘contribution’ and ‘innovation’.
More specifically we define as S, criteria linked to soundness as clarity, reproducibility, correctness, and the absence of misconduct.Footnote 8
In the criteria contribution, C, we include elements linked to the impact and value added of the paper; while novelty-related criteria are denoted as I. In other words, each paper is defined by three criteria, S, C and I, so that the true value of a project is:
Where V is the value of the project i, S represents the scientific soundness of the project, C the scientific contribution, and I is the innovative element of the project.Footnote 9
The weight given to these three criteria are not similar in all fields or editing committees. Some prefer to put emphasis on ‘soundness’, other might want to focus on the ‘contribution’ of a paper. We therefore analyze in this model the effects of having different weights on these criteria. In the first case, we check when \( \alpha = \beta = \gamma = 1/3 \). Later on, we also check five other sets of weights.
Referees valuation of the projects and papers
The referees have different subsets of projects, usually selected based on their expertise. The referees try to estimate the ‘true’ values of the projects. We denote Uij the value given by the referee j to the project i. Note that referees are different in their subjective value of time, as well as their degree of homophily to the project. So, Uij is a function of the time spent by the referee analyzing the project. It is also a function of the referee’s opinion on how innovative the project is, which is influenced by homophily.
We now present in more details the way referees value project. First, we assume that the referees evaluate Si without error, since committees report that there are no big debates about the ‘soundness’ of a project.
Contribution criteria, C
About the contribution and value added of a project, there is usually a debate between referees. Indeed the scientific contribution of a paper, Ci, is not easily evaluated.
We define Tij as the time that referee j takes to investigate the project i, and assume that if the time invested is higher than the contribution value, i.e., Ci ≤ Tij, then the referee can correctly estimate the true value of the project. However, if Ci > Tij, then he/she does not appreciate the true value.
In other words, we assume that the more time a referee spends analyzing the project, the closer he gets to the true value Ci; and the greater the difference between Ci and Tij, the larger the error in valuation is.
Without loss of generality, we assume that Tij depends on both the reviewer and the project, so that it can be represented as:
where Tj represents the average time the referee j spends on review and εij represents the project-dependent fraction of time. In the following, we set εij = 0 for the sake of simplicity.
Innovation criteria, I
About the innovative value of a project and the effect of homophily on the valuation, we assume that some of the referees are more innovative and have a tendency for more innovative ideas, while other referees are more orthodox in their essence and do not like unorthodox projects.
We call Iij the homophilic index of scientist j w.r.t. project i, which is distributed normally on the range [0, Z]. We can compute homophily between the referee and the project as the similarity between the set of traits related to innovations they have. In general, similarly to Tij we can split Iij into two components:
where γij represents the homophily effect, while Ij represents the conformity, i.e., how receptive the referee is to innovative ideas.
When considering the inventive element, Iij, we assume that γij = 0, i.e., homophily affects the valuation of referee in the following manner: (1) the more creative (or receptive to non-orthodox ideas) the referee is, the better he estimates the invention element; (2) if the referee is more creative that the project proposed, he makes no error on the value; and (3) the error is an increasing function of the difference between the true value and his creative possibilities.
The total valuation of referees
Taking into account the various elements described above, we get that the valuation given by a referee is:
The results of the model
This simple model permits us to show some of the implications of the peer review process, based on Eq. (4). The two main results are the following.
Proposition 1
The peer review process leads to arbitrariness: For the same given papers, when the reviewers are different, then we get a different ranking of the papers.
The model reproduces the results of the NIPS experiment.
Proposition 2
Innovative projects are not highly ranked in the existing peer review process, mainly due to the homophilic trait of reviewers.
Instead of presenting formal proofs, we will show the results for more than 200 simulations. We present the simulations in the next section, but, let us start with a simple example which is more intuitive and allows us to understand the various claims of the propositions.
An example
There is one committee and two referees who have to choose 3 papers out of 10 (k = 10 and h = 3), an acceptance rate of 30%. This acceptance rate is consistent with the acceptance rate for computer science conferences, as shown above.Footnote 10
We assume that all criteria are equal in their weight (and assume that α, β and γ are equal to 1). We order all the papers in an increasing value such that:
The two referees chosen are different in their preferences. The first referee spends much time on each of the papers (his T1 is 70, so that all papers with C lower than 70 will be reviewed accurately). But his homophilic index related to unorthodox views is low (his I1 is 40, so that all papers with innovation index higher than 40 will not be judged accurately).
The second referee does not spend much time (T2 = 40), but her homophilic index is high (I2 = 120). The consequences of the fact that these two referees are quite dissimilar in the time spent on refereeing, and in their homophilic index is that they will differ in their choice of papers. In Table 2, we present the 10 papers, their ‘true’ value, and how they were ranked by the two referees.
Results of the example
Table 2 permits us to compare the ranking of papers chosen by each referee, as well as their average. First, we see that reviewer 1 will choose the three papers: 7, 8, 10; while reviewer 2 will choose the three papers: 5, 9, 10 (recall that the referees have to pick 3 papers out of 10).
What is striking is that the referees agree only on 1 paper out of 3. Indeed, both reviewers have in common only the paper #10 (1/3!).
In case the committee chooses the papers by average then, the final choice of the papers will include papers 5, 7, 10, while the best 3 papers are: 8, 9, 10. The referees should have chosen papers 8, 9, 10. In fact they have chosen, 5, 7, 10: a mistake of 66%.
As stressed in Proposition 1, there is Arbitrariness in the peer review process. This is exactly what happened in the NIPS experiment. Our example replicates the results of the NIPS experiment.
Moreover, the three innovative papers are #8, 9, and 10. Only the paper #10 is chosen. As stated in Proposition 2, peer review leads to a bias against innovative papers and projects.
This example highlights the bias in the peer review system. We turn now to present the 200 simulations performed.
Simulations
Introduction
We now present the simulations performed. The number of papers is 100 (k = 100). The number of papers accepted, h, is either 5, 10 or 15 (i.e., 5%, 10% or 15% acceptance rate). We present different acceptance rates in order to check whether the acceptance rate has an impact on arbitrariness.
The Committee chooses 30 referees to referee the 100 papers. The committee sends each referee 10 papers, so that each paper will be read by 3 referees.Footnote 11
Recall that Eq. (1) represents the true value of the paper:
where S is soundness, C contribution of the paper and I, innovativeness of the paper. We first explain the size of the coefficients, and then how C, S, and I are generated.
The coefficients
The coefficients given to the various criteria can be different. These coefficients account for varying emphasis on certain aspects of the paper (innovation, contribution, and soundness). Indeed, different reviewers, heads of project financing and conferences, each put the emphasis on different elements. Some may care more about innovation than contribution, or vice versa.
Hence, we test five different sets of coefficients:
In Table 3, we present the five sets of coefficients, each labelled respectively coeff. 1–5.
Below, we show that despite big differences in the value of the coefficients, the results for the various coefficients are almost the same.
The value of the papers
There are three elements to be generated: the soundness, S; the scientific contribution, C, and the inventive part, I. We have generated these elements in a random way. The elements S and C are generated from a normal distribution on the range (0, 100). The element I is generated from a 1/x distribution, to reflect the fact that there are many “below average” and “average” papers, while there are only few very innovative papers. The graphs of the density of the values of the elements of the 100 projects, along with an explanation on why we chose these distributions, are presented in "Appendix 1".
The referees
The referees are picked from a long list of people. Randomly, we picked 30 referees who have different Tj’s (time spent refereeing a paper), and Ij’s (level of innovation homophily).
Note from Eq. (4) that the referee will not be capable of accurately measuring a paper with a greater degree of innovation than himself/herself. The same is true for the time spent by a referee in regards to the contribution of the paper.
The Tj and Ij were generated randomly as well. The distribution of Tj and Ij of the referees are presented in "Appendix 2". The actual value of Tj and Ij for the 30 referees are presented in Table 4.
The selection of papers by the referees
We divide the 30 referees in 10 groups of 3, and for each group we allocate them to 10 papers, so that each paper will be refereed by 3 referees, and each referee will give a grade to 10 papers.
We repeat this exercise 10 times, to analyze how different will be the choices of the referees under the 10 various iterations.Footnote 12
We simulate these 10 iterations, for the 5 different coefficients of Table 3. So in total, we had 200 various rankings of these 100 papers. We start by presenting the results of the 10 iterations for the coefficients equal to 1/3; which we have coined “coeff. 1”.
The results of the 10 iterations for coeff. 1: (1/3, 1/3, 1/3)
We present the results of iterations 1 and 2 in Tables 5 and 6, while the other iterations are presented succinctly in Table 7.
Table 5 presents the top 15 papers chosen by each of the three referees and also the average of the three referees. In column (1), we present the ranking. In column (2), we present the 15 best papers in the draw we got. In parentheses, we present the value of the papers.
Iteration #1
The papers chosen by the three referees for iteration #1 are presented in columns (3) to (5). For iteration 1, we got that only the paper #90 was recognized as a top 5% paper. So, when the committee asks for 100% agreement between the three referees, then there is only one paper accepted, which means a success of 1/5 of recognizing the best papers.
When the committee requires a total agreement on the 10% best papers, then there is an agreement on papers #90, 48 and 85, that is: 3/10. And when we check for the acceptance rate of 15%, then they agree on 6/15 papers (90, 48, 85, 14, 52, 21).
This means that total agreement is very difficult to get, exactly as in the example presented in the previous section. Therefore, most committees do not ask for total agreement, but rank the papers using the average of the grades given by the referees.
When the committee examines the average of the grades given by the three referees, we get that three papers are recognized as top 5% (90, 14, 21)—a success of 60% (see column 6). When we check for the 10% top papers, the committee chose 8 papers—a success of 80%, and for 15% top, a success of 87%. So this seems to be a positive result.
What happens when the committee sends the papers to different referees? Let us check iteration 2.Footnote 13
Iteration #2
For iteration 2, we got that only the paper #14 was recognized as a top 5% paper (see Table 6, columns 3–5). So, when committee asks for 100% agreement, then there is only one paper they can agree on (#14).
What is striking is that the paper chosen in iteration 2 is different than the paper chosen in iteration 1, where paper #90 was the one chosen. In other words, there is arbitrariness.
When the committee fixes an acceptance rate of 10%, then they are in agreement on papers #14, 21, 17, 68, 65 (different than #90, 48 and 85 in iteration 1).
When the committee asks for the average of the grades given by the three referees, we get that three papers are recognized among the top 5% (21, 65, 14), a success of 60%. What is striking is that in iteration 1 it was also 60%, but different papers: #90, 14, 21, so that there was a complete agreement on only two papers.
When we check for the 10% top papers, the committee chose 7 papers (while in the first iteration it was 8 papers)—a success of 70%, and for top 15%, a success of 80%.
The 10 iterations
The 10 iterations are summarized in Table 7. We present the average of the grades given by the three referees, which succeeds finding the good papers with a probability of 60%. But, each iteration picks different papers.
To conclude and to summarize our results: there is complete arbitrariness in the peer review process. These simulations and iterations lead us to present the following results:
- 1.
There is not even one paper among the top 5, which is accepted by all the committees in these 10 different iterations. It means that there is no robustness at all in the choice of the papers.Footnote 14 This confirms the result in Pier et al. (2018), whose replication study of the NIH peer review process has shown a very low level of agreement among the reviewers in both their written critiques and the ratings.
- 2.
The best paper (#14) is chosen among the top 5% by only 4 committees out of the 10 iterations.
- 3.
Averaging the referees’ grades is better than asking for consensus, but does not eliminate arbitrariness.
- 4.
Each iteration (committee) succeeds in picking between 1 and 3 top 5% papers, which means that 2–4 ‘not-top’ papers will be selected as top. A mistake of 40–80%.Footnote 15
- 5.
Increasing the acceptance rate of papers (moving from top 5% to top 10%, or top 15%) leads to accept more papers.Footnote 16 It is clear that while reducing the tightness of selection of papers to conferences is not too costly—(one has to add more sessions at the same time, and admittedly big conferences are not easy to handle); For projects to be financed, increasing the number of projects funded could be almost impossible.
- 6.
We have also checked the results for the 5 coefficients presented in Table 3. In Table 8, we present the results for coeff. 2, (1/4, 3/8, 3/8). As can be seen, the committees pick between 1 and 4 top papers. Again, none of the top papers will be chosen by all. We get similar results for the other coefficients 3–5.
Table 8 The results of the 10 iterations for coeff. 2, and for the average of 3 referees - 7.
The papers and projects with more innovation are the ones with the highest variance among the 10 iterations. In consequence, their probability of being accepted is low.
- 8.
In conclusion, arbitrariness is a robust result of this paper.
Conclusions and policy remarks
Peer review has come under scrutiny in the last few years; and it has become acknowledged that the system is not optimal. This paper has focused on one of the problems: The arbitrariness of projects and papers chosen through peer review.
The problem of arbitrariness has already been raised in the past: The NIPS experiment has raised the alert about the arbitrariness of the peer review process underlining that changing reviewers lead to choosing different projects. Moreover, several previous studies have shown that the reviewers’ ratings do not correlate with subsequent citations of the paper.Footnote 17
This paper focuses on the reasons for the robustness of arbitrariness, by modeling the phenomenon, and by emphasizing that the heterogeneity of the reviewers is the main reason for the arbitrariness. There are two main types of heterogeneity leading to arbitrariness. The first is homophily in the trait related to innovation, and the second is the time dispensed by reviewers to peer review. We have stressed that heterogeneity in these two elements is sufficient to generate arbitrariness.
We have shown that if we have 10 different committees formed with the same 30 referees, but a different draw of papers sent to them, and for an acceptance rate of 5%, we get that there is agreement on only one paper out of five, so 20% agreement. We have also underlined that changing the weight of the various criteria does not change the results: Arbitrariness is a phenomenon related to peer review.
Can the problem be even more acute than arbitrariness? Unfortunately, yes. The second result emphasized by our paper is that the probability of accepting innovative papers is low. The peer review process leads to conformity, i.e., selection of less controversial projects and papers. This may even influence the type of proposals scholars will propose, since scholars need to find financing for their research as discussed by Martin (1997): “a common informal view is that it is easier to obtain funds for conventional projects. Those who are eager to get funding are not likely to propose radical or unorthodox projects. Since you don’t know who the referees are going to be, it is best to assume that they are middle-of the road. Therefore, a middle of the road application is safer”.
Can we reduce arbitrariness and the bias against innovative projects? There are some alternative models proposed, and see in particular (Kovanis et al. 2017; Birukou et al. 2011; Brezis 2007), which try to reduce the bias against innovative projects, by introducing some randomness in the process of peer review. More recent approaches suggest using a modified lottery to partially eliminate bias (see Avin 2015; Gross and Bergstrom 2019; Roumbanis 2019). Still, the problem persists.
About arbitrariness, our model does not propose a panacea to the problems raised in this paper. Yet, our model can pinpoint worse solutions, as proposing to increase the numbers of criteria. This would increase the variance among the reviewers.
In conclusion, it is not easy to improve the peer review process. But, to conclude on an optimistic note, it could be that Artificial intelligence which is expanding these last years could revolutionize the peer review process. Maybe the revolution is at our gate.Footnote 18
Notes
Their dataset included 9000 reviews on ca. 2800 papers submitted to computer science conferences.
See Francois (2015).
There are also studies which have included the Weneger’s hypothesis of continental drift (see Hallam 1975).
See also Ragone et al. (2013).
Our model is also consistent with the one described in Ragone et al. (2013), where they consider q criteria used by the reviewers. In our case, q = 3.
One of the reasons why reviewer have different taste related to the time they want to invest in reviewing can be either having a different utility function, or they have different time constraints.
As we will discuss later on, adding more criteria is leading to more arbitrariness. So having only one category of ‘soundness’ and not three different ones as correctness, reproducibility and clarity is good.
I is similar to the degree of disruption the paper introduces, as described by Wu et al. (2019).
In the simulation, in the next section, the number of papers is k = 100, and the acceptance rate is either h = 5, 10, or 15%. These acceptance rates are consistent with acceptance rates for project funding which are between 1 and 20%.
Note that having at least 3 reviewers is a normal practice in computer science conferences.
The draw we got was that for instance, in iteration 1, papers 1–10 are read by referees #19; 13; and 10. In iteration 2, papers 1–10 are sent to referees 16; 22 and 29. In fact, Referee #1 will grade papers 21–30 in iteration 1; and papers 61–70 in iteration 2.
Recall that in iteration 2, the papers 1–10 are sent to referees 16, 22, and 29.
This result of our paper will probably give a good feeling to all readers of this paper: If your paper was rejected lately; it is mostly due to the specific referees who have read your paper; other referees would have accepted your paper. We thank Judit Bar-Ilan, our friend who passed away lately, for this remark.
In all iterations it is either 2 or 3 papers among the top, except for iterations 9, in which only 1 top paper was selected! Imagine that the committee which judges research in medicine looks like committee 9: it means that breakthroughs will be postponed, alas!.
In the case of 10%, the number of not-top papers published will be between 10 and 40%, while for the top 15%, it will be between 13 and 33%. Obviously, when we increase the acceptance rate, we increase the number of “top” papers, and the errors are tautologically reduced. When we accept all papers, the error is then nil! So the decision about the acceptance rate is crucial, for the trade-off between arbitrariness and tightness.
We already see the applications of AI for detecting research topics of the paper (see Salatino et al. 2019) and carrying out the statistical review (Heaven 2018). The use of automated methods during some parts of the peer review process has been already mentioned by Garfield (1986), but is still not widely adopted. However, the AI revolution can also change the whole peer process, by knowing to drop papers with false proofs, and accepting papers with some new approach. Indeed, we would like to warn our readers—without calming those fearing from the AI revolution and robots taking our jobs—the revolution is soon at our gate.
References
Avin, S. (2015). Breaking the grant cycle: On the rational allocation of public resources to scientific research projects. Ph.D. Thesis, University of Cambridge. https://doi.org/10.17863/CAM.16172.
Bartneck, C. (2017). Reviewers’ scores do not predict impact: bibliometric analysis of the proceedings of the human–robot interaction conference. Scientometrics,110(1), 179–194. https://doi.org/10.1007/s11192-016-2176-y.
Birukou, A., Blanzieri, E., Giorgini, P., & Giunchiglia, F. (2013). A formal definition of culture. In K. Sycara, M. Gelfand, & A. Abbe (Eds.), Models for intercultural collaboration and negotiation (Vol. 6)., Advances in group decision and negotiation Dordrecht: Springer.
Birukou, A., Wakeling, J., Bartolini, C., Casati, F., Marchese, M., Mirylenka, K., et al. (2011). Alternatives to peer review: Novel approaches for research evaluation. Frontiers in Computational Neuroscience,5, 56.
Boudreau, K., Eva, J., Guinan, C., Lakhani, K. R., & Riedl, C. (2016). Looking across and looking beyond the knowledge frontier: Intellectual distance, novelty, and resource allocation in science. Management Science,62(10), 2765–2783. https://doi.org/10.1287/mnsc.2015.2285.
Brezis, E. S. (2007). Focal randomization: An optimal mechanism for the evaluation of R&D projects. Science and Public Policy,34(9), 691–698.
Francois, O. (2015). Arbitrariness of peer review: A Bayesian analysis of the NIPS experiment.
Garfield, E. (1986). Refereeing and peer review: Opinion and conjecture on the effectiveness of refereeing. Essays of an Information Scientists,9, 3–11.
Garfield, E. (1987). Refereeing and peer review: How the peer review of research grant proposals works and what scientists say about it. Essays of an Information Scientists,10, 21–26.
Gross, K., & Bergstrom, C. T. (2019). Contest models highlight inherent inefficiencies of scientific funding competitions. PLoS Biology. https://doi.org/10.1371/journal.pbio.3000065.
Hallam, A. (1975). Alfred Wegener and the hypothesis of continental drift. Scientific American,232(2), 88–97.
Heaven, D. (2018). The age of AI peer reviews. Nature,563, 609–610. https://doi.org/10.1038/d41586-018-07245-9.
Hirshman, B. R., Birukou, A., Martin, M. A., Bigrigg, M. W., & Carley, K. M. (2008). The impact of educational interventions on real and stylized cities. Technical Report CMU-ISR-08-114, Carnegie Mellon University.
Kovanis, M., Trinquart, L., Ravaud, P., & Porcher, R. (2017). Evaluating alternative systems of peer review: A large-scale agent-based modelling approach to scientific publication. Scientometrics,113(1), 651–671.
Linton, Jonathan. (2016). Improving the peer review process: Capturing more information and enabling high-risk high-return research. Research Policy,45, 1936–1938.
Luukkonen, Tertu. (2012). Conservatism and risk-taking in peer review: Emerging ERC practices. Research Evaluation,21(2), 48–60. https://doi.org/10.1093/reseval/rvs001.
Malički, M., Mihajlov, M., Birukou, A., & Bryl, V. (2017). Peer review in computer science conferences. In Eighth international congress on peer review and scientific publication (PRC8), Chicago, IL.
Martin, B. (1997). Peer review as scholarly conformity. Suppression Stories,5, 69–83.
McPherson, M., Lovin, L. S., & Cook, J. M. (2001). Birds of a feather: Homophily in social networks. Annual Review of Sociology,27(1), 415–444.
Pier, E., Brauer, L. M., Filut, A., Kaatz, A., Raclaw, J., Nathan, Mitchell J., et al. (2018). Low agreement among reviewers evaluating the same NIH grant applications. Proceedings of the National Academy of Sciences of the United States of America,115(12), 2952–2957.
Ragone, A., Mirylenka, K., Casati, F., & Marchese, M. (2013). On peer review in computer science: Analysis of its effectiveness and suggestions for improvement. Scientometrics,97(2), 317–356.
Roumbanis, L. (2019). Peer review or lottery? A critical analysis of two different forms of decision-making mechanisms for allocation of research grants. Science, Technology and Human Values,44(6), 994–1019. https://doi.org/10.1177/0162243918822744.
Salatino, A. A., Osborne, F., Birukou, A., & Motta, E. (2019). Improving editorial workflow and metadata quality at springer nature. In C. Ghidini, et al. (Eds.), The semantic web—ISWC 2019 (Vol. 11779)., Lecture notes in computer science Cham: Springer. https://doi.org/10.1007/978-3-030-30796-7_31.
Shah, N. B., Tabibian, B., Muandet, K., Guyon, I., & von Luxburg, U. (2018). Design and analysis of the NIPS 2016 review process. Journal of Machine Learning Research,19, 1–34.
Squazzoni, F., Brezis, E., & Marusic, A. (2017). Scientometrics of peer review. Scientometrics,113(1), 501–502.
Travis, G. D. L., & Collins, H. M. (1991). New light on old boys: Cognitive and institutional particularism in the peer review system. Science, Technology and Human Values,16(3), 322–341. https://doi.org/10.1177/016224399101600303.
Wu, L., Wang, D., & Evans, J. A. (2019). Large teams develop and small teams disrupt science and technology. Nature,566, 378–382. https://doi.org/10.1038/s41586-019-0941-9.
Acknowledgements
We are grateful to Judit Bar-Ilan, Ana Marusic, Flaminio Squazonni, as well as participants at the Peere conference in Rome and workshop at the Technion, the European Public Choice Society meeting, the CESifo workshop on Political Economy, and the ICOPEAI conference, for their valuable remarks. We thank the editor and the reviewers for helpful comments, and we thank Jason Tang for his excellent research assistance. This research was funded by COST Action TD1306, New Frontiers of Peer Review (PEERE). The second author also acknowledges the support of the “RUDN University Program 5–100”.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: the values of the various projects
The distribution of C, S and I we use in this paper are as presented in Figs. 1, 2, and 3 below. Recall that the distribution of C and S are generated from a normal distribution on the range (0, 100), so that the frequency of papers with S and C values in the middle range should be the greatest. The element I is generated from a 1/x distribution, so that there will be plenty of not-so innovative papers and few incredibly innovative papers. The exact numeric value is presented in the website of the paper. The exact numeric C, S, and I values can be seen in the first three columns of Table 1 (see website). We have also checked a whole new round of simulations with another draw of these variables. The results were similar. The distribution of C, S and I are presented in the following figures.
Appendix 2
The frequency value for the referees of the I and T values are presented in Figs. 4 and 5.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brezis, E.S., Birukou, A. Arbitrariness in the peer review process. Scientometrics 123, 393–411 (2020). https://doi.org/10.1007/s11192-020-03348-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11192-020-03348-1