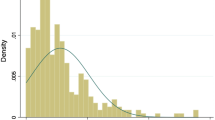
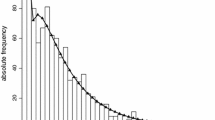
Abstract
Using an exhaustive database on academic publications in mathematics all over the world, we study the patterns of productivity by mathematicians over the period 1984–2006. We uncover some surprising facts, such as the weakness of age related decline in productivity and the relative symmetry of international movements, rejecting the presumption of a massive “brain drain” towards the US. We also analyze the determinants of success by top US departments. In conformity with recent studies in other fields, we find that selection effects are much stronger than local interaction effects: the best departments are most successful in hiring the most promising mathematicians, but not necessarily at stimulating positive externalities among them. Finally we analyze the impact of career choices by mathematicians: mobility almost always pays, but early specialization does not.

Similar content being viewed by others
Notes
To our knowledge, Borjas and Doran (2012) are the only ones to use the same source of data. They study the effects of the collapse of the Soviet Union and the influx of Soviet mathematicians after 1992 on the productivity of their American counterparts.
In all tables, *** means that the coefficient estimate is significantly different from zero at 1 percent level, ** at 5 percent and * at 10 percent.
Recall that in our individual output measure, the impact of each paper is shared between the authors.
References
Adler, R., Ewing, J., & Taylor, P. (2009). Citation statistics: A report from the international mathematical union (IMU) in cooperation with the international council of industrial and applied mathematics (ICIAM) and the Institute of Mathematical Statistics (IMS). Statistical Science, 24, 1–14. http://dx.doi.org/10.1214/09-STS285.
Agrawal, A., & Goldfarb, A. (2008). Restructuring research: Communication costs and the democratization of university innovation. American Economic Review, 98, 1578–1590.
Borjas, G. J., & Doran, K. B. (2012). The collapse of the soviet union and the productivity of american mathematicians. Technical report, National Bureau of Economic Research.
Combes, P. P., & Linnemer, L. (2003). Where are the economists who publish? Publication concentration and rankings in Europe based on cumulative publications. Journal of the European Economic Association, 1, 1250–1308.
Coupé, T. (2003). Revealed performances: Worldwide rankings of economists and economics departments, 1990–2000. Journal of the European Economic Association, 1, 1309–1345.
Davis, G. (1997). Mathematicians and the market. Notices American Mathematical Society, 44, 1307–1315.
Ellison, G. (2010). How does the market use citation data? The Hirsch index in economics. CESifo working paper series 3188, CESifo Group Munich, http://ideas.repec.org/p/ces/ceswps/_3188.html.
Ellison, G. (2011). Is peer review in decline?. Economic Inquiry, 49, 635–657.
Ellison, G. (2012). Assessing computer scientists using citation data. Technical report, http://economics.mit.edu/files/7784.
Hill, D., Rapoport, A. I., Lehming, R. F., & Bell, R. K. (2007). Changing US output of scientific articles: 19882003. Technical report NSF 07-320, National Science Foundation, Division of Science Resources Statistics.
Hirsch, B. T., Austin, R., Brooks, J., & Moore, J. B. (1984). Economics departmental rankings: Comment. The American Economic Review, 74, 822–826.
Hirsch, J. E. (2005). An index to quantify an individual’s scientific research output. In Proceedings of the national academy of sciences, 102, 16569.
Jones, B. (2010). As science evolves, how can science policy? Technical report, National Bureau of Economic Research.
Kim, E. H., Morse, A., & Zingales, L. (2009). Are elite universities losing their competitive edge? Journal of Financial Economics.
Korevaar, J. C. (1996). Validation of bibliometric indicators in the field of mathematics. Scientometrics, 37, 117–130.
Laband, D. N., & Tollison, R. D. (2000). Intellectual collaboration. Journal of Political Economy, 108, 632–662.
Levin, S. G., & Stephan, P. E. (1991). Research productivity over the life cycle: Evidence for academic scientists. The American Economic Review, 81, 114–132.
Lotka, A. J. (1926). The frequency distribution of scientific productivity. Journal of the Washington Academy of Science, 16, 317–323.
Neary, J. P., Mirrlees, J. A., & Tirole, J. (2003). Evaluating economics research in Europe: An introduction. Journal of the European Economic Association, 1, 1239–1249.
Oyer, P. (2006). Initial labor market conditions and long-term outcomes for economists. The Journal of Economic Perspectives, 20, 143–160.
Palacios-Huerta, I., & Volij, O. (2004). The measurement of intellectual influence. Econometrica, 72, 963–977.
Stephan, P. (2008). Job market effects on scientific productivity. Conferences on New Political Economy, 25, 11–29.
Waldinger, F. (2012). Peer effects in science—evidence from the dismissal of scientists in nazi germany. The Review of Economic Studies, 79, 838–861.
Wuchty, S., Jones, B. F., & Uzzi, B. (2007). The increasing dominance of teams in production of knowledge. Science, 316, 1036–1039.
Author information
Authors and Affiliations
Corresponding author
Additional information
We are grateful to Mathematical Reviews, published by the American Mathematical Society, for allowing us to use large data from their base to conduct the study presented here.
Appendices
Appendix 1: additional tables
See Tables 8, 9, 10, 11, 12,13,14,15,16,17, 18, 19, 20, 21, 22, 23 and 24 .
Appendix 2: results based on the Impact factor
The data presented in this section are similar to those obtained in other parts of the paper. However, the basic indicators are based on the IF rather than on MCQ. More precisely, the weight attributed to each article is equal to the number of its pages times the IF of the journal where it is published, rather than the square of the MCQ.
Table 19 is the analog of Table 8.
Similarly, we have the analog of Table 9 in Table 20 with the impact of authors based on the IF.
We now consider the factors playing a part in a mathematician’s scientific productivity. Table 21 is the analog of Table 10 based on the IF rather than the MCQ.
The analog of Table 11 with the impact of authors based on the IF is in Table 22 . Finally, Table 23 is the analog of Table 7 based on the IF.
Appendix 3: more on the data
Table 24 contain the list of journals used here. With each journal we list the total number of pages published in the sample period, the number of articles, the 2007 M.C.Q., the mean number of pages by article, and the mean number of authors by article. The code used for each journal (in the first column) should make it easy, for those who are familiar with the mathematical literature, to identify each journal.
Rights and permissions
About this article
Cite this article
Dubois, P., Rochet, JC. & Schlenker, JM. Productivity and mobility in academic research: evidence from mathematicians. Scientometrics 98, 1669–1701 (2014). https://doi.org/10.1007/s11192-013-1112-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11192-013-1112-7