Introduction

It is well known that the cumulative number of various items (for example, articles, journals and authors) in a database or citations of the publication output of an author initially increases rapidly with time, followed by a maximum level attained after a certain time (Avramescu 1979; Gupta 1990; Egghe et al. 1995; Bharathi 2011). In terms of the absolute number of items per unit time (e.g. citations per year of an author), initially they increase, then, after going through a maximum value, slowly decrease and finally attain a zero value with increasing time. This phenomenon is usually called obsolescence (Avramescu 1979; Gupta 1990; Egghe 1993; Egghe et al. 1995), aging (Egghe et al. 1995) or decay.

The decay process of items is usually explained (Avramescu 1979; Gupta 1990; Egghe et al. 1995) by using decreasing exponential functions. For the dependence of citations L of individual articles on time t, Avramescu (1979) proposed the empirical function

$$ L(t) = C_{0} [\exp \,( - \lambda t) - \exp ( - m\lambda t)], $$
(1)

where C 0 is the citation amplitude, λ is the age decrement time constant, and m > 1 is the initial increment. However, different exponential functions used for the growth of items as well as the exponential functions employed to describe their decaying behavior contain empirical constants to which it is difficult to assign any physical significance. For example, in Eq. 1 it remains unclear why C 0 of individual articles is attained and what factors determine the values of parameters λ and m for individual articles.

Sangwal (2011a) suggested that the combined growth and decay L(t) curve of citations can be described as the product of fractions α 1 and α 2 of citations corresponding to growth and decay processes in the form of the empirical relation

$$ \alpha (t) = \alpha_{1} \alpha_{2} = \frac{{L_{1} (t)}}{{C_{1} }} \times \frac{{L_{2} (t)}}{{C_{2} }} = \frac{L(t)}{C} = \left[ {1 - \exp \left\{ { - \left( {\frac{t}{{\Uptheta_{1} }}} \right)^{{q_{1} }} } \right\}} \right] \times \left[ {1 - \exp \left\{ { - \left( {\frac{t}{{\Uptheta_{2} }}} \right)^{{ - q_{2} }} } \right\}} \right], $$
(2)

where L(t) is the number of citations at time t, C is the maximum number of possible citations, Θ is the time constant, the constant q > 1, and the lower indexes 1 and 2 denote growth and decay processes, respectively. The time constants Θ1 and Θ2 are given by Eq. 4 whereas the exponents q 1 and q 2 are given by Eq. 5. In Eq. 2 the first and the second terms in the square brackets denote the growth and decay processes, respectively. The first term follows from the progressive nucleation mechanism (PNM) advanced originally to describe overall crystallization kinetics. Equation 2 predicts a maximum value of α(t) at a particular value of t/Θ, but the values of α* and (t/Θ)* corresponding to the maximum in the α(t) plot are determined by the relative values of q 1 and q 2.

The PNM has been described previously by the present author (Sangwal 2011a, b) and applied to analyze the growth of citations of individual authors (Sangwal 2011b), the growth of articles in three randomly selected databases in humanities, social sciences and science and technology (Sangwal 2011a) and the growth of journals, articles and authors in malaria research (Sangwal 2011a). The basic concepts of the mechanism have been described in detail in a more recent paper (Sangwal 2012). The aim of the present study is to apply the PNM to describe the growth behavior of cumulative L(t) citations and ΔL(t) citations per year of individual papers of four selected Polish professors. The choice of citations of individual papers of selected authors for the analysis is associated with the fact that citations of a paper are prototypes of items generated in an individual systems as considered by the PNM.

Basic concepts and equation of PNM for growth behavior of items

In the case of growth of items (such as articles of an author, citations of individual paper of an author or authors working in a research field) with time t in an individual system since the year Y 0, the fraction α(t) number of items L(t) at time t for the system producing the items may be given by (Sangwal 2012)

$$ \alpha (t) = \frac{L(t)}{C} = \left[ {1 - \exp \left\{ { - \left( {\frac{t}{\Uptheta }} \right)^{q} } \right\}} \right], $$
(3)

where C is the maximum number of items that can be produced in the system, the time constant

$$ \Uptheta = \frac{{q^{1/q} }}{{\kappa J_{\text{s}} }}, $$
(4)

the exponent

$$ q = 1 + \nu d. $$
(5)

In the above equations, J s is the rate of stationary nucleation and κ is the shape factor (e.g. κ = 4π/3 for a sphere), d is the dimensionality of the growing nuclei, and the time

$$ t = Y - Y_{0} , $$
(6)

where Y is the year of the item L(t) and Y 0 is the actual publication or extrapolated year when α(t) = 0. In the case of growth of nuclei by diffusion and mass transfer processes, ν = 1/2 and 1, respectively. Therefore, for 0 < d < 3, q lies between 1 and 2.5 and 1 and 4 for the above processes, respectively.

Equation 3 provides a static picture of the fraction α occurring at time t in the system. One can obtain a dynamic picture of the process at different t by differentiating Eq. 3 with respect to t, in the form of the velocity v of generation of items:

$$ v(t) = \frac{d\alpha (t)}{dt} = \frac{1}{C}\frac{dL(t)}{dt} = \frac{q}{{\Uptheta^{q} }}t^{q - 1} \exp \left\{ { - \left( {\frac{t}{\Uptheta }} \right)^{q} } \right\} = \frac{q}{{\Uptheta^{q} }}t^{q - 1} \left[ {1 - \alpha (t)} \right]. $$
(7)

Equation 7 describes the change of generation of items L(t) with time t. This equation predicts an initial increase followed by a decrease in the velocity v with an increase in time t. By differentiating Eq. 7 one obtains the change in the velocity v(t) of generation of items (i.e. acceleration a(t) in the process) in the form

$$ a(t) = \frac{{{\text{d}}v(t)}}{{{\text{d}}t}} = \frac{1}{C}\frac{{{\text{d}}^{2} L(t)}}{{{\text{d}}t^{2} }} = \frac{q}{{\Uptheta^{q} }}t^{q - 1} \exp \left\{ { - \left( {\frac{t}{\Uptheta }} \right)^{q} } \right\}\left[ {\frac{q - 1}{t} - \frac{q}{{\Uptheta^{q} }}} \right] = v(t)\left[ {\frac{q - 1}{t} - \frac{q}{{\Uptheta^{q} }}} \right] . $$
(8)

The plots of α(t), v(t) and a(t) as functions of generation time t of items according to Eqs. 3, 7 and 8, respectively, are shown in Fig. 1.

Fig. 1
figure 1

Plots of α(t), v(t) and a(t) as functions of generation time t of items, according to Eqs. 3, 7 and 8, respectively, for two different values of exponent q

Full size image

It may be seen from Fig. 1 that α(t) increases with an increase in t for q ≥ 1 and approaches a saturation value, which is attained at a lower t with an increase in q (curves 1 and 1′). However, the behavior of v(t) depends on the value of q. For q = 1 the value of citation velocity v steadily decreases with an increase in t, but for q > 1 the value of v increases first and then decreases with increasing t, exhibiting a maximum value of citation velocity v at a particular time t, denoted hereafter by v* and t*, respectively. In contrast to the dependences of α(t) and v(t) on t, the citation acceleration a is negative for q = 1 but it is positive for q > 1 in the entire range of t. In both cases however, a approaches zero at sufficiently long citation durations t. Moreover, in the case of q > 1, the values of t when v and a approach zero decrease with increasing values of q.

The value of t when v attains the maximum value v* may be obtained by maximizing Eq. 7 i.e. when a(t) = dv(t)/dt = 0:

$$ t* = \frac{(q - 1)}{q}\Uptheta^{q} . $$
(9)

Substitution of t* from Eq. 9 in Eq. 7 gives the maximum value of v in the form

$$ v* = \left( {\frac{\alpha (t)}{dt}} \right)^{*} = \frac{{(q - 1)^{q - 1} }}{{q^{q} }}\Uptheta^{q(q - 2)} \exp \left[ {\left( {\frac{q - 1}{q}} \right)^{q} \Uptheta^{q(q - 1)} } \right]. $$
(10)

For sufficiently high values of q they may be expressed as

$$ t* = \Uptheta^{q} , $$
(11)
$$ v* = \Uptheta^{{q^{2} }} \exp (\Uptheta^{{q^{2} }} ). $$
(12)

According to the above equations t* and v* depend on parameters q and Θ, but Eqs. 11 and 12 are too crude to calculate t* and v* because usually q < 4.

It should be noted that a maximum value in the velocity v of generation of items according to Eq. 3 is obtained when the term (t/Θ)q ≫ 1. However, when (t/Θ)q ≪ 1, Eq. 3 reduces to the traditional power law:

$$ \alpha (t) = \frac{L(t)}{C} = \frac{1}{{\Uptheta^{q} }}t^{q} , $$
(13)

and the velocity

$$ v = \frac{{{\text{d}}\alpha (t)}}{{{\text{d}}t}} = \frac{1}{C}\,\frac{{{\text{d}}L(t)}}{{{\text{d}}t}} = \frac{q}{{\Uptheta^{q} }}t^{q - 1} . $$
(14)

In this case, for all values of q > 1, both α(t) and v(t) increase with the generation time t of items without attaining a limiting value.

Using the relationship between the fraction α(t) of items and their maximum value C i.e. L(t) = Cα(t) and ΔL(t) = CΔα(t), Eqs. 3 and 7 may be written in the form:

$$ L(t) = C\left[ {1 - \exp \left\{ { - \left( {\frac{t}{\Uptheta }} \right)^{q} } \right\}} \right], $$
(15)
$$ \Updelta L(t) = \frac{{{\text{d}}L(t)}}{{{\text{d}}t}} = \frac{Cq}{{\Uptheta^{q} }}t^{q - 1} \exp \left\{ { - \left( {\frac{t}{\Uptheta }} \right)^{q} } \right\}. $$
(16)

For the analysis of real data on the dependence of cumulative citations L(t) and citation ΔL(t) per year on time t, Eqs. 15 and 16 can be used.

Citation data of selected authors

We used Thomson Reuters’ ISI Web of Knowledge (Web of Science) to collect and analyze the citations ΔL i (t) of individual most cited i papers of four selected Polish professors: T. Dietl (Institute of Physics, Polish Academy of Sciences, Warsaw, and University of Warsaw), J. Barnaś (Adam Miśkiewicz University, Poznań, and Institute of Molecular Physics, Polish Academy of Sciences, Poznań), M. Kosmulski (Lublin University of Technology), and K. Sangwal (Lublin University of Technology). For the analysis 10, 7, 4 and 6 papers of these authors were chosen. The data on the number ΔL i (t) of citations of papers i of these authors are given in Tables 1, 2, 3, 4. The data were collected on 19–20 December 2010. From the data of Tables 1, 2, 3, 4 the cumulative L i (t) citations at time t were calculated. The research fields, the total number N of papers, the cumulative citations L of N papers, the Hirsch index h, and the year Y 0 of the first publication of the above authors are given in Table 5. The publications of these professors have spanned over a period t varying from 28 to 40 years.

Table 1 Citations L i of ten most cited papers of Dietl
Full size table
Table 2 Citations of seven most cited papers i of Barnaś
Full size table
Table 3 Citations of four most cited papers i of Kosmulski
Full size table
Table 4 Citations of six most cited papers i of Sangwal
Full size table
Table 5 Some other relevant data for different authors
Full size table

The data were analyzed according to Eqs. 15 and 16 using the standard Origin program. The best-fit values of different constants of these equations for the data were obtained by taking the publication year as the value of Y 0. When the best fit was not achieved with a fixed value of Y 0, two values are given in Table 6. However, it was observed that the selection of the values of Y 0 was very critical for the citation data of papers endowed with low values of time constant Θ. A typical example of this type is paper 4 of Dietl (see Table 6; Fig. 5b).

Table 6 Constants of Eq. 3 for the citation data of individual papers
Full size table

Results and discussion

Time dependence of cumulative number L i (t) of citations

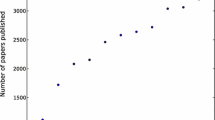
Figure 2 shows typical examples of the dependence of cumulative number L i (t) of citations of 6 papers published by Dietl as a function of publication year Y. Figure 2a presents the data for the first four highly cited papers. In this figure, the highest number ΔL i (t) of citations per year is 493 for Paper 1 whereas this number is lower by a factor of 4–6 for the remaining three papers and lies between 76 and 137. These most cited papers were published relatively recently between 2000 and 2004. Figure 2b shows the data for papers 5 and 6. Here the highest number of yearly citations is practically one half of that of paper 4 and lies between 33 and 40. These data can be represented reasonably well by Eq. 15 with the best-fit values of the parameters given in Table 6.

Fig. 2
figure 2

Normal growth behavior of cumulative number L i (t) of citations of papers i published by Dietl; papers a 1–4 and b 5–6

Full size image

Figure 3 shows the growth behavior of cumulative number L i (t) of citations of most cited papers i published by Barnaś, Kosmulski and Sangwal. The highest number ΔL of yearly citations in these papers lies between 10 and 27. The data of Fig. 3 can equally be described by Eq. 15. The best-fit values of the constants of Eq. 15 for these data are listed in Table 6.

Fig. 3
figure 3

Normal growth behavior of cumulative number L i (t) of citations of most cited papers i published by: a Barnaś, b Kosmulski and c Sangwal

Full size image

In the above papers where the growth behavior of the citations is satisfactorily represented by Eq. 15 in the entire citation period (Y − Y 0), their citation period is less than 15 years and it is even 6–8 years in several cases. In contrast to the above papers with “normal citation” behavior, there are papers where their citations cannot be described by Eq. 15 in the entire citation durations. Papers 7–9 of Dietl and papers 3 and 4 of Sangwal are typical examples of this type of “anomalous” growth behavior of cumulative number L i (t) of citations, as shown in Fig. 4. The citation periods of these papers lie between 24 and 28 years for Dietl and between 20 and 33 years for Sangwal.

Fig. 4
figure 4

Examples of anomalous growth behavior of cumulative number L i (t) of citations of papers i published by: a Dietl and b Sangwal. See text for details

Full size image

It may be noted that the citations of paper 7 of Dietl (Fig. 4a) follow practically two linear dependences below and above 1987, whereas paper 8 shows at least linear citation regions separated at 1988 and 1997. Similarly, paper 10 shows three distinct citation durations between: (1) 1983 and 1992, (2) 1992 and 1998, and (3) 1998 and 2010. Well-defined citation regions can also be discerned for paper 9, but these citation data may be presented by Eq. 15. In the case of paper 3 of Sangwal (see Fig. 4b), there are two citation regions covering the period before and after 1997, where both of them may be described by Eq. 15. However, after its publication in 1978, the citations of paper 4 of Sangwal has an initial period of sudden growth up to 1980, followed by a relatively stagnant period up to 1993, then a slow growth up to 1999 and finally a steady, relatively fast growth.

It should be mentioned that, except for papers 5 and 6 of Sangwal, the fit of the data for papers 7–10 of Dietl and papers 3 and 4 of Sangwal according to Eq. 15 is not only extremely poor but is unreliable due to different citation regions and small increase in the values of ΔL i citations per year. For the citations of these papers, data fitting gives even unrealistic values of q less than 1 (see Table 6). Therefore, the data are represented by curves drawn with the calculated values of parameters C and Θ, keeping q = 1. The curves for the citation data of paper 9 of Dietl and paper 3 of Sangwal are drawn with the constants for the entire citation period.

From Figs. 2 and 3 it may be seen that the PNM satisfactorily describes the time dependence of cumulative citations L in the case of papers with sufficiently high citations ΔL, as represented by the highest yearly citations ΔL max during the citation period t. However, as seen from Fig. 4, there are distinct citation periods in the plots of cumulative citations L as a function of citation time t for papers corresponding to relatively low ΔL max and relatively long citation durations t. From these observations it may be concluded that cumulative L(t) of citations of an individual paper i of an author is followed in the case of short citation durations less than about 15 years where the condition of stationary nucleation is more or less satisfied. The causes of deviations in stationary nucleation in the citations of a paper may be internal as well as external factors. The internal factors are associated with the author of the paper whereas the external factors are related to the paper itself. According to the PNM, these internal and external factors are related to the generator of items and their quality, respectively. For example, self-citations of a paper by its author in his subsequent papers published during a short period and citations in new collaborative papers are two of the main internal factors, whereas recognition of the importance of the results of a paper at a later date after its publication is one of the key external factors.

From Table 6 one observes that, for the authors considered in this study, the value of the exponent q for different papers showing normal growth behavior lies between 1.07 and 2.69. This is in good agreement with 1 < q < 2.5 predicted by PNM when the growth of items in an individual system occurs by diffusion (Sangwal 2012). The value of time constant Θ lies between 3 and 44 years. Using Eq. 4 one finds that J s lies between 2.4 × 10−10 and 3.6 × 10−9 s−1 (assuming that the citation nuclei are spherical i.e. the shape factor κ = 4π/3, and the term q 1/q = 1.42; cf. Sangwal 2012). The values of Θ and J s are similar to those observed in the case of growth behavior of cumulative N(t) papers published by the above authors (Sangwal 2012).

Time dependence of number ΔL i of citations per year

Figure 5 shows the dependence of the number ΔL i (t) of citations per year as a function of citation duration for different papers i of Dietl, while the curves are drawn according to Eq. 16 with the best-fit values of the constants given in Table 6. It may be noted that Eq. 16 represents the data of Fig. 5 reasonably well.

Fig. 5
figure 5

Time dependence of number ΔL i (t) of citations per year for different papers of Dietl; papers: a 1, b 2–5 and c 5 and 6. In (b) the curve for paper 4 is drawn with Y 0 = 2003.8. In (c) the data of paper 5 presented in (b) are shown at a different scale

Full size image

The main conclusion of the curves of Fig. 5 is that citations of an article have an initial growth period followed by a relatively long decay period. This means that the PNM also explains the growth and decay of citations ΔL of papers corresponding to ΔL max above about 10 citations approaching in about 5 years.

Summary and conclusions

Based on the PNM of items described previously (Sangwal 2012), Eq. 15 is proposed to analyze the dependence of cumulative citations L(t) of individual papers of an author on time t. Differentiation of Eq. 15 with respect to t yields Eq. 16 to describe the dependence of citation ΔL(t) per year (i.e. citation velocity v) of an individual paper on time t. It is shown that Eq. 16 predicts an initial increase followed by a decrease in the plots of velocity v ≡ ΔL(t) against citation time t. These equations of the PNM are applied to analyze the time dependence of cumulative citations L of individual papers of four selected Polish professors.

The PNM satisfactorily describes the time dependence of cumulative citations L of the papers published by different authors with sufficiently high citations ΔL, as represented by the highest yearly citations ΔL max during the entire citation period t (normal citation behavior). The citation period for these papers is less than 15 years and it is even 6–8 years in several cases. However, for papers with citation periods exceeding above about 15 years, the growth behavior of citations does not follow the PNM in the entire citation period (anomalous citation behavior), and there are regions of citations in which the citation data may be described by the PNM. The anomalous citation behavior is associated with the lack of stationary nucleation of citations for citation durations longer than about 15 years.

The PNM explains the growth and decay of yearly citations ΔL of papers corresponding to ΔL max above about 10 citations approaching in about 5 years. However, in the case of relatively low ΔL max and relatively long citation durations t, there are distinct citation periods in the plots of cumulative citations L as a function of citation time t.

The most important feature of the PNM applied in this paper is that the citation behavior of various individual papers of different authors can be characterized in terms of the maximum number C of citations, the time constant Θ and the exponent q of Eqs. 15 and 16 of the mechanism, and all of these parameters have well-defined physical significance. The value of q between 1.07 and 2.69 for the citations of different papers (see Table 6) indicates that the growth of citations of an individual paper occurs by volume diffusion because q lies between 1 and 2.5 for the growth of crystallites by diffusion.

According to the original PNM for overall crystallization, the crystallites developed during the growth have discrete values of d = 1, 2 and 3. Consequently, the values of q are also expected to be quantized as 1, 1.5, 2 and 2.5. In the case of citation behavior of individual paper where the values of q > 1 are not quantized, the condition of dimensionality of citations should be relaxed.