1 Introduction

Scholars and policymakers are enmeshed in a growing debate about the impact of climate change on socioeconomic systems (Choi et al., 2020; Cortés & Strahan, 2017; Dell et al., 2014; Dessaint & Matray, 2017). By increasing the frequency of rare and harmful weather phenomena, climate change poses a major threat to industries, economies, and societies (Cevik & Jalles, 2022; Felbermayr & Groschl, 2014; Hong et al., 2019; Hsiang et al., 2017). Motivated by weather experts’ increasingly alarming projections, lenders are focusing more attention on environmental issues (Ali et al., 2022; Cortés & Strahan, 2017; Fard et al., 2020; Houston & Shan, 2022; Nguyen & Wilson, 2020) and incorporating firms’ exposure to climate risks into their loan decisions (Dal Krueger et al., 2020; Maso et al., 2022). After all, weather-related disasters can cause severe damage to firms’ proprietary assets or disrupt their business operations (Kousky, 2014). Hence, lenders are adjusting their credit allocation strategies (Berg & Schrader, 2012) and charging a risk premium to hedge against borrowers’ exposure to harmful weather. These changes can potentially compromise firms’ activities and impair their solvency (Kling et al., 2021).

Researchers have attempted to understand the relationship between firms’ exposure to climate risk and their access to financing (Huang et al., 2018). While the empirical literature has associated climate vulnerability with the cost of corporate financing (e.g., Davlasheridze & Geylani, 2017; Huang et al., 2022; Javadi & Masum, 2021; Kling et al., 2021), most studies have focused on the borrowing implications of firms’ direct exposure to severe climate events. However, there is a paucity of evidence regarding the potential spillover effects stemming from geographical proximity to highly exposed enterprises.

One factor in such spillover effects seems to be the structure of local credit markets. Extant research has shown that local credit markets’ structure is likely to influence the internalization of negative spillovers associated with supply chain interconnections (Giannetti & Saidi, 2019). Indeed, scholars have claimed that supplier-customer links act as a potential climate-risk transmission channel (Henriet et al., 2012) and lenders are expected to adjust their debt pricing decisions in response to disaster shocks through them (Javadi & Masum, 2021). Far-sighted lenders that serve a large share of local credit markets are more likely to internalize negative spillovers (Giannetti & Saidi, 2019). Backed by high bargaining power, they can implement a credit pricing strategy suited to providing liquidity to distressed firms’ customers and suppliers when supply chains expect costly disruptions. In addition, banks that have long-term relationships with local firms may exhibit opportunistic behaviors (Kysucky & Norden, 2016) once private information is disclosed, especially when borrowers are small and thus more likely to rely on local financial intermediaries (see, e.g., Detragiache et al., 2000; Ongena & Smith, 2000; Ozkan, 2001).

Assuming that lenders will hedge against the potential propagation of distress, we want to empirically test whether firms’ cost of borrowing is influenced by not only their own direct exposure to the risk of climate-related disasters, but also by the exposure of neighboring firms. We then aim to explore whether smaller companies are more susceptible to negative spatial effects, presuming that lenders’ pricing strategies are expected to burden less financially diversified borrowers.

To answer these questions, we used a sample of non-financial private firms operating in Italy. Italy is as an ideal setting because its geomorphological characteristics and intense urbanization make the country highly vulnerable to hydrogeological risks. Approximately 91% of Italian municipalities are affected by landslide and/or flood hazard zones, while 16% of the national territory features areas classified as high and very high landslide and/or medium flood hazards (Iadanza et al., 2021). In May 2023, for instance, heavy rainfall impacted the Italian region of Emilia-Romagna, with more than 450 mm of rain recorded in several localities. These extreme natural events triggered severe floods and landslides throughout the region, forcing hundreds of people to evacuate their homes.Footnote 1 Later, in September 2023, the region of Marche suffered severe flash floods that killed 13 people and caused huge damages.Footnote 2 Similarly, Tuscany recorded 257 mm of rain in just 24 h—more than the monthly average rainfall for this time of year.Footnote 3

Additionally, Italian enterprises are significantly dependent on debt financing, particularly through traditional sources like bank loans (Aristei & Gallo, 2017). Italian entrepreneurs have traditionally been reluctant to take on equity partners due to their fear of undesired interferences and loss of control (Martin et al., 2002). Bank loans thus represent a significant proportion of Italian firms’ financial liabilities, reflecting the historical relevance of bank credit for corporate financing (Aristei & Gallo, 2017). In 2019, bank loans accounted for more than 51% of all debt of Italian non-financial corporations—a percentage far exceeding the European average (Bank of Italy, 2020). Thus, the country presents a good backdrop for investigating whether borrowing costs are affected by firms’ exposure to the risk of natural disasters.

For our analysis, we combined firm-level accounting data with granular information on the flood risk faced by Italian municipalities. To determine whether flood risk exposure directly or indirectly affects firms’ debt costs, we estimated a correlated random effects model, augmented with the spatial difference between a firm’s neighborhood flood risk and its own risk, while controlling for both time-varying and time-invariant heterogeneity. In line with previous evidence, we found a positive association between a firm’s climate risk (proxied by flood risk) and the cost of debt (e.g., Kling et al., 2021). According to our findings, an increase in flood risk of one standard deviation is associated with an increase of 18.5-basis points in the firm’s borrowing costs. In other words, companies in the highest-risk municipalities may face borrowing costs that are 1.24% higher than those in the lowest-risk municipalities.

By focusing on the average flood risk faced by enterprises within a 10-km radius of the focal firm, we also show that companies located close to riskier areas may incur additional debt costs.Footnote 4 More precisely, an increase in neighbors’ flood risk of one standard deviation is associated with at least a 10-basis point increase in the firm’s borrowing costs. Most importantly, when disentangling the spillover effect of physical climate risk by firm size, we find that smaller enterprises bear the additional cost of operating in a risky neighborhood, whereas larger enterprises do not. We conducted a battery of robustness tests, which are available in the Electronic Supplementary Material (available online), to validate our results. First, after having discussed the econometric foundations of our approach, we used the nearest neighborhood estimator to further address omitted variable issues. Second, we exploited the average distance from neighbors to control for measurement errors in the flood risk variable. Third, we analyzed the flood risk affecting individuals and areas separately in order to dismiss the possibility that factor analysis influenced our findings. Finally, we performed a mechanism analysis to support the hypothesis that flood risk spatial effects are the result of a bargaining process between businesses and financial intermediaries.

In short, this study provides a comprehensive analysis of the direct and indirect implications of climate risk on firms’ borrowing costs. By accounting for firms’ direct exposure to flood risk and the spatial spillover effects of natural disasters, this study sheds new light on the financial implications of firms’ exposure to climate risk. In line with previous evidence on lenders’ sensitivity to climate-related issues, we find that borrowers’ exposure to flood risk is associated with the cost of rising debt (e.g., Huang et al., 2022; Kling et al., 2021). Importantly, we also observe that climate-related risks propagate through regional environments and burden neighboring firms—particularly small businesses, which are likely to face stringent credit constraints (Kirschenmann, 2016).

The remainder of this paper is organized as follows: We review the literature and develop the related research questions in Section 2, and then present our data and empirical strategy in Sections 3 and 4, respectively. We discuss our results in Section 5 and conclude the paper in Section 6.

2 Related literature and research questions

Several studies have examined how physical climate risks affect firms’ borrowing costs. Kling et al. (2021) noted a positive correlation between the two, finding that a firm’s exposure to climatic events has an additional indirect effect on the cost of borrowing because it restricts access to financing. Javadi and Masum (2021) proved that the exposure to drought risk is priced by lenders and associated with an increase in the cost of bank loans. Poorly rated firms suffer the most from the negative effects of drought risk exposure. Similarly, Huang et al. (2022) showed that the costs of corporate financing rise in tandem with the risk of being hit by climate change–related natural disasters.

While numerous studies have established a link between firms’ direct exposure to natural disasters and higher borrowing costs, there remains a gap in understanding how the spatial effects of natural disaster risk influence financing costs. Correa et al. (2022) recently established that lenders charge higher costs even to firms located near disaster areas, pointing to the transmission of the negative effects of extreme events across units. Nonetheless, the field still lacks a definitive answer to whether lenders charge firms based on their geographical proximity to climate-vulnerable firms. In that vein, the present study seeks to determine whether these spatial effects arise before the occurrence of a negative event, such as flooding.

The interplay of concomitant factors may explain why firms’ climate vulnerability is partially transferred to spatially proximate units. First, supplier-customer links act as a potential risk transmission channel. Previous studies have provided theoretical and empirical support to the propagation of climate risk through supply chain connections (Elliott et al., 2019; Henriet et al., 2012; Hertzel et al., 2008; Javadi & Masum, 2021). For instance, Javadi and Masum (2021) showed that a firm’s cost of debt is higher when the firm’s customers are more likely to be hit by natural disasters. The preparations that firms undertake to manage the indirect consequences of natural disasters seem to affect lenders’ perceptions of creditworthiness (Henriet et al., 2012). Second, the extent to which lenders take actions to anticipate and counteract the potential propagation of distress from natural disasters is thought to stem from the structure of the local credit market. Giannetti and Saidi (2019) noted that credit market concentration at the local level facilitates the internalization of negative spillovers associated with supply chain interconnections and asset fire sales. Because high-market-share lenders are prominent providers of credit, they are more likely to provide liquidity to the customers and suppliers of distressed firms when the disruption of supply chains is expected to be costly. In addition, prominent lenders may impose higher rates on borrowers in order to accumulate resources that will serve as liquidity insurance during times of distress (Kysucky & Norden, 2016). Indeed, forward-looking lenders should anticipate the occurrence of negative shocks by implementing a risk management framework that mitigates their adverse effects. Third, such behaviors may be also backed by the nature of lender-borrower relationships. Financial intermediaries engaging in relationship lending may take advantage of lower information opacity to adjust their credit-pricing strategy (Berger et al., 2008). As argued by Kysucki and Norden (2016), a strong lender-borrower relationship can be a double-edged sword for borrowers. On the one hand, a long-term relationship may reduce inefficiencies related to information asymmetries. On the other hand, lenders might pursue an intertemporal pricing strategy whereby they attract firms with seemingly advantageous credit terms and then raising the borrowing costs once the private information is revealed. According to Kysucki and Norden (2016), the former (vs. latter) effect is more likely to be observed in economies with higher (vs. lower) levels of bank competition. Relying on the above conjectures, we test whether the firms’ cost of borrowing incorporates neighboring units’ exposure to the risk of natural disasters. Specifically, we intend to answer the following research question:

  • RQ.1: Does spatial proximity to climate-vulnerable neighbors affect a firm’s cost of debt?

According to the literature on financing decisions (Ozkan, 2001) and borrower-lender relationships (Berger & Udell, 2002; Kysucky & Norden, 2016), there is another element that may exacerbate the transmission of climate risk across proximate units: firms’ size. Kysucki and Norden (2016) highlighted that economies with a high number of small and medium enterprises (SMEs), which face difficulties diversifying their financial sources, are more likely to exhibit higher borrowing costs associated with long-term credit relationships. In this respect, smaller firms typically struggle to raise funds and face credit rationing because of asymmetric information issues and more firm-specific risks (Kirschenmann, 2016; Ozkan, 2001). Unlike larger enterprises, which are more prone to diversifying their debt sources to satisfy complex and varied financial needs (Detragiache et al., 2000; Ongena & Smith, 2000), SMEs may struggle to diversify their financial sources; hence, SMEs tend to have lower bargaining power and higher exposure to negative externalities. Drawing external capital from diverse providers can mitigate larger enterprises’ exposure to single intermediaries’ loan-pricing policies, thus providing protection against localized extreme weather events. In this vein, Davlasheridze and Geylani (2017) investigated the impact of natural disasters on the survival of SMEs in the US. The authors found that small businesses are particularly susceptible to adverse weather events, with disaster loans provided by the Small Business Administration playing a significant role in their survival. Meanwhile, Basker and Miranda (2018) confirmed that smaller firms bear the brunt of natural disasters: for instance, smaller firms in Mississippi exhibited lower survival rates in the aftermath of Hurricane Katrina compared to their larger counterparts.

What existing research lacks, however, is an understanding of how firm size might affect a firm’s vulnerability to the indirect effects of spatial climate spillovers. This gap highlights the need to explore whether smaller firms exacerbate the risks of natural disasters that spill over to neighboring firms. We aim to fill this void by addressing the following research question:

  • RQ. 2: Does proximity to risky neighbors affect smaller firms’ cost of debt to a greater extent than larger firms?

3 Data

3.1 Sample and data collection

We created our dataset using Orbis (Bureau van Dijk) accounting data and the ISTAT database for municipality-level data.Footnote 5 Table 1 features a description of the main variables used along with their sources. Our sample selection process began with all Italian firms covered by Orbis during the period 2016–2019.Footnote 6 We started our sample period in 2016 because the flood risk measure provided by ISTAT refers to 2018, whereas we stopped in 2019 to avoid the influence of COVID-19. Our final sample consists of 419,040 firm-year observations (i.e., 104,760 firms). Tables A1 and A2 in the Electronic Supplementary Material respectively describe the sample selection criteria and the distribution of observations by year-NACE general category.

Table 1 Definitions of variables
Full size table

3.2 Cost of borrowing

Following previous literature (e.g., Kling et al., 2021; Palea & Drogo, 2020), we proxied firms’ cost of debt as the ratio of interest expenses to total financing liabilities at the fiscal year-end. While previous studies have adopted specific bank loan term data (e.g., loan spread) as a proxy for the cost of borrowing (e.g., Huang et al., 2022; Javadi & Masum, 2021), we relied on accounting measures due to the data available for private Italian companies.

3.3 Measuring flood risk

We used data provided by ISTAT to measure flood risk. As of June 2018, ISTAT has distributed an integrated framework on natural risks in Italy at the municipality level, along with demographic, housing, territorial, and geographical information. Similar to Dessaint and Matray (2017), we matched firm-level data with local flood risk using firms’ headquarters municipality name.

ISTAT considers two types of flood risk: those faced by residents of a municipality and those faced by areas within a municipality. For each type of risk, ISTAT defines the following three classes of risk: low risk (P1), medium risk (P2), and high risk (P3). The level of risk is determined by the frequency of floods. Those areas and individuals who are characterized as high risk (P3) are likely to experience floods every 20–50 years; those categorized as medium risk (P2) are likely to experience floods every 100–200 years, while those classified as low risk are unlikely to experience floods at all.

Based on the standard loan duration, we expect that lenders would primarily price high-risk scenarios. Therefore, we constructed our synthetic measure of flood risk (FR) by applying factor analysis to two separate, but related indicators of municipality risk: the fraction of areas at high hydraulic risk (FRarea) and the fraction of residents exposed to a high hydraulic risk (FRpop).Footnote 7 The objective of this data reduction technique is to identify the common factors that underlie a set of covariates. Specifically, it reduces the number of covariates describing a certain phenomenon by identifying linear combinations of variables that provide most of the information contained in the initial variables and, hopefully, enable meaningful interpretation. A factor analysis based on two covariates is considered reliable only if the two variables are highly correlated with each other (i.e., a correlation coefficient greater than 0.7) and relatively uncorrelated with other predictors (Yong & Pearce, 2013). Both conditions are met in our case; however, we use both indicators of flood risk separately as a robustness test. The first common factor (FR) corresponds to the only factor with an eigenvalue greater than 1 (i.e., 1.506) and loading factors of 0.868 for both area and population risk measures. Factor scores were generated using standardized information, resulting in standardized scores as well.

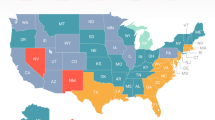
Figure 1 presents an infographic of hydrogeological risk in Italian municipalities. By dividing the overall flood risk into quartiles, we observe that Northern Italy exhibits a higher degree of heterogeneity in hydrogeological risk; by contrast, flood risk in Southern Italy is relatively high and diffused. In light of recent floods, it is not surprising that some municipalities in the Emilia-Romagna region were classified as high-risk areas. Finally, we want to note a lack of data in the mountainous areas and certain inner areas of Sicily and Sardinia.

Fig. 1
figure 1

Hydrogeological risk at the municipality level. The figure shows a map of Italy in which the colors correspond to each municipality’s flood risk level. Flood risk is categorized into quartiles

Full size image

3.4 Defining firms’ neighbors

We considered firm j to be a neighbor of firm i when j falls within a critical distance band from i. Our choice of the optimal distance band flowed from two considerations: First, the distance band should be selected so that each firm has at least one neighbor (so as to prevent firms from being isolated by overly restrictive cutoffs). Second, the critical distance should not feature too much autocorrelation in order to ensure a sufficient degree of heterogeneity in hydrogeological risk.

With s denoting the standardized value of flood risk, and considering that the covariance of standardized variables corresponds to their correlation, we wrote the correlation between a pair of firms i–j as a function of their geodetic distance as follows: \({s}_{{\text{i}}}{s}_{{\text{j}}}=f\left({d}_{{\text{ij}}}\right)+u\), where \(f\left(\bullet \right)\) is an a priori unknown function, \({d}_{{\text{ij}}}\) is the distance between pair i and j, and u is the error term.Footnote 8 We estimated \(f\left(\bullet \right)\) using a non-parametric kernel estimator (Bjørnstad & Falck, 2001). In contrast to other parametric estimators, this approach does not rely on a predetermined spatial weight matrix, but instead allows data to endogenously determine the optimal distance band.

The top panel of Fig. 2 displays the spatial correlogram of hydrogeological risk and represents the non-parametric estimation of \(f\left(\bullet \right)\). This correlogram constitutes an alternative measure of global spatial autocorrelation. As expected, hydrogeological risk exhibited the highest correlations for pairs of firms located within a radius of 5 km. There was also a significant decline in autocorrelation after 10 km, which continued until 25 km.Footnote 9 Unexpectedly, the spatial autocorrelation of hydrogeological risk increased at a distance of 35 km.

Fig. 2
figure 2

Spatial autocorrelation for hydrogeological risk. The upper panel illustrates the change in spatial correlation of flood risk as the distance from pairs of firms increases. The lower panel shows how firm pairs are distributed according to their distance

Full size image

This latter result can be explained by the bottom panel of Fig. 2, which illustrates the proportion of firm pairs that are located at a certain distance from each other. Most firms were located between 7.5 and 12.5 km from neighbors; thus, the distance cutoff of 10 km gives firms enough neighbors to allow for robust inference. In contrast, only a few companies were located above 30 km, which is why the corresponding autocorrelation reported in the top panel is relatively noisy. In general, Italian businesses tend to be concentrated within a radius of 25–30 km.

After having determined the optimal distance band, we computed the average flood risk for all other firms within the neighborhood: \({\overline{{\text{FR}}} }_{{{\text{N}}}_{{\text{i}}}}=\frac{{\sum }_{j\in {N}_{i}}{{\text{FR}}}_{{\text{j}}}}{{N}_{{\text{i}}}}\), with \(j\ne i\). Given \({\overline{{\text{FR}}} }_{{{\text{N}}}_{{\text{i}}}}\), we also computed the difference between the average flood risk for all other firms located in a neighborhood of firm \(i\) (i.e., \(j\in {N}_{{\text{i}}}\), and \(j\ne i\)) and the flood risk faced by firm \(i \left({\text{i}}.{\text{e}}., {{\text{FR}}}_{{\text{i}}}\right):\) \({\overline{{\text{DFR}}} }_{{{\text{N}}}_{{\text{i}}}}\equiv {\overline{{\text{FR}}} }_{{{\text{N}}}_{{\text{i}}}}-{{\text{FR}}}_{{\text{i}}}\). In Section 4 and in the Electronic Supplementary Material, we discuss the reasons for using \({\overline{{\text{DFR}}} }_{{{\text{N}}}_{{\text{i}}}}\) instead of \({\overline{{\text{FR}}} }_{{{\text{N}}}_{{\text{i}}}}\) to capture spatial effects.

3.5 Control variables

Prior literature points to several control variables associated with the cost of debt (e.g., Huang et al., 2022; Jung et al., 2018; Kling et al., 2021). Therefore, we controlled for firm size, performance, liquidity, and financial risk. We accounted for firm size using the natural logarithm of total assets (SIZE) and the ratio of total fixed assets to total assets (TA). As established by previous studies (e.g., Jung et al., 2018; Kling et al., 2021), larger companies are less likely to go bankrupt; therefore, it might be assumed to have a negative correlation with the cost of borrowing. We measured a firm’s profitability as operating income divided by total assets (ROA) (Huang et al., 2022) and operating income divided by total interest expenses (IC) (Ali et al., 2022). We expected that more profitable firms are less likely to go bankrupt; hence, we expected a negative correlation between profitability and borrowing costs. We measured liquidity using the ratio of working capital (operating current assets minus operating current liabilities; WC) to total assets (e.g., Kling et al., 2021; Palea & Drogo, 2020). We expected firms with lower liquidity to pay a higher spread on the cost of debt. Finally, we used the total debt-to-assets ratio (LEV) to account for financial risk. Accordingly, firms with high leverage are riskier, which results in higher debt costs.Footnote 10 Finally, following Huang et al. (2018) and Kling et al. (2021), we added a dummy variable for firms in climate-sensitive sectors (e.g., oil, gas, energy, agriculture) to account for their greater cash flow volatility and the related impacts on borrowing cost.

3.6 Descriptive statistics

Table 2 presents the main descriptive statistics for the dependent and independent variables. As reported, our average sample firm had a borrowing cost of 5.8%, a return on assets of 5.2%, a weight of tangible assets of 24.8%, a debt-to-assets ratio of 23.8%, and interest coverage of 14.2%. Concerning flood risk, on average, 17.7% of areas present a high flood hazard risk (\({{\text{FR}}}_{{\text{area}}}\)), while 14.7% of the population lives in areas with a high flood hazard risk (\({{\text{FR}}}_{{\text{pop}}}\)).Footnote 11

Table 2 Descriptive statistics (Obs. = 419,040)
Full size table

4 Econometric specification

To identify the effect of time-invariant heterogeneity, specifically flood risk, on firms’ borrowing costs, we estimated a cross-regressive model re-written in terms of differential spatial effect. This methodology allowed us to control for unobserved neighborhood attributes that could potentially influence firms’ location and borrowing costs.Footnote 12 Following Mundlak (1978), we also included firm-level, time-averaged variables in the model to consistently estimate both the within- and between-effects of time-varying factors. With respect to a model incorporating firm-specific fixed effects, this approach allowed us to account for the correlation between time-invariant factors and time-varying firm attributes without removing the effects of time-invariant regressors, such as flood risk measures. Formally, we estimated the following linear model:

$${{\text{KD}}}_{{\text{it}}} = {\beta }_{0}+ {\beta }_{1}{{\text{FR}}}_{{\text{i}}}+{\beta }_{2}{\overline{{\text{DFR}}} }_{{{\text{N}}}_{{\text{i}}}}+ {\gamma }^{\prime}{X}_{{\text{it}}}+{\delta }^{\prime}{\overline{{\text{X}}} }_{{\text{i}}}+ {\mu }_{{\text{t}}}+{\varepsilon }_{{\text{it}}}$$
(1)

where \({{\text{KD}}}_{{\text{it}}}\) is the cost of debt by firm \(i\) at time \(t\), \({{\text{FR}}}_{{\text{i}}}\) is the flood risk faced by firm \(i\), \({\overline{{\text{DFR}}} }_{{{\text{N}}}_{{\text{i}}}}\) is the difference between the average flood risk for all other firms located in a neighborhood of firm \(i\) (i.e., \(j\in {N}_{{\text{i}}}\), and \(j\ne i\)) and the flood risk faced by firm \(i ({\text{i}}.{\text{e}}., {{\text{FR}}}_{{\text{i}}})\), \({X}_{{\text{it}}}\) is a set of time-varying control variables (as described in Section 3.3), \({\overline{{\text{X}}} }_{{\text{i}}}\) is the panel-level means of \({X}_{{\text{it}}}\), \({\mu }_{{\text{t}}}\) is the time-fixed effects, and \({\varepsilon }_{{\text{it}}}\) is the error term. All the inferences are based on cluster-robust standard errors.Footnote 13 As mentioned, we considered firms within a 10-km radius as neighbors. If our conjecture on spatial spillovers is true, then the coefficient of \({\overline{{\text{DFR}}} }_{{{\text{N}}}_{{\text{i}}}}\) should be positive. In other words, firm i should face higher financial costs when its neighbors are riskier.

We also estimated a restricted form of Eq. (1) by imposing \({\beta }_{2}=0\). In this way, we tested the existence of a positive effect of flood risk on borrowing costs without considering spatial effects (Kling et al., 2021; Palea & Drogo, 2020). We re-estimated Eq. (1) by removing observations for which \({\overline{{\text{DFR}}} }_{{{\text{N}}}_{{\text{i}}}}\) was zero so as to avoid inflating our estimates with firms whose neighborhoods are entirely located within the same municipality or surrounded by municipalities that are as risky as their own.

After having estimated Eq. (1), we take advantage of the fact that our flood risk measure is at the municipal level, but the spatially lagged variable extends beyond municipal boundaries, so as to be able to control for time-invariant omitted variables at the municipality level that may correlate with both \({{\text{FR}}}_{{\text{i}}}\) and \({{\text{KD}}}_{{\text{it}}}\). This concept is illustrated in Fig. 3, where riskier municipalities are represented with darker shades; some firms in municipality A have neighbors located in municipalities B to F that have different levels of flood risk. In other words, we exploited the fact that firms located within the same municipality differ in terms of neighborhood riskiness. Depending on the number of these firms and the variability of the flood risk measure, we may be able to estimate spatial effects consistently.Footnote 14

Fig. 3
figure 3

Addressing municipality-level omitted variables

Full size image

Thus, Eq. (1) becomes:

$${{\text{KD}}}_{{\text{it}}} = {\beta }_{0}+ {\beta }_{2}{\overline{{\text{DFR}}} }_{{{\text{N}}}_{{\text{i}}}}+ {\gamma }{\prime}{X}_{{\text{it}}}+{\delta }{\prime}{\overline{{\text{X}}} }_{{\text{i}}}+ {\mu }_{{\text{t}}}+ {\mu }_{{{\text{m}}}_{{\text{i}}}}+{\varepsilon }_{{\text{it}}}$$
(2)

where \({\mu }_{{{\text{m}}}_{{\text{i}}}}\) is the fixed effect for the municipality in which firm i is located.

We concluded the analysis related to our first research question by investigating whether spatial effects are symmetric. More precisely, we tested whether negative effects from riskier neighbors are stronger or weaker than positive effects from safer neighbors. Accordingly, we separately estimated Eq. (2) for firms characterized by a safer neighborhood (i.e., \({\overline{{\text{DFR}}} }_{{{\text{N}}}_{{\text{i}}}}<0\)) and firms characterized by a riskier neighborhood (i.e., \({\overline{{\text{DFR}}} }_{{{\text{N}}}_{{\text{i}}}}>0\)).Footnote 15

To answer our second research question, we augmented our specifications with two interaction terms: \({\text{SIZE}}\bullet {{\text{FR}}}_{{\text{i}}}\) and \({\text{SIZE}}\bullet {\overline{{\text{DFR}}} }_{{{\text{N}}}_{{\text{i}}}}\). Both terms are expected to have negative coefficients, indicating that smaller firms incur higher debt costs than larger firms due to their own and their neighbors’ exposure to climate risk. Even in this case, we will also consider the asymmetric effects for firms surrounded by safer or riskier neighbors.

5 Results

5.1 Flood risk externalities

Table 3 reports the estimation results for Eq. (1) with and without spatial difference in flood risk. Column (1) only considers the effect of a firm’s flood risk, without accounting for the possibility of spatial effects. Column (2) also includes the difference between the average flood risk for all other firms located in a neighborhood of firm \(i\) and the flood risk faced by firm \(i\) (i.e., DFR). Finally, compared to Column (2), Column (3) excludes firms with neighborhoods entirely located within the same municipality or surrounded by municipalities with the same risk level. All columns include firm-specific control variables, year-fixed effects, and Mundlak’s correction.

Table 3 Flood risk and cost of borrowings
Full size table

In line with previous studies, the coefficient of FR reported in Column (1) indicates that the firm’s flood risk and cost of debt are positively correlated, while most of the coefficients of the control variables align with previous studies (e.g., Kling et al., 2021). On average, an increase in flood risk by one standard deviation is associated with increased borrowing costs of approximatelyFootnote 16 11.1 basis points (Column 1).Footnote 17 If we consider that FR ranges between − 1.45 and 4.76, firms located in the most dangerous areas are likely to pay 0.745% more than firms located in the safest areas.Footnote 18

Columns (2) and (3) show two important results. First, once we include the spatial difference in flood risk into the model, the coefficient of FR significantly increases. In this case, firms located in the most dangerous areas are likely to pay 1.24% more than firms located in the safest areas.Footnote 19 Second, the coefficient of the differential flood risk for companies located within a 10-km radius of the focal firm is positive and statistically significant. This means that proximity to risky neighborhoods also contributes significantly to firms’ debt costs. Specifically, firms are likely to pay 0.18% more for every unit change in the differential flood risk (i.e., Column 3 of Table 3). Although the coefficients of FR and DFR have similar magnitudes, Table 2 indicates that the former has a higher standard deviation of 0.927 than the latter (with a standard deviation of 0.563). Therefore, using the estimates reported in Column 3 of Table 3, we see that one standard deviation variation of FR leads to an increase of 18.5 basis points in KD, while one standard deviation variation of DFR leads to an increase of 10 basis points in KD. The control variables show firm-level diversity, with the SIZE coefficient revealing that larger firms enjoy lower borrowing costs, likely due to better capital market access (Ozkan, 2001). We will further explore the influence of SIZE on borrowing costs in the next section.

Table 4 reports the estimated coefficients of Eq. (2). Notice that, because the inclusion of municipality fixed effects completely absorbs the effect of direct flood risk on the cost of debt, our results account exclusively for the effect of spatially lagged differences in flood risk on a firm’s cost of debt. The coefficient of DFR in Column (1) is consistent with those in Table 3, demonstrating that our findings are robust to the omission of time-invariant variables at the municipality level. Therefore, even when we control for the time-invariant effects at the municipal level, our previous conclusions regarding the existence of spillover effects from risky neighbors and their negative consequences for small firms remain valid.

Table 4 Flood risk and cost of borrowings (municipality fixed effects)
Full size table

To determine whether negative spillovers from riskier neighbors are stronger or weaker than positive spillovers from safer neighbors, we divided our sample into two subsamples. Specifically, Column (2) only considers firms surrounded by safer neighbors (i.e., DFR < 0), whereas Column (3) only considers firms surrounded by riskier neighbors (i.e., DFR > 0). As shown in these two columns, spatial effects are significant only for firms characterized by riskier neighbors. The coefficient of DFR reported in Column (3) indicates that firms that exhibit the greatest differential risk with respect to their neighbors (i.e., DFR = 3.084) pay 1.23% more on loans (on average) than firms surrounded by neighbors with the same flood risk (i.e., DFR = 0).

5.2 Flood risk, firm size and cost of borrowings

We now examine whether small companies are more vulnerable to climate risk, both directly and indirectly. Table 5 reports the estimates of Eqs. (1) and (2), with and without the spatially lagged difference in flood risk, and augmented by the inclusion of an interaction term between flood risk measures and SIZE. According to all columns, a negative relationship exists between a firm’s size and the marginal impact of flood risk on its borrowing costs. The same result holds for spatial differential risk, especially when considering firms that are surrounded by riskier neighbors (i.e., those whose DFR is greater than zero).

Table 5 Flood risk, firm size, and cost of borrowings
Full size table

As in Table 4, the inclusion of municipality-fixed effects in Column 3 of Table 5 does not significantly alter the estimated impact of the spatial differential risk on the borrowing costs. Moreover, we observe that spatial effects are significant only for firms surrounded by riskier neighbors (Column 5).

Based on the estimated coefficients reported in Columns (2), (4), and (5) of Table 5, Fig. 4 illustrates how the impact of firms’ flood risk and spatially lagged differences in flood risk varies as a function of firm size. The solid black line is derived from Column (2) and shows how the effect of FR changes with firm size. The dashed grey line is derived from Column (4) and shows how the effect of DFR changes with firm size when DFR < 0 (i.e., when we restrict our sample to firms that are riskier than their neighbors). The solid grey line is derived from Column (5) and shows how the effect of DFR changes with firm size when DFR > 0 (i.e., when we restrict our sample to firms with riskier neighbors).Footnote 20 The histogram shows the distribution of firms according to their size, while the vertical reference lines indicate the first, second, and third quartiles of the SIZE distribution.

Fig. 4
figure 4

Spatial spillovers and firms’ size. The point estimates illustrate how the marginal effects of FR and DFR vary with the firm size. The figure distinguishes between spatial effects when DFR < 0 (dashed grey line) and when DFR > 0 (solid grey line). Capped spikes denote the 95% confidence intervals. The histogram shows the distribution of firms according to their size

Full size image

According to Fig. 4, most firms in our sample are small businesses, as expected given the well-known structural characteristics of the Italian economy. The dashed grey line indicates that firms with safer neighbors face no spatial effects. On the other hand, the solid grey line indicates that small businesses face additional borrowing costs due to their riskier neighbors. Vice versa, larger firms on the upper tail of the distribution are not subject to negative externalities associated with their neighborhood. As indicated by the solid black line, large companies do not even pay borrowing costs associated with their own flood risk. As discussed in Section 2, large firms may be able to reduce their exposure to lenders’ climate-risk loan pricing policies by leveraging their bargaining power. This may be due in part to the fact that larger companies are more likely to borrow from different sources and have less opaque financial information.Footnote 21 The pairwise correlation coefficients reported in the Electronic Supplementary Material show that large firms tend to have higher financial leverage, greater interest coverage, less working capital, and lower returns on assets.Footnote 22

In order to corroborate our conjectures, we conducted a mechanism analysis that exploited local concentrations of financial intermediaries.Footnote 23 As expected, we found that spatial effects are concentrated in areas with a small number of financial institutions (i.e., those with greater monopolistic power). Nevertheless, large firms are less susceptible to the bargaining power of these intermediaries.

6 Conclusion

Using Italian firm data and a municipality flood risk metric, this article examined whether firms’ borrowing costs are affected by the climate-related risks faced by their neighbors. The empirical evidence indicates that a one-standard deviation increase in flood risk causes a firm’s debt cost to increase by about 18 basis points. As a result, firms in the highest-risk areas face borrowing costs that are 1.24% higher than those in the lowest-risk areas. In addition, we found that firms’ borrowing cost increases with the flood risk faced by firms located within a 10-km radius of the focal company. To be more specific, an increase of one standard deviation in the neighbor’s flood risk is associated with an increase of 10 basis points in the firm’s borrowing cost. Hence, we provide a comprehensive view of the topic whereby borrowing money implies a cost that varies significantly based on both the firm’s direct exposure to the risk of natural disasters (i.e., floods) and its spatial proximity to climate-vulnerable units.

This study also showed that only small businesses with riskier neighbors are subject to higher borrowing costs, while larger firms are less exposed to neighboring risks. In line with the existing literature, we interpret this result as indirect evidence that a small business’ limited financial diversification reduces its bargaining power (Ozkan, 2001). In this vein, policymakers should enhance local credit markets’ competitiveness to reduce these negative spatial effects. Government aid can provide general and temporary relief, but long-term strategies are essential to support businesses in adapting to mounting disaster risks, thus minimizing their financial exposure and the spread of risk to nearby firms.

Despite its contributions, our study has some limitations. First, our data are limited to Italian firms between 2016 and 2019, which limits the generalizability of our findings. Second, we used municipality-level data for flood risk; hence, future research could benefit from creating more accurate, firm-specific climate risk assessments. Lastly, data constraints prevented us from investigating small businesses’ increased vulnerability to spatial spillovers—an area that merits further exploration.