1 Introduction

Using an aggregate production function, Solow (1957) found that only around 13% of US growth in GDP was due to increases in measured inputs, labor, and capital. The remainder was unexplained, and he proposed that the large residual, 87% of the change in growth, represented technological change. But, explaining the determinants of, and measuring, this technological change has proved to be elusive. Thus, the original notion of inputs generating outputs through an aggregate production function has been extended by more sophisticated measures of inputs, including human capital (Barro 1991), as well as more complex conceptualizations of the functional relationship and the factors underlying it (Barro and Sala-i-Martin 1995). Models of endogenous growth have also extended the framework to consider research and development, patents, and policy (Romer 1986; Aghion and Howitt 1992; Aghion 2017). However, less attention has been paid to the joint role of entrepreneurship and institutions in the growth process.

In a little cited article by Martin L. Weitzman, we have a clue to how these might affect economic growth. Weitzman (1970) replicated the Solow model for the Soviet Union. He estimated that the Solow residual was only in the range of 20%. In other words, in the Soviet Union, increases in factor inputs explained most of economic growth. On this basis, Weitzman correctly foresaw a decline in Soviet growth rates because per worker capital accumulation cannot sustain positive aggregate growth in a Solow framework. What was different between the Soviet Union and the USA was not so much the availability of new technology (as the quality of technical research in the former country was high) but rather in the institutional structure and the incentives for entrepreneurs.

The idea that entrepreneurship and institutions are pivotal in explaining the variation in economic growth not accounted for by changes in factor inputs was a central implication of the ideas of Baumol (1990, 1993; see also Bjørnskov and Foss 2013, 2016). Baumol argued that, even if all countries had similar supplies of entrepreneurs, the institutional structure would determine the allocation to productive, unproductive, and destructive forms of activity. Countries with weak institutions would not incentivize productive entrepreneurship but rather either unproductive or even destructive entrepreneurship (see also Murphy et al. 1993; Parker 2009). Furthermore, Baumol and Strom (2007) went on to argue that as a result of these differing incentives for entrepreneurs, economic growth and performance would vary along with heterogeneity in institutions. Similarly, Aidis et al. (2008) argue that, because the Soviet Union had poor “market supporting institutions” (Acemoglu and Robinson 2012) as well as weak incentives for wealth-creating entrepreneurship, much of its entrepreneurship was indeed of the unproductive or even destructive type. Aidis et al. (2008) showed that even post-transition, productive entrepreneurial activity has remained extremely low in many former socialist economies, especially the former Soviet Union.Footnote 1

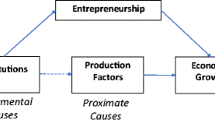
There has been a longstanding literature linking entrepreneurship and growth (Schumpeter 1934; Leibenstein 1968), and over the past 25 years, a large literature has also emerged on institutions and economic growth (North 1990; Acemoglu and Johnson 2005; Acemoglu and Robinson 2012). However, most of the literature has focused on either entrepreneurship (e.g. Koellinger and Thurik 2012) or institutions (e.g. Fatas and Mihov 2013), with less emphasis on the joint effects of entrepreneurship and institutions on economic growth. This leads us to consider whether entrepreneurship and institutions, in combination as an ecosystem, might represent the “missing link” in explaining cross-country differences in economic growth (Braunerhjelm et al. 2010; Acs et al. 2017a, b; Sussan and Acs 2017). The idea is that the stronger the entrepreneurial ecosystem, the more productive will be the technology, and hence the stronger the impact of technology on economic growth. Entrepreneurs thereby act as the agents who, by commercializing innovations, provide the transmission mechanism transferring advances in knowledge into economic growth. However, even where entrepreneurial initiative is present, this process of transmission may be either hampered or facilitated by the institutional environment (Baumol and Strom 2007). To formalize these ideas empirically, we measure entrepreneurship and institutional arrangements independently and combine them in a National System of Entrepreneurship (NSE). The NSE brings together human agency and the institutional context and therefore allows us to compare the combined roles of entrepreneurship and institutions in economic growth.Footnote 2

To develop these ideas, we need also to consider what we mean by entrepreneurship at the national level. Is it self-employment (Reynolds et al. 2005), or is it firm-level behavior (Lumpkin and Dees 1996; Henrekson and Sanandaji 2014), or individual-level cognitive behavior (Shane and Venkataraman 2000; Shane 2012).Footnote 3 According to Acs et al. (2014: 476), “The measurement challenge becomes even more complex when discussing entrepreneurship in countries. If we have difficulty defining entrepreneurship as an individual or firm-level phenomenon, what hope do we have of deciding what ‘entrepreneurship’ means as a county-level phenomenon?” Researchers at the country-level use measures of self-employment, new firm startups, or the Global Entrepreneurship Monitor defined as Total Entrepreneurship Activity (TEA) rate (Carree and Thurik 2003; Erken et al. 2016). In contrast, we propose that country-level entrepreneurship should be treated as a systemic phenomenon similar to the way the literature on National Systems of Innovation (NSI) treats country-level innovation, institutions, and policies. A key message of NSI was that the structure rather than individual processes ultimately determines the innovation productivity of nations (Nelson 1993).

We make three contributions to the literature about the relationship between entrepreneurship and economic growth. First, we review and develop the literature about the relationship between entrepreneurial activity, institutions, and economic growth. One stream has highlighted the crucial role of institutions (e.g. Acemoglu et al. 2005; Acemoglu and Robinson 2012) but has not focused on the impact of entrepreneurship. On the other hand, some analysts have sought to associate entrepreneurial activity with economic growth (see Parker 2009), but the underlying mechanisms have rarely been spelt out and there is as yet limited convincing empirical evidence of the relationship (Carree and Thurik 2003; van Praag and Versloot 2007; Acs and Sanders 2013). We consider whether entrepreneurship and institutions in combination in an ecosystem can improve the explanation provided by an aggregate production function analysis of cross-country differences in economic growth.

Further, we suggest a mechanism whereby greater rates of entrepreneurship in the context of inclusive institutions might raise economic growth. We return to the notion of the entrepreneur as the coordinator of the production process, bringing together labor, capital, and technology to produce output. As Solow (1957) understood, there is an important distinction between replicating existing economic activities in which case growth relies solely on the supply of inputs, and changing the production function which links inputs to output, which generates technical change, raising levels of aggregate productivity (Lafuente et al. 2016). The entrepreneur achieves this by introducing new forms of technology to the production process, but if the rewards to such innovations depend on the institutional arrangements, increased entrepreneurial activity will only raise growth if the institutional environment is benign. We propose a construct which seeks to encapsulate the joint ecosystem of entrepreneurial activity and institutions and which influences the process of economic growth independently from the traditional factor inputs.

Our final contribution is empirical. We use the Global Entrepreneurship Index (GEI) as a measure of the NSE (Acs et al. 2014) and use this construct to test our ideas about the individual and combined impacts of entrepreneurship and institutions on economic growth. We use a panel fixed effects model (Islam 1995) to test the hypothesis that a NSE as measured by the GEI is positively associated with economic growth. We find support for the role of the entrepreneurial ecosystem in economic growth but only a marginal role for the entrepreneur or institutions acting independently.

2 The theoretical background

Solow (1957) proposed to separate variation in national output per head due to technical change from that due to changes in the availability of capital per head. Thus, if Q represents output and K and L represent capital and labor inputs in physical units, then, the Solow aggregate production function can be written as

$$ Q=F\left(K,L;A(t)\right). $$
(1)

The variable A(t) allows for productivity to rise over time without additional factor inputs, technical change. Solow explored empirical specifications of the function

$$ \frac{\dot{q}}{q}=\frac{\dot{A}}{A}+{w}_k\frac{\dot{k}}{k}, $$
(2)

using output per man hour, capital per man hour, and the share of capital to decompose growth into the elements caused by capital inputs and technical change, respectively. Using American data for the period 1909–1949, Solow concludes the following: technical change (A(t)) during that period was neutral on average; the upward shift in the production function was, apart from fluctuations, at a rate of about 1% per year for the first half of the period and 2% per head for the last half; Gross output per man hour doubled over the interval with 87.5% of the increase attributed to technical change and the remaining to increased use of capital.

Technological change is the product of endeavor, especially in the fields of science and engineering. The literature has sought to explain the mechanism enabling the transition from inventions to economic applications which raise total factor productivity (Aghion 2017). The process is not automatic; in practice, many inventions have never been commercialized, and many economies have been for long periods stagnant (Acemoglu and Robinson 2012). We argue that this prolonged absence of convincing and unambiguous results on this mechanism of transition arises because the modeling fails to take sufficient account of potential complementarities and bottlenecks in the relationship between institutions and entrepreneurship. In an early attempt to address this problem, Leibenstein (1968) pointed out that the standard theory of competition gives the impression that there is no need for entrepreneurs. If all inputs and outputs are marketed and their prices are known, and if there is a production function that relates inputs to outputs, then we can always predict the returns for any activity that transforms inputs into outputs. But, one to one correspondence between sets of inputs and outputs is a very strong assumption (see also March and Simon 1993). There are many reasons why that correspondence is broken. Contracts for labor are incomplete, the production function is not completely specified or known, and not all factors of production are marketed (Stiglitz 1989). Returning to the question of the Solow residual, we are left with the issue of what constitutes growth-generating technical change. According to Weitzman (1970: 686), writing about the Soviet economy, “It is at the point that our ignorance of what constitutes the residual becomes really annoying. What is it that should be pushed—increasing returns, labor skills, new innovations, optimal use of resources, better organization, or what?” Jones and Romer (2009) identify two types of attempts to explain the Solow residual. The first is to include the stock of human capital in the production function for a cross section of countries. The switch from a time series for one country (as in Solow 1957) to a cross section has certain advantages. It allows us to look at different levels of development. Barro (1991) in a series of studies for almost 100 countries for the period 1960–1985 found that the growth rate of real per capita GDP was positively related to initial human capital, proxied by school enrolment rates, and negatively related to the initial (1960) level of real per capita GDP, suggesting convergence in growth rates.

The more recent advance—endogenous growth theory—has been based on the emergence of research and development focused models of growth in the seminal papers of Romer (1990) and Aghion and Howitt (1992). This class of models explicitly aims to explain the role of technological progress in the growth process. R&D-based models view technology as the primary determinant of growth yet treats it as an endogenous variable. These are two-sector-models, in which the stock of ideas is an input in the knowledge production function and the variety of ideas creates value (Romer 1990).Footnote 4 In the Romer model, long-run per capita growth is driven by technological progress, but the latter is conditioned by growth in knowledge.

Jones and Romer (2009) bring these points together arguing that progress in growth theory resulted from a tractable description of production possibilities based on a production function and a small list of inputs. Modern growth theory has added ideas, institutions, population, and human capital. Physical capital has been pushed to the periphery. Summarizing the stylized facts, they list the following:

  • Increased flows of goods, ideas, finance, and people—via globalization and urbanization—have increased the extent of the market for all workers and consumers.

  • The variations in rate of growth of per capita GDP increase with the distance from the technological frontier (convergence).

  • Large income and TFP differences persist. Differences in measured inputs explain less than half of the enormous cross-country differences in per capita GDP.

  • Poor countries are poor not only because they have less physical and human capital but also because they use their inputs much less efficiently.

They conclude their paper with the observation that “there is very broad agreement that differences in institutions must be the fundamental source of the wide differences in growth rates observed for countries at low levels of income and for low income and TFP levels themselves” (p. 20).

What exactly are institutions? North (1990: 3) offers the following definition: “Institutions are the rules of the game in a society or, more formally, are the humanly devised constraints that shape human interaction....In consequence they structure incentives in human exchange, whether political, social or economic.” In their survey of institutions as a fundamental cause of growth, Acemoglu et al. (2005: 385) write:

…though this theoretical tradition is still vibrant in economics and has provided many insights about the mechanics of economic growth, it has for a long time seemed unable to provide a fundamental explanation of economic growth. As North and Thomas (1973, p.2) put it: “the factors we have listed (innovation, economies of scale, education, capital accumulation etc.) are not causes of growth; they are growth” (italics in original). Factor accumulation and innovation are only proximate causes of growth. In North and Thomas’s view, the fundamental explanation of comparative growth is differences in institutions.

Of particular importance to growth are the economic institutions in society such as the structure of property rights and the presence of effective market frameworks, “inclusive or market supporting institutions” (Acemoglu and Robinson 2012). Without property rights, individuals will not have the incentive to invest in physical or human capital or adopt more efficient technologies. More generally, economic institutions are important because they help to allocate resources to their most efficient uses; they determine who gets profits, revenues, and residual rights of control. As we noted for the Soviet Union, when markets were highly restricted, there was little substitution between labor and capital and technological change was limited.

How can we think about the combined role of entrepreneurship and institutions in growth? Baumol (1990) argued that entrepreneurial talent can be allocated among a range of choices with varying effects from productive to destructive effects on economic welfare. If the same actor can be engaged in such different activities, then the mechanism through which talent is allocated has important implications for economic outcomes (Desai et al. 2013), and the quality of this mechanism becomes the key criterion in evaluating a given set of institution with respect to growth. Murphy et al. (1993: 506) proposed that countries’ institutions create incentives and that the entrepreneurial talent is allocated to activities “with the highest private return, which need not have the highest social returns”.Footnote 5 The comparison of the USA and the Soviet Union is important in this context because it enables us to isolate the impact of technological innovation from the institutional change.

What was different between the Soviet Union and the USA was not so much in their generation of technology (they both had nuclear weapons and successful space programs) but in technological progress in economic applications. We follow many others, for example Hayek (1945) and Ofer (1987), in proposing that the explanation for this rests upon the institutional system and the incentives that it created for agents to generate decentralized knowledge; we differ in simultaneously stressing the role of entrepreneurs. In the USA, institutions of private property and contract enforcement gave entrepreneurs the incentive to invest in physical and human capital, to combine inputs in ways to create new production functions, and to complete markets. In the Soviet Union, there was also entrepreneurship, but it tended to take unproductive and destructive forms (Aidis et al. 2008).

We therefore propose that entrepreneurs, operating in productive institutional environments, provide the transmission mechanism from innovation to economic growth. This leaves open the question of how to operationalize the features which make the economic system efficient in this process. If we accept that the entrepreneurs are important for the efficient working of the system, to create or carry on an enterprise where not all the markets are well established or clearly defined and in which the relevant parts of the production function are not completely known, an obvious way to approach the problem is to try to incorporate this into an aggregate production function. However, this is not a simple task. We suggest that one way to explore the efficiency of the process is to incorporate entrepreneurship into a system that combines institutions and agency (Acs et al. 2014). The basic Solow model has already been extended to take account of the quality of factor inputs, such as human capital (e.g. Barro 1991; Barro and Lee 1993). Indeed, according to Bergeaud et al. (2017), the quality of labor and capital and the diffusion of innovation explain slightly more than half the share of TFP growth 1913–2010. However, the unexplained residual remains large and this leads us to ask the question: Does entrepreneurship within a context of specific institutions supplement the explanation of the growth process offered by factor inputs?

In particular, we consider the role of entrepreneurship and institutions jointly within an ecosystem. On the institutional side, we build on the ideas of National Systems of Innovation (NSI) (Acs et al. 2017a, b) though entrepreneurship remains mostly absent from this literature with its institutional-centric focus. The other side of the coin has been the tendency of the entrepreneurship literature to concentrate on individual agency but with insufficient reference to the wider, system-level constraints and outcomes of entrepreneurial action.Footnote 6 Central to the entrepreneurship process is not whether opportunities exist but rather, what is done about them and by whom (McMullen et al. 2007). Thus, action by individuals and regulations thereof (bottlenecks) becomes key to the entrepreneurial process. This leads us to think about the role of the entrepreneur’s context not only as a regulator of opportunities and personal feasibility but also as the regulator of outcomes. From a systems perspective, we emphasize the interactions between individuals and their institutional contexts in producing entrepreneurial action. Entrepreneurship can be viewed as individual-led behavior that mobilizes resources for opportunity exploitation through the creation of a new production function. This is subject to complex population-level interactions between attitudes, abilities, and aspirations embedded within a multifaceted economics social and institutional context that drives productivity through the allocation of resources to efficient ends. This leads us to propose the following definition of National Systems of Entrepreneurship (NSE) (Acs et al. 2014):

A NSE is the dynamic institutionally embedded interaction between entrepreneurial attitudes, abilities and aspirations, by individuals, which drives the allocation of resources through the creation and operation of new ventures.

The NSE can be conceived of as a dynamic interaction between entrepreneurial attitudes, abilities, and aspiration. It must also consider entrepreneurial processes within their institutional contexts and recognize the multifaceted multi-level nature of the phenomenon. In our empirical counterpart, we present an empirical measure of the NSE across countries and explore whether it represents a significant additional phenomenon explaining differences in cross-country rates of growth using an aggregate production function.

3 National Systems of Entrepreneurship

Composite indices can capture the multifaceted characteristics like those of NSE (OECD 2008). Our measure of NSE, the Global Entrepreneurship Index (GEI), further incorporates (1) systemic combination of the elements, (2) system dynamics (interaction), and (3) the optimal resource allocation to improve the system performance. We assume that the system of entrepreneurship does not work perfectly, with system failure operationalized by recognizing bottlenecks (Miller 1986; Casadio Tarabusi and Guarini 2013).Footnote 7 Hence, we propose that the building blocks (pillars) of entrepreneurial activity constitute a system where the final outcome is moderated by the weakest performing pillar. Index building is at four levels: (1) variables, (2) pillars, (3) sub-indices, and finally (4) the super-index. All three sub-indices contain several pillars, which can be interpreted as quasi-independent building blocks. The sub-indices of attitudes, abilities, and aspiration constitute the entrepreneurship super-index (GEI). The detailed structure of the GEI is presented in Acs et al. (2014).

To summarize, the GEI scores are calculated as follows:

  1. 1.

    Selection of variables: These variables can be at the individual-level (personal or business) derived from the Global Entrepreneurship Monitor (GEM), Adult Population Survey, or the institutional/environmental level. We employ 16 individual and 15 institutional variables.

  2. 2.

    The construction of the pillars: We calculate pillars by multiplying the individual variable with the appropriate institutional variable. All pillars were normalized and capped.

$$ {z}_{i,j}={ind}_{i,j}\ x\ {ins}_{i,j} $$
(3)

for all j = 1 ... k, the number of pillars, individual, and institutional variables

where zi, j is the original pillar value for country i and pillar j, indi, j is the original score for country i and individual variable j, insi, j is the original score for country i and institutional variable j.

  1. 3.

    Average pillar adjustment: The different averages of the normalized values of the indicators imply that reaching a given value requires different effort and resources. The additional resources for the same marginal improvement of the indicator values should be the same for all indicators. Therefore, we need a transformation to equate the average values of the components.

Pillars are adjusted so the potential minimum value is 0 and the maximum value is 1, calculated for the 2002–2011 time period.

  1. 4.

    Penalizing: The penalty for bottleneck (PFB) methodology was used to create indicator-adjusted values; a loss in one pillar is compensated by the same increase in another pillar at an increasing rate. Modifying Casadio Tarabusi and Palazzi (2004), we define the penalty function as

$$ {h}_{(i),j}=\mathit{\min}\ {y}_{(i),j}+\mathrm{a}\left(1-{e}^{-\mathrm{b}\left({y}_{(i)j}-\mathit{\min}\ {y}_{(i),j}\right)}\right) $$
(4)

where hi, j is the modified, post-penalty value of pillar j in country i, yi, j is the normalized value of index component j in country i, ymin is the lowest value of yi, j for country i. i = 1, 2,……n is the number of countries. j = 1, 2,.……m is the number of pillars. 0 ≤ a and b ≤ 1 are the penalty parameters; the basic setup is a = b = 1.

  1. 5.

    Pillars and sub-indices: The pillars are the basic building blocks of t. The value of the three sub-indices—entrepreneurial attitudes, entrepreneurial abilities, and entrepreneurial aspirations—is the arithmetic average of its PFB-adjusted pillars for that sub-index multiplied by a 100. The maximum value of the sub-indices is 100 and the potential minimum is 0.

  2. 6.

    GEI: This is simply the average of the three sub-indices.

The description of individual variables used in GEI is presented in Table 1.

Table 1 The description of the individual variables used in the GEI (Acs et al. 2015)
Full size table

4 Data and estimation issues

4.1 Specification

To explore empirically whether the entrepreneurial ecosystem helps in an explanation of cross-country growth, we start from Eq. (1) augmented with the National System of Entrepreneurship. This gives us

$$ Q=F\ \left(K,L, NSE;A(t)\right). $$
(5)

For estimation, more specifically, we adopt a standard Cobb-Douglas function based on a product of independent variables. Transforming the latter into logarithms leads to additive functional form. We explore the relevance of the entrepreneurial ecosystem in aggregate growth via the sign and significance of the coefficient on logarithm of NSE in Eq. (5). To address potential omitted variable bias, we also consider in some specifications L to be proxied by both employment and labor quality (human capital).

We noted in our theoretical framework that much of the literature has proposed the relevance of either institutions or entrepreneurship, or both, in the growth process, without reference to the need for an entrepreneurial ecosystem. We therefore also propose to test a version of this idea, namely that growth is influenced by entrepreneurship and institutions separately rather than via an ecosystem. Hence, we suggest, as an alternative specification to that indicated in Eq. (5), that, in addition to the standard factor inputs, output is determined by national-level institutions and/or individual-level entrepreneurial activity, separately. The alternative specification is

$$ Q=F\ \left(K,L,I,E;A(t)\right) $$
(6)

where I is country-level institutions and E represents an indicator of entrepreneurial activity at the country-level. Once again, Eq. (6) is estimated in logarithms. If neither entrepreneurship nor institutions affect the growth process, net of factor inputs, then neither E nor I will be significant in the estimation of Eq. (6). We may also wish to compare the impact of the NSE against the separate institutional and entrepreneurial factors. However, Eqs. (5) and (6) are non-nested, so our comparison in this case is based on a J-test (Davidson and MacKinnon 1981, 1993).

4.2 Data

The data on real GDP growth, fixed capital investment, and labor derive from the Penn World Table (PWT version 8).Footnote 8 For robustness, we also used data derived from the World Bank to measure GDP growth. As noted above, the Global Entrepreneurship Monitor (GEM) forms the individual basis for measures of E and NSE (Reynolds et al. 2005), and the institutional dimensions are largely derived from the World Bank and the World Economic Forum. Our sample for the table is drawn on the 2003–2011 period that is available for all indicators. Note that GEI measures both the NSE as a whole, while its components include E—average country-level individual entrepreneurship—and I—institutions—denoted individual and institutions, respectively. The definitions of variables used in our regression analysis and their descriptive statistics are presented in Table A0 in the online appendix and Table 2, respectively.

Table 2 Variable definitions and descriptive statistics
Full size table

4.3 Estimation issues

We face serious data constraints that limit both the range of feasible estimators and the power of econometric tests we can apply to investigate the relationship between our proposed empirical measure of NSE, individual entrepreneurship, institutions, and economic growth. Despite possible endogeneity, these data limitations make the application of estimation techniques which rely on instrumenting hard to implement. For example, successfully applying dynamic panel data models based on generalized methods of moments proved to be impossible, due to the fact that we do not have a sufficient number of longer sequences of data for countries in our sample. For that reason, we use the robust, if less efficient, fixed effects estimators. At the same time, to make the tests stronger, we apply one additional measure in our base regressions: We take all our variables in first differences—therefore, we have economic growth regressed on changes in employment, fixed capital, the measure of the NSE, and its components. Two issues of estimation are worthy of note. The first is whether to estimate the GEI in logs or levels. It is not clear whether it is appropriate to put an index into logs, though it is often done for consistency. Our aim is to test for robustness, so we present both logs and levels for the GEI and its components.

The second estimation issue has to do with the use of both first differences and fixed effects in our estimation of the underlying production function, a strong specification applied to handle unexplained country-specific heterogeneity in the growth process across countries. This exacting specification is suitable to test our hypothesis on this dataset because data limitations mean that our time period is not very long and the panel is not balanced. If we had a longer time period and a balanced panel, we could regress growth averages on values of the independent variables measured at the beginning of the period, as for example in Sala-i-Martin et al. (2004).

We therefore start by estimating the first differenced, fixed effects specification. We believe it to be more convincing to obtain significant results about the effects of entrepreneurship and institutions on growth in such a demanding specification. Our findings can be compared with those obtained using first differencing only and those based on fixed effects only, as reported in the Appendix (Online Resource).

5 Empirical results

We first estimate a model which only includes our (first difference) measures of the log of capital and labor in column (1) of Table 3. Next, we introduce the full system version of the logged GEI index, estimated in column (2). Finally, we investigate the separate effects of agency and institutions, in which the components making up the GEI index—the individual system (entrepreneurs) index and the institutional system index—enter the equation independently in columns (3) and (4).Footnote 9

Table 3 Fixed effects estimates of economic growth model
Full size table

We observe in Table 3 that the effect of log capital and labor always comes as positive and highly significant. The estimated coefficient on GEI is positive and statistically significant at the 5% level in column (2), the institutional component is mildly significant at the 10% level in column (3), and the entrepreneurial component is also mildly significant at the 10% level.

The comparison of the GEI ecosystem variable as against the individual components is non-nested, so we apply a Davidson-MacKinnon (1981, 1993) J-test to choose between them as better representations of the data. We find that the inclusion of the predicted values from GEI equation into the components specification leaves the institutional components insignificant at the 10% level, but applying the reverse does not eliminate the significance of the GEI index at the 5% level. On this basis, we conclude that GEI does stand against the two sub-components separately for the dataset, as a whole, but the components do not hold against the GEI variable. Hence, while both representations are found to have some significance in explaining the growth process, for the entire sample, the Davidson-MacKinnon test indicates that the specification based on independent components is not preferred to that of the ecosystem. This is in line with our theoretical argument stressing a distinctive role of entrepreneurial ecosystems.

We have undertaken numerous additional regressions to explore our results in more depth. These results on GEI hold when the dependent variable is specified as GDP per capita rather than GDP (always in logs) and the factors are loaded as capital per unit of labor (hence assuming the production function is linearly homogeneous). Thus, in regressions reported in Appendix (Table A.1, Online Resource), we re-estimate columns (1)–(4) using capital per employee instead of capital and labor separately. In these models, GEI is significant at 0.01 level, individual entrepreneurship component loses all significant, and the institutional component gains in significance. Next, we estimate the models utilizing data in levels rather than rate of change. The GEI index is statistically marginally significant in this specification. The institutional variable is significant, while the individual entrepreneurship variable is not. In turn, when we apply first difference but without fixed effect, GEI index is significant at the 1% level, the individual (entrepreneurship) component is not, and the institutional component is. One might also be concerned about the effects of the recession given that our sample covers this period. When a time dummy for the years of the recession is included, the results of interest are not statistically altered, and the recession variable is negative and statistically significant for the years 2008–2011.Footnote 10

The first three columns of Table 4 show results for using first differences of GEI as an alternative and the first logarithmic differences for other variables as before. The results in column (4) replicate the specification from Table 3 for comparison with model (5), which has human capital variable added (Barro and Lee 1993). The human capital variable taken from the Penn Tables is not statistically significant, while the ecosystem variable retaining significance. Similar to Table 3, all these models are replicated in the Appendix (Online Resource), applying per capita specifications, models in levels with fixed effects, and models in first differences without fixed effects (Tables A.1b, A.2b, and A.3b).

Table 4 Fixed effects estimates of economic growth model without logs
Full size table

6 Discussion and conclusions

The original theoretical insight that entrepreneurship should have a positive effect on growth comes from Schumpeter (1934). He argued that entrepreneurship represents the introduction of new combinations of factors in the economy and that the role of the entrepreneur is to shift the production function upwards. Therefore, for Schumpeter, innovation is at the heart of growth and development. The key role of efficiency in growth was also emphasized by Leibenstein (1968). However, most growth theory scholars do not consider the role of entrepreneurship but concentrate on human capital and in endogenous growth theory, R&D, and innovation. We used the example of growth in the USA and the Soviet Union to suggest that they both had technological development via R&D, and the crucial difference for their long-run growth performance was perhaps in the quality of institutions and the implications for entrepreneurship. This leads us to suggest considering entrepreneurship and institutions in combination in explaining the growth process.

In this paper, we used the concept of the entrepreneurial ecosystem measured by the GEI and it is important to note its limitations as well as its strengths. The GEI is a composite index that combines both agency and institutions, a way of thinking consistent with the work of De Soto (2000, 2017), Andersson and Waldenström 2017). With any composite index, there are necessary ambiguities regarding certain components. For instance, in GEI, if we consider the domestic market indicator, in what ways is it good or bad for institutional entrepreneurship if the domestic market is big or small? The Likert scale on which much of the index is based can be thought of being rather opaque. It may be that the appropriate measurement of GEI should be at a more disaggregated level, such as a city, MSA, or some other region that represents an agglomeration which takes account of knowledge spillover and density. We have sought to explain the source of the Solow residual in terms of institutions and entrepreneurship, whether singly or in combination. Explanations of the Solow residual over the past almost 50 years have focused on stocks of capital, labor, human capital, and knowledge, but none of them have provided a full explanation of the variance in growth. We therefore explored the question of whether the interaction of private initiative and adequate institutional frameworks shaped by collective choice captured by the concept of the entrepreneurial ecosystem may be important in the growth process. We provided a preliminary empirical exploration of this idea based on the inclusion of a measure of an NSE, the GEI, in an aggregate production function framework. We have shown that the NSE is positively and significantly associated with economic growth. Hence, though the number of countries under consideration is relatively small and the estimation methods employed are relatively unsophisticated, our results suggest that analyses of entrepreneurial ecosystems could be a promising way forward to understanding variation in cross-country growth rates as well as providing a systemic basis for policy interventions.