Abstract
This paper investigates whether new venture performance becomes easier to predict as the venture ages: does the fog lift? To address this question we primarily draw upon a theoretical framework, initially formulated in a managerial context by Levinthal (Adm Sci Q 36(3):397–420, 1991) that sees new venture sales as a random walk but survival being determined by the stock of available resources (proxied by size). We derive theoretical predictions that are tested with a 10-year cohort of 6579 UK new ventures in the UK. We observe that our ability to predict firm growth deteriorates in the years after entry—in terms of the selection environment, the ‘fog’ seems to thicken. However, our survival predictions improve with time—implying that the ‘fog’ does lift.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Economic dynamics are characterised by a noisy selection environment that (imperfectly) rewards superior performance. This paper investigates whether the selection environment becomes clearer—more predictable—in the years after entry. The benefits of greater predictability accrue to business owners, to providers of finance and to governments. For business owners, the value is the availability of a route-map to enable them to plan ahead and check progress over time (Dencker et al. 2009). For providers of finance, being able to more accurately estimate the optimal date to provide finance is valuable, because too early an investment may be too risky, whereas delay may mean the opportunity is seized by a rival (Cumming et al. 2015). Finally, governments are continually faced with the choice of using taxpayer’s funds to support and stimulate start-ups, or instead to delay support until performance metrics become clearer (Pons Rotger et al. 2012). An optimal combination of support at different stages as new ventures evolve could provide considerable social and economic returns.
This paper is motivated by a desire to explain and then to use these explanations to predict, post-start performance so providing the benefits of greater predictability to all three parties. It takes two alternative measures of performance (Miller et al. 2013)—survival and sales growth—and assesses whether, over time, our ability to explain these two performance variables improves. In the phrasing of this paper—does the fog lift with time? If so, when does this greater clarity appear? Is it after 1 year, or 10 years? Or, does the fog lift only gradually but continually? Is there a clear ‘step’ at a clearly-identified point in time?
Our theoretical starting point is the Levinthal (1991) random walk model which we apply to new, as opposed to well-established, ventures. Here, each enterprise has an initial stock of resources which expands or contracts depending on post-entry growth, which is determined by stochastic shocks. Exit takes place when the stock falls below a minimum threshold.Footnote 1
Given these assumptions we distinguish between new venture sales growth and survival. Following Levinthal (1991), if the sales growth of a new venture follows a random walk, there is no improvement in our ability to predict growth in the years after entry—hence the fog is thick and remains thick over time. However, we assume new ventures have different (financial) resource endowments, enabling those with more resources to survive shocks that would lead to the exit of those with fewer resources. These financial endowments are either present at start-up, or accumulated through post-entry growth. Survival rates are therefore expected to increase and become more predictable, in the years after entry, as surviving new ventures acquire the financial resources that enable them to ‘ride out’ the inevitable vicissitudes of trade that characterise their early months and years.
These predictions for growth and survival are tested using a cohort of 6579 new ventures in the UK, all of which began to trade in the same quarter of 2004, where every financial transaction is tracked over 10 years. With this unique data we show that our ability to explain sales growth decreases as the venture ages, because as time goes by this becomes more random. When we focus only on firms that survive until the end of year 10; however, for this subsample of surviving firms, our ability to predict growth remains constant over time. Regarding survival, our ability to predict which firms will remain in operation increases slightly in the years after entry. Our results are therefore broadly consistent with our model.
Our specific contribution is then to demonstrate that, even if the sales growth of a new venture increasingly approximates a random walk, its survival becomes more predictable. The growth fog becomes thicker over time, but the survival fog becomes less dense. Perhaps the paper most closely related to ours is Lotti et al. (2009), who present evidence that firms converge to a random growth model (i.e. Gibrat’s (1931) ‘Law of Proportionate Effect’) in the years after entry. In our paper, however, we look more widely at our ability to explain growth and survival in the years after entry. Another related paper is Wiklund et al. (2010), who observe that the explanatory power of financial indicators decreases in the years after entry, when the task is to explain survival. In our analysis, we include other variables (beyond financial indicators) as explanatory variables for performance (measured in terms of both survival and growth), and present finer-grained evidence on the year-by-year evolution of the model fit statistics.
The remainder of the paper is set out as follows: Sect. 2 provides the theoretical context that is used in Sect. 3 to derive hypotheses. Section 4 presents our methodology. Section 5 presents the dataset, and we test our hypotheses in Sect. 6. Section 7 concludes.
2 Theory development
Conceptualising firm performance as a random walk has a long history in economics (Gibrat 1931; Ijiri and Simon 1964; Levinthal 1991; Denrell et al. 2015). Random processes produce results that closely match the outcomes of many top performing companies, to the extent that investigating whether or not performance is purely random remains a valid research question (Henderson et al. 2012; Denrell et al. 2015; Storey 2011). This need not imply that managers do not put thoughtful planning and effort into their business decisions, because it could be that competition is so fierce, and businesses are all more or less ‘neck-and-neck’, that there may not be any easily observed systematic factors that allow new ventures to enjoy prolonged above-average performance in the years after entry. ‘Chance models are, in fact, compatible with effortful managers who carry out deliberate actions’ (Denrell et al. 2015, p. 936). Our preference for chance models in this paper is because random walk models offer useful approximations to real-world phenomena (Levinthal 1991; Henderson et al. 2012; Denrell et al. 2015), and also because random walk models can provide simple and clear theoretical predictions that can be developed into testable hypotheses.
Levinthal (1991) was amongst the first to formally explore how random processes could shed light on venture survival in a managerial context. His model had two key assumptions. The first was that firm growth was modelled as a random walk, and the second was that survival depended upon access to resources or assets that could be used to finance the shocks experienced by the business in a random walk.Footnote 2
Levinthal emphasised that the random walk model is compatible with variations in competence amongst enterprises. He writes (p. 399):
While variation in competence should shift the mean of the possible distribution of outcomes, and perhaps the variance as well, the presence or absence of competence does not fundamentally alter the stochastic nature of the process.
The Levinthal (1991) model also puts forward that the amount of the assets is determined by two factors—past performance and initial resources. We assume that access to more financial resources improves the chances of survival. However, there are two key respects in which the assets of the new venture differ from that in an established firm. The first is that, in an established venture, the assets primarily comprise those accumulated over time, whereas those available to the new venture are considerably more likely to be those in place when the venture begins. Second, in an established firm the accumulated assets constitute a ‘track-record’ which can help internal and external parties assess future performance, whereas no such record exists for a new venture. This is particularly problematic for external suppliers of finance—banks, trade creditors—who then seek ‘signals’ of credibility, such as collateral (Voordeckers and Steijvers 2006).
Our model therefore assumes the returns from venture creation are a random walk and this payoff structure attracts individuals who are optimistic and favour situations where, although the expected returns may be negative (Hamilton 2000), the variance is high and positively skewed. Survival, in turn, reflects the availability of resources (i.e. resources available at start-up, as well as those obtained from post-entry performance).
More formally expressed, growth occurs through the following random process:
where x t is the logarithm of firm size at time t, and ε is a random shock (additive in logs, but multiplicative on a linear scale) with mean µ and standard deviation σ.
Survival is a function of the stock of accumulated resources, so survival, S, depends on whether a firm’s resources exceed a minimum threshold size x*:
where x l is a latent variable that corresponds to x if x l > x*, but remains unobserved if x l ≤ x*. If the exit threshold is positive, i.e. x* > 0, then players will not persist until their resources reach zero, but quit the ‘gambling table’ even when resources are positive (Gimeno et al. 1997).
3 Hypotheses derivation
Our primary interest is in whether the selection environment for new ventures improves—becomes more predictable—in the years after entry. To do this we investigate the explanatory power (or goodness-of-fit, represented by the R 2 statistic) of models that seek to explain the growth and survival of new ventures.
3.1 Growth
If new venture growth is a random walk, à la Levinthal, the dynamics of (log) size are x t = x t−1 + ε t , the growth rate (in log-differences; Tornqvist et al. 1985) is expressed entirely in terms of a random shock: x t − x t−1 = ε t . Growth is well approximated by a random walk in the years after start-up, and our inability to make systematic predictions for post-entry growth implies that the expected R 2 from growth regressions is low and remains low in the years after entry.Footnote 3
Hypothesis 1
The R 2 from regressions of the determinants of new venture growth does not increase in the years after entry.
3.2 Survival
To examine survival, firm size at time t is xt, with start-up size being denoted as x 0. In a random walk model à la Levinthal (1991), firm size evolves, with x t = x t−1 + ε t , where ε t is distributed with mean μ and variance σ 2. When μ = 0, we have a pure random walk, whereas when μ > 0 (following Le Mens et al. 2011) then there is a steady increase in expected resource stock over time.
Firms are assumed to exit when their size (proxied by their resource stock) reaches zero. The time taken until the firm first exhausts its resources (i.e. x l ≤ x*, for the case when x* = 0) is expressed as the cumulative distribution function of a random variable in the following way (known as the Bachelier–Lévy formula):
where N(·) represents the cumulative density of the standard normal distribution (Levinthal 1991; Coad et al. 2014). Time to exit is thus a function of three parameters: the trend in the random walk μ, the variance σ 2 of the growth shocks, and start-up size x 0. Footnote 4 Even if growth is a random process, expected survival time can be increased by increasing the size at start-up x 0 (Levinthal 1991; Coad et al. 2014). The R 2 from survival regressions therefore depends on both start-up size and growth since start-up.
We now apply a simulation model to derive implications of the Levinthal random walk model for the evolution of the R 2. We generate an artificial dataset of 50,000 firms, whose start-up size is calibrated according to the lognormal distribution with mean 10.55 and standard deviation 1.5, in order to closely follow the start-up size distribution observed in our data. We then generate a distribution of growth rates, distributed according to the Laplace or ‘symmetric exponential’ (Stanley et al. 1996; Bottazzi and Secchi 2006), with mean µ = −0.1 and standard deviation σ = 0.9 (again, closely following the values observed in our data).Footnote 5 Firm size evolves as a random walk, x t = x t−1 + ε t , given the distributions of start-up size and growth rates given above, for t = 60 periods. The exit threshold x* is set at 7 in the baseline case, which is deliberately chosen to be a relatively high value that will guarantee that in each period some firms will exit (thus avoiding a degenerate value for the R 2 in any year’s survival regression in which all firms survive). For each individual period up to t = 60, we estimate a probit survival regression (with a constant term and a single explanatory variable: lagged size) and record the Nagelkerke R 2 statistic.
Figure 1 shows that the R 2 clearly increases in the years following start-up. This is because, with the passage of time, surviving firms overcome the liability of newness and grow to become sufficiently large that they have accumulated a ‘buffer’ stock of resources, and no longer operate on the brink of the exit threshold. Firms that start small, on the other hand, are more likely to be quickly weeded out through a selection effect. As these chaotic, short-lived firms are removed, the selection environment becomes less ‘foggy’. The central point here is that the R 2 value rises over time even when growth is a random walk.
Evolution of the Nagelkerke R 2 using simulated data, for 60 periods. y-axis: Nagelkerke R 2 obtained from probit regressions where exit depends on lagged size. x-axis: time period. Baseline case (with exit threshold x* = 7) appears as a solid line; x* = 8 for the long-dash line; x* = 9 for the short-dash line. Linear trend-line plotted for the baseline case
Hypothesis 2
The R 2 from regressions of the determinants of new venture survival increases in the years after entry.
4 Testing for changes in the density of the fog
Of crucial interest for our paper is measuring what we call ‘fog’—the coefficient of determination, or R 2 statistic. The standard R 2 statistic is expressed in terms of how well an OLS regression model can explain the total variation in the data:
where SSreg is the regression sum of squares (i.e. the explained sum of squares), SStot is the total sum of squares, and SSres is the residual (i.e. unexplained) sum of squares. The R 2 statistic provides meaningful information on how well a set of variables can explain a given outcome, or how well we can predict real-world outcomes on the basis of our available information (Bertrand and Schoar 2003; see also Syverson 2011, p. 340). Cox and Snell (1989) suggested that the R 2 statistic be generalised to other regression models (such as regression models with binary dependent variables) where maximum likelihood is the criterion of fit. They suggested the following R 2 statistic:
where L(\(\hat{\beta }\)) and L(0) denote the likelihoods of the fitted and ‘null’ models, respectively. The Cox–Snell R 2 statistic has a number of desirable properties (e.g. it is asymptotically independent of the sample size), although a drawback is that it reaches a maximum value that is lower than unity for discrete models (Nagelkerke 1991). Therefore, it has been suggested that the Cox–Snell R 2 be adjusted as follows, to obtain what has become known as the Nagelkerke R 2 statistic, after Nagelkerke (1991):
Because of its desirable statistical properties we use the Nagelkerke R 2 statistic, although we check that our results are not sensitive to this choice of R 2 statistic.
We begin by running regressions on cross sections corresponding to each year, where the dependent variable is either growth rate or survival probability.Footnote 6 For each year we obtain a Nagelkerke R 2 statistic. We then plot the evolution of the Nagelkerke R 2 over time using line charts—one chart for growth, one for survival.
5 The dataset: Barclays bank customer accounts
5.1 Start-up: definition
We exploit a rich and unique dataset drawn from non-financial firms identified as start-ups or new ventures that entered the business customer base of Barclays Bank between March and May 2004. At that time about one in four UK start-ups banked with Barclays. The sample excludes established businesses that switched from another Bank. We are aware that a new business does not necessarily start trading immediately upon opening an account. Indeed, for Barclays’ customers, approximately five per cent of start-ups show no activity through their account in the subsequent 12 months. We addressed this by only including firms that showed activity in the month following entry to the customer base.Footnote 7 , Footnote 8
We therefore focus on a cohort of 6579 firms that have the same start date. We consider this to be important, because firms starting in different years may not be readily comparable (especially if the macroeconomic conditions at start-up have persistent effects on firm development in subsequent years). Focusing on a single cohort means that firms face the same macro-economic conditions at each year of their development and can therefore be meaningfully compared (Ryder 1965; Anyadike-Danes et al. 2015). We then track the cohort for a maximum of 10 years, a period of time that we consider to be sufficiently long for our purposes, given that over 80 % of the ventures will have exited in that time (Anyadike-Danes and Hart 2014).
5.2 Start-up: data
Prior to opening the new business account, data were collected on the founder(s) gender, age, highest level of educational qualifications; prior business experience; previous ownership; and/or ownership amongst immediate family members. Finally, to capture access to non-financial resources, owners were asked about the sources of advice and support they used prior to start-up.
These data were then supplemented by the bank as part of its general account opening process. This covers the legal form of the business, the activity type (sector/branch/market) and its location (standard region) within the UK. Table 2 in ‘Appendix’ sets out the data definitions in full.
5.3 Ongoing data
To measure the size of the business we used credit turnover—the value of payments into a current account,Footnote 9 which we will refer to as ‘sales’. This serves as a very close approximation to sales revenue inclusive of taxes.Footnote 10 The much greater granularity of sales compared with using measures of employee numbers is a particular strength.Footnote 11 It is also reliable, comprehensive and, because every financial transaction is documented, the scale of volatility can be reliably quantified. Although credit turnover was initially observed by the bank at monthly intervals, the data we have have been aggregated over 12 months to analyse annual values, since our focus here is to explain long-run, rather than short-run changes.
5.4 Exit and closure
Establishing precisely when a business has closed is perhaps the most challenging aspect of any study of new ventures. Even for datasets taken from near comprehensive official sources, the date at which exit occurs may be some time after actual closure.Footnote 12
When using bank records, there are two main issues to resolve. The first is to distinguish between those businesses that have closed, and those that have switched to another bank. For our dataset we used Barclays closure-reason-codes that record why any given account has been closed. 1.38 % of our initial sample switched over the 10 years covered by the dataset, i.e. they had closed their account with Barclays, but continued to trade.Footnote 13 These were dropped from our sample before we started the analysis.
The second issue is judging when a given business has actually closed. While the majority of Barclays customers ceasing to trade clearly close at a specific time when no more transactions take place, an important minority become dormant, i.e. their account remains open, but with no activity.Footnote 14 For the firms in our sample we used a simple rule—if the business had shown no sales in consecutive 6-month periods, then it was deemed to have closed in the first of these periods.Footnote 15
It is important to note that this process identifies closures. It is not limited to business ‘failures’. By the latter we mean those firms that cease to trade with some external financial liability. Of course, as noted earlier, a closing firm may, or may not, have met the objectives of its owner(s), although closure may equally reflect that a better opportunity has presented itself to the business owner(s) (Headd 2003; Harada 2007). Finally, cases of entrepreneurial exit (but business continuation) such as an initial public offering (IPO), merger or acquisition (M&A) or trade sale will not have a confounding effect on our measurement of business exit (Wennberg et al. 2010; Coad 2014), because if the firm continues operations with the same bank account, it will be treated in our dataset as a continuing firm, whereas if it switches its bank account to a different bank, it will be treated in our dataset as a ‘switcher’ and dropped prior to analysis. Nevertheless, cases of IPOs, M&As and even trade sales are negligible because our new ventures are both young, small and representative of all sectors (apart from financial services). The tech-based services in which these outcomes are particularly characteristic constitute only a tiny proportion of the sample.Footnote 16
5.4.1 Dependent variables
We take two dependent variables as alternative indicators of new venture ‘performance’ (Miller et al. 2013). Survival is a binary variable, equal to 1 if the enterprise continues to trade at end of period (=0 if the enterprise exited). The Growth Rate is measured in terms of growth in credit turnover (or ‘sales’, the value of payments into a current account) excluding payments from a related account (deposit account).Footnote 17 Sales growth has many advantages over other metrics of growth, such as employment, for new ventures. The first is because growth in terms of employment is ‘clunky’ (Coad et al. 2015, p. 6) due to integer constraints in terms of employee headcounts. These are particularly important for new ventures (e.g. a solo self-employed individual contemplating her first hire, who can either remain static or double her size—and nothing in between).Footnote 18 Second, the decision to take on a new/first employee is a huge decision by a NV and presents problems of interpretation since it reflects a, difficult to specify, combination of past and current performance as well as future expectations. Finally, most new ventures, in our sample, are too small to employ others—certainly when they start to trade.Footnote 19
We calculate the annual growth rate in the usual way (see e.g. Tornqvist et al. 1985; Coad 2009) by taking log-differences of sales, i.e.
We estimate regression equations 1 year at a time, one cross section at a time, to obtain an R 2 statistic for each year. A logistic regression model is applied for our survival estimations (Jenkins 1995; Wiklund et al. 2010), which is compatible with our focus on survival/death within a single year (rather than survival durations over many years). Our regression equations for the growth and survival of firm i in year t are as follows:
where our explanatory variables can be grouped together at the entrepreneur level (age, education, business experience, sources of advice), the business level (number and gender of owner(s), legal form, industry, region), and the bank account level (volatility, overdraft behaviour).Footnote 20
5.4.2 Independent variables
The independent variables used in the analysis are defined in Table 2 in ‘Appendix’. It also sets out where these variables have been used in previous work on survival/growth of new/small enterprises and the results obtained. The first group are the ‘usual suspects’ such as Legal form (Company, Partnership, Sole Trader); Number of owners; Gender; Age (and Age squared); Education level categories; Sources of advice (EABL scheme, Accountant, Solicitor, College, SR Seminar, PYBT scheme, Family, or Other), and a full set of dummies for industry and geographical region.
A second group is information on bank account activity: sales volatility, availability and extent of use of authorised overdraft facilities, and the use and extent of use of unauthorised overdrafts. These variables have not been explored in previous work that seeks to explain firm growth and survival, and so their inclusion can be considered to be a strength of this paper.Footnote 21
Table 2 in ‘Appendix’ does not point to the omission of key variables that might cause our regression equations to be grossly misspecified. Prior work on firm growth generally has low values for the R 2 statistic (usually lower than 15 %, see the survey in Coad 2009, Table 7.1) so although there remains a risk of specification error and omitted variable bias, there are no clear guidelines in the literature as to which (if any) variables or regression specifications would be more appropriate.
5.5 Summary statistics
Table 1 provides an overview of the size and growth of new ventures in our sample which, it will be recalled, all began trading in the second quarter of 2004. The median sales in year 1 (i.e. 2005) are £38,712 which is far smaller than the threshold for value-added tax (VAT) registration (set at £58,000 for the 12 months from 1 April 2004, and rising to £73,000 by 1 April 2011), above which firms start to appear in UK administrative datasets. Around 50 % of new ventures will exit within 3 years of starting to trade, which is similar to that observed from UK administrative data on new ventures (Anyadike-Danes and Hart 2014).
To investigate the impact of our rich coverage of micro firms, we complement our baseline results with those obtained from restricting our sample of new ventures to those of above-median start-up size. This makes our sample more similar to other work on new ventures that has a disproportionate coverage of larger new ventures (Yang and Aldrich 2012). The significance of this is that, only by year 10, would the median surviving firm from this dataset have had sales sufficient for them to be included in official data.
A second key fact to emerge from the lower section of Table 1 is that (positive) growth in sales is by no means the ‘norm’ for new ventures. The mean growth rate is negative in every single year, although the median growth rate is only negative in 3 years. The term ‘sales growth,’ when applied to NVs, is for this reason potentially misleading if it is not understood that growth rates can be negative (Davila et al. 2015). Indeed, negative growth rates (i.e. decline) are very common.
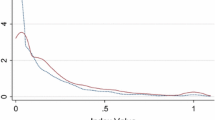
Figure 2 presents the growth rate distribution, which resembles the usual Laplace or symmetric exponential distribution found in other work (Bottazzi and Secchi 2006; Coad and Tamvada 2012; Daunfeldt and Halvarsson 2015). In every year, about half of the firms will have negative growth rates, which emphasises further that our use of the term ‘sales growth’ does not imply that new ventures all have (positive) growth, but that there are many cases of decline (i.e. negative growth rates).
Summary statistics for the explanatory variables are presented in Table 3 in ‘Appendix’.
6 Testing the hypotheses
This section presents the crux of our empirical contribution, which can be found in our plots of the evolution of the R 2 statistic over time (see Figs. 3a, b, 4). We present the evolution of the Nagelkerke R 2 statistic for four regression specifications—in some cases we include lagged growth as an explanatory variable (at the cost of losing an extra year’s results), and in some cases we focus on a subsample of relatively large firms (i.e. those with above-median sales in year 1). Regression results tables for the baseline specification are also presented for the sake of completeness as Tables 4, 5 and 6 in ‘Appendix’.
a OLS growth regression Nagelkerke R 2 statistics for individual cross sections for the first 10 years, for 4 different growth rate regression specifications and b OLS growth regression Nagelkerke R 2 statistics for the first 10 years, for 4 different growth rate regressions (NVs that survive until the end of year 10). Key: Baseline: full sample. Baseline + lag: full sample controlling for lagged growth. Largest startup size: above-median start-up size only. Largest startup size + lag: above-median start-up size subsample, controlling for lagged growth
Logit survival regression: Nagelkerke R 2 statistics for individual cross sections for first 10 years, for 4 different survival regression specifications. Key to regression specifications: the baseline model refers to the full sample with or without controlling for lagged growth. Regressions labelled ‘large startup size’ refer to a subsample of firms with above-median start-up size (i.e. above-median values of sales in the first year)
6.1 Plotting the R 2 statistics
6.1.1 Sales growth
Figure 3a shows how the Nagelkerke R 2 statistic for sales growth regressions evolves over the first 10 years. It starts off in year 2 at values of 28–37 % (depending on the regression specification), which is considerably higher than normally found in the literature on growth rate regressions (no doubt due to our unusually rich information on business behaviour). A closer look at the regression coefficients, reported in Table 4 in ‘Appendix’ for the baseline model, shows that the most significant variables are the bank account activity variables (volatility and overdraft behaviour).
Figure 3a shows that the R 2 decreases in the years after entry for the four specifications shown. In year 2 it is in the range of 27–37 %, whereas by year 10 it is in the range of 13–22 %. Year 5, which corresponds to the deep recession of 2009, does not stand out or interrupt the overall trend. As new ventures age, it seems to become increasingly difficult to accurately predict their growth. This implies the fog seems to thicken and is in line with Lotti et al. (2009), who observe that Gibrat’s Law appears to hold as a ‘long-run regularity’ as time goes by, and growth becomes harder to predict.
Another observation is that, from both Fig. 3a, b, for nearly all years, the Nagelkerke R 2 values for the equations that only include the larger enterprises (i.e. the ‘large startup size’ subsample) are higher than for the baseline sample. This implies it is harder to explain the growth performance of smaller firms, which exhibit greater volatility. This may explain, at least in part, why analyses using relatively large and well-established ‘new ventures’ (Hmieleski and Baron 2009; Dencker et al. 2009; Baum and Bird 2010) are able to show higher explanatory power than those included here.
Table 4 in ‘Appendix’ shows this decreasing trend in the explanatory power of our regressions is observed for alternative indicators of goodness of fit—the standard R 2 statistic as well as the Cox–Snell R 2 statistic—for the baseline case. Further explorations show that this is also the case for the 3 other regression specifications (results available upon request).
Figure 3a shows that the explanatory power of growth rate regressions decreases over time, but it does not explain why. Changes in the ‘fog’—our ability to predict growth—could be due to internal developmental factors in new firms, or they could reflect selection effects—whereby the composition of the sample of survivors is affected by the selective exit of certain types of firms.
Indeed, previous research has shown that many firms will exit in the years after entry (Audretsch et al. 1999; Santarelli and Vivarelli 2007), and it could be that changes in our ability to explain growth are due to changes in the sample composition over time. One way of eliminating the role of selection effects is to restrict the analysis to only those firms that survive the full 10-year period. Any change in the ability to explain growth for this subsample would then be due to internal developmental factors rather than selection effects.
The results are plotted in Fig. 3b (and the regression results for the baseline case are presented in Table 5 in ‘Appendix’). For the subsample of surviving firms, the R 2 shows no clear trend over time. For surviving firms, there is no clear change in our ability to explain their growth in the years after entry. Any deterioration in our ability to explain growth in the years after entry (shown in Fig. 3a) would therefore seem to be driven by the relative ease of explaining the growth (or perhaps more precisely: the decline) of short-lived firms.Footnote 22
Overall, therefore, the evidence in Fig. 3a, b suggests that our ability to explain growth deteriorates in the years after entry, with this becoming closer to random over time. This seems to be driven by the changing composition of the sample of surviving firms (i.e. selection effects) rather than any internal developmental factors within firms. Focusing on a core subsample of NVs that survive until the end of year 10 (and thus removing any sample composition effects because we have the same number of observations in each year), our ability to explain growth remains roughly constant over time (Fig. 3b). Overall, this mixed evidence is in keeping with Hypothesis 1.
6.1.2 Survival
To test Hypothesis 2 we run year-by-year regressions (presented in detail in Table 6 in ‘Appendix’ for the baseline case) and plot the evolution of the Nagelkerke R 2 statistics in Fig. 4. The ‘fog’ regarding survival—i.e. our ability to explain the survival of firms—seems to clear in the years after entry. Figure 4 shows how the Nagelkerke R 2 starts off at around 15 % in year 2 and increases to 26–36 % by year 10. This is consistent with our simulation model and the predictions of Hypothesis 2.
The key difference between the growth rate regressions (Fig. 3a, b), on the one hand, and the survival regressions (Fig. 4), on the other hand, is that ‘the fog clears’ in the years after entry when the task is to explain survival, yet it remains dense when the task is to explain growth.
6.2 Robustness analysis
Further evidence on the robustness of our findings comes from considering alternative measures of goodness of fit, in addition to the Nagelkerke R 2. These are shown at the bottom of Tables 4, 5 and 6 in ‘Appendix’. For the growth regressions, the R 2 and Cox–Snell R 2 statistics closely mirror the Nagelkerke R 2, with no clear trend in the R 2 statistic. For survival, we report the Cox–Snell R 2, as well as information on the percentage of cases correctly classified: the latter increase in most years after start-up, hence confirming our earlier results using the Nagelkerke R 2 statistic. The Cox–Snell measure provides results that are less clear-cut, however: although it rises during the early years, it reaches a peak in year 6.
Another way of exploring the robustness of our results is by taking an alternative regression specification with a different set of explanatory variables. Earlier we commented on the fact that our database contains a number of variables relating to bank account activity, which constitute a rich and unique source of information on firm behaviour, although these variables remain little-known in the literature, and also they may raise concerns of endogeneity (e.g. risky unauthorised overdraft behaviour may be a cause or a consequence of poor performance in terms of growth or survival prospects). We repeated the analysis excluding the variables relating to bank account volatility and obtained the following results. For the growth rate regressions, a first observation was that the Nagelkerke R 2 statistics were very low, in the range of 3–7 % for our baseline specification. If anything, the Nagelkerke R 2 statistics appeared to increase slightly in the years after entry, although this increase was not monotonic. When the growth rate regressions were performed on the core sub-sample of firms surviving until the end of the 10-year period, the Nagelkerke R 2 generally decreased, if anything, in the years after entry. Our clearest results were observed in our survival regressions, where the Nagelkerke R 2 followed an increasing trend in the years after entry. All in all, when we repeated the analysis without the bank account activity variables, our results for survival were relatively clear in showing that the survival ‘fog’ tends to clear in the years after entry (i.e. that the Nagelkerke R 2 generally increases in the years after entry). Our results for growth were less clear-cut, probably because after dropping the bank account variables the overall explanatory power was very low (Nagelkerke R 2 statistics of around 5 % or lower) and hence the lower signal-to-noise ratio made it hard to detect any clear trend.
7 Conclusion
Business owners, providers of finance, and governments have much to gain from developing a better understanding of the factors influencing the performance of new ventures (NVs) in the years after entry. The starting point for this paper was that the post-entry performance of new ventures is highly diverse, the selection environment is noisy (characterised by imperfect mechanisms of survival/growth of the fittest), and that our ability to explain and perhaps forecast the survival/growth in new ventures is weak. In the terminology of this paper, the fog was thick. The challenge therefore was to examine whether, as the new venture aged, it became easier to explain performance: did the fog lift? Our final question was, if the fog does lift with time, did visibility improve in steps or stages (Phelps et al. 2007; Levie and Lichtenstein 2010) or was the process more continuous?
To address these questions we primarily drew upon a theoretical framework that sees new venture sales growth as a random walk (Levinthal 1991; Le Mens et al. 2011), and survival being determined by the stock of available resources (proxied by size), where these resources are either present at start-up or accumulated after entry. We used this theory to derive testable hypotheses that our ability to explain growth (i.e. the R 2 from growth regressions) should remain low over time, but that our ability to explain survival should increase in the years after entry.
We conducted our tests on 6579 new ventures which, because they were genuinely representative of NVs, were on balance considerably smaller than those identified in prior work. These NVs were tracked over the years 2004–2014, generating two key findings. First, in the sales growth regressions, the goodness-of-fit measure (Nagelkerke R 2) decreases in value in the years after entry—implying that our ability to explain firm growth deteriorates, or that ‘the fog thickens’. However, when we sidestep issues of ‘selection’ and focus only on a subsample of NVs that we know will survive until the end of the period of observation, then our ability to explain the growth in this subsample of survivors remains low but does not change over time. Hence, any decrease in our ability to explain growth in the years after entry appears to be driven by the presence of short-lived firms, rather than being due to internal developmental factors within surviving firms. In any case, our ability to explain growth remains low throughout the period investigated.Footnote 23 Second, in the survival equations, using three performance metrics we find that, on balance, the goodness-of-fit increases in years since start-up. This suggests that the fog does lift somewhat with time when the task is to predict survival.
In terms of the questions posed at the start of the paper, we take our evidence as showing that the growth rate fog is always thick and shows no signs of improvement with time, in line with our theory. Survival visibility, however, does seem to improve with time, but not in a clear ‘step’ fashion.
Finally, we see important areas for developing this approach. Currently our data track a cohort of new ventures during an unusual period—beginning in benign macro-economic conditions that are followed by a deep recession. Ideally we would like to know whether our findings hold under different macro-conditions. However, future efforts in this direction will face challenges of obtaining comprehensive datasets on NVs (from year 1) that also include a rich set of explanatory variables.
Notes
Gimeno et al. (1997) extend this framework to allow for individual-specific thresholds, according to which some individuals with attractive outside options may exit before they reach a minimum level of resources. Furthermore, one could conceive possible extensions in which the exit threshold is not exogenous but endogenous and potentially time-variant.
The Levinthal (1991) model assumes that exit takes place when the business cannot meet its financial obligations. However, Gimeno et al (1997) shows that the ability to assemble these resources is endogenous in the sense that they vary according to the alternative employment options open to the business owner(s).
We consider it trivial that the R 2 will be low and driven by stochastic noise, therefore we do not see the need to use a simulation model here to demonstrate the evolution of the R 2.
It was correctly pointed out to us by a Referee that this does not capture the situation where “a wealthy entrepreneur operates a very small firm (with a low amount of annual sales). Such a small firm could experience negative shocks which are then financed by the personal wealth of the entrepreneur”. We acknowledge that this highlights a mismatch between the theoretical construct and the empirics. However we do not see how this could be resolved, since even the Bank has an imperfect idea of the wealth of its clients and would only be incentivised to quantify that wealth in the unlikely event that this particular NV were seeking large funding.
See Table 1 for summary statistics on our dataset.
Note that, in contrast to a large body of research on survival models, we do not investigate the determinants of a firm’s total survival duration, but instead the chances of survival for any one particular year.
We also included a small proportion of firms who did not show activity in their first full month, but in either May or June 2004. In these cases the start month of the firm was recorded as the month prior to activity.
The UK, unlike many countries in continental Europe, is not characterised by multiple banking (Ongena and Smith 2000). The account at a single bank is therefore likely to capture the full trading activities of the new venture.
Excluding payments from related accounts, e.g. deposit accounts held by the business.
Prior empirical work has measured growth in terms of numerous metrics such as employment, sales, profits, business valuation. We follow Zimmerman and Zeltz (2002, p. 417) who explain that “growth in sales is especially important for new ventures since their economies of scale are too important for them to continue without increasing their scale of operations.”
These strengths are discussed in more detail shortly.
For example Storey et al (1987, p. 45), in a study of the closure of 177 Limited Companies that “failed”, identified seven decision-rules that were required to identify the year in which the enterprise ceased to trade.
This could be an understatement of the true number if there were imperfections in the reporting process meaning that some switchers were not recorded. However, our rates are broadly in line with Fraser (2005, p. 90) for all types of UK (SME) businesses.
Indeed, some of these may have switched rather than closed.
Some Barclays customers can show little or no activity for a number of months before seeing turnover return to non-negligible levels. This reflects the nature of many ‘micro’ businesses.
It has been pointed out to us, both by referees and others, that this procedure of retaining the same bank account number is not the case in other countries and contexts. We think our classification is a clear benefit, since it also includes the tiny proportion of new ventures that might grow by acquisition in their early years.
Our indicator of growth rates is continuous and can be positive or negative (i.e. decline). We agree with Davila et al. (2015) that the research community has focussed disproportionately upon both growth and high growth.
Detailed data on fractional or part-time employees, total wage bill, or total hours worked, are extremely unusual in longitudinal databases on new venture performance.
Datasets which identify new ventures as those taking their first employee are therefore likely to be both larger and longer-established than those identified as making sales for the first time.
We do not claim to have resolved the endogeneity between the explanatory variables and the performance outcome variables. We also do not claim to have discovered causal effects regarding growth or survival. Instead, we are interested in describing how the R 2 statistics change in the years after entry.
However, their inclusion may introduce endogeneity into the analysis of growth and survival (e.g. although bank account activity may affect survival and growth, future survival and growth prospects may precede or co-evolve with bank account activity). We therefore remind the reader that the coefficient estimates for our variables reflect partial correlations (i.e. associations) rather than causal effects. We also investigate how our results change according to whether or not these bank account variables are included.
More specifically, it appears that our ability to explain the relative growth performance of short-lived firms is largely due to the bank account activity variables. When these variables are omitted, we can no longer observe that our ability to explain growth decreases in the post-entry years. (If anything, it seems that our ability increases post-entry, when bank account activity variables are not included.) These extra results are available from the corresponding author upon request.
Our finding that there is little predictability in sales growth is in itself a valuable finding, with many implications for scholars and providers of finance. Some (admittedly speculative) possible implications can be mentioned here. First, stakeholders might be encouraged to take a broad-based approach to investing, rather than trying to invest in just one firm suspected of soon embarking on fast growth; and second, it hints that there might be little to be gained for investors from investing too heavily in collecting detailed information on firms to predict their growth performance—because growth is so hard to predict.
References
Anyadike-Danes, M., Bjuggren, C.-M., Gottschalk, S., Hölzl, W., Johansson, D., Maliranta, M., & Myrann, A. (2015). An international cohort comparison of size effects on job growth. Small Business Economics, 44, 821–844. doi:10.1007/s11187-014-9622-0.
Anyadike-Danes, M., & Hart, M., (2014). All grown up? The fate after 15 years of the quarter of a million UK firms born in 1998. Sept 14th, Mimeo.
Audretsch, D. B., Santarelli, E., & Vivarelli, M. (1999). Start-up size and industrial dynamics: Some evidence from Italian Manufacturing. International Journal of Industrial Organization, 17, 965–983.
Baum, J. R., & Bird, B. J. (2010). The successful intelligence of high growth entrepreneurs: Links to new venture growth. Organization Science, 21(2), 397–412.
Bertrand, M, & Schoar, A. (2003), Managing with style: The effect of managers on firm policies. MIT Sloane School of Management, Working Paper 4802-02.
Botham, R., & Graves, A. (2011). Regional variations in new firm job creation: The contribution of high growth start-ups. Local Economy, 26(2), 95–107.
Bottazzi, G., & Secchi, A. (2006). Explaining the distribution of firm growth rates. Rand Journal of Economics, 37(2), 235–256.
Chrisman, J. J., & McMullan, W. E. (2004). Outsider assistance as a knowledge resource for new venture survival. Journal of Small Business Management, 42(3), 229–244.
Coad, A. (2009). The growth of firms: A survey of theories and empirical evidence. Cheltenham: Edward Elgar.
Coad, A. (2014). Death is not a success: Reflections on business exit. International Small Business Journal, 32(7), 721–732.
Coad, A., Frankish, J. S., Nightingale, P., & Roberts, R. G. (2014). Business experience and start-up size: Buying more lottery tickets next time around? Small Business Economics, 43(3), 529–547.
Coad, A., Frankish, J. S., Roberts, R. G, & Storey D. J. (2016 forthcoming). Why should banks provide entrepreneurship training seminars? International Small Business Journal. doi: 10.1177/0266242615593138.
Coad, A., Frankish, J. S., Roberts, R. G., & Storey, D. J. (2013). Growth paths and survival chances: An application of Gambler’s Ruin theory. Journal of Business Venturing, 28(5), 615–632.
Coad, A., Frankish, J. S., Roberts, R. G., & Storey, D. J. (2015). Are firm growth paths random? A reply to “Firm growth and the illusion of randomness”. Journal of Business Venturing Insights, 3, 5–8.
Coad, A., & Tamvada, J. P. (2012). Firm growth and barriers to growth among small firms in India. Small Business Economics, 39, 383–400.
Cox, D. R., & Snell, E. J. (1989). The analysis of binary data (2nd ed.). London: Chapman and Hall.
Cumming, D. J., Ari Pandes, J., & Robinson, M. J. (2015). The role of agents in private entrepreneurial finance. Entrepreneurship Theory and Practice, 39(2), 345–374.
Daunfeldt, S.-O., & Halvarsson, D. (2015). Are high-growth firms one-hit wonders? Evidence from Sweden. Small Business Economics, 44, 361–383.
Davila, A., Foster, G., He, X., & Shimizu, C. (2015). The rise and fall of start-ups: Creation and destruction of revenue and jobs by young companies. Australian Journal of Management, 40(1), 6–35. doi:10.1177/0312896214525793.
Dencker, J. C., Gruber, M., & Shah, S. K. (2009). Pre-entry knowledge, learning and the survival of new firms. Organization Science, 20(3), 516–537.
Denrell, J., Fang, C., & Liu, C. (2015). Chance explanations in the management sciences. Organization Science, 26(3), 923–940.
Frankish, J. S., Roberts, R. G., Coad, A., Spears, T. C., & Storey, D. J. (2012). Do entrepreneurs really learn? Or do they just tell us that they do? Industrial and Corporate Change, 22(1), 73–106.
Frankish, J. S., Roberts, R. G., & Storey, D. J. (2010). Enterprise profiles in deprived areas: are they distinctive? International Journal of Entrepreneurship and Small Business, 9(2), 127–142.
Frankish, J. S., Roberts, R. G., & Storey, D. J. (2011). Enterprise: A route out of disadvantage and deprivation? In A. Southern (Ed.), Enterprise, deprivation and social exclusion: The role of small business in addressing social and economic inequalities. London: Routledge.
Fraser, S. (2005). Finance for small and medium-sized enterprises. CSME, University of Warwick, UK.
Gibrat, R. (1931). Les inégalités économiques: applications, aux inégalités des richesses, à la concentration des entreprises, aux populations des villes, aux statistiques des familles, etc.: d’une loi nouvelle la loi de l’effet proportionnel. Recueil Sirey, Paris.
Gilbert, B. A., McDougall, P. P., & Audretsch, D. B. (2006). New venture growth: A review and extension. Journal of Management, 32(6), 926–950.
Gimeno, J., Folta, T. B., Cooper, A. C., & Woo, C. Y. (1997). Survival of the fittest? Entrepreneurial human capital and the persistence of underperforming firms. Administrative Science Quarterly, 42(4), 750–783.
Greene, F. J. (2009). Assessing the impact of policy interventions: The influence of evaluation methodology. Environment and Planning C, 27(2), 216–229.
Hamilton, B. H. (2000). Does entrepreneurship pay? An empirical analysis of self-employment. Journal of Political Economy, 108(3), 604–631.
Harada, N. (2007). Which firms exit and why? An analysis of small firm exits in Japan. Small Business Economics, 29, 401–414.
Headd, B. (2003). Redefining business success: Distinguishing between closure and failure. Small Business Economics, 21, 51–61.
Henderson, A. D., Raynor, M. E., & Ahmed, M. (2012). How long must a firm be great to rule out chance? Benchmarking sustained superior performance without being fooled by randomness. Strategic Management Journal, 33, 387–406.
Hmieleski, K. M., & Baron, R. A. (2009). Entrepreneurs’ optimism and new venture performance: A social cognitive perspective. Academy of Management, 52(3), 473–488.
Ijiri, Y., & Simon, H. (1964). Business firm growth and size. American Economic Review, 54(2), 77–89.
Jenkins, S. P. (1995). Practitioners corner: Easy estimation methods for discrete-time duration models. Oxford Bulletin of Economics and Statistics, 57(1), 129–138.
Klotz, A. C., Hmieleski, K., Bradley, B. H., & Busenitz, L. W. (2014). New venture teams: A review of the literatureand roadmap for future research. Journal of Management, 40(1), 226–255.
Le Mens, G., Hannan, M. T., & Pólos, L. (2011). Founding conditions, learning, and organizational life chances: Age dependence revisited. Administrative Science Quarterly, 56(1), 95–126.
Levie, J., & Lichtenstein, B. B. (2010). A terminal assessment of stages theory. Introducing a dynamic states approach to entrepreneurship. Entrepreneurship Theory and Practice, 34(2), 317–350.
Levinthal, D. (1991). Random walks and organizational mortality. Administrative Science Quarterly, 36(3), 397–420.
Lotti, F., Santarelli, E., & Vivarelli, M. (2009). Defending Gibrat’s Law as a long-run regularity. Small Business Economics, 32, 31–44.
Miller, C. C., Washburn, N. T., & Glick, W. H. (2013). The myth of firm performance. Organization Science, 24(3), 948–964.
Mole, K. F., Hart, M., Roper, S., & Saal, D. S. (2011). Broader or deeper? Exploring the most effective intervention profile for public small business support. Environment and Planning A, 43(1), 87–105.
Nagelkerke, N. J. D. (1991). A note on a general definition of the coefficient of determination. Biometrika, 78(3), 691–692.
Ongena, S., & Smith, D. C. (2000). What determines the number of bank relationships? Cross-country evidence. Journal of Financial Intermediation, 9(1), 26–56.
Parker, S. C. (2009). The economics of entrepreneurship. Oxford: Oxford University Press.
Persson, H. (2004). The survival and growth of new establishments in Sweden, 1987–1995. Small Business Economics, 23(5), 423–440.
Phelps, R., Adams, R., & Bessant, J. (2007). Life cycles of growing organizations: A review with implications for knowledge and learning. International Journal of Management Reviews, 9(1), 1–30.
Pons Rotger, G., Gørtz, M., & Storey, D. J. (2012). Assessing the effectiveness of guided preparation for new venture creation and performance: Theory and Practice. Journal of Business Venturing, 27(4), 506–521.
Ryder, N. B. (1965). The cohort as a concept in the study of social change. American Sociological Review, 30(6), 843–861.
Santarelli, E., & Vivarelli, M. (2007). Entrepreneurship and the process of firms’ entry, survival and growth. Industrial and Corporate Change, 16(3), 455–488.
Solomon, G. T., Bryant, A., May, K., & Perry, V. (2013). Survival of the fittest: Technical assistance, survival and growth of small businesses and implications for public policy. Technovation, 33, 292–301.
Stanley, M. H. R., Amaral, L. A. N., Buldyrev, S. V., Havlin, S., Leschhorn, H., Maass, P., et al. (1996). Scaling behavior in the growth of companies. Nature, 379, 804–806.
Storey, D. J. (1994). The role of legal status in influencing bank financing and new firm growth. Applied Economics, 26(2), 129–136.
Storey, D. J. (2011). Optimism and chance: The elephants in the entrepreneurship room. International Small Business Journal, 29(4), 303–321.
Storey, D. J., Keasey, K., Watson, R., & Wynarczyk, P. (1987). The performance of small firms: Profits, jobs and failures. London: Croom Helm.
Syverson, C. (2011). What determines productivity? Journal of Economic Literature, 49(2), 326–365.
Tornqvist, L., Vartia, P., & Vartia, Y. O. (1985). How should relative changes be measured? American Statistician, 39(1), 43–46.
Voordeckers, W., & Steijvers, T. (2006). Business collateral and personal commitments in SME lending. Journal of Banking and Finance, 30(11), 3067–3086.
Wennberg, K., Wiklund, J., Detienne, D. R., & Cardon, M. S. (2010). Reconceptualizing entrepreneurial exit: Divergent exit routes and their drivers. Journal of Business Venturing, 25, 361–375.
Wiklund, J., Baker, T., & Shepherd, D. (2010). The age-effect of financial indicators as buffers against the liability of newness. Journal of Business Venturing, 25(4), 423–437.
Yang, T., & Aldrich, H. E. (2012). Out of sight but not out of mind: Why failure to account for left truncation biases research on failure rates. Journal of Business Venturing, 27(4), 477–492.
Zimmerman, M. A., & Zeltz, G. Z. (2002). Beyond survival: Achieving new venture growth by achieving legitimacy. Academy of Management Review, 27(3), 414–431.
Acknowledgments
We are grateful to Jose Garcia Quevedo, Gabriele Pellegrino, Maria Savona, Karl Wennberg, and participants at the RATIO Institute Stockholm and DRUID 2013 (ESADE, Barcelona) for many helpful comments. A.C. gratefully acknowledges financial support from the ESRC, TSB, BIS and NESTA on grants ES/H008705/1 and ES/J008427/1 as part of the IRC distributed projects initiative, as well as from the AHRC as part of the FUSE project. The views expressed are purely those of the authors and may not in any circumstances be regarded as stating an official position of the European Commission. J.S.F. and R.G.R. write only in a personal capacity and do not necessarily reflect the views of Barclays Bank. Any remaining errors are ours alone.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Coad, A., Frankish, J.S., Roberts, R.G. et al. Predicting new venture survival and growth: Does the fog lift?. Small Bus Econ 47, 217–241 (2016). https://doi.org/10.1007/s11187-016-9713-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11187-016-9713-1
Keywords
- Entrepreneurship
- Firm growth
- Survival analysis
- Coefficient of determination
- Selection environment
- Gambler’s Ruin theory