1 Introduction

Endogenous growth theory has given a central role to R&D and innovation (e.g. Romer 1987, 1990; Aghion and Howitt 1992), though rarely addressed its interaction with entrepreneurship (Braunerhjelm et al. 2010). At the same time, entrepreneurship research has increasingly recognized that it is not only the quantity, or level, of new business formation that matters. Also the quality is of importance, as entrepreneurs with better business ideas should be able to survive longer and possibly create more jobs higher up the value chain (Storey and Tether 1998; Fritsch and Mueller 2004). In particular, new technology-based firms (NTBFs) are widely held as agents that introduce innovation, promote technology transfer, intensify market competition, and speed up industrial evolution and ultimately induce economic growth (Schumpeter 1934; Saxenian 1994; Lindholm Dahlstrand 1997; Autio and Parhankangas 1998; Licht and Nerlinger 1998; Storey and Tether 1998; Rickne and Jacobsson 1999). Such firms can be seen as an expression of ‘quality.’ While the link from inventive activity to growth has been intensively studied, the reverse direction of effects, how growth impacts on inventive activity, has not. In this article we study one set of such effects, namely how economic fluctuations affect the post-entry performance of new businesses. Little is also known about how different quality levels of entrepreneurship are affected by business cycles. The key interest in this article is whether one expression of such quality entrepreneurship, NTBFs, is affected differently by the business cycle in terms of survivability than other entrepreneurial firms. Since NTBFs and other high-quality firms arguably have better growth prospects, a finding that they are more vulnerable to recessions suggests that business cycle downturns may also weaken long-term growth.

In order to examine this research issue, we first define entrepreneurial firms as new, small, independent businesses based on entrepreneurial opportunities. Generally, an empirical challenge rests in how to define and identify NTBFs, since they lack a consistent methodological framework (Storey and Tether 1998). This has also been a main reason for the deterred development of research in this field. Earlier studies use a definition based on taxonomy of sectors. But this approach has apparent disadvantages including a high level of heterogeneity of technological activities within each sector (Storey and Tether 1998) or a selection of firms in high-tech sectors. We propose a method for identifying NTBFs by matching inventors with data on new firm formation for the Swedish economy. The motivation for identifying NTBFs through this method is the presumption that new firms with inventors embody ‘quality’ characteristics in technology.

Previous studies have proposed three arguments to support the presumption. The first is that inventions with high technological opportunities are more likely to be commercialized through new firm formation (Shane 2001) than other alternatives. Furthermore, we argue that the presence of inventor entrepreneurs in new firms can be regarded as a further quality indicator in technology when considering the opportunity costs of being entrepreneurs (Lucas 1978) and the associated risk and uncertainty of technological projects (Arrow 1962; Audretsch 1997; Jaffe 1998). The second argument is that inventors bring fresh human capital to new firms, especially tacit knowledge (Zucker et al. 1998). Tacit knowledge can be transferred to technical capital in new firms by training or face-to-face communication with inventors (Levin and Stephan 1991). Third, inventors also transfer their social capital to new firms, facilitating network formation in new firms (Murray 2004).

New firm dynamics are characterized by high turbulence in terms of entry and exit (Geroski 1995; Caves 1998). Previous studies identify a set of factors that impact on firms’ post-entry performance. Some focus on founders’ individual traits, such as human capital (Colombo et al. 2004; Colombo and Grilli 2005); others on firm-specific characteristics, such as firm age and size (Evans 1987; Hall 1987; Dunne and Hughes 1994); yet others on industry-specific characteristics, such as the nature of technology (Audretsch 1991, 1995; Malerba and Orsenigo 1999), the R&D intensity (Audretsch 1995; Licht and Nerlinger 1998), industry life cycles (Utterback and Suárez 1993; Jovanovic and MacDonald 1994; Klepper 1996; Agarwal and Gort 2002) or entry barriers (Geroski 1995). However, little effort has been devoted to explore empirically how the business cycle impacts on the survival performance of entrepreneurial firms. Even less is known about how it affects the evolution of NTBFs over time. Boeri and Bellmann (1995) adopt longitudinal data on the establishment level for West German manufacturing industries to investigate the relationship between macroeconomic fluctuations and post-entry performance of new firms entering in 1979–1992. Based on logit models, their results do not show cyclical patterns of exit. But they find that the longer firms survive, the more sensitive their growth becomes to business fluctuations. Fotopoulos and Louri (2000) find that firms born during economic downturns have higher exit rates. Box (2008) follows seven birth cohorts of new firms established from 1899 to 1950 in Sweden. His findings furthermore confirm that firms born under favorable macroeconomic conditions have higher survival rates, and vice versa. Licht and Nerlinger (1998) link patterns of entry and exit of NTBFs with the business cycle based on firm-level data for Germany, but find a rather weak and ambiguous pattern of entry and exit of new firms over the business cycle. They point out that one potential explanation is that data are disturbed by the 1989 German reunification.

The lack of study on the relationship between entrepreneurship and the business cycle can be attributed to a shortage of high-quality and/or comprehensive longitudinal data. Boeri and Bellmann (1995) complain that most databases on firm dynamics are recent constructions and do not even cover a full business cycle. In this article, our data span over almost two decades and comprise the complete set of new firms, which allow us to identify entrepreneurial firms from 1991 to 2002 and trace their performance until 2007. The long time series covers two recessions and two expansions, providing a long enough time span for analyzing effects stemming from the business cycle. More specifically, our research questions are: (1) whether NTBFs have a higher survival probability than other entrepreneurial firms; (2) whether entrepreneurial firms in general have a higher hazard probability in recessions; (3) whether NTBFs in particular respond differently to macroeconomic shocks than other entrepreneurial firms in terms of survival performance. We employ discrete-time duration models to explore the research questions. Our main findings are that entrepreneurial firms follow a pro-cyclical pattern of survival performance over the business cycle. With respect to NTBFs, our results confirm that they indeed embody ‘quality’ characteristics that make them survive longer than other entrepreneurial firms, even after controlling for the level of human capital. In particular, NTBFs are found to be more pro-cyclically affected by macroeconomic shocks than other entrepreneurial firms. When further dividing entrepreneurial firms into self-employed entrepreneurial firms and non-self employed, we obtain further insights. We find that the pro-cyclical effect mainly pertains to self-employed NTBFs. This suggests to us that the technological risk carried by NTBFs among self-employed firms imposes an extra burden on the survival of these firms during recessions. On the other hand, these firms have more strength to go on during good economic times, possibly due to their intrinsic technological strength. With respect to general survivability, NTBFs survive to a higher extent only among non-self-employed, which suggests that their higher survivability is only revealed after a threshold size has been exceeded.

We believe our study makes three contributions to the existing literature. First, we propose and adopt a method for identifying NTBFs by linking new firm information with data on inventors. Second, we improve on the understanding of new firm survival more broadly over the business cycle. Third, in particular we examine whether NTBFs survive differently from other entrepreneurial firms in response to macroeconomic fluctuations. The rest of the article is organized as follows. Section 2 sets out the theoretical framework and puts forward the hypotheses to be tested. Section 3 introduces the data and methods. Section 4 presents the results, and Sect. 5 concludes.

2 Theoretical framework and investigated hypotheses

2.1 Key factors behind firm entry

New firms are started for many reasons. Several of these factors impact on the performance and more specifically their survivability. Some may be viewed as working “progressively,” others “regressively” (Santarelli and Vivarelli 2007). Among the regressive factors, we find motivations that are based on unemployment or fear of unemployment. Thus, starting an own firm provides a possible source of income that may be better than nothing or low unemployment benefits. Similarly, low wages may drive people to start their own firm, even if this entails living only on a subsistence income. Evidence clearly shows that previous unemployment does not provide a favorable basis for high-quality entrepreneurship and leads to higher exit rates and worse economic outcomes (Carrasco 1999; Pfeiffer and Reize 2000; Andersson and Wadensjö 2007). Andersson and Wadensjö (2007) also find that unemployed are highly represented among the self-employed, suggesting that the firms started by previously unemployed represent entrepreneurship of ‘lower’ quality.

Progressive factors include favorable economic conditions, which raise profit expectations, and technological opportunities. The former make it more likely to become profitable, given a high demand. Technological opportunities encourage prospective entrepreneurs with a potentially more long-term mindset toward their business to start a firm. There are also studies that show that innovative start-ups have a higher performance (Vivarelli and Audretsch 1998; Arrighetti and Vivarelli 1999).

The psychological traits and background of entrepreneurs have been studied extensively. The desire to be independent encompasses aspects such as self-sufficiency and individualism, which have been listed as key factors, especially in US studies (Zacharakis et al. 2000). Other studies also show that many entrepreneurs tend to have overoptimistic visions of their future business prospects (e.g. Åstebro 2003).

2.2 Main hypotheses

We believe that new technology-based firms are more likely to reside in the category of high-quality entrepreneurship, with a better articulated business plan. They are also less likely to stem from regressive factors such as the risk of unemployment. We therefore formulate

Hypothesis 1:

Chances of survival of new technology-based firms are higher than for other firms.

Unemployment, as well as its impact on the type of business formation, is intertwined with the business cycle. Parker (2009, p.143–144) distinguishes two opposite effects with respect to how unemployment affects entrepreneurship. The recession push effect implies that periods of high unemployment reduce the probability of paid employment and lowers the cost of capital, and both factors push individuals towards entrepreneurial entry. An alternative scenario is that low demand and less availability of capital during periods of high unemployment shake out some entrepreneurs from the market, i.e. leading to exits. This prosperity pull effect induces a negative association between unemployment and entrepreneurial activities in general. Santarelli and Vivarelli (2007, p. 461) list studies that report about 20 % of new firms to be linked to unemployment and/or fear of unemployment. The next hypothesis is therefore natural:

Hypothesis 2:

Exits of new firms are more common in recessions.

Does NTBFs exit behavior differ from that of other types of firms in recessions? Three aspects can be highlighted. First, capital requirements may differ between NTBFs and other types of new firms. Some NTBFs may require larger investments in complementary capital assets, such as laboratory equipment, but there are many cases where NTBFs require less. For instance, only a computer might be needed where another firm may require heavy machinery to set up. However, and secondly, NTBFs are more likely to need risk-willing capital, and if venture capital is what is needed for the NTBF to uphold the business, investors may be particularly reluctant to support NTBFs during recessions. This factor suggests that NTBFs’ survival may be more sensitive relative to other new firms in recessions. Access to venture capital is intrinsically related to the formation of new firms. For instance, Audretsch and Acs (1994), Gompers and Lerner (1998), and Jeng and Wells (2000) all report that macroeconomic expansions lead to higher start-up numbers, with higher demand for venture capital. Romain and Van Pottelsberghe (2004) finds that venture capital supply is positively related to GDP across the OECD countries (Félix 2013). Third, a factor that favors NTBFs during recessions is that their business, based on technological opportunities, may be less vulnerable to economic downturns. However, it is likely that the full potential of technological opportunities does not reveal itself shortly after the business has been founded. Therefore, we believe that the risk capital argument dominates, which should make NTBFs more vulnerable in recessions.

Hypothesis 3:

NTBFs exit more frequently than other entrepreneurial firms during recessions.

However, both NTBFs and non-NTBFs have self-employed among their firms. As highlighted above, these firms are very often started out of necessity and lack of capital during recessions. This could potentially have detrimental effects on these firms. We therefore propose:

Hypothesis 4:

Self-employed firms are more sensitive to the business cycle than non-self-employed firms.

Also in line with the above reasoning, because NTBFs are more likely to be burdened by a technological risk on top of being small, we claim:

Hypothesis 5:

Self-employed NTBFs have a lower rate of survival than other self-employed firms during recessions.

However, the fact that NTBFs are based on technology should generally be useful for both self-employed and non-self-employed firms. Therefore:

Hypothesis 6:

Both self-employed and non-self-employed NTBFs should have a higher survivability than their corresponding non-NTBF counterparts.

2.3 Secondary hypotheses

The survival performance of entrepreneurial firms is affected by many other aspects. The level of human capital is highlighted as one of the most important founder-specific factors. Human capital has been widely evidenced to affect the post-entry performance of start-ups positively (Bates 1990; Boden and Nucci 2000). We use the share of employees with any tertiary education or above as our indicator of human capital and state:

Hypothesis 7:

The level of human capital available to the firm impacts positively on firm survival.

Nevertheless, we believe that NTBFs’ quality characteristics extend beyond those provided by the level of human capital, because they embody inventive experience and technological opportunities. Hence:

Hypothesis 8:

An NTBF has a survival probability that extends over and above those given by their level of human capital.

Jovanovic (1982) proposes a model with asymmetric information in the market with divergent efficiency among firms, but fixed efficiency within firms. Firms learn about their efficiency only after entering the market. Feedback from the market enables firms to learn about their ability and inform them on whether to stay, grow, shrink or exit. This model predicts that the likelihood of survival increases with firm age (Pakes and Ericson 1998; Cefis and Marsili 2006). In addition, another widely discussed determinant of post-entry performance is firm size, which is usually indicated by the number of employees. Gibrat’s law (Parker 2009) argues that firm growth and size are not correlated, but this postulate has been rejected for small firm populations in many studies (Evans 1987; Hall 1987; Dunne and Hughes 1994). Empirical studies support that the probability of survival increases with firm size, measured either by entry size of employment (Audretsch et al. 2000) or current size of employment (Mata et al. 1995).

Hypothesis 9:

The larger the size of a firm, the higher is its survivability.

Among industry-specific factors, substantial structural differences affect entry and exit behavior across industries. A higher entry rate reflects competitiveness and market turbulence, which should have a negative effect on the survival likelihood of new firms (Geroski 1995). In our study, we include the entry rate defined as the number of new firms in each two-digit sector (NACE v.1.1) divided by the total number of new firms within manufacturing and service sectors each year.

Hypothesis 10:

A higher industry entry rate in which the firm started affects its survivability negatively.

Moreover, according to industrial life cycle models, firm survival is also affected by the stage of development of an industry. In early phases, firm entry and survival likelihood are high. But during the mature stages of an industry, shake-out mechanisms lower both entry and survival performance (Utterback and Suárez 1993; Jovanovic and MacDonald 1994; Klepper 1996; Agarwal and Gort 2002). We include employment growth for each two-digit sector (NACE v.1.1) to capture industrial-life-cycle effects.

Hypothesis 11:

A higher industry growth rate in which the firm started affects its survivability positively.

Concerning the impact of R&D intensity on survival performance, previous studies have shown ambiguous results. Audretsch (1995) finds that in industries characterized by a high innovative environment, competition is higher, which for entrants leads to higher failure rates. However, if firms survive this initial shake-out period, their survival rates are higher than in other industries. Licht and Nerlinger (1998) employ firm-level data from 1980 to 1992 and focus on NTBFs in German technology-intensive sectors. Their study distinguishes “very-high-tech” industries, “high-tech” industries and “high-tech” services from other manufacturing industries and services, based on R&D intensity.Footnote 1 They find that start-ups in high-tech manufacturing industries have lower hazard rates than those in other manufacturing industries. But in “very-high-tech” industries, hazard rates of start-ups are much higher than those found in other manufacturing industries. Moreover, structural differences also exist between manufacturing and service sectors. Low entry barriers and low switching costs (Headd 2003; Bates 2005) make entrepreneurial firms in service sectors more fragile to exit. In our study, we control for sector effects following the OECD classification (Eurostat 2011)Footnote 2 and divide industries into high-tech manufacturing, medium–high-tech manufacturing, medium–low-tech manufacturing, low-tech manufacturing, knowledge-intensive services (KIS) and less knowledge-intensive services (LKIS) using dummy variables and taking low-technology manufacturing as the reference group.

Hypothesis 12:

Firms started in low-tech and medium–low-tech sectors should experience a lower probability of survival. Firms in high-tech sectors may have a lower probability of survival than medium–high-tech firms.

3 Data, methods and descriptive statistics

3.1 Data

We constructed a unique micro-level data set that links Swedish inventors, matched with an employer-employee database and data on economic growth. The information on inventors is from a newly constructed database that identifies approximately 80 % of inventors in Sweden from 1985 to 2007 by matching inventor records of addresses listed in PATSTAT (European Patent Office 2012) from the EPO (European Patent Office) with population register data from Statistics Sweden (Ejermo 2011, Jung and Ejermo 2013). A systematic missing part consists of inventors employed at Astra (later AstraZeneca), a pharmaceutical company. These inventors (about 5 %) could not be identified because they state the company’s rather than their home address. Since this concerns an incumbent, the omission should not be serious in the current context. The match rate is fairly stable around 80 % over time. We do not have indications that we consistently sample inventors in a way that is misrepresentative for entrepreneurship, although this cannot be ruled out.

The matched employer-employee database comes from Statistics Sweden and consists of annual information of all registered Swedish firms and their employees since 1987. By tracing the flows of employees among workplaces from each pair of years, firms/workplaces are identified as surviving, new or exiting each year. The database covers demographic information for both firms and employees. The inventors and matched employer-employee data are linked by a unique identifier: the social security number (Swedish: personnummer). We use real GDP per capita growth to indicate macroeconomic fluctuations, derived from Statistics Sweden and added each year.

The method of identifying new firms is based on the information provided by the matched employer-employee database combined with the appearance of a new firm ID. Similar methods have been used in studies by Eriksson and Kuhn (2006) and Andersson and Klepper (2013). Following these two studies, we add two criteria to Statistics Sweden’s definition in order to focus on entrepreneurial firms. First, entrepreneurial firms should not belong to any business groups when they were founded, which distinguishes independent entrepreneurship from diversifying entrants by established firms. Second, new firms with more than ten employees are regarded as divestitures (Eriksson and Kuhn 2006) instead of “genuine” entrepreneurship and are excluded from our data. So far, we have identified the population of entrepreneurial firms in the Swedish economy. The next step is to add information on inventors. We examine the employees of identified entrepreneurial firms when they were established. If an entrepreneurial firm has at least one employee who has been listed as inventor on a patent application to the EPO within the past 5 years, we define it as an NTBF. Otherwise it is categorized as an “other entrepreneurial firm.”

Our definition of NTBFs is based on the presence of inventor entrepreneurs and does not cover all new firms with inventive or innovative activities. New firms can be R&D intensive and inventive without intent to patent. They can also rely on inventions without the presence of inventors, e.g. based on licensed patents. Thus, our sample of NTBFs is a subset of the whole population of inventive entrepreneurship. Nevertheless, assuming that patenting experience is an indicator of quality, and the presence of inventor entrepreneurs is a further quality indicator of new firms, our definition of NTBFs should capture the high-end group of the whole population of inventive entrepreneurship. Also, while our grouping of firms is dichotomous and instances of inventive new firms may be found among “other” entrepreneurial firms, their share among all other new firms is small and should not be the cause of misleading inferences.Footnote 3

Our data allow us to distinguish exit by bankruptcy or termination from exit by split or merger by tracing employment flows. Our focus is on exit by bankruptcy or termination, which accounts for more than 90 % of all exit events in the data. Therefore, we follow the common approach to simply treat the observations that experienced exit by split or merger as censored (Allison 1984) and define exit by bankruptcy or termination as the relevant category for firm exit in this article.

Our data identify entrepreneurial firms entering from 1991 to 2002, in total 12 birth cohorts, which are followed separately until 2007. There are two reasons for the choice of the 12 cohorts of firms. First, there is a distinct change in the industrial classification system from 1990 in Statistics Sweden. We therefore choose 1991 as our start year for observing entering firms to keep the industrial classification scheme consistent. Second, we drop entrepreneurial firms entering after 2002 in order to gauge the survival performance of each birth cohort over at least 5 years.

Furthermore, we select entrepreneurial firms in manufacturing and service sectors based on sectoral codes at year of entry, but exclude recycling and public service sectors. We exclude 112 firms with missing observations during the period. The final data set is a dynamic panel consisting of 340,199 entrepreneurial Swedish firms entering from 1991 to 2002 which we follow until 2007. The unbalanced panel has 1,254,034 observations over the whole period. Figure 1 shows the entry numbers of all entrepreneurial firms and NTBFs over time. First, it can be noted that more entrepreneurial firms including NTBFs were founded over time. A spike in the number of NTBF entrants can be observed in 2000 compared with 1999, which corresponds to the peak of the Information Technology Bubble. Second, compared with entry numbers of all entrepreneurial firms, only a small number of NTBFs enter each year. Further descriptive statistics will be discussed in Sect. 3.3.

Fig. 1
figure 1

Entry Numbers: 1991–2002

Full size image

3.2 Discrete-time duration models

In order to explain survival performance, we apply duration models to explore whether the business cycle impacts on the probability of exit. The data set we have constructed records the history of entrepreneurial firms from entry to exit (if any) and relevant explanatory variables from 1991 to 2007. The dependent variable is the length of time over which a new firm stays in the economy. These are typical event history data. One of the main advantages of duration models is that they account for the problem of incomplete information of event occurrence (Singer and Willett 1993). This means that some firms cannot be observed to experience an event’s occurrence in a given observation period. Such firms are termed as right-censoring observations in duration models. Another advantage is that such models consider state dependence (time dependence), which means that time elapsed potentially affects the probability of staying in a particular state. This is important for the study of firm survival, as previous literature has shown that the probability of firm failure decreases with age because of the learning process involved (Jovanovic 1982; Evans 1987).

Duration models can be divided into continuous-time and discrete-time models. We have access to register data where time elapses as discrete annual change. It is thus appropriate to use discrete-time models. In addition, the panel form structure of our data allows us to easily fit discrete-time models. As mentioned by Allison (1982), discrete-time models have two additional advantages. First, the methodology is easier to understand than the alternatives. Second, the models can easily accommodate time-varying explanatory variables. The discrete-time hazard function is specified in Eq. (1),

$$h(t) = \Pr [T = t|T \ge t]$$
(1)

where \(h(t)\) is the hazard function. The hazard rate at time t is the probability that a subject will experience an event in a given time interval, conditional on being at risk at the beginning of that interval (Singer and Willett 2003).

3.2.1 The Kaplan-Meier estimator

Usually, non-parametric models are used for descriptive purposes. Their main advantage is that they do not impose a priori assumption regarding the distribution of the hazard function or the survivor function. We choose the Kaplan-Meier estimator (Kaplan and Meier 1958), one of the most common non-parametric methods, to describe the survivor function before introducing any covariates. Equation (2) shows the basic Kaplan-Meier function where \(S_{t}\) refers to the survivor function, \(n_{j}\) is the number of subjects at risk (the risk set) at time interval \(t_{j}\), and \(d_{j}\) is the number of failures at time interval \(t_{j}\) (Cleves et al. 2010).

$$S_{t} = \prod\nolimits_{{j|t_{j} \le t}} {\left( {\frac{{n_{j} - d_{j} }}{{n_{j} }}} \right)}$$
(2)

3.2.2 The logit (proportional hazard odds) model

Due to the discrete-time nature of the data, we follow Singer and Willett (2003) to adopt the proportional hazard odds model to explore the research questions; see Eq. (3). The hazard rate when all covariates equal zero is the baseline hazard rate that all firms face. When introducing explanatory variables, the model imposes a proportional hazard odds assumption.

$$\frac{{h(t|X_{t} )}}{{1 - h(t|X_{t} )}} = \frac{{h_{0} \left( t \right)}}{{1 - h_{0} \left( t \right)}} \cdot \exp \left( {\beta^{'} X_{t} } \right),$$
(3)

where \(X_{t}\) is a vector of covariates, and h 0 (t) is the baseline hazard rate. A major strength of the proportional hazard odds model is that we do not need to assume any particular form of the baseline hazard function. Instead, duration dummies are included to allow the baseline hazard to vary over time. After a logarithmic transformation, the hazard odds and covariates are linked by a linear form, see Eq. (4).

$$\ln \left( {\frac{{h_{t} }}{{1 - h_{t} }}} \right) = \alpha_{i} 'D_{i} + \beta^{'} X_{t}$$
(4)

where \(D_{i}\) refers to a vector of dummies for duration time (age in our study) and \(\alpha_{i}\) is a vector of parameters of the baseline logit hazard function at each age. The coefficient vector \(\beta\) represents the effect of the covariate vector X relative to the baseline logit hazard, which is assumed to be constant over time. The logit model is estimated by maximum likelihood. In order to give a more intuitive relationship between the coefficient \(\beta\) and the hazard probability, Eq. (4) can also be expressed with the hazard probability as the dependent variable, see Eq. (5).

$$h_{t} = \frac{1}{{1 + {\text{e}}^{{ - (\alpha_{i} 'D_{i} + \beta^{'} X_{t} )}} }}$$
(5)

From Eq. (5), it can be noted that any positive (negative) coefficient in \(\beta\) will increase (decrease) the hazard probability when the associated covariate increases (decreases) after controlling for the baseline hazard and other covariates (Singer and Willett 2003).

3.3 Descriptive statistics

We include both time-invariant and time-varying variables in our analysis. Time-invariant variables do not change over time, such as the dummy variables of sector classification and the dummy variable of NTBFs. In order to avoid the simultaneity problem,Footnote 4 with the exception of age, we treat all founder-specific and firm-specific variables as time invariant, including human capital and size. All time-invariant variables are coded at their entry level. Time-varying variables exhibit variation over time, e.g. age, entry rate, industry growth and real GDP per capita growth.

In panel A of Table 1, we list the statistics by distinguishing the whole population of entrepreneurial firms from NTBFs. In the whole population, the difference between the mean and median values of entry size reveals a highly skewed distribution of firm size. We thus include another dummy variable to account for the share of self-employed firms. In our data, about 76.2 % of observations enter as self-employed. NTBFs only account for around 0.3 % of all observations. In comparison with all entrepreneurial firms, there are about 60.7 % self-employed firms among NTBFs, which is less than the share of self-employed in the whole population. We also find that NTBFs are slightly older and have larger entry size in terms of employment on average. It is not surprising that we find that NTBFs have a much higher share of employees with tertiary education or above (55 % on average) when they were established, because inventors tend to be highly educated (Ejermo 2012). In terms of industry classification, almost 90 % of observations are in service sectors with about 40 % in knowledge-intensive service sectors and about 49 % in less-knowledge-intensive service sectors in the whole population. For NTBFs, about 66 % of observations are found in knowledge-intensive service sectors. In panel B of Table 1, we report summary statistics of real GDP per capita growth. As the observation period lasts from 1991 to 2007, the variable real GDP per capita growth has 17 observations, with values ranging from −2.6 % to +4.6 % annually.

Table 1 Variables description and descriptive statistics
Full size table

4 Results

4.1 Patterns of the business cycle and firm survival

We depict the business cycle indicated by real GDP per capita growth in Sweden from 1990 to 2007 in Fig. 2. From the dynamics of real GDP per capita growth, a depression from 1990 to 1993 in the Swedish economy is notable. This depression was regarded as a financial crisis and attributed to the deregulation of financial markets and unreasonable monetary policies by economic historians (Schön 2010). After the depression, the Swedish economy experienced a fairly stable period of sound economic growth until 2000. In 2001, real GDP per capita growth dropped to almost 1 % compared to the preceding year. However, the economy rebounded in 2002 and kept a moderate pace until 2007.

Fig. 2
figure 2

The business cycle in Sweden: 1990–2007

Full size image

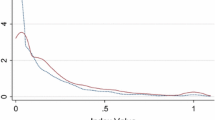
Next, we plot the survival probability against age by distinguishing NTBFs from other entrepreneurial firms based on the Kaplan-Meier estimator in Fig. 3. The Kaplan-Meier survival curves show the proportion of firms that have survived up to each age. Figure 3 shows clearly that NTBFs have a higher survival probability than other entrepreneurial firms at each age.

Fig. 3
figure 3

Kaplan-Meier survival estimates

Full size image

4.2 Determinants of survival

In panel A of Table 2, we report the estimation results of the whole population of entrepreneurial firms, based on the discrete-time proportional hazard odds model. In Specification A1, we only include duration (age) dummies before introducing any covariates to estimate the baseline logit hazard at each age, i.e. the vector of parameters \(\alpha_{i}\) in Eq. (4). The estimated parameters are shown for different ages in Fig. 4 that imply that the baseline logit hazard decreases monotonically with age until age 13.

Table 2 Estimation results
Full size table
Fig. 4
figure 4

Estimated baseline logit hazard function

Full size image

We now introduce covariates into the model. First, we include the dummy variable of NTBFs in Specification A2. The dummy variable reports a significantly negative coefficient at the 1 % level, which means that NTBFs have a lower logit hazard than other entrepreneurial firms. This also implies a lower hazard rate for NTBFs than for other entrepreneurial firms according to Eq. (5). We can also antilog the coefficient to obtain the relative odds ratio to facilitate interpretation. The relative odds ratio is exp (−0.273) or about 0.761, which means that the estimated hazard odds of NTBFs is roughly 76.1 % of the odds for other entrepreneurial firms on average at each age. This supports Hypothesis 1.

In Specification A3, we include real GDP per capita growth, human capital, entry rate, industry growth and industry dummies. The coefficient of the NTBF dummy variable is still negative and significant, although the effect decreases somewhat. With the exception of the dummy variable for less knowledge-intensive service sectors, all other covariates report significant coefficients. More specifically, the consistently negative coefficient of real GDP per capita growth across specifications (through A3–A5) indicates that firm survival follows a pro-cyclical pattern. This supports our Hypothesis 2. Higher levels of human capital and industry growth always promote firm survival probability, which is consistent with findings from previous studies and Hypothesis 7 and 11. Also, hypothesis 8 is supported, i.e. the “quality” embedded in NTBFs extends over the human capital level in these firms.

However, higher entry rates in an industry raise the firm’s survival probability. It should be noted that the whole population of entrepreneurial firms is dominated by self-employed firms (about 76.2 %) and that the entry rate effect reverses in regressions B4 and B5 when excluding self-employed firms. Also, the growth of the industry impacts positively when including self-employed firms. Our interpretation is that, when including self-employees, the positive entry rate effect stems from better business opportunities not captured entirely by the industry growth effect. One reason for this could be that self-employed firms act quicker on business opportunities than other new firms. This results in higher survival rates among, in particular, self-employed firms. Re-estimation of Specification A3 based on self-employed firms only (reported as C3) confirms that the positive effect from the entry rate on survival exists mainly for self-employed firms. Therefore, the unexpected sign of the entry rate can be attributed to the high share of self-employed firms in the whole population.

In terms of sector dummies, we find, with the exception of knowledge-intensive and less knowledge-intensive service sectors, that all other sectors exhibit lower hazard rates than the reference group—low-tech manufacturing sectors, and firms in medium–high-tech manufacturing sectors have the highest survival probability at each age. This result, that we do not find the highest survivability among the high-tech firms, is reminiscent of the finding reported by Licht and Nerlinger (1998) and confirms Hypothesis 12.

In Specification A4, we further control for entry size. The extant variables retain their respective sign and significance. The coefficient for entry size is significantly negative, which means that larger entry size lowers the hazard probability of entrepreneurial firms, consistent with previous literature and Hypothesis 9; see Sect. 3.3.

Specification A5 further includes interaction terms between (1) NTBF and age, (2) NTBF and size, and (3) NTBF and real GDP per capita growth to test for structural differences between NTBFs and other entrepreneurial firms. The dummy for NTBFs now loses significance. This effect is thus taken over by the interaction variables. The interaction term between NTBFs and age shows a significantly positive coefficient, suggesting that the advantage that NTBFs have over other entrepreneurial firms at the beginning becomes less pronounced over time. This is not strange as surviving firms in the group of other firms should have a higher quality and from that perspective thus become increasingly similar to NTBFs. The coefficient for the interaction term between NTBFs and size is significantly negative, indicating that NTBFs have an advantage that goes beyond their larger size, since the coefficient for size remains negative and significant. We also find a negative coefficient in terms of the interaction effect between NTBFs and the business cycle, which means NTBFs are more pro-cyclically affected by the business cycle than other entrepreneurial firms, although only at the 10 % significance level. This gives some support for Hypothesis 3.

In panel B, we therefore re-estimate Specifications A4 and A5 but exclude self-employed entrepreneurial firms (reported as B4 and B5). We find that most of the covariates retain their sign. The exception is the entry rate, which now turns into a negative effect. Entry therefore has a primarily competitive effect when excluding self-employed firms. In addition, we find that the interaction term between NTBFs and size loses significance at conventional confidence level. By excluding self-employed firms, NTBFs and non-NTBF start-ups become similar such that the previously seen size-advantage disappears. However, the interaction term between NTBFs and real GDP per capita growth becomes insignificant in the restricted sample.

In panel C, we re-estimate Specifications A3 and A5, but only on self-employed entrepreneurial firms (reported as C3 and C5). The main results are the following. With respect to the effects of real GDP per capita growth, we do find that self-employed firms in general have a higher sensitivity in line with our expectations set out in Hypothesis 4. We also find that the interaction term between NTBFs and real GDP per capita growth, which was insignificant when we looked at non-self-employed, has a stronger effect for self-employed firms. This supports Hypothesis 5, i.e. that self-employed NTBFs are more pro-cyclically affected by the business cycle than non-NTBF self-employed. A difference with respect to our expectations in Hypothesis 6 is that the “NTBF effect” only pertains to non-self-employed. Thus, it seems as if NTBFs need to move beyond the initial self-employment stage in order to experience a higher survivability than other new firms.

As the specifications are nested, we adopt likelihood ratio tests based on the deviance statistics to test whether unnecessary control variables are included. The statistics of likelihood tests confirm that Specification A5 is the preferred specification for the whole population. Moreover, Specification B5 is also found to be preferred for the sample of non-self-employed firms. But when comparing Specification C5 and C3 based on self-employed firms only, the likelihood test fails to support that C5 is preferred at conventional significance levels.

5 Discussion and conclusions

In this article, we explore the survival performance of entrepreneurial firms in Sweden from 1991 to 2007. More specifically, we examine whether NTBFs have a higher survival probability and respond differently to macroeconomic shocks than other entrepreneurial firms. Based on estimated discrete-time proportional hazard odds models, our findings show that entrepreneurial firms follow a pro-cyclical pattern of survival performance. NTBFs have a higher survival likelihood than other entrepreneurial firms even after controlling for the level of human capital. Arguably, they embody qualitative features expressed by the presence of inventors and superior business ideas that these firms bring to the market. We also find that NTBFs are more pro-cyclically affected by macroeconomic shocks than other entrepreneurial firms. When dividing our data between self-employed and non-self-employed firms, we find that this sensitivity to macroeconomic activity pertains solely to self-employed NTBFs. Thus, during recessions, being active in new technologies is particularly risky for small firms. Also when dividing the sample, we find that NTBFs’ higher general level of survivability only pertains to non-self-employed firms.

Our findings are indicative that NTBFs are clearly superior to other entrepreneurial firms in the economy in terms of survivability, but this superiority is only fully revealed if they are able to survive beyond the stage of self-employment. Their survival is also particularly sensitive to recessions during this stage.

Although NTBFs are small in numbers, we believe that our findings are broader than what might seem to be the case. While our method has succeeded in finding a group of firms of higher ‘quality,’ other high-quality firms exist among the broader group “other entrepreneurial firms” that have not been captured by our definition. Another limitation of our study is that we do not yet know whether NTBFs have higher growth rates than other surviving firms. Nevertheless, surviving firms also tend to grow, and therefore the results suggest that making NTBFs survive may impact positively on long-term growth. Thus, downturns in business cycles may have long-term growth effects and vice versa. Therefore, policymakers may want to direct support to NTBFs and other entrepreneurial ‘high-quality’ firms rather than pursuing policies that support entrepreneurship more broadly. Future research efforts should focus on investigating the growth effects of NTBFs and enable identification of high-quality firms.