Advertisement

Small Business Economics

, Volume 34, Issue 2, pp 105–125 | Cite as

The missing link: knowledge diffusion and entrepreneurship in endogenous growth

  • Pontus Braunerhjelm
  • Zoltan J. Acs
  • David B. Audretsch
  • Bo Carlsson
Open Access
Article
First Online:

Abstract

The intellectual breakthrough contributed by the new growth theory was the recognition that investments in knowledge and human capital endogenously generate economic growth through the spillover of knowledge. However, endogenous growth theory does not explain how or why spillovers occur. This paper presents a model that shows how growth depends on knowledge accumulation and its diffusion through both incumbents and entrepreneurial activities. We claim that entrepreneurs are one missing link in converting knowledge into economically relevant knowledge. Implementing different regression techniques for the Organisation for Economic Co-operation and Development (OECD) countries during 1981 to 2002 provides surprisingly robust evidence that primarily entrepreneurs contributed to growth and that the importance of entrepreneurs increased in the 1990s. A Granger test confirms that causality goes in the direction from entrepreneurs to growth. The results indicate that policies facilitating entrepreneurship are an important tool to enhance knowledge diffusion and promote economic growth.

Keywords

Endogenous growth Knowledge Innovation and entrepreneurship 

JEL Classifications

O10 L10 L26 

1 Introduction

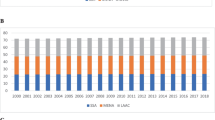
Endogenous growth theory has provided two fundamental contributions that constitute intellectual breakthroughs. The first is that the formation of knowledge and human capital takes place as a response to market opportunities. The second is that investment in knowledge is likely to be associated with large and persistent spillovers to other agents in the economy. However, empirical evidence supporting the hypotheses derived from these models is ambiguous at best.1 The simple correlation between research and development (R&D) expenditure and gross domestic product (GDP) growth reveals no systematic relationship (Fig. 1).2 Thus, the model seems to offer no explanation as to why countries with large R&D stocks grew slowly (such as Sweden in the 1980s and Japan in the 1990s), while other countries less endowed with knowledge—such as Ireland and Denmark—experienced persistent and high growth rates. We believe that the ambiguous empirical support for endogenous growth models is associated with far too mechanistic a view on the spillover of knowledge (Acs et al. 2009, Carlsson et al. 2009).
Fig. 1

Expenditures on R&D and economic growth in 29 OECD countries 1981–2000. Source: OECD, Statistical Compendium on CD, 2002:2

We go back to Arrow’s (1962) recognition that knowledge is not the same thing as economically relevant knowledge. The endogenous growth proponents (Romer 1986, 1990, Lucas 1988, Rebelo 1991, and others) picked up the thread suggested in the earlier literature.3 Their aim was to introduce spillovers explicitly into models of growth. Aggregate knowledge capital was defined as a composite of R&D and human capital, not embodied in processes or products. Accumulation of capitalized knowledge assets was shown to lead to increased growth in a general equilibrium setting. This result could be traced to the assumptions of nonexcludability and nonrivalry attached to knowledge, implying that marginal productivity of knowledge capital does not need to diminish as it becomes available to more users.

Still, the first wave of endogenous growth models paid little attention to how spillovers actually took place and treated the process as exogenous. Their emphasis was on the influence of knowledge spillovers on growth without specifying how knowledge spills over.4 However, as pointed out by Schumpeter (1947), “the inventor produces ideas, the entrepreneur ‘gets things done’ … an idea or scientific principle is not, by itself, of any importance for economic practice.” Indeed, the Schumpeterian entrepreneur, by and large, remains absent in those models. We intend to highlight how the introduction of the “pure” Schumpeterian entrepreneur influences knowledge spillover and how knowledge thereby can be more or less smoothly turned into business activity.

The purpose of this paper is to explain how knowledge is converted into economic knowledge and how economic knowledge influences growth. First, in contrast to previous endogenous growth models, we explicitly introduce a transmission mechanism—entrepreneurship—that influences the rate at which the stock of knowledge is converted into economically useful firm-specific knowledge. Thus, whether regions or countries experience higher growth depends just as much on the distribution between entrepreneurial activities and R&D in the economy as on how much resources are spent on knowledge creation. Second, we implement different regression techniques over different periods to assess the impact of entrepreneurs and researchers on growth. Third, we claim that this implies a new policy approach that reduces the obstacles to entrepreneurship to enhance commercialization of knowledge.

The paper is organized as follows. The next section discusses exogenous knowledge diffusion in endogenous growth models, and provides a suggestion as regards the missing link in the knowledge spillover process. Section 3 presents models for how the individual decision to become an entrepreneur is linked to the risk–reward possibilities that potential entrepreneurs encounter, while Sect. 4 provides a link between microbehavior, entrepreneurship, and growth. In Sect. 5 we provide empirical support for the contribution of entrepreneurship to economic growth. The following Sect. 6 discusses the implications of growth policy. The final section provides a summary and conclusions.

2 The missing link in the endogenous growth models

In the endogenous growth models the opportunity to exploit knowledge spillovers accruing from aggregate knowledge investment is not adequately explained. In essence, these models assume that knowledge (normally defined as codified R&D) is automatically transformed into commercial activities, or what Arrow (1962) classifies as economic knowledge.

New knowledge indisputably leads to opportunities that can be exploited commercially. Economic growth, however, requires that new knowledge be converted into economic knowledge that constitutes a commercial opportunity, a considerably more unpredictable and complex process. For example, only about half of the invention disclosures in US universities result in patent applications; half of the applications result in patents; only one-third of patents are licensed, and only 10–20% of licenses yield significant income (Carlsson and Fridh 2002). In other words, only 1% or 2% of inventions are successful in reaching the market and yielding income.

Hence, opportunities rarely present themselves in neat packages; rather they have to be discovered and applied commercially. Notably such discoveries are made in all types of economic activities, not only in R&D-intensive activities, even though knowledge is used—or combined—in new ways. Precisely for this reason, the nexus of opportunity and enterprising individuals is crucial in order to understand economic growth (Shane and Eckhardt 2003). This implies that knowledge by itself is only a necessary condition for the exercise of successful enterprise in a growth model. The ability to transform new knowledge into economic opportunities involves a set of skills, aptitudes, insights, and circumstances that is neither uniformly nor widely distributed in the population.5

In particular, the uncertainty, asymmetries, and high transaction costs inherent to knowledge generate a divergence in the assessment and evaluation of the expected value of new ideas (Arrow 1962). This divergence in the valuation of knowledge across economic agents and within the decision-making process of incumbent firms can induce agents to start new firms as a mechanism to appropriate the (expected) value of their knowledge. This would suggest that entrepreneurship facilitates the spillover of knowledge in the form of starting a new firm.

That entrepreneurship may constitute a missing link in contemporary growth models corroborates with recent empirical studies that have found an empirical regularity in the form of a positive relationship between various measures of entrepreneurial activity, most typically start-up rates, and indicators of economic growth (Figs. 2, 3).6 Other measures are small and medium-sized enterprises (SMEs), self-employment, and business ownership rates in relation to total population or labor force. For instance, Thurik (1999) provides empirical evidence from a 1984–1994 cross-sectional study of 23 OECD countries. He shows that increased entrepreneurship, as measured by business ownership rates, is associated with higher rates of employment growth at the country level. In another study for the OECD, Audretsch and Thurik (2002) undertake two separate empirical analyses to identify the impact of changes of entrepreneurship on growth.7
Fig. 2

Entrepreneurship and employment growth

Fig. 3

High growth firms and employment growth

There are undoubtedly many mechanisms that impede the commercialization of knowledge. By serving as a conduit for the spillover of knowledge that might not otherwise be commercialized, entrepreneurship is one conceivable mechanism that links knowledge to commercialization and economic growth.

3 Incumbents, entrepreneurs, and knowledge

3.1 Basic assumptions

In order to model the role of the entrepreneur in the endogenous growth process, the mechanisms that impede knowledge exploitation contribution, and the choice of economic agents to become entrepreneurs or remain employees, we impose the following assumptions:

  1. 1.

    A given set of individuals \( \overline{L} \) can either be employed in the goods producing sector (L F), the knowledge (invention) producing sector (L R) or in the entrepreneurial (innovation) sector (L E).

     
  2. 2.

    Entrepreneurial ability is distributed unevenly (and exogenously) across individuals. They deploy their endowments of entrepreneurial capabilities to evaluate the knowledge accessible to them in reaching a decision on how best to appropriate the returns from that knowledge, i.e., they make profit-maximizing intertemporal choices of whether to remain employees or become entrepreneurs (see the following section).

     
  3. 3.

    Efficiency (σ) in transforming knowledge into economic knowledge is impacted by a nation’s or region’s policy, institutions, and path dependence, which influences technology transfer mechanisms.

     
  4. 4.

    There are two channels to develop and transform knowledge (A) into economically useful knowledge. The first involves incumbent firms and the second involves the entrepreneurial start-up of new (Schumpeterian) firms.

     
  5. 5.
    Incumbent firms develop and transform available knowledge into economically useful knowledge by employing researchers (L R), which results in new inventions and new varieties of products (x i ). How smoothly incumbents develop and transform knowledge into goods and services (commercialization) is determined by the efficiency variable σ R,
    $$ 0 \prec \sigma_{R} \prec 1.$$
    The closer σ R is to zero, the less efficient the exploitation of knowledge.
     
  6. 6.
    A start-up (innovation) represents any kind of new combination of existing or new knowledge, where individuals (L E) draw on their (given) entrepreneurial ability (\( \overline{e}_{i} \)) and the aggregate stock of knowledge (A) to develop new products.8 Also, entrepreneurial activities are governed by how efficiently knowledge is exploited and transformed into goods,
    $$ 0 \prec \sigma_{E} \prec 1. $$
    Entrepreneurs do not engage in research but develop new products and new business models (organizing production).
     
  7. 7.

    The production activities of incumbents and entrepreneurs imply that the societal stock of nonrivalrous and partly nonexcludable knowledge increases.

     

These assumptions imply that two conditions are decisive for an increasing stock of knowledge to materialize higher economic growth. First, knowledge has to be transformed into economically useful knowledge, and, second, an economy must be endowed with factors of production that can select, evaluate, and transform knowledge into commercial use. If these conditions are not fulfilled, an increase in the knowledge stock may have little impact on growth. Moreover, economies endowed with small knowledge stocks may experience higher growth than regions more abundantly endowed with knowledge due to a higher efficiency in converting knowledge into products.

3.2 The entrepreneurial choice

Consider an economy endowed with a population of L individuals that live for two periods. In the first period incumbents employ all individuals, but between periods they make intertemporal choices as regards remaining an employee or becoming an entrepreneur.

Individuals at the higher end of the distribution of entrepreneurial ability identify more opportunities to exploit commercially as compared with individuals with lower ability. By combining given entrepreneurial capacity \( (\overline{e} ) \)with the aggregate knowledge stock (A) in an economy operating at an efficiency level (σ E), a certain number of the population (L E) will identify profitable opportunities in running their own firms and become entrepreneurs (e i ). Thus, at a given point in time,
$$ e_{i} = f(\overline{{e_{i} }} ,A,\sigma_{E} ),\mathop {}\nolimits_{{}} \sum\limits_{i = 1}^{L} {e_{i} \equiv }_{{}} L_{E}, $$
(1)
where aggregate entrepreneurial ability in an economy is increasing in e, A, and σ E.
The intertemporal choice between becoming an entrepreneur or remaining an employee depends on the expected payoff accruing to the respective alternatives. Suppose that individuals’ preferences are characterized by von Neumann–Morgenstern utility functions allowing a strictly increasing utility representation of the expected utility form. Moreover, assume that individuals are strictly risk-averse and that u(0) = 0. The decision regarding whether to become an entrepreneur or not is illustrated in Fig. 4.9
Fig. 4

Expected utility of becoming an entrepreneur

The individual who chooses to remain an employee will receive a wage (w) with certainty, yielding utility
$$ U^{{{\text{Wor}}\ker }} = u\left( w \right)_{{}} =_{{}} u_{{}}^{w} (x), $$
(2)
which we will refer to as the individual’s expected utility from remaining an employee, allowing consumption of x goods. If, on the other hand, the individual chooses to become an entrepreneur, expected utility is dependent on the probability of success (\( \varphi \in \left[ {0,1} \right] \)) and the expected pay-off (π),
$$ U^{\text{Entrepreneur}} = \varphi_{{}} u\left( \pi \right) = \varphi_{{}} u^{\pi } (x). $$
(3)

To engage in entrepreneurial activities the individual’s expected net payoff from entrepreneurial activities (\( \varphi_{{}} u^{\pi } \)) must be larger than the expected net payoff from remaining an employee (\( u^{w} \)). As shown in Fig. 4, if \( \pi_{{}} \ge w, \) then there exists a probability \( \varphi * \) such that the choice of being an entrepreneur is optimal for the individual for all\( \varphi > \varphi * \). Assume that there exist a π > w and a \( \varphi > \varphi * \) for a subset of individuals (since \( \bar{e} \) is assumed to be unequally distributed). Then a share of the population will shift from employees to entrepreneurs, thereby using knowledge to commercialize new products, which simultaneously also result in new knowledge.10

At the aggregate level, entrepreneurial activity in the economy (L E) depends on entrepreneurial ability and factors influencing the filter (σ E). A policy that increases the probability of success (φ)—given π—e.g., reducing the regulatory burden or making knowledge more accessible, increases the expected utility from becoming an entrepreneur. This can be illustrated as a move along the straight line in Fig. 4 toward the “northeast” corner.

The share of entrepreneurs can also increase due to a policy that increases the expected payoff (π) for an entrepreneur (e.g., through lowered taxes). In the figure, this implies a shift downwards of the straight line and the intersection with the u-curve would take place further to the “east” in Fig. 4. Thus, even though the probability of success is held constant, the expected utility of becoming an entrepreneur may increase through other measures.

4 A simple endogenous growth model with entrepreneurship

In Sect. 3 we modeled individuals’ intertemporal occupational choice, i.e., providing the analysis with a solid microeconomic base. Linking individual behavior to the macrolevel, and to illustrate the role of entrepreneurs in growth, we suggest a modification of the Romer (1990) model to incorporate “pure” Schumpeterian entrepreneurs (Schumpeter 1911).11 Hence, there are now two methods of developing new products: research laboratories in incumbent firms (inventions) and entrepreneurs (innovations). Just as in Romer’s original work we think of these products as either new types of physical capital, blueprints or “business models” that are being rented or sold to final goods producers, thus making production of final goods more effective. As, e.g., Grossman and Helpman (1991) have shown, the new varieties of capital goods can just as well be thought of as new varieties of consumer goods entering consumers’ utility function directly. The different varieties appear on markets characterized by monopolistic competition, meaning that they never become obsolete and earn an infinite stream of profits.
Table 1

Notation and definitions of variables in the theoretical model

Variable notation

Definition

Y

Final good

x j

Capital good j

A

Aggregate knowledge stock

K

Capital stock

L

Total population, assumed constant

L Y

Number of people in final good production

L E

Number of entrepreneurs

L R

Number of researchers

\( \overline{{e_{i} }} \)

Given entrepreneurial ability of individual i

e i

Probability that individual i becomes an entrepreneur

σ

Efficiency level of economy

Z

Production function, new technology

\( \mathop A\limits^{ \bullet } \)

Change in aggregate stock of knowledge

\( \mathop K\limits^{ \bullet } \)

Change in capital stock

κ

Units of capital goods to produce one unit of capital

ρ

Subjective discount rate

θ

Inverse of intertemporal elasticity of substitution

4.1 Linking entrepreneurs to knowledge exploitation

Before the role of entrepreneurs in knowledge exploitation and growth is considered, we first briefly recapitulate the production function for researchers working in incumbent firms. Research departments within incumbent firms employ labor (L R) as the only production factor, and research activities are influenced by the available stock of knowledge (A) and an efficiency parameter (σ R) related to research activities.12 The latter is a composite of a multitude of different factors. Thus, in its simplest form, the production function for research activities can be written
$$ Z_{\text{R}} \left( {L_{\text{R}} } \right) = \sigma_{\text{R}} L_{\text{R}} A, $$
(4)
where research production is positively influenced by a larger knowledge stock and higher efficiency.
In order to include the Schumpeterian entrepreneur, we first assume that entrepreneurial ability is embodied in labor, but in contrast to raw labor, it is distributed unevenly across the population. Thus, entrepreneurial activities are assumed to be characterized by decreasing returns to scale (γ < 1). The production function for entrepreneurial activities takes the following form:
$$ Z_{\text{E}} (L_{\text{E}} ) = \sigma_{\text{E}} L_{\text{E}}^{\gamma } A,\,\gamma < 1. $$
(5)
Hence, similar to R&D workers, the representative entrepreneur takes advantage of existing knowledge. On the other hand, the production technology differs (decreasing returns to scale), and they do not engage in research. Rather, they combine their entrepreneurial ability with the existing stock of knowledge to introduce new products and business models.13 The different varieties of capital goods (x i ) produced by entrepreneurs and researchers are employed in the final goods (Y) sector together with labor,
$$ Y = (L - L_{\text{E}} - L_{\text{R}} )^{\alpha } \int\limits_{0}^{A} {x(i)^{1 - \alpha } \text{d}i}, $$
(6)
where α (0 < α < 1) represents the scale parameter. Given that the demand for all varieties in equilibrium is symmetric, i.e., \( x_{i} = \bar{x} \) for all i ≤ A, we rewrite Eq. 6 as
$$ Y = (L - L_{\text{E}} - L_{\text{R}} )^{\alpha } A\overline{x}^{(1 - \alpha )}. $$
(7)
Assume that capital goods (K) are produced with the same technology as final goods and that it takes κ units of capital goods to produce one unit of capital (Chiang 1992). Then it can be shown that
$$ K = \kappa A\bar{x}, $$
(8)
and substituting Eq. 8 into Eq. 7 gives
$$ Y = (L - L_{\text{R}}^{{}} - L_{\text{E}} )^{\alpha } A^{\alpha } K^{1 - \alpha } \kappa^{\alpha - 1}. $$
(9)
Thus, the economy employs three factors of production, i.e., raw labor (producing finals), together with researchers and entrepreneurs that produces varieties of capital goods. Labor market equilibrium is attained when employment in R&D, entrepreneurship, and final production equals total supply:
$$ L = L_{\text{F}}^{{}} + L_{\text{E}} + L_{\text{R}}. $$
(10)

4.2 Knowledge production in an economy

As a side-effect of their efforts, researchers and entrepreneurs produce new knowledge that will be publicly available for use in future capital good development, positively influencing coming generations of research and entrepreneurial activities. Equation 11 describes the production of new knowledge, i.e., the evolution of the stock of knowledge, in relation to the amount of labor channeled into R&D (L R) and entrepreneurial activity (L E).
$$ \mathop A\limits^{ \bullet } = Z_{\text{R}} (L_{\text{R}} ) + Z_{\text{E}} (L_{\text{E}} ). $$
(11)
Substituting from Eqs. 4 and 5 yields
$$ \mathop A\limits^{ \bullet }/A = \sigma_{\text{R}} L_{\text{R}} + \sigma_{\text{E}} L_{\text{E}}^{\gamma }, $$
(12)
where, again, σ:s represents the knowledge efficiency in invention activities (R&D) and innovation (entrepreneurship), whereas A is the stock of available knowledge at a given point in time. The rate of technological progress is thus an increasing function in R&D, entrepreneurship, and the efficiency of these two activities.

4.3 Endogenous growth with knowledge-exploiting entrepreneurs

Assuming that demand is governed by consumer preferences characterized by constant intertemporal elasticity of substitution (1/θ), the maximization problem can be expressed in following way:
$$ \mathop {\max }\limits_{{C,L_{\text{E}} ,L_{\text{R}} }} \int_{0}^{\infty } {{\frac{{C^{1 - \theta } }}{1 - \theta }}} \text{e}^{ - \rho t} {\text{d}}t $$
(13)
subject to the laws of motion for knowledge and capital
$$ \mathop A\limits^{ \bullet } = \sigma_{\text{R}} L_{\text{R}} A + \sigma_{\text{E}} L_{\text{E}}^{\gamma } A, $$
(14a)
$$ \mathop K\limits^{ \bullet } = Y - C = \left( {L - L_{E} - L_{R} } \right)^{\alpha } A^{\alpha } K^{1 - \alpha } \kappa^{\alpha - 1} - C. $$
(14b)
The current value Hamiltonian for the representative consumer is then
$$ H_{\text{C}} = {\frac{{C^{1 - \theta } }}{1 - \theta }} + \lambda_{\text{A}} \left( {\sigma_{\text{R}} L_{\text{R}} A + \sigma_{\text{E}} L_{\text{E}}^{\gamma } A} \right) + \lambda_{\text{K}} \left( {\kappa^{\alpha - 1} A^{\alpha } K^{1 - \alpha } \left( {L - L_{\text{R}} - L_{\text{E}} } \right) - C} \right). $$
(15)
The first-order conditions for a maximum, letting \( \Updelta \equiv \left( {L - L_{\text{E}} - L_{\text{R}} } \right)^{\alpha } A^{\alpha } K^{1 - \alpha } \kappa^{\alpha - 1} \), are as follows:
$$ {\frac{{\partial H_{\text{C}} }}{\partial C}} = C^{ - \theta } - \lambda_{\text{K}} = 0, $$
$$ \lambda_{\text{K}} = C^{ - \theta } \to {\frac{{\dot{\lambda }_{\text{K}} }}{{\lambda_{\text{K}} }}} = - \theta {\frac{{\dot{C}}}{C}}, $$
(16)
$$ {\frac{{\partial H_{\text{C}} }}{{\partial L_{\text{E}} }}} = \lambda_{\text{A}} \gamma \sigma_{\text{E}} L_{\text{E}}^{\gamma - 1} A - \lambda_{\text{K}} \alpha \left( {L - L_{\text{E}} - L_{\text{R}} } \right)^{ - 1} \Updelta = 0, $$
(17)
$$ {\frac{{\partial H_{\text{C}} }}{{\partial L_{\text{R}} }}} = \lambda_{\text{A}} \sigma_{\text{R}} A - \lambda_{\text{K}} \alpha \left( {L - L_{\text{E}} - L_{\text{R}} } \right)^{ - 1} \Updelta = 0. $$
(18)
Combining Eqs. 17 and 18 gives
$$ L_{\text{E}} = \left( {{\frac{{\sigma_{\text{R}} }}{{\gamma \sigma_{\text{E}} }}}} \right)^{{{\frac{1}{\gamma - 1}}}}. $$
(19)
Thus, on a balanced growth path, where both R&D and entrepreneurship are profitable, the amount of resources engaged in entrepreneurial activities is independent of consumer preferences (ρ). As γ is less than 1, entry into entrepreneurship is increasing in σ E and decreasing in σ R.
Maximization of Eq. 15 also gives the equations of motion for the shadow prices of capital (K) and knowledge (A) as
$$ {\frac{{\partial H_{\text{C}} }}{\partial A}} = \lambda_{\text{A}} \left( {\sigma_{\text{R}} L_{\text{R}} + \sigma_{\text{E}} L_{\text{E}}^{\gamma } } \right) + \lambda_{\text{K}} \alpha A^{ - 1} \Updelta = \rho \lambda_{\text{A}} - \mathop {\lambda_{\text{A}} }\limits^{ \bullet }, $$
$$ {\frac{{\mathop {\lambda_{\text{K}} }\limits^{ \bullet } }}{{\lambda_{\text{K}} }}} = \rho - \left( {1 - \alpha } \right)K^{ - 1} \Updelta, $$
(20)
\( {\frac{{\partial H_{\text{C}} }}{\partial K}} = \lambda_{\text{K}} \left( {1 - \alpha } \right)K^{ - 1} \Updelta = \rho \lambda_{\text{K}} - \mathop {\lambda_{\text{K}} }\limits^{ \bullet }, \)
$$ {\frac{{\mathop {\lambda_{\text{A}} }\limits^{ \bullet } }}{{\lambda_{\text{A}} }}} = \rho + \sigma_{\text{R}} L_{\text{E}} - \sigma_{\text{R}} L - \sigma_{\text{E}} L_{\text{E}}^{\gamma }, $$
(21)
$$ {\frac{{\partial H_{\text{C}} }}{{\partial \lambda_{\text{A}} }}} = \mathop A\limits^{ \bullet }, $$
(22)
$$ {\frac{{\partial H_{\text{C}} }}{{\partial \lambda_{\text{K}} }}} = \mathop K\limits^{ \bullet }. $$
(23)
A balanced growth path, i.e., where \( {\frac{{\mathop Y\limits^{ \bullet } }}{Y}} = {\frac{{\mathop C\limits^{ \bullet } }}{C}} = {\frac{{\mathop K\limits^{ \bullet } }}{K}} = {\frac{{\mathop A\limits^{ \bullet } }}{A}} \), requires that \( {\frac{{\dot{\lambda }_{\text{K}} }}{{\lambda_{\text{K}} }}} = {\frac{{\dot{\lambda }_{\text{A}} }}{{\lambda_{\text{A}} }}} \). From (16) and the law of motion for knowledge (14a),
$$ {\frac{{\mathop {\lambda_{\text{K}} }\limits^{ \bullet } }}{{\lambda_{\text{K}} }}} = - \theta {\frac{{\mathop C\limits^{ \bullet } }}{C}} = - \theta {\frac{{\mathop A\limits^{ \bullet } }}{A}} = - \theta \left( {\sigma_{\text{R}} L_{\text{R}} + \sigma_{\text{E}} L_{\text{E}}^{\gamma } } \right). $$
(24)
Equating Eqs. 20 and 21, using Eq. 24, yields the following expression:
$$ - \theta \left( {\sigma_{\text{R}} L_{\text{R}} + \sigma_{\text{E}} L_{\text{E}}^{\gamma } } \right) = \rho + \sigma_{\text{R}} L_{\text{E}} - \sigma_{\text{R}} L - \sigma_{\text{E}} L_{\text{E}}^{\gamma }. $$
(25)
Solving for employment in the research sector gives
$$ L_{\text{R}} = {\frac{1}{{\theta \sigma_{\text{R}} }}}\left( {\sigma_{\text{R}} \left( {L - L_{\text{E}} } \right) + \left( {1 - \theta } \right)\sigma_{\text{E}} L_{\text{E}}^{\gamma } - \rho } \right). $$
(26)
Inserting the expressions for equilibrium employment in the entrepreneurial (19) and research sectors (26) into the law of motion for knowledge, the steady-state growth rate (g) can be derived as
$$ g = {\frac{{\mathop A\limits^{ \bullet } }}{A}} = \sigma_{\text{R}} L_{\text{R}} + \sigma_{\text{E}} L_{\text{E}}^{\gamma }, $$
$$ g = \sigma_{\text{R}} \left( {{\frac{1}{{\theta \sigma_{\text{R}} }}}\left( {\sigma_{\text{R}} \left( {L - L_{\text{E}} } \right) + \left( {1 - \theta } \right)\sigma_{\text{E}} L_{\text{E}}^{\gamma } - \rho } \right)} \right) + \sigma_{\text{E}} L_{\text{E}}^{\gamma }, $$
$$ g = \sigma_{\text{R}} \left( {{\frac{1}{{\theta \sigma_{\text{R}} }}}\left( {\sigma_{\text{R}} \left( {L - \left( {{\frac{{\sigma_{\text{R}} }}{{\gamma \sigma_{\text{E}} }}}} \right)^{{1/\left( {\gamma - 1} \right)}} } \right) + \left( {1 - \theta } \right)\sigma_{\text{E}} \left( {{\frac{{\sigma_{\text{R}} }}{{\gamma \sigma_{\text{E}} }}}} \right)^{{\gamma /\left( {\gamma - 1} \right)}} - \rho } \right)} \right) + \sigma_{\text{E}} \left( {{\frac{{\sigma_{\text{R}} }}{{\gamma \sigma_{\text{E}} }}}} \right)^{{\gamma /\left( {\gamma - 1} \right)}}, $$
$$ g = {\frac{1}{\theta }}\left( {\sigma_{\text{R}} L - \rho + \left( {1 - \gamma } \right)\gamma^{{\gamma /\left( {1 - \gamma } \right)}} \left( {{\frac{{\sigma_{\text{E}} }}{{\sigma_{\text{R}}^{\gamma } }}}} \right)^{{1/\left( {1 - \gamma } \right)}} } \right). $$
(27)
Note that some entrepreneurial activity (Eq. 19) will always be profitable, i.e., \( L_{\text{E}} > 0, \)as long as the stock of knowledge exceeds zero (\( A > 0 \)), which does not, however, always apply to R&D activities (Eq. 26).14 The model shares a number of characteristics with previous models, e.g., growth is decreasing in the discount factor (\( \rho \)) and increasing in a larger labor force.

Apart from these properties, the specification of the model implies that the impact on growth of the distribution of labor between R&D and entrepreneurial activities can be derived. Similarly, the optimal distribution of labor between final goods production and knowledge production (R&D and entrepreneurs) can also be inferred from the model. The following propositions follow from the model:

Proposition 1

Given that an economy has an optimal distribution of workers between the final goods sector and the knowledge producing sectors (R&D and entrepreneurs), optimal steady-state growth implies that a marginal redistribution between entrepreneurship and R&D workers has no effect on growth (assuming that the efficiency parameters is constant and that the knowledge stock exceeds zero).

Proof

In steady state \( {\frac{{\mathop A\limits^{ \bullet } }}{A}} = {\frac{{\mathop K\limits^{ \bullet } }}{K}} \Rightarrow {\frac{{\mathop Y\limits^{ \bullet } }}{Y}} = {\frac{{\mathop A\limits^{ \bullet } }}{A}} \), i.e., an optimal distribution of labor between final goods and knowledge production implies that a marginal increase in either sector is exactly counterbalanced by a decrease in the other sector. This is, however, not equivalent to an optimal distribution of labor in the knowledge producing sector (\( L_{A} \)) between R&D workers and entrepreneurs, \( L_{\text{A}} = L - L_{\text{F}} = L_{\text{R}} + L_{\text{E}} \). Using this relationship and Eqs. 27 and 10, growth can be rewritten as\( g = {\frac{{\mathop A\limits^{ \bullet } }}{A}} = \sigma_{\text{R}} (L_{\text{A}} - L_{\text{E}} ) + \sigma_{\text{E}} L_{\text{E}}^{\gamma } \). Differentiating with respect to \( L_{\text{E}} \) yields \( {\frac{\partial g}{{\partial L_{\text{E}} }}} = - \sigma_{\text{R}} + \gamma_{{}} \sigma_{\text{E}} L_{\text{E}}^{\gamma - 1} = 0 \), which is equivalent to Eq. 19, \( L_{\text{E}}^{*} = ({\frac{{\sigma_{\text{R}} }}{{\gamma \sigma_{\text{E}} }}})^{1/(\gamma - 1)} \), where \( L_{\text{E}}^{*} \) represents an optimal allocation between R&D workers and entrepreneurs. Consequently, \( {\frac{\partial g}{{\partial L_{\text{E}} }}} > 0 \Rightarrow L_{\text{E}} < \left({\frac{{\sigma_{\text{R}} }}{{\gamma \sigma_{\text{E}} }}}\right)^{1/(\gamma - 1)} = L_{\text{E}}^{*} \), i.e., social optimum is not attained. Given that there is an optimal allocation of labor between the final goods sector and the knowledge sector (\( dL_{\text{A}} = 0 \)), there is also a direct mapping to R&D workers (\( dL_{\text{R}} = - dL_{\text{E}} \)); too few entrepreneurs is mirrored by too many R&D workers.

A second, and rather obvious, implication of the model concerns the efficiency of an economy in accumulating and exploiting knowledge, which should influence the rate of growth. Moreover, if the efficiency in converting knowledge to commercial use is influenced asymmetrically over time due to events that are exogenous to firms (national and international institutional change), there may be time-inconsistent effects of R&D and entrepreneurship on growth over time.

Proposition 2

Growth is increasing in higher efficiency of research (\( \sigma_{\text{R}} \)) and of entrepreneurship (\( \sigma_{\text{E}} \)).

Proof

First, differentiating the growth Eq. 27 with respect to the efficiency parameter of research,
$$ {\frac{\text{d}g}{{\text{d}\sigma_{\text{R}} }}} = {\frac{1}{\theta }}\left[ {L - \left({\frac{{\sigma_{\text{R}} }}{{\gamma \sigma_{\text{E}} }}}\right)^{{{\frac{1}{\gamma - 1}}}} } \right] = {\frac{1}{\theta }}\left[ {L - L_{\text{E}}^{{}} } \right], $$
which is unambiguously nonnegative.
Second, differentiating the growth Eq. 27 with respect to the efficiency parameter of entrepreneurial activities,
$$ {\frac{\text{d}g}{{\text{d}\sigma_{\text{E}} }}} = {\frac{1}{\theta }}\left[ {\left({\frac{{\sigma_{\text{R}} }}{{\gamma \sigma_{\text{E}} }}}\right)^{{{\frac{\gamma }{\gamma - 1}}}} } \right] = {\frac{1}{\theta }}\left[ {L_{\text{E}}^{\gamma } } \right], $$
which is unambiguously nonnegative.

From these two propositions the following testable hypotheses emerge: If countries have attained an optimal growth path there will be no growth effect of a (i) marginal redistribution of labor between sectors (the final goods sectors and the knowledge producing sectors), (ii) marginal redistribution of labor within the knowledge producing sectors (R&D and entrepreneurial activities), (iii) marginal redistribution of knowledge workers between time periods, while growth should be positively influenced by (iv) altering variables that influence how efficiently an economy works.

5 Empirical analysis

5.1 Variables

The dependent variable is defined as the annual difference in log real GDP growth (expressed in 1995 prices) for 17 OECD countries over the period 1981–2002. The main explanatory variables of interest and relevance to the model derived in the previous section include measures of R&D activities and entrepreneurship. These variables are defined as either the number of (full-time equivalent) scientists and entrepreneurs in the respective country, which most closely corresponds to the model, or normalized by population.15

Measuring entrepreneurship (ENT) is at least as challenging and elusive as measuring knowledge. While start-up rates are perhaps the ideal measure capturing entrepreneurship, no such comparable measure exists across the sample of countries chosen for the current analysis. When such measures do exist, they normally comprise a limited subset of countries and tend to be measured in significantly differently ways, rendering their application in cross-country comparisons and regressions inappropriate and misleading. Instead, the same measure as Evans and Jovanovic (1989), Evans and Leighton (1989), and Blanchflower and Oswald (1998) is used: the nonagricultural self-employed. Self-employment is a proxy reflecting underlying entrepreneurial activity and has the advantage of being available for a cross-country time-series context. Obviously there are differences across countries, but we argue that our chosen econometric method to a large extent controls for these differences provided that they are consistent over time. The number of self-employed is used to represent L E in the model introduced in the previous section.

The degree of trade union activity will be used as a measure of how efficiently an economy work (the \( \sigma :s \) used in the model). The prevalence of trade unions (TUD), measured as the share of employment in the labor force belonging to a trade union, is expected to be negatively related to growth since trade unions may pose institutional rigidities and poorly functioning labor markets. Thereby optimal allocation of labor between different occupations may be distorted. In addition, labor market rigidities have been shown to correlate strongly with other market regulations that impede productivity and the functioning of an economy (Nicoletti et al. 1999).

Barro and Sala-i-Martin (2004) include a number of variables controlling for other influences. We follow their approach by including variables reflecting the human capital endowment of an economy (average years of schooling), its openness (imports and exports in relation to GDP), the degree of urbanization (population living in urban areas), and other factors of production (capital–labor ratio). All control variables are expected to exert a positive impact on growth. In addition dummies are used to control for time-specific effects, either annual or defined as periods. Definitions of the variables, and their sources, are shown in Table 2.
Table 2

Notation and definition of variables in the empirical model

Growth

Difference in log real GDP, 1995 year’s prices and in purchasing power parity (PPP)

OECD, Statistical Compendium on CD, 2004-2002

Entrepreneurs (ENT)

Total nonagriculture self-employed

EIM, The COMPENDIA database.

Researchers (R&D)

Total number of researchers, full-time equivalent

OECD, Statistical Compendium on CD, 2004-2

Trade union density (TUD)

Share of labor force that is unionized

Visser (2006), Schnabel and Wagner (2003), OECD Labour Market Statistics

Capital stock per worker (CAPW)

Business capital stock divided by employment valued at 1995 price level and in PPP

OECD, Statistical Compendium on CD, 2004-2

Openness (OPEN)

The sum of exports and imports of goods and services measured as a share of gross domestic product

OECD, Statistical Compendium on CD, 2004-2

Urban population (URBAN)

The share of total population living in areas defined as urban in each country

OECD, Statistical Compendium on CD, 2004-2

Average years of schooling (TYR)

Average years of schooling among population aged 25 years and above

Barro and Lee (2000), International Data on Educational Attainment. Updates and Implications, CID Working Paper No. 42

Population (POP)

Total population

OECD, Statistical Compendium on CD, 2004-2

5.2 Econometric specification

Data has been pooled over countries and years for the period 1981–2002. In the regressions generalized least-squares (GLS) techniques, taking into account “within” and “between” effects simultaneously as we control for heteroskedastic panels and panel autoregressive (AR) error structures, will be implemented together with ordinary least squares (OLS).16 The regressions will use both 5-year averages of the data and annual observations.

The following growth (\( g \)) equation will be estimated:
$$ g_{jt} = \beta_{0} + \beta_{1} \text{ENT}_{j,t} + \beta_{2} \text{R\&D}_{j,t} + \beta_{4} \text{TUD}_{j,t} + \delta 'Z_{j,t} + \varepsilon_{j,t}, $$
(28)
where \( j \) refers to country and \( t \) to the time period. The error term either has a common AR1 structure where the error terms for the different panels follow a common process \( \varepsilon_{j,t} = \rho \varepsilon_{j,t - 1} + \mu_{j,t} \), (\( \mu_{j,t} \) is white noise) or a panel-specific AR1 structure which allows for the correlation coefficient to differ between panels, \( \varepsilon_{j,t} = \rho_{j} \varepsilon_{j,t - 1} + \mu_{j,t} \). Besides the key variables, defined as the numbers of entrepreneurs (ENT), the numbers of researchers (R&D), and the efficiency variables (TUD), a set of control variables is contained in the vector Z.

The regression analysis will implement both levels of data—which closely corresponds to the theoretical model—and estimations where the data are normalized by country size for the variables of principal interest in the analysis, i.e., entrepreneurs and researchers. The bivariate correlations when the variables are expressed in levels are sufficiently low as not to suggest any problems with multicollinearity. We will also control for different lag structures on the ENT and R&D variables. The population variable will be implemented in all estimations to control for country size.

5.3 Regression results

We start by presenting the results when the variables are defined as 5-year averages. The first run of regressions is presented in Table 3 where only the level of entrepreneurs and researchers, together with population and period dummies, are used. The entrepreneurship coefficient turns out to be positive and strongly statistically significant, irrespective of econometric specification, albeit somewhat lower when OLS estimation techniques are used, suggesting that there is a positive relationship between economic growth and the degree of entrepreneurial activity. Due to the limited degrees of freedom, the estimations implementing a common autoregressive structure can be expected to yield the most robust results. Turning to the variable capturing researchers, a conspicuous result is that in no case does this variable reach significance.
Table 3

General least-squares regressions with heteroskedastic panels and panel-specific and common AR1 structures, and OLS regressions

 

GLS, common AR1

GLS, panel-specific AR1

OLS

Level

Share

Level

Share

Level

Share

Self-employed,

1,000

1.10***

(3.88)

1.10***

(3.88)

1.15***

(6.85)

1.15***

(6.87)

1.21**

(2.12)

1.20**

(2.11)

Researchers,

1,000

0.18

(0.88)

0.18

(0.88)

−0.14

(−0.11)

−0.02

(−0.12)

0.12

(0.45)

0.13

(0.44)

Population

−1.40***

(−3.65)

−0.12*

(−1.63)

−1.31***

(−5.95)

−0.17***

(−3.81)

−1.15**

(−2.06)

−0.23*

(−1.89)

Time dummy,

Period 2

1.11***

(7.77)

1.11***

(7.77)

1.27***

(18.76)

1.27***

(19.01)

1.12***

(2.87)

1.13***

(2.87)

Time dummy,

Period 3

−0.49***

(−3.20)

−0.49***

(−3.20)

−0.22**

(−2.25)

−0.23**

(−2.28)

−0.34

(−0.82)

−0.34

(−0.81)

Time dummy,

Period 4

0.48***

(2.88)

0.48***

(2.87)

−0.72***

(−0.03)

0.72***

(5.03)

0.63

(1.40)

0.63

(1.41)

Constant

7.80***

(3.85)

1.99*

(1.89)

7.20***

(5.62)

1.95***

(2.88)

8.97**

(2.48)

2.84**

(2.03)

Wald

181***

181***

1329***

1432***

–

–

F

–

–

–

–

4.12

4.11

Adj.\( R^{2} \)

–

–

–

–

0.20

0.20

No. of obs.

74

74

74

74

74

74

Note: Standard errors are in parentheses; ***, **, and * indicate significance at the 1%, 5%, and 10% level, respectively. All variables expressed in logarithms

Regressions based on the following 17 OECD countries: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Ireland, Italy, Japan, The Netherlands, Norway, Spain, Sweden, UK, and USA

Levels and shares of entrepreneurs and researchers, 5-year averages (1981–1985, 1986–1990, 1991–1995, 1996–2002), 17 OECD countries. Dependent variable: difference in log real GDP, 1995 year’s prices, multiplied by 100

In Table 4 the full model is tested with all the control variables included. Similar results appear, where it is shown that entrepreneurial activities exert a strongly significant and positive impact on growth, while no such effect could be found for researchers. As regards the efficiency variable captured by trade union density, it attains a negative value but remains insignificant in all estimations. Thus, the econometric results presented in Tables 3 and 4 involving the main variables of the analysis (entrepreneurs, researchers, and the efficiency variable) seem to exhibit a satisfactorily level of robustness irrespective of the definitions of variables (levels or shares) or the econometric specification implemented. The Wald statistics are also satisfactorily high. The results for the control variables fluctuate somewhat and the results are not always as expected.
Table 4

General least-squares regressions with heteroskedastic panels and panel-specific and common AR1 structures, and OLS regressions

 

Specific AR, 5-year average

Common AR, 5-year average

OLS

Level

Share

Level

Share

Level

Share

Self-employed, 1,000

1.35***

(5.15)

1.36***

(5.17)

1.23***

(2.90)

1.23***

(2.89)

1.51**

(2.59)

1.51**

(2.59)

Researchers, 1,000

−0.34

(−1.31)

−0.34

(−1.31)

0.26

(0.65)

0.26

(0.65)

0.24

(0.48)

0.24

(0.47)

Trade union density, %

−0.09

(−0.49)

−0.09

(−0.49)

−0.20

(−0.82)

−0.20

(−0.82)

−0.31

(−0.78)

−0.31

(−0.78)

Population

−0.95**

(−2.13)

0.06

(0.45)

−1.47**

(−2.03)

0.02

(0.12)

−1.80*

(−1.90)

−0.04

(−0.19)

Capital stock per worker, 1,000 USD

−0.85*

(−1.93)

−0.85*

(−1.92)

−1.41**

(−2.35)

−1.42**

(−2.35)

−1.51**

(−2.23)

−1.51**

(−2.23)

Openness, %

0.42

(1.27)

0.42

(1.29)

0.73*

(1.71)

0.73*

(1.71)

1.10**

(2.53)

1.11**

(2.53)

Average years of schooling

1.25**

(2.37)

1.26**

(2.40)

0.60

(0.64)

0.59

(0.63)

0.51

(0.43)

0.51

(0.43)

Urban population, %

−1.81***

(−3.41)

−1.83***

(−3.44)

−1.48*

(−1.66)

−1.48*

(−1.65)

−3.46***

(−3.53)

−3.46***

(−3.53)

Time dummy, Period 2

1.27***

(9.97)

1.27***

(9.93)

1.09***

(4.71)

1.09***

(4.71)

0.89**

(2.30)

0.89**

(2.30)

Time dummy, Period 3

−0.04

(−0.18)

−0.04

(−0.20)

−0.33

(−1.02)

−0.33

(−1.02)

−0.40

(−0.85)

−0.40

(−0.85)

Time dummy, Period 4

0.84***

(2.71)

0.84***

(2.69)

0.50

(1.05)

0.47

(1.05)

0.40

(0.61)

0.38

(0.61)

Constant

10.95**

(2.41)

6.28**

(1.87)

16.33**

(2.43)

9.49**

(1.97)

26.01***

(3.34)

17.95***

(3.05)

Wald

1357***

1359***

99***

99***

–

–

F

–

–

–

–

4.44

4.43

Adj. \( R^{2} \)

–

–

–

–

0.35

0.35

No. of obs.

70

70

70

70

70

70

Note: Standard errors are in parentheses; ***, **, and * indicate significance at the 1%, 5%, and 10% level, respectively. All variables expressed in logarithms

Regressions based on the following 17 OECD countries: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Ireland, Italy, Japan, The Netherlands, Norway, Spain, Sweden, UK, and USA

Levels and shares of entrepreneurs and researchers, 5-year averages (1981–1985, 1986–1990, 1991–1995, 1996–2002), 17 OECD countries. Dependent variable: difference in log real GDP, 1995 year’s prices, multiplied by 100

We then rerun the regressions for annual data but retain the remaining specifications. The results are presented in Tables 5 and 6. The results are almost identical for our core variables (entrepreneurship, researchers, and efficiency), while the significance of some of the control variables is affected. Considering the increased degrees of freedom, the estimations implementing specific autoregressive structure should be the focus. The entrepreneurial variable is shown to display a strong impact on growth, while researchers fail to attain significance. Again the definition of variables (levels or shares) does not influence the results, and the choice of econometric method only marginally changes the results between the different regressions.
Table 5

General least-squares regressions with heteroskedastic panels and panel-specific and common AR1 structures, and OLS regressions

 

GLS, common AR1

GLS, panel-specific AR1

OLS

 

Levels

Shares

Levels

Shares

Levels

Shares

Self-employed,

1,000

0.69

(1.31)

0.70

(1.31)

1.29***

(3.16)

1.29***

(3.16)

1.45***

(3.67)

1.44***

(3.67)

Researchers,

1,000

0.28

(1.10)

0.28

(1.10)

0.22

(0.74)

0.22

(0.74)

0.15

(0.71)

0.16

(0.71)

Population

−1.09

(−1.53)

−0.11

(−0.92)

−1.51

(−2.80)

−0.01

(−0.03)

−1.90***

(−3.68)

−0.30***

(−3.64)

Annual dummies

Yes

Yes

Yes

Yes

Yes

Yes

Constant

5.62*

(1.68)

1.11

(0.94)

6.08**

(2.17)

−0.87

(−0.67)

9.52***

(3.79)

2.16**

(2.13)

Wald

242***

242***

292***

293***

–

–

F

–

–

–

–

6.82

6.82

Adj. \( R^{2} \)

–

–

–

–

0.27

0.27

No. of obs.

371

371

371

371

371

371

Note: Standard errors are in parentheses; ***, **, and * indicate significance at the 1%, 5%, and 10% level, respectively. All variables expressed in logarithms

Regressions based on the following 17 OECD countries: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Ireland, Italy, Japan, The Netherlands, Norway, Spain, Sweden, UK, and USA

Levels and shares of entrepreneurs and researchers, annual data (1981–2002), 17 OECD countries. Dependent variable: difference in log real GDP, 1995 year’s prices, multiplied by 100

Table 6

General least-squares regressions with heteroskedastic panels and panel-specific and common AR1 structures, and OLS regressions

 

Specific AR

Common AR

OLS

Level

Share

Level

Share

Level

Share

Self-employed,

1,000

1.24***

(2.65)

1.24***

(2.65)

1.16**

(2.02)

1.16**

(2.02)

1.72***

(4.28)

1.73***

(4.28)

Researchers,

1,000

0.25

(0.55)

0.25

(0.55)

0.24

(0.58)

0.25

(0.58)

0.41

(1.16)

0.40

(1.15)

Trade union density, %

−0.26

(−0.84)

−0.26

(−0.84)

−0.18

(−0.59)

−0.18

(−0.59)

−0.40

(−1.44)

−0.40

(−1.44)

Population

−1.48*

(−1.77)

0.10

(0.54)

−1.42*

(−1.61)

−0.02

(−0.05)

−2.23***

(−3.45)

−0.09

(−0.56)

Capital stock per worker,

1,000 USD

−1.60**

(−2.48)

−1.60**

(−2.48)

−2.06***

(−3.29)

−2.06***

(−3.29)

−1.65***

(−3.60)

−1.65***

(−3.61)

Openness, %

0.93**

(2.13)

0.94**

(2.13)

1.01**

(2.28)

1.01**

(2.28)

1.31***

(4.28)

1.31***

(4.28)

Average years of schooling

0.77

(0.75)

0.77

(0.75)

0.04

(0.03)

0.04

(0.04)

0.39

(0.45)

0.39

(0.45)

Urban population, %

−1.95*

(−1.91)

−1.95*

(−1.91)

−2.08

(−2.28)**

−2.08**

(−2.28)

−3.73***

(−5.48)

−3.73***

(−5.48)

Annual dummies

Yes

Yes

Yes

Yes

Yes

Yes

Constant

17.00**

(2.23)

10.10*

(1.88)

20.36***

(2.86)

13.87***

(2.66)

28.69***

(5.36)

18.86***

(4.66)

Wald

310***

310***

292***

291***

–

–

F-test

 

–

–

–

8.65

8.65

Adj. \( R^{2} \)

 

–

–

–

0.38

0.38

No. of obs.

371

371

371

371

371

371

Note: Standard errors are in parentheses; ***, **, and * indicate significance at the 1%, 5%, and 10% level, respectively. All variables expressed in logarithms

Regressions based on the following 17 OECD countries: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Ireland, Italy, Japan, The Netherlands, Norway, Spain, Sweden, UK, and USA

Levels and shares of entrepreneurs and researchers, annual data (1981–2002), 17 OECD countries. Dependent variable: difference in log real GDP, 1995 year’s prices, multiplied by 100

The period dummies implemented in Tables 3 and 4 suggest that there are reasons to suspect a structural break in the data over time. It may be that the sources of growth shifted from accumulation of knowledge towards exploiting the stock of knowledge, rendering the role of conduits facilitating the spillover of the knowledge, such as entrepreneurship, more important in the latter period. Thus, in Table 7 results are presented, estimating the model where data has been distributed on two decades: the 1980s (1981–1993) and the 1990s (1994–2002).17 The results reveal some interesting dynamics between the two periods. First, entrepreneurial activities seem to have become increasingly important in the 1990s, while researchers continue to have negligible impact on growth. In addition, the efficiency variable is shown to be statistically significantly negative in the 1990s, but not so in the 1980s. In addition, even though research fails to impact growth, education becomes strongly significant in the 1990s. The results suggest a change in the sources that promotes growth between the two decades, where entrepreneurship, trade union density (efficiency proxy), and education have become more important. That is likely to reflect the structural changes that most OECD countries have undergone in the 1990s, characterized by globalization and increased competition.
Table 7

General least-squares regressions with heteroskedastic panels, panel-specific and common AR1 structures, and OLS regressions

 

Specific AR

Common AR

OLS

1981–1993

1994–2002

1981–1993

1994–2002

1981–1993

1994–2002

Self-employed, 1,000

1.09*

(1.73)

1.66***

(2.89)

1.27*

(1.70)

1.81***

(2.77)

1.03*

(1.79)

2.16***

(3.97)

Researchers, 1,000

0.06

(0.11)

−0.85

(−1.50)

−0.10

(−0.16)

−71

(−0.99)

0.01

(0.01)

−1.03

(−1.48)

Trade union density, %

−0.25

(−0.58)

−1.05**

(−2.30)

−0.29

(−0.79)

−0.86**

(−2.10)

−0.25

(−0.65)

−1.12***

(−2.78)

Population

−1.08

(−1.02)

−1.55*

(−1.81)

−0.99

(−0.91)

−1.92*

(−1.76)

−0.90

(−1.03)

−2.08*

(−2.01)

Capital stock per worker, 1,000 USD

−1.71**

(−1.98)

0.44

(0.46)

−2.02**

(−2.37)

−0.18

(−0.21)

−1.64***

(−2.58)

0.08

(0.11)

Openness, %

0.72

(1.30)

0.57

(1.22)

0.88

(1.49)

−0.04

(−0.08)

0.75*

(1.70)

1.03**

(2.27)

Average years of schooling

0.79

(0.68)

6.89***

(3.07)

1.04

(0.75)

4.28**

(2.07)

0.37

(0.37)

5.66***

(3.02)

Urban population, %

−2.70***

(−2.45)

−3.25***

(−3.11)

−2.30**

(−2.11)

−1.38

(−1.18)

−2.74***

(−2.93)

−4.64***

(−5.17)

Annual dummies

Yes

Yes

Yes

Yes

Yes

Yes

Constant

19.06**

(2.07)

9.12

(1.05)

16.24*

(1.80)

13.14

(1.30)

18.80***

(2.61)

19.24**

(2.19)

Wald

159***

203***

173***

154***

−

−

F-test

–

–

–

–

6.31

10.96

Adj.\( R^{2} \)

–

–

–

–

0.33

0.52

No. of obs.

221

150

221

150

221

150

Note: Standard errors are in parentheses; ***, **, and * indicate significance at the 1%, 5%, and 10% level, respectively. All variables expressed in logarithms

Regressions based on the following 17 OECD countries: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Ireland, Italy, Japan, The Netherlands, Norway, Spain, Sweden, UK, and USA

Levels of entrepreneurs and researchers, annual data, distributed on two time periods (1981–1993 and 1994–2002), 17 OECD countries. Dependent variable: difference in log real GDP, 1995 year’s prices, multiplied by 100

To conclude, the empirical analysis basically rejects the hypotheses presented in Sect. 3: In particular, there seems to have been a suboptimal distribution of labor between sectors and within the knowledge producing sector. According to the regression results, more labor should have been shifted towards entrepreneurial activities. Similarly, low efficiency seems to have hampered growth in the latter part of the time period we are considering, and entrepreneurial activities are indicated to exert a stronger impact on growth over time. The results indicate a wedge between private and social welfare optimization. These results also imply that a different set of policy instruments should be used in order to attain sustainable higher growth rates.

5.4 Testing for robustness

In order to check the robustness of the results and how causality runs between growth and entrepreneurship, some additional results will be presented. First, a Granger causality test is presented in the appendix, showing that causality runs predominantly from entrepreneurial activities to growth and not the other way around.

We have also implemented different lag structures on the variables (from 1 to 4 years) on our key variables entrepreneurship and researchers to control for growth effects appearing in subsequent periods. Table 8 reports some of the findings when the variables are lagged 1 and 4 years, respectively.18 The results for the remaining variables are quite stable and not shown in the table. Similarly, the results change only marginally if we define the variables in terms of shares, or if we split the data set between the 1980s and the 1990s. As shown in Table 8, the entrepreneurial variable attains significance in all but one regression, while the number of researchers remains insignificant in all estimations. The results support our previous findings.
Table 8

Regression results. General least-squares regressions with heteroskedastic panels and panel-specific AR1 structures, and OLS

Regression

Variable

SpecificAR1

OLS

1

Self-employed lagged 1 period

0.93**

(1.98)

1.51***

(3.70)

Researchers

0.20

(0.43)

0.36

(1.02)

2

Self-employed

0.98*

(1.93)

1.57***

(3.78)

Researchers lagged 1 period

0.23

(0.46)

0.29

(0.78)

3

Self-employed lagged 1 period

0.60

(1.17)

1.35***

(3.22)

Researchers lagged 1 period

0.16

(0.33)

0.24

(0.64)

4

Self-employed lagged 4 periods

1.11**

(2.27)

1.37***

(3.27)

Researchers

0.23

(0.51)

0.30

(0.84)

5

Self-employed

1.13*

(1.95)

1.49***

(3.38)

Researchers lagged 4 periods

−0.70

(−1.24)

−0.23

(−0.56)

6

Self−employed lagged 4 periods

1.30**

(2.15)

1.33***

(2.97)

Researchers lagged 4 periods

−0.79

(−1.44)

−0.39

(−0.94)

Note: Standard errors are in parentheses; ***, **, and * indicate significance at the 1%, 5%, and 10% level, respectively. All variables expressed in logarithms. In addition to self-employed and researchers, the regressions contain the following variables: population, trade union density, capital stock per worker, openness, average years of schooling, and urban population

Regressions based on the following 17 OECD countries: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Ireland, Italy, Japan, The Netherlands, Norway, Spain, Sweden, UK, and USA

Annual data, different lag structure of self-employed and researchers, levels; 17 OECD countries. Dependent variable: difference in log real GDP, 1995 year’s prices, multiplied by 100

Finally we have checked for different kinds of spurious correlations between the independent variables. Again, the results remain stable as we run the regressions excluding some of the variables. One obvious candidate is the education variable, which could be linked to both the variable capturing researchers but also to the urbanization variable. The results when we exclude the education variable are presented in Table 9. The remaining variables are barely affected; particularly, the research variable remains insignificant while the entrepreneurial variable continuous to display a positive and statistically significant impact on growth. These results are independent with respect to the definition of the variables or the specification of the autoregressive structure. Hence, we conclude that the regression results are robust.
Table 9

General least-squares regressions with heteroskedastic panels, excluding the education variable

 

Specific AR, annual data

Common AR, 5-year average

Level

Share

Level

Share

Self-employed, 1,000

1.18**

(2.53)

1.18**

(2.53)

1.21***

(2.82)

1.20***

(2.82)

Researchers, 1,000

0.43

(1.20)

0.43

(1.19)

0.41

(1.28)

0.41

(1.28)

Population

−1.61**

(−2.00)

0.002

(0.01)

−1.61**

(−2.35)

0.006

(0.004)

Trade union density, %

−0.23

(−0.75)

−0.23

(−0.74)

−0.18

(−0.75)

−0.18

(−0.75)

Capital stock per worker, 1,000 USD

−1.79***

(−2.97)

−1.79***

(−2.97)

−1.59***

(−2.89)

−1.59***

(−2.89)

Openness, %

0.94**

(2.14)

0.94**

(2.14)

0.77*

(1.80)

0.77*

(1.79)

Average years of schooling

−

−

−

−

Urban population, %

−1.77*

(−1.78)

−1.77*

(−1.78)

−1.41

(−1.58)

−1.41

(−1.58)

Time dummy, period 2

–

–

1.10***

(4.78)

1.10***

(4.78)

Time dummy, period 3

–

–

−0.29

(−0.91)

−0.29

(−0.91)

Time dummy, period 4

–

–

0.52

(1.18)

0.52

(1.18)

Annual dummies

Yes

Yes

–

–

Constant

19.58***

(2.93)

12.16***

(2.58)

18.85***

(3.46)

11.42***

(2.99)

Wald

308***

308***

100***

100***

No. of obs.

371

371

70

70

Note: Standard errors are in parentheses; ***, **, and * indicate significance at the 1%, 5%, and 10% level, respectively. All variables expressed in logarithms

Regressions based on the following 17 OECD countries: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Ireland, Italy, Japan, The Netherlands, Norway, Spain, Sweden, UK, and USA

Annual data (1981–2002) and 5-year averages (1981–1985, 1986–1990, 1991–1995, 1996–2002), 17 OECD countries. Dependent variable: difference in log real GDP, 1995 year’s prices, multiplied by 100

6 Policy implications

A significant and compelling contribution of the endogenous growth theory was to refocus the policy debate away from the emphasis on enhancing capital and labor with a new priority on knowledge and human capital—in particular through a combination of taxes and subsidies. As Lucas (1993) concluded, “The main engine of growth is the accumulation of human capital—of knowledge—and the main source of differences in living standards among nations is differences in human capital. Physical capital accumulation plays an essential but decidedly subsidiary role.”

Lucas also elaborates on specific policy instruments designed to enhance investments in human capital and knowledge. Thus, the policy debate on how to generate growth revolves around the efficacy of a combination of taxes and subsidies in order to promote education, public and private investments in research and development, training programs, and apprentice systems.

By contrast, the extension of the endogenous growth model suggested in this paper implies the central, although not exclusive, role played by a very different set of policy instruments. This policy focus is on instruments that will influence the “entrepreneurial choice” as discussed in Sect. 3, thereby converting knowledge into economic knowledge. Such institutional changes are targeted to enhance the commercialization of knowledge.19

The point emphasized in this paper is that entrepreneurship policies are important instruments in the arsenal of policies to promote growth. As this paper suggests, while generating knowledge and human capital may be a necessary condition for economic growth, it is not sufficient. Rather, a supplementary set of policies focusing on enhancing the conduits of knowledge spillovers also plays a central role in promoting economic growth.

7 Conclusion

A careful examination of the basic structure of the knowledge-based endogenous growth theory reveals that the model is limited by the assumption that knowledge not only spills over but also that it is automatically transformed from knowledge to economic knowledge. Such an assumption violates the basic premise of Arrow’s (1962) insights into the economics of knowledge. These misspecifications may account for the somewhat ambiguous empirical results the model has generated in explaining growth differences across countries.

Recent literature on entrepreneurship suggests that it may serve as a conduit for the spillover of new knowledge. Thus, entrepreneurship is one mechanism that may augment the effect of knowledge investments. This is certainly consistent with the recent wave of statistical regularities that provide compelling, systematic empirical evidence linking measures of entrepreneurship to economic growth. Implementing different regression techniques we find surprisingly robust support for entrepreneurship being one important source of growth, while no such relationship could be established for researchers. In addition, it was also shown how R&D seems to have been overemphasized in the 1990s as compared with entrepreneurial activities, while a somewhat different picture emerged for the 1980s.

We have suggested a modification of the endogenous growth model that we believe will narrow the gap between the model and real-world behavior. The role that entrepreneurship plays in increasing the arrival intensity of innovations, thereby generating economic growth, implies a whole new policy approach. Hence, even though the major part of entrepreneurs do not engage in R&D activities, they contribute to growth by exploiting knowledge in a way that resembles Schumpeter’s approach.

In this paper we have made a first preliminary attempt to separate the contribution to growth that emanates from entrepreneurial spillovers relative to the commercialization by incumbent firms. Future research needs to identify more rigorously the different contributions to growth by entrepreneurial and incumbent firms.

Footnotes

  1. 1.

    See Jones (1995a, b), Young (1998), and Greenwood and Jovanovic (1998). Jones proposed a semi-endogenous growth model in which it becomes more difficult over time to discover new products. Educational variables have been more successful in explaining growth (Barro and Sala-i-Martin 2004). See Dinopoulos and Thompson (1998) and Aghion and Howitt (1998b) for a discussion of empirical problems.

  2. 2.

    In Fig. 1, changing or removing the time lag does not materially change the results.

  3. 3.

    A version of a R&D-driven growth model was first presented by Shell (1967).

  4. 4.

    This was to some extent remedied in the second generation of endogenous growth models (Segerstrom et al. 1990, Segerstrom 1991, Aghion and Howitt 1992, 1998a, b, 2005, Cheng and Dinopoulos 1992, Segerstrom 1998, Aghion and Griffith 2005). These neo-Schumpeterian models design entry as an R&D race where a fraction of R&D is turned into commercially successful innovations. While this implies a step forward, the essence of the Schumpeterian entrepreneur is missed. The innovation process stretches far beyond R&D races that predominantly involve large incumbents and concern quality improvements of existing goods. An alternative mechanism was presented by Schmitz (1989), where imitative behavior of entrepreneurs fostered growth.

  5. 5.

    An interesting approach presented by Michelacci (2003) focuses on the matching mechanism between inventors (doing R&D) and entrepreneurs who commercialize such inventions. Michelacci stresses the importance of having access to both R&D and entrepreneurial skills.

  6. 6.

    See, for instance, Callejon and Segarra (1999), Audretsch and Fritsch (2002), Acs and Armington (2004), Audretsch and Keilbach (2004), Braunerhjelm and Borgman (2004), and Beck et al. (2005). The Global Entrepreneurship Monitoring (GEM) report has found a similar correlation at the country level (Reynolds et al. 2003).

  7. 7.

    See Braunerhjelm (2008) for a recent survey on the entrepreneurship-growth literature.

  8. 8.

    Schumpeter (1911).

  9. 9.

    The concave curve in Fig. 2—the Bernoulli utility function—is associated with certain outcomes and the straight line—the von Neumann–Morgenstern utility function—with uncertain outcomes. The certain utility of π is u π (x) and the certain utility of a zero payoff is u(0) = 0. If, as is the case for the entrepreneur, the outcomes are uncertain and can only be described in probability terms, we have to look at the von Neumann–Morgenstern utility function. This utility function gives the expected utility of becoming an entrepreneur as the linear weighted average of the certain outcomes (wage earner), where the weights are the probabilities of the respective outcomes. The expected utility of the choice to become an entrepreneur is therefore \( \varphi \,u^{\pi } (x) + (1 - \varphi )u(0) = \varphi \,u^{\pi } (x). \)

  10. 10.

    Compare Murphy et al. (1991).

  11. 11.

    The model involves a large number of variables. To simplify for the reader, these variables are—in addition to being explained in the text—listed and defined in Table 1.

  12. 12.

    Following Romer we ignore the distinction between new knowledge created in incumbent firms and that created in academic institutions. For simplicity we assume constant returns to scale in knowledge production by incumbents. Choosing decreasing returns to scale—which is more likely—would not qualitatively affect the results but yields expressions that are less transparent and harder to interpret.

  13. 13.

    Starbucks (USA) and Ikea (Sweden) would be two examples of entrepreneurial start-ups that exploit the current knowledge stock with regard to logistics, distribution, and organization of the production in an innovative way, while the products have no R&D content.

  14. 14.

    This depends in a nontrivial way on a range of parameters. The degree of entrepreneurial activity is, for instance, decreasing in the productivity of R&D as long as R&D is profitable. Thus, R&D and entrepreneurship are to some extent substitutes. If R&D is not sufficiently profitable, then we cannot combine Eqs. 16, 17, 20, and 21 to derive the reduced-form growth. The resulting expression provides little insight and is not shown here.

  15. 15.

    As an alternative we have also used only R&D undertaken in the business sector in the estimations which, however, only had a marginal impact on the results. The reason is of course that the business sector accounts for the overwhelming part of R&D in most countries.

  16. 16.

    An autoregressive (AR) structure implies that the error term is serially correlated, such that the current error term is partly a function of previous error terms. Autoregressive structures are likely to occur in growth estimations. An AR1 process implies that the current error term depends on just one lagged error term. The panel-specific autoregressive structure is considered to be most adequate for regressions using annual-level data, while the common AR1 structure is preferred for the 5-year average estimations due to fewer degrees of freedom. As will be shown in the next section, the results are quite similar irrespective of the assumption of the autoregressive error structures.

  17. 17.

    The time periods are chosen such that they start and end in roughly the same sequence in the business cycle.

  18. 18.

    Regression results for other lag structures are very similar to those in Table 8 and are available on request.

  19. 19.

    Storey (2003) provides a set of examples.

Notes

Acknowledgements

We would like to thank seminar participants at seminars in Amsterdam, Athens, Helsinki, Bologna, Milan, and Sophia Antipolis (Schumpeter conference 2006) for helpful comments. The paper has particularly benefited from comments by Paul Segerstrom and Henrik Braconier. We also like to thank Benny Borgman and Per Thulin, for excellent assistance. Finally, generous financial support by the Marianne and Marcus Wallenberg Foundation is gratefully acknowledged.

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

References

  1. Acs, Z. J., & Armington, C. (2004). Employment growth and entrepreneurial activity in cities. Regional Studies, 38, 911–927.CrossRefGoogle Scholar
  2. Acs, Z. J., Braunerhjelm, P., Audretsch, D., & Carlsson, B. (2009). The knowledge spillover theory of entrepreneurship. Small Business Economics, 32(1), 15–30.CrossRefGoogle Scholar
  3. Aghion, P., & Griffith, R. (2005). Competition and growth: Reconciling theory and evidence. Cambridge, MA: MIT Press.Google Scholar
  4. Aghion, P., & Howitt, P. (1992). A model of growth through creative destruction. Econometrica, 60, 323–351.CrossRefGoogle Scholar
  5. Aghion, P., & Howitt, P. (1998a) Appropriate growth policy: A unifying framework. In mimeo. Boston: Harvard University.Google Scholar
  6. Aghion, P., & Howitt, P. (1998b). Endogenous growth theory. Cambridge, MA: MIT Press.Google Scholar
  7. Aghion, P., & Howitt, P. (2005). Growth with quality-improving innovations: An integrated framework. In P. Aghion & S. Durlauf (Eds.), Handbook of economic growth. North-Holland/Elsevier: Amsterdam.Google Scholar
  8. Arrow, K. (1962). The economic implication of learning by doing. Review of Economics and Statistics, 80, 155–173.Google Scholar
  9. Audretsch, D., & Thurik, R. (2002). Linking Entrepreneurship to Growth. OECD STI Working Paper, 2081/2.Google Scholar
  10. Audretsch, D., & Fritsch, M. (2002). Growth regimes over time and space. Regional Studies, 36, 113–124.CrossRefGoogle Scholar
  11. Audretsch, D., & Keilbach, M. (2004). Entrepreneurship capital: Determinants and impact, papers on entrepreneurship, growth and public policy 2004-37. Max Planck Institute of Economics, Entrepreneurship, Growth and Public Policy Group.Google Scholar
  12. Barro, R., & Lee, J-W. (2000). International data on educational attainment. Updates and Implications, CID Working paper No. 42. Google Scholar
  13. Barro, R. J., & Sala-i-Martin, X. (2004). Economic growth (2nd ed.). New York: McGraw Hill.Google Scholar
  14. Beck, T., Demirguc-Kunt, A., & och Levine, R. (2005). SMEs, growth and poverty: Cross country evidence. In mimeo.Google Scholar
  15. Blanchflower, D. G., & Oswald, A. (1998). What makes an entrepreneur? Journal of Labor Economics, 16, 26–60.CrossRefGoogle Scholar
  16. Braunerhjelm, P. (2008). Entrepreneurship, knowledge and growth. Foundations and Trends in Entrepreneurship, 4, 451–533.Google Scholar
  17. Braunerhjelm, P., & Borgman, B. (2004). Geographical concentration, entrepreneurship, regional growth. Evidence from regional data in Sweden 1975–1999. Regional Studies, 38, 929–947.CrossRefGoogle Scholar
  18. Callejon, M., & Segarra, A. (1999). Business dynamics and efficiency in industries and regions: The case of Spain. Small Business Economics, 13(4), 253–271.CrossRefGoogle Scholar
  19. Carlsson, B., Acs, Z. J., Audretsch, D., & Braunerhjelm, P. (2009). Knowledge creation, eentrepreneurship, and economic growth: A historical review. Industrial and Corporate Change (in press).Google Scholar
  20. Carlsson, B., & Fridh, A.-C. (2002). Technology transfer in United States universities: A survey and statistical analysis. Journal of Evolutionary Economics, 12(1–2), 199–232.CrossRefGoogle Scholar
  21. Cheng, L., & Dinopoulos, E. (1992). Schumpeterian growth and international business cycles. American Economic Review, 82, 409–414.Google Scholar
  22. Chiang, A. (1992). Elements of dynamic optimization. New York: McGraw-Hill.Google Scholar
  23. Dinopoulos, E., & Thompson, P. (1998). Schumpeterian growth without scale effects. Journal of Economic Growth, 3, 315–335.CrossRefGoogle Scholar
  24. Evans, D., & Jovanovic, B. (1989). An estimated model of entrepreneurial choice under liquidity constraints. Journal of Political Economy, 97, 808–827.CrossRefGoogle Scholar
  25. Evans, D., & Leighton, L. (1989). Some empirical aspects of entrepreneurship. American Economic Review, 79, 519–535.Google Scholar
  26. Greenwood, J., & Jovanovic, B. (1998). Accounting for growth. NBER WP No. 6647.Google Scholar
  27. Grossman, G., & Helpman, E. (1991). Innovation and growth in the global economy. Cambridge, MA: MIT Press.Google Scholar
  28. Jones, C. I. (1995a). R&D-based models of economic growth. Journal of Political Economy, 103, 759–784.CrossRefGoogle Scholar
  29. Jones, C. I. (1995b). Time series test of endogenous growth models. Quarterly Journal of Economics, 110, 495–525.CrossRefGoogle Scholar
  30. Lucas, R. (1988). On the mechanics of economic development. Journal of Monetary Economics, 22, 3–39.CrossRefGoogle Scholar
  31. Lucas, R. (1993). Making a miracle. Econometrica, 61, 251–272.CrossRefGoogle Scholar
  32. Michelacci, C. (2003). Low returns in R&D due to the lack of entrepreneurial skills. The Economic Journal, 113(January), 207–225.CrossRefGoogle Scholar
  33. Murphy, K., Schleifer, A., & Vishny, R. (1991). Thee allocation of talent: The implications for growth. Quarterly Journal of Economics, 56, 503–530.CrossRefGoogle Scholar
  34. Nicoletti, G., Scarpetta, S., & Boylaud, O. (1999). Summary indicators of product market regulation and with an extension to employment protection legislation. Economic Department, WP No. 226, OECD, Paris.Google Scholar
  35. Rebelo, S. (1991). Long-run policy analysis and long-run growth. Journal of Political Economy, 99, 500–521.CrossRefGoogle Scholar
  36. Reynolds, P., Bygrave, W. D., Autio, E., Cox, L. W., & Hay, M. I. (2003). Global entrepreneurship monitoring. London Business School.Google Scholar
  37. Romer, P. (1986). Increasing returns and economic growth. American Economic Review, 94, 1002–1037.Google Scholar
  38. Romer, P. (1990). Endogenous technical change. Journal of Political Economy, 98, 71–102.CrossRefGoogle Scholar
  39. Schmitz, J. (1989). Imitation, entrepreneurship, and long-run growth. Journal of Political Economy, 97, 721–739.CrossRefGoogle Scholar
  40. Schnabel & Wagner (2003). Determinants of trade union membership in West Germany: Evidence from micro data 1980–2000. Socio-Economic Review, 3, 1–24.CrossRefGoogle Scholar
  41. Schumpeter, J. (1911). Theorie der Wirtschaftlichen Entwicklung. [The theory of economic development] (English Trans.). Cambridge, MA: Harvard University Press (1934).Google Scholar
  42. Schumpeter, J. (1947). The creative response in economic history. Journal of Economic History, 7, 149–159.Google Scholar
  43. Segerstrom, P. (1991). Innovation, imitation and economic growth. Journal of Political Economy, 99, 190–207.CrossRefGoogle Scholar
  44. Segerstrom, P. (1998). Endogenous growth without scale effects. American Economic Review, 88(5), 1290–1310.Google Scholar
  45. Segerstrom, P., Anant, T. C., & Dinopoulos, E. (1990). A Schumpeterian model of the product life cycle. American Economic Review, 80, 1077–1091.Google Scholar
  46. Shane, S., & Eckhardt, J. (2003). The individual-opportunity nexus. In Z. J. Acs & D. Audretsch (Eds.), Handbook of entrepreneurship research (pp. 161–194). Kluwer: Boston.Google Scholar
  47. Shell, K. (1967). Inventive activity, industrial organization, and economic activity. In J. Mirrlees & N. Stern (Eds.), Models of economic growth. London: MacMillan.Google Scholar
  48. Storey, D. (2003). Entrepreneurship, small and medium sized enterprises and public policies. In Z. J. Acs & D. Audretsch (Eds.), Handbook of entrepreneurship research (pp. 473–514). Kluwer: Boston.Google Scholar
  49. Thurik, R. (1999). Entrepreneurship, industrial transformation and growth. In G. D. Libecap (Ed.), The sources of entrepreneurial activity (pp. 29–65). Stamford, CT: JAI Press.Google Scholar
  50. Visser, J. (2006). Union membership statistics in 24 countries. Monthly Labour Review, 129, 38–49.Google Scholar
  51. Young, A. (1998). Growth without scale effects. Journal of Political Economy, 106, 41–63.CrossRefGoogle Scholar

Copyright information

© The Author(s) 2009

Authors and Affiliations

  • Pontus Braunerhjelm
    • 1
  • Zoltan J. Acs
    • 2
  • David B. Audretsch
    • 3
  • Bo Carlsson
    • 4
  1. 1.Department of Transport and EconomicsRoyal Institute of TechnologyStockholmSweden
  2. 2.George Mason UniversityFairfaxUSA
  3. 3.Indiana University BloomingtonBloomingtonUSA
  4. 4.Case Western Reserve UniversityClevelandUSA

Personalised recommendations