Learning your own risk preferences

Abstract

Do people know their own risk preferences, or do risk choices change with experience and observation? We provide a straightforward test in the laboratory. People make an initial decision concerning a lottery choice and then experience 24 unpaid practice periods in which they roll the dice, record the outcome, and record the would-be payoff. They then make a final decision for the lottery choice; one of the first and last periods is randomly chosen for payment. Our primary hypothesis is that people will become less risk-averse by having made and experienced the practice rolls. We do find that people are significantly more likely to become less risk-averse than more risk-averse over time. We note that this move towards assuming increased risk goes in the opposite direction from what is at least arguably predicted by loss aversion and reference dependence. We find that women’s preferences change much less during a session than men’s preferences change. We feel that our literally hands-on approach ensures a degree of engagement that helps to accelerate the learning process. We argue that measures obtained after people have had experience with a mechanism are more meaningful, and that this principle might well extend more generally to other elicitation tasks.

1 Introduction

Risk preferences have an essential role in understanding individuals’ financial and economic decisions. Economic agents must decide how much risk they are willing to take in their daily lives. Given the importance and relevance of risk, many economic models include risk parameters in the agent's utility function in an effort to model an agent’s decisions under risk; one example is the prospect theory in Kahneman and Tversky (1979). Economists have developed many experimental methods to elicit this risk parameter, which can then be used to predict decisions in risky environments.

Yet, risk elicitation is challenging and there are unresolved methodological issues. For example, the risk-elicitation puzzle (Pedroni et al., 2017) stems from numerous investigations showing significant inconsistencies in risk preferences when elicited using different or similar methods. It questions the validity of these methods and the degree to which these preferences are stable. In the standard neoclassical view, one has stable risk preferences that are self-known. But there is evidence that factors such as shocks can influence risk-taking preferences in different environments; for example, Beine et al. (2020) finds evidence that exogenous shocks—two earthquakes occurring during their study—can affect risk preferences.

Nevertheless, research in this area is still developing. The effect of experience and learning on one’s risk choices should be systematically explored. We advocate first giving people experience with a task or mechanism in the hope of obtaining better comprehension and a more meaningful measure of risk attitude. Furthermore, we suggest that doing this in a manner that is literally hands-on may accelerate the process.

We take a step in this direction with a straightforward experiment that gives people experience with risk choices. We offer each participant a choice of six possible gambles in a slight modification of the Dave et al. (2010) version of the original Eckel and Grossman (2002, 2008) mechanism. These gambles reflect trade-offs between expected value and variance so that one should, in principle, choose the gamble that best suits their own self-perceived risk preferences. This method is known for its simplicity in that 1) all gambles are 50%, avoiding probability-weighting issues (see Gonzalez & Wu, 1999), and 2) a subject makes a choice in only one row (instead of in 10, as in Holt & Laury, 2002). The modified version distinguishes between risk-seeking and risk-neutral choices a bit more sharply than the previous payoff numbers used; specifically, we lower the expected value of the riskiest gamble so that choosing this gamble in effect means one is willing to sacrifice expected value to take on more risk.

In a nutshell, our question is whether repeated hands-on and unpaid experience with a relatively simple risk-elicitation task affects the choices and, by extension, the implied risk preferences. We first display and explain the gambles and their choices. Each person then chooses one of the rows for a gamble; either this first gamble or the final gamble, but not both, will be paid (50% chance for each; in doing so, we try to eliminate hedging behavior). We then require people to acquire experience by having them execute 24 practice rolls of the dice. To increase engagement, we had them physically make these practice rolls themselves and then record the choice of rows, the outcome of the roll, and the payoff consequences had this roll been chosen for actual payoff. After the practice periods, they then make a final choice of rows. One of the two non-practice choices is then selected by the subject by rolling the dice at the time of payment; the dice are rolled again to determine the outcome of the gamble. All this information was conveyed in the instructions and was read aloud at the beginning of the session.

To account for the role of experience and learning in risk elicitation, we consider two effects that might influence participants. First, experience and learning could make participants understand the risk-elicitation task better and thus reduce some errors that players might make in a one-shot task. Being unfamiliar with tasks could make players more risk-averse in their decision simply due to uncertainty about the task structure. It seems natural to be cautious when one is just having one’s first experience with a task. So, an inexperienced participant may display a degree of risk aversion that is transitory. Second, perhaps the most critical information that people fail to understand in the one-shot task concerns the expected payoffs and variance of the lotteries. With more experience with the lotteries, the player might learn or at least have a better feel for these, thereby making a more informed decision .

Table 1 Our risk elicitation choices

A related approach to overcoming inexperience was used in Engelmann and Hollard (2010) in considering the endowment effect. Their idea was that people who did not have experience with trading might be reluctant to trade their endowed good for another of equal (or even more) value. In their treatment condition, people were endowed with a good that would have no value if not traded for a good that would have value. Doing this trade gave them some experience. While there was a significant endowment effect present in the control treatment, there was no significant endowment effect for the group with trading experience. The conclusion is that providing familiarity and experience with a mechanism can change behavior. It is not obvious that people really know their own preferences, despite the usefulness of this assumption. At the limit, how can we know our feelings about something never experienced?

If negative outcomes during the practice periods are experienced as losses compared to a reference point between the high and low payoffs for the gamble chosen, reference dependence and loss aversion (“losses loom larger than gains”) suggest that people should become more risk-averse with experience. But if uncertainty or inexperience leads to people being less willing to take risks than their “true” preferences recommend, one would expect choices to become less risk-averse. Our hypothesis is that the latter force will dominate—experience will lead people to later choose lotteries with higher expected payoffs. Experience could simply allow players to explore their own preferences and perhaps change them. One could consider this to be the case of a player not being fully aware of their own risk preferences, and so potentially benefitting from exploration. In the end, becoming fully aware of one’s risk attitude should be beneficial.

The main contributions of this article: People change their risk preferences over the course of a session, in combination with having unpaid practice periods. An unanticipated result is that this significant change is largely driven by males. No shocks are needed, and the structure of the choices and outcomes are clear. This is not just measurement error because the change significantly favors a decrease in risk aversion. The positive or negative outcomes in the practice periods do not affect the final lottery choice, which is comforting in the absence of any psychological affect that could presumably be present for paid rounds. As do other studies, we find that people with more cognitive ability are less risk-averse. Finally, the comments made by the subjects offer evidence that people indeed learned about their preferences and the task.

The remainder of this article is organized as follows. Section 2 provides background in the related literature, while section 3 describes the experimental design and hypotheses. We present the experimental results in section 4, and we conclude in section 5.

2 Background

2.1 Elicitation methods

Holt and Laury (2014) states that Binswanger (1981a) was “one of the first to use choices with high cash payoffs to elicit measures of risk aversion”. These stakes were feasible with farmers in rural Bangladesh. Subjects make choices in a series of binary options that were arranged to lead less risk-averse subjects to select gambles with higher expected values. Since then, economists have developed many experimental methods to elicit risk preferences. The most common ones are variations of Gneezy and Potters (1997), Holt and Laury (2002), and Eckel and Grossman (2002, 2008), although the bomb task (Crosetto & Filippin, 2013) is growing in popularity.

Holt and Laury (2014) characterizes the approaches used to elicit risk preferences. One type of method is the “investment-portfolio” approach (e.g., Binswanger, 1981b): People decide how much of an endowment to invest in a risky asset and how much to keep. Gneezy and Potters (1997) offers subjects the chance to invest up to 100 in a risky asset with higher expected value than the safe investment. Eckel and Grossman (2008) present rows of binary gambles and asks subject which gamble they prefer. These are also classified as investment-portfolio approaches. A second type of method involves a list with rows of binary choices between ordered gambles, with risk preferences being surmised from the choices made in these rows. This corresponds to the mechanism in Holt and Laury (2002), whereby subjects are presented with 10 ordered rows of binary choices and make selections in each one. For a detailed discussion of these and other methods, we refer the interested reader to Charness et al. (2013) and Holt and Laury (2014).

2.2 The risk-elicitation puzzle

What we term “the risk-elicitation puzzle” stems from numerous investigations showing major inconsistencies in risk preferences when elicited using different or similar methods (Pedroni et al., 2017). This inconsistency is troubling and raises many crucial questions. What is the source of this inconsistency? Successfully addressing this question might help economists to better understand people's risk preferences and to find better ways to elicit them.

While various methodologies may have been designed for different purposes and to address different problems, all methodologies are assumed to measure the same constant risk attitudes. Results would need to be consistent across time and contexts to be useful in economic applications. Furthermore, the measures should be predictive of decisions in different settings (particularly field settings) to be relevant.

However, the literature highlights a weak relation between the risk attitudes elicited and significant changes, depending on the characteristics of the method. For example, using a multiple-price list, the seminal paper by Holt and Laury (2002) finds payoff-magnitude effects for real payoffs, with more risky choices made for lower payoffs and even riskier choices made for hypothetical payoffs. A follow-up paper by Holt and Laury (2005) then found that the effect of high payoffs was only present with real payoffs. Given these effects in a single task, it may not be so surprising that the correlation among measures is low.

Friedman et al. (2014) found a correlation of 0.27 between the original Holt-Laury and Eckel-Grossman studies, and no correlation between the balloon task (each incremental puff into the balloon pays incrementally more unless the balloon explodes, in which case the payment is zero; the stopping point is observed) and the deal-or-no-deal task. According to Friedman et al. (2022), a lower-than-expected correlation is still present even when controlling for measuring error using the ORIV method developed by Gillen et al. (2018)—the highest correlation (0.55) between the closely-related tasks Lottery and Project was still low, even after correcting for measurement error and considering uncensored data.

Charness et al. (2020) used the adult Dutch population to compare five risk-measuring tasks: a non-incentivized questionnaire willingness-to-take-risk task, Gneezy-Potters, Eckel-Grossman, Holt-Laury, and multiple-price lists involving paired lotteries. There was a correlation between task and laboratory financial decisions with a higher predictive power for simpler tasks, but no explanatory power for field behavior. Holzmeister and Stefan (2019) found small correlations between four risk measures; however, subjects are aware of the variation in their risk attitudes. It may well be that people tend to be more cautious in more complex one-shot tasks. They write: “In particular, we are not the first to report that subjects, on average, tend to be significantly more risk-averse in the Bret [Bomb Risk Elicitation Task] and the MPL [Holt-Laury] than in the SCL [Eckel-Grossman].” They conjecture that people might have task-dependent or reference-dependent preferences.

Given the evidence, Holt (2019) states that “numerical risk aversion should not be taken too seriously”, highlighting the importance of using the same measure for a particular question since risk preferences could be multi-dimensional and different characteristics of the context might affect the decision process and preferences. With this question in mind, we feel that experience/learning will shed some light if the inconsistency of players' decisions among various tasks reflects an incomplete understanding of the task structure and of their own preference. By exploring these, they could potentially converge on a more consistent choice.

2.3 Related work on risk-preference change

An extensive discussion in the economic literature, led by Plott (1996), puts forth the notion that people learn their own preferences through experience. Besides learning something about the task structure, agents may not be fully aware of their own risk preferences; but they may become more aware by receiving experience. Delaney et al. (2019) provide experimental evidence on preference discovery, suggesting that preference-discovery processes can explain choice observed instabilities in behavior. If agents are unfamiliar with making such decisions, the preference-discovery effect would be larger. In addition, there is a vein of work (led by Elke Weber and Paul Slovic) in the psychology literature that compares learning from experience and learning from information provided to subjects. However, to our knowledge, this literature does not consider the effect of providing experience to people who have been given sufficient information, as in our experimental design.

Many experimental papers, starting with Eckel et al. (2009), have found that shocks affect risk preferences. For example, the Beine et al. (2020) lab-in-the-field experiments in Tirana, Albania in 2019 obtained data from before either of two earthquakes, between the two earthquakes, and after the second one. Strong effects on risk preferences were found, with each earthquake leading to greater risk-aversion.¹ Since the objective odds of a favorable coin flip were clearly 50/50 and no one participated more than once, there could be no learning with this simple mechanism. Reynaud and Aubert (2020) study “how experiencing a natural disaster affects individual attitudes towards risk” in Vietnam. People experiencing a flood in recent years were more risk-averse, although this was only true in the loss domain.

Bradbury et al. (2015) conducted risk simulations based on experience sampling to investigate how this affected investment decisions under risk. These appear to significantly improve participants’ understanding of the underlying risk-return profile and prompt them to reconsider their investment decisions and choose significantly riskier (and higher expected return) financial products. Of particular interest for our study, they find that the experience of a simulation has a much more rapid effect on the adjustment of the investment strategy than simply informing investors descriptively. In the latter case, multiple investment periods are necessary before they show “the stable average risk-taking behavior and similar allocations to the risky asset as investors informed via risk simulations”.

The article most closely-related to our work is Ert and Haruvy (2017). The article explores the impact of repetitions of the Holt-Laury risk-elicitation task on risk preferences, finding that players become more risk-neutral over time. Our experiment differs from theirs in some respects. First, we choose a much simpler risk-elicitation task. Given the relative complexity of Holt-Laury, we might see less of a learning effect with EG (Eckel-Grossman). Second, subjects in Ert and Haruvy (2017) performed 200 repetitions with the HL task, receiving feedback about payoffs every period. In the end, subjects received payment according to the realization of their choice in one randomly-chosen trial, so that they in fact are potentially paid for any period in question.

We used a different learning mechanism with minimal intervention and without any incentives for outcomes per se during the learning process. Our main goal was to provide a clean learning environment that allows participants to explore the task and make decisions. We find significant changes in choices, with a clear directional trend, even without learning incentives.

We have two explanations for the learning/experience effect. First, experience and learning could make participants understand the risk-elicitation task better and thus reduce some errors that players may make in a one-shot task without fully understanding the full information given to them. We note again that Engelmann and Hollard (2010) used a similar approach to overcoming inexperience in relation to the endowment effect.

We suspect that experience also helps the subject learn more about the task structure (expected payoffs). Only 68% of the subjects correctly identified Gamble 5 as having the highest expected payoffs, so there is some scope for learning. This strengthens the argument that even in the simplest one-shot risk-elicitation task, where all the information is given to the participants, some errors are due to subjects failing to learn/use this information in a one-shot decision.

Overall, the literature suggests that risk preferences are not necessarily consistent over time and may well be subject to experience and comprehension.

3 Experimental design and hypotheses

3.1 Design and implementation

We conducted our experiments in person in early 2022. We made the design choice to conduct this experiment using pen-and-paper and actual dice rolled by the participants. Our view is that the best way for people to absorb their experience is to have them as involved as possible in the data-generation process. Watching dice being rolled on a computer screen and having the outcomes automatically entered are naturally less engaging and may well be less effective.

We wished to explore how learning and experience with an elicitation task could influence players’ risk preferences even when there is no external shock and when this experience had no financial consequences. For our experimental design, we wished to use an easy-to-comprehend method. Gneezy and Potters (1997) is perhaps the simplest, but we were also interested in risk-seeking behavior, which is not picked up with this mechanism. While the Eckel-Grossman mechanism is not quite as simple as Gneezy-Potters, it is still relatively easy in that one makes just one decision that involves a 50-50 gamble. The six-row version presented in Dave et al. (2010) includes a row that would be an attractive gamble for a risk-seeking subject. In addition, we felt it might be better to have a menu of just a few choices that than the 101 integer choices possible with Gneezy-Potters.

We adapt the Dave et al. (2010) choice options by having 66 rather than 70 for the high payoff in row 6, so that one must sacrifice some expected payoff (relative to row 5) to be more risk-seeking. This draws a sharper distinction between rows 5 and 6, so that people who choose row 6 should be substantially risk-seeking.² Note that a purely risk-neutral subject would be indifferent between rows 5 and 6 with the Dave et al. (2010) payoffs (Table 1).

We recruited participants using ORSEE (Greiner, 2015) from the Experimental and Behavioral Economics Laboratory database at UCSB. We had 99 participants, paying an average of about $13 per person (including a $5 show-up fee) for sessions lasting about 45 min. Each person was seated at a distance from everyone else, so that choices were not observed by others. The instructions are provided in Appendix A. People were shown the table of gambles, with the higher (lower) payoff resulting from the total of two rolled dice being even (odd). We used two dice instead of a coin because we felt that rolling dice was a more familiar environment for people than flipping a coin (and coins might end up on the floor). We explained the payoff consequences of choices in detail. Each point in the table was worth $0.15. Thus, the highest payoff from a gamble was $10.50 and the lowest was $0.30. This compares to $3.85 and $0.10 in the low-payoff treatment of HL, while the mean payoff in Eckel and Grossman (2008) was considerably higher ($16) and there was higher pay with a low-income community in Dave et al. (2010). Our stakes were modest, but they seemed meaningful for a short experiment. In line with the results in Holt and Laury (2002), lower stakes seem to lead to less risk aversion.³

After taking questions, we instructed the participants to choose one of the six rows, informing them that there was a 50% chance that the outcome from this choice would be implemented for cash payoff at the end. Each person recorded 24 practice rolls on a record sheet (see Appendix A). The row choice was already made for 12 of these rolls (twice for each row); for these, each person rolled the dice, recorded the outcome, and then wrote the would-be payoff on the sheet. For the other 12 rolls, each person chose a row, rolled the dice, and recorded the outcome and payoff information. After 24 practice rolls, each person came to the front of the room and then rolled to determine whether the first or last choice would be implemented for cash payoff and then rolled to determine the outcome for the row that had been selected.

After the completion of the choices, we also administered the Cognitive Reflection Test (CRT, Frederick, 2005) and a brief questionnaire to examine the effect of individual characteristics on choice behavior. We paid people to complete a questionnaire about why they did (did not) change their choices.⁴ We paid $1 for each correct answer to the CRT, and we also paid $1 if the subject had correctly recorded the outcome in a randomly-selected practice period.

3.2 Hypotheses

Standard theory predicts that people will not change their preferences. Given that all information is known initially, experience should not tell the participants anything new. If agents have stable risk preferences, the prediction is that participants will not change the row voluntarily selected after experiencing the practice periods. Yet when we first discussed the idea for this experiment, we had in mind the notion that in many cases people may not really know their own preferences without becoming familiar and experienced with the process or goods involved. This may well apply to preference elicitation using standard laboratory or lab-in-the-field methods.

To a certain extent, one must become familiar with a mechanism before being ready to fully engage with it. Consider the idea of training wheels on a bicycle, where the wheels help to guide the rider along (more) safely. When one asks non-academic friends such a stylized question about risk preferences, these friends are typically lost for an answer to such a strange question. Insisting on elicitation in this manner may not be as meaningful as it is when people have some experience with it.⁵ This insight leads to our first hypothesis, which contrasts the standard presumption that one’s risk preferences are fixed.

Hypothesis 1: Individuals frequently choose different rows for their first and last gambles.

Assuming individuals do change their selected rows, a particularly interesting question is whether there is a pattern to the observed changes. Uncertainty is typically considered to lead to more conservative choices, so that familiarity with the mechanism could per se lead to less conservative choices. In addition, if people are reacting to the 24 practice-period outcomes and observing the mean outcome, we might expect them to move towards rows with higher expected value. This is our second hypothesis and the one that motivated our study.

Hypothesis 2: There will be significantly more switches to gambles with higher expected value than to gambles with lower expected value.

However, we note a countervailing influence: If one sees unfavorable dice rolls as losses and favorable ones as gains, reference-dependence would predict movement towards row choices with less variance (perhaps even the top row), since losses are felt more strongly than gains. Still, we felt that increased familiarity would lead over time to choices with higher expected values.

While researchers might assume that everyone readily calculates expected value, this may not be the case. In fact, we will present evidence that many people think the bottom row has the highest expected payoff. To the extent that this is true, we can state an alternative formulation:

Hypothesis 2a: There will be significantly more switches to gambles lower in the table (higher-numbered gambles) than to gambles higher in the table (lower-numbered gambles).

Since beliefs or even superstitions (see, e.g., Fudenberg & Levine, 2006, and the experimental “god games” in Hajikhameneh & Iannaccone, 2023) about luck are common, perhaps people form beliefs about the dice. Still, the direction is unclear; some subjects might expect positive serial correlation (the “hot hand”) and others might expect negative serial correlation (the “law of averages”); this was confirmed in the comments made. So, we have a null hypothesis about the effect of observing a high proportion of favorable practice rolls.

Hypothesis 3: The proportion of favorable practice rolls observed will not affect the action taken in the final choice of rows.

Do individual characteristics matter? We expected people with higher CRT scores to be less risk-averse, in keeping with previous experimental work (e.g., Dohmen et al., 2010). We also expected them to move more to gambles with higher expected payoffs.

Hypothesis 4: 1) People with higher CRT scores will be less risk-averse in both initial and final gambles. 2) For those who change their gambles, people with higher CRT scores will have a higher proportion of changes towards higher expected payoffs/lower gambles in the table.

Our final hypothesis concerns gender differences. Previous work has found pervasive differences in risk preferences across gender (although these effects seem modest or insignificant with the Holt-Laury mechanism), with males less risk-averse than females. However, there is no evidence concerning gender and changing one’s risk preferences.

Hypothesis 5: 1) Males will choose higher rows for both their initial and final gambles. 2) There will be no difference across males and females in terms of switching behavior for these gambles.

4 Results

In this section, we present summary statistics and non-parametric tests to analyze behavior.⁶

4.1 Gambles and changes in gambles

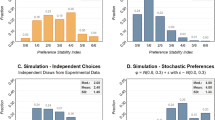
Table 2 and Fig. 1 provide a first look at the choices made for initial and final gambles. We see overall movement towards higher gambles. A Kolmogorov-Smirnov test of cumulative distribution gives ${\chi }_{2}^{2}=4.454,$ p = 0.103 on a two-tailed test or p = 0.051 on the one-tailed test justified by our hypothesis. The same test statistic results if we instead use expected value as the metric (combining Gamble 4 and Gamble 6, with the same expected value). The change direction is driven substantially by people initial choosing Gamble 3 and moving to higher numbers.⁷ The correlation between the initial and final gamble chosen in the experiment was 0.546 (p < 0.001).

Table 2 Initial and final gambles chosen

Fig. 1

CDF of the gambles chosen before and after observing the realizations

Table 3 confirms this impression, with the shaded diagonal indicating no change. We see that 45 people of 99 (on the diagonal) did not change their choice of gamble, whereas 54 of 99 people did change; this supports Hypothesis 1. Since more than half the population changed over time, we can easily reject the standard view that risk preferences do not change. Furthermore, Table 3 shows that 36 of the 54 people who changed gambles chose a higher gamble. A simple binomial test gives z = 2.449, p = 0.007, one-tailed test. A Wilcoxon signed-ranks test on the individual level gives z = 2.392, p = 0.008, one-tailed test. So, we do in fact find more movement towards riskier lotteries, supporting hypothesis 2a.

Table 3 Individual changes in Gambles

We can instead consider expected value (Table 4). There are 33 (19) entries above (below) the diagonal. The binomial test gives z = 1.941, p = 0.026, one-tailed test, and a Wilcoxon signed-ranks test on the individual level gives z = 1.992, p = 0.023, one-tailed test, supporting Hypothesis 2.

Table 4 Individual changes in expected value of gambles

So, there is significant movement towards higher expected value. The overall expected payoffs improved over time: The average expected payoff was 31.495 (std. deviation 2.292) for the initial decision and 33.131 (std. deviation 2.558) for the final decision. Since the expected payoffs ranged only from 28 to 36, this difference of 1.636 represents more than a 20% increase overall and 36.3% of the possible increase above the initial expected value.⁸

We conducted an additional survey of our participants (see Appendix A) after the experiments were concluded and can link the survey responses to the individual experimental choices. We also incentivized a guess about the average guess made by the participants, paying the most accurate guesses. To our surprise, 23 of 74 respondents (31.1%) stated that Gamble 5 did not have the highest payoff and 15 of these 23 people stated that Gamble 6 had the highest expected payoff, helping to explain the prevalence of Gamble 6 choices.⁹ This lack of comprehension most likely contributed to the slightly weaker test statistic given by Table 4.

4.2 CRT results

We next consider the relationship between CRT scores and gamble choices. In principle, higher scores indicate better cognitive ability, although it seems to be more of a test about resisting one’s impulse to make the immediate and seemingly-obvious-but-incorrect response.

Table 5 shows that the “average” row of the initial gamble was 3.51, 3.41, 3.50, and 4.08 for respective CRT scores of 0, 1, 2, and 3, averaging 3.717. A Wilcoxon ranksum test for CRT = 3 against the combined other scores gives z = 1.982, p = 0.047, two-tailed test; no other comparison approaches significance. The average row chosen for the final gamble was 3.00, 4.227, 4.056, and 4.324, averaging 3.960. People with CRT = 0 reduce the riskiness of the lottery, while all other groups increase it. A Wilcoxon ranksum test for CRT = 0 against the combined other scores gives z = 3.345, p = 0.001, two-tailed test. The final gamble chosen is significantly different for CRT = 0 in pairwise tests with all other scores. z = 2.356, z = 2.093, and z = 3.245 for respective comparisons with CRT = 1, 2, and 3, all significant at p = 0.050. These results generally support Hypothesis 4.

Table 5 CRT scores and gambles chosen

4.3 Gender results

Previous work (e.g., Charness & Gneezy, 2012) has found gender differences in risk attitudes. Our data support this view. Figure 2 presents the cumulative distributions of initial and final rows chosen by males and females.

Fig. 2

Difference in chosen rows before and after practice, by favorable realizations. Note: We exclude the observations with exactly 12 realizations since for them the results were neither favorable nor unfavorable

We see differences across gender in both the initial and final choices of rows. A Kolmogorov-Smirnov test for the initial choice gives ${\chi }_{2}^{2}=5.491,$ p = 0.064 (0.032) on a two-tailed (one-tailed) test. Not only are females more risk-averse initially, but the difference widens considerably with experience. For the final row selected, the Kolmogorov-Smirnov test for the initial choice gives ${\chi }_{2}^{2}=12.050,$ giving p = 0.002 (0.001) on a two-tailed (one-tailed) test. Of the 20 cases (of 38) where males changed gambles, 16 were increases in the row chosen. The binomial test gives z = 2.683, p = 0.006, one-tailed. This supports the first part of Hypothesis 5. Of the 34 cases (out of 61) where females changed gambles, 20 were increases in the row chosen (z = 1.029, p = 0.196, one-tailed). The correlation between the initial and final gambles was higher among females (0.557) than the correlation among men (0.441), but the difference is not statistically significant (p = 0.471).

We can also examine differences regarding the expected value of rows. The differences across gender are like the ones using row numbers. For initial choices, the Kolmogorov-Smirnov test gives ${\chi }_{2}^{2}=5.956,$ p = 0.025 on the one-tailed test justified by our hypothesis. For the final row selected, the Kolmogorov-Smirnov test gives ${\chi }_{2}^{2}=7.798,$ p = 0.010 on the one-tailed test.¹⁰

So, the males who changed rows are significantly more likely to move to increasing row numbers, while females are not. We can only speculate about why this is the case. It is interesting to consider the final choices for people who chose rows 1 or 2 for their initial gamble. There were five males who did so, and none of them chose rows 1 or 2 for their final gamble. On the other hand, there were 12 females who chose row 1 or 2 for their initial gamble, and nine of them chose the same gamble for their final gamble. Even with this tiny sample, the test of proportions gives z = 2.823, p = 0.005, two-tailed test, for this difference across gender. This rejects the second part of Hypothesis 5.

This suggests that risk-conservative females are more likely than risk-conservative males to stick to their initial views. Perhaps females simply have a better perception of their risk preferences than males do prior to the practice rounds. But all of this is speculation and a topic for future research.

4.4 Practice outcomes and final gambles

One issue concerns the effect of (un)favorable outcomes in the 24 practice periods. Given the common belief in the “hot hand” (and its apparent existence: see Bennett et al., 2010; Gallistel, 2012; Miller & Sanjurjo, 2018), one might expect a positive serial correlation in the dice rolls. However, there may also be a common belief in the “law of averages”, which would correspond to negative serial correlation. On balance, even if these effects are present, they may wash out in the data. And it is likely that 24 rolls of the dice give roughly equal the same number of positive and negative outcomes; if extreme outcomes are necessary to trigger such beliefs, there might be little evidence in the data. And beliefs about dice having a memory may not be that prevalent in the population.

In fact, we find no evidence of an effect from the proportion of positive outcomes during the practice periods. Figure 2 shows a CDF of the difference between the row of the final and initial gambles depending on whether more than half or less than half of the practice rolls were favorable. There is no evidence that change in row choices are driven by the outcomes of the practice rolls, supporting Hypothesis 3. The Kolmogorov-Smirnov test of cumulative distributions gives ${\chi }_{2}^{2}=0.374,$ so p = 0.829 on a two-tailed test. If anything, when the outcomes have been lopsided, there appears to be more anticipation that the law of averages, rather than the hot dice hand, is in effect. These results are confirmed with an ordinal regression analysis of the final chosen gamble on the number of even realizations. The coefficients on gender and the initial gamble selected were statistically significant. This can be seen in Appendix D.

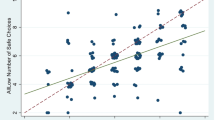
We might also wonder if people are consistent with their beliefs about the most common gambles chosen. This might be a useful predictor if there is a high degree of consistency and beliefs are readily elicited. In fact, the correlation between the incentivized guess about the most frequent gamble chosen and the final gamble one chooses is high (0.53) and quite significant.

A final point is that evidence in the marketing literature (e.g., see Neumann et al., 2016) shows that when people are not fully aware of their preferences or do not pay too much attention, they might choose a neutral decision somewhere in the middle. A “middle decision” avoids extremes. So, one would expect people who make these intermediate choices to be less confident in these choices. In fact, we find that participants who initially choose a lottery in the middle (row 3 or row 4) are nearly three times as likely (81.6% versus 27.5%) to choose a different lottery in the end than those choosing other rows for the initial lottery. The test of proportion shows this difference in switch rates is statistically significant (z = 3.708, p = 0.000).

4.5 What did subjects learn?

An open question is what people learned that induced them to change their decision and become more risk-tolerant? Were they learning about the task or their own preferences?

We chose the EG-based risk-elicitation task because of its simplicity. Given this simplicity, one might expect that there is not much to learn about the task, since all the information is given and (we thought) easy to follow. The probabilities of the events are 50% each, and the payoff structure is straightforward. However, our follow-up survey suggests that even with this “simple” task and a reasonably-sophisticated subject pool, a considerable number subjects struggled to understand the expected payoffs and the variance of the lotteries.

To shed some light on what people learned, the exit survey asked the subjects: “Why did you change, or maintain, your decision between the 1st and 3rd sections?” The responses to this question were useful and point to some different learning directions. To analyze these comments, we classified them based on the categories shown in Table B5 in Appendix B.¹¹

In our experiment, 54 subjects changed their final decision after the learning section, and based on their comments, our classification process sorted them, as seen in Table 6. We can see that the subject learning process went in different directions, and some of them learned undesirable outcomes that we tried to avoid in our design.

Table 6 Proportions who changed their decision and the direction of change, by category

First, some subjects decided to hedge (diversify) their initial and final decisions even though we tried to eliminate hedging behavior by paying for only one gamble. Another learning issue was that people may form biased beliefs about the die, suffering either from positive serial correlation (the “hot hand”) or negative serial correlation (the “law of averages”). To minimize this effect, we tried to have significant enough learning trials to reduce this undesirable learning process. However, as shown in the previous section, there is no evidence that the outcomes of the practice rolls drive change in row choices, at least in the aggregate, so that this learning pattern does not explain why subjects become more risk tolerant.

Finally, based on the comments, we observe two learning processes that we mentioned before that could be the central role of experience and learning in risk elicitation. The first is knowing the risk-elicitation task better, which, based on the comments, we observed few subjects in this category LT. These subjects mentioned directly that they learned/understood that task better, especially the payoff structure (expected payoffs and the variance of the lotteries.). The second is knowing your preferences which we label as category LP. Based on these categories, we can compare how those different learning patterns affect the decisions and if they made subjects to become more (or less) risk tolerant, as seen in Table 6.

Based on Table 6, we can see that learning either your own preferences (LP) or about the task (LT) are the main drivers that made the subjects more risk tolerant. In those two cases, 18 of 20 people (90%) chose more risk in the final gamble than initially. This difference is not random, according to a binomial test (z = 3.58, p < 0.001). By comparison, the rate of choosing increased risk was 64% (22 of 34). These rates differ significantly), with z = 2.05, p = 0.040 on a two-tailed test of proportions, so that learning about one’s preferences or about the task in hand leads to significantly more of an increase in risk-taking than otherwise.

5 Discussion

We find that most people (54 of 99) change their choice of lotteries after they have received the experience of hypothetical choices, outcomes, and payoffs. Furthermore, the pattern of these changes is not random: For those who change, there is a strong tendency for people to select lotteries with more risk and higher expected payoffs. We believe that the latter choices are more likely to reflect more informed preferences that may better proxy for the field environment. We make our experiment as hands-on as possible for the participants, requiring them to roll the physical dice themselves and enter the outcomes by hand. We wonder about the extent to which elicitation with these tasks (or perhaps many others) can be made more informative by giving the subjects experience with the task or the consumption choice involved.

We see no evidence that people base their final gamble choice on whether the dice have been “lucky”. In principle, the dice should have no memory, but people may expect with positive (“hot hand”) or negative (“law of averages”) serial correlation. To the extent that these beliefs are present, they appear to be offsetting and there is no difference in behavior depending on whether more (or less) favorable practice outcomes occurred. Nevertheless, we also have diverse evidence from the comments made by the subjects after the experiment. Some people made comments in which they said that they tried to pick the lottery with the highest expected payoffs, which is why they changed their choice of lotteries. On the other hand, some students stated that they chose a safer final lottery even though they noticed that row 5 had the highest expected payoff. We do find that people who made comments about learning preferences or learning about the task increased the riskiness of the final gamble significantly more than others.

If loss aversion applies to hypothetical gambles and the reference point is intermediate between the high and low payoffs, one would expect losses to “loom larger than gains” and people to make more conservative choices after their experience. But if this effect is present, it is overwhelmed by the immersion in the task.

It seems clear that choices made after having just practice-round experience with our task change in the direction of more risk and higher expected payoffs. We feel strongly that researchers should explore better elicitation methods in the lab and elsewhere. A one-shot task may not be sufficient: It takes time for the subjects to understand what is going on, even with straightforward tasks like ours. We propose that researchers consider these findings when designing and implementing elicitation tasks.