Abstract
It has been a longstanding goal of the behavioral sciences to measure and model people’s risk preferences. In this article, we adopt a novel theoretical perspective of doing so and test to what extent specific types of individuals share similar risk profiles (i.e., configurations of multidimensional risk preferences). To this end, we analyzed data of a U.S. sample (N = 3,123) in a comprehensive and rigorous way, resulting in a twofold contribution. First, based on data from the Domain-Specific Risk-Taking scale (DOSPERT) and using a cross-validation procedure, we established a multidimensional trait space including general and domain-specific dimensions of risk preference. Second, we employed model-based cluster analyses in this multidimensional trait space, finding that 66% of participants can be described well with four basic risk profiles. In sum, the typological perspective proposed in this article has important implications for current theories of risk preference and the measurement of individual differences therein.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Risk preference constitutes a key construct of the behavioral sciences (Bernoulli, 1954; Kahneman & Tversky, 1979), and for both scientific and applied reasons there has been great interest in measuring and modeling interindividual differences in this construct (Appelt et al., 2011; Frey et al., 2017, 2021). Yet, despite decades of research on the measurement and modeling of people’s risk preferences, two fundamental theoretical issues still remain poorly understood (see Fig. 1).
Two outstanding issues concerning the construct of risk preference. Psychometric structure (left panel): is risk preference best modeled as a uni- or a multidimensional construct, or even a combination of both? Capturing individual differences (right panel): assuming at least some degree of multidimensionality (e.g., two dimensions), is a variable-centered approach necessary to describe individuals with highly idiosyncratic profiles, or does a small set of risk profiles account for a substantial portion of people (i.e., types) in the population?
The first issue concerns the psychometric structure of risk preference, with an ongoing debate whether this construct should be modeled exclusively as a unidimensional trait–potentially explaining variance in risk taking across diverse behaviors and circumstances (Weber, 1999; Zhang et al., 2018)–or rather as a multidimensional construct, implying that people’s risk preferences may vary substantially across different situations and domains of life (e.g., finance, health; Blais & Weber, 2006; Weber et al., 2002). Recent psychometric investigations have suggested that these two views may not be mutually exclusive, as people’s risk preferences appear to be best modeled by simultaneously accounting for general and domain-specific dimensions (Frey et al., 2017; Highhouse et al., 2016). The observation that the construct of risk preference may comprise both a general trait as well as multiple narrow traits is in line with how other psychological constructs are conceptualized: intelligence, for instance, is typically modeled as a general factor (“g”) and various facets (Deary, 2012). To date, however, the diverse theoretical perspectives on the construct of risk preference have only rarely been compared rigorously and by means of state-of-the-art data-analytic methods, such as cross-validation using separate hold-out samples. And yet, a solid understanding of the trait space of risk preference is naturally the prerequisite for the successful modeling of interindividual differences therein.
The second and related issue concerns the origin and conceptualization of interindividual differences within a multidimensional trait space of risk preference–provided that this construct does not consist of a broad and general trait only, but at least to some extent also comprises multiple narrow traits (i.e., akin to different facets of intelligence, or akin to the Big-Five personality dimensions; Costa & MacCrae, 1992; Deary, 2012; Weber et al., 2002). Importantly, in psychological research the predominant view is that the various dimensions of such multidimensional trait spaces tend to be orthogonal from each other, implying that each person may have a highly unique configuration in a given trait space. According to this view it is thus necessary to describe each person with an idiosyncratic profile of traits to be able to properly account for interindividual differences. But do indeed all trait profiles emerge empirically that are theoretically possible? An alternative view–which we adopt and test in this article–is that certain groups of people may share similar configurations of traits. Such prototypical profiles might have evolved (phylogenetically) or may develop (ontogenetically) because groups of people were and are exposed to shared environments. In other words, adaption processes may give rise to regularities within types of persons in terms of their multidimensional risk preferences. Crucially, when not taking into account such potential types of persons, an interdependence of traits may be hidden at the population level, and traits will misleadingly appear uncorrelated (cf. Simpson’s paradox; Simpson, 1951).
In line with these arguments, in personality research it has already been questioned whether people are as “exquisitely different as to defy a useful categorization” (Block & Haan, 1971; Robins et al., 1996), thus challenging the predominant variable-centered approach (Costa & MacCrae, 1992; Goldberg, 1990). In fact, recent empirical evidence using sophisticated modeling methods supports a person-centered view, suggesting the existence of a relatively small number of types of people who share similar configurations of personality traits (Asendorpf & van Aken, 1999; Gerlach et al., 2018). Conversely, typological approaches to modeling individual differences in risk preference have not yet been considered thus far. As such, it remains an open question whether a small set of prototypical risk profiles potentially accounts well for a large portion of individuals in the population.
1.1 Overview and research questions
In this article, we aim to address the two issues reviewed above by modeling self-reported risk preferences of 3,123 adults sampled from the U.S. general population. Specifically, we pursue the following two main research questions (RQs):
First, we aim to further clarify how to best model the construct of risk preference (RQ1). To this end, we revisit the psychometric structure as captured by one of the most commonly implemented questionnaires of risk preference, the Domain-Specific Risk-Taking scale (DOSPERT; Blais & Weber, 2006; Weber et al., 2002). The DOSPERT scale constitutes an ideal test bed for addressing our RQs: on the one hand, it has been designed to capture people’s risk preferences in five specific domains of life–thus, potentially tapping multiple narrow traits of risk preference–which, on the other hand, does not preclude the possibility that this scales also captures a general dimension of risk preference (see Highhouse et al., 2016). In our attempt of establishing a robust trait space of risk preference and addressing RQ1, we compare a series of theory- and data-driven models using separate exploratory and confirmatory subsamples (i.e., cross-validation). This approach promises to provide conclusive evidence whether the construct of risk preference is best modeled exclusively as a broad, general trait, exclusively as multiple independent dimensions, or as a combination of both. To the best of our knowledge, the current study is the largest investigation on the DOSPERT scale and the psychometric structure of risk preference it captures that has been conducted to date.
Second, within the newly established trait space we conduct latent profile analyses (Oberski, 2016) using model-based cluster algorithms (Gerlach et al., 2018; Pedregosa et al., 2011), to thus examine whether individual differences cover all niches of a potentially multidimensional trait space of risk preference–or, alternatively, whether groups of people (i.e., types) with similar configurations of risk preference can be identified (RQ2). The latter would substantially challenge current (variable-centered) theories of risk preference and simultaneously have important implications for the future measurement of risk preferences. That is, to the extent that particular risk profiles may be systematically associated with certain socio-demographic indicators, in the future it may be possible to infer the configurations of risk preference for groups of persons in a fast and frugal manner–without assessing idiosyncratic profiles by means of extensive measurements.
2 Methods
2.1 Participants and procedure
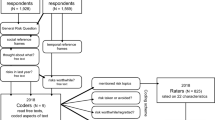
Three thousand and seven hundred participants aged 18 and over were recruited via Amazon’s Mechanical Turk (mTurk). The inclusion criteria were as follows: at least 50 Human Intelligence Tasks (HITs) completed with a 95% approval rate, and location in the U.S. The study was presented with Qualtrics, starting with the most recent version of the DOSPERT scale (see next subsection), followed by one to four brief questionnaires unrelated to risk preference and the present analyses, and finally, six one-item questions regarding general and domain-specific risk taking (for a subset of participants; see next subsection). The study ended with a battery of demographic questions. Overall, participants took approximately 15 minutes to complete the study and they were paid USD 1.70 on average, with a range from USD 1.25 to USD 4. Only participants who completed all parts of the study were included in our analyses, making the total sample 3,123 individuals (50.2% female, mean age: 35.6 years, age range: 18–77 years). Table S1 provides the full sample characteristics.
2.2 Materials
2.2.1 Domain-specific risk-taking scale (DOSPERT)
The DOSPERT scale (Blais & Weber, 2006; Weber et al., 2002) is a psychometric questionnaire with 30 items, each of which representing a risky activity from one of five different domains of life (i.e., six items per domain): ethical, financial (further subdivided into three investment and three gambling items), health/safety, recreational, and social. To illustrate, “going camping in the wilderness” represents an item of the recreational domain and, “investing 5% of your annual income in a very speculative stock” represents an item of the financial domain (see Table S4 for all items). Participants responded to the items in a fixed order and in the sequence of domains specified above.
Within each domain, the items were presented three times, once for each of three subscales: The first subscale assessed participants’ risk-taking propensities as follows: “Please indicate the likelihood that you would engage in the described activity or behavior if you were to find yourself in that situation.” Participants could answer anywhere from “Extremely unlikely” to “Extremely likely” on a Likert scale ranging from 1 to 7. The second subscale assessed participants’ risk perception: “People often see some risk in situations that contain uncertainty about what the outcome or consequences will be and for which there is the possibility of negative consequences. However, riskiness is a very personal and intuitive notion, and we are interested in your gut level assessment of how risky each situation or behavior is.” Participants could answer anywhere from “Not at all risky” to “Extremely risky” on a Likert scale ranging from 1 to 7. Finally, the third subscale assessed participants’ expected benefits: “Please indicate the benefits you would obtain from each situation.” Participants could answer anywhere from “No benefits at all” to “Great benefits” on a Likert scale ranging from 1 to 7. In line with most implementations of the DOSPERT scale, the present analyses primarily focus on the first subscale (i.e., risk-taking propensity).
2.2.2 Risk items of the German socio-economic panel (SOEP)
The last 991 participants (i.e., approximately one-third of all participants) were additionally asked to answer a single-item question concerning general risk taking, as well as five single-item questions concerning domain-specific risk taking. Some of these questions are routinely implemented in large panel studies such as in the German Socio-Economic Panel (SOEP; Dohmen et al., 2011; Falk et al., 2016) as well as in recent studies aimed at better understanding the cognitive underpinnings of people’s risk preferences (e.g., Arslan et al., 2020; Steiner et al., 2021). To assess general willingness to take risks, participants were asked to respond to the following question (using a Likert scale ranging from 0 to 10): “How do you see yourself: Are you generally a person who is fully prepared to take risks or do you try to avoid taking risks?” Using the same response scale participants also responded to five questions on their domain-specific risk taking in terms of driving, financial matters, leisure and sports activities, career decisions, and health behaviors.
2.3 Open research practices and multi-stage analysis plan
We followed a pre-registered multi-stage analysis plan to reduce our degrees of freedom in the exploratory analyses and to thus increase the likelihood of obtaining robust results. At the onset of the project, we detailed the specification of the theoretical rationale and a conceptual analysis plan in a stage-I registration (available from https://osf.io/pjt57).
We then split the full sample into an exploratory subsample A (1,500 randomly selected participants) and a confirmatory subsample B (the remaining 1,623 participants).
For the exploratory analyses informing the data-driven models 3, 5, and 6 (see Sect. 3), only the data of subsample A were made available to the main data analyst (R.F.). This exploratory dataset had blinded variable labels, with blinding conducted by S.M.D. The intermediate results (e.g., model structures) were reported in a stage-II registration (available from https://osf.io/pjt57).
The final analyses used the dataset with the unblinded variable labels. To assess whether any of the data-driven models overfitted the data, we compared the respective fits in the exploratory subsample A with those in the confirmatory subsample B. As Fig. S7 shows, there was no indication of systematic declines in the model fits in subsample B, suggesting that the analyses were robust, likely due to the large exploratory sample. We, therefore, report the model fits across the full sample (see SM for a discussion of the different fit criteria).
After having selected the best-performing model based on confirmatory factor analysis (CFA) across the full sample, we proceeded with the latent profile analyses to identify groups of people with similar profiles in the established multidimensional space of risk preference (see SM for methodological details and simulation analyses). We also repeated these analyses in the two separate subsamples to test the robustness of the identified clusters.
As detailed in the stage-II registration, at the onset of our analyses we compared two different correlation matrices across the 30 items of the DOSPERT scale, one using Pearson correlations and one using polychoric correlations. The latter treat the DOSPERT ratings as ordinal variables and consequently estimate correlations by assuming that continuous latent variables underlie the observed ordinal ratings. For the risk-taking propensity subscale, the polychoric correlations between the 30 ratings were on average 0.04 higher (range: -.09 to .17). As this difference was relatively small, we used the Pearson correlations for the subsequent exploratory factor analysis (EFA).
All details concerning the stage-I and stage-II registrations, the full dataset, and the analysis code are available from https://osf.io/pjt57.
3 Results
3.1 RQ1: How best to model the psychometric structure of risk preference?
To revisit the psychometric structure of risk preference and to establish a robust trait space thereof, we tested six models using confirmatory factor analysis (CFA; for an overview of all models, see Table S2). These models cover the full theoretical spectrum, at one extreme assuming risk preference to be a unitary trait (thus implying that a single factor will be sufficient to capture this construct), and at the other extreme assuming that risk preference is exclusively domain-specific (thus implying that multiple factors are required to capture this construct). To bridge the gap between these two extremes, we also implemented different bifactor models (Frey et al., 2017; Highhouse et al., 2016; Holzinger & Swineford, 1937; Jennrich & Bentler, 2011). Bifactor models can account for general and domain-specific variance simultaneously and, thus, permit quantifying to what extent risk preference is general or specific. Moreover, as the general factor in a bifactor model accounts for the common variance across measures, it renders the specific factors more distinct. As such, bifactor models in principle promise to cover a wider range of the trait space of risk preference. As outlined in Section 2, we followed a preregistered, multi-stage analysis plan and used blinded variable labels to extract all of the data-driven models.
3.1.1 Model 1 (theory-driven)
The first model (M1) comprised only a general factor, implying that there exists no domain-specificity in risk preference (Fig. S1). This model accounted for 19% of the total variance and did not achieve a solid model fit according to all fit criteria (e.g., RMSEA = .12, CFI = .43; see Table S3).
3.1.2 Model 2 (theory-driven)
The second model (M2) implemented the factor structure originally proposed for the DOSPERT scale, namely, five specific factors capturing ethical, financial, health/safety, social, and recreational risk-taking propensity (Fig. S2). Each factor was composed of six items, and the factors were permitted to be correlated with each other. M2 accounted for 38% of the total variance and approached but did not quite achieve a satisfactory model fit (e.g., RMSEA = .07, CFI = .80; see Table S3). The five factors were correlated relatively strongly with each other, with a mean factor-intercorrelation of .32 and a range from .01 to .69.
3.1.3 Model 3 (data-driven)
The third model (M3) retained the assumption that risk preference is best modeled with a series of domain-specific factors, but the optimal number of factors and the factor structure were determined in a data-driven way (i.e., during the exploratory stage-II analyses using only subsample A with blinded variable labels). M3 had six factors, which were composed of between two and six items. We only included items that loaded at least .2 on any of the factors in the preceding exploratory factor analysis (EFA) during the stage-II analyses, which resulted in retaining 26 of the 30 items. This model accounted for 41% of the total variance (i.e., slightly more than M2) and achieved a satisfactory fit (e.g., RMSEA = .05, CFI = .90; see Table S3). As in M2, the factors were correlated relatively strongly with each other, with a mean factor-intercorrelation of .34, and a range from .04 to .68.
3.1.4 Model 4 (theory-driven)
To test the extent to which the intercorrelations between the domain-specific factors (as observed in M2 and M3) can be modeled with a general factor (R) while simultaneously accounting for domain-specific variance, we next tested a bifactor model. Specifically, the fourth model (M4) had the same factor structure as originally proposed for the DOSPERT scale (i.e., the structure of M2) yet with an additional general factor modeling all items, and forcing all factors to be orthogonal (as is required in bifactor models; Fig. S4). M4 accounted for 43% of the total variance (i.e., again slightly more than the previous models) and approached a satisfactory fit (e.g., RMSEA = .06, CFI = .86; see Table S3). In M4, the general factor accounted for 35% of the explained variance, whereas the five specific factors cumulatively accounted for the remaining 65% of the explained variance.
3.1.5 Model 5 (data-driven)
We implemented the fifth model (M5) as another bifactor model (i.e., like M4), yet with a factor structure determined in a data-driven way (i.e., during the exploratory stage-II analyses using only subsample A with blinded variable labels). M5 had a general factor and six specific factors (Fig. 2). This model accounted for 44% of the total variance and achieved a satisfactory fit (e.g., RMSEA = .05, CFI = .89; see Table S3). In M5, the general factor accounted for 38% of the explained variance, whereas the six specific factors cumulatively accounted for the remaining 62% of the explained variance.
Model 5 implementing a data-driven bifactor structure. All factors were implemented to be orthogonal. Loadings and factor intercorrelations were obtained from confirmatory factor analysis using the full sample. The red shaded areas depict the proportion of variance accounted for by the general factor, and the green shaded areas depict the proportion of variance accounted for by the domain-specific factors. R = general factor of risk preference; SOC = social; REC = recreational; GAM = gambling; INV = investment; ETH = ethical; HEA = health
3.1.6 Model 6 (data-driven)
Finally, we implemented the sixth model (M6) as a reduced bifactor model (Fig. S6) because the preceding EFAs during the exploratory stage-II analyses indicated that a model with only four specific factors (instead of six, as in M5 described above) may account for about the same amount of variance. In the confirmatory analyses using the full sample, M6 accounted for 41% of the total variance and achieved an approximately satisfactory fit (e.g., RMSEA = .06, CFI = .87; see Table S3). The general factor accounted for 41% of the explained variance, whereas the four specific factors cumulatively accounted for the remaining 59% of the explained variance.
3.1.7 Model-comparison and -selection
To gauge how strongly the six different models captured the same or similar constructs, we computed and compared the correlations between all domain-specific and general latent variables (i.e., factors) from all models. The combined trait space is displayed in Fig. 3. The center of this network plot shows a convergence of several factors, namely, the general factor of M1 as well as the three general factors of the bifactor models (M4, M5, and M6). Moreover, several of the supposedly domain-specific factors clustered close to the center of this “positive manifold,” such as the factors ETH and HEA of M2, or ETH, HEA, and REC of M3. However, there were also clearly domain-specific clusters, such as the SOC factors of all models (except for M1, which did not comprise any domain-specific factors). As a general pattern, the domain-specific factors of the bifactor models (M4, M5, and M6) tended to be the most dispersed across the entire network, reflecting the fact that they were specified to be orthogonal from each other as well as from the general factors.
Network plot of the combined trait space across the implemented models, showing the correlations between all general and domain-specific factors, as well as the intercepts from the risk–return framework (see supplemental materials; SM), and the general and domain-specific risk items of the socio-economic panel (SOEP; see SM). The factors of the selected model (M5) are highlighted with black circles. ETH = ethical; FIN = financial; HEA = health; SOC = social; REC = recreational; GEN = general; OCC = occupational; DRI = driving; I = intercept of the risk–return framework
We proceeded with selecting a model for the further analyses, striving for a balance between reasonable fit criteria and conceptual interpretability of the model. We dismissed M1 given its bad fit and low proportion of explained variance. That is, we could clearly reject the assumption that risk preference is exclusively unidimensional. For the remaining five models, the differences in model fit and proportion of explained variance were smaller (Table S3 and Fig. S7). Specifically, among the two models without a general factor (i.e., M2 and M3) there existed small differences in terms of model fit and proportion of explained variance, yet the resulting factor structures were very similar. That is, in the data-driven M3 the factor structure originally proposed for the DOSPERT scale was recovered almost perfectly, with only two differences: first, the factor capturing financial risk-taking propensity was split into a “gambling” (GAM) and an “investment” (INV) factor–an observation that has already been made previously (Weber et al., 2002). Second, four of the six items supposedly capturing recreational risk-taking propensity were removed in M3, as they did not load with at least .2 on any of the factors in the EFA. In sum, M3 included fewer items, which potentially improved some of the fit indices, but overall there were only minor differences in terms of factor structure.
Among the three models with a general factor, the differences in model fit were also relatively small. However, a comparison of M4 (Fig. S4) and M5 (Fig. 2) indicated that the general factor in the latter was broader, that is, capturing variance across more measures. Moreover, the fit indices and the proportion of explained variance slightly favored M5. Conversely, the reduced bifactor model with fewer items (as implemented in M6) achieved a similar fit as compared to M5, but explained slightly less variance.
Finally, a direct comparison between M5 and M2–both including all 30 DOSPERT items and thus being nested models–favored the bifactor model M5 in terms of most fit indices (e.g., smaller BIC and AIC), and also from a conceptual perspective. That is, due to their orthogonality the specific factors in M5 may be cleaner indicators of people’s domain-specific risk preferences and, thus, easier to interpret, as opposed to the factors of M2 that were correlated relatively strongly with each other (see Fig. S8 for a direct comparison of all within- and across-model correlations of these factors). The distributions of the seven factor scores extracted from the selected model (M5) are depicted in Fig. S9.
3.1.8 Relationship between factor scores (M5) and traditional scores of the DOSPERT scale
We further examined the relationship between the factor scores of the selected model (M5) and the indicators that are traditionally computed for the DOSPERT scale (i.e., sum or mean scores across items of the various domains)–in order to clarify the extent to which these traditional scores are reasonable approximations of their conceptual counterparts resulting from the more extensive modeling approach. As a sanity check, panel A of Fig. 4 depicts the intercorrelations of all factor scores extracted from M5, confirming that the general and the various domain-specific factors of M5 are essentially uncorrelated.
Intercorrelations between the factor scores of the selected model (M5; panel A), as well as correlations between these factors scores and the traditional scores computed for the original DOSPERT scale (panel B) and a revised version of the DOSPERT scale (panel C). Correlations between conceptually identical scores are highlighted with red circles
Next, panel B of Fig. 4 depicts the correlations between the factor scores obtained from M5 and the scores traditionally computed for the DOSPERT scale, namely, the means across all items within each of the five domains (as well as a sum score across all items that may reflect a general dimension of risk preference in the DOSPERT scale). The correlations between the factor scores (M5) and their conceptually equivalent scores traditionally computed for the DOSPERT scale (highlighted with red circles) range between .36 and .96, suggesting that overall the traditional DOSPERT scores may be reasonable approximations of the more elaborate factor scores. However, panel B also illustrates that most of the traditional (domain-specific) DOSPERT scores are quite highly correlated with the general factor extracted from M5 (range: .15 to .85). This observations indicates that the traditional DOSPERT scores do not reflect purely domain-specific dimensions of risk preference.
Finally, panel C of Fig. 4 depicts the correlations between the factor scores of M5 and the scores computed for a revised version of the DOSPERT scale. The latter scores are based on the items that were retained in M5, that is, the sum across all retained items reflecting a total score, as well as the means across the items retained in each of the six factors of M5. The resulting correlations between the conceptually equivalent scores (highlighted with red circles) range between .62 and .94 and, thus, tend to be slightly higher as compared to the respective correlations based on the original DOSPERT scale. However, most of these supposedly domain-specific scores are still highly correlated with the general factor extracted from M5 (range: 0.15 to .76).
3.2 RQ2: Do types of people with distinct risk profiles exist?
Using the newly established multidimensional space of risk preference we next examined whether there exists a finite number of types of persons with similar configurations of risk preferences–and whether such potential types are systematically associated with specific socio-demographic variables. To this end, we conducted a latent profile analysis based on the continuous factor scores extracted from M5 (i.e., the bifactor model specifying a slightly revised factor structure for the DOSPERT scale plus a general factor). We implemented this analysis with a Gaussian-mixture model and Bayesian estimation methods, using the mixture package from the Python library scikit-learn (Pedregosa et al., 2011).
At the onset of this analysis we screened solutions ranging from one to ten clusters, and a comparison of the resulting BICs indicated that the solution with seven clusters achieved the best fit (Fig. S10). We next subjected these seven clusters to an enrichment analysis using a permutation test (see Gerlach et al., 2018), in which we repeatedly shuffled bootstrapped datasets to estimate the density under the null-model while keeping the marginal distributions constant (i.e., implementing the assumption that there exist no clusters in the data; see Fig. S11). This analysis indicated that only four of the seven clusters were robust. However, the majority of 66% of participants were best described by one of these four clusters, and these participants were assigned to one of the four clusters with very high classification probabilities (i.e., on average with p = .98, .93, 87, and .92 for the four clusters, respectively). Conversely, the average probability that these participants were assigned to any of the other clusters was only .06 (see Fig. S12). Thus, overall these results imply a very clear cluster solution.
The risk profiles (i.e., profiles I–IV) of the four identified clusters are depicted in Fig. 5. Specifically, the colored bars in the upper panel show the factor scores (for each dimension extracted from M5) at the centers of the four clusters, with the grey vertical lines indicating the separate factor scores for the two subsamples (i.e., robustness check). Moreover, the black marks indicate the mean empirical factor scores of all participants assigned to the clusters (including two standard errors of the mean as error bars). Profile I represents the largest cluster (containing 21% of participants), and participants assigned to this cluster can be described as the “cautious”–that is, people who are relatively more risk-averse in all domains except the social and ethical domains (where their risk preference is at average level). Profile II (18% of participants) represents people who are relatively more risk-averse in general, but more risk-seeking in the recreational domain (i.e., “recreational adventurers”). Profile III (15% of participants) represents “financial gamblers,” who are relatively more risk-seeking regarding financial investments and gambling, but more risk-averse regarding health, and about average otherwise. Finally, profile IV (13% of participants) represents the “daredevils,” who are more risk-seeking than average in most domains, except for investment where their risk preference is at an average level, and in the social domain, where they are relatively more risk-averse.
A multinomial log-linear model provided evidence that several socio-demographic variables were systematically associated with these four risk profiles (see lower panel of Fig. 5; values represent odds-ratios relative to the reference profile I). For example, an increase of one standard deviation in age was associated with monotonically decreasing odds-ratios of .84, .77, and .41 of being assigned to the profiles II, III, or IV, relative to profile I. In other words, older people are about half as likely to belong to the “daredevil” type than to the “cautious” type. Gender was also systematically associated with particular profiles: for instance, men were 5.87 times more likely to be “daredevils” than “cautious.” Finally, people with higher income were relatively more likely to be “financial gamblers,” whereas people with (more) children were relatively less likely in this group.
The four identified risk profiles, ordered according to their cumulative degree of risk preference from left to right. Colored bars represent the mean factor scores at the cluster centers, and the black indicators depict the empirical means of factor scores of all participants assigned to the respective clusters (including two standard errors of the mean as error bars). Gray bars depict the cluster centers as extracted independently for the two subsamples. The lower panel depicts the odds-ratios for various predictors, indicating the relative probability of being assigned to a specific profile over being assigned to the reference profile I (i.e., with N = 654 the largest cluster). The coefficients depict the change of a one-unit increase in the predictor variable (e.g., one standard deviation of age) or the change from the reference level to the effect level in the case of categorical variables (e.g., from “independent” to either “democrat” or “republication”). Significant odds-ratios are marked with an asterisk
4 Discussion
This article makes two key contributions with direct implications for current theories of risk preference and the assessment of people’s risk preferences in scientific and applied settings. First, in line with recent research (Frey et al., 2017; Highhouse et al., 2016) our results decisively suggest that risk preference comprises both a general as well as multiple domain-specific dimensions–or, in other words, a combination of a broad, general trait, and multiple narrow traits. The existence of a general trait has always been theoretically attractive and practically desirable, as both researchers and the general public have strong intuitions about being able to evaluate different individuals on their general level of risk-aversion or risk-seeking (Weber & Milliman, 1997). Second, we identified four types of persons with similar configurations of (multidimensional) risk preferences. Specifically, four basic risk profiles accounted for two-thirds of the participants in our large and diverse sample of the U.S. population. A typological approach to gauging interindividual differences in risk preference may prove valuable in several applications: for instance, the possibility of targeting specific types (e.g., based on socio-demographic proxy variables) may constitute a promising alternative for addressing large-scale problems at the population level (e.g., behavioral change), where targeting individuals based on extensive individual assessments is rarely feasible. Moreover, the new evidence for a typology of risk preference may inform future work on the origins and the development of traits, suggesting that certain traits may evolve or develop according to systematic patterns in subgroups of the population. Such an interdependence of traits remains masked when only studying interindividual differences at the population level.
4.1 Risk preference: General, domain-specific, or both?
In the past, the view of preferences as stable and enduring (cf. Stigler & Becker, 1977) has implied that people’s appetite for risk may originate from a general and unidimensional trait. Conversely, from research assuming that preferences are largely constructed (Lichtenstein & Slovic, 2006) it followed that people’s risk preferences may vary substantially across different domains of life (e.g., health, finance, etc.)–for instance, because people perceive consistently different risks and benefits in such domains (Weber & Milliman, 1997). Instruments including the DOSPERT scale (Weber et al., 2002), or a brief battery of questions capturing domain-specific risk preferences (Falk et al., 2016), have repeatedly provided evidence in this regard.
Yet, when “controlling” for differences in perceived risks and benefits that may emerge across various life domains, people’s perceived risk-attitudes were found to reflect a relatively general dimension of risk preference (Weber & Milliman, 1997). Alike, more recently psychometric modeling analyses implementing bifactor models (Frey et al., 2017; Highhouse et al., 2016) have provided evidence that risk preference comprises general and domain-specific dimensions–an observation that has also been made for other major psychological constructs (e.g., intelligence; Deary, 2012). Our observations are in line with these results and, thus, challenge theories of risk preference that do not predict any domain-specific variation (e.g., traditional economic theories of risk preference); clearly, future measurement efforts will profit from modeling both general and specific components of people’s risk preferences. As our analyses have illustrated, a simple bifactor model succeeds in doing so, rendering time-consuming assessments of people’s risk perceptions and expected benefits obsolete–as was necessary to employ a risk–return framework to extract people’s general perceived risk-attitudes (Weber & Milliman, 1997).
4.2 Towards a typology of risk preference
Our latent profile analyses resonate with recent efforts in personality research, which has started to examine the possibility that different individuals may not be as unique as previously thought, in the sense that configurations of personality characteristics potentially do not vary from person to person in an entirely unpredictable way (Gerlach et al., 2018). Rather, in line with many lay persons’ intuitions, there appears to be a small set of distinct personality types (Asendorpf & van Aken, 1999; Robins et al., 1996).
Some of these approaches have originally used relatively simplistic methods to model typologies (Asendorpf & van Aken, 1999; Robins et al., 1996), but others have meanwhile shifted to using sophisticated and robust machine-learning algorithms (Gerlach et al., 2018). Following the latter approach, our analyses yielded similar conclusions for the construct of risk preference: specifically, our model-based cluster analyses suggest that 66% of the participants in our sample could be classified confidently to one of four basic risk profiles (i.e., the “cautious,” the “recreational adventurers,” the “financial gamblers,” and the “daredevils”). These profiles were systematically associated with socio-demographic indicators, such as a person’s age or gender.
Clearly, these profiles and their predictive value for particular economic or social behaviors remain to be further validated in future research. Moreover, as in all instances of unsupervised learning (i.e., when no absolute criterion for a “correct” classification is available), certain degrees of freedom exist. Yet, in our approach we have implemented a robust model-based approach and conducted extensive simulation analyses, in order to identify potential spurious clusters (see SM; Gerlach et al., 2018). We are thus confident that the four identified risk profiles are meaningful, in particular given their high “face validity,” that is, their clear associations with relevant socio-demographic indicators, and the high probabilities by which classified participants were assigned to one of the profiles but not to the others (Fig. S12). In sum, these findings constitute an important first step in substantiating the novel theoretical view that we have proposed in this article, namely, that a relatively small number of types of persons may share similar configurations of multidimensional risk preferences.
4.3 Conclusions
This article suggests a novel typological approach to modeling individual differences in risk preference. To this end, we established a robust trait space of risk preference comprising general and domain-specific dimensions. Although a minority of people appears to have highly idiosyncratic configurations of risk preferences, two-thirds of participants could be described well with one of the four identified risk profiles. These findings have important implications for current theories of risk preference, and challenge theories that assume that risk preference is either an exclusively general or domain-specific construct, as well as theories assuming that most people have highly idiosyncratic configurations of risk preferences.
It follows that future measurement approaches will profit from assessing general and domain-specific dimensions of risk preference. Moreover, in scientific and applied settings where detailed assessments of people’s multidimensional risk preferences are not feasible, the shortcut of predicting risk profiles based on socio-demographic indicators may turn out to be a promising alternative.
Availability of data and material
The dataset and additional materials can be retrieved from https://osf.io/pjt57.
Code availability
The analysis code is available from https://osf.io/pjt57.
References
Appelt, K. C., Milch, K. F., Handgraaf, M. J., & Weber, E. U. (2011). The decision making individual differences inventory and guidelines for the study of individual differences in judgment and decision-making research. Judgment and Decision Making, 6(3), 252–262.
Arslan, R. C., Brümmer, M., Dohmen, T., Drewelies, J., Hertwig, R., & Wagner, G. G. (2020). How people know their risk preference. Scientific Reports, 10(1), 15365.
Asendorpf, J. B., & van Aken, M. A. G. (1999). Resilient, overcontrolled, and undercontrolled personality prototypes in childhood: Replicability, predictive power, and the trait-type issue. Journal of Personality and Social Psychology, 77(4), 815–832.
Bernoulli, D. (1954). Exposition of a new theory on the measurement of risk. Econometrica, 22(1), 23–36. Original work published 1783.
Blais, A.-R., & Weber, E. U. (2006). A domain-specific risk-taking (DOSPERT) scale for adult populations. Judgment and Decision Making, 1(1), 33–47.
Block, J., & Haan, N. (1971). Lives through time. Bancroft Books.
Costa, P. T., & MacCrae, R. R. (1992). Revised NEO personality inventory (NEO PI-R) and NEO five-factor inventory (NEO-FFI): Professional manual. Psychological Assessment Resources, Incorporated.
Deary, I. J. (2012). Intelligence. Annual Review of Psychology, 63(1), 453–482.
Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J., & Wagner, G. G. (2011). Individual risk attitudes: Measurement, determinants, and behavioral consequences. Journal of the European Economic Association, 9(3), 522–550.
Falk, A., Becker, A., Dohmen, T. J., Huffman, D., & Sunde, U. (2016). The Preference Survey Module: A validated instrument for measuring risk, time, and social preferences. Institute for the Study of Labor, Bonn. Discussion Paper No. 9674.
Frey, R., Pedroni, A., Mata, R., Rieskamp, J., & Hertwig, R. (2017). Risk preference shares the psychometric structure of major psychological traits. Science Advances, 3, e1701381.
Frey, R., Richter, D., Schupp, J., Hertwig, R., & Mata, R. (2021). Identifying robust correlates of risk preference: A systematic approach using specification curve analysis. Journal of Personality and Social Psychology, 120(2), 538–557.
Gerlach, M., Farb, B., Revelle, W., & Amaral, L. A. N. (2018). A robust data-driven approach identifies four personality types across four large data sets. Nature Human Behaviour, 2(10), 735–742.
Goldberg, L. R. (1990). An alternative “description of personality”: The big-five factor structure. Journal of Personality and Social Psychology, 59(6), 1216.
Highhouse, S., Nye, C. D., Zhang, D. C., & Rada, T. B. (2016). Structure of the DOSPERT: Is there evidence for a general risk factor? Journal of Behavioral Decision Making.
Holzinger, K. J., & Swineford, F. (1937). The bi-factor method. Psychometrika, 2(1), 41–54.
Jennrich, R. I., & Bentler, P. M. (2011). Exploratory bi-factor analysis. Psychometrika, 76(4), 537–549.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263–291.
Lichtenstein, S., & Slovic, P. (Eds.). (2006). The construction of preference. Cambridge University Press.
Oberski, D. (2016). Mixture models: Latent profile and latent class analysis. In J. Robertson & M. Kaptein (Eds.), Modern Statistical Methods for HCI (pp. 275–287). Springer International Publishing.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., & Duchesnay, É. (2011). Scikit-learn: Machine learning in python. Journal of Machine Learning Research, 12, 2825–2830.
Robins, R. W., John, O. P., Caspi, A., Moffitt, T. E., & Stouthamer-Loeber, M. (1996). Resilient, overcontrolled, and undercontrolled boys: Three replicable personality types. Journal of Personality and Social Psychology, 70(1), 157–171.
Simpson, E. H. (1951). The interpretation of interaction in contingency tables. Journal of the Royal Statistical Society: Series B (methodological), 13(2), 238–241.
Steiner, M. D., Seitz, F., & Frey, R. (2021). Through the window of my mind: Mapping information integration and the cognitive representations underlying self-reported risk preference. Decision, 8(2), 97–122.
Stigler, G. J., & Becker, G. S. (1977). De gustibus non est disputandum. The American Economic Review, 67(2), 76–90.
Weber, E. U. (1999). Who’s afraid of a little risk? New evidence for general risk aversion. In J. Shanteau, B. A. Mellers, & D. A. Schum (Eds.), Decision Science and Technology (pp. 53–64). Springer US.
Weber, E. U., & Milliman, R. A. (1997). Perceived risk attitudes: Relating risk perception to risky choice. Management Science, 43(2), 123–144.
Weber, E. U., Blais, A. R., & Betz, N. E. (2002). A domain-specific risk-attitude scale: Measuring risk perceptions and risk behaviors. Journal of Behavioral Decision Making, 15(4), 263–290.
Zhang, D. C., Highhouse, S., & Nye, C. D. (2018). Development and validation of the General Risk Propensity Scale (GRiPS). Journal of Behavioral Decision Making.
Acknowledgements
We thank the members of the Center for Cognitive and Decision Sciences (University of Basel) for valuable input and Laura Wiles for proofreading the manuscript.
Funding
Open access funding provided by University of Zurich. The present work was supported by two grants of the Swiss National Science Foundation to Renato Frey (#174042 and #194540). The Center for Decision Sciences at Columbia Business School funded the data collection.
Author information
Authors and Affiliations
Contributions
R.F. and E.U.W. conceptualized the research. S.M.D. collected and blinded the dataset. R.F. conducted the formal analyses and wrote the paper. E.U.W. and S.M.D. provided critical revisions.
Corresponding author
Ethics declarations
Ethics approval
The study was approved by the institutional review board of Columbia University.
Conflicts of interest
The authors declare no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frey, R., Duncan, S.M. & Weber, E.U. Towards a typology of risk preference: Four risk profiles describe two-thirds of individuals in a large sample of the U.S. population. J Risk Uncertain 66, 1–17 (2023). https://doi.org/10.1007/s11166-022-09398-5
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11166-022-09398-5