Abstract
The Description-Experience gap (DE gap) is widely thought of as a tendency for people to act as if overweighting rare events when information about those events is derived from descriptions but as if underweighting rare events when they experience them through a sampling process. While there is now clear evidence that some form of DE gap exists, its causes, exact nature, and implications for decision theory remain unclear. We present a new experiment which examines in a unified design four distinct causal mechanisms that might drive the DE gap, attributing it respectively to information differences (sampling bias), to a feature of preferences (ambiguity sensitivity), or to aspects of cognition (likelihood representation and memory). Using a model-free approach, we elicit a DE gap similar in direction and size to the literature’s average and find that when each factor is considered in isolation, sampling bias stemming from under-represented rare events is the only significant driver of the gap. Yet, model-mediated analysis reveals the possibility of a smaller DE gap, existing even without information differences. Moreover, this form of analysis of our data indicates that even when information about them is obtained by sampling, rare events are generally overweighted.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we present an experimental investigation into the nature and causes of the so-called Description-Experience gap (DE gap for short). The DE gap is a widely-documented tendency for people to act as if they have systematically different preferences over risks, depending on whether their information about those risks is derived from explicit descriptions or, alternatively, acquired through sampling or other experience that permits learning. Classic references in psychology include Barron and Erev (2003), Hertwig et al. (2004), and Weber et al. (2004). Examples of more recent interest among economists include Abdellaoui et al. (2011b), Kopsacheilis (2018), and Aydogan and Gao (2020). Wulff et al. (2018) provides a meta-analytic review.
The distinction between description and experience is pertinent for a wide range of human decisions because, in everyday life, people tend to acquire information about risks via both description and experience. Practitioners, such as doctors, insurance brokers or investment advisors, often provide clients with written numerical information about different types of risk. Yet, people also continually learn about risks from a multitude of experiences: examples include seeing your investments go up and down; observing people returning from skiing trips with injured limbs; and living through one more day without being burgled or mugged. Hence, if there is a significant DE gap, it may influence many decisions. With that in mind, our primary motivation in this paper is to assess what sort of, and how serious, a challenge the DE gap poses for theoretical and applied work by investigating the contributions of different possible causes of the DE gap and measuring its footprint in choices and in risk-preference functions.
While existing research provides widespread evidence of DE gaps in experimental studies, the exact form and implications of the phenomenon remain controversial. For example, estimates of the size and even the direction of the gap vary across studies. Moreover, while there is ample evidence that misperceptions of objective probabilities in decisions from experience (due to biases in information captured in sampling experiences) explain some component of the DE gap, it is less clear whether - and, if so, how far - other contributory factors related to preferences and/or cognitive processes also play a role. We discuss the relevant evidence in the next section, simply noting here that our experimental design is motivated by two sources of diversity in the prior evidence: that the DE gap may be influenced by multiple, importantly distinct, causal mechanisms that have been triggered differentially by competing designs; and that different studies have measured the gap in different ways. For example, some studies use measures of the gap based on choice frequencies alone whereas other studies rely on parameter comparisons within particular preference models. We refer to these approaches as model-free and model-mediated respectively.
The experiment that we present here tests, in a single unified design, for the operation of four distinct causal mechanisms that may drive the DE gap. Our data analysis uses both model-free and model-mediated approaches to assess the effects of the mechanisms and the size of the DE Gap itself.Footnote 1
The mechanisms we examine are, respectively, effects of: sampling bias; attitudes to ambiguity in probability information; the representation of that information; and memory. The first of these mechanisms explains the DE gap in terms of differences in the information available to decision makers at the point of choice, comparing description and experience; the second attributes the DE gap to features of preference; the third and fourth effects explain the DE gap as arising from features of human cognition.
These channels are not mutually exclusive, as we explain. Yet, identifying which actually operate, and to what degree, is important because the implications for decision theory vary markedly depending upon which of the information, preference or cognition channels are most at play. If the DE gap is simply caused by differences in information about objective risks that result from properties of small samples, that would be a reason to pay close attention to information available to agents, but not a fundamental challenge to preference theory. If the DE gap arises from ambiguity sensitive preferences, it would become an important, but so far under-appreciated, part of the rationale for the numerous models of such preferences that have emerged in the last 30 years. However, if the DE gap is caused by cognitive processes and constraints, a full understanding of it may require models of decision processes, rather than pure preference models.
Our main findings are as follows. Our model-free analysis replicates a significant DE gap, similar in magnitude and direction to the literature’s average. Also, in line with existing literature, we find that sampling bias contributes importantly to the DE gap. In fact, in our experiment, sampling bias - in the form of under-representation of rare events - is the only one of the four causal factors we consider that generates a statistically significant gap by itself in our model-free analysis. Our model-mediated analysis uses the framework of rank-dependent utility theory (RDU; Quiggin, 1982; Wakker, 2010) to capture effects of our causal factors on probability weighting, while allowing for utility curvature (and for any effects of our treatments on the latter). It supports two findings. First, in all treatments that control for sampling bias, we find inverse-S probability weighting, consistent with overweighting of rare events for both description and experience; by contrast, sampling bias tends to create the appearance of more linear probability weighting via the under representation of rare events in experienced samples. Second, we find some evidence of DE gaps caused by factors besides sampling bias: this arises from treatment comparisons that implicate a mixture of cognitive factors and ambiguity sensitive preference.
In the next section, we discuss existing literature. This provides the background to our experiment. Section 3 presents our experimental design and details on the methods of analysis. In Sect. 4 we show results, with discussion and conclusions in Sect. 5.
2 Background
Much of the evidence for the DE gap derives from lab experiments using variants of the so-called “sampling paradigm” (Hertwig et al., 2004) in which participants make one-off choices between safer and riskier options in one of two different treatments: “Description” or “Experience.”Footnote 2 In “Description,” gamble properties are fully stated, leaving no uncertainty regarding the set of possible payoffs or their associated probabilities.Footnote 3
In contrast, in “Experience,” participants are not given stated information about consequences and/or their probabilities but must garner it via some form of sampling. In a typical implementation of “Experience,” the two gambles might appear on screen in the form of two buttons. Participants then sample by pressing the buttons in some sequence of their choice and, each time a button is pressed, one of the outcomes of the selected gamble appears on screen with outcome likelihoods controlled by the gambles objective probabilities. Note that, in this framework, relative frequencies of experienced outcomes may not always coincide with the objective probabilities (though in some designs, as in some of our treatments, they may be controlled to do so).
A standard test for the DE gap has been to compare choice proportions across the two conditions. The “canonical finding” is that subjects in the “Description” condition tend to prefer the riskier option when the rare event gives a desirable outcome, and to prefer the safer option when the rare event gives an undesirable outcome; whereas the opposite is observed in the “Experience” condition. Taken together, this pattern has been commonly interpreted as reflecting a tendency to overweight rare events in “Description” but to underweight them in “Experience” (Hertwig et al., 2004).
There is now a considerable amount of research investigating the DE gap, with a recent meta-analysis (Wulff et al., 2018) adding authority to the claim that the DE gap exists. However, this meta-analysis also demonstrates striking heterogeneity across studies with respect to the size of the gap, ranging from very small to very large. In fact, some papers even find a reversed DE gap, with subjects in “Experience” appearing to overweight rare events more than in “Description” (e.g. (Glöckner et al., 2016)). How can we make sense of these diverse findings?
One possible contributor to the diversity of findings is the wide variation in design features such as the structure of sampling, characteristics of gambles and the ways in which they are evaluated. Another is the fact that different studies have employed different measurement approaches to quantify their findings.
2.1 Variation in design of studies
The idea that variation in study design accounts for the variation in measured DE gaps is plausible given that existing literature has suggested several potential causes of the DE gap. To the extent that there are multiple causes at work, different designs may have triggered subsets of them to different degrees. We taxonomise causal factors that may drive the DE gap into three channels: sampling bias; preference; and cognition.
Sampling bias is perhaps the most obvious candidate explanation. This attributes the DE gap to individuals acting on the basis of biased information in “Experience” treatments. As already noted, in these treatments, the relative frequency with which gamble outcomes are observed may not always match their objective probabilities. Moreover, because people usually choose to collect only quite small samples in “Experience” treatments (e.g. the median subject of (Hills & Hertwig, 2010), samples each option only 9 times), rare events tend to be under-represented due to a property of the binomial distribution.Footnote 4 In such circumstances, we should expect the impact of rare events on choices to be attenuated, in line with the canonical finding.
There is considerable existing evidence that sampling bias contributes to the DE gap. Perhaps the most prominent, early evidence for this is the study of Fox and Hadar (2006). In this study, the authors reanalyse the data of Hertwig et al. (2004) and point out that if objective probabilities are replaced by either experienced relative frequencies or judged probabilities (each sensitive to samples), then aggregate choices in Experience can be explained sufficiently well with a standard, inverse S-shaped probability weighting function.
Were sampling bias the full story, the significance of the DE Gap would largely derive from the potential for sub-optimal search intensity by agents and the dangers of environments that generate biased information. But, there is evidence that DE gaps can also arise, albeit typically weaker, in the absence of sampling bias, from studies that control for it by engineering ‘Experience’ treatments to ensure that experienced and objective probabilities coincide (e.g. Hau et al., 2010; Ungemach et al., 2009; Barron & Ursino, 2013; Aydogan & Gao, 2020). DE gaps observed in such setups require an explanation that goes beyond biased information, prompting consideration of preferences, cognitive processes or both.
The most obvious candidate for a preference-based account of the DE gap is some form of attitude toward ambiguity.Footnote 5 This is so because, in terms of the classic Knightian distinction (Knight, 1921), decisions in a “Description” treatment are choices among risks whereas those in an “Experience” treatment are more naturally interpreted as involving other forms of uncertainty, in which probabilities are ambiguous or only imprecisely known. If agents are (subjective, where necessary) expected utility maximisers, the distinction would be irrelevant in situations where subjective, experienced and objective probabilities coincide. But, the presence of ambiguous information about probabilities may affect behaviour if individuals have non-expected utility attitudes towards ambiguity. For example, paralleling Ellsberg (1961)’s famous urn experimentsFootnote 6 where people are often ambiguity averse in the sense of being more willing to gamble on “known” than “unknown” urns, willingness to take risks may be lower in “Experience” (where distributions are unknown) than in “Description”. There is some existing evidence that ambiguity attitudes play a role in the DE gap. Specifically, Abdellaoui et al. (2011b), find that, in the absence of sampling bias, estimated probability weights for a prospect theory model are systematically smaller (less optimistic) in “Experience” compared with “Description.” While this result might be due to ambiguity aversion, as suggested by (Abdellaoui et al., 2011b), Sections 2.3.2 and 7.1.2), so far, the evidence for such an effect being an important driver of the DE gap is limited. If the finding were to generalise, the DE gap might be an important exhibit of ambiguity sensitivity, along with the Ellsberg paradox.
A third class of explanation attributes the DE gap to factors that have their roots in human cognition (as opposed to preference). We consider two such candidates: response to likelihood representation and memory. Recall that gamble information is represented in different ways across “Description” and “Experience.” In “Description,” probabilities are communicated through written information often in the form of percentages (e.g. “£16 with 10% chance”) but in “Experience,” gamble information is obtained through sequential sampling experiences which must be interpreted by the receiver (e.g. “this option gave me a good prize 1 out of 10 times”). While there is considerable evidence that representation of chance can affect decisions in different contexts (e.g. Gigerenzer & Hoffrage, 1995; Slovic et al., 2000), it is not yet clear how important differences in likelihood representations are as drivers of DE gaps, when the underlying information represented is held constant. A related consideration arises from noticing that, when likelihoods are discovered through sequential sampling, claims about what information subjects have in mind are contingent on assumptions about their recall. As such, imperfect memory of sampling is a further possible driver of the DE gap. While the possible role of imperfect memory in the DE gap has been noted in previous literature (e.g. Rakow et al., 2008; Frey et al., 2015) its actual role is hard to assess based on existing evidence (see (Wulff et al., 2018) p.156, for a relevant discussion).
2.2 Variation in measurements
While most studies in this literature have used direct choice comparisons to assess the DE gap (e.g. comparing choice proportions as described above), studies in a slightly different genre have estimated behavioural models (usually based on cumulative prospect theory; Tversky & Kahneman, 1992) to examine the impact of “Description” versus “Experience” on parameters of estimated preference functions, often focussing on differences in the resulting probability-weighting functions. It seems possible that different measurement approaches may support different conclusions. Notwithstanding this possibility, there remains considerable variation across the results of studies even within each of these genres. For example, while DE gap studies that estimate prospect theory weighting functions have generally reported inverse S-shaped probability weighting curves in “Description,” there is considerable heterogeneity in the shapes of curves elicited in “Experience” conditions: Abdellaoui et al. (2011b), and Kemel and Travers (2016) reported inverse-S shaped weighting; Ungemach et al. (2009) reported S-shaped weighting; while Hau et al. (2008) found linear weighting. More recently, Kopsacheilis (2018) put forward the “Relative Underweighting Hypothesis,” according to which people overweight rare events in “Experience” but less so than in “Description,” a hypothesis that was later corroborated by findings in Aydogan and Gao (2020). This hypothesis is accommodated by an inverse S-shaped probability weighting function in “Experience” that is closer to the diagonal for probabilities closer to 0 or 1, when compared to “Description.”
Our experiment is designed to facilitate direct tests for the influence of each of: sampling bias, ambiguity attitude, likelihood representation, and memory. These factors are tested by pairwise comparisons of treatments in a unified design which, by varying a single factor in each comparison, isolates their separate influences. Our setup is designed to facilitate evaluation via model-free tests of effects and via comparisons of the impact of factors on probability-weighting functions. By using four different “Experience” treatments, our design also permits tests of four distinct forms of DE gap.
3 Design and methods
3.1 Treatments
In our experiment, subjects evaluate a series of binary gambles via a process described below. Payoffs are (non-negative) sums of money which are always known to the decision maker at the point of evaluation. Gambles are represented by virtual decks of cards, each containing two types of card, demarcated by colour.Footnote 7 Within each gamble, there are two possible outcomes, each associated with one of the two colours in the deck; the relative frequencies of the two colours represent the probabilities of the two outcomes. The design involves five treatments: one Description (Desc) treatment plus four variants of “Experience” which we label Unambiguous (E-Unamb), No Records (E-NR), Ambiguous (E-Amb), and Restricted (E-Res). As we summarise in the top part of Fig. 1, the treatments differ in how subjects obtain information about the contents of the deck.
In Desc, gamble probabilities are communicated in explicit, numerical form (as percentages) during evaluation (e.g. “90% of the deck’s cards are grey and 10% are yellow”). By comparison, in the Experience treatments, subjects are not told the relative frequencies of the colours in each deck but have opportunities to investigate and/or discover this information by sampling deck contents. The sampling environment varies by treatment as we now explain.
The E-Unamb treatment provides a version of “Experience” which is informationally equivalent to Desc. This involves two key ingredients. The first is that, in E-Unamb, subjects sample the entire deck, without replacement, and are told that they see the full deck with each card appearing once and only once. Hence, subjects in this treatment have access to full information about the chances of the two outcomes which is logically identical to that available to subjects in Desc. However, subjects having seen the full set of cards exactly once is no guarantee that subjects have accurate perceptions of the colour composition of the deck at the point of gamble evaluation: they may not have paid full attention to the sampling experience and they might have forgotten aspects of it, prior to the evaluation phase. To control for the influence of such cognitive constraints in E-Unamb, we introduce, as the second key ingredient, a history table that remains on screen during the evaluation phase.Footnote 8 This records the colours of cards that were sampled in the order they were sampled. This record is shown on the screen where subjects evaluate gambles and, for this treatment, a message on top of the history table reads: “This is the entire deck with its cards displayed in the order you sampled them.”Footnote 9
Figure 2 illustrates how the sampling process was displayed to subjects, depicting three instances of the experimental procedure for E-Unamb. Panels a. and b. capture before and after instances of a single sample event, while panel c. demonstrates an example of the evaluation phase. Notice that -once sampling is complete- the history table encodes mathematically identical probability information to that provided, in a different format, in the Desc treatment. Hence, comparing behaviour in the Desc and E-Unamb treatments provides a test of whether behaviour depends on the way in which given likelihood information is represented and acquired.
As illustrated at the bottom of Fig. 1, treatments branch along two different routes as a consequence of variations relative to E-Unamb. The E-NR treatment is identical to E-Unamb, except that no history table is presented. Hence, while the information contained in the sampled deck remains equivalent to Desc and E-Unamb, memory or other cognitive limitations (including lack of attention) might lead individuals to act on assessments of gambles based on misperceptions of objective probabilities. As a convenient shorthand we refer to any such influences of cognition, as “memory” effects. The comparison of E-Unamb with E-NR isolates such effects.
E-Amb branches in a different way from E-Unamb. E-Amb retains the history table and all other features of E-Unamb except that, in E-Amb, subjects are not told that the 40 cards they sampled comprise the entire deck. In this treatment, the line of text immediately above the history table just says: “These are the colours you sampled in the order you sampled them,” instead of the text shown in Fig. 2c. Hence, while these subjects do in fact see the full deck and the record of it, they do not know that they see the full deck. From their perspective, the situation has a degree of ambiguity because they are not informed that the relative frequencies they experience match objective probabilities. Hence, the comparison between E-Unamb and E-Amb isolates the effect of the presence of ambiguity, keeping constant the actual samples experienced and the presence of the history table record of them. This is our cleanest test for the impact of ambiguity. However, if subjects are ambiguity sensitive and also (aware that they) suffer from imperfect recall, they might experience ambiguity in E-NR too. Our shorthand term ‘memory’ should be interpreted as including this additional effect of withdrawing the history table.
Our final treatment, E-Res, is identical to E-Amb except that the number of cards sampled was restricted. Specifically, unlike E-Unamb, E-NR and E-Amb that featured 40-card samples, sampling in E-Res was restricted to 18 cards. In consequence, a unique feature of this treatment is that the experienced relative frequency of colours sampled cannot exactly match the objective one.Footnote 10Therefore, the E-Res treatment necessarily introduces sampling bias and the comparison of it to E-Amb isolates the effect of that factor. Notice that sampling bias can arise in two directions: a particular event can be either over- or under-represented in a given sample, relative to its objective probability. Since we should expect the effects of under- and over-representation to be different, in the analysis we split observations in E-Res into two subsets: E-Over and E-Under. Since rare events are our loci of interest, we taxonomise observations according to whether the event with the smallest probability to occur was over- or under-represented.Footnote 11
We are now in a position to summarise the full logic of the set of treatments introduced in Fig. 1. In essence, pairwise comparisons of treatments which are adjacent in the bottom panel of Fig. 1 provide a series of tests designed to isolate causal effects due to: likelihood representation, memory, ambiguity, and sampling bias.We refer to these as tests for “effects.” Since we have multiple variants of Experience implemented in our design, and since it is possible that the factors we isolate might also work in combination, we also conduct a set of tests for DE gaps by comparing behaviour in our Desc treatment with that in each of our different Experience conditions. Lastly, in order to get an estimate of the average DE gap we elicit, we compare Desc with E-All, a compilation of observations across all four variations of Experience.
The distinct DE gaps we elicit - each based on comparison of Desc with one of our Experience treatments - relate to previous literature in interesting ways. Since in E-Unamb the subject ultimately has access to precise information about gamble probabilities (visible in one place, even though acquired gradually through an experiential process), comparison of Desc with E-Unamb investigates a case of a possible DE gap in which - unusually - both treatments are in the domain of risk. This contrasts with the more usual case in which the Description and Experience treatments cross the risk-uncertainty divide, a possibility that features in our comparisons of Desc with, respectively, E-Amb, E-NR and E-Res. Each of these Experience treatments gives subjects different reasons to be unsure of gamble probabilities at the moment of choice, as explained above.
The design of our Experience treatments bears some noticeable differences from the sampling paradigm. For example, during the sampling phase, subjects explore only one source of uncertainty at a time instead of two. The second option is always a sum of money offered with certainty. Moreover, as we explain below, subjects make repeated choices for each lottery in our decision set - instead of a one-off choice - so that we can infer an indifference between the risky-option and a certain amount. The advantage of these adaptions is that they allow us to elicit a more precise account of subjects’ risk-preferences (see Abdellaoui et al., 2011b for further discussion).
Also, in our design, subjects do not decide when to stop sampling but, instead, draw a fixed number of cards (i.e. all 40 or just 18) from the deck without replacement. This gives us complete control over the information they obtain by sampling. It is interesting to relate our use of this feature, especially when the fixed number is 40, to designs reported by Aydogan and Gao (2020) and Barron and Ursino (2013). We focus on Aydogan and Gao’s “complete sampling paradigm,” but a similar argument applies to the “Experience” treatment of Barron and Ursino’s Experiment 1 which shares some salient features with Aydogan and Gao’s design. In Aydogan and Gao (2020)’s “Description” treatment, subjects were fully informed of the set of balls in an urn; whereas, in their “Sampling” treatment, subjects sampled every ball from the urn one after another. They were not provided with any record of the sampling but were allowed to take their own notes. Therefore, this “Sampling” treatment is a hybrid of our various Experience treatments: a subject who kept a complete record would be in a position akin to our E-Unamb treatment; one who kept no records would be in a position akin to our E-NR treatment; whereas, the position of one who kept an incomplete record (or had less than full confidence in their record) is harder to characterise. Our design gives us more control of the information subjects have in these treatments and, by using four such treatments, enables us to isolate distinct effects in the way we have explained.Footnote 12
3.2 Incentives and other procedures
We now explain how gambles were evaluated by subjects. An example of the evaluation phase is depicted in panel c of Fig. 2. This illustrates one step in the evaluation of a gamble (denoted Option A in this figure) which gives a 10% chance of winning £16 (otherwise zero). Note that while the presentation of probability information on this screen would have differed between treatments, once probability information was acquired, the protocol for evaluation of gambles was essentially the same for all five treatments. Gambles were evaluated by a series of five choices between the gamble and a sure sum of money (such as Option B in the figure). We achieve this by implementing a version of the bisection method of Abdellaoui et al. (2011b) in which sums of money are updated according to the subjects’ previous choice. At the first iteration of each evaluation, the certain amount is set equal to the expected value of the gamble (Option A). In the second iteration, this amount is revised upwards (downwards) to the mid-point of the gamble’s highest (lowest) outcome and the certain amount just rejected (accepted). After the fifth iteration, we impute - for each gamble a subject evaluates - a certainty equivalent that is the certain amount that would have been displayed under Option B if a 6th iteration were to take place.Footnote 13
The set of lotteries evaluated is summarized in the column of Table 1 headed “Risky,” using the notation explained in the legend of the figure. We selected these lotteries in order to comply with the semi-parametric estimation protocol of Cumulative Prospect Theory that was implemented by Abdellaoui et al. (2011b) (see Sect. 3.3.2 for more details). One noticeable adaption from the set of lotteries suggested by Abdellaoui et al. (2011b) is that we increase the number of lotteries involving rare events - a feature that allows us to zoom further into this region of probability weighting.
The order of these lotteries was randomized within two clusters for each subject. Lotteries in the first cluster (\(1.1 - 1.7\)) had varying outcomes but with a winning probability fixed at \(p = 0.25\). To make this common structure clear to subjects in the Experience treatments, this first cluster of lotteries was associated with only one deck and one sampling process. Seven evaluations were then based on that one sampling process. Lotteries in the second cluster (\(2.1 - 2.9\)) had a pair of fixed outcomes and varying probabilities. A subset of this second cluster (\(2.4 - 2.9\)) feature “rare” events which will be important in our analysis. Following the convention in this literature we consider an event rare if its corresponding probability is less than 0.20 (Hertwig et al., 2004). Notice that all of the lotteries with rare events have just one non-zero payoff and sometimes the rare event is associated with the desirable prize [lotteries 2.4, 2.5, 2.6] and sometimes the rare event is undesirable [lotteries 2.7, 2.8, 2.9]. The role of lotteries without rare events will emerge in the next sub-section.
In total, 198 participants were recruited through ORSEE (Greiner, 2015) and randomly assigned to one of the five treatments summarized in Table 1. The experiment was programmed in Z-tree (Fischbacher, 2007) and sessions were conducted in the CeDEx laboratory (University of Nottingham) and lasted for approximately one hour. Subjects’ payments depended on their choices and on gamble resolutions. At the end of the experiment, one choice was selected at random for payment.Footnote 14 If participants had chosen the Safe option, then they would receive the corresponding certain amount. Otherwise, if they had chosen the Risky option, they would play out the lottery, with the outcome determined by the probabilities implied by the relevant colour mix of the cards for the specific lottery. On average, subjects were paid £11.50 including a flat £2 participation fee.
3.3 Methods of analysis
3.3.1 Model-free methods
In the model-free analysis, we make cross-treatment comparisons using tests that do not rely on any particular behavioural or preference model, but instead let the raw choice data speak.
Another important motivation for the model-free analysis is that it allows us to relate our findings to several previous studies that used a similar measurement approach. To facilitate this comparison we use only the data from the first iteration of each bisection in the evaluation phase. This choice-structure is similar to that of the early studies in the sampling paradigm where participants often made one-off choices between the gamble (risky choice) and the certain amount equal to the gamble’s expected value (safe choice). Moreover, as these early studies focused only on situations involving rare events, for comparability, this part of our analysis will focus only on the subset of decision problems involving lotteries containing a rare event (those highlighted grey in Table 1).
We summarise each individual’s behaviour through an overweighting score. The score is constructed, for each individual, based on their evaluations of the six gambles which feature rare events. Consider a binary index: \(C_i\in \{0,1\}\), with i indexing one of the 6 problems in Table 2 that contain a rare event. \(C_i=1\) (0) when the subject’s choice in decision problem i is consistent with overweighting (underweighting) of rare events. A choice is consistent with overweighting when the riskier option is selected (over the safer one) when the rare event was desirable or when the safer option was selected when the riskier alternative featured an undesirable rare event. We then calculate the overweighting score as:
We interpret the %Overweighting score as a measure of the propensity to overweight, which varies from 0 (no choice was consistent with overweighting) to 100 (all choices were consistent with overweighting).Footnote 15 While this index is in some ways simplisticFootnote 16, it is intuitive, does not require committing to any preference model, avoids issues associated with inference from repeated observations, and allows us to benchmark against behaviour reported in earlier literature where the DE gap was established using comparable measures. Using this measure, we test for effects and for DE gaps by comparing the average %Overweighting scores across the individuals facing each relevant treatment.
3.3.2 Model-mediated methods: RDU
To the extent that the DE gap reflects variation in the weighting of events across different environments, it is natural to consider modelling it using theories which, in the tradition of prospect theory, embody a concept of decision weighting. We follow this approach exploiting a simple and now rather standard RDU framework. One important benefit of the model-mediated analysis is that it allows for more refined inferences, e.g. by separating effects that are representable as coming via utility curvature from ones that come through probability weighting. In our design, a second advantage of this level of analysis is that it takes into account a richer information set, incorporating all 5 iterations of the bisection method (instead of only the first one) and more probability targets (instead of only the ones containing a rare outcome). A third benefit is that this analysis facilitates comparison with more recent literature on the DE gap (discussed above) which has exploited related approaches.
To formalise our approach, consider binary lotteries of the form \(x_{E_p}y\) which give one of two monetary outcomes x, y where \(x>y>0\). Outcome x arises in event E which occurs with probability p; otherwise the outcome is y. The rank dependent expected utility of any such lottery is given by the expression:
where \(u(\cdot )\) is a strictly increasing utility function, \(W(\cdot )\) is a weighting function and \(W(E_p)\) is the decision weight associated with event \(E_p\). This model reduces to expected utility theory in the special case where \(W(E_p)=p\), for all events.
To study the DE gap using the RDU model, we follow the source method (Tversky & Fox, 1995; Abdellaoui et al., 2011a) which was specifically adapted for this purpose by Abdellaoui et al. (2011b). A key feature of this approach is to allow weighting functions to depend on the source of uncertainty. So, for example, different weighting functions might apply to decisions under risk than apply under different forms of experienced uncertainty, even if the underlying probability distributions over outcomes are otherwise identical. In our setting, we apply this idea by interpreting our various treatments as potentially different sources.
More formally, for an event \(E_p\), such as drawing a yellow card from a deck in a specific treatment, where \((100 \times p)\%\) of its cards are yellow, the decision weight is given by:
In Eq. (2), \(w_\sigma\) is a source function which transforms probabilities into decision weights according to the source of uncertainty, \(\sigma\). In this expression, \(\pi (\cdot )\) is the individual’s belief of the likelihood of \(E_p\). In line with standard practice, we assume that in Desc, \(\pi (E_p)=p\).
In Experience conditions on the other hand, this belief depends on a variety of other factors, including the relative frequency (\(f_p\)) of each event \(E_p\) that is observed by the individual. Following common practice, we assume that \(\pi (E_p)=f_p\) for decisions from Experience.Footnote 17 Under this assumption, Eq. (2) can be re-written as:
For the three variations of Experience which control for sampling bias we set \(f_p=p\) and so, for these cases, Eq. (3) reduces to:
In our treatment E-Res, \(f_p\ne p\), by construction. Although in principle, operating under Eq. (3) for E-Res could allow us to control out the role of sampling bias, this would defy the purpose of this treatment, i.e., quantifying the effect of sampling bias. Therefore, we choose to operate under Eq. (4) for E-Res too, thereby incorporating a sampling bias of magnitude: \(|p-f_p|\). We return to this point in the Results section.
Though, formally, Eq. (4) gives us decision-weights for the more desirable of each gamble’s outcomes, those weights can only vary across our gambles (within a given treatment) with the probability p of that outcome. Hence, we will use the term “probability-weighting” when we are referring to how the decision-weight varies with p.
In our analysis, we estimate (parametrically) utility curvature first and then calculate (non-parametrically) decision weights at the individual level. The set of gambles in Table 1 is tailor-made for this approach. Following Abdellaoui et al. (2008)’s semi-parametric method for eliciting RDU components, we use the seven certainty equivalents elicited from evaluations of risky options in problems \(1.1 - 1.7\) to fit the utility curvature parameter of a power utility function: \(u(x)=x^\alpha\). We do so by minimizing: \(\sum _{j=1}^{7}(z_j-\hat{z_j})^2\), where \(z_j\) and and \(\hat{z_j}\) are, respectively, the observed and estimated certainty equivalents for decision problem 1.j, with j ranging from 1 to 7. Using Eq. (1), the power utility function and the fact that the probability of the better outcome of the lottery is 0.25 in all of problems \(j=1,\dots ,7\), we obtain the following expression for \(\hat{z_j}\) which we can use to estimate \(\alpha\) for every subject:
Hence, we can treat the corresponding decision weight: \(W(E_{0.25})\) as a free parameter to be estimated together with the utility curvature parameter: \(\alpha\).
Having obtained an estimate of each subject’s utility curvature, we proceed to calculate (i.e. non-parametrically) decision-weights for the risky options in 2.1 - 2.9. Notice that these options have fixed outcomes: \(x^*=16\) and \(y^*=0\) and varying probability: \(p_r\), with r indexing the risky option in decision problems 2.1 - 2.9. Using Eq. (5), we can therefore calculate the decision weight for the better outcome of each risky option, given the probability level \(p_r\) of the event on which it is considered, obtaining:
where \(z_r^{'}\) is the elicited certainty equivalent for risky option r (\(r=1, 2,\dots ,9\)).
Taking the median weight across individuals, we obtain an aggregated source function for each treatment. By studying the shape of the elicited weighting curves and comparing them across treatments, we examine the DE gap and its driving forces from the perspective of a model that allows for probability weighting. This combination, derived from Abdellaoui et al. (2008); Abdellaoui et al. (2011b) and explained above, allows us to control for utility curvature while letting the data speak on the exact form of probability-weighting in different treatments (without any commitments to functional forms).
4 Results
4.1 Model-free analysis
We begin our analysis by examining choice proportions through the lens of the %Overweighting scores. Recall that these scores derive from choices made in the first iteration of each bisection process and, in line with the discussion of Sect. 3.3.1, we interpret the average %Overweighting for each treatment as representing a treatment-level propensity to overweight rare events. The results are presented in Fig. 3.
We highlight three features of the data evident from the barplot of Fig. 3. First, and in line with the canonical finding, the propensity to overweight is higher in Desc than in any variant of Experience. Second, the %Overweighting scores (depicted at top of each bar) fall as we introduce extra features of “Experience” one by one along the two branches away from Desc in Fig. 1: Desc \(\longrightarrow\) E-Unamb \(\longrightarrow\) E-NR; and Desc \(\longrightarrow\) E-Unamb \(\longrightarrow\) E-Amb \(\longrightarrow\) E-Res. This is consistent with each extra feature expanding the DE gap. We explore the statistical significance of these changes below. Finally, a third salient feature of Fig. 3 is the comparatively low score for E-Under: this is consistent with the intuition that rare-events carry less weight in decisions from Experience, when they are under-represented in the sample.Footnote 18
The Table in the bottom half of Fig. 3 details the size and statistical significance of the various DE gaps and effects that our experiment was designed to measure. Its top row reports the overall average DE gap in our experiment by comparing Desc vs E-All. This measure of the gap is statistically significant (p-value \(= 0.041\); MW) and its size at 9.35 percentage points is very close to the literature’s average of 9.7 percentage points, based on a large meta-analysis from 80 data sets (Wulff et al., 2018). We view this close correspondence to the reported central tendency of existing evidence as a reassuring indication that we are capturing a familiar DE gap in our experimental setup. In line with the canonical finding, we find less overweighting of rare events in Experience than in Description. These observations lead to Result 1.
Result 1
We replicate a DE gap. It has the same direction as the canonical finding and, in terms of the %Overweighting measure, a very similar size to the literature’s average.
The next six rows of Fig. 1 test for a set of DE gaps via pairwise comparisons of the %Overweighting score for Desc with each of the individual Experience treatments including the two sampling bias derivatives (E-Over and E-Under). Across these comparisons, statistically significant differences are identified only in cases where sampling bias is present (i.e., the cases involving E-Res and E-Under). Not surprisingly, the gap is widest when rare events are under-represented rather than when they are over-represented. In comparisons that do not involve sampling bias (i.e., those comparing Desc with each of E-Unamb, E-NR or E-Amb), while the direction of each effect is in the typical direction of the DE gap, we find no statistically significant differences, although the comparison between Desc and E-NR is slightly bigger in magnitude than the literature average gap.
The bottom section of the table in Fig. 3 provides analogous tests, but focussing on treatment comparisons capturing effects associated with specific mechanisms as summarised in Fig. 1. Based on this analysis, while each factor again moves the average %Overweighting in the direction consistent with the canonical finding, the only statistically significant effect is that of under-representation - where the effect is both large and highly significant.Footnote 19 This leads to our second main result.
Result 2
The most important single driver of the DE gap in our data is sampling bias, in the form of under-representation of rare events.
While the results we have presented so far are consistent with claims made elsewhere (e.g. Fox & Hadar, 2006; Rakow et al., 2008) to the effect that sampling bias is the predominant driver of the gap, we hold short of such a firm conclusion at this point for two reasons. First, while no factor other than sampling bias was statistically significant in isolation, the measured DE gap nevertheless consistently widens with each factor introduced in our design. That is, the difference in %Overweighting is positive for each gap and effect reported in the table of Fig. 3, with the exception of over-representation where we expect an opposing effect. Moreover, combinations of other factors sometimes come close to producing a significant change in the gap (see the comparison between Desc and E-NR, which captures the combination of likelihood representation and memory). This suggests the DE gap might be partly driven by a range of other factors beyond sampling bias, even if these are relatively weak when operating in isolation. Second, in the next section we present a model-mediated analysis which involves a different and more detailed examination of the DE gap and its underpinning causes. We turn to this analysis now.
4.2 Model-mediated analysis
In this analysis, we use certainty equivalents derived from the bisection elicitation process to estimate a best fitting RDU model for each individual. We obtain parametric estimates for the utility curvature first (as per Eq. 5) and then calculate -non-parametrically- decision weights (as per Eq. 6).
Table 2 reports median values for the utility curvature parameter (\(\alpha\)) across treatments. In aggregate, our estimations suggest near linear utility over money which is a not-uncommon finding.Footnote 20 Median values are very similar across treatments and a Kruskal-Wallis test does not reject the null hypothesis of equal utility curvature across treatments (p-value \(= 0.708\)). Despite this, the size of the interquartile ranges (IQR) suggests that there was considerable heterogeneity of utility curvatures across individuals - a result that demonstrates the importance of our having controlled for this when assessing probability-weighting. We also consistently fail to reject the null of no difference in utility curvature in pairwise comparisons of treatments.Footnote 21 This suggests that potential treatment effects are more likely to occur due to differences in probability weighting rather than due to differences in preferences over money.
Next, we calculate decision weights \(W(E_{p_r})\) for each subject at each probability level \(p_r\), following Eq. (6). Median values for these decision weights are reported in Table 3.
In this table, we use upward sloping arrows to indicate cases where estimated decision weights are statistically significantly above the diagonal line (i.e. the line consistent with linear decision weights where \(W(E_{p_r})=p_r\) for all events, where EUT coincides with RDU), and we use downward arrows to indicate cases where weights are significantly below the diagonal (in each case, the number of arrows indicates the critical value). The shaded cells highlight cases where weights do not deviate significantly from the diagonal. Although unconventional, this labelling makes it easy to see that, if we confine attention to cases that control for sampling bias (i.e. the first 4 of the 8 data columns in Table 3), then probability weighting generally takes an inverse S-shape: weights tend to be above the diagonal for small probabilities and below them for high probabilities with a cross-over at, or in the vicinity of, \(p = 0.25\).Footnote 22 This inverse S-shaped probability weighting is consistent with a general tendency to overweight rare events.Footnote 23 This leads to Result 3.
Result 3
Controlling for sampling bias and utility curvature, probability weighting is generally inverse S-shaped, consistent with overweighting of rare events in both Description and Experience.
Things look different when we consider cases with potential for sampling bias. In particular, E-Under stands out by having a pattern of median weights consistent with an S-shaped weighting function: for low probabilities, median weights are nominally below the diagonal, rising above it for high probabilities. If we confine attention to the analysis of statistical significance, however, almost none of the weights associated with rare events depart significantly from the diagonal; and hence, an interpretation of this analysis is that sampling bias is counteracting an underlying behavioural tendency to overweight rare events. That is, the overweighting is a property of preferences that is disguised by the sampling bias.
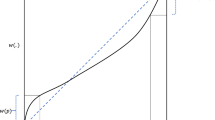
We complement the analysis of Table 3 by providing a visualisation of the weighting functions implied by the weights reported there by fitting a parametric weighting function to the set of median decision weights for each treatment, using the linear-in-log-odds specification of the weighting curve (Goldstein & Einhorn, 1987; Gonzalez & Wu, 1999):
In this specification, the parameter \(\delta\) is largely responsible for the elevation of the curve and \(\gamma\) for its curvature (Gonzalez & Wu, 1999). When \(\gamma <1\), the weighting function takes its characteristic inverse S-shape, suggesting overweighting of rare events. As \(\gamma\) approaches the value 1, the weighting curve becomes increasingly linear. Finally, values where \(\gamma >1\) suggest an S-shaped curve that is consistent with underweighting of rare events.
The fitted functions are presented in Fig. 4 where each of the seven panels provides a comparison of a pair of functions, thereby giving a qualitative impression of the impact of an individual factor manipulated in our design. We also include a comparison of Desc versus E-all for completeness. The top three panels use data from treatments which control for sampling bias and show the impacts of, respectively, likelihood representation, ambiguity, and memory. The top left panel reveals that the treatments Desc and E-Unamb generate almost identical inverse-S functions; hence our treatment manipulation capturing the impact of likelihood representation has no discernible impact on the fitted function. The middle and rightmost panels of the top row both use E-Unamb as a benchmark: the introduction of ambiguity (middle panel) slightly depresses the revealed weighting function throughout much of its range. The impact of removing the memory aid (history table) in our design, depresses weights more markedly (top right panel).
The bottom three panels provide a similar exercise but focused on the impact of sampling bias. Here we highlight, in particular, the impact of under-representation of rare events: in line with the discussion of Table 3, relative to the E-Amb treatment, we see the under-representation of rare events reducing the weights associated with both desirable and undesirable rare events (i.e. the weighting function for E-Under lies below the E-Amb function for low probabilities and above it for high ones). Finally, the comparison in the central panel, capturing the visual effect of the average DE gap, provides support for the “relative underweighting hypothesis” (Kopsacheilis, 2018). Although both weighting functions are inverse S-shaped, that of E-All exhibits less overweighting - i.e, it is closer to the diagonal - when compared to Desc for small enough and high enough probabilities.
An obvious question is how far the suggestion of treatment differences is supported by more formal statistical analysis. We address this via Table 4 which reports the p-values from a series of 2-tailed Mann-Whitney (MW) U tests. The set of tests mirrors the structure of the treatment-level comparisons presented in Fig. 3: we compare the same pairs of treatments testing for gaps and effects, but we use the RDU approach to conduct a series of tests at each probability level for every treatment comparison.
We highlight three main observations based on this analysis. First, considering the bottom half of the table which tests the impact of individual factors operating in isolation, we corroborate the finding of our model-free analysis that sampling bias, in the form of under-representation of rare events, has a major impact on the revealed weights. Second, and again in line with the model-free analysis, the bottom half of the table shows little evidence to support the impact of any factor beyond sampling bias.Footnote 24 Third, the RDU analysis presented above offers some new insights too. Based on the results presented in the top half of Table 4, we now can detect a significant DE gap in some cases where there was no sampling bias. Specifically, we find evidence of a significant gap in the comparison of Desc vs E-NR for small values of p (desirable rare events). This confirms the visual impression (from top right panel of Fig. 4) that desirable rare events receive lower weights in treatment E-NR relative to E-Unamb and Desc (the latter two functions being almost identical). We take these results as indicating that there may be a replicable effect worthy of further investigation. On that assumption, it is helpful to reflect on the differences in weighting between Desc and E-NR.
Referring back to Fig. 1, note that we get from Desc to E-NR in two steps: one changes the likelihood representation; the other removes the history table. The evidence presented in Fig. 4 and Table 4 provides tentative support for thinking that the removal of the history table may be the more important of the two manipulations: memory has a more marked effect on the shape of the weighting functions (comparing top left and top right panels of Fig. 4) and in the bottom of Table 4, the memory effect in isolation does reach significance at 5% at one probability level (p = 0.1). As noted earlier, removal of the history table may be interpreted as not purely cognitive if subjects are aware of their forgetfulness and react to the resulting ambiguity. Hence, to the extent that removing the history table has a genuinely distinct effect, we are not entitled to interpret it as a purely cognitive one, as there may be some preference component too. This leads to Result 4.
Result 4
We find some evidence that there are factors other than sampling bias that contribute to the DE gap. These factors are most clearly seen when our memory aide is removed and, thus, involve cognitive factors and responses to them.
5 Conclusion
Past research has consistently demonstrated that revealed risk preferences vary according to whether risky options that decision makers face are described or experienced: that is, there is a Description-Experience (DE) gap. Yet the causes, nature, size - and even the direction - of the DE gap remain matters of ongoing debate.
This study was designed to provide an integrated investigation of three types of factor whose influences may contribute to the DE gap: probability information (which may differ according to whether experienced risks display sampling bias); ambiguity sensitive preferences; and cognitive factors (responses to likelihood representation and memory constraints). We implemented an experiment designed to isolate the separate impacts of these factors; and measured their effects using two different approaches - a model-free one and a parametric one based on the Rank Dependent Expected Utility (RDU) model - allowing us to map our results to those reported in different branches of the extant literature.
Reassuringly, our model-free analysis finds an average DE gap very similar in size and direction to the average across studies reported in a recent meta-analysis (Wulff et al., 2018). While each causal factor that we isolate contributes positively to the DE gap, the only one whose effect is statistically significant when considered in isolation is sampling bias due to under-representation of rare events. If this were the full explanation for the DE gap, its implications for core risk preference models would be limited: though the gap would have important implications for how to apply them in settings where sampling bias might arise, those models would not require revision, at the theoretical level, in order to accommodate it. From some perspectives, this might seem a convenient conclusion. Yet, we cannot endorse it unreservedly because, though preference and cognitive factors left only faint traces in our data, when considered in isolation, we still detected effects when multiple factors could operate in tandem, especially when memory limitations were potentially at play. While these effects are modest in our data, they were detectable and it would be naive to assume they would always be negligible across all contexts of interest, especially given the totality of other evidence considered in Sect. 2.
Using the RDU approach, we established that the DE gap operates mainly via its impact on probability-weighting functions, rather than on utility curvature. Though we found variation in probability-weighting functions across our treatments, we also found that, in all those conditions that control for sampling bias, probability-weighting was inverse S-shaped. This is consistent with over-weighting of rare events in both Description and Experience conditions. More specifically, our analysis of probability-weighting is consistent with the “relative underweighting hypothesis” (Kopsacheilis, 2018) whereby rare events are over-weighted in Experience, but less so than in Description. In contrast with interpretations of the DE gap common in the earlier literature, it strengthens the accumulating recent evidence that overweighting of rare events generalises beyond the domain of described risks, even in the presence of a DE Gap (Glöckner et al., 2016; Kopsacheilis, 2018; Aydogan & Gao, 2020).
The finding of consistently inverse-S shaped weighting in the absence of sampling bias coheres with the interpretation that overweighting of rare events is a robust feature of preferences which sampling bias -in the form of under-representation of rare events and possibly reinforced by memory limitations - has some tendency to offset. In principle, this means that the probability-weighting curve resulting from a small sample could become indistinguishable from the diagonal in the vicinity of rare events (as in our E-Under treatment). While this might tempt speculation that overweighting (as captured by several non-expected utility models such as Prospect Theory) originates as an evolved response to the problem of under-sampling (or recalling) rare events, caution is required as our evidence is only supportive of the two biases cancelling out under quite particular circumstances and so does not license any general cancelling-out claim.
The sensitivity of revealed risk preference to whether information about uncertainty is obtained from descriptions or experience has intriguing implications. For example, outside the laboratory, the potentially available information often combines elements from both types of source; and the mix of the two types is not always fixed. The latter point opens the way for manipulation of behaviour, for good or ill, by firms, organisations or policy-makers hoping to “nudge” citizens, by influencing the form of information they have. People also make choices for themselves that influence the mix of description and experience they will be exposed to, with consequences they may or may not foresee.
Data Availability
Data and other additional materials are available at https://osf.io/frsa9/.
Notes
Our study is the first to consider all four of the causal mechanisms in a single experimental design. However, using multiple measurement approaches is an ambition shared by other recent papers. One example is Aydogan and Gao (2020), which prefaces an “individual data” analysis of probability-weighting functions with an “aggregate data” analysis based on choice frequencies. Yet, their aggregate analysis is not entirely model-free, as it uses a model to control for utility curvature. In contrast, as we explain later in this paper, our first mode of analysis uses no preference model at all, while our second one includes utility curvature among other model-parameters.
Note, however, that this is not the only paradigm. One notable alternative to the “sampling paradigm” is the “partial feedback paradigm” (Barron & Erev, 2003) where participants in Experience make repeated instead of one-off choices between safer and riskier options.
Here, and unless otherwise stated, we use “Description” to refer to cases where there is a unique and complete description of the set of payoffs and their probabilities for each gamble. However, other lines of research have considered other possibilities, such as: imprecise descriptions of probabilities in Ellsbergian investigations of ambiguity (e.g. Trautmann & Van De Kuilen, 2015); or multiple, competing, descriptions in studies of risk perception (e.g. Viscusi & Magat, 1992; Viscusi, 1997).
As a simple demonstration, consider drawing a single ball from an urn that contains 90 black and 10 red balls. On average, red balls will be under-represented in 90% of such single-observation (small) samples.
See Etner et al. (2012) for a review of the theoretical literature on modelling ambiguity sensitive preferences.
See Trautmann and Van De Kuilen (2015) for a recent review of the subsequent literature.
Each gamble’s outcomes are demarcated by a different pair of colours - Fig. 2 displays one such pair. The correspendence between colours and outcomes for each lottery was randomized for each subject. This was done to avoid systematic influence of connotations associated with particular colours such as “danger” with red or “environmental risk” with green. Moreover, the order of cards within each sample from each deck was randomised by subject.
See "Instructions" section in Appendix for details of instructions.
As will become clearer in the following subsection, the set of objective probabilities that we chose for this study cannot be accurately represented in samples of 18 observations.
There is one exception. For the one 50-50 gamble, we classify the observation according to the observed relative frequency of the event corresponding to the better outcome.
To illustrate the possible significance of this, note that Aydogan and Gao (2020) interpret their investigation as one of a DE gap in the domain of risk; yet, as acknowledged in their fn. 3 and Section 6.2, this relies on their subjects recording (or recalling) all the balls they sampled - a condition which their online archive of subjects’ notes supports for some subjects, but not for others. In contrast, our interpretations only rely on subjects having a full record of sampling in cases where the history table gave them such a record.
See Table 5 in the "Bisection method" section of the Appendix for a demonstration.
Glöckner et al. (2016) refer to the same index as p(overweighting) and interpret it as the probability of making a choice consistent with overweighting.
We are not entitled to assume that choices consistent with overweighting are fully explained by overweighting as other factors may be at work.
Previous papers that operate under the same assumption include Fox and Hadar (2006), Hadar and Fox (2009) and Abdellaoui et al. (2011b). Moreover, Fox and Hadar (2006) report a very high correlation (0.97) between experienced and judged probabilities. Aydogan (2021) offers an interesting examination of this assumption.
See Table 6 in the "Sampling Bias" section in the Appendix for more details on sampling bias.
We confirm this pattern of findings with a robustness check using a different, but conceptually similar, model-free overweighting index (see the section: An alternative model-free measure to %Overweighting in the Appendix). Although not directly comparable to previous literature, this alternative measure exploits data from all five iterations. We thank an anonymous referee for suggesting this additional form of analysis.
See "Utility curvature" section in the Appendix for more details on these tests (Tables 7 and 8) and for a plot of all subjects’ utility curves (Fig. 5).
Note that only one of the 36 cells in these four columns of data - that associated with E-NR for \(p=0.025\) - is inconsistent with this inverse-s pattern.
Recall that rare events lie in two sets: for \(p \in \{0.025, 0.05, 0.10\}\) and for \(p\in \{0.90, 0.95, 0.975\}\). As p is the probability of the better outcomes, rare events in the first set have desirable outcomes; rare events in the second set have undesirable outcomes.
Except for the role of Memory when p=0.10, no other factor registers a statistically significant effect.
The italicised text was present on in E-Unamb and E-NR, where there was no ambiguity regarding the representativeness of the sampled cards. In E-Amb and E-Res this message was replaced by the following: “However by the end of this process you will have discovered something more about this mix because you will have seen a selection of draws from that deck”. All references to seeing or exploring “all” cards were replaced appropriately in E-Amb and E-Res.
References to this “History Table” did not feature in E-NR where there was no such visual aid.
References
Abdellaoui, M. (2000). Parameter-free elicitation of utility and probability weighting functions. Management Science, 46, 1497–1512.
Abdellaoui, M., Baillon, A., Placido, L., & Wakker, P. P. (2011a). The rich domain of uncertainty: Source functions and their experimental implementation. American Economic Review, 101, 695–723.
Abdellaoui, M., Bleichrodt, H., & L’Haridon, O. (2008). A tractable method to measure utility and loss aversion under prospect theory. Journal of Risk and Uncertainty, 36, 245.
Abdellaoui, M., L’Haridon, O., & Paraschiv, C. (2011b). Experienced vs. described uncertainty: Do we need two prospect theory specifications? Management Science, 57, 1879–1895.
Aydogan, I. (2021). Prior beliefs and ambiguity attitudes in decision from experience. Management Science, Articles in Advance.
Aydogan, I., & Gao, Y. (2020). Experience and rationality under risk: Re-examining the impact of sampling experience. Experimental Economics, 23, 1100–1128.
Bardsley, N., Cubitt, R., Loomes, G., Moffatt, P., Starmer, C., & Sugden, R. (2010). Experimental economics: Rethinking the rules. Princeton University Press.
Barron, G., & Erev, I. (2003). Small feedback-based decisions and their limited correspondence to description-based decisions. Journal of Behavioral Decision Making, 16, 215–233.
Barron, G., & Ursino, G. (2013). Underweighting rare events in experience based decisions: Beyond sample error. Journal of Economic Psychology, 39, 278–286.
Bates, D., Chambers, J., & Hastie, T. (1992). Statistical models in s. In Computation Science and Statistics Proceedings of the 19th Symposium on the Interface. Wadsworth & Brooks California.
Bates, D. M., & Watts, D. G. (1988). Nonlinear regression analysis and its applications 2. New York: Wiley.
Booij, A. S., Van Praag, B. M., & Van De Kuilen, G. (2010). A parametric analysis of prospect theory’s functionals for the general population. Theory and Decision, 68, 115–148.
Cubitt, R. P., Starmer, C., & Sugden, R. (1998). On the validity of the random lottery incentive system. Experimental Economics, 1, 115–131.
Ellsberg, D. (1961). Risk, ambiguity, and the Savage axioms. The Quarterly Journal of Economics, 75, 643–669.
Etchart-Vincent, N. (2004). Is probability weighting sensitive to the magnitude of consequences? An experimental investigation on losses. Journal of Risk and Uncertainty, 28, 217–235.
Etner, J., Jeleva, M., & Tallon, J.-M. (2012). Decision theory under ambiguity. Journal of Economic Surveys, 26, 234–270.
Fischbacher, U. (2007). Z-tree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10, 171–178.
Fox, C. R., & Hadar, L. (2006). "Decisions from experience" = sampling error + prospect theory: Reconsidering Hertwig, Barron, Weber & Erev (2004). Judgment and Decision Making, 1, 159–161.
Frey, R., Mata, R., & Hertwig, R. (2015). The role of cognitive abilities in decisions from experience: Age differences emerge as a function of choice set size. Cognition, 142, 60–80.
Gigerenzer, G., & Hoffrage, U. (1995). How to improve Bayesian reasoning without instruction: Frequency formats. Psychological Review, 102, 684–704.
Glöckner, A., Hilbig, B. E., Henninger, F., & Fiedler, S. (2016). The reversed description-experience gap: Disentangling sources of presentation format effects in risky choice. Journal of Experimental Psychology: General, 145, 486–508.
Goldstein, W. M., & Einhorn, H. J. (1987). Expression theory and the preference reversal phenomena. Psychological Review, 94, 236–254.
Gonzalez, R., & Wu, G. (1999). On the shape of the probability weighting function. Cognitive Psychology, 38, 129–166.
Greiner, B. (2015). Subject pool recruitment procedures: Organizing experiments with ORSEE. Journal of the Economic Science Association, 1, 114–125.
Hadar, L., & Fox, C. R. (2009). Information asymmetry in decision from description versus decision from experience. Judgment and Decision Making, 4, 317.
Hau, R., Pleskac, T. J., & Hertwig, R. (2010). Decisions from experience and statistical probabilities: Why they trigger different choices than a priori probabilities. Journal of Behavioral Decision Making, 23, 48–68.
Hau, R., Pleskac, T. J., Kiefer, J., & Hertwig, R. (2008). The description-experience gap in risky choice: The role of sample size and experienced probabilities. Journal of Behavioral Decision Making, 21, 493–518.
Hertwig, R., Barron, G., Weber, E. U., & Erev, I. (2004). Decisions from experience and the effect of rare events in risky choice. Psychological Science, 15, 534–539.
Hills, T. T., & Hertwig, R. (2010). Information search in decisions from experience: Do our patterns of sampling foreshadow our decisions? Psychological Science, 21, 1787–1792.
Kemel, E., & Travers, M. (2016). Comparing attitudes toward time and toward money in experience-based decisions. Theory and Decision, 80, 71–100.
Knight, F. H. (1921). Cost of production and price over long and short periods. Journal of Political Economy, 29, 304–335.
Kopsacheilis, O. (2018). The role of information search and its influence on risk preferences. Theory and Decision, 84, 311–339.
Moré, J. J. (1978). The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical analysis (pp. 105–116). Springer.
Murad, Z., Sefton, M., & Starmer, C. (2016). How do risk attitudes affect measured confidence? Journal of Risk and Uncertainty, 52, 21–46.
Quiggin, J. (1982). A theory of anticipated utility. Journal of Economic Behavior & Organization, 3, 323–343.
Rakow, T., Demes, K. A., & Newell, B. R. (2008). Biased samples not mode of presentation: Re-examining the apparent underweighting of rare events in experience-based choice. Organizational Behavior and Human Decision Processes, 106, 168–179.
Slovic, P., Monahan, J., & MacGregor, D. G. (2000). Violence risk assessment and risk communication: The effects of using actual cases, providing instruction, and employing probability versus frequency formats. Law and Human Behavior, 24, 271–296.
Trautmann, S. T., & van de Kuilen, G. (2015). Ambiguity attitudes. In G. Keren, & G. Wu (Eds.), The Wiley Blackwell handbook of judgment and decision making (Vol. 1, pp. 89–116). John Wiley & Sons, Ltd.
Tversky, A., & Fox, C. R. (1995). Weighing risk and uncertainty. Psychological Review, 102, 269–283.
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–323.
Ungemach, C., Chater, N., & Stewart, N. (2009). Are probabilities overweighted or underweighted when rare outcomes are experienced (rarely)? Psychological Science, 20, 473–479.
Viscusi, W. K. (1997). Alarmist decisions with divergent risk information. The Economic Journal, 107, 1657–1670.
Viscusi, W. K., & Magat, W. A. (1992). Bayesian decisions with ambiguous belief aversion. Journal of Risk and Uncertainty, 5, 371–387.
Wakker, P. P. (2010). Prospect Theory: For Risk and Ambiguity. Cambridge University Press.
Weber, E. U., Shafir, S., & Blais, A.-R. (2004). Predicting risk sensitivity in humans and lower animals: Risk as variance or coefficient of variation. Psychological Review, 111, 430–445.
Wulff, D. U., Mergenthaler-Canseco, M., & Hertwig, R. (2018). A meta-analytic review of two modes of learning and the description-experience gap. Psychological Bulletin, 144, 140–176.
Acknowledgements
We thank Mohammed Abdellaoui, Simon Gaechter, an anonymous referee and the editor as well as participants in various conferences and workshops for useful comments. The research was supported by the Economic and Social Research Council [grant numbers ES/K002201/1, ES/P008976/1].
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Instructions
Instructions were handed to participants in printed form and were read out loud by the experimenter prior to the start of the experiment. Before the start of the experiment and after the instructions had been read out loud, subjects played one trial round.
1.1.1 Instructions for Description
In this study you are asked to make choices that involve lotteries. For each choice, just pick the option you prefer as there are no “right” or “wrong” answers. Overall you are going to consider a total of 19 lotteries which are described by virtual decks of cards. Each deck contains exactly two types of cards represented by two different colours. Each deck has its own mix of these two types of cards.
The information about the relative frequency and the monetary value of each type of card will be provided to you (in the form of percentages) prior to making a choice. This information is seen on the bottom of the screen.
The first 7 lotteries are all associated with the same deck of cards. This guarantees that the relative frequency of each colour is the same for Lotteries 1 to 7. Notice however that the rewards associated with each outcome will differ from one lottery to another.
Later in the experiment, you may have the opportunity to “play” a lottery. That would mean drawing once more from a deck you have sampled and receiving the sum of money assigned to the colour of the drawn card.
Your task is to choose each time between playing the Lottery and receiving the Certain Outcome. Each Lottery entails 5 such choices between the Lottery (Option A) which remains constant across these 5 Choice-Rounds and a Certain Outcome (Option B) that will be changing from each choice to the next.
Payoff Stage
At the end of the experiment one choice is going to be randomly selected to be played out for real. All choices are equally likely to be drawn so each choice you make has equal chances of affecting your final payment. There are two cases:
Case 1: If in the randomly selected choice you chose Option B (the Certain Outcome) then the monetary value of this choice is going to be added directly to your final payment.
Case 2: If in the randomly selected choice you chose Option A (the Lottery) then the deck of cards corresponding to that choice will reappear on the screen. You will then be asked to draw one card from it. Then the monetary value assigned to the colour of the card you just drew will be added to your final payment.
1.1.2 Instructions for the E-Unamb version of Experience
In this study you are asked to make choices that involve lotteries. For each choice, just pick the option you prefer as there are no “right” or “wrong” answers. Overall you are going to consider a total of 19 lotteries which are described by virtual decks of cards. Each deck contains exactly two types of cards, represented by two different colours. Each deck has its own mix of these two types of cards.
For every lottery you go through two stages:
Stage 1: the “Sampling Stage”
Stage 2: the “Choice Stage”
Exception: The first 7 Lotteries all share the same “Sampling Stage” because they relate to the same deck. This means that you will only sample once for the first seven lotteries. Each of the lotteries 8 - 24 has its own Sampling Stage (because it relates to its own deck).
Stage 1: “Sampling Stage”
In each Sampling Stage you go through a particular computerized deck and explore one by one all of their cards. The information about the relative frequency of each type of card is unknown to you prior to the start of the sampling process. However by the end of the process, this information will be completely revealed to you as you will have seen every card in the deck exactly once.Footnote 25 As mentioned earlier, the first 7 lotteries relate to the same deck. This guarantees that the relative frequency of each colour is the same for Lotteries 1 to 7. We recommend that you pay attention during this sampling process as this information is relevant for your decisions later on and hence your final payment.
Every time you click on the “Draw” button you will observe a new card from the deck. Once you observe its colour click on “Proceed with the next card” for the “Draw” button to reappear. You will repeat this process until you go exactly once through all the cards in each deck. Once you have done so, a message will appear on the screen verifying that you have seen all the cards in this deck and a button that reads: “Go to the Choice Stage” will become accessible at the bottom of the screen. Once you click on that button you will move on to the “Choice Stage”.
Stage 2: "Choice Stage"
At this stage a monetary value is assigned to the colour of each card. This information is seen on the bottom of the screen. Later in the experiment, you may have the opportunity to “play” a lottery. That would mean drawing once more from a deck you have sampled and receiving the sum of money assigned to the colour of the drawn card.
On the top of the screen you will observe a “History Table” where you can track your sampling history from each lottery’s “Sampling Stage.” As mentioned earlier, the first 7 lotteries are all associated with the same deck of cards and hence share the same “History Table.”Footnote 26Notice however that although the relative frequency of each colour of card is the same for lotteries 1 to 7, the rewards associated with each outcome will differ from one lottery to another.
Your task in this stage is to choose each time between playing the Lottery and receiving the Certain Outcome. Each Lottery entails 5 such choices between the Lottery (Option A) which remains constant across these 5 Choice-Rounds and a Certain Outcome (Option B) that will be changing from each choice to the next.
Payoff Stage
At the end of the experiment one choice is going to be randomly selected to be played out for real. All choices are equally likely to be drawn so each choice you make has equal chances of affecting your final payment. There are two cases:
Case 1: If in the randomly selected choice you chose Option B (the Certain Outcome) then the monetary value of this choice is going to be added directly to your final payment.
Case 2: If in the randomly selected choice you chose Option A (the Lottery) then the deck of cards corresponding to that choice will reappear on the screen. You will then be asked to draw one card from it. Then the monetary value assigned to the colour of the card you just drew will be added to your final payment.
1.2 Bisection method
The following illustrative choices demonstrate an example of the bisection process for the lottery: (16, 0.1; 0). Illustrative choices are represented in bold. The elicited CE for the process of this example will be the mid-point between 0.7 (the last certain outcome preferred over the lottery) and 0.6 (the last certain outcome that the lottery was preferred over). This yields a CE equal to 0.65.
1.3 Sampling bias
1.4 Utility curvature
1.5 An alternative model-free measure to %Overweighting
We provide here a supplementary analysis related to Result 2, based on an alternative, model-free index to %Overweighting, namely, the “Overweighting_RiskPremium” index. It is constructed as the difference between the elicited certainty equivalent and the expected value of the lottery when the rare event is desirable (\(CE-EV\); positive risk premium) and the difference between the expected value of the lottery and the certainty equivalent when the rare event is undesirable (\(EV-CE\); negative risk premium). Like the %Overweighting index, the Overweighting_RiskPremium index can be interpreted as a measure of overweighting of the rare event. While this alternative index retains the attraction of being model-free (by using only raw data and a property of the gamble), it differs from %Overweighting in using using choices from all iterations of the bisection method instead of only the first one.
Although our use of %Overweighting in the main text enabled Result 1 to link to model-free analyses in previous literature, the alternative measure considered here permits an important robustness check for Result 2. As Table 9 demonstrates, using this alternative measure leaves unchanged the conclusion that the only statistically significant driver of the DE gap in our data, is sampling bias, in the form of under-representation of rare events.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cubitt, R., Kopsacheilis, O. & Starmer, C. An inquiry into the nature and causes of the Description - Experience gap. J Risk Uncertain 65, 105–137 (2022). https://doi.org/10.1007/s11166-022-09393-w
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11166-022-09393-w
Keywords
- Decisions from Description
- Decisions from Experience
- Risk preferences
- Cumulative prospect theory
- Ambiguity