Strength of preference and decisions under risk

Abstract

Influential economic approaches as random utility models assume a monotonic relation between choice frequencies and “strength of preference,” in line with widespread evidence from the cognitive sciences, which also document an inverse relation to response times. However, for economic decisions under risk, these effects are largely untested, because models used to fit data assume them. Further, the dimension underlying strength of preference remains unclear in economics, with candidates including payoff-irrelevant numerical magnitudes. We provide a systematic, out-of-sample empirical validation of these relations (both for choices and response times) relying on both a new experimental design and simulations.

1 Introduction

Economics has by now embraced the view that economic choices are subject to noise (e.g., McFadden, 2001). Research in stochastic choice has provided extensive evidence that human beings often make different choices even when repeatedly confronted with the same set of options¹ (e.g., Hey & Orme, 1994; Ballinger & Wilcox, 1997; Agranov & Ortoleva, 2017). There is, however, no universally-accepted view on the origins and determinants of noise or errors in economic decision making.² How often do economic agents make mistakes, and what does the number of mistakes depend on?

The key question is whether error rates are associated with directly or indirectly measurable economic variables. Evidence from other disciplines suggests so. In the domain of psychophysics, decades of research have concentrated on perceptual discrimination tasks, where two stimuli are presented and human participants are asked to estimate which one scores higher along an objective scale, for instance which of two sounds is louder, which of two lights is brighter, or which of two lines is longer. In such simple tasks, there is an objective, direct measure of choice difficulty: choices become gradually harder as the difference between the stimuli becomes smaller (along the objective scale). There are two firmly-established stylized facts in this literature. The first is that the percentage of correct choices is strictly decreasing with choice difficulty, that is, error rates are larger when stimuli are more similar (Laming, 1985; Klein, 2001; Wichmann & Hill, 2001). The second is that choices are slower for harder choices, that is, response times are larger when the stimuli are more similar (Dashiell, 1937; Moyer & Landauer, 1967).

In this work, we ask the question of whether these gradual effects are relevant for economic choices and, if so, which economic variables do determine them. This question is obviously important for conceptual reasons, as the phenomena we discuss imply a cardinal effect of economic variables on choices, as opposed to the classical, purely-ordinal view of preferences.

Our main contribution is to empirically demonstrate the gradual relation between underlying economic variables (specifically, differences in expected utilities) and both choice frequencies and response times relying in a confound-free, out-of-sample approach. Previous work has already pointed at these relationships, starting with Mosteller and Nogee (1951). However, those works have typically employed within-sample, fitting approaches which are not appropriate to test the basic hypothesis that gradual effects exist. The reason is that the estimation method transforming utility differences into economic choices might create apparent regularities where none exists. After all, a monotonic relation between utility differences and error rates is already implicit in random utility models of stochastic choice (McFadden, 1974, 2001; Anderson et al., 1992), where underlying utility differences for a choice pair (x, y) are perturbed by a noise term $\varepsilon$ and actual choice follows the realization $u(x)-u(y)+\varepsilon$. As a consequence, the probability of a choice which goes against the underlying utility difference (hence an error) is larger if $u(x)-u(y)$ is closer to zero, that is, errors are more likely as choice pairs are closer to indifference.³ Since applied work in discrete choice microeconomics assume such a gradual, monotonic relation from the onset, fitting them to data will necessarily produce patterns in agreement with the assumed relation just because the underlying dimension (e.g., imputed utilities in random utility models, or fitted drift rates in evidence accumulation models; see Fudenberg et al., 2020)⁴ is estimated in order to produce a good fit. While these within-sample, fitting approaches are invaluable to compare the fit of different utility- or payoff-based models of choice, they assume (and hence do not demonstrate) the gradual effects we are interested in. To drive this point home, in Sect. 3.2 we conduct a simulation exercise showing that it is possible to obtain apparently systematic, gradual effects from purely random choices. In contrast, our analysis relies on an out-of-sample approach, where individual utilities are estimated using a set of choices, and the postulated gradual relationships are tested using a different set of choices.

The second objective of our work is to compare different candidate explanatory variables for the gradual effects of interest. A priori, it is by no means clear what the gradual effects predicted by psychology and neuroscience should depend on for economic choices, where a natural scale as weight, brightness, or length is usually not part of the problem’s formulation, and utilities are neither directly observable nor objective. For decisions under risk, expected utilities are a natural candidate, but they involve a subjective underlying dimension, since widespread evidence shows that risk attitudes are highly heterogeneous (e.g., Bougherara et al., 2021; de Oliveira, 2021; Mentzakis & Sadeh, 2021; Bandyopadhyay et al., 2021). This subjective nature creates the need for out-of-sample estimation. Alternatively, expected values provide an objectively-defined candidate (which would not need any estimation). A third candidate is given by differences in numerical magnitudes. A number of contributions in the cognitive sciences (Moyer & Landauer, 1967; Dehaene et al., 1990; Dehaene, 1992) show that people make more mistakes and take longer to decide when asked whether 6 is larger than 5 than when asked whether 9 is larger than 2. This observation has been recently reproduced by Frydman and Jin (2022) and has motivated the work of Khaw et al. (2021) (see Sect. 2).

To accomplish our objectives, we designed a new experimental task where we can independently vary the (subjective) value of the options available to the participant and the (payoff-irrelevant) numerical magnitudes of the stimuli. If we would use a standard lottery choice task, as previously done in the literature, every change in each numerical magnitude (payoffs or probabilities) would directly translate into changes in expected payoffs and utilities. On the contrary, we implement a naturalistic environment where stimuli are represented using decks of cards and participants need to decide whether to bet (or not) on whether a subsequent extracted card is larger than another. In this way the values of the options are not directly related to the numerical symbols represented on the cards, i.e., we can vary independently the perceptual and the value-based dimensions of the stimuli.

Our results show that, in an economically relevant situation (betting choices), choice frequencies and response times are monotonically related to cardinal differences in expected utilities, where the latter are estimated out of sample. This substantiates the claim that the gradual effects of psychophysics are relevant for economic choices, in the sense that “strength of preference” drives error rates and response times. At the same time, we show that these effects are mostly determined by expected utility differences and not expected value differences or (payoff-irrelevant) perceptual effects. This result validates the ideas and assumptions behind random utility models and other approaches. Crucially, we also show that our results do not hinge on the particular functional form of the utility function or error specification. That is, we perform our analysis using random utility and random parameter models as well as assuming different functional forms of the utility functions (CARA or CRRA) and even present a robustness check which relies on certainty equivalents. Further, the relation to response times shows that the effects are more than “as if” accounts of decision making and might have their origin in brain processes of a gradual nature, as assumed e.g. by evidence accumulation models (Ratcliff, 1978; Fudenberg et al., 2018).

The paper is structured as follows. Section 2 briefly reviews the related literature. Section 3 discusses the experimental design and the results of the experiment. Section 4 concludes.

2 Related literature

Our work is related to long-standing problems in economics and to several strands of the recent literature. Classical studies of stochastic choice endorsed the view that utilities should be understood as reflecting choice probabilities (e.g., Debreu, 1958; Luce, 1959), in direct opposition with the neoclassical view that they reflect preferences of an exclusively ordinal nature (Hicks & Allen, 1934).

The gradual relation between underlying preferences and choice frequencies has also been repeatedly illustrated in a domain which bridges the gap between psychophysics and decisions under risk. In experimental studies on consumer choice (typically snack food items), participants make choices based on their personal preferences. Although they generally have a very different focus, several works in this domain have illustrated a relation between differences in subjective, self-reported ratings and choice frequencies (e.g., Krajbich et al., 2010; Fisher, 2017; Clithero, 2018; Polania et al., 2019). However, the approach in those works is typically to fit an evidence accumulation model, which assumes a relation of this sort (as discussed above) and is hence inadequate to test for the postulated effects, and in any case does not extend to decisions under risk.

To the best of our knowledge, the first study to point at a connection between utility differences and choice frequencies in decisions under risk was the inspiring experiment of Mosteller and Nogee (1951) on poker dice gaming, which aimed to “test the validity of the construct” represented by (expected) utility. Their analysis included illustrations which suggested a sigmoidal relation between utility differences and choice frequencies, although, as the authors admitted, those were at the individual level and cherry-picked among all experimental participants. While suggestive, their illustrations were not a test for the presence of gradual effects (and were actually not meant to be), because their utility functions were constructed through an interpolation procedure relying exclusively on observed indifferences. For instance, although their illustrations map zero utility difference to 50 percent choice frequency, “this finding was built into the expected utilities by the construction leading to the utility curves” (Mosteller & Nogee, 1951, p.202).

Conceptually, our work is also related to the studies of Khaw et al. (2021) and Frydman and Jin (2022). The former carried out an experiment on risky choice where participants chose between a sure amount and lotteries with a single non-zero outcome and a fixed probability of winning varying amounts (that is, the winning probability was identical for all choices). By varying the sure amount and the lottery outcome, Khaw et al. (2021) explored the reaction of choice frequencies to changes in payoffs and argued that the data could be explained assuming an imprecise internal representation of numerical magnitudes, in line with Moyer and Landauer (1967) and Dehaene (1992). Hence, their work speaks in favor of a direct effect of numerical magnitudes on error rates.⁵ However, by design, their numerical magnitudes stand in a monotonic relation to payoffs: each lottery is mapped to a single number, which in turn maps monotonically to economic value. Further, because probabilities were fixed, participants only needed to evaluate a single number for each lottery, hence making the type of choices implemented in Khaw et al. (2021) and Frydman and Jin (2022), by design, a perceptual discrimination task. In particular, in their data it is not possible to disentangle the effects of numerical magnitudes and expected values (or utilities) on choice frequencies and response times.

It should also be remarked that, for concreteness, Khaw et al. (2021) concentrate on the perception of payoffs and assume probabilities to be objective in their analysis. It is conceivable that an an extension of the models proposed by Khaw et al. (2021) and Frydman and Jin (2022) to account for distortions in both payoffs and probabilities might provide a foundation for the effects of subjective variables (expected utilities) that we demonstrate. We follow a different approach by using a design such that different numerical magnitudes are associated with the same expected payoffs and vice versa, allowing us to study perceptual (but payoff-irrelevant) and utility effects separately. Further, the choices in our experiment vary both payoffs and probabilities.

In a related paper, Alós-Ferrer and Garagnani (2021) consider decisions under dominance, where what is correct is objectively defined and, in particular, independent of risk attitudes. In that task, gradual effects as described by psychophysics are also present, and can be shown to be determined by expected values. As in our task, payoff-irrelevant numerical magnitudes play only a minor role.

3 Design and procedures

Participants were $N=96$ (different) university students (66 females, age range $18-36$, mean 24). Sessions lasted around 60 minutes and the average payoff was EUR 13.45 (around USD 14.40 at the time of the experiment). Three participants were unable to understand the task and were excluded from the analysis.

Fig. 1

Each trial starts by extracting two black cards, a red card, and displaying a prize. Participants then decide whether to bet or not (betting is costly). After a bet, a black card is extracted, and the participant wins if and only if it is strictly larger than the red card

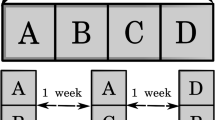
All decisions are embedded within a fixed, naturalistic environment using betting decisions (as, e.g., Mosteller & Nogee, 1951; Alós-Ferrer & Garagnani, 2021), and, in addition, the decision task allows us to disentangle numerical differences from economic incentives, which would not be possible using, e.g., a lottery choice task (because in the latter every change in each numerical magnitude influences payoffs). Further, in order to concentrate on the effects of strength of preference, we again strive to streamline the choice environment to reduce possible additional sources of variability in choice frequencies. The experimental task is as follows. Participants are confronted with two decks of cards, a red one (Diamonds) and a black one (Clubs), containing ten cards each (numbered 1 to 10). At the beginning of each of the 170 trials, two cards are extracted from the black deck, one red card is extracted from the red deck, and a monetary prize is displayed (see Fig. 1). The participants’ task is to decide whether to bet or to pass. After this decision, a further black card will be extracted from the remaining eight cards in the black deck, and the objective is to beat the red card with that new card. Betting is costly: placing a bet costs EUR 0.10 (fixed for all trials), independently of the outcome of the trial. If the participant bets and if the newly-extracted black card is strictly larger than the displayed red card, the participant receives the displayed monetary prize (minus the cost). Otherwise, the payment is zero (resulting in a net loss equal to the cost of betting). If the participant does not bet, there is neither a payment nor a cost (but the new black card is still extracted and the participant observes the outcome). Before a new trial starts, all cards are returned to their respective decks and those are reshuffled. Hence, each trial reflects an independent decision situation. All trials were paid. In our particular context, this payment mechanism is incentive-compatible under mild assumptions on the participants’ preferences, as shown by Azrieli et al. (2018, 2020).⁶

The set of initial stimuli (red card, first two black cards, and prize) was predetermined and pseudorandomized across trials to achieve adequate stimuli variance with a manageable number of trials. Red cards were extracted in such a way that there was always some probability of winning, so as to avoid trivial decisions. Hence, there were eight possible distinct probabilities of winning, ranging from 12.5% to a sure win. Prizes ranged from 10 to 120 cents, and were determined trial-by-trial as deviations from the actuarially-fair prize, the amount that leaves a risk-neutral agent indifferent between betting and passing. Eleven different distortions from the fair prize were implemented, ranging from 50% below to 50% above, in 10% steps. Stimuli were selected to ensure that every participant faced every combination of winning probability and distortion from the fair prize at least twice. The crucial third black card was randomly selected among the cards remaining in the deck.

In each trial, at the moment of the decision, the black deck contains eight cards, and the two already-extracted cards are displayed. The probability to win when betting depends on the magnitude of the red card and on whether the displayed black cards are winning or losing cards. In the example depicted in Fig. 1, the red card is an 8 and the two extracted black cards are a 2 and a 4, hence both are losing cards. That is, the black deck contains two winning cards and six losing ones, yielding a probability of winning of 1/4. Since the cost of betting is 10 cents, the actuarially-fair prize is 40 cents, but the offered prize is 24 cents. Hence, a risk-averse or risk-neutral agent should decline to bet, while a risk-loving one might rationally decide to bet. That is, there are no objectively-correct decisions in this task; rather, what is “correct” depends on the individual risk attitude. Therefore, we hypothesized that the natural underlying dimension or subjective economic distance would be the difference between the expected utilities of betting and passing, referred to as EU distance for clarity, which requires us to estimate the underlying individual utilities of money.

By design, however, the expected value of betting depends on the distortion of the fair prize. For risk neutral individuals, the difference in expected value between passing and betting reflects how far away from “indifference” the participants were, and are hence a natural, alternative measure for “strength of preference.” Therefore, another candidate determinant of gradual effects is simply the absolute value of the expected value differences between betting and passing, which we refer to as EV distance.

We remark also that the probability of winning does not depend on the numerical distances between the black cards and the red one, but only on whether the former are larger or smaller than the latter. Hence, numerical distances in themselves are payoff-irrelevant (but the sign of the numerical differences is not). This allows us to disentangle the numerical closeness of stimuli as a further possible determinant of choice frequencies, which is the closest one to standard measures of perceptual similarity used in psychophysics. Since there are two black cards, we have different possible candidates for numerical distance. We present here the analysis using the distance between the red card and the second, more recent black card, since a large literature has advocated the prominence of the recency effect (Deese & Kaufman, 1957; Murdock, 1962). There are ten possible perceived distances between the red card and the second black card, ranging from 0 to 9. We refer to this magnitude as numerical distance. We also carried out analyses with other definitions of numerical distance; the main results described below are unaffected.⁷

3.1 Utility estimation

We estimate out-of-sample risk attitudes for each subject. Specifically, we use the choices made in odd trials to estimate risk attitudes and use this estimation to predict the expected utility in the even trials, and vice versa.⁸ Crucially, our results do not hinge on the particular functional form of the utility function or error specification. Following a standard approach, we the main analysis estimates an additive random utility model (RUM) which considers a given utility function plus an additive noise component (e.g., Thurstone, 1927; Luce, 1959; McFadden, 2001). The estimation procedure employs well-established techniques as used in many recent contributions (Van Gaudecker et al., 2011; Conte et al., 2011; Moffatt, 2015; Alós-Ferrer & Garagnani, 2020; Garagnani, 2020; Alós-Ferrer et al., 2019, 2021). We provide a short description in Appendix A.

For the functional form of the utility function, we adopt a normalized constant absolute risk aversion (CARA) function, which is given by

$$u(x) = {\left\{ \begin{array}{ll} \frac{1-\exp (-rx)}{1-\exp (-rx_\text {max})}, &{}\text{ if } r \ne 0\\ \frac{x}{x_\text {max}}, &{}\text{ if } r=0, \end{array}\right. }$$

For the noise term, we consider normally-distributed errors. In Appendix C, we repeat the analysis assuming CRRA utilities instead of a CARA functional form. In Appendix D, and since random utility models have been recently criticized (see Wilcox, 2011; Apesteguía & Ballester, 2018), we again repeat the analysis, this time using a random parameter model (RPM; Loomes & Sugden, 1998; Apesteguía & Ballester, 2018), which follows a different approach for the specification of noise. As a last robustness check, in Appendix E we repeat the analysis using certainty equivalents instead of (CARA) utilities. In all cases, all our results remain qualitatively unchanged.

The estimated risk propensities (absolute risk aversion) in our dataset using CARA have an average $r=0.026$ (SD $=0.016$, median 0.025, min $=-0.007$, max $=0.086$; see Appendix A for details on the estimation). The risk propensity estimated on odd trials ($r= 0.027$) is not significantly different from the one estimated on even trials ($r= 0.025$; Wilcoxon Signed-Rank test, $N=93, \, z=0.738, \, p=0.463$). Given the estimated risk attitudes, the majority of subjects are estimated to be risk averse, with only 3 subjects classified as risk-seeking. Appendix C reproduces the estimation on the basis of CRRA functions instead and finds an average relative risk aversion parameter of $r=0.215$ (SD $=0.190$, median 0.146, min $=0.011$, max $=0.749$).

3.2 Fitting is not testing: A simulation exercise

Fig. 2

Analysis of a dataset of random, simulated choices. Left-hand panel: Choices as function of expected utility difference using a standard, within-sample procedure. An appearance of order and gradual effects of expected utility differences on error rates emerges, even though no regularity is present in the data. Right-hand panel: The same choices as function of expected utility difference using an out-of-sample procedure. No regularity can be identified. Gray areas indicate 95% binomial proportion confidence intervals

Before we proceed to the analysis of the actual data, we report on a simulation exercise that illustrates the need for out-of-sample estimation procedures as the ones described above.

We simulated a dataset where each of 93 fictitious subjects randomly chose 170 times between accepting the bets. That is, the dataset contains the same choice pairs for the same number of actual participants as in the experiment, but actual choices in this dataset were fully random (50% probability for each choice) and unrelated to the options. We then treated the dataset as if it would come from actual decision makers and used a standard fitting approach following the same procedures described above, but using the entire data for each simulated decision maker. That is, we estimated a CARA utility function using an additive random utility model and heteroskedastic, normally-distributed errors, following the specification and procedures explained in Sect. 3.1.

The left-hand panel of Fig. 2 plots the simulated choice frequencies against the estimated utility differences following this within-sample, fitting approach. That is, we used the estimated risk attitudes to compute, within sample, the expected utility difference between the two options (betting minus passing), and then plotted this difference against the proportion of times one option was chosen over the other. We observe a regular sigmoidal curve (as in any logit or probit model), which creates the appearance of order (and gradual effects arising from utility differences) for the nonsensical dataset. Actually, this appearance is a mere artifice of the method, as can be shown by estimating utility out of sample, i.e., using part of the choices for estimation purposes and plotting the rest of the choices against the resulting estimated utility differences, as we will do for the actual data from the experiment. The right-hand panel of Fig. 2 depicts the result of this out-of-sample estimation, performed exactly as our actual analysis for the experiment. Specifically, we estimated a CARA utility function from even-numbered choices and used it to plot data from odd-numbered choices, and vice versa. As demonstrated by the figure, this approach shows that there is no actual regularity in the dataset. We conclude that structural models where utility is estimated can mistakenly create an appearance of gradual effects, and hence direct tests are needed.⁹

In summary, the difference between within-sample (fitting) and out-of-sample estimations shows that the estimation procedure might create apparent gradual effects simply because they are assumed in the underlying random utility model. Our out-of-sample procedure ensures that the regularities we uncover below correspond to actual features of the data.

3.3 Choices and errors

We define an error as a choice which gives a negative expected utility, e.g. deciding to bet when the expected utility (as estimated out of sample) of betting is strictly smaller than the expected utility of passing. The mean error rate across participants was 27.31%, with a median of 28.24% (SD = 8.44, max 44.12%, min 10.00%). Figure 3 plots the frequency of betting decisions for each possible value of each variable. As in previous pictures, to facilitate the comparison, in all figures and regressions the various distances are normalized to be between 0 and 1. The left-hand panel plots the dependence on expected utility differences.¹⁰ The shaded areas correspond to errors with the definition above. We observe that the relation between betting frequency and expected utility differences has a sigmoidal shape resembling a cumulative normal distribution or a logistic curve. This shape indicates that error rates decrease gradually as the difference in expected utilities between the options becomes larger. For very large differences, error rates are close to zero. For differences close to zero, error rates are close to 50%. This stands in sharp contrast to deterministic, neoclassical models, which would predict that subjects always bet when expected utility differences are positive and always pass when they are negative.

Fig. 3

Proportion of betting decisions as a function of expected utility differences (left) and expected value differences (right). Gray areas indicate 95% binomial proportion confidence intervals. Shaded areas indicate the proportion of errors

Since the left-hand panel of Fig. 3 pools utility differences of different subjects on the same scale, raising questions of interpersonal comparability, in Appendix E we reproduce this figure and the entire analysis using certainty equivalents instead, which yield a monetary (hence comparable) scale for every subject. The results are qualitatively unchanged. The right-hand panel of Fig. 3 plots the proportion of betting choices as a function of the differences in expected value (betting minus passing). We observe a positive but non-monotonic trend with greater expected values corresponding roughly to a higher frequency of betting.¹¹ This is not surprising, since as long as utility is increasing on monetary amounts, there will be some positive correlation between expected utility and expected values in a dataset. However, the figure strongly suggests that expected utility differences better explain gradual effects on error rates than differences in expected values. This is noteworthy since, as commented above, the estimates of (absolute) risk aversion parameters using CARA are relatively low. In other words, the fact that our estimated risk aversion parameters are relatively low but still a clear difference between expected utility and expected value is observed supports the view that strength of preference effects are better explained by expected utility differences.¹² Appendix C carries out a robustness analysis assuming CRRA instead of CARA and finds that the estimates of (relative) risk aversion are not close to risk neutrality, but our results are qualitatively unchanged. The same applies when considering random parameter models instead of RUMs (Appendix D).

One can depict the proportion of betting decisions as a function of numerical distances as defined above (errors, however, cannot be derived from numerical distance alone in this experiment). For the sake of brevity, we omit this figure (see Fig. B.1 in Appendix B) and simply comment that a graphical representation suggests a weak, noisy monotonic relation which might hint to second-order effects but offers no strong evidence of an impact of purely numerical, payoff-irrelevant perceptions on choice frequencies.

In summary, our data shows that there is a gradual relation between economic distance and error rates, but the former now corresponds to differences in expected utilities. Again, we remark that this and subsequent results do not hinge on the specific functional form or error structure that we assume (Appendices C, D, E).

We now turn to a regression analysis. The data form a strongly balanced panel with 170 trials for each of the 93 participants. We ran random-effects panel Probit regressions where the dependent variable is 1 in case of a correct answer. For completeness, we provide separate analyses for expected utility (Table 1) and expected value differences (Table 2), while controlling for numerical distance in both. Recall that Expected Utility distance (EU distance), Expected Value distance (EV distance), and numerical distance are all normalized to range from 0 to 1. The various regression models are built in a completely analogous way, and hence we discuss them simultaneously below. The definitions of errors is the natural one in each table, i.e. choices against expected utility differences in Table 1 and choices against expected value differences in Table 2. Note that, for the models in Table 1, the dependent variable specifies whether each actually-observed choice was consistent with the estimated utility or not, but our out of sample approach guarantees that the utility function used for each given choice has been estimated using different choices only (that is, not including the given choice).

In Model 1 of both tables we see that larger economic distances lead to less errors, confirming the basic prediction. However, there is a considerable difference in the magnitude of the estimated coefficients, with EU distance having a coefficient almost 30 times bigger than EV distance. To conduct a proper comparison, we calculated the relative elasticities. A $1\%$ variation in EU distance increases the probability of a correct answer by an average of $0.183\%$, while the analogous percentage for EV distance is only $0.120\%$. This confirms the message from Fig. 3 that differences in expected utility, and not in expected value, are the relevant dimension of strength of preference in this context.¹³

Table 1 Random-effects Probit regressions on correct answers for expected utility. $EU\_Dist$ is the distance between the expected utilities of the options. A correct answer is passing or betting when that option has larger expected utility. We further control for numerical distance ($Num\_Dist$), defined as the absolute value of the difference between the numerical values of the red card and the second black card

Model 2 in both tables introduces numerical distance as an additional control. In the presence of EU distance, numerical similarity does not seem to play a role. The effect is also insignificant when controlling for the interaction between numerical distance and EU distance (Model 3), and when controlling for gender, age, native language, and other characteristics (Model 4; Table B.2 in Appendix B contains the details on the controls). In the presence of EV distance, numerical effects are not statistically significant. They only become significant when we further control for the interaction between numerical distance and EV distance (Model 3) as well as other controls (Model 4). The results for numerical distance should be attributed to the fact that there is a (mechanical) correlation between the expected value and numerical distance across all decisions in the dataset (Spearman’s $\rho =0.145$; $N=170$, $p= 0.059$), but there is no correlation between numerical distance and expected utility (Spearman’s $\rho =0.093$, $N=170$, $p= 0.227$). In all models we control for learning effects. Participants appear to improve as the experiment advances (Trial, 1–170).

Table 2 Random-effects Probit regressions on correct answers for expected value. $EV\_Dist$ is the distance between the expected values of the options. A correct answer is passing or betting when that option has larger expected value. We further control for numerical distance ($Num\_Dist$), defined as the absolute value of the difference between the numerical values of the red card and the second black card

3.4 Response times and the underlying processes

The previous section shows that differences in expected utilities are the best candidate as an explanatory determinant of gradual effects on errors. Expected value differences and numerical differences also display significant effects, but those are of a smaller magnitude and appear less robust. In this section, we further compare the gradual effects of all three variables by focusing on response times. The main objective is to show that, while there appears to be a strong, clear correspondence between expected utility differences and actual human decision processes as reflected by response times, that relation is far from clear when it comes to other alternative variables.

The variable of interest is the time participants took to decide whether to bet or to pass. The average across individual average response times for this decision was 2.051 seconds (SD $=0.150$, median $=2.090$, min $=1.354$, max $=2.200$). Figure 4 plots average response times as a function of expected utility differences (left) and of expected value differences (right).¹⁴ Response times and EU distance clearly show an inverted U-shaped relation. Decisions associated with smaller expected utility differences result in longer response times. However, the figure shows no systematic relation with EV differences (the corresponding coefficient is not significantly different from zero, coef. $=0.012, z=0.85, p=0.393$). Analogously, there is no relation with numerical distance (coef. $=0.017, z=0.25, p=0.803$; see Fig. B.1 in Appendix B). This provides an independent confirmation of the relation between a larger strength of preference, in the sense of larger subjective economic distance, and smaller error rates reflects fundamental characteristics of the underlying decision process (and, in particular, is not an artifact of the econometric estimation). Again, the results are robust to using alternative utility functions, specifications of noise, or certainty equivalents instead of utilities (Appendices C, D, and E). We remark that comparable results for response times as a function of estimated utility differences where found by Moffatt (2005) in an experiment on lottery choice using rank-dependent expected utility, and by Chabris et al. (2009) in an experiment on intertemporal choice with utility differences estimated using a functional form with hyperbolic discounting.

Fig. 4

Average response times as a function of expected utility differences (left) and expected value differences (right). Gray areas indicate 95% confidence intervals

We conducted a panel regression analysis for log-transformed response times. Tables 3 and 4 report the corresponding regressions using expected utility distances and expected value distances as a measure of strength of preference, respectively. In all models with further control for individual differences in mechanical swiftness using the log of the response time for pressing the space bar to move to the next trial.

Response times are significantly shorter for larger EU distances across all models in Table 3. This effect is robust to controlling for numerical distance and additional controls. Additionally, numerical distance does have an effect on response times, validating the view from psychophysics (Moyer & Landauer, 1967; Dehaene et al., 1990) that even payoff-irrelevant perceptual differences might influence the choice process. That is, in addition to the effects of subjective economic distance, response times are shorter for more perceptually distinguishable stimuli (larger numerical distance).

In contrast, the effect of expected value differences is less clear. In Model 1 of Table 4, we observe larger response times for higher values of EV distance, contrary to expectations if EV distance was taken to explain the gradual effects of strength of preference. However, the effect becomes non-significant when we control for the relation between EV distance and numerical distance as well as other controls (Models 3 and 4; Table B.3 in Appendix B adds details on the controls). Again, the analysis is consistent with the view that expected utility differences are the key variable explaining the gradual effects that we investigate. In all models we control for time trends, reproducing the standard observation that subjects become slightly faster over time. Other controls deliver no additional insights.

Table 3 Random-effects regressions on log response times (Log RT) for expected utility. $EU\_Dist$ is the distance between the expected utilities of the options. We further control for numerical distance ($Num\_Dist$), defined as the absolute value of the difference between the numerical values of the red card and the second black card

Table 4 Random-effects regressions on log response times (Log RT) for expected value. $EV\_Dist$ is the distance between the expected values of the options. We further control for numerical distance ($Num\_Dist$), defined as the absolute value of the difference between the numerical values of the red card and the second black card

4 Discussion

Homo oeconomicus does not play dice (but homo sapiens might). A fully rational economic agent would be consistent, choosing an option 100% of the time if it delivered a slightly larger payoff than the alternative, and 0% if a minute payoff reduction left it worse than the alternative. However, considerable evidence suggests that the implementation of decision processes in the human brain follows processes of a more gradual nature (e.g., Shadlen & Kiani, 2013). Using an out-of-sample approach, we have demonstrated the existence of a stable, gradual relation between error rates in decisions under risk and an underlying, cardinal “strength of preference,” and shown that the latter is best represented by integrated variables of an exclusively economic nature. That is, decisions become more error-prone as the economic distance between the alternatives becomes smaller in line with firmly-established facts from psychophysics (e.g., Weber’s Law). This is true even in the standard economic context of decisions under risk (betting), which are an example of preferential choice where there is no objectively correct alternative.

Moreover, these effects are robust and obtain even though we use a strictly out-of-sample approach, that is, they are not an artifice of the estimation method. The results are unaffected by the particular utility function assumed (CARA or CRRA), the error specification adopted (RUM vs. RPM), as well as by whether choice difficulty is represented by differences in utilities or certainty equivalents. Further, the link to response times shows that the relationship between expected utility differences and choice frequencies reflects the characteristics of actual decision processes, rather than being just “as if” modeling. Numerical distance, seen as a more perceptual dimension influencing choice frequencies, plays a minor role. The effects of this dimension on choices are small and not robust to the addition of controls. Response times suggest that a second-order effect is present, but expected utility differences are the major determinant of the effects we study.

Of course, our experiment is (on purpose) stylized and, by design, shuts down a number of additional determinants of choice frequencies that are bound to also play a role in economic decisions. Those range from the complexity of the options’ description to the presence of transparent relationships (e.g., dominance) and whether the decision environment cues in cognitive shortcuts or not. Our claim is merely that strength of preference is one of the relevant dimensions influencing choice frequencies, and in particular that it is a dimension that can be characterized by measurable variables with an explicitly economic content.

Conceptually, our results agree with earlier studies as Mosteller and Nogee (1951) and with recent contributions as Khaw et al. (2021). Both report gradual increases in the proportion of risky choices in lottery experiments as the reward increases. Khaw et al. (2021) argue these effects are due to an imprecise perception of stimuli and not to an intrinsically economic variable such as differences in expected utilities or certainty equivalents. However, the experiment of Khaw et al. (2021) concentrates on the perception of payoff-relevant numerical magnitudes. Their task varies only payoff magnitudes, which in turn determine expected payoffs and utilities; hence the former and the latter cannot be disentangled. In contrast, we show that perceptual effects of payoff-irrelevant numerical magnitudes add little to the effects of expected utility differences. It is conceivable that an extension of the model of Khaw et al. (2021) allowing for noisy perception of both payoffs and probabilities might be used to provide a perceptual foundation of the effects of expected utilities that we demonstrate here, but our evidence suggests that such a foundation should build upon the perception of payoff-relevant magnitudes.

Our results are further aligned with the neuroscience literature, which has repeatedly found direct evidence for the neural encoding of cardinal differences between options (e.g., Padoa-Schioppa & Assad, 2006; Kurtz-David et al., 2019; Ballesta et al., 2020). In turn, those vindicate pre-neoclassical views from economists as Daniel Bernoulli, Adam Smith, and Jeremy Bentham (Niehans, 1990), who proposed that economic choices rely on the computation and comparison of subjective values.

For response times, our findings are aligned with Chabris et al. (2009), who found similar effects for intertemporal decisions (using a hyperbolic-discounting utility function), and with Moffatt (2005), who viewed response times as reflecting cognitive effort. They are also aligned with the theoretical argument of Fudenberg et al. (2018), which implies that it should take longer to distinguish utilities if they are closer, and with the assumptions in Alós-Ferrer et al. (2020), which postulate a decreasing relation between utility differences and response times.

The implications of our results are of broad significance for economic modeling. First, the systematic demonstration of the gradual relation between economic integrated variables and errors provides a foundation for theories of stochastic choice and empirical approaches to preference revelation alike. Second, the fact that these effects are a natural extension of those observed in psychophysics provides a tangible bridge to other disciplines, most notably neuroscience, through which new techniques and ideas can travel (in both directions). Third, the results pose a significant conceptual challenge to traditional, neoclassic as if modeling, because the latter is based on deterministic and, more importantly, purely ordinal preferences.