1 Introduction

Economic models of decision making in risky settings largely assume that a decision maker’s preferences are exogenous to the problem and exhibit a few key properties. Perhaps the most commonly asserted property is risk aversion, which in the expected utility framework implies a concave utility function. Increasingly researchers have identified a wide class of problems in which prudence (Kimball 1990) is also a key property of preferences. In the expected utility framework, prudence implies that marginal utility functions are concave.Footnote 1 We investigated when and how these two key traits—risk aversion and prudence—emerge and are shaped during human development. We did this by experimentally testing for the presence of these traits in 362 Chinese children and adolescents aged 8 to 17 years and then examining the correlation of these results with same tests for their parents—collected as hypotheticals in a survey—as well as with cognitive abilities and household attributes.

The direct measurement of higher-order risk preferences, such as prudence, has been sparked by the lottery-based and model-free definition by Eeckhoudt and Schlesinger (2006; see also Eeckhoudt and Schlesinger 2013 for a comprehensive review). For an individual with initial positive wealth W, they define risk aversion and prudence (as well as higher-order risk preferences more generally) in terms of preferences over pairs of lotteries. Each lottery has two potential outcomes x and y and is denoted by [x; y]. Eeckhoudt and Schlesinger (2006) define risk aversion as weakly preferring a lottery [W-k1; W-k2] over a lottery [W-k1-k2; W], where k1 > 0 and k2 > 0 are sure losses. They define prudence as weakly preferring a lottery [W-k1; W + ε] over a lottery [W-k1+ ε; W], where ε is a zero-mean risk (i.e., a lottery with an expected value of zero). While risk-averse individuals like to disaggregate two sure losses, prudent individuals like to disaggregate a sure loss and an additional zero-mean risk. In other words, risk aversion corresponds to a preference for a lower spread in payoffs and prudence to a preference for facing additional risk in better states of the world (prudence is therefore sometimes also called downside risk aversion).

Based on these definitions, risk aversion and prudence have been measured in a series of papers (see Trautmann and van de Kuilen (2018) for a survey). Most of these papers elicit risk preferences in the gain domain using choices between lottery pairs (Ebert and Wiesen 2011; Noussair et al. 2014; Deck and Schlesinger 2014; Breaban et al. 2016; Haering et al. 2020; Ebert and van de Kuilen 2017; Baillon et al. 2018). Some alternatively elicit risk and prudence premia using a multiple price list (Ebert and Wiesen 2014; Heinrich and Mayrhofer 2018) or elicit preferences in the loss domain (Maier and Rüger 2012; Bleichrodt and van Bruggen 2018). With respect to the loss domain the evidence is ambiguous, but with respect to the gain domain most studies find a majority of choices to be risk averse and prudent for binary choices, as well as for a multiple price list.Footnote 2 For the sake of comparability with the majority of studies, we opt to elicit risk preferences in the gain domain using binary lottery choices.

When comparing risk aversion across age groups, the evidence from previous experiments does not show a clear age effect. In an initial study, Harbaugh et al. (2002) analyze risk aversion of children and adolescents aged 5 to 20 as well as that of adults aged 21 to 64. They observe no correlation between age and a preference for gambles over certain amounts of equal expected value. Levin et al. (2007) compare the risky choices made by 9- to 11-year-old children to the choices the same children made three years earlier. They find a significant within-subject correlation but also no age effects for risk aversion. Furthermore, Sutter et al. (2013) do not observe age effects in their study with children and adolescents ranging from 10 to 18 years. Khachatryan et al. (2015) find a gender-dependent age effect. They study risk aversion of boys and girls in two age groups (7 to 12 years and 12 to 16 years). In their sample, risk aversion of boys decreases with age, while girls’ risk aversion stays constant.Footnote 3

Several survey-based investigations have found positive correlation between the risk aversion of adult children and that of their parents (see, e.g., Kimball et al. 2009, Dohmen et al. 2011, Necker and Voskort 2014), providing evidence for the intergenerational transmission of risk aversion. In addition, experimental studies that correlate decisions in incentivized tasks observe correlations between children’s and their parents’ risk aversion: Levin and Hart (2003) find a significant correlation between the risk aversion of 6- to 8-year-old children and that of their parents (79% of them mothers). However, this correlation is insignificant in their follow-up study with the same subjects three years later, as reported in Levin et al. (2007). Alan et al. (2017) study risk aversion in 7- to 8-year-old children and their mothers. They find that the risk aversion of girls (but not of boys) correlates with their mothers’ risk aversion.

There is evidence that a considerable part of variability of decision making under uncertainty is determined genetically, as documented, for example, in twin studies on risk aversion (Cesarini et al. 2009; Zhong et al. 2009; Zyphur et al. 2009) and on financial investments (Cesarini et al. 2010; Barnea et al. 2010). Heritability may explain the transmission of risk preferences from parents to their children. However, the environment also appears to be an important driver of risk-taking. A recent study by Black et al. (2017) on adoptees finds that the portfolio risk adoptees take on is more strongly correlated with that of their adoptive than their biological parents (see also Fagereng et al. 2018). In addition, a number of studies suggest that risk preferences are influenced by the general characteristics of the household within which children grow up. Deckers et al. (2019) observe that 7- to 9-year-old children who grow up in households of parents with low income or low education are less risk averse than other children. Falk and Kosse (2016) interpret breastfeeding duration as a measure of quality of the early childhood environment. In a sample of preschool children aged 5.9 years on average, they find that shorter breastfeeding is associated with lower risk aversion (and lower levels of patience and altruism).

In this study, we connect the emerging literature on higher-order risk preferences with previous work on the development and transmission of risk aversion. We measure risk aversion and prudence in two primary schools, one middle school and one high school in the mainland Chinese sub-provincial city of Xiamen. For this purpose, we developed a simple preference elicitation task suitable for young children. We ran all experiments during the usual class time and are thus able to rule out self-selection in the experiment. We also used a survey to collect the stated risk preferences of parents and household information. Furthermore, we obtained additional information from the school records.

Our results with respect to the preferences of children and adolescents reveal that subjects from grades 5 to 11 (10 to 17 years) make mostly risk-averse and prudent choices. With respect to risk aversion, behavior of 3rd graders (8 to 9 years) does not differ statistically from risk neutrality. We also find 3rd graders to make mostly prudent choices; however, this effect is driven by one of the two primary schools we sampled from. We also find evidence for a transmission of preferences: children’s risk aversion is significantly correlated with stated preferences of their parents. Also, prudence of girls (but not boys) is significantly correlated with stated preferences of their parents.

In Section 2, we will describe our elicitation method and process of data collection. In Section 3, we present the results. After describing the summary statistics, we first focus on the basic question of whether children and adolescents are risk averse and prudent. We then present our results on the transmission of risk preferences and consider the development of risk preferences with age. In Section 4, we present estimates of a structural model of stochastic mean-variance-skewness expected utility to explore whether grade variation in behavior is driven by changing deterministic utility parameters or shrinking decision errors. Section 5 concludes with a discussion of our findings.

2 Study design

2.1 Preference elicitation

Our goal is to test for risk aversion and prudence in a classroom setting. For this purpose, we need a method that can be explained quickly and is easy to understand for participants with little knowledge of mathematics. Nevertheless we also want to build on established methods so that our results are readily comparable to existing studies.

Various tools have been applied to measure risk preferences in experiments with adults (see Harrison and Rutström 2008; Charness et al. 2013; and Haering and Heinrich 2017, for overviews). We also use lottery pairs to measure risk preferences. As pointed out above, most studies on higher-order risk preferences do as well. This approach fulfills our need for simplicity, and it also has been applied successfully with young children (Deckers et al. 2019).Footnote 4

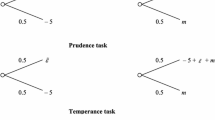
In the design of our elicitation method, we build on Deck and Schlesinger’s (2014) study. They have developed 38 random lottery pairs that allow measuring first to sixth order risk preferences that are also used in subsequent studies (Deck and Schlesinger 2018; Haering et al. 2020). We select seven of their lottery pairs: one first-order dominance task, three risk aversion tasks and three prudence tasks. Table 1 shows the parameters of the tasks.Footnote 5 We would expect all participants to make the dominant choice of option B in order 1. Following the definition of Eeckhoudt and Schlesinger (2006), risk-averters will prefer to disaggregate two sure losses and thus choose option B in all tasks of order 2. Prudent individuals will prefer to disaggregate a sure loss and an additional zero-mean risk. Thus, they will choose option B in all tasks of order 3.

Table 1 Parameters of the pair-wise lottery choice tasks
Full size table

We deviate from the task frame of Deck and Schlesinger (2014). Most lotteries in these pairs are compound lotteries. Deck and Schlesinger depicted and resolved uncertainty through a sequence of binary lotteries, represented as a series of random wheel spins. We presented the same lotteries in their reduced form, represented as a random draw from an opaque bag containing four marbles of different colors.

All choices were displayed using four marbles, as illustrated in Fig. 1. This shows the two options available in Task 11 by Deck and Schlesinger (2014) as it was operationalized in our experiment. Both options have the same expected payoff and the same variance, while differing in their skewness. The lottery on the left has lower skewness (i.e., a larger downside risk). The letters indicate the color of each marble (green, blue, yellow and white), which were replaced with the symbol for the respective color in the original Chinese version of the instructions.

Fig. 1
figure 1

Prudence lottery task. G: green, B: blue, Y: yellow, W: white; in the original instructions these letters were replaced with the Chinese symbol for the respective color

Full size image

2.2 Experimental procedures

We conducted all experiments during regularly scheduled class times by the same lead experimenter, who was supported by six extensively trained assistants. We held all sessions in either the school’s library or in a classroom. At the beginning of each session, the rules of the experiment were carefully explained by the lead experimenter. We stressed that we wanted participants to understand all procedures, encouraged questions, and took ample time to answer them. We also made clear that choices had to be made individually and that talking to other students was forbidden.

All participants had to successfully answer two control questions to demonstrate comprehension of the tasks. These questions asked for the payoff of the degenerate lottery and for the highest potential payoff from a skewed distribution. All answers were individually checked by the research assistants before the experiment continued. Subjects who did not answer these questions correctly or showed a lack of understanding during the conversation with the research assistants were excluded from the analysis.

The students proceeded to make their choices by noting them in a paper booklet illustrating the different lotteries.Footnote 6 We randomized the presentation of the left and right lotteries between booklets. We use the dummy variable Flipped to indicate which of the two presentations was used. There was no feedback over the course of decision-making, and payments were only determined at the very end. For this purpose, one task was drawn for payment. This task was the same for all participants; it was determined by a draw from a bingo cage. At this point, the assistants approached the students one by one and determined the outcome of their chosen lottery in the respective task. To accomplish this, one marble was drawn from an opaque bag containing the four marbles, and the student was then paid accordingly.Footnote 7

The students’ grades, their Hukou status and their gender were collected directly from the schools’ administrations. The Hukou is a household registration and categorization system used in China to distinguish between locals and non-locals, as well as between urban and rural citizens. We use the local/non-local Hukou status as a proxy for migratory experience. As observed by Jaeger et al. (2010), among others, migrants tend to be more risk seeking.Footnote 8

The third data set we collected uses a survey instrument given to the students’ parents. After the experiment, student participants received an envelope containing a questionnaire for their parents. It was explained that the envelope questionnaire was to be filled out by their parents.Footnote 9 It then had to be placed in the sealed envelope signed by them. Parents also had to sign the sealed envelope before the student returned it to their respective teachers. Parents received RMB 40 (approximately US$ 6.45 at the time) for returning the questionnaire. In this questionnaire, parents were presented with the same lottery pairs. We were not, due to human resource limitations, able to incentivize their decisions, but rather scaled up the hypothetical payoffs by a factor of 1000 (relative to those of the primary school children) to make payoffs more salient.Footnote 10 In addition, we included an extensive set of questions. Some of the questions, whose responses we report in this paper, asked who filled out the questionnaire (the mother, the father or someone else), how many members of the household had a high school degree, and how many had a university degree (none, one, two or more). We also asked about the number of houses or apartments the members of the family owned altogether (none, one, two or more). We use this as a proxy of wealth, as this is the primary store of wealth for Chinese citizens.

Table 2 presents our experimental design. We collected data at six grade levels, covering children in the age range from 8 to 17 years. Across schools, we used the same experimental procedures. After consulting with several teachers, we decided to pay all students in cash (see Brosig-Koch et al. 2015 and Geng et al. 2015 for a similar procedure). Based on these consultations, we used the same incentives within each school, but we doubled the primary school’s pay for the middle school and tripled it for the high school. Thus, lotteries paid between RMB 1 and RMB 19 for 3rd and 5th graders (between US$ 0.16 and US$ 3.06), between RMB 2 and RMB 38 for 7th and 8th graders (between US$ 0.32 and US$ 7.12) and between RMB 3 and RMB 57 for 10th and 11th graders (between US$ 0.48 and US$ 9.19). Note that Vieider (2012) finds no influence of variations up to 20% in payoffs on second-order risk aversion.

Table 2 Experimental design
Full size table

A challenge of cross-sectional studies that compare different age groups lies in finding comparable samples. We selected four schools from urban districts of Xiamen (which in the official census in 2010 had a total population of approximately 3.5 million people): a primary school from the Huli district, a middle school from the Haicang district, and a high school from the Siming district. These are three similarly urbanized districts with Xiamen, consisting of mostly upper and middle class households, and are the only districts where the municipal government imposes drastic curbs on manufacturing.

The public Xiamen school system has approximately 300 primary, 60 middle and 35 high schools. In Xiamen, and largely across school districts in China, primary and middle school enrollment is based solely upon catchment areas—the registered household address. However, high school admission is determined by a student’s performance on a Xiamen-wide entrance exam. High school students often take places at the most selective school, by entrance exam thresholds, they gain admission to within the district. High schools often have highly utilized dormitories for weekly boarding for those students who do not live close by, thus potentially injecting issues of selection bias for our high school sample. The high school in our experiment typically ranks around 10th out of 35 in terms of entrance exam score threshold.

Based on the results from our first sample, we also collected data from a second primary school in the Huli district of Xiamen, due to a strong imbalance between the proportion of local and non-local Hukou holders. Relative to the two other schools, migrants represented a larger share of participants at the first primary school. We therefore collected a follow-up sample at another primary school with a share of migrants that is similar to that in the middle and the high school. At this school, we used identical experimental procedures, and the study was conducted by the same lead experimenter. In the following, we present the results of the full samples, including regressions that control for Hukou status. If not mentioned otherwise, our main observations persist when using data from either one of the two primary schools. Online Appendix E includes additional analyses using only data from one of the two primary schools at a time.

3 Results

3.1 Summary statistics

Overall 362 subjects were recruited for the experiment, as shown in Table 2. However, we excluded six subjects from our analysis because they were not able to answer the control questions correctly (three subjects from grade 3, two from grade 5, and one from grade 8). Furthermore, two more subjects were excluded because of missing personal data (one subject in grade 3 and one in grade 10). This leaves us with 354 subjects at six grade levels. Table 3 summarizes these observations. Next to the number of subjects, it displays summary statistics of their individual characteristics, namely the average age in months and their average grade in math. Math performance is graded on a scale from 0 to 100 in primary school (grades 3 and 5) and on a scale from 0 to 150 in middle and high school (grades 7 to 11).Footnote 11 Additionally, Table 3 shows the share of female subjects. The last three columns show the average number of choices in line with first-order stochastic dominance, risk aversion and prudence.

Table 3 Summary statistics student subjects
Full size table

We provide some summary statistics from the survey given to parents. Only 9 parents did not return the questionnaire, 51 of the 345 returned questionnaires were not filled out completely and 5 were filled out by someone other than the mother or the father. Table 4 contains the summary statistics of the remaining 289 questionnaires that we use to characterize the children’s environment at home. “Low education,” “medium education,” “high education” and “house owner” are dummies that are constructed from the answers in the parent questionnaire. All households in which parents indicated that no household member has at least a high school or university degree are classified as “low education” households. If at least one member has a high school degree but no one holds a university degree they are classified as “medium education” households. The remaining households with at least one member holding a university degree are classified as “high education” households. The indicator “house owner” takes the value of one if the parents indicate that the household members own at least one house or apartment altogether.

Table 4 Summary statistics household characteristics and parents’ choices
Full size table

The Hukou status was collected directly from the official school records. “Local Hukou address” takes a value of one if the child has the Hukou of the school’s local municipality (i.e., a Hukou from Xiamen for all four schools). The last two columns show the average number (out of three) of risk-averse or prudent choices.

The summary statistics reveal some heterogeneity between the households in the different grades and schools. In all grades, the minority of questionnaires was answered by the mothers. The asymmetry is most pronounced in grade 7 of the middle school. The share of families with low education ranges from 3% in grade 10 to 38% in grade 8. Rates of high education and house ownership are less dispersed: they range from 17 to 31% and from 74 to 86%. After merging the data sets from two primary schools, the share of local students is still somewhat lower in grades 3 and 5: 34% of children in grade 3 and 31% in grade 5 have a local Hukou address, while at least 43% in higher grades have one. We will control for these differences in our regression analyses.

The summary statistics also reveal that across grades a large majority of subjects follow first-order stochastic dominance, and the proportion across grades does not monotonically decrease. Choosing the dominated option can be interpreted as an additional test of understanding. Yet, as there is only one first-order dominance task in our experiment we cannot disentangle a lack of understanding from choice errors (cf. Section 4). We chose not to exclude the respective subjects and rather opted for the larger yet noisier data set. Unreported analysis duplicating what we report, except excluding the first-order stochastic dominance violators, yields very similar results.

Table 3 also shows that the number of risk-averse choices is higher than the number of prudent choices in all grades. Recent evidence would lead us to expect the opposite relationship: Deck and Schlesinger (2014) have observed that lottery choices can be explained surprisingly well by a preference for either combining “good” with “bad” or “good” with “good,” implying mixed risk-averse and mixed risk-loving behavior (Crainich et al. 2013). People with one of these two preference types differ in their lottery choices in even orders but coincide in odd orders (i.e., risk averters and risk lovers are both prudent).Footnote 12 In a related study, Haering et al. (2020) observe less temperate and less prudent choices in the reduced lotteries, which is consistent with the pattern observed in our study.

3.2 Are children and adolescents risk averse and prudent?

3.2.1 Risk aversion

Behavior in the risk aversion tasks 2, 3 and 4 suggested that choices are not made randomly but with a general preference for the less risky option. Pooling choices across tasks 2, 3 and 4, binomial tests reject the null hypothesis that only half the choices are risk averse within all grades (p < 0.001, two-sided binomial tests) except in grade 3 (p = 0.503).Footnote 13 Fig. 2 displays the distribution of the number of risk-averse choices within the six grade levels we examine. If participants are risk averse and this preference is deterministic, we would expect them to make three risk-averse choices (or zero risk-averse choices if they are risk-loving). In fact, the most frequent choice pattern in all grades except grade 3 consists of perfectly risk-averse choices.

  • Observation 1: Subjects in grades 5 to 11 (but not in grade 3) make predominantly risk-averse choices.

Fig. 2
figure 2

Distribution of number of risk-averse choices within grades

Full size image

Figure 3 displays the number of risk-averse choices by girls and boys across grades. It reveals that female and male students differ only marginally in their behavior. When comparing the number of choices within grades, we do not find any significant differences between boys and girls (p ≥ 0.326, two-sided Mann-Whitney-U tests).

Fig. 3
figure 3

Average number of risk-averse choices by gender

Full size image

3.2.2 Prudence

As in the risk aversion tasks, behavior in the prudence tasks 5, 6 and 7 suggests that choices are not made randomly. Instead, most choices are prudent. Pooling choices across tasks 5, 6 and 7, binomial tests reject the null hypothesis that half the choices are prudent within all grades, including grade 3 (p ≤ 0.004, two-sided binomial tests). However, the tendency of 3rd graders to choose prudently is driven by the second primary school we sampled. Third graders in the second school make prudent choices (p < 0.001) while choices of 3rd graders in the first school do not differ from random behavior (p = 0.929).Footnote 14 Fig. 4 displays the distributions of the number of prudent choices within grades of the joint sample. If participants are prudent and this preference is deterministic, we would expect them to make three prudent choices (or zero prudent choices if they are imprudent). Yet, in terms of prudence, the mode of the choice distributions varies across grades: it is one for 3rd graders, two for 5th and 8th graders, and three for 7th, 10th and 11th graders.

  • Observation 2: Subjects in grades 5 to 11 make predominantly prudent choices. The behavior of subjects in grade 3 differs by school.

Fig. 4
figure 4

Distribution of number of prudent choices within grades

Full size image

Figure 5 displays the average number of prudent choices made by girls and boys across grades. Again, there appears to be no pronounced gender gaps. Boys and girls do not differ in the number of prudent choices in any of the grades (p ≥ 0.151, two-sided Mann-Whitney-U tests).

Fig. 5
figure 5

Average number of prudent choices by gender

Full size image

3.3 How does the household influence risk preferences?

In this subsection, we focus on the transmission of preferences, while controlling for characteristics of the children’s household and for individual differences in regressions. Therefore, the following analyses are based on the subset of subjects for whom all household information was available (summarized in Table 4).

Table 5 provides initial evidence of the transmission of preferences by examining the joint distribution of the children’s and parents’ lottery choices. It shows two contingency tables: number of risk-averse choices on the left and number of prudent choices on the right. We observe a small but significant correlation within the risk tasks (Spearman’s Rho of 0.248, p < 0.001) and within the prudence tasks (Spearman’s Rho of 0.173, p = 0.003). Furthermore, Chi-squared tests reject the null hypothesis of independence in both cases (p ≤ 0.036).

Table 5 Contingency tables for share of risk-averse and prudent choices by children and parents
Full size table

Additionally, we run several regressions that also shed more light on potential age effects. We run ordered logit regressions to identify the influences on the number of risk-averse or prudent choices. We first focus on risk aversion before considering the influences of individual and household characteristics on prudence.

3.3.1 Risk aversion

Table 6 presents six ordered logit regressions on the number of risk-averse choices. The results are reported as average marginal effects and standard errors are clustered on the grade level. We estimated models (1) and (2) using the whole sample, while we estimated models (3) and to (6) using only girl and/or boy participants respectively.

Table 6 Ordered logit regressions on the children’s number of risk-averse choices (average marginal effects)
Full size table

We present models with and without controls for household characteristics. We first focus on models (2), (4) and (6), which include these controls. The three regression models indicate the existence of age effects within our sample: The joint F-tests of the Grade and Grade 3 coefficients are significant in all three models (p < 0.001). The regressions also reveal gender-specific age effects: in the overall sample, we find third graders to be significantly less risk averse than the remaining children (p < 0.001), while the Grade effect is insignificant (p = 0.742). When splitting the regressions by gender, a significant Grade 3 effect is observed only in the male sample (p < 0.001 for boys and p = 0.167 for girls). The Grade variable reveals a significantly positive effect for girls and a significantly negative effect for boys (p ≤ 0.038). We find two differences between the two primary schools, which are not presented in Table 6. Participants at the second school make significantly fewer risk-averse choices (p ≤ 0.002). Furthermore, we find a significant positive correlation between math grade and the number of risk-averse choices made by girls (p = 0.015).

With respect to the household parents’ preferences, we confirm the finding of a positive and significant correlation between the number of risk-averse choices made by parents and their children (cf. Table 5) when controlling for household characteristics. In the whole sample, one more parental risk-averse choice leads to 0.094 more risk-averse choices by their children (p < 0.001). For girls, the increase is somewhat smaller than for boys (0.075 versus 0.104), but both increases are significant (p = 0.036 and p = 0.008).Footnote 15

  • Observation 3: Risk aversion is significantly correlated between parents and their children, after controlling for individual and household characteristics.

The remaining household characteristics (parental education level, house ownership status, and Hukou status) also influence children’s choices significantly: the joint F-tests of these remaining variables are significant in all of the three models (p ≤ 0.001). A high level of education in parents is associated with more risk-taking in the complete sample relative to the baseline of medium education households (p = 0.048). Splitting the sample reveals that the effect is driven by the girls in our sample: we find a significant influence for girls (p = 0.008) but not for boys (p = 0.539). Parents’ house ownership is significantly associated with less risk-taking in the complete sample (p < 0.001). In the subsamples, this effect is significant for girls (p < 0.001) and weakly significant for boys (p = 0.090). A local Hukou address is neither associated with risk-taking in the complete sample nor in one of the subsamples (p ≥ 0.220). As parents’ preferences may be correlated with household characteristics, we also present models without the respective controls in columns (1), (2) and (3). These regressions indicate a similar level of correlation of parents’ and children’s choices as the models in columns (2), (4) and (6).

3.3.2 Prudence

While we observe a robust influence of individual characteristics, parents’ preferences and household characteristics with respect to risk aversion, their influence on prudence is less clear. Table 7 presents the regression results of our first specification that regresses the number of prudent choices on these characteristics.

Table 7 Ordered logit regressions on the children’s number of prudent choices (average marginal effects)
Full size table

First of all, when considering models (2), (4) and (6) that control for household characteristics, we also observe some significant age effects on prudence, after controlling for further individual differences and for household differences: The joint F-tests of the Grade and Grade 3 coefficients are significant in full data set (p = 0.002) and for girls (p < 0.001) but insignificant for boys (p = 0.965). However, we do not find a significant effect of the Grade 3 variable (p ≥ 0.627) in any of the samples. There is a significant positive Grade effect in the complete sample (p = 0.045). Yet, Grade is weakly significant in the female subsample (p = 0.088) and insignificant in the male subsample (p = 0.793). Even though they affected risk-taking, we neither find a systematic effect of the second primary school (p ≥ 0.484) nor a gender effect with respect to the complete sample (p = 0.729). A better math grade, however, is significantly associated with a larger number of prudent choices in the whole sample (p = 0.004) and in the female subsample (p = 0.032). In the male subsample, the correlation is only weakly significant (p = 0.056).

Considering the household parents’ preferences, the regressions confirm the positive and significant correlation between the number of prudent choices made by parents and their children (cf. Table 5). In the whole sample, one more parental prudent choice leads to 0.061 more prudent choices by their children (p = 0.064). But this effect is driven by the girls: it is only significant for them (p = 0.009 for girls and p = 0.302 for boys) and it is more than twice as large for girls than for boys (0.090 versus 0.041).Footnote 16

  • Observation 4: Prudence is significantly correlated between parents and their daughters (but not their sons) after controlling for individual and household characteristics.

The remaining household characteristics affect children’s choices significantly in the whole sample (p < 0.001) but not in the separate samples (p ≥ 0.446), as the F-tests reveal. With respect to the individual effects, we find that girls who grow up in a household with low educational level make weakly significantly less prudent choices (p = 0.099). This effect is neither found in the complete sample (p = 0.648), nor in the male subsample (p = 0.228). None of the remaining household characteristics is found to be significant on its own.Footnote 17 Considering the models without the respective controls in columns (1), (2) and (3) again reveals a similar level of correlation of parents’ and children’s choices as the models in columns (2), (4) and (6).

4 Evolving deterministic or random utility?

We observe an, at least weakly, increasing trend of risk averse and prudent choices across grades. We also observe that a substantial portion of individuals do not make perfectly consistent risk averse/loving or prudent/imprudent choices; suggesting a stochastic element partly drives their choices. Two possible drivers of these choice patterns are (i) emerging deterministic risk averse and prudent preferences and (ii) a diminishing variance in the stochastic element of choice. We report on structural estimates of expected cubic utility functions that vary in the degree by which they permit group specific coefficients and variances of the random component.Footnote 18

Consider the following data description. Each participant i in grade g ∈ G = {3, 5, 7, 8, 10, 11} completes a sequence of seven binary lottery choice tasks, indexed by l = 1, 2, …, 7, as presented in Table 1. The choice of i in task l is between the lotteries Alg and Blg. The g subscript indicates the grade appropriate monetary incentive multiplier as indicated in Table 2. We denote i’s choice in task l,

$$ {y}_{il}=\left\{\begin{array}{cc}1& \mathrm{if}\ \mathrm{lottery}\ {A}_{lg}\ \mathrm{is}\ \mathrm{chosen},\mathrm{and}\\ {}0& \mathrm{if}\ \mathrm{lottery}\ {B}_{lg}\ \mathrm{is}\ \mathrm{chosen}\end{array}\right. $$

We assume a participant chooses the lottery that maximizes his expected utility function. This utility function is the sum of a deterministic and stochastic component. The deterministic component is a cubic polynomial, and the stochastic component is a zero-mean normally distributed random variable. Specifically, for a lottery Z

$$ {U}_i(Z)={\alpha}_{1i}E\left[Z\right]+{\alpha}_{2i}E\left[{\left(Z-{\mu}_Z\right)}^2\right]+{\alpha}_{3i}E\left[{\left(Z-{\mu}_Z\right)}^3\right]+{\varepsilon}_{iZ} $$

The participant chooses lottery Alg if his realized utility for Alg exceeds that of Blg. The probability of this event is

$$ \Pr \left[{y}_{il}=1\right]=\Pr \left[{U}_i\left({A}_{lg}\right)-{U}_i\left({B}_{lg}\right)>0\right]=\Pr \left[\frac{\sum_{j=1}^3{\alpha}_{ij}{x}_{lg}^j}{\sigma_g}>{\epsilon}_{il g}\right], $$
(1)

where \( {x}_{lg}^j \) is the difference between the jth moment of the lotteries Alg and Blg, and \( {\epsilon}_{ilg}={\varepsilon}_{iA_{lg}}-{\varepsilon}_{iB_{lg}} \). We assume realizations of the standardized random innovation, ϵilg, are independent across participants and tasks. Thus its distribution is N(0, 1). We consider two possibilities for the variance-covariance structure: homoscedastic, in which \( {\sigma}_g^2 \) is constant for all grades, and heteroscedastic with grade specific variance. With respect to the moment coefficients we consider two cases: homogeneous preferences, HomPrefs for short, indicates there is a common set of population moment coefficients and heterogeneous preferences, HetPrefs for short, indicates there are grade specific moment coefficients.

This formulation allows for two potential channels for development of risk aversion and prudence in our data sample. In the HetPref channel, coefficients on the second moment are negative and decreasing over grades—increasing risk aversion—and coefficients on the third moment are positive and increasing over grades—increasing prudence. Second, with heteroscedacity, the variance of the random component of utility decreases with the grade level. These are two distinct patterns of preference development: changing preferences or shrinking decision errors. We evaluate these two channels by estimating probit models under varying homoscedastic and HomPrefs restrictions.

We present three estimated probit models in Table 8. In model (1), homoscedastic-HomPref, the estimated coefficients on the three moments have sensible signs: positive for the mean and skewness and negative for variance. When allowing for grade specific moment coefficients, model (2), we find almost uniformly decreasing coefficients for the variance, and increasing coefficients for skewness, with the grade level. We note the biggest jumps occur between grade 3 and 5 for risk aversion, and grade 5 and 7 for prudence. A likelihood ratio tests rejects the homoscedastic-HomPref model in favor of the homoscedastic-HetPref model (LR-stat of 43.29, 15 degrees of freedom, p value <0.001). This statistical evidence supports evolving deterministic risk averse and prudent preferences.

Table 8 Probit regressions of children’s mean-variance-skewness stochastic utility functions
Full size table

Model (3) allows for varying variances of the stochastic choice component of utility, while assuming HomPref. The estimated coefficients for the difference in moments are quite similar to model (1), particularly for the differences in variance and skewness. The estimate grade specific variances, 3rd grade is the baseline and normalized to one, also suggest there is heteroscedasticity. However, the monotonic decline is not as consistent as expected. The estimated deviations for the 2nd and 11th grade specific variances, while negative, are not statistically significant. While the estimated deviations for the 7th, 8th and 10th grade specific variances are statistically significant and reflect a reduction of approximately forty to 50% from the baseline. These grade differences are consistent with the more frequent first order stochastic dominance choice violations we noted for grades 5th, and 11th graders, as reported in Table 3, and the roughly fifty percentage risk averse choices of 3rd graders. We reject homoscedasticity in favor of heteroscedasticity, i.e. model (3) versus model (1), via a Likelihood Ratio test (LR-stat of 16.67, 5 degrees of freedom, p value = 0.005).

This hypothesis test is conditional upon the assumption of HomPref, and it would be more informative if that test could be conducted allowing for HetPref. Unfortunately, we could not obtain reliable estimates for a Heteroscedastic-HomPref model. We did not obtain consistent estimates from various initial values, and for many of these the procedure did not converge. Thus, the only comparisons we can offer are comparisons of the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC) for models (2) and (3). These comparisons do not provide clear evidence in favor of either model; model (2) has the higher AIC and model (3) the higher BIC. In summary, we find evidence in support of both evolving deterministic preferences and heteroskedastic decision errors. These decision errors have a higher variance with the primary school participants but also with the participants from the 11th grade, which is less consistent with the shrinking variance hypothesis.

5 Conclusion

In this study, we measure risk aversion and prudence in Chinese children and adolescents in two primary schools, one middle school and one high school. Choices by 3rd graders do not differ significantly from choices under risk neutrality, but 5th to 11th graders make significantly risk-averse choices. Furthermore, 5th to 11th graders make significantly prudent choices. We also find 3rd graders to make significantly prudent choices. However, this effect is driven by the second primary school we recruited from. We do not find any gender differences with respect to risk aversion or prudence. Yet, risk aversion appears to increase more gradually with age in girls than in boys. In addition, we find evidence for the transmission of risk preferences from parents to children: risk aversion correlates between parents and their sons and daughters, while prudence correlates between parents and their daughters (but not their sons).

It is interesting to note that we do not observe any gender differences with respect to risk aversion and prudence. Often adult men are described as less risk averse than women (see, e.g., the overview by Croson and Gneezy 2009, and the results from China reported by Gong and Yang 2012 and Zhang 2019). Yet the difference appears to be small and depends on the elicitation task as pointed out in the meta-study by Filippin and Crosetto (2016). With respect to children and adolescents, the evidence suggests a similar pattern. Cárdenas et al. (2012) study risk aversion in children aged 9 to 12 years in samples from Columbia and Sweden. They find boys to be less risk averse than girls. A similar observation is made by Borghans et al. (2009) for Dutch adolescents aged 15 to 16 years and by Sutter et al. (2013) for Austrian children and adolescents aged 10 to 18 years. In the USA, Harbaugh et al. (2002) find no gender differences in their samples of children and adolescents aged 5 to 20, while Eckel et al. (2012) find male high school students in grades 9 and 11 to be less risk averse than girls. Risk preferences may be shaped by environmental factors. Booth and Nolen (2012) study risk preferences of adolescents in grades 10 and 11 (15 years old on average) in the UK. They only find a gender difference for students in mixed schools, but not when comparing children from single-sex schools. Furthermore, they find that girls make somewhat less risk-averse choices, when preferences are elicited in all-girls groups.

While we do not observe gender differences in the levels of risk aversion and prudence, the transmission of preferences differs by gender: the correlation in the number of prudent choices is driven by the girls in our sample. Alan et al. (2017) report a similar finding for risk aversion. They only find a significant correlation between mothers and their daughters, but not between mothers and their sons. We also find differences with respect to prudence between the two primary schools. These may be driven by unobserved differences in the school environment. Eckel et al. (2012) have reported differences between schools in risk aversion between high schools. In an experimental study conducted in nine different high schools in the USA, they find that risk aversion varies with characteristics like class size and teachers’ levels of education.

Our findings are important with respect to field behavior and the design and timing of potential policy measures. Risk preferences are not only central to many economic models. They have also been shown to influence outcomes across the lifespan. For example, those who report lower risk aversion in surveys also choose careers with higher variance of income, as observed by Bonin et al. (2007) and Fouarge et al. (2014). When measuring risk preferences of children and adolescents between 10 and 18 years, Sutter et al. (2013) find that less risk-averse subjects have a higher body mass index (while there is no significant correlation with whether or not they save money, smoke or spend money on alcohol, or with their conduct at school). Furthermore, 7 to 9 year old children who grow up in households with low income or low education are less risk averse, as observed by Deckers et al. (2019). In a follow-up survey conducted 4 to 5 years later, they also find that lower risk aversion in the initial experiment is positively correlated with lower grades and juvenile offences. Castillo et al. (2018) also correlate adolescents’ experimentally elicited risk preferences with field behavior. They find that less risk-averse 8th graders (14 years old on average) have more disciplinary referrals one to two years later and are less likely to graduate from high school.

There is much less direct evidence on the relevance of prudence for field behavior. Only Noussair et al. (2014) find more prudent lottery choices to be correlated with greater wealth, a greater likelihood of having a savings account, and a lower likelihood of credit card debt in a representative survey of the adult Dutch population. Note, however, that our finding of prudence in children and adolescents is also important when designing policies that relate to inter-temporal decision-making. Sutter et al. (2013), for example, find more impatient children and adolescents to be less likely to save money and more likely to smoke and to spend money on alcohol. More impatient children also receive worse grades for their conduct at school (while there is no significant correlation with their body mass index). But in inter-temporal optimization, higher-order risk preferences determine today’s reaction to future changes in risk, as shown by Leland (1968) and Sandmo (1970). For a given level of risk aversion and a given discount factor, an increase in (second-order) risk of future income, for example, yields an increase in today’s savings if and only if the decision maker is prudent.