Abstract
We consider the external validity of laboratory measures of risk attitude. Based on a large-scale experiment using a representative panel of the Dutch population, we test if these measures can explain two different types of behavior: (i) behavior in laboratory risky financial decisions, and (ii) behavior in naturally-occurring field behavior under risk (financial, health and employment decisions). We find that measures of risk attitude are related to behavior in laboratory financial decisions and the most complex measures are outperformed by simpler measures. However, measures of risk attitude are not related to risk-taking in the field, calling into question the methods currently used for the purpose of measuring actual risk preferences. We conclude that while the external validity of measures of risk attitude holds in closely related frameworks, this validity is compromised in more remote settings.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Risk is at the core of economic decisions. For example, risk preferences are an essential element in any discussion regarding finance, insurance and the asset markets. It is thus necessary to understand how individuals behave in risky environments in order to properly understand financial decision-making. To address this, numerous experimental methodologies dedicated to measuring individual risk attitudes have emerged (for a survey, see Harrison and Rutström 2008). In this study, we assess the external validity of five of the most influential risk-preference-elicitation procedures by testing whether they can explain laboratory financial decisions and behavior in the field. A great deal of research has pursued the question of how to best measure risk preferences, yet one question that has received insufficient attention is how well these attempts actually map into behavior by people in the field.
While the default assumption seems to be that these measurements are useful, this has been called into question by works such as Friedman et al. (2014). The first work on this topic was conducted by Binswanger (1980), which attempted to measure risk preferences of farmers in India. The method he designed presented a choice of seven lotteries, which involved a coin flip and which varied the payoffs for heads and for tails. Regressions on choices made indicate that “the independent variable which most consistently correlated with the ordinal risk measure turned out to be ‘luck’ – that is, past coin flip realizations during earlier trials of the Binswanger procedure,” and so does not inspire confidence that a stable trait is being measured. Friedman et al. (2014) note: “Subsequent investigators, notably Jacobson and Petrie (2009), would have even greater difficulty getting estimates from the Binswanger procedure to predict out-of-sample data.”
They also mention historical problems with the most common contemporary measure (Holt and Laury 2002, hereafter HL), with pie-chart displays (Hey and Orme 1994), and with physiological measures (Sapienza et al. 2009). There is sometimes little correlation between the HL measure and, e.g., investment behavior in the laboratory (Viscusi et al. 2011). Or the correlation between the HL measure and psychometric methods is significant for students but not for other categories such as farmers (Maart-Noelck and Musshoff 2013).
Overall, Friedman et al. (2014) note: “The different ways of eliciting risk parameters in cash-motivated, controlled economics experiments yield different general results.” (see He et al. 2018 for a review). Loomes (1988) is one of the first studies to notice such inconsistencies when evaluating risk attitudes using certainty equivalents, and Loomes and Pogrebna (2014) show a large variability within and between elicitation methods when the underlying preferences are imprecise.
More recently, in a large cross-country study Vieider et al. (2015) identify correlations between incentivized decisions in binary lotteries and self-reported risk attitudes in most countries. By contrast, Deck et al. 2013 find considerable within-subject variation in behavior between four measures of risk attitude: HL, Eckel and Grossman (2008, hereafter EG), “the deal or no deal” method from Deck et al. (2008) and the “balloon analogue” risk task from Lejuez et al. (2002, hereafter BART). Crosetto and Filippin (2016) confirm this finding by comparing behavior in EG, HL, Gneezy and Potters (1997, hereafter GP) and the procedure introduced by Crosetto and Filippin (2013). The inconsistency is robust when also considering measures from psychology and cognitive neuroscience as shown by the comparisons of decisions in HL, BART, Columbia card task, marbles tasks and two developed in-house measures conducted in Pedroni et al. (2017).Footnote 1 Finally, similar conclusions are reached based on the comparisons between HL and the procedure introduced by Andreoni and Harbaugh (2009) (see Dulleck et al. 2015) or the self-reported risk measure introduced by Dohmen et al. (2005, hereafter WTR for Willingness to Take Risks; see Lönnqvist et al. 2015). These findings raise the question: Can one’s underlying (“true”) risk preferences be accurately measured in the laboratory?
A critical aspect of laboratory experiments is their generalizability, i.e., that insights gained in the lab can be extrapolated to the world beyond (Levitt and List 2007). However, the adequacy between some measures of risk attitude and other behavior under risk has been analyzed almost exclusively in studies focusing on a single risk measure.
In particular, based on their stated risk preference approach, Dohmen et al. (2005) report that investment in stocks, actively engaging in sports, being self-employed, and smoking are related to risk attitude.Footnote 2 Using the same measure in rural Thailand, Hardeweg et al. (2013) confirm its relation to being self-employed and also find a relation to the purchase of lottery tickets. Ding et al. (2010) identify a correlation between this self-reported risk measure, parental income and the reservation price of a hypothetical lottery ticket, but they also note that this correlation is low. Franken et al. (2017) find a correlation between self-reported risk attitudes in a survey and marketing arrangements in the hog industry. Caliendo et al. (2009) identify a positive relationship between the decision to start a business and a lower stated risk aversion.
Lusk and Coble (2005) and Andersen et al. (2008) find that risk aversion measured with HL is negatively correlated with the consumption of genetically-modified food, cigarette smoking, heavy drinking, being overweight and seat belt non-use. Guiso and Paiella (2008) highlight a positive link between a direct measure of absolute risk aversion based on a willingness to pay and the likelihood to face income uncertainty or to become liquidity constrained. Lejuez et al. (2002) find that the measure of risk aversion introduced in their study correlates with the self-reported frequency of addictive, unsafe and unhealthy behavior. Verschoor et al. (2016) use GP on a sample of farmers and find that it correlates with some risky choices (e.g., the purchase of fertilizer) but not others (e.g., growing of cash crops).
Falk et al. (2018) use an index of risk preferences based on certainty equivalents and WTR that correlates with self-employment and smoking. Based also an certainty equivalents, Fairley and Weitzel (2017) find that risk aversion is not related to student borrowing behavior. Finally, Sutter et al. (2013) study the impact of children and adolescents’ risk aversion on smoking, drinking, the body mass index (BMI), savings, and conduct at school using an elicitation method based on certainty equivalents (Wakker 2010). Risk aversion is only related to the BMI.
Therefore, while consistency between measures has been extensively and systematically studied, an extensive and systematic analysis of their ability to explain risky behavior in other settings is missing in the literature.
To the best of our knowledge, the only other study in economics aiming to provide a systematic evaluation of the measures of risk attitude is Galizzi et al. (2016)Footnote 3 (see Galizzi and Navarro-Martínez 2019 for a similar investigation of the external validity of experimental games in the domain of social preferences). They test the relation between three measures (HL, GP, and WTR) and field behavior based on a UK representative sample. They find that none of these measures are related to smoking, junk-food consumption, regularly saving, or savings horizons. HL and EG are related respectively to the regular consumption of fruits and vegetables, and having a private pension fund. WTR is associated with heavy alcohol drinking. Overall, they thus find mixed evidence of a link between measures of risk attitude and field behavior. In comparison, we consider a larger range of measures of risk attitude. We use different types of behavior as a benchmark (risky financial decisions in the laboratory and field behavior). Finally, we also focus more on financial decisions as field behavior that can possibly be explained by risk aversion.
Two valuable characteristics of a measure of risk attitude can be identified: simplicity and theoretical compliance (Charness et al. 2013). Simplicity is thought to decrease measurement errors and misunderstanding. Relying on more elaborate theories is thought to permit measures to describe behavior more precisely. However, achieving both objectives can be difficult, since compliance with advanced theory often requires the implementation of complex procedures. Risk measures can thus be ranked according to this trade-off between simplicity and theoretical refinement. We select five of the most popular procedures currently in use in experimental economics, which vary regarding their level of complexity.
At one end of the spectrum is the complex procedure described by Tanaka et al. (2010, hereafter TCN), which allows the researcher to identify the utility-curvature and probability-weighting parameters of prospect theory. At the other end of the spectrum, the non-incentivized survey questions introduced by Dohmen et al. (2011) have no specific relation to any particular economic theory. Between these two extremes, we also consider three incentivized methods: an investment task proposed by Gneezy and Potters (1997) and adapted by Charness and Gneezy (2010), a choice of one lottery out of six introduced by Eckel and Grossman (2008), and finally a more complicated procedure based on ten choices between paired lotteries proposed by Holt and Laury (2002).
We test the external validity of measures of risk attitude based on two different types of risk-related behavior. The first set of risky behavior is composed of laboratory financial decisions: a portfolio task, an insurance task, and a mortgage task. In contrast to measures of risk attitude, their instructions are context-rich in the sense that the type of decision is explicitly mentioned when describing the tasks. These tasks thus constitute an intermediate step between standard laboratory measures and field behavior, since they introduce some context but are still artificial situations. The second set of risky behavior is composed of naturally-occurring field behavior that reflects the risk exposure that individuals are willing to bear in their everyday lives. The risk attitude in the field is assessed based on insurance decisions, employment decisions, and investment decisions that can be either monetary or in properties.
We collect decisions in both settings using a representative sample of the Dutch population: subjects in our experiment are part of the Longitudinal Internet Studies for the Social sciences (LISS) panel. Studying a representative sample of the population increases the likelihood that subjects face major financial decisions under risk such as investing or purchasing insurance compared, for example, to a student sample. Moreover, more complex measures of risk attitude perform better for individuals with high numeracy skills. Thus using a representative sample makes it more likely that our conclusions are not biased by numeracy.
Noussair et al. (2013) used this panel to study whether risk aversion, prudence, and temperance are related to six types of financial decisions. They implement a single measure of risk aversion based on five binary choices between a lottery and a safe amount. They find that owning real-estate, long-term insurance, or loans are unrelated to any of the risk measures. Individuals with higher temperance are more likely to have a savings account and are less likely to have unpaid balances on a credit card. Neither risk aversion, prudence nor temperance are related to real-estate investments, risky investments or having a loan. In comparison, we do not consider higher-order risk attitudes but we vary how risk aversion is measured. We find that measures of risk attitude are indeed related to behavior in laboratory financial decisions. We also find that more complex measures under-perform. However, the measures of risk attitude in the lab—either simple or complex—consistently fail to predict risk attitude in the field. Our conclusion highlights an apparent lack of external validity of these common measures of risk attitude.
The remainder of this paper is organized as follows: Section 2 describes the experimental design. The data-analysis methodology and the results are reported in Section 3. Section 4 concludes.
2 Experimental design
In this section, we first present our sample of subjects and experimental procedures. Then, we describe our measures of risk attitude in the laboratory: risk-attitude elicitation procedures and framed laboratory financial decisions. Finally, we introduce our measures of risk attitude in the field.
2.1 Sample of subjects and experimental procedures
We conducted our experiment on a sample of the LISS panel composed of 1122 individuals from different households. The distributions of the age and income of our sample confirm its diversity. Subjects are on average 51 years old (s.d. = 16.44). The youngest of our subjects is 18 years old while the oldest is 92 years old. Their net monthly incomes are on average €1473 (s.d. = 2291). Monthly incomes range from no revenue to a maximum of €69054. Finally, 46% of our sample is male.
Our experiment is composed of five measures of risk attitude, three laboratory financial decisions and six measures of risk exposure in the field. The risk attitude of each subject is measured using a single procedure (between-subject design). It enables us to guarantee that our main focus of interest is not affected by a carry-over between procedures (Charness et al. 2012).
All subjects make decisions for the three laboratory financial tasks. Subjects were paid based on their answers in one of these four parts. Their earnings were on average €9.03 (s.d. = 10.67). Subjects were paid by bank transfer at the end of the experiment. The survey questions used to assess risk attitude in the field were asked of all subjects. Instructions of the experimental measures are in Appendix A and our design is summarized in Figure A1 of Appendix B.
2.2 Our measures of risk attitude
The five measures we use to measure risk attitude are: WTR, GP, EG, HL, and TCN.
- Self-reported measure::
-
Dohmen et al. (2011). The simplest of all procedures consists of asking subjects directly if they are willing to take risks. Subjects rank their willingness to take risks on a 0 to 10 scale with 0 being the lowest willingness and 10 the highest. The exact phrasing of the question is: “How do you see yourself: are you generally a person who is fully prepared to take risks or do you try to avoid taking risks?” this question is completed by a similar question specifically targeting financial decisions: “How would you rate your willingness to take risks concerning financial matters?” subjects also answer on a 0 to 10 scale. The general question is referred to hereafter as “WTR–G (for General)” while the specific question is referred to as “WTR–S (for Specific)”. In contrast to the procedures below, this mechanism is not incentivized and is based on reported preferences rather than revealed preferences. As this measure is based on a scale, it does not provide a cardinal measure in the strictest sense. We thus consider in the result section one dummy variable equal to 1 if the reported willingness to take risk is strictly higher than 5, and 0 otherwise.Footnote 4
- Investment task::
-
This procedure taken from Gneezy and Potters (1997) and adapted by Charness and Gneezy (2010) is perhaps the most straightforward procedure based on revealed preferences. Subjects receive an endowment of €8. They are offered to invest in a lottery that pays 2.5 the amount invested with a 50% chance and that pays €0 otherwise. For practical issues, their investment must be divisible by 0.01 (i.e., 801 different options). Whatever is not invested is kept. Formally, subjects choose an investment k ∈ [0,8] with \((100\times k)\in \mathbb {N}\). They are paid according to the lottery (8 − k, 0.5; 8 + 1.5 × k, 0.5). The expected earning and the earning variance are thus increasing with the investment. Risk-neutral and risk-seeking subjects should invest all their endowments. Investment should decrease as risk aversion increases.
- Ordered lottery selection::
-
Eckel and Grossman (2008). This procedure is close to Binswanger (1980), and also comparable to that of Gneezy and Potters (1997) but with a more narrow decision space. Subjects select one two-outcome lottery out of six possibilities, as introduced in Table 1. The first lottery is a safe lottery paying €7. The next four lotteries are obtained by adding €2 to one outcome and deducting €1 from the other outcome. Both outcomes being equally likely, the expected value and the variance are increasing from one lottery to the next. Risk-averse subjects should select one of the five first lotteries depending on their degrees of risk-aversion. Only risk-neutral (or very slightly risk-averse/risk-seeking individuals) should select the fifth lottery. The last lottery is obtained by adding and deducting the same amount of €2.5 to the two outcomes of the fifth lottery. While it is impossible to fully discriminate between risk-neutral and risk-seeking people, the last lottery is the unique choice for people who are at least moderately risk-seeking.
- List of paired lotteries::
-
Holt and Laury (2002). This procedure requires subjects to make 10 decisions. It is more complicated than previous procedures, but it does enable us to completely disentangle risk-seeking subjects from risk-neutral subjects. Ten ordered choices between two lotteries denoted A or B are presented to subjects (Table 2). Lottery A always pays either €8.0 or €6.4 while Lottery B pays €15.4 or €0.4. The probability that both lotteries pay the high payoff is varied between choices from 0.1 to 0.9. Lottery A is safer than Lottery B; however, the expected value of lottery A increases from €6.56 to €8 while the expected value of Lottery B increases from €1.9 to €15.4. For the first four decisions, only risk-seeking subjects should choose Lottery B as this lottery has a lower expected value and more risk than Lottery A. After these decisions, risk-averse subjects might switch to Lottery B. The later they switch to Lottery B, the more risk averse they are. The last decision is singular, as no risk is involved. It tests if subjects have understood the instructions. If this procedure is selected for payment in our experiment, one decision is randomly selected for payment. Note that there should be (at most) one crossing from the left side to the right side. A serious issue is that there are often multiple crossings in the experimental population, particularly in rural areas of undeveloped nations, suggesting a lack of comprehension.
- Multiple lists of paired lotteries::
-
Tanaka et al. (2010). The procedure introduced by Tanaka et al. (2010) is the most complicated procedure implemented in this study, as it consists of two lists of 14 decisions each.Footnote 5 This higher level of complexity is explained by the fact that this procedure relies on prospect theory as an alternative framework to expected utility. While the expected utility is characterized only by the concavity of a utility function, prospect theory is also characterized by a probability weighting parameter. Each combination of decisions in the two price lists determines a combination of prospect theory parameters.
Both lists are composed of a constant lottery (Lottery A) and a lottery for which one outcome is increasing from one row to another (Lottery B). In the first list introduced in the upper part of Table 3, Lottery A always pays €8 with probability 0.3 and €2 with probability 0.7. Lottery B pays €1 with probability 0.9 and, with probability 0.1, an amount increasing from €13.6 (first decision) to €340 (last decision). In the second list introduced in the lower part of Table 3, the Lottery A always pays €8 with probability 0.9 and €6 with probability 0.1. The Lottery B pays €1 with probability 0.3 and, with probability 0.7, an amount increasing from €10.8 (first decision) to €26 (last decision). For both price lists, more subjects should choose Lottery B when proceeding down the list as the value of Lottery A is constant while the value of Lottery B increases. Contrary to HL, this procedure enforces monotonic switching by asking subjects at which question they want to switch from Lottery A to Lottery B in each list.Footnote 6 If this procedure is selected for payment, one decision is randomly selected in one of the two lists for payment.
2.3 Laboratory financial decisions
The three laboratory financial decisions reproduce three types of financial decisions under risk in the laboratory: a portfolio decision, an insurance decision, and a mortgage decision.
- Portfolio task::
-
The portfolio task reproduces an investment decision. Subjects are told that they have to manage a fund of €100. To invest this money, they have the choice between three projects. The first project pays a safe amount of €0.6 for each euro invested. The second project pays, for each euro invested, €0.2 with probability 0.5 and €1.4 with probability 0.5. The last project pays, for each euro invested, €0.2 with probability 0.8 and €4.2 with probability 0.2. Subjects can freely divide the €100 between the projects, but they have to invest all the money. For practical issues, investments must be non-negative integers.
Formally, they are paid according to the lottery Lj,k, defined as:
$$ L_{j,k}=\left\{ \begin{array}{ll} 0.6\times(100-j-k)+0.2\times(j+k) \text{ with }p=0.4\\ 0.6\times(100-j-k)+0.2\times j+4.2\times k \text{ with }p=0.1\\ 0.6\times(100-j-k)+1.4\times j+0.2\times k \text{ with }p=0.4\\ 0.6\times(100-j-k)+1.4\times j+4.2\times k \text{ with }p=0.1 \end{array} \right. $$They choose (j,k) ∈⟦0,100⟧2 such that j + k ≤ 100.
Projects are increasing in expected value (€0.6 for the first, €0.8 for the second, and €1 for the third), but are also increasing in their payoff variances. Thus, investments in the second and third projects should decrease as risk aversion increases. We summarize the decision in a single measure given by the expected value of the lottery Lj,k. The expected value should decrease as risk aversion increases.
- Insurance task::
-
The insurance task captures how subjects cover risks. Subjects are given an endowment of €10. However, this endowment may be lost with probability 0.1. They can partially insure themselves against this risk. They choose one insurance scheme out of five possibilities. Insurance schemes cost either €0, €0.5, €1, €1.5, and €2.5. If the endowment is lost, the insurance pays three times the insurance fee. Subjects are thus paid according to one of the five lotteries described in Table 4. Risk-seeking and risk-neutral subjects should choose not to buy any insurance (Lottery 1). The chosen insurance fee should increase as risk aversion increases.
- Mortgage task::
-
The mortgage task assesses the repayment profile that subjects would prefer when investing in real estate. Subjects are told that they have taken out a loan of €10 that must be repaid in 10 years. Every year, they receive an income of €1.5, and they have to pay the interest on the loan. They have the choice between three options that vary regarding the interest rate of the first year and the volatility of following interest rates. With the first option, the interest rate is fixed at 7%. They thus pay €0.7 per year (€10 × 7%). With the second option, the interest rate is at 6% for the first year. The first year, they thus pay €0.6. Any following year, this rate may vary, up to two percentage points below its value of the previous year and up to two percentage points above its value of the previous year. With the third option, the interest rate is at 5% for the first year. Any following year, this rate may vary, up to four percentage points below its value of the previous year and up to four percentage points above its value of the previous year. To facilitate understanding, a figure showing the interest rates over 100 years is part of the instructions. Options are increasing regarding the risk taken but decreasing regarding the expected total payment. The number of the chosen option is thus decreasing as risk aversion increases.
2.4 Field behavior
We have six measures of risk exposure in the field. Three of them target investment decisions, two involve insurance choices, and one involves employment choice. Risk aversion is expected to have an unambiguous impact on four of these measures in the field (savings, risky investments, insurance, and deductible), as they are directly related to the variance of the final outcome and widely used to assess risk-taking in the field. For the remaining two measures (self-employed and owning real-estate) the expected relationship is less straightforward. However, some previous studies have shown that risk attitudes may influence the decision to become self-employed or to invest in real estate. We thus include these measures to diversify our investigation of financial domains. There may be potential specific risk attitudes across these. We discuss each of the field behavior in turn below.
The first measure gives the total balance that subjects have in their current accounts, savings accounts, term deposit accounts, savings bonds or savings certificates, and bank savings schemes. It is expressed in thousands of euros.Footnote 7 One would expect that a more risk-averse individual would have a higher degree of (precautionary) savings, to guard against short-term financial reverses. Thus, we feel that savings will increase as risk aversion increases (for a given income) since savings are safe, and so this should be positively correlated with one’s measured financial risk preferences. This measure has previously been used to link experimental and field behavior by, for example, Noussair et al. (2013), Sutter et al. (2013), and Galizzi et al. (2016).
The second measure tells us the percentage of earnings that is invested in risky accounts. Risky accounts include, but are not limited to, growth funds, share funds, bonds, debentures, stocks, options, or warrants. In general, we expect that the percentage of earnings invested in risky accounts will decrease with risk-aversion, so that one would expect risky financial investments in the field to be positively correlated with risky financial decisions in our own (smaller-stake) investment tasks. This measure has been used previously in Dohmen et al. (2011), Noussair et al. (2013), and Drerup et al. (2017).
The last investment measure concerns owning real estate investment properties. It is equal to one if subjects own real estate that is not used as their own home, second home or holiday home. While real estate typically increases in value over time (and so might be considered non-risky), many of us remember the collapse in prices in the late 2000’s, with properties losing as much as 75% of their value, and the large losses in our own financial portfolios. One could also consider that the relative irreversibility of real estate investment and its lack of liquidity make it riskier. So owning investment real estate, generally speaking, involves more risk than savings but less than stocks. These factors lead us to expect that owning investment real estate will be negatively correlated with risk aversion. This measure has been used previously in Noussair et al. (2013).
People who dislike risk are more likely to wish to insure against loss, even paying a substantial premium to do so. Our first insurance measure is related to financial insurance. It tells us if subjects have a single-premium insurance policy, a life annuity insurance, or endowment insurance (not linked to a mortgage). This measure is equal to one if the subject possesses any financial insurance. Since a physical calamity could be disastrous, leaving one’s family without income, risk aversion would seem to be closely linked to the desire to purchase such insurance. We expect that the likelihood of being insured will increase as risk aversion increases. This measure has also been used previously in Noussair et al. (2013).
The second insurance measure concerns health insurance. It is equal to one if subjects have chosen a voluntary deductible for their health insurance. A higher deductible increases the variance of outcomes. We thus expect that the likelihood of choosing a deductible will decrease as risk aversion increases. While we are not aware of any studies using this measure to assess the performance of laboratory measures of risk attitude, some studies use insurance deductible choices directly to estimate risk attitude (e.g., Cohen and Einav 2007; Sydnor 2010; Barsegghyan et al. 2013).
Finally, we consider whether individuals are self-employed. This measure is equal to one if subjects are freelancers or have another independent profession. Since owning one’s own business has considerably more uncertainty than receiving a regular paycheck, we would expect entrepreneurial people to be less risk averse than others. Indeed, Dohmen et al. (2005) and Hardeweg et al. (2013) or Falk et al. (2018) found that self-employment decreases as risk aversion increases. However, studies on entrepreneurship have provided less clear findings on the link between entrepreneurship and risk taking, with many finding that risk attitudes between entrepreneurs and non-entrepreneurs differ in surveys but not in measures elicited in lab experiments (Holm et al. 2013; Andersen et al. 2014; Koudstaal et al. 2015). We thus include this variable to study if we can identify a relationship between our risk attitudes and self-employment.
The field measures are statistically described in Table 5. The number of observations per measure shows that not all variables are measured for all subjects. Before answering each block of questions, subjects were given the option to answer if they were willing to answer. If subjects were not willing to answer, the measure is not available.
Table 6 gives the Pearson’s rank-correlation coefficient between pairwise combinations of field behavior. Each behavior is related to, at least, two other behaviors. Field behaviors are globally related to one another but correlation coefficients are far from perfect correlation (the highest coefficient is equal to 0.17). It means that each behavior has its own determinants and thus, it makes sense to study if risk aversion can explain each field behavior.
3 Results
First, we present the methodology used to compute a risk-aversion parameter based on decisions in the tasks measuring risk attitude and we compare the value of this parameter between measures. Second, we study correlations between measures of risk attitude and laboratory financial decisions. Finally, we study correlations between measures of risk attitude and field behavior.
3.1 Aggregate risk-aversion parameter
Each measure of risk attitude is expressed on its own scale. To measure risk aversion on a common scale, we estimate a risk-preference parameter for all procedures measuring risk attitude (with revealed preferences). This enables us to make between-procedure comparisons and to create a single measure of risk preferences available for most of our sample. For all incentivized procedures, we use a CRRA specification for the utility function following influential literature in the estimation of risk attitude (Andersen et al. 2008; Wakker 2008; Dohmen et al. 2011). The parameter r represents the concavity of the utility function. Risk aversion increases as the value of r decreases.
All incentivized procedures except Tanaka et al. (2010) measure risk aversion based on expected-utility maximization. Tanaka et al. (2010) is designed to allow for probability weighting. Instead of maximizing the expected value, individuals are modeled as maximizing the expected prospect value. We reproduce their approach by using the functional form of Prelec (1998) for the probability function: π(p) = exp[−(−lnp)α]. α gives the probability sensitivity.Footnote 8
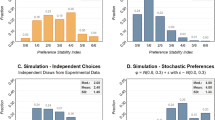
Estimation methods of the risk-aversion parameter are presented in Appendix C. This parameter is computed for 872 subjects and its mean value is equal to 0.060 (s.d. = 1.40). We refer to this parameter as the “aggregated risk parameter” since it aggregates risk-aversion parameters estimated with different methods (even if, for each subject, the risk aversion parameter is estimated with a single procedure). Estimated values for each procedure are presented in Table 7, along with statistics describing our laboratory measures. Bar plots of the decisions and risk-aversion parameters are available in Appendix D. Note that our results are robust to the exclusion of subjects switching multiple times (see Section E.4 of the Appendix).
Let us introduce our first result.
Result 1
There is no consistency across incentivized measures of risk attitude.
We compare the estimated risk parameter across the incentivized risk-elicitation procedures (thus excluding the WTR measure). We make pairwise comparisons using two-sided t-tests since the risk-elicitation procedures have been implemented on different subjects. TCN is significantly different from HL (p < 0.001) and from GP (p= 0.051). The only measures that are not statistically different are HL and GP (p= 0.141). We reject that EG is similar to the other measures at a 1% level for each pairwise comparison. This can be explained by the surprisingly high proportion (43%) of subjects that have chosen to take no risk in the EG task. This proportion is much higher than usually found in the literature (e.g., in Eckel and Grossman (2008) 4.3% of the subjects choose the option with no risk). Overall, we find that the measures of risk attitude are mainly inconsistent with each other.
3.2 Measured risk attitude and financial laboratory decisions
In this subsection, we study whether our measures of risk attitude can explain laboratory financial decisions. In order to lead the analysis in a meaningful and intuitive way, we reverse-code the decisions of the insurance task so that decisions in all three tasks are decreasing as risk aversion increases.
We regress the outcome of each measure of risk attitude on each laboratory financial decision. We also include demographic and income characteristics as controls. Regressions are described by the following model:
Lab Financial is consecutively equal to the decision in the insurance task, the decision in the mortgage task or the expected value of the lottery in the portfolio task. Risk Attitude is consecutively equal to the dummy variable based on one of the Dohmen et al. (2011)’s questions (WTR–G and WTR–S), to the estimated aversion parameter with one of the procedures (HL, GP, Tanaka, EG) or to the estimated aversion parameter with any of the procedures (aggregated parameter).
Regressing independently the risk-aversion parameters of each incentivized procedure on the laboratory financial decisions enables us to compare the performances of the different procedures. Regressing pooled estimations allows us to go beyond the specificity of each procedure to study if, overall, these procedures explain decisions in the laboratory financial decisions. Results are presented in Table 8. We only display the effect of the measure of risk attitude for each of the 21 regressions, since the other independent variables are controls.
Result 2
Most measures of risk attitude correlate with the laboratory financial decisions.
We first analyze which measures explain which laboratory financial decisions. Behavior in both the portfolio task and in the mortgage tasks is explained by almost all risk-elicitation procedures. There is no major difference in how well these tasks explain decisions. The insurance task is, however, singular. Behavior in this task is explained only by one measure (HL) and even the aggregated risk-aversion parameter cannot explain it (p= 0.294). This task can be summarized as a single lottery choice among mean-decreasing and variance-decreasing lotteries. In that sense, it is closely related to the GP and EG procedures. However, the framing is different, as subjects are told that they can insure themselves against a loss. This loss framing combined with an insurance framing may explain the behavioral change. Finally, we find that all statistically significant effects are in the expected direction as the value of the decision in the laboratory financial decisions has been ordered to decrease with risk-aversion.
We then compare performances between risk-elicitation procedures. GP, WTR–G, WTR–S and EG perform equally well, as their impact on behavior in the mortgage and the portfolio tasks is significant at the 5% level. They also explain at least one of these tasks at a 1% level. However, they do not explain behavior in the insurance task and HL is the only measure that has a significant impact on this task (p= 0.034). The HL measure also helps to explain behavior in the portfolio task at the 5% level (p= 0.033), but not in the mortgage task (p= 0.527) and it does not explain any laboratory financial decision at a 1% level. Based on this approach, TCN has the weakest performance of all measures; its impact on behavior in the portfolio task is only marginally significant (p= 0.070).Footnote 9 This analysis suggests that the most complex procedures are outperformed by simpler procedures. It is possible that the structure of the laboratory financial decisions is closer to the structure of the simpler procedures, which may also contribute to explain their higher performance.
Result 3
The most sophisticated measures of risk attitude are less able to explain behavior in laboratory financial decisions.
3.3 Measures of risk attitude and field measures
We present whether our measures of risk attitude can explain field decisions. Following previous methodology, we regress the outcome of each measure of risk attitude on each field measure:
Field Measure is consecutively equal to the amount of savings, the percentage of risky investments, having real estate, having financial insurance, having health insurance deductible and being self-employed. As in the previous subsection, Risk Attitude is consecutively equal to each measure of risk attitude or to the aggregated risk parameter.
Result 4
None of the measures of risk attitude explain field behavior.
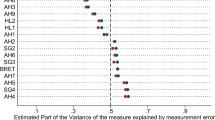
We first analyze regressions of the different measures on field behavior reported in Table A2 in the Appendix. The lack of explanatory power of the different risk-elicitation procedures is striking: no measure of risk attitude is statistically significant at even a 10% level in any of the thirty-six regressions. As a result, we are not able to discriminate among procedures since they all consistently fail to explain field measures. Based on our sample, this analysis raises serious concerns about how well common measures of risk attitude explain field behavior.
To challenge these findings, we then focus on the aggregated risk parameter. This aggregated parameter is less affected by the specificity of each procedure, and it is estimated for a larger number of subjects than each individual procedure. Table 9 reports the results of regressions of the aggregated parameter on our different field measures. These regressions reveal a trend suggesting that being insured and owning real-estate investments are negatively impacted by the aggregated risk parameter (p= 0.084 and p= 0.098, respectively). This result for insurance goes in the expected direction: purchasing insurance allows people to decrease the risk, so that more risk-averse individuals should be more insured.
The aggregated risk parameter has no statistically significant impact on the other field measures at any conventional levels. Thus, the estimated risk parameter has overall little explanatory power. Could it stem from a lack of statistical power? To address this point, we calculated the effect size and the statistical power of the risk parameter in the different regressions. The effect size is measured using marginal effects for logistic regressions, standardized coefficients and f2 for OLS regressions.Footnote 10 Reported power tests are the estimated statistical power and the estimated number of observations needed to find a statistically significant effect at a 5% level with a statistical power of 80%.Footnote 11 Analyzing statistical power provides us with an estimation of how reliable our findings are. Our conclusion regarding the absence of effect of the aversion parameter on the probability of being self-employed is deeply rooted, since the statistical power is above the threshold of 80%. For the other variables, our statistical power is below this threshold. For these variables, obtaining a p-value under 5% with a power above 80% would require a great increase in the sample size (between 1763 and 142857 observations).Footnote 12
In conclusion, we observe that the effects of the aggregated parameter on field behavior are small at best and are either statistically-insignificant or weakly significant. The inability of our standard measures of risk attitude to explain field behavior goes beyond the specificity of each procedure since even the aggregated risk-preference parameter does a poor job of explaining risky decisions in the field.
4 Discussion and conclusion
Based on a large-scale experiment, we evaluate if experimental measures of risk attitude are able to explain risky behavior in both experimental settings and naturally-occurring settings. First, we confirm previous findings on the inconsistency between measures of risk attitude. Second, we find that these measures have some predictive power on behavior in experimental settings, and that the most complex procedure (TCN) is outperformed by simpler procedures. Finally, we find no correlation between field behavior and measures of risk attitude. This finding is confirmed for all of the implemented measures, either simple or complex. We thus conclude that while measures of risk attitude can explain behavior in the laboratory, they fail to explain behavior in external settings.
These findings may result from several potential explanations such as the domain-specific nature of risk attitudes, different drivers of risky behavior in the field, weaknesses of the expected-utility-theory paradigm on which most measures are built, and cognitive processes.
Regarding the first possible explanation, studies in experimental psychology approach risk attitudes as being content—and context—dependent. In particular, Weber et al. (2002) developed a scale measuring risk-taking across six domains: financial, health, ethical, recreational, investment and gambling decisions. Using this scale, several studies have found that risk-taking is indeed domain-specific (Weber et al. 2002; Hanoch et al. 2006). In the economics literature, Reynaud and Couture (2012) and Deck et al. (2013) investigated whether domain-dependence could explain the inconsistency between measures of risk attitude. While Reynaud and Couture (2012) conclude that domain-dependence may explain this inconsistency, the results from Deck et al. (2013) do not support this finding.
In our study where we investigate decisions in various financial domains, one could claim that the experimental measures are perceived as gambling decisions in contrast with field measures. However, the lack of explanatory power of the measures of risk attitude for any field financial behavior investigated—independently of the domain—and the absence of difference between the general and domain-specific questions of Dohmen et al. (2011) provide little evidence that our results are due to the domain-specific nature of risk attitudes.
A second possible explanation could be that behavior under risk in natural settings is mainly driven by other factors than risk preferences. A major difference between experimental measures and field behavior is that in the field the “perception of risk” (Slovic 1987) is more difficult to evaluate than in an experimental setting. In an experimental setting, probabilities are defined exogenously, whereas they are subjectively evaluated in the field and they arise endogenously. Risk perception has been found to differ widely between cultural backgrounds, while risk attitude was much more stable (Weber and Hsee 1998). Differences in perceived risk may also be related to moral values, peer effects or external constraints. Many important risky decisions in the field, like buying a house, investing in the stock market and choosing a pension plan are much more complex than the relatively simple lottery choices that subjects face in an experiment. For such complex problems, decisions may result from household preferences more than individual ones, and people may also seek advice (for example 56% of the American households ask for advice from financial professionals, see Egan et al. (2019) or copy the choices of people that they consider successful (social learning). They may thus end up displaying a different risk attitude than they would if they were confronted with a simple problem where social sampling is not available (Offerman and Schotter 2009).
If the risk perceptions are the primary driver of risky decisions in the field and if they differ from objective risks, it might contribute to explain why risk preferences elicited experimentally fail to explain actual behavior. Similarly, Noussair et al. (2013) highlight that the complexity of field behavior might be better captured by higher-order risk attitudes than by the second order-risk attitudes.
Third, most of the measures of risk attitude tested are based on expected-utility maximization. Perhaps such specifications may not be adequate, as probability weighting is important in guiding decision making (Kahneman and Tversky 1979). However, in our study the only measure of risk attitude that relies on prospect theory (TCN) performs as badly as other measures concerning the explanation of field behavior. Furthermore, it has the weakest performance in explaining laboratory financial decisions. Our results thus do not provide evidence that prospect theory is an improvement over the expected-utility framework.
A final possible explanation involves cognitive processes. Many subjects may process their answer depending on the framing of the questions. Thus, a given elicitation method may perform well when it is structurally similar to the task it is predicting, so that both types of answers are processed similarly. But if the elicitation method is -or if it is perceived as- structurally different, answers may be processed differently and this may lead to answers that do not seem to reveal the same risk attitudes. To explain that different elicitation methods produce different risk preferences, Pedroni et al. (2017) invoke different cognitive processes leading individuals to follow different strategies across methods. This cognitive explanation could also apply to our findings.
Our findings shed light on the existing gap between laboratory and field decisions under risk. Risk preferences seem to depend on the setting in which they are expressed. They are particularly difficult to evaluate for researchers, since both methods based on revealed preferences and methods based on the self-reported willingness to take risk do not seem to predict actual behavior. In line with the conclusions of Friedman et al. (2014), it appears that the mechanisms developed to measure risk preference do not accurately reflect financial behavior in the field. An ambitious research challenge will be to find a better match between measurement mechanisms and field behavior.
Notes
Tynan (2018) reports also generally weak correlations between the Blais and Weber (2006) Domain Specific Risk Taking scale (DOSPERT), based on self-reports and widely used in psychology, and laboratory tasks with either hypothetical or real earnings, and no correlation with self-reported risky behavior in life, except for heavy alcohol use and gambling.
However, many studies in psychology have found major differences in risk attitudes across such domains (e.g., Weber et al. 2002).
Both studies were developed at about the same time. We designed and conducted our experiment prior to the release of this working paper, without being aware of their project.
The original procedure is composed of three price lists. The additional price list is dedicated to estimating a loss aversion parameter. As loss attitude was not in the scope of our study, we have not implemented this last price list.
Note that this by no means ensures comprehension.
The value of the savings can be negative to capture the position of an individual with more debts than deposits.
In following analyses, we only consider the curvature parameter estimated with TCN as all other measures only estimate this parameter. However, under prospect theory, the risk attitude is not driven only by this parameter. In Section E.1, we also consider the probability-sensitivity parameter either independently or jointly with the curvature parameter.
The lack of explanatory power of TCN is confirmed when considering also the probability weighting parameter.
f2 is the variation of Cohen’s f2 associated with the aggregated risk parameter (Cohen 1988). This measure reports the increase in the explained variance due to adding a given variable in the regression, divided by the unexplained variance for normalization.
We used G*Power (Faul et al. 2009) to compute statistical-power measures. Thresholds for α and β were chosen following conventional standards for adequacy.
The magnitudes of marginal effects range between 0.001 (for self-employment) and 0.017 (for being insured). An increase in one unit of the risk parameter (approximately two-thirds of its standard deviation) increases the odds of field behavior to between 1% and 2%. For the continuous measures, an increase of one standard deviation of the parameter (1.5 units) leads to an increase of respectively 4.2% and 3.2% of standard deviation for the amount of savings or the percentage of risky investments. A rather large variation in estimated risk aversion has thus a rather small impact on field measures. The variations in Cohen’s f2 classify the effects on continuous field measures as no more than that one-tenth of an effect characterized as small (\(f^{2}_{small}\)= 0.02).
References
Andersen, S., Harrison, G.W., Lau, M.I., & Rutström, E.E. (2008). Eliciting risk and time preferences. Econometrica, 76(3), 583–618.
Andersen, S., Girolamo, A., & Harrison, G. (2014). Risk and time preferences of entrepreneurs: Evidence from a Danish field experiment. Theory and Decision, 77(3), 341–357.
Andreoni, J., & Harbaugh, W. (2009). Unexpected utility: Experimental tests of five key questions about preferences over risk. Working Paper University of Oregon, Dept of Economics.
Barseghyan, L., Molinari, F., O’Donoghue, T., & Teitelbaum, J.C. (2013). The nature of risk preferences: Evidence from insurance choices. American Economic Review, 103(6), 2499–2529.
Binswanger, H.P. (1980). Attitudes toward risk: Experimental measurement in rural India. American Journal of Agricultural Economics, 62(3), 395–407.
Blais, A., & Weber, E. (2006). A domain-specific risk-taking (dospert) scale for adult populations. Judgment and Decision Making, 1(1), 33–47.
Caliendo, M., Fossen, F., & Kritikos, A.S. (2009). Risk attitudes of nascent entrepreneurs—New evidence from an experimentally validated survey. Small Business Economics, 32, 153–167.
Charness, G., & Gneezy, U. (2010). Portfolio choice and risk attitudes: an experiment. Economic Inquiry, 48(1), 133–146.
Charness, G., Gneezy, U., & Kuhn, M.A. (2012). Experimental methods: Between-subject and within-subject design. Journal of Economic Behavior & Organization, 81(1), 1–8.
Charness, G., Gneezy, U., & Imas, A. (2013). Experimental methods: Eliciting risk preferences. Journal of Economic Behavior & Organization, 87, 43–51.
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. 2nd edn.
Cohen, A., & Einav, L. (2007). Estimating risk preferences from deductible choice. American Economic Review, 97(3), 745–788.
Crosetto, P., & Filippin, A. (2013). The “bomb” risk elicitation task. Journal of Risk and Uncertainty, 47(1), 31–65.
Crosetto, P., & Filippin, A. (2016). A theoretical and experimental appraisal of four risk elicitation methods. Experimental Economics, 19(3), 613–641.
Deck, C., Lee, J., & Reyes, J. (2008). Risk attitudes in large stake gambles: Evidence from a game show. Applied Economics, 40(1), 41–52.
Deck, C., Lee, J., Reyes, J.A., & Rosen, C.C. (2013). A failed attempt to explain within subject variation in risk taking behavior using domain specific risk attitudes. Journal of Economic Behavior & Organization, 87, 1–24.
Ding, X., Hartog, J., & Sun, Y. (2010). Can we measure individual risk attitudes in a survey? IZA Discussion Paper No. 4807.
Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J., & Wagner, G.G. (2011). Individual risk attitudes: Measurement, determinants, and behavioral consequences. Journal of the European Economic Association, 9(3), 522–550.
Dohmen, T.J., Falk, A., Huffman, D., Sunde, U., Schupp, J., & Wagner, G.G. (2005). Individual risk attitudes: New evidence from a large, representative, experimentally-validated survey. IZA Discussion Paper, 1730.
Drerup, T., Enke, B., & Von Gaudecker, H.-M. (2017). The precision of subjective data and the explanatory power of economic models. Journal of Econometrics, 200(2), 378–389.
Dulleck, U., Fooken, J., & Fell, J. (2015). Within-subject intra-and inter-method consistency of two experimental risk attitude elicitation methods. German Economic Review, 16(1), 104–121.
Eckel, C.C., & Grossman, P.J. (2008). Forecasting risk attitudes: an experimental study using actual and forecast gamble choices. Journal of Economic Behavior & Organization, 68(1), 1–17.
Egan, M., Matvos, G., & Seru, A. (2019). The market for financial adviser misconduct. Journal of Political Economy, 127(1), 233–295.
Fairley, K., & Weitzel, U. (2017). Ambiguity and risk measures in the lab and students’ real-life borrowing behavior. Journal of Behavioral and Experimental Economics, 67, 85–98.
Falk, A., Becker, A., Dohmen, T., Enke, B., Huffman, D., & Sunde, U. (2018). Global evidence on economic preferences. The Quarterly Journal of Economics, 133(4), 1645–1692.
Faul, F., Erdfelder, E., Buchner, A., & Lang, A.-G. (2009). Statistical power analyses using g* power 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41(4), 1149–1160.
Franken, J.R., Pennings, J.M., & Garcia, P. (2017). Risk attitudes and the structure of decision-making: Evidence from the Illinois hog industry. Agricultural Economics, 48(1), 41–50.
Friedman, D., Isaac, R.M., James, D., & Sunder, S. (2014). Risky curves: On the empirical failure of expected utility. New York:Routledge.
Galizzi, M.M., Machado, S.R., & Miniaci, R. (2016). Temporal stability, cross-validity, and external validity of risk preferences measures: Experimental evidence from a Uk representative sample. Working Paper.
Galizzi, M.M., & Navarro-Martínez, D. (2019). On the external validity of social preference games: a systematic lab-field study. Management Science, 65 (3), 976–1002.
Gneezy, U., & Potters, J. (1997). An experiment on risk taking and evaluation periods. The Quarterly Journal of Economics, 112(2), 631–645.
Guiso, L., & Paiella, M. (2008). Risk aversion, wealth, and background risk. Journal of the European Economic Association, 6(6), 1109–1150.
Hanoch, Y., Johnson, J.G., & Wilke, A. (2006). Domain specificity in experimental measures and participant recruitment: an application to risk-taking behavior. Psychological Science, 17(4), 300–304.
Hardeweg, B., Menkhoff, L., & Waibel, H. (2013). Experimentally validated survey evidence on individual risk attitudes in rural Thailand. Economic Development and Cultural Change, 61(4), 859–888.
Harrison, G.W., & Rutström, E.E. (2008). Risk aversion in the laboratory. In Risk aversion in experiments (pp. 41–196): Emerald Group Publishing Limited.
He, P., Veronesi, M., & Engel, S. (2018). Consistency of risk preference measures: an artefactual field experiment from rural China. The Journal of Development Studies, 54(11), 1955–1973.
Hey, J.D., & Orme, C. (1994). Investigating generalizations of expected utility theory using experimental data. Econometrica, 62(6), 1291–1326.
Holm, H.J., Opper, S., & Nee, V. (2013). Entrepreneurs under uncertainty: an economic experiment in China. Management Science, 59(7), 1479–1724.
Holt, C.A., & Laury, S.K. (2002). Risk aversion and incentive effects. American Economic Review, 92(5), 1644–1655.
Jacobson, S., & Petrie, R. (2009). Learning from mistakes: What do inconsistent choices over risk tell us? Journal of Risk and Uncertainty, 38, 143–158.
Kahneman, D., & Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica, 47(2), 263–292.
Koudstaal, M., Sloof, R., & Van Praag, M. (2015). Risk, uncertainty, and entrepreneurship: Evidence from a lab-in-the-field experiment. Management Science, 62(10), 2765–3084.
Lejuez, C.W., Read, J.P., Kahler, C.W., Richards, J.B., Ramsey, S.E., Stuart, G.L., Strong, D.R., & Brown, R.A. (2002). Evaluation of a behavioral measure of risk taking: the balloon analogue risk task (bart). Journal of Experimental Psychology: Applied, 8(2), 75–84.
Levitt, S.D., & List, J.A. (2007). What do laboratory experiments measuring social preferences reveal about the real world? Journal of Economic Perspectives, 21(2), 153–174.
Lönnqvist, J.-E., Verkasalo, M., Walkowitzc, G., & Wichardt, P.C. (2015). Measuring individual risk attitudes in the lab: Task or ask? an empirical comparison. Journal of Economic Behavior & Organization, 119, 254–266.
Loomes, G. (1988). Different experimental procedures for obtaining valuations of risky actions: Implications for utility theory. Theory and Decision, 25 (1), 1–23.
Loomes, G., & Pogrebna, G. (2014). Measuring individual risk attitudes when preferences are imprecise. The Economic Journal, 124(576), 569–593.
Lusk, J.L., & Coble, K.H. (2005). Risk perceptions, risk preference, and acceptance of risky food. American Journal of Agricultural Economics, 87(2), 393–405.
Maart-Noelck, S.C., & Musshoff, O. (2013). Measuring the risk attitude of decision-makers: are there differences between groups of methods and persons? The Australian Journal of Agricultural and Resource Economics, 58, 336–352.
Noussair, C.N., Trautmann, S.T., & Van de Kuilen, G. (2013). Higher order risk attitudes, demographics, and financial decisions. Review of Economic Studies, 81(1), 325–355.
Offerman, T., & Schotter, A. (2009). Imitation and luck: an experimental study on social sampling. Games and Economic Behavior, 65(2), 461–502.
Pedroni, A., Frey, R., Bruhin, A., Dutilh, G., Hertwig, R., & Rieskamp, J. (2017). The risk elicitation puzzle. Nature Human Behaviour, 1 (11), 803.
Prelec, D. (1998). The probability weighting function. Econometrica, 66(3), 497–527.
Reynaud, A., & Couture, S. (2012). Stability of risk preference measures: Results from a field experiment on French farmers. Theory and Decision, 73(2), 203–221.
Sapienza, P., Zingales, L., & Maestripieri, D. (2009). Gender differences in financial risk aversion and career choices are affected by testosterone. Proceedings of the National Academy of Sciences, 106(36), 15268–15273.
Slovic, P. (1987). Perception of risk. Science, 236(4799), 280–285.
Sutter, M., Kocher, M.G., Glätzle-Rützler, D., & Trautmann, S.T. (2013). Impatience and uncertainty: Experimental decisions predict adolescents’ field behavior. American Economic Review, 103(1), 510–31.
Sydnor, J. (2010). (Over) insuring modest risks. American Economic Journal: Applied Economics, 2(4), 177–99.
Tanaka, T., Camerer, C.F., & Nguyen, Q. (2010). Risk and time preferences: Linking experimental and household survey data from Vietnam. American Economic Review, 100(1), 557–571.
Thunström, L., & Ritten, C.J. (2019). Endogenous attention to costs. Journal of Risk and Uncertainty, 59(1), 1–22.
Thunström, L., Nordström, J., Shogren, J.F., Ehmke, M., & van’t Veld, K. (2016). Strategic self-ignorance. Journal of Risk and Uncertainty, 52(2), 117–136.
Tynan, M. (2018). The domain-specific risk-taking scale lacks convergence with alternative risk-taking propensity measures. Graduate Theses and Dissertations, Iowa State University, 16477.
Verschoor, A., D’Exelle, B., & Perez-Viana, B. (2016). Lab and life: Does risky choice behaviour observed in experiments reflect that in the real world? Journal of Economic Behavior & Organization, 128, 134–148.
Vieider, F.M., Lefebvre, M., Bouchouicha, R., Chmura, T., Hakimov, R., Krawczyk, M., & Martinsson, P. (2015). Common components of risk and uncertainty attitudes across contexts and domains: Evidence from 30 countries. Journal of the European Economic Association, 13(3), 421–452.
Viscusi, W.K., Phillips, O., & Kroll, S. (2011). Risky investment decisions: How are individuals influenced by their groups? Journal of Risk and Uncertainty, 43(2), 81–106.
Wakker, P.P. (2008). Explaining the characteristics of the power (crra) utility family. Health Economics, 17(12), 1329–1344.
Wakker, P.P. (2010). Prospect theory: For risk and ambiguity. Cambridge University Press.
Weber, E.U., Blais, A.-R., & Betz, N.E. (2002). A domain-specific risk-attitude scale: Measuring risk perceptions and risk behaviors. Journal of Behavioral Decision Making, 15(4), 263–290.
Weber, E.U., & Hsee, C. (1998). Cross-cultural differences in risk perception, but cross-cultural similarities in attitudes towards perceived risk. Management Science, 44(9), 1205–1217.
Acknowledgements
This research has benefited from the support of IDEXLYON from Université de Lyon (project INDEPTH) within the Programme Investissements d’Avenir (ANR-16-IDEX-0005) and of the LABEX CORTEX (ANR-11-LABX-0042) of Université de Lyon, within the program Investissements Avenir (ANR-11-IDEX-007) operated by the French National Research Agency (ANR). The views expressed here do not necessarily represent the opinions of the Banque de France.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Charness, G., Garcia, T., Offerman, T. et al. Do measures of risk attitude in the laboratory predict behavior under risk in and outside of the laboratory?. J Risk Uncertain 60, 99–123 (2020). https://doi.org/10.1007/s11166-020-09325-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11166-020-09325-6