Abstract
One of the stylized facts underlying prospect theory is a fourfold pattern of risk preferences. People have been shown to be risk seeking for small probability gains and large probability losses, while being risk averse for large probability gains and small probability losses. Another fourfold pattern of risk preferences over outcomes, postulated by Harry Markowitz in 1952, has received much less attention and is currently not integrated into prospect theory. In two experiments, we show that risk preferences may change over outcomes. While we find people to be risk seeking for small outcomes, this turns to risk neutrality and later risk aversion as stakes increase. We then show how a one-parameter logarithmic utility function fits such stake effects significantly better under prospect theory than the power or exponential functions mostly used when fitting prospect theory models. We further investigate the extent to which the use of ill-suited functional forms to represent utility may result in violations of prospect theory, and whether such violations disappear when using logarithmic utility.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Almost any important real world decision involves considerable levels of risk. It thus comes as no surprise that attitudes toward such risks and how to model them have received considerable attention in economics. After the axiomatization by von Neumann & Morgenstern (1944) of Daniel Bernoulli’s 1738 expected utility theory (reprinted in Bernoulli 1954), it soon became clear that a setup richer than a function with one subjective dimension defined over lifetime wealth would be needed to model real world behavior such as the coexistence of insurance uptake and lottery play (for an early discussion of these issues, see Vickrey 1945). Markowitz (1952) provided such a framework by allowing preferences to differ between gains and losses relative to a reference point given by current wealth. Psychologists Preston & Baratta (1948) proposed a different solution, involving the subjective transformation of probabilities instead of outcomes—a solution that they considered to be psychologically more realistic (Lopes 1987).
The two approaches of subjectively transforming changes in wealth into utilities and subjectively transforming probabilities into decision weights were finally combined in prospect theory (Kahneman & Tversky 1979; Tversky & Kahneman 1992). Prospect theory is recognized by most scholars to be the leading descriptive theory of decision making under risk today (Barberis 2013; Starmer 2000; Wakker 2010). Nevertheless, its descriptive accuracy continues to be debated. Scholten & Read (2014) recently pointed out how prospect theory has generally neglected the type of changes in risk attitudes taking place purely over outcomes while keeping probabilities constant, as originally proposed by Markowitz (1952). Fehr-Duda et al. (2010) uncovered issues in the separability principle underlying prospect theory—a principle according to which changes in preferences over outcomes ought to be reflected purely in utility, while changes in preferences over probabilities ought to be reflected in probability weighting.
We set out to revisit the issue of whether a double-fourfold pattern of risk preferences—changes from risk seeking to risk aversion over the probability spectrum, and changes from risk seeking to risk aversion over the outcome spectrum—can be accommodated within a prospect theory framework without increasing the number of parameters. We thereby expand on the insights provided by Scholten & Read (2014) by generalizing the results to probabilities larger than their p ≤ 0.1 and by discussing the economic and psychological underpinnings of the candidate utility functions. This further allows us to revisit the separability violations pinpointed by Fehr-Duda et al. (2010), and thus to examine the descriptive validity of prospect theory in our setup. Indeed, while a good fit of functional forms is necessary for separability to hold, it is not sufficient, so that separability does not necessarily follow from a good fit of functional forms to the data.
We conduct two experiments to investigate these issues. The first one is an incentivized experiment over gains. While this has the advantage of rendering the decision real for subjects, it suffers the drawback of restricting our stake range and to make the investigation of losses problematic. We thus supplement the insights gained from experiment 1 with a second, hypothetical experiment. This allows us to examine the whole fourfold pattern of risk preferences over outcomes, including gains as well as losses. Furthermore, it serves the purpose of testing the stability of the results obtained in experiment 1 to truly large stakes, beyond what we could provide under real incentives.
In both experiments, we find relative risk aversion to increase in stakes at all probability levels, with qualitative reversals from risk seeking to risk aversion as stakes increase for some probability levels, as described in Markowitz’s original thought experiment. We also replicate qualitatively similar probability distortions across different stake levels, as originally found by Preston & Baratta (1948). We then proceed to fit functional forms to our data. We find the frequently used power utility function to provide the worst fit to our data—perhaps unsurprisingly, given how that function assumes constant relative risk aversion, while we find relative risk aversion to increase in stakes for gains. The logarithmic utility function proposed by Scholten & Read (2010) for intertemporal decisions, and applied to risk by Scholten & Read (2014), is found to fit our data best. The reason for this may lie in the psychological insight that the subjective sensation derived from a physical stimulus often tends to be proportional to the logarithm of the physical stimulus itself (known as the Weber-Fechner law). From an economic point of view the logarithmic utility function, which can be traced all the way back to Bernoulli’s 1738 essay, incorporates both increasing relative risk aversion and decreasing absolute risk aversion, which constitute the most common empirical finding (Wakker 2010).
Our results in terms of separability violations are more nuanced. Examining risk preferences over low and high stakes, Fehr-Duda et al. (2010) found stake effects and the resulting increase in relative risk aversion to be reflected in probability weighting rather than in utility curvature (see also Hogarth and Einhorn 1990). This violates the separability precept of prospect theory, whereby changes in outcomes ought to be purely reflected in utility curvature. We replicate their finding of high stakes shifting probability weighting downwards using a setup similar to the original one. We then show that, when combining our two-parameter weighting function with a logarithmic utility function, these stake effects on probability weighting disappear in experiment 1. This shows that one issue underlying separability violations can be found in the traditional neglect of qualitative changes in risk attitudes over outcomes, and from the inability of traditional power and exponential utility functions to account for such patterns. In experiment 2, however, the use of a logarithmic utility function does not eliminate the issue completely. Indeed, we still observe a separability violation for some stake levels, an issue that seems to be driven by different reactions to changes in outcomes across probabilities.
2 Theory and econometrics
2.1 Theoretical setup
We start from a description of our theoretical setup. We work with experimentally elicited indifferences c e i ∼ (x i ,p i ;y i ) throughout, whereby c e i is the certainty equivalent of a prospect giving a p i chance to obtain x i , and a complementary chance of 1 − p i at |y i | < |x i |. We are interested in particular in three models: i) Markowitz-expected utility (MEU); ii) Dual-expected utility (DEU); and iii) prospect theory (PT).
We start from MEU. For our experimental setup, the function takes the following form:
Other than under expected utility theory, where utility is formulated over total wealth, u under MEU captures a reference-dependent utility function over changes in wealth. This form of utility was motivated by the observation that people may take out insurance and play the lottery, and they often do so at the same time and regardless of their wealth levels. This led Markowitz to conclude that utility must be first convex and then concave over positive changes of wealth, while utility would be first concave and then convex for losses. To illustrate the plausibility of these patterns, Markowitz conducted the following thought experiment. Given the choice between a 10% probability of obtaining $10 and $1 for sure, most people would likely take the gamble. Scaling up all outcomes, most people might still prefer a 10% chance of obtaining $100 over $10 for sure. Continuing this exercise, however, one would invariably reach a point where almost everyone would prefer the sure amount—few people indeed would turn down $1 million for sure for a 10% chance at $10 million. Similarly, for losses most people may pay $1 rather than taking a 10% chance of losing $10, but very few would (or indeed could) pay if the amounts were scaled up by one million. Furthermore, Markowitz suggested that utility would also be steeper for losses than for gains, reflecting a general aversion to losses of wealth.
An alternative way of representing preferences was proposed a few years previously by psychologists Preston & Baratta (1948). Observing that risk preferences varied systematically over the probability scale for several different stake levels, they proposed to subjectively transform probabilities into decision weights instead of transforming outcomes into utilities. Mathematically, this constitutes the dual function of expected utility. This function has been axiomatized for the dual of rank-dependent utility by Yaari (1987). Schmidt & Zank (2007) provide an axiomatization for the dual of the reference-dependent MEU. This can be represented as follows:
where π represents a subjective decision weight associated to a given probability p that is not necessarily equal to the probability p itself, and the subscript s indicates the sign of the outcomes, allowing for different decision weights for gains and for losses. Risk preferences in this setup are thus completely represented by the decision weight.
Finally the combination of the primal (MEU) and the dual (DEU) results in PT, which incorporates nonlinear transforms of both outcomes and probabilities and takes the following form:
where v(.) represents a utility or value function with a fixed point at 0, which is not necessarily the same function as indicated by u above under the linear probability assumption (Bleichrodt et al., 2007; Schmidt & Zank 2008). Prospect theory’s separability precept then implies that changes in outcomes x i and y i ought to affect only the utility function v, with the decision weights π s invariant to such changes. Whether changing risk preferences over outcomes for constant probabilities can be accommodated by the utility function v will now depend inter alia on the functional forms adopted to represent utility—the issue which we discuss next.
2.2 The utility function and probability-outcome separability
We want to investigate the two connected issues of 1) whether we can fit the double fourfold pattern over outcomes and over probabilities in a prospect theory framework; and 2) whether we can do so without violating probability-outcome separability. Given this focus, the choice of functional form has important substantive implications. This is particularly true for the form of the utility function, since it is the fourfold pattern over outcomes which has not received much attention in the prospect theory literature.
Our task will now be to find a utility function that can accommodate qualitative changes in risk preferences over the outcome space while holding probabilities constant, assuming decision weights π(p) that are invariant over such changes (i.e., they only depend on p, and not on x or y). To do this, it is useful to represent the decision weight in its fully general form according to Eq. 3:
where we dropped the subscript s for notational convenience. Given that decision weights in this formulation are invariant to outcomes by definition, our task will now be to find a utility function v that allows us to accommodate patterns of changing risk preferences.
To organize our ideas, let us start from DEU, where u(x) = x. Treating outcomes linearly, that model can clearly not explain patterns of relative risk aversion that change over outcomes. Let us assume without loss of generality that y = 0, thus giving us c e i = π(p)x i . For example, if π(0.5) = 0.4 and x i = 10, we will observe c e i = 4. If we now increase the outcome such that x i = 100, assuming separability to hold we will observe c e i = 40, i.e. the increase in the certainty equivalent must be directly proportionate to the increase in the outcome. Clearly, such directly proportionate changes are at odds with Markowitz’s observation that preferences can change from risk seeking to risk averse (and vice versa for losses) while holding probabilities constant.
Looking at nonlinear utility transformations we can start from arguably the most popular functional form, power utility. This function owes its popularity to the ease with which it can be manipulated and fit to data, and the good fit it has been found to provide in many cases (Wakker 2008). This functional form was for instance used by Tversky & Kahneman (1992) to estimate prospect theory parameters, and also constitutes the main functional form employed by Fehr-Duda et al. (2010) in their investigation of separability (although they also tested the stability of the phenomenon to other functional forms, an issue to which we will return below). The function takes the following normalized form
with ρ > 0 indicating concave utility for gains, and 𝜃 > 0 indicating convex utility for losses (decreasing sensitivity), while λ > 1 indicates loss aversion. For values of ρ = 1, the function converges to l o g(x) (and if 𝜃 = 1 to − λ l o g(−x) for losses) (Wakker 2008). This function is also known as the constant relative risk aversion (CRRA) function, since its coefficient of relative risk aversion for gains is simply equal to ρ, and hence independent of the function’s argument x.Footnote 1 To determine whether this utility function can accommodate changing patterns of risk aversion over outcomes, take two stake levels, designated by s for small stakes, and ℓ for large stakes. Let us assume that large stakes are given by k > 1 times small stakes. Using Eq. 4 and substituting the utility from Eq. 5, we obtain that for power utility |c e ℓ | = |k c e s ∣, i.e. the certainty equivalent for high stakes must be directly proportional to the certainty equivalent for low stakes. This, however, directly contradicts Markowitz’s thought experiment, which predicts |c e ℓ | < |k c e s |. We thus conclude that power utility is not suited to capturing changing patterns of risk preferences over outcomes.
In order to accommodate the type of pattern that emerges from Markowitz’s thought experiment, we thus need to look at utility functions able to accommodate increasing relative risk aversion (IRRA). Importantly for our purpose, such functions can accommodate patterns that change from risk seeking to risk aversion, implying that for small stakes it can accommodate risk seeking for gains by π(p)v(x) > v(p x), while this pattern may reverse as all outcomes are increased so that π(p)v(k x) < v(p k x) for some k > 1 (and vice versa for losses).Footnote 2 This captures the intuition that as outcome magnitude increases, the utility of the outcomes increases less than proportionally.
A prime candidate exhibiting this property is the exponential function. The normalized version takes the following form for values of μ,ν > 0, indicating decreasing sensitivity:
For μ = 0 and ν = 0 the functional form is linear and becomes v(x) = x and v(x) = −λ(−x) for gains and losses respectively. This functional form was used for instance by Köbberling & Wakker (2005) to fit data from mixed gain-loss prospects, and by Choi et al. (2007) to fit data from portfolio selection tasks implemented in a laboratory experiment. One potential drawback of the exponential function is that it is bounded, with a bound from above of 1/μ for gains, and a bound from below of −λ/ν for losses. If the function approaches this bound too rapidly, then it may increase quickly for relatively small changes from the reference point, while changes above a certain amount may no longer increase utility at all (Scholten & Read 2014). A further limitation of the function when fitting data over large outcome ranges may be that it exhibits constant absolute risk aversion (CARA). Most empirical results, on the other hand, indicate that decreasing absolute risk aversion (DARA) is a more accurate description of behavior (see Wakker 2010, and references therein).
An alternative is then the normalized logarithmic utility function (Rachlin 1992; Scholten and Read 2010, 2014). Under the usual decreasing sensitivity assumption the function takes the following form:
where γ > 0 indicates concavity for gains, and δ > 0 convexity for losses, while for γ = 0 and δ = 0 the function becomes again v(x) = x and v(x) = −λ x for gains and losses respectively. This function has the desirable empirical property of combining IRRA with DARA. It is also unbounded, meaning subsequent increases in outcomes will always further increase utility, no matter to what amount they are added. It furthermore captures an insight on human perception of physical stimuli such as brightness and loudness, known as the Weber-Fechner law. The Weber-Fechner law states that the subjective sensation deriving from a physical stimulus is proportional to the logarithm of the stimulus intensity itself (see Kontek 2011, for a discussion). Whether this insight generalizes to the perception of monetary outcomes under risk is a question we endeavor to answer below.
Some papers in the literature have also used two-parameter utility functions. The most popular among these is arguably the so-called expo-power function developed by Saha (1993). It can be constructed based on Eq. 6, by simply adding a power to the exponential formulation:
The power parameter ρ can be interpreted as an indicator of absolute risk aversion for gains, with ρ < 1 indicating decreasing absolute risk aversion, ρ = 1 constant absolute risk aversion, and ρ > 1 increasing absolute risk aversion. The parameter μ indicates levels of relative risk aversion, with μ < 0 indicating decreasing relative risk aversion, and μ > 0 increasing relative risk aversion. The interpretation for losses is similar. We are interested in the use of this function mainly under MEU, where it may allow us to capture changing patterns of risk attitudes over outcomes in the absence of probability weighting. Under PT this is not strictly needed, as discussed above, so that we will restrict ourselves to one-parameter functions in the interest of parsimony.
Before moving on, we need to devote some more attention to the issue of separability. The conditions on the utility function set out above constitute necessary rather than sufficient conditions for separability. Intuitively, we will need two more conditions for separability to hold. Imagine we would measure point estimates of utilities and decision weights rather than fitting functions to the data. Since we will always need nonzero lower outcomes to uniquely identify decision weights separately from utilities, a minimal condition will be that the utility estimated for a given outcome x will be the same whether this is the higher outcome in a small-stake prospect, or the smaller outcome in a large-stake prospect. A further complication arises when we proceed to estimating a whole probability weighting function, w, that traces decision weights over the whole probability spectrum. Indeed, we now need the changes in utility following changes in outcomes to be consistent across different probability levels. Both conditions are far from trivial, so that we may still observe separability violations even if we were to find a utility function that fits the patterns of changing risk aversion over outcomes quite closely. Accommodating qualitative changes in risk preferences and satisfying separability are thus two quite separate and different issues.
Finally, we need to select functional forms for the probability weighting function. We use the two-parameter probability weighting function developed by Prelec (1998):
where β governs mostly the elevation of the weighting function, with higher values indicating a less elevated function. This parameter can thus be interpreted as capturing probabilistic pessimism for gains, and probabilistic optimism for losses. The parameter α governs the slope of the probability weighting function and hence probabilistic sensitivity. A value of α = 1 indicates linearity of the weighting function, and α < 1 represents the typical case of probabilistic insensitivity (Abdellaoui 2000; Tversky & Fox 1995; Wu & Gonzalez 1996). All results presented below remain qualitatively unchanged if we use an alternative two-parameter function developed by Goldstein & Einhorn (1987) instead. However, the two-parameter function by Prelec provides a significantly better fit to our data.Footnote 3 One-parameter functions, such as the one proposed by Tversky & Kahneman (1992), are generally not suitable in our context, since we want to fit the variation over probabilities in the most flexible way possible, and allow for shifts of the probability weighting function as outcomes vary to provide a strong test of separability.
2.3 Econometric approach
The model just presented is deterministic in nature. To accommodate the possibility that people make mistakes, we now develop an explicit stochastic structure. Given that we aim to model preference relations c e i ∼ (x i ,p i ;y i ), we can represent the certainty equivalent predicted by our model, \(\hat {ce}_{i}\), as follows:
The actual certainty equivalent we observe will now be equal to the certainty equivalent calculated from our model plus some error term, or \(ce_{i}=\hat {ce}_{i}+\epsilon _{i}\). We assume this error to be normally distributed with mean zero, 𝜖 i ∼ N(0,σ i2) (see Train 2009). We can now express the probability density function ψ(.) for a given subject n and prospect i as follows
where ϕ is the standard normal density function, and 𝜃 indicates the vector of parameters to be estimated. The subscript i indicates that we allow the error term to depend on the specific prospect, or rather, on the difference between the high and low outcome in the prospect, such that σ i = σ|x i − y i |.Footnote 4 This allows the error term to differ for choice lists of different lengths, since the sure amount always varies in equal steps between x i and y i in our experimental design.
These parameters can now be estimated by standard maximum likelihood procedures. To obtain the overall likelihood function, we now need to take the product of the density functions above across prospects for each subject:
where 𝜃 is the vector of parameters to be estimated such as to maximize the likelihood function, and the subscript n indicates the subject-specific likelihood. The subscript s to the error term further indicates that we allow for heteroscedasticity across decision domains (i.e. differences in errors for gains and losses). Taking logs and summing over decision makers n we obtain
We estimate this log-likelihood function in Stata 13 using the Broyden-Fletcher-Goldfarb-Shanno optimization algorithm. Errors are always clustered at the subject level.
3 experiment 1: Incentivized gains
3.1 Experimental setup
Participants and setting The experiment was run as a classroom experiment at the beginning of a class in Advanced Microeconomics at the University of Reading, UK, in the fall term 2015. A total of 47 students showed up on the first day of class and participated in the experiment. We eliminate two students because they exhibited multiple switching behavior in some choice lists. Students had been taught the basics of expected utility theory in Intermediate Microeconomics the previous year. This discussion followed a standard exposition, and stressed neither initial wealth integration, nor were any violations of EUT discussed in class.
Students were told that their answers were to be kept anonymous and would not be traced back to them. Students were also told that there were no right and wrong answers, and that they only needed to record their preferences. They were also told that the lecturer would be using average responses (but never individual ones) as examples of behavior during class, and that they may find it interesting to look at their preferences as the course progressed.
Stimuli
We use two-outcome prospects throughout. The stimuli used in the experiment are reported in Table 1. We included three different probability levels, 0.1, 0.5, and 0.9. The stakes ranged from £10 to £200. High stakes were needed in order to meaningfully test the Markowitz patterns over outcomes with constant probability. Finally, non-zero lower outcomes were needed to separate utility curvature from probability weighting in parametric estimates of prospect theory. The stimuli were balanced in the sense that all stake levels were included for all probabilities. The order of the tasks was counterbalanced.
Incentives
Participants were told that two individuals in the class would be randomly selected to play one of their choices for real money. The selection took place based on random numbers attached to the questionnaires, in order to guarantee the anonymity of the selected students. Although paying for one randomly selected task may raise theoretical concerns under non-expected utility models, it is the standard procedure in this type of experiment. Empirically, tests of this issue did not find a difference between deterministic incentives and incentivization based on randomly chosen rounds (Bardsley et al., 2010; Cubitt et al., 1998). They constitute the only solution if one wants to obtain rich measurements of preferences for each subject. Randomization between subjects is also a standard procedure followed in the literature when high stakes are offered (Abdellaoui et al., 2008; Harrison et al., 2007). Some papers explicitly tested whether paying only some randomly selected subjects made a difference, and found none (Armantier 2006; Bolle 1990; Harrison et al., 2007). Full instructions are included in the online appendix.
3.2 Nonparametric analysis of results
We start by showing some descriptive results. To this end we obtain a nomalized risk premium as follows. First, we normalize the certainty equivalent to \(\frac {ce_{i}-y_{i}}{x_{i}-y_{i}}\). This is a measure of risk tolerance, and has the advantage that it is comparable across outcome levels. Conveniently, it corresponds to a decision weight, π(p i ), under DEU. To obtain also comparability across probabilities, we further subtract this risk tolerance measure from the probability of winning in a given prospect, to obtain the relative risk premium \(r_{i} = p_{i}-\frac {ce_{i}-y_{i}}{x_{i}-y_{i}}\). This can be interpreted as a measure of risk aversion. It is a measure of whether the decision weight for a given prospect under linear utility is a) lower than the probability itself (r i > 0, risk aversion); b) higher than the probability (r i < 0, risk seeking); or c) equal to the probability (r i = 0, risk neutrality). The risk premia are now perfectly comparable across both stakes and probabilities.
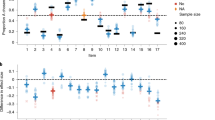
Figure 1 shows the mean normalized risk premia for all prospects with zero lower outcomes. Two general patterns stand out. First, within each stake level risk aversion clearly increases in probabilities. For the smallest probability of p = 0.1, we find significant risk seeking for all stake levels. For p = 0.9, we find significant risk aversion across all stake levels. Risk preferences for p = 0.5 are always intermediate between those of the more extreme probabilities. Second, across stakes the mean risk premia move up for every probability, indicating relative risk aversion increasing in stakes. For the intermediate probability of p = 0.5 we indeed find qualitatively different patterns across stakes as predicted by Markowitz—risk seeking for the smallest prize, and risk aversion for the largest prize, with risk neutrality for intermediate stakes.Footnote 5 The levels of risk aversion we find may seem low. The trend of relatively low levels of risk aversion is, however, consistent with the results from the international comparison of risk preferences reported by L’Haridon & Vieider (2016), where Britain constituted an outlier among rich countries.Footnote 6
We can represent these preferences non-parametrically by assuming either MEU or DEU. Since utility is only unique up to an affine transformation, we can normalize the lowest and highest outcomes in a series of prospects arbitrarily. By choosing u(x) ≡ 1 and u(y) ≡ 0, we can plot the non-parametric functions that result from probability variations while keeping the outcomes in the prospect constant. While not corresponding to Markowitz’s original thought experiment (where probabilities were held constant and outcomes varied), this representation is perfectly legitimate in terms of Markowitz’s theory. Figure 2a shows such a plot of utility for two stake levels (plots for other stake levels are similar), with monetary amounts on the abscissa and utility of money on the ordinate. In both cases, we observe the expected pattern of risk seeking for relatively small expected outcomes, and risk aversion for larger expected outcomes.
Problems become apparent when comparing the stake ranges over which we observe these patterns. For the low stake prospect offering a chance at £20 or else 0, we observe risk seeking up to an expected outcome of £10.8, and risk aversion from £16.8, with preferences changing somewhere in between. If one looks at the curve drawn using the £200 stake level, however, risk seeking ranges to well above £43. This is a clear contradiction with the risk aversion starting at £16.8 in the lower stake prospect. What this goes to show is simply that Markowitz-expected utility is not good at handling variation in probabilities.Footnote 7 Subjectively transforming probabilities likely constitutes a better way of capturing this type of variation (Preston & Baratta 1948; Yaari 1987).
Probability transformations combined with linear utility are shown in Fig. 2b for the same two stake levels, with probabilities shown on the abscissa and decision weights on the ordinate. These nonparametric representations are obtained for prospects with 0 lower outcomes from Eq. 4 under the linear utility assumption underlying DEU. For both stake levels, risk seeking for small probabilities is now reflected in a subjective weight that is larger than the objective probability, π(0.1) > 0.1. This is the probability attributed to winning the prize, and can thus be interpreted as a measure of optimism. For the largest probability, this pattern is inverted, i.e. π(0.9) < 0.9. Problems surface when looking at differences in stakes. Passing from £20 to £200, the function shifts systematically downwards. However, this cannot be captured in any of the subjective transformations, since the probabilities remain identical. In other words, we observe dual violations for the dual theory—it performs very badly at handling outcome variations.
3.3 Fitting prospect theory parameters
The issues just shown constituted the rationale for the development of prospect theory (Kahneman & Tversky 1979; Tversky & Kahneman 1992), which combines the non-linear reference-dependent outcome transformations proposed by Markowitz with non-linear transformations of probabilities into decision weights. This, however, raises the issue of whether differences across stake levels will purely be reflected in utility curvature, and differences across probabilities purely in probability weighting. Using state-of-the-art structural estimation techniques, Fehr-Duda et al. (2010) indeed found increases in stake sizes to register in probability weighting rather than in utility curvature. Prospect theory has also typically not incorporated the qualitative changes from risk seeking to risk aversion over outcomes emphasized by Markowitz (Scholten & Read 2014), which as we have seen above cannot be handled by the popular power utility function. In this section, we will start fitting functional forms to the data.
Table 2 shows parameter estimates of our main models. Testing PT with exponential utility against PT with power utility, we find the former to perform significantly better (p < 0.001, Clarke test).Footnote 8 Notice also how the confidence intervals estimated around the point estimates are much narrower with exponential utility than under power utility, which may indicate collinearity between utility curvature and the elevation of the probability weighting function using the power function. Indeed, PT with power utility performs no better than DEU in our setting—notwithstanding the clear violations of DEU we showed in the nonparametric analysis above (p = 0.190, likelihood-ratio test). Directly comparing MEU and DEU yields a clear verdict in favor of the Dual (p < 0.001, Clarke test). This reflects the fact that for the stake sizes here employed, variation of risk preferences across the probabilistic dimension is much more important than variation across stakes (Fehr-Duda & Epper 2012). This could change when stakes get truly important—an issue to which we will return in experiment 2.
Scholten & Read (2014) found a PT model with logarithmic utility to fit their data involving probabilities smaller than or equal to 0.1 significantly better than power utility. We confirm this result (p < 0.001, Clarke test), and extend it to exponential utility (p < 0.001, Clarke test). This result obtains because for small stakes the probability weights overpower the utility function, thus accommodating risk seeking pattern. For larger stakes, on the other hand, utility trumps weighting. Since this pattern in risk preferences holds especially for moderate probabilities of p = 0.5, a two-parameter probability weighting function is essential to accommodate the behavioral patterns observed in our data. Notice also that a similar elevation of the probability weighting function is observed in combination with the exponential utility function. This reflects the generally high levels of risk taking we find in our data—we will further discuss the implications of this below.Footnote 9
We have modeled the gain part of the double fourfold pattern of risk preferences across stakes and probabilities using a prospect theory formulation combining a logarithmic utility function with a two-parameter probability weighting function, which we indeed found to provide the best fit for the data. Nevertheless, stake effects have been shown to result in a more fundamental challenge to this type of modeling. Fehr-Duda et al. (2010) used low and high stake prospects of a type similar to the ones employed here to estimate a prospect theory model. Letting the parameters of the model depend linearly on a high stakes treatment dummy, they found that stake effects were reflected in the probability weighting function rather than in the utility function. Their results thus cast doubt on the separability of outcome and probability transformations underlying models such as prospect theory and rank-dependent utility.
We can now attempt to replicate this pattern in our data. Since we only have nonzero lower outcomes for the highest stakes in our data, however, we cannot follow their approach of making both the utility parameter and the weighting parameters dependent on stake levels. Instead we always estimate the utility function over the whole outcome range, without making it a function of the stake level. Probability weighting, on the other hand, can be made a function of stakes, since we have variation over probabilities at all stake levels. We hereby follow the same strategy of Fehr-Duda et al. (2010), by letting the two parameters of the weighting function (as well as the noise parameter) be a linear function of a stake-level dummy. If utility fully picks up our outcome variation, no stake effects on probability weighting should be found. If, on the other hand, separability is violated, we would expect to find stake effects in our data.
We estimate this model using power utility like Fehr-Duda et al. (2010), exponential utility, and with our best-fitting logarithmic utility function from above. As an independent variable, we use a dummy indicator for high stakes, which takes the value 1 if the stakes are £60 or higher (the results are not sensitive to where the line between high and low stakes is drawn exactly; they are also stable to inserting the monetary outcomes directly as an independent variable). Table 3 shows the regressions. The upper panel shows the results using power utility. We find a strong and highly significant effect of stakes on the probability weighting function. The effect goes in the direction of pessimism increasing in stakes. This effect replicates the effect found by Fehr-Duda et al. (2010). The strength can be seen from Fig. 3a—the high stakes weighting function is shifted downwards relative to the low stakes one, and crosses the 45 degree line at a much lower point. Indeed, we do no longer find probabilistic optimism (or risk seeking, given the linearity of utility) for p = 0.5 under high stakes. We do not find a significant difference in probabilistic sensitivity. Similar effects obtain with an exponential utility function, shown in the second panel in Table 3. While the effect on the elevation of the weighting function appears to be somewhat weaker quantitatively, it remains statistically highly significant.Footnote 10
We next look at the regression results using log utility, shown in the lower panel of Table 3. We now do not find any significant effect of stakes on the probability weighting function. Panel Fig. 3b shows graphically how the weighting function for high stakes remains as elevated as the one for low stakes. This is due to the better fit of the utility function, which is capable of accommodating the two-fold pattern of risk preferences over outcomes we found. The log utility function used thus absorbs all the stake variations over outcomes in our data.
3.4 Discussion of experiment 1
The data obtained for gains in experiment 1 show a double two-fold pattern of risk preferences. First, they show risk seeking for small stakes and risk aversion for large stakes at intermediate probabilities, as well as a general increase of relative risk aversion with stakes. Second, we found that relative risk aversion systematically increases in probabilities, thus replicating typical patterns of risk seeking for small probabilities and risk aversion for large probabilities at different stake levels. Modeling approaches relying on a single subjective dimension, such as Markowitz-expected utility and Dual-expected utility, were clearly shown to be rejected in the nonparametric analysis. Nonetheless, Dual-EU showed a clearly better fit, showing that for this type of stake range variations over probabilities are significantly more important than variations over outcomes.
Proceeding to parametrically fitting the data, a single parameter logarithmic function provided the best fit to our data. This extends a recent insight by Scholten & Read (2014) to moderate and large probability levels. This insight also goes beyond a mere fitting exercise, and tells us something substantive about how our subjects perceived the experimental stimuli. Indeed, the pattern of increasing relative risk aversion found cannot possibly be fitted using a power utility function, which encompasses constant relative risk aversion. Relative to the exponential function, the data are found to exhibit decreasing absolute risk aversion, which the latter cannot accommodate. This provides an indication that the observation of monetary stimuli indeed seems to follow something akin to the patterns postulated in the Weber-Fechner law—the subjective perception of a stimulus is proportional to the log of the stimulus itself. Using the logarithmic utility function in conjunction with a two-parameter weighting function furthermore made the effect of stake size on probability weighting disappear.
In contrast to Scholten & Read (2014), we used a two-parameter probability weighting function. In our setting such a function was indeed found to be essential, given the low levels of risk aversion we found, and the observation of the twofold pattern over outcomes for p = 0.5. Such high levels of risk taking may not be exceptional. L’Haridon & Vieider (2016) examined prospect theory functionals across 30 countries with students, and found quite elevated weighting functions to be the norm in developing and middle income countries. Vieider et al. (2013) and Vieider et al. (2016a) found these patters to extend to rural populations in developing countries. This may indeed also explain the more elevated weighting function found by Fehr-Duda et al. (2010) in their Chinese data.
The general elevation of the function may be dependent on the general level of risk aversion observed, and hence on the probabilities for which the two-fold pattern over outcomes is observed. In our case and given our stimuli, we observed this pattern most strongly for p = 0.5. This requires an elevated weighting function to a point where w(0.5) > 0.5, so as to guarantee that w(0.5)v(2x) > v(x) for low stake levels, as described by Scholten & Read (2014). Prospect theory can easily accommodate such an elevated weighting function under its modern form. While for instance the original formulation of prospect theory required subcertainty to explain violations such as the Allais paradox (see Kahneman and Tversky 1979, p. 281-282), under the modern version incorporating rank-dependance (Tversky & Kahneman 1992), this principle is replaced by a considerably milder condition that does not rely on w(0.5) < 0.5.Footnote 11
4 Experiment 2: Hypothetical gains and losses
4.1 Motivation
The results in experiment 1 present a clear verdict in favor of log utility. Nonetheless, that experiment suffered from some limitations. Most importantly perhaps, using incentivized tasks limited us to the examination of gains only, thus really only considering a ‘two-fold pattern’ over outcomes for gains. The stake variation we could use was also limited due to the incentives used, which resulted in not being able to replicate Markowitz’s thought experiment for small probabilities. We thus designed experiment 2 to complement experiment 1 on these issues. In particular, using hypothetical tasks will allow us to investigate losses as well as gains, and to use wider stake ranges.
4.2 Experimental setup
Participants and setting We recruited 51 students from a standing subject pool at the University of Reading. Most participants were new to experiments and studied economics or business. The general conditions were made to be as similar as possible to experiment 1. The experiment was again run using paper and pencil, and the instructions followed those for experiment 1 closely. The one major difference was that choices were hypothetical, and subjects were paid a fixed fee of £15 for their participation. The experiment lasted about 1 hour.
Stimuli
The stimuli are shown in Table 4. The outcomes range from £200—the highest outcome in experiment 1—to £100,000. Paralleling the design for experiment 1, all stake levels are present for all probabilities, and we added prospects with non-zero lower outcomes to be able to econometrically separate utility curvature from probability weighting. The stakes for gains are exactly replicated for losses. We did not include any mixed prospects, so that the loss aversion parameter λ cannot be identified.
4.3 Nonparametric analysis of results
We start from a nonparametric analysis of the data. Out of our 51 subjects, 10 (or 19.6%) switched multiple times between the sure outcome and the prospect at least in some cases. This rate is quite high for certainty equivalents, and significantly higher than in experiment 1 (p < 0.001, binomial test). Increased levels of noise are quite typical when using hypothetical stakes (Smith & Walker 1993), and Vieider (2017) specifically observed increased levels of multiple switching under hypothetical as compared to real payoff conditions. There is also a possibility, however, that the difference may at least in part be due to differences in subject pools. Consistent with experiment 1, we eliminate multiple switchers from the data, leaving us with 41 subjects.
Figure 4 shows the relative risk premia for gains. Compared to experiment 1, we find higher levels of risk taking for the stake level of £200, which was included in both experiments. This is particularly evident for the 50-50 prospect over that stake level, for which we cannot reject risk neutrality in experiment 2, while we found clear risk aversion in experiment 1. Other than that, however, the qualitative pattern looks very similar to the one found in experiment 1. For a given probability level, we can see risk aversion to increase steadily in stakes. For p = 0.1, we find risk seeking for lower stake levels, which turns into risk neutrality for the largest stakes. This pattern is consistent with Markowitz’s thought experiment, although for the stakes used we do not yet observe fully fledged risk aversion for the smallest probability. For p = 0.9 we find risk aversion throughout. For p = 0.5, the initial risk neutrality turns into risk aversion as the stakes increase. However, the increase over stakes is also less regular than seen in experiment 1. This is largely due to outliers and the relatively high levels of noise in the data. There is also a clear pattern of risk aversion increasing in the probability of winning for all stake levels.
Figure 5 shows the corresponding risk premia for losses, where a positive value now indicates risk seeking. Across probabilities, we find a pattern that is the mirror image of the one observed for gains. For the smallest probability of p = 0.1, we find risk aversion to be the prevalent pattern throughout. For p = 0.9, we find risk seeking across the outcome spectrum. For the intermediate probability of p = 0.5, risk neutrality cannot be rejected. This pattern is consistent with the fourfold pattern of risk preferences over probabilities incorporated into prospect theory. When it comes to Markowitz’s fourfold pattern over outcomes, however, we cannot replicate the patterns we found for gains. In particular, there does not appear to be a clear pattern to risk preferences as outcomes change for any of the probability levels. This finding is in agreement with previous evidence, with most studies investigating stake effects for losses finding no stake effects (Bouchouicha et al., 2017; Etchart-Vincent 2004; Fehr-Duda et al., 2010; Scholten & Read 2014).Footnote 12
4.4 Econometric fitting of functional forms
We now proceed to fitting functional forms to the data. We follow the same approach as for experiment 1, except that we normalize outcomes by dividing them by the highest outcome in the stimuli. This makes the utility coefficients easier to interpret given the wide stake range, and does not otherwise affect our results.
Table 5 shows the estimates of the functional forms. We start by discussing the models transforming only a single dimension subjectively—DEU and MEU. Once again, DEU can clearly be seen to fit our data significantly better than the primal (p < 0.001, Clarke test), thus confirming the results from experiment 1. Notice how this result is now stronger than it was before, seeing how the outcome range is much larger. Nonetheless, the variation of risk preferences found over outcomes is of second order importance relative to the variation we observe over probability levels. We also confirm another surprising result from experiment 1, namely that PT with power utility fits the data no better than the DEU model assuming linear probability (p = 0.485, likelihood-ratio test).
Among the full PT specifications, exponential utility clearly outperforms power utility (p < 0.001, Clarke test), as does logarithmic utility (p < 0.001, Clarke test). Among the latter two, logarithmic utility fits the data significantly better (p = 0.009, Clarke test), thus providing further support for the conclusions drawn from experiment 1. This difference appears to derive mainly from gains, however, since for losses utility is estimated to be linear under both exponential and logarithmic utility. Linear utility has indeed been found frequently for losses (see Abdellaoui 2000, for a discussion).
This leaves separability to be discussed. Table 6 shows regressions for our three PT models, where the parameters of the probability weighting function are made to depend on a dummy indicating high stakes (defined as a high outcome larger than £2,000 in absolute value). At first glance, the results appear to be once again perfectly in line with those of experiment 1. Indeed, we find separability to be clearly violated for gains when adopting a power function for utility. Adopting an exponential utility function instead, this violation appears to be somewhat reduced, and finally the violation disappears once we adopt the logarithmic utility function.
This result is, however, not quite as stable as in experiment 1. While the results presented for experiment 1 were indeed invariant to the cut-off point for the definition of high stakes, this is not the case for experiment 2. In particular for the smallest stakes of £200 and £400 we do find violations of separability. Table 7 shows the regressions from Table 6, except that the stake dummy is now defined such as to capture all but the two lowest stake levels. Other than in the results shown above, we now find that probabilitistic sensitivity is lower under high stakes than it is under low stakes. This clearly violates one of the conditions necessary for separability to hold, and indeed we also find the elevation parameter β to be affected by stake size, with more probabilistic pessimism for gains for higher stakes. This effect still appears to be strongest for power utility and weakest for log utility, but there remains a clear violation in the last case, and the differences between the utility functions are now quantitative rather than qualitative.
4.5 Discussion of experiment 2
Compared to experiment 1, experiment 2 fielded much larger (hypothetical) stake sizes, and losses in addition to gains. For gains, we found very similar patterns to those observed in experiment 1. Fitting functional forms to the data, we once again found a logarithmic utility function combined with a two-parameter probability weighting function to fit the data best. The results thus broadly confirm the insights obtained from experiment 1. For losses, we observed systematic variations over probabilities, but not over stakes. This is in line with most of the literature investigating stake effects for losses. Together, these findings confirm the existence of a fourfold pattern of risk preferences over probabilities. Over outcomes, we confirm the existence of a two-fold pattern over gains, but we are unable to reproduce the whole fourfold patterns over gains and losses as postulated by Markowitz. This may well be due at least in part to the unfamiliarity of decisions over large losses in our subject pool. It may be difficult to contemplate losses over amounts that a respondent is unlikely to have.
Our conclusions about separability are more nuanced. We observe separability violations over the whole outcome range when using either power or exponential utility. These violations are eliminated when adopting a logarithmic utility function. However, other than in experiment 1, this is only the case for some stake levels, while we still observe violations when allowing the weighting function to differ between the lowest two stake levels and the higher ones. Interestingly, this violation seems to be driven by a tilt in the weighting function for higher outcomes—an effect that was also observed by Fehr-Duda et al. (2010). In particular, high stake levels appear to reduce probabilistic sensitivity. This insight is consistent with studies finding such a rotation of the weighting function when stimuli are affect-rich or salient (Hsee & Rottenstreich 2004; Rottenstreich & Hsee 2001; Vieider et al., 2016b).
5 Conclusion
Risk attitudes have been found to vary significantly with the characteristics of the decision problem. Historically, Markowitz (1952) proposed to model such variations using a reference-dependent utility function defined over changes in wealth, while treating probabilities linearly. Psychologists, on the other hand, proposed early on to model risk preferences using subjective transformations of probabilities into decision weights, while treating outcomes linearly (Preston & Baratta 1948). While prospect theory combined these two different traditions into one unified framework (Kahneman & Tversky 1979; Tversky & Kahneman 1992), Markowitz’s fourfold pattern over outcomes has generally been neglected in this setup (Scholten & Read 2014). Indeed, power utility—the most popular utility function used in the prospect theory literature (Wakker 2008)—cannot accommodate changes in relative risk aversion over outcomes while keeping probabilities constant.
In two experiments, we revisited the issue of relative risk aversion changing over outcomes, and to what extent such changes can be accommodated using a prospect theory framework. We found clear changes in risk preferences for gains as stakes increased, including qualitative changes from risk seeking to risk aversion. We did not find any changes in relative risk aversion over stakes for losses. Fitting functional forms to this pattern, we found probability transformations to provide a better fit than outcome transformations. This result held even when (hypothetical) stakes ranged up to £100,000, and provides an indication that variations in risk preferences over probabilities are generally more important than variations over outcomes. The best-fitting function, however, was a prospect theory function combining a two-parameter weighting function with a logarithmic utility function as proposed by Scholten & Read (2014). The latter combined increasing relative risk aversion with decreasing absolute risk aversion—an empirically desirable quality (Wakker 2010).
We further revisited violations of prospect theory deriving from the observation that variations over stakes may result in changes in probability weighting (Fehr-Duda et al., 2010). Our conclusions in this respect are mixed. Logarithmic utility could indeed absorb such violations in some cases, showing how a good functional fit to the data is essential. In at least one case, however, logarithmic utility could not fully eliminate this violation. This was found to be due to differing reactions to stake variations dependent on the level of probability, which resulted in a change in probabilistic sensitivity as well as probabilistic pessimism. This indeed seems to be an essential element in separability violations, which appears to be driven by an increase in probabilistic insensitivity when outcomes are affect-rich or salient.
Notes
Technically, the reference to risk aversion is wrong in the context of PT, since risk aversion under prospect theory is determined jointly by utility curvature and decision weights, so that a reference to concavity would be more appropriate (Wakker 2010). We nevertheless continue using this terminology here for continuity with discussion in the expected utility literature.
Coming from the literature on intertemporal decision making, Scholten & Read (2014) discuss this requirement in terms of decreasing elasticity. Elasticity is thereby defined as \(\epsilon _{v} = \frac {\frac {d}{dx}\left (log[v(x)] \right )}{\frac {d}{dx}\left (log(x) \right )}\).
4Wilcox (2011) pointed out a potential problem when applying such a model in a discrete choice setup, whereby the probability of choosing the riskier prospect may be increasing in risk aversion in some cases. This problem does not apply in our setting. Also, Apesteguia & Ballester (2014) have shown that this problem does not occur even in discrete choice models when a derived certainty equivalent is compared to a sure amount, as in our setup.
Markowitz used a small probability of p = 0.1 in his thought experiment. The fact that we find uniform risk seeking behavior for this probability level reflects the issue that our real stakes are much smaller than those used by Markowitz in his hypothetical thought experiment. Experiment 2 below will address this difference.
It is still somewhat unclear why that may be the case. L’Haridon & Vieider (2016) speculated that this may be due to the large proportion of students of foreign origin participating in the study. However, Bouchouicha & Vieider (2017) also found Britain to be relatively more risk tolerant than other countries with similar GDP per capita based on survey questions answered by representative samples.
One could imagine that the curve may be initially convex, then concave, and then convex again. Originally proposed as a solution for the contradictions found in original expected utility theory by Friedman & Savage (1948), such a fix quickly runs into contradictions itself. We can show this in our own data recurring to other stake levels. For instance, the prospect offering £60 with a 0.9 probability shows clear risk aversion at £47—very close to the risk seeking for £43 found for £200 obtaining with a probability of 0.1.
Test results are qualitatively unaffected if we use a parametric Vuong test instead. We will henceforth report Clarke tests whenever the models are non-nested, while we will use likelihood ratio tests for nested models.
It is also possible to estimate our PT model in combination with the expo-power utility function, although this leads to a proliferation of parameters. We find in our data that—while such a model significantly outperforms the power and exponential utility formulations—it still performs less well than log utility (p < 0.001; Clarke test).
We do not show any regression results using the two-parameter expo-power function for space reasons. Using such a function, we do, however, still find a significant violation of separability. This confirms the conclusion of Fehr-Duda et al. (2010) that the phenomenon carries over to such functions.
Following the example used by Kahneman & Tversky (1979), assume we observe the preferences 2400 ≻ (0.33, 2500; 0.66, 2400; 0) and (2400, 0.34; 0) ≺ (2500, 0.33; 0). Subcertainty would have required w(0.34) + w(0.66) < 1. Under PT in its modern formulation, this is replaced by the condition w(0.34) + [w(0.99) − w(0.66)] < 1. This condition is much milder, and generally compatible with w(0.5) > 0.5. It can also easily be calculated that this condition is fulfilled by the weighting function estimated using our data.
An exception is constituted by Bosch-Domènech & Silvestre (2006), who found strong stake effects for losses as well as for gains.
References
Abdellaoui, M. (2000). Parameter-free elicitation of utility and probability weighting functions. Management Science, 46(11), 1497–1512.
Abdellaoui, M., Bleichrodt, H., L’Haridon, O. (2008). A tractable method to measure utility and loss aversion under prospect theory. Journal of Risk and Uncertainty, 36(3), 245–266.
Apesteguia, J., & Ballester, M.A. (2014). Discrete choice estimation of risk aversion. Working Paper.
Armantier, O. (2006). Do wealth differences affect fairness considerations?. International Economic Review, 47(2), 391–429.
Barberis, N.C. (2013). Thirty years of prospect theory in economics: A review and assessment. Journal of Economic Perspectives, 27(1), 173–96.
Bardsley, N., Cubitt, R.P., Loomes, G., Moffatt, P.G., Starmer, C., Sugden, R. (2010). Experimental economics: Rethinking the rules. Princeton: Princeton University Press.
Bernoulli, D. (1954). Exposition of a new theory on the measurement of risk. Econometrica, 22(1), 23–36.
Bleichrodt, H., Abellan-Perpiñan, J.M., Pinto-Prades, J.L., Mendez-Martinez, I. (2007). Resolving inconsistencies in utility measurement under risk: Tests of generalizations of expected utility. Management Science, 53(3), 469–482.
Bolle, F. (1990). High reward experiments without high expenditure for the experimenter? Journal of Economic Psychology, 11(2), 157–167.
Bosch-Domènech, A., & Silvestre, J. (2006). Reflections on gains and losses: A 2 x 2 x 7 experiment. Journal of Risk and Uncertainty, 33, 217–235.
Bouchouicha, R., & Vieider, F.M. (2017). Growth, entrepreneurship, and risk tolerance: A risk-income paradox. Reading: University of Reading Working Paper.
Bouchouicha, R, Martinsson, P., Medhin, H., Vieider, F. (2017). Stake effects on ambiguity attitudes for gains and losses. Theory & Decision, 83(1), 19–35.
Choi, S., Fisman, R., Gale, D., Kariv, S. (2007). Consistency and heterogeneity of individual behavior under uncertainty. The American Economic Review, 97(5), 1921–1938.
Cubitt, R.P., Starmer, C., Sugden, R. (1998). On the validity of random lottery incentive systems. Experimental Economics, 1, 115–131.
Etchart-Vincent, N. (2004). Is probability weighting sensitive to the magnitude of consequences? An experimental investigation on losses. Journal of Risk and Uncertainty, 28(3), 217–235.
Fehr-Duda, H., Bruhin, A., Epper, T.F., Schubert, R. (2010). Rationality on the rise: Why relative risk aversion increases with stake size. Journal of Risk and Uncertainty, 40(2), 147–180.
Fehr-Duda, H., & Epper, T. (2012). Probability and risk: Foundations and economic implications of probability-dependent risk preferences. Annual Review of Economics, 4(1), 567–593.
Friedman, M., & Savage, L.J. (1948). The utility analysis of choices involving risk. Journal of Political Economy, 56(4), 279–304.
Goldstein, W., & Einhorn, H. (1987). Expression theory and the preference reversal phenomena. Psychological Review, 94, 236–254.
Harrison, G.W., Lau, M.I., Rutström, E.E. (2007). Estimating risk attitudes in Denmark: A field experiment. Scandinavian Journal of Economics, 109, 341–368.
Hogarth, R.M., & Einhorn, H.J. (1990). Venture theory: A model of decision weights. Management Science, 36(7), 780–803.
Hsee, C., & Rottenstreich, Y. (2004). Music, pandas, and muggers: On the affective psychology of value. Journal of Experimental Psychology: General, 133(1), 23–30.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263–291.
Köbberling, V., & Wakker, P.P. (2005). An index of loss aversion. Journal of Economic Theory, 122(1), 119–131.
Kontek, K. (2011). On mental transformations. Journal of Neuroscience, Psychology, and Economics, 4(4), 235–253.
L’Haridon, O., & Vieider, F.M. (2016). All over the map: Heterogeneity of risk preferences across individuals, contexts, and countries. EM-DP2016-04. Reading: University of Reading.
Lopes, L.L. (1987). Between hope and fear: The psychology of risk. Advances in Experimental Social Psychology, 20, 255–295.
Markowitz, H. (1952). The utility of wealth. Journal of Political Economy, 60 (2), 151–158.
Prelec, D. (1998). The probability weighting function. Econometrica, 66, 497–527.
Preston, M.G., & Baratta, P. (1948). An experimental study of the auction-value of an uncertain outcome. The American Journal of Psychology, 61(2), 183.
Rachlin, H. (1992). Diminishing marginal value as delay discounting. Journal of the Experimental Analysis of Behavior, 57(3), 407–415.
Rottenstreich, Y., & Hsee, C.K. (2001). Money, kisses, and electric shocks: On the affective psychology of risk. Psychological Science, 12(3), 185–190.
Saha, A. (1993). Expo-power utility: A flexible form for absolute and relative risk aversion. American Journal of Agricultural Economics, 75(4), 905–913.
Schmidt, U., & Zank, H. (2007). Linear cumulative prospect theory with applications to portfolio selection and insurance demand. Decisions in Economics and Finance, 30(1), 1–18.
Schmidt, U., & Zank, H. (2008). Risk aversion in cumulative prospect theory. Management Science, 54(1), 208–216.
Scholten, M., & Read, D. (2010). The psychology of intertemporal tradeoffs. Psychological Review, 117(3), 925–944.
Scholten, M., & Read, D. (2014). Prospect theory and the forgotten fourfold pattern of risk preferences. Journal of Risk and Uncertainty, 48(1), 67–83.
Smith, V.L., & Walker, J.M. (1993). Monetary rewards and decision cost in experimental economics. Economic Inquiry, 31(2), 245–261.
Starmer, C. (2000). Developments in non-expected utility theory: The hunt for a descriptive theory of choice under risk. Journal of Economic Literature, 38, 332–382.
Train, K. (2009). Discrete choice methods with simulation. Cambridge: Cambridge University Press.
Tversky, A., & Fox, C.R. (1995). Weighing risk and uncertainty. Psychological Review, 102(2), 269–283.
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–323.
Vickrey, W. (1945). Measuring marginal utility by reactions to risk. Econometrica, 13(4), 319.
Vieider, F.M. (2017). Certainty preference, random choice, and loss aversion: A comment on violence and risk preference: Experimental Evidence from Afghanistan. American Economic Review, forthcoming.
Vieider, F.M., Beyene, A., Bluffstone, R.A., Dissanayake, S., Gebreegziabher, Z., Martinsson, P., Mekonnen, A. (2016a). Measuring risk preferences in rural Ethiopia. Economic Development and Cultural Change, forthcoming.
Vieider, F.M., Villegas-Palacio, C., Martinsson, P., Majia, M. (2016b). Risk taking for oneself and others: A structural model approach. Economic Inquiry, 54(2), 879–894.
Vieider, F.M, Truong, N., Martinsson, P., Khanh, N.P. (2013). Risk preferences and development revisited. WZB Discussion Paper SP II 2013–403.
von Neumann, J., & Morgenstern, O. (1944). Theory of games and economic behavior. New Heaven: Princeton University Press.
Wakker, P.P. (2008). Explaining the characteristics of the power (CRRA) utility family. Health Economics, 17(12), 1329–1344.
Wakker, P.P. (2010). Prospect theory for risk and ambiguity. Cambridge: Cambridge University Press.
Wilcox, N.T. (2011). Stochastically more risk averse: A contextual theory of stochastic discrete choice under risk. Journal of Econometrics, 162(1), 89–104.
Wu, G., & Gonzalez, R. (1996). Curvature of the probability weighting function. Management Science, 42(12), 1676–1690.
Yaari, M.E. (1987). The dual theory of choice under risk. Econometrica, 55 (1), 95–115.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bouchouicha, R., Vieider, F.M. Accommodating stake effects under prospect theory. J Risk Uncertain 55, 1–28 (2017). https://doi.org/10.1007/s11166-017-9266-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11166-017-9266-y
Keywords
- Fourfold pattern of risk preferences
- Prospect theory
- Stake effects
- Probability-outcome separability
- Markowitz