Abstract
We examine the relationship between confidence in own absolute performance and risk attitudes using two confidence elicitation procedures: self-reported (non-incentivised) confidence and an incentivised procedure that elicits the certainty equivalent of a bet based on performance. The former procedure reproduces the “hard-easy effect” (underconfidence in easy tasks and overconfidence in hard tasks) found in a large number of studies using non-incentivised self-reports. The latter procedure produces general underconfidence, which is significantly reduced, but not eliminated when we filter out the effects of risk attitudes. Finally, we find that self-reported confidence correlates significantly with features of individual risk attitudes including parameters of individual probability weighting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we report an experiment investigating relationships between measures of individuals’ confidence assessments of their own performance and their risk attitudes.
Our broad motivation flows from a large literature originating in psychology in the 1970s and documenting apparently systematic biases in individuals’ assessments of their own abilities, both relative to others and in absolute terms. For example, a classic experimental approach to eliciting absolute confidence might ask subjects to respond to various quiz questions with right and wrong answers and then to report assessments of their own performance (e.g., by responding to questions of roughly the form “how many questions do you think you got right?” or “how likely is that you got this question right?”). A range of studies using approaches like this, starting with the classic study of Fischhoff et al. (1977), document systematic miscalibration, usually in the form of either overconfidence (i.e., over-predicting own actual success rate) or a hard-easy effect (i.e., overestimating success for ‘hard’ tasks and underestimating success for ‘easy’ ones).Footnote 1
This literature has, in turn, stimulated significant streams of work in both empirical and, more recently, theoretical economics. For example, findings of overconfidence in own performance relative to that of others (e.g., Svenson 1981) has motivated many studies by experimental economists on the relationship between relative confidence, relative ability, and willingness to take risks in strategic environments (e.g., Camerer and Lovallo 1999; Hoelzl and Rustichini 2005; Moore and Cain 2007; Niederle and Vesterlund 2007). Confidence about own abilities has been shown to affect many important spheres of economic behaviour including consumer decision making (Grubb 2015), trading in financial markets (Biais et al. 2005; Kent and Hirshleifer 2015), innovative activity (Herz et al. 2014), investment in education (Dunning et al. 2004), and decision making among managers and CEOs (Malmendier and Tate 2015). Given this, it is not surprising that economists have shown interest in developing theoretical models to examine the implications of biases in confidence (e.g., Compte and Postlewaite 2004; Dubra 2004; Gervais et al. 2011; Ludwig et al. 2011).Footnote 2
Our study has two primary motivations. One flows from an apparent clash between particular stylized findings from the established psychological literature and more recent evidence emerging from experimental economics. We discuss the relevant evidence in more detail in the next section, but the crucial motivating feature to note is that the recent evidence from experimental economics has tended to reveal either much less evidence of systematic miscalibration or strikingly different patterns of miscalibration where it does occur. So, what might account for this difference? One distinctive feature of much of the newer literature is that it employs various (financial) incentive mechanisms to motivate revelation of confidence, whereas the psychology studies tended to rely on non-incentivised self-reported confidence. One possibly tempting—though in fact it will turn out misleading—diagnosis would be that the newer evidence provides more accurate confidence measurement as a consequence of incentivised revelation techniques. In this paper, however, we investigate another possibility: that some of the differences between findings of economists and psychologists may be a consequence of biases in measured confidence induced by incentive mechanisms which fail to control for the influence of individual risk attitudes.
Our second motivation is to explore the possibility that confidence judgements may be intrinsically related to risk attitudes. It seems plausible that there could be a positive association between individuals being more confident in their own performance and being more willing to take risks. For example, overconfidence about own abilities and a willingness to take risks might be common consequences of particular personality traits (e.g., egotism), emotional states or dispositions (e.g., optimism). While these considerations suggest a possible linkage between individual confidence assessments and risk attitudes, as far as we know, there is no existing evidence to support such linkage.
In Section 2, we underpin the two motivations just highlighted with a more detailed discussion of key aspects of the background experimental literature, with particular focus on evidence related to assessments of absolute confidence.
Section 3 then introduces our experimental design. This has two core components: one involves the use of two distinct methods for the elicitation of (absolute) confidence; the other involves procedures for independently measuring individual risk attitudes. One of our confidence measurement tools is a non-incentivised tool designed to be analogous to procedures that have been used extensively in psychological research; the other is an incentivised choice based procedure. We designed the latter to be incentive compatible for revelation of confidence for risk neutral subjects but, in common with other incentive mechanisms that have been used in the recent literature, our procedure will result in biased confidence measurements for non-risk-neutral subjects. Thus, we use elicited risk attitudes to adjust incentivised confidence measures for departures from risk neutrality. We also examine whether individual risk attitudes predict self-reported (non-incentivised) confidence judgements. In the implementation of the design (explained in detail in Section 3), measurement of risk attitudes precedes elicitation of confidence. In presenting the design, however, we begin by introducing our tools for confidence measurement.
In Section 4 we present our results. There are three primary findings. First, our two tools produce markedly different patterns of confidence miscalibration, mimicking the stylised facts of existing research (the non-incentivized tool reproduces the familiar hard-easy effect, while our incentivised tool reveals general underconfidence). Second, when we filter out the effects of risk attitudes on incentivised measurements of confidence, we find that measured miscalibration is much reduced. This shows that incentivised mechanisms for confidence elicitation can be biased in the absence of suitable controls for risk preferences. Finally, we find that confidence, as measured by non-incentivized self-reports, correlates significantly with features of individual risk attitudes including parameters of individual probability weighting functions. Moreover the directions of association are intuitively plausible: for example, reported confidence is positively associated with risk parameters that imply greater willingness to take risk. Section 5 discusses broader implications and concludes.
2 Background literature
In this section, we review dimensions of the literature relating to confidence miscalibration which are most closely related to, and motivate, our contribution. Because we are interested in possible relationships between individuals’ confidence judgements and their risk attitudes, which we interpret as features of individuals, we focus mainly on evidence related to the calibration of own absolute performance.Footnote 3
We begin by looking more closely at our earlier assertion that recent research by experimental economists has revealed rather different patterns in (absolute) confidence miscalibration compared to the earlier psychology literature. One of the first papers in experimental economics to study absolute confidence miscalibration is by Blavatskyy (2009). In his experiment, subjects answer a set of 10 multiple choice quiz questions before choosing between two payment schemes. Either one question is selected at random and the subject receives a payoff if they answered this question correctly, or the subject receives the same payoff with a stated probability set by the experimenter to be equal to the percentage of correctly answered questions (although the subject does not know this is how the probability is set). Subjects could also indicate indifference. The majority choose the second payment scheme which Blavatskyy interprets as reflecting a tendency towards underconfidence. He also elicits risk attitudes in a separate part of the experiment but finds no significant relationship between these risk attitudes and choices of payment scheme. In our study, by contrast and as explained below, we do find significant correlations between risk attitudes and confidence.Footnote 4
In a related contribution, Urbig et al. (2009) elicit confidence about own performance over a set of 10 multiple choice quiz questions. They use an incentivized mechanism that elicits confidence via probability equivalents for bets based on own performance. In their data the average elicited probability equivalent is extremely close to the actual rate of success. Both Blavatskyy (2009) and Urbig et al. (2009) note the difference between their findings and those from the earlier psychology literature, and speculate that the difference may be due to the introduction of incentivized elicitation devices. However, neither study contains a benchmark treatment for comparing the elicited confidence with a non-incentivized tool. Our study includes such a comparison.
Clark and Friesen (2009) study subjects’ confidence in relation to two types of real effort tasks involving verbal and numerical skills. They study forecasts of own performance using quadratic scoring rule (QSR) incentives and find that underconfidence is more prevalent than overconfidence. One potential limitation of QSR incentives, however, is that they may result in biased measurements of confidence if subjects are not risk neutral. Recognizing this Clark & Friesen use a binary lottery incentive procedure which, for an expected utility maximizer, induces risk neutrality. However, departures from expected utility theory—for example due to non-linear probability weighting—may result in the procedure failing to induce risk neutrality (we return to this point below in more detail).Footnote 5
A potentially significant feature of the three experiments discussed in the last three paragraphs is that they all elicit confidence in relation to performance across sets of tasks. By contrast, much of the earlier psychological literature investigating confidence calibration assessed it with reference to performance in single tasks. This may be a significant distinction because there is evidence that miscalibration varies between measurements based on single versus sets of tasks. For example, Gigerenzer et al. (1991), Liberman (2004) and Griffin and Brenner (2008) report that when beliefs are elicited about aggregate performance in sets of tasks most subjects are either well-calibrated or underconfident whereas overconfidence is evident when elicitation is at the single task level. We study confidence on a single task level. Hence our evidence is more directly comparable with the original confidence calibration studies.
Hollard et al. (2015) elicit absolute confidence in relation to single tasks and compare confidence in visual perception and quiz tasks contrasting three elicitation tools: non-incentivized self-reports; the QSR; and the Becker-deGroot-Marschak (BDM) mechanism. They find highest overconfidence in the non-incentivized self-reports followed by BDM and then QSR. BDM-elicited confidence being higher than QSR-elicited confidence is consistent with the effects of risk aversion, but since they do not elicit risk attitudes we cannot tell whether that difference is caused by risk attitudes or something else, such as differences in understanding of the elicitation procedures. With our methodology we will be able to identify the extent to which elicited confidence is affected by risk attitudes.
Our study is also related to a growing literature on elicitation of subjective beliefs. Offerman et al. (2009); Trautmann and van de Kuilen (2015) and Andersen et al. (2014) elicit subjects’ beliefs about uncertain events in a two-step process, using estimates of individual risk attitudes to filter out the effect of risk attitudes from measured beliefs. Our experiment also uses estimated risk attitudes to filter out the effect of risk attitudes from beliefs but a key difference is that we are concerned with biases in subjective estimates of confidence in own performance (not biases in assessments of naturally determined chance events). A second difference from these studies is that we use the parametric method developed by Fehr-Duda et al. (2006) to estimate individual risk attitudes under rank-dependent utility (RDU) theories. This method gives us a rich measure of risk attitudes which separates attitudes to consequences from attitudes to probabilities. In our analysis, we use the measured risk attitudes for two distinct purposes: first, by comparing risk-adjusted to unadjusted confidence we are able to track the effect of risk attitudes on confidence elicited using our incentivized mechanism; second, by relating measured risk attitudes to (non-incentivised) self-reported confidence we are able to test for an intrinsic relationship between confidence and risk attitudes.
Our exploration of the relationship between risk attitudes and confidence connects with previous studies investigating links between other individual characteristics and confidence. Some studies have focused on gender differences and find that overconfidence is more pronounced among men than women (see Croson and Gneezy 2009 for a discussion of some of these). However other studies, for example Clark and Friesen (2009), find no gender differences in confidence. More recently, there has been interest in how personality traits and economic preferences interact. For example, it has been found that personality traits such as openness and extraversion predict confidence and overconfidence, respectively (Schaefer et al. 2004); neuroticism and cognitive ability predict risk taking (Rustichini et al. 2012); and narcissism predicts higher confidence and more willingness to bet on one’s own performance (Campbell et al. 2004). Becker et al. (2012) review the relationships between economic preferences and psychological personality traits, finding mixed evidence on associations between risk preferences and personality traits. In their own data, these authors find only weak correlations between risk preferences and personality traits, and their best model for predicting life outcomes such as health, earnings and education includes both personality traits and risk preferences. None of these studies, however, report how risk attitudes correlate with elicited confidence at the individual level. This is a significant gap which our study seeks to address.
3 Methods
Our experiment had two parts. In the first part, we used a procedure (common across all subjects, and explained in detail later) to elicit risk attitudes. In the second part, we measured confidence about own performance in the context of a standard quiz framework, using two different techniques, which we now explain.
In Part 2 of the experiment, subjects responded to a series of two-item multiple-choice questions, each of which asked them to judge which of a pair of cities had the highest population. Subjects could earn £0.50 for each correct answer. The quiz is included as Appendix A.
For each quiz response, we elicited a measure of confidence. We employed two different procedures for measuring confidence implemented in two treatments in a between subjects design. In the Reported Confidence treatment, we elicited confidence using a simple non-incentivised self-report. Our method was as follows: alongside each quiz answer the subject completed the statement:
I am ___% confident that my answer is correct.
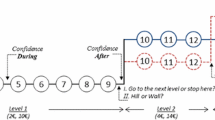
In the Inferred Confidence treatment we measured confidence using a new incentivised procedure. Figure 1 illustrates the tool which has a choice list format.Footnote 6 At the top of the figure, the subject has to choose which of two cities has the higher population. They are then required to complete the table below the quiz question choosing either A or B in each of the 20 rows.
Given the construction of the table, subjects are expected to choose Option B in the first row and Option A in the last row. At some point they will likely switch from Option B to A, and this switchpoint is used to measure their confidence in their answer. For example, suppose a subject thinks she has a 67% chance of being correct. Her expected earnings from Option A are £6.70 and so if she wants to maximise her expected earnings she should switch from B to A at row 8. We will refer to these switchpoints as certainty equivalents (CE) and under expected value maximisation (EV) the CE can be interpreted as revealing an individual’s subjective probability of success (±2.5%).
More generally, the CE picks up some mix of assessment of their chances of success with (possibly several) aspects of risk attitudes including non-linear attitudes to consequences and probabilities. For example, if the subject is a risk averse expected utility maximiser she will switch at a later row. If we were to incorrectly assume that this subject makes choices according to the EV model, we would interpret this later switchpoint as indicating a lower subjective probability of success. In this case our estimate of the subject’s confidence would be biased and, even if the individual is perfectly calibrated in that her subjective probability accurately reflects her underlying performance, we would incorrectly record underconfidence. Similarly, if choices are made based on non-linear attitudes to probabilities, we would obtain biased measures of confidence if we were to infer confidence through the lens of a model that fails to incorporate these attitudes, and as a result we would attribute systematic miscalibration to well-calibrated subjects.
To allow for non-linear attitudes to consequences and/or probabilities we infer confidence from CEs using one of the most common and parsimonious specifications for risk preferences, Rank Dependent Utility (RDU) theory. Under RDU, there should be a unique switchpoint at which the utility of the certainty equivalent will be (approximately) equal to the value of the lottery.Footnote 7 Hence, under the RDU model (which contains expected utility and expected value theories as special cases) we may write:
where CE i is an individual’s certainty equivalent for question i, U(.) is a utility function defined on money payoffs and w(.) is an RDU probability weighting function. In expression (1) we treat confidence as a subjective probability judgement that underlies choices, but may be prone to biases and miscalibration. The function w(.) is then interpreted as capturing attitudes to chance distinct from miscalibration.Footnote 8 Rearranging Eq. (1) we obtain the probability that a subject assigns to being correct in question i, denoted Conf i , as:
Under the EV model both the value function and the probability weighting function are linear so confidence can be inferred directly from an observed CE as Conf i = CE i /10. Estimation under the RDU model requires knowledge of both the utility function and the probability weighting function.
Part 1 of the experiment required subjects to make a series of lottery choices, from which we estimate individual risk attitudes in the form of their utility and probability weighting functions. We use these estimates to filter out the effects of risk attitudes on elicited confidence in our incentivized procedure and to study the relationship between individual confidence and risk attitude. For the purpose of estimating U(.) and w(.), we use a simple and easy to understand procedure introduced in Fehr-Duda et al. (2006) and successfully employed to estimate utility function and probability weighting function parameters in several subsequent studies (including: Bruhin et al. 2010; Fehr-Duda et al. 2010; and Epper et al. 2011). Because it uses a choice list elicitation task which is very similar in structure to our incentivised confidence elicitation task, it is particularly well suited to our study as its use minimises the cognitive load involved in subjects learning how to respond to the two types of task.
The procedure requires each subject to complete 25 tables of the form given in Fig. 2. Each table consists of 20 rows, where each row is a choice between a two-outcome lottery and a guaranteed amount of money, with the guaranteed amount of money decreasing from the high outcome to the low outcome of the lottery in equal increments moving down the rows. The subject’s certainty equivalent, CE L , of lottery L can be written as in (3), where the high prize of the lottery x 1L occurs with probability p 1L and the low prize of the lottery x 2L occurs otherwise:
We use the switching point from choosing the guaranteed amount (Option B) to the lottery L (Option A) as our estimate of the subject’s certainty equivalent of the lottery. The 25 lotteries are summarized in Table 1 and were adapted from Fehr-Duda et al. (2006).
To estimate U(.) and w(.) we first specify functional forms for utility and probability weighting functions. We follow Bruhin et al. (2010) in their choice of flexible and interpretable functions which have been widely used elsewhere in the empirical literature. On this basis we use the power form for the utility function:
This specification is parsimonious in modelling risk attitudes via a single curvature parameter, α, and has been shown to provide a good fit to a wide range of choice data. To allow for non-linear probability weighting in the estimation of RDU parameters, we use the linear-in-log-odds function of Goldstein and Einhorn (1987):
This specification is credited with providing a good account of individual heterogeneity (Wu et al. 2004) and its two parameters have the advantage of having clear intuitive interpretations (Lattimore et al. 1992; Bruhin et al. 2010): the parameter β captures ‘elevation’ of the probability weighting function (with greater β reflecting more ‘optimism’); the parameter γ controls curvature (for γ < 1, the smaller is γ the stronger is the deviation from linearity).
Finally, operationalizing the model requires specification of some stochastic element in the decision process. Following Epper et al. (2011) we assume that the observed switching point, \( {\widehat{CE}}_L \) is given by:
where the error terms, ϵ L , are independent draws from a normal distribution with zero mean. Heteroskedasticity in the error variance across elicitation tables is accounted for, as in Epper et al. (2011), by assuming the standard deviation of the distribution of the error term, v L , is proportional to the difference between the guaranteed amounts in Option B as one moves down the rows of the table. Hence, v L = v(x 1L − x 2L ), where v denotes an additional parameter to be estimated. The normalized standard deviation v, and the parameters of U(.) and w(.), are then obtained by maximum likelihood estimation.
To summarise our setup, in Part 1 we elicited risk attitudes (i.e., utility and probability weighting parameters) for every subject, using versions of Fig. 2 and the parameter sets of Table 1. These tasks were identical for all subjects except that the order of tasks was randomized across subjects. In Part 2 we elicited confidence, varying the way we did this across two between-subject treatments. In the Reported Confidence treatment we used simple, non-incentivized self-reports. In the Inferred Confidence treatment we used Fig. 1 and Eq. (2), using the elicited risk attitudes from Part 1 for measuring confidence under RDU.Footnote 9
After answering all quiz questions and providing their confidence levels (either by reporting or filling in the table), subjects completed a questionnaire while we checked their answers. Via this questionnaire, we elicited a variety of things including demographic information and a basic measure of ambiguity attitudes using a simple (non-incentivized) version of Ellsberg’s (1961) urn problems.Footnote 10 Details of the questionnaire are provided in Appendix B. At the end of the experiment, we used a random incentive system to pay subjects.Footnote 11 Subjects were paid based on one randomly drawn row in one randomly drawn table in one randomly drawn part of the experiment. We used physical objects (dice, numbered balls and poker chips) to make the independence of the randomization devices salient, and we explained the randomization procedures with simple examples and diagrams.
The experiment was conducted at the University of Nottingham, CeDEx lab in 2011. Subjects were recruited using ORSEE (Greiner 2004). In total 86 subjects participated; 40 in the Inferred Confidence treatment (25 male), and 46 in the Reported Confidence treatment (23 male). The experiment was conducted in pen and paper format with subjects seated in cubicles. The experiment lasted approximately 1 hour and the average payment to participants was £9. The full experimental instructions are available on request.
4 Results
We structure the results under three subheadings. In Section 4.1, we compare and contrast the data on average confidence elicited in the two treatments. In Section 4.2, we present our findings on individual risk attitudes and risk-adjusted confidence. Finally, in Section 4.3, we examine the relationship between risk attitudes and reported confidence.Footnote 12
4.1 Reproducing standard results
Figure 3 provides a quick eye-balling tool for comparing confidence measured using non-incentivized self-reports with confidence elicited using our incentivised mechanism (on the assumption that individuals are risk neutral). Consider first the top left panel. This plots, for each quiz question, the mean of reported confidence against the average success rate. The 45-degree line provides a natural benchmark in the sense that a general tendency towards overconfidence would result in points located above the line whereas a general tendency towards underconfidence would result in points below it.Footnote 13
Confidence and success. Top panels: Each dot represents a question. For a given question, Bias = (Average Confidence) − (Average Success) across subjects. Average Bias is the mean across questions and the reported p-value is for a two-tailed t-test that the mean of the distribution of biases equals zero. Bottom panels: Each dot represents a subject. For a given subject, Bias = (Average Confidence) − (Average Success) across questions. Average Bias is the mean across subjects and the reported p-value is for a two-tailed t-test that the mean of the distribution of biases equals zero
The reported confidence data have a pattern consistent with the familiar ‘hard-easy effect’. To highlight this, we have drawn a vertical (dashed) line through the question which is the median in terms of its success rate (at around 68%). If we define ‘hard’ (‘easy’) questions as those with lower (higher) than median success rates it is then apparent that, on average, there is overconfidence for all but one of the hard questions and underconfidence for all of the easy ones. For each question we measure miscalibration bias as average confidence minus the proportion of correct answers. We then test whether the mean of the distribution of biases is equal to zero using a simple t-test. For easy questions there is significant underconfidence (average bias = −0.115, p = 0.002) while for hard questions there is significant overconfidence (average bias = 0.070, p = 0.001). Pooling hard and easy questions we cannot reject the null of zero expected bias (average bias = −0.027, p = 0.312), evidently because the negative bias on easy questions offsets the positive bias on hard questions.
The top right panel of Fig. 3 provides corresponding analysis for confidence inferred from our incentivised elicitation tool, but on the assumption that individuals are expected value maximizers. We refer to this measure as Conf EVi and, from expression 2 above, it is easy to see that this can be calculated directly from an individual’s switchpoint in any given table because Conf EVi = CE i /10. Here, all of the observations sit below the 45-degree line indicating a systematic and highly significant tendency towards underconfidence (average bias = −0.212, p = 0.000).
The bottom two panels provide corresponding analysis, but in this case, each dot represents a single subject with each individual’s average reported confidence across tasks plotted against their actual success rate. For the Reported Confidence treatment, individuals with less than median success rate are overconfident (p = 0.085) and individuals with more than median success rate are underconfident (p = 0.041). For the Inferred Confidence treatment, across all individuals, there is general underconfidence (p = 0.000).
Taken together, the results presented in Fig. 3 reproduce the standard pattern of findings that motivated our study: using a procedure based on non-incentivised self-reports of confidence, similar to those used in a range of psychological studies, we reproduce a hard-easy effect; in contrast, using an incentivised procedure to elicit confidence we find a marked tendency towards underconfidence.
4.2 Risk preferences and risk-filtered confidence
As explained above, if individuals have non-linear utility or probability weighting functions then confidence measures elicited via our incentivised mechanism will, in part, reflect risk attitudes. This section takes account of this possibility by implementing analysis to filter out the effects of risk attitudes on our incentivised confidence measures.
To this end, we exploit the data from Part 1 of the experiment to fit risk preference models separately for each individual. As described in Section 3, we do this using one of the leading models of risk preference, rank-dependent utility theory (RDU). We estimate four parameters per experimental subject: the three parameters of the RDU model (α, β, γ) assuming the power utility function (Eq. 4) and the linear-in-log-odds probability weighting function (Eq. 5); plus the normalized standard deviation of the decision errors (v). We omit discussion of the error distribution parameter from the results since this is not central to our analysis.
Figure 4 summarises the results from fitting these models to individuals in our (‘Nottingham’) study; as a benchmark for our estimates we also report parameters obtained by applying the same econometric method to the data reported in Bruhin et al. (2010) and Epper et al. (2011) (these are labelled the ‘Zurich’ estimates). The results for Nottingham and Zurich are, qualitatively, very similar. The mean of the utility function parameter distribution is close to one and for most of the Nottingham subjects (67 out of 86) we cannot reject the null hypothesis that α = 1 at the 5% level of significance (two-tailed test). Based on the same test procedure, however, for a very large majority of subjects we do reject linearity of the probability weighting function: for roughly half the subjects (44 of 86) we reject β = 1; for 78 out of 86 subjects we reject γ = 1 and for all except four subjects we reject the joint hypothesis that β = γ = 1.
The graph presented in Fig. 4 plots the probability weighting function based on the median estimates of β and γ of the sample. The Nottingham and Zurich plots both display the inverse-S shape which overweights (underweights) small (large) probabilities; this is quite typical of the broader empirical literature estimating probability weighting functions, at least for data gathered from tasks with stated (as opposed to learned) probabilities (for a review see Starmer 2000; Fehr-Duda et al. 2006). This correspondence between our estimates and those obtained in Zurich provides some reassurance that our procedures for estimating the risk preference measures are reliable (or at least comparably reliable to those based on similar procedures elsewhere in the literature).Footnote 14
The significant non-linearity in utility and probability weighting functions for the majority of our subjects strongly suggests that risk attitudes will be a component of confidence measured via Conf EVi . Also notice that from the bottom right panel of Fig. 3 it is apparent that Conf EVi < 0.5 for a significant proportion of individuals (47.5%). Given that each task involved a choice between two options, one of which was right, confidence below 50% is implausibly low. In our incentivised task, however, risk aversion (say as measured by concavity of the utility function) would tend to depress Conf EVi . In other words, the data obtained from our incentivised mechanism might seem more plausible were we to filter out the effect of departures from risk neutrality.
Using the independent measures of individuals’ risk parameters (based on responses to Part 1 of the experiment) we estimate risk-adjusted measures of inferred confidence, based on expression (2) above, as follows:
The results of filtering out risk in this way are shown in Fig. 5. This figure plots inferred confidence against actual success rates for each question, with separate panels for the EV and RDU models. For comparison, we also reproduce the reported confidence in the bottom panel. We observe that (i) the extent of underconfidence falls as we move from EV to RDU (p = 0.025), (ii) the difference between mean biases of reported and inferred confidence decreases as we filter out risk attitudes (p = 0.023), and (iii) inferred confidence is significantly more noisy than reported confidence (Levene (1960) variance equality test: p = 0.009). These results suggest that, in the absence of filters for risk attitude, the extent of underconfidence is exaggerated. By filtering out components of these measures attributable to risk attitudes, the overall mean bias falls from −0.212 (inferred confidence under EV) to −0.086 (inferred confidence under RDU).
Risk adjusted confidence and success. Each dot represents a question. For a given question, Bias = (Average Confidence − Average Success) across subjects. Average bias is the mean across all questions and the reported p-value is for a two-tailed t-test that the mean of the distribution of biases is zero. Absolute Bias = Absolute (Average Confidence − Average Success) across subjects
While confidence miscalibration is reduced as a consequence of allowing for risk attitudes, it is not eliminated and the mean (underconfidence) bias remains significant for both measures of inferred confidence. Averaging across questions, subjects’ success rates are 8.6 percentage points higher than their inferred confidences under our RDU specification. For comparison, success rates are 2.7 percentage points higher than reported confidence.
Note, however, that zero bias does not imply perfect calibration. If, as in the bottom panel of Fig. 5, bias is positive for hard questions and negative for easy questions, the average bias measure may not reveal the extent of miscalibration. Thus, for a different overall measure of miscalibration we use the average absolute bias (i.e., the sum of vertical deviations from the 45-degree line). On this measure, inferred RDU confidence (11.6%) and reported confidence (10.2%) are not significantly different (p = 0.666).
4.3 Relationship between reported confidence and risk attitudes
So far we have focussed on the relation between risk attitudes and measured confidence elicited via an incentivised mechanism. Next we explore a possible connection between risk attitudes and self-reported confidence. It seems plausible to suppose that confidence might be related to risk attitudes. One reason for thinking this flows from the fact that various popular contemporary theories of risk preference allow departures from risk neutrality to arise as consequences of the way that people assess and/or respond to probabilities. For example, in prospect theory (Kahneman and Tversky 1979; Tversky and Kahneman 1992) decisions can be interpreted as being influenced either by misperception of objective probabilities or by subjective attitudes to whatever probabilities are perceived. To the extent that such processes reflect generic properties of the way that humans perceive and respond to risks, that provides reason to expect that similar processes might operate in relation to confidence judgements because those judgments are assessments of probabilities. We investigate this possibility by examining the correlation between individual level risk parameters and reported confidence. Notice that, while we have a reason to believe that Conf EV and Conf RDU may be correlated with risk attitudes because of an influence introduced via the measurement technique, in the case of reported confidence, there is no such transmission mechanism. As such, a correlation between risk attitudes and reported confidence would be suggestive of an intrinsic link between confidence and risk attitudes.
Table 2 presents the results of OLS regressions where the dependent variable is average reported confidence (subject level). The table reports two model specifications. Model 1 uses estimated RDU parameters as regressors, and Model 2 includes additional controls for average success rates, demographic variables and the measure of ambiguity aversion elicited from the questionnaire. Since some of the regressors are estimated, we use bootstrapped standard errors to account for measurement error in the independent variables.
Estimates of Model 2 show no significant association between average reported confidence levels and average success rates across subjects.Footnote 15 None of the other control variables have any significant predictive power for confidence levels. Turning to the risk parameter estimates, curvature of the utility function is positively related to reported confidence levels in both specifications, with greater risk seeking (as captured by higher α) associated with higher confidence. We do not find a robust significant effect of the probability weighting elevation parameter β.Footnote 16 The significant positive effect of γ in both specifications has a natural interpretation. Recall that γ controls curvature of the weighting function, then notice that, for our tasks, success rates are such that we are typically operating in a region where the median subject’s weighting function underweights probabilities. In this region, increases in γ reduce underweighting. Hence, the positive sign here is consistent with a positive association between underweighting and underconfidence.Footnote 17 We believe the analysis in this section is novel, and scientifically interesting, suggesting the possibility of common psychological mechanisms underpinning risk attitudes and confidence judgements.
5 Discussion
There is a very large empirical literature investigating confidence judgements and much of this points to the presence of overconfidence in a range of judgements or the existence of a hard-easy effect. The bulk of this literature, however, rests on data generated from non-incentivised self-reports of confidence. More recently, the robustness of conclusions from this line of research has been challenged by studies from experimental economists which use incentivised tasks to elicit confidence judgements and find that overconfidence is considerably reduced. Indeed, in these recent studies, underconfidence is the typical finding.
Our study contributes to this literature, and its central novelty lies in combining two key design features. First, we compare miscalibration of confidence in own absolute performance across incentivised and non-incentivised confidence elicitation tasks. Second, our design incorporates procedures for measuring the risk attitudes of our participants coupled with techniques that allow us to track how filtering out risk attitudes affects the measurement of confidence via the incentivised procedure. With the data generated from our design, we are also able to investigate a possible link between reported confidence and risk attitudes at the individual level.
Using a non-incentivised procedure, designed to be very similar to those used in much of the background psychology literature, we reproduce the standard finding of a hard-easy effect. With our new incentivised confidence measurement, regardless of whether or not we filter for risk attitudes, and in line with the recent experimental economics literature, we observe a general tendency towards underconfidence and the hard-easy effect disappears.
Our primary novel findings then relate to the impacts of risk aversion on measured confidence. In the context of incentivised confidence elicitation, we find that filtering out risk attitudes from inferred confidence reduces the degree of underconfidence. We also observe a striking association between risk attitudes inferred from incentivised decisions about lotteries and confidence measured using the non-incentivized tool. Specifically, individuals who are more risk averse tend to express lower confidence.
As far as we know, we are the first to provide direct evidence that risk attitudes play a significant role in determining confidence judgements. While we have argued that some such connection is intuitively plausible, the fact that the association appears to work through both attitudes to consequences and attitudes to chance is striking: in our data confidence is associated with parameters of both the utility function and the probability weighting function. In our view the discovery of an association between probability weighting and confidence is particularly intriguing. To those who tend to think of probability weighting as reflecting more general underlying principles of cognition, the manifestation of those principles in another domain will be reassuring but perhaps not especially surprising. However, we suspect that many economists previously aware of evidence of probability weighting may, quite reasonably, think of it as an essentially empirical regularity derived mainly from observing choices among simple gambles, with stated probabilities. To those who do interpret it in this more limited way, our results are arguably much more surprising by establishing a clear empirical connection between responses to probabilities in two very different domains: one involving attachment of certainty equivalents to gambles with stated probabilities (Part 1 of our experiment); the other involving self-reported probability judgements about one’s own success rate in a given question (Part 2 of our experiment). We suggest that the ability of measured (non-linear) probability weighting to predict behaviour in these very different tasks and domains is a positive signal of the explanatory scope and significance of the concept of probability weighting within economics.
Given this association between probability weighting and confidence judgements, it is natural to ask whether other ‘non-standard’ aspects of preference in relation to risk or uncertainty might also co-vary with confidence judgements. In this respect, an obvious candidate to consider is ambiguity aversion, particularly since confidence judgments appear to be intrinsically ambiguous (as opposed to risky). Although this raises issues beyond the boundaries of the present study, our post-experimental questionnaire did include a task intended to assess attitudes to ambiguity. Using these data we found that subjects identified as ambiguity averse did not switch differently in the confidence elicitation tables compared to ambiguity neutral subjects. Nor did we find any relationship between ambiguity attitudes and self-reported confidence. This is, of course, far from conclusive evidence that there is no relationship to discover, and there is certainly scope for further research into this issue and the broader question—previously highlighted by Hoelzl and Rustichini (2005); Offerman et al. (2009) and Kothiyal et al. (2011)—of how to assess and control the potential impact of ambiguity attitudes in the context of incentivised belief elicitation.
We conclude with a brief cautionary remark. Whether or not people’s confidence judgements are well calibrated is clearly an important issue in a range of economically relevant field contexts (Harrison and Phillips 2014). As such, economists have, understandably, shown an interest in the large volume of evidence supporting overconfidence in the lab and field. While it seems entirely appropriate to analyse the consequences of confidence miscalibration, it now looks naïve to proceed, as some have done in the past, by simply assuming overconfidence as a reasonable empirical assumption (Odean 1999; Compte and Postlewaite 2004; Malmendier and Tate 2005; Galasso and Simcoe 2011; Gervais et al. 2011). In contrast, our results, alongside other recent work (e.g., Hoelzl and Rustichini 2005; Moore and Healy 2008; Blavatskyy 2009; Clark and Friesen 2009; Merkle and Weber 2011), support the following conclusion: while miscalibration of confidence judgements occurs and persists in controlled incentivised decisions, there is currently—and perhaps ironically—apparent overconfidence regarding the empirical significance of overconfidence. We hope that our work provides helpful input for recalibration.
Notes
A related literature in psychology has challenged the interpretation of findings from miscalibration studies, arguing that observed overconfidence and the hard-easy effect may be partly artefacts of the confidence elicitation tools and/or methods used to analyse data, rather than biases in individual information-processing (see Olsson (2014) for a review).
In our experiment we focus exclusively on absolute, rather than relative, confidence judgements. Note that biases in judgements about relative performance may reflect misperceptions about own performance or the performance of others, and measurement of judgements about relative performance may be complicated by strategic and/or social comparison concerns. Our focus on absolute confidence avoids such complications.
There are various differences between our methodologies that might explain this key difference in findings. For example, Blavatskyy (2009) does not directly elicit confidence measures, as we do, but rather infers underconfidence from the choice of payment scheme. As such, his measure of an individual’s confidence is rather coarse, potentially limiting his analysis of the relation between individual risk attitudes and confidence. Our measurement of risk attitudes is more detailed and also allows us to distinguish attitudes to consequences and attitudes to chance.
Clark and Friesen (2009) also study forecasts of relative performance and compare (QSR) incentivized forecasts with non-incentivized forecasts. They find little if any effect of incentives on calibration.
A choice list elicitation procedure was used as early as Cohen et al. (1987) to elicit risk preferences. Andersen et al. (2006) and Isoni et al. (2011) extensively discuss the advantages and disadvantages of using choice lists as elicitation tools. We use choice lists mainly because of the clear interpretable framework of the decision environment (the value of betting on one’s own answer) and the relative ease with which subjects may see that truthful revelation is in their best interest.
For compactness, the discussion now proceeds as if CE is revealed accurately by our procedure but the reader should keep in mind that there is, of course, an element of approximation.
In the literature on prospect theory, probability weights are sometimes interpreted as reflecting misperception of underlying probabilities, sometimes reflecting subjective attitudes to chance, and sometimes a mixture of the two. For discussion and a formalisation following the latter mixed approach, see Abdellaoui et al. (2011). For a thorough discussion of prospect theoretic models see Wakker (2010).
We did not randomize the order of risk and confidence elicitations since we wanted to ensure a common experience prior to confidence measurement across treatments.
We included a basic tool for classifying subjects according to ambiguity attitudes because we conjectured that such attitudes might play some role in responses to our confidence elicitation tasks. We found no evidence to support this, however. Summary statistics of the ambiguity data are reported in Appendix B.
The random incentive system is a widely used experimental procedure. For a discussion of its rationale and possible limitations see Bardsley et al. (2010).
Before proceeding with the analysis, we dropped the data for four quiz questions that were potentially misleading because the success rate on each of these questions was less than 40% (whereas reported confidence judgements were constrained to the interval 50–100%; see Appendix A). We also excluded data from tables where subjects switched on one row and then switched back again at a later row. Reassuringly, however, less than 2% of the tables of Part 1 and no table in Part 2 included such non-monotonic responses.
Histograms of average, subject-level, reported and inferred confidence are also presented in Appendix C.
Histograms of the estimated parameters can be found in Appendix D.
The lack of a significant effect may reflect low power due to our relatively limited sample size. We also checked the relation between confidence and success in a more disaggregate analysis using responses to each question (rather than averages) as the dependent variable. In this analysis, there is a positive and significant association between success and expressed confidence levels; confidence is about 8.5% higher when a subject’s answer to a question is correct. This relationship fades away in average subject-level analysis which is consistent with the findings by e.g., Kruger and Dunning (1999) and Massoni and Roux (2012).
In Table 2 we report our most parsimonious model, using just the risk attitude variables, and our most general model. We also examined intermediate cases excluding some of the questionnaire variables. We found that the significant effects captured by α and γ are robust across model specifications, but the effect captured by β is sensitive to model specification. For example, if the gender dummy is excluded from Model 2, β becomes significantly positive at the 5% level. Lack of significance in this specification may also reflect low power due to our modest sample size.
We also examined the relationship between reported confidence and another simple proxy for risk attitudes represented as the individual’s average switch point (ASP) in Part 1 of the experiment. This revealed significant positive association between ASP and reported confidence consistent with higher confidence for less risk averse individuals. Notice that this ASP measure of risk attitude does not rely on any particular model of risk preference. Results of this analysis are reported in Appendix E.
References
Abdellaoui, M., L’Haridon, O., & Paraschiv, C. (2011). Experienced vs. described uncertainty: Do we need two prospect theory specifications? Management Science, 57, 1879–1895.
Alba, J. W., & Hutchinson, J. W. (2000). Knowledge calibration: What consumers know and what they think they know. Journal of Consumer Research, 27, 123–156.
Andersen, S., Harrison, G. W., Lau, M. I., & Rutstrom, E. E. (2006). Elicitation using multiple price list formats. Experimental Economics, 9, 383–405.
Andersen, S., Fountain, J., Harrison, G. W., & Rutström, E. E. (2014). Estimating subjective probabilities. Journal of Risk and Uncertainty, 48, 207–229.
Bardsley, N., Cubitt, R., Loomes, G., Moffatt, P., Starmer, C., & Sugden, R. (2010). Experimental economics: Rethinking the rules. New Jersey: Princeton University Press.
Becker, A., Deckers, T., Dohmen, T., Falk, A., & Kosse, F. (2012). The relationship between economic preferences and psychological personality measures. Annual Review of Economics, 4, 453–478.
Biais, B., Hilton, D., Mazurier, K., & Pouget, S. (2005). Judgemental overconfidence, self-monitoring, and trading performance in an experimental financial market. Review of Economic Studies, 72, 287–312.
Blavatskyy, P. (2009). Betting on own knowledge: Experimental test of overconfidence. Journal of Risk and Uncertainty, 38(1), 39–49.
Bruhin, A., Fehr-Duda, H., & Epper, T. (2010). Risk and rationality: Uncovering heterogeneity in probability distortion. Econometrica, 78(4), 1375–1412.
Camerer, C., & Lovallo, D. (1999). Overconfidence and excess entry: An experimental approach. The American Economic Review, 89, 306–318.
Campbell, W. K., Goodie, A. S., & Foster, J. D. (2004). Narcissism, confidence, and risk attitude. Journal of Behavioural Decision Making, 17, 297–311.
Clark, J., & Friesen, L. (2009). Overconfidence in forecasts of own performance: An experimental study. The Economic Journal, 119, 229–251.
Cohen, M., Jaffray, J. Y., & Said, T. (1987). Experimental comparison of individual behavior under risk and under uncertainty for gains and for losses. Organizational Behavior and Human Decision Processes, 39, 1–22.
Compte, O., & Postlewaite, A. (2004). Confidence-enhanced performance. The American Economic Review, 94, 1536–1557.
Croson, R., & Gneezy, U. (2009). Gender differences in preferences. Journal of Economic Literature, 47, 448–474.
Dubra, J. (2004). Optimism and overconfidence in search. Review of Economic Dynamics, 7, 198–218.
Dunning, D., Heath, C., & Suls, J. M. (2004). Flawed self-assessment: Implications for health, education, and the workplace. Psychological Science in the Public Interest, 5, 69–106.
Ellsberg, D. (1961). Risk, ambiguity, and the Savage axioms. The Quarterly Journal of Economics, 75, 643–669.
Epper, T., Fehr-Duda, H., & Bruhin, A. (2011). Viewing the future through a warped lens: Why uncertainty generates hyperbolic discounting. Journal of Risk and Uncertainty, 43, 169–203.
Fehr-Duda, H., de Gennaro, M., & Schubert, R. (2006). Gender, financial risk and probability weights. Theory and Decision, 60, 283–313.
Fehr-Duda, H., Bruhin, A., Epper, T., & Schubert, R. (2010). Rationality on the rise: Why relative risk aversion increases with stake size. Journal of Risk and Uncertainty, 40, 147–180.
Fischhoff, B., Slovic, P., & Lichtenstein, S. (1977). Knowing with certainty: The appropriateness of extreme confidence. Journal of Experimental Psychology: Human Perception and Performance, 3, 552–564.
Galasso, A., & Simcoe, T. S. (2011). CEO overconfidence and innovation. Management Science, 57, 1469–1484.
Gervais, S., Heaton, J. B., & Odean, T. (2011). Overconfidence, compensation contracts and capital budgeting. The Journal of Finance, 66, 1735–1777.
Gigerenzer, G., Hoffrage, U., & Kleinbolting, H. (1991). Probabilistic mental models: A Brunswikian theory of confidence. Psychological Review, 98, 506–528.
Goldstein, W. M., & Einhorn, H. J. (1987). Expression theory and the preference reversal phenomena. Psychological Review, 94, 236–254.
Greiner, B. (2004). An online recruitment system for economic experiments. In K. Kremer & V. Macho (Eds.), Göttingen :Ges. fürsWiss. Datenverarbeitung (pp. 79–93).
Griffin, D., & Brenner, L. (2008). Perspectives on probability judgment calibration. In D. J. Koehler & N. Harvey (Eds.), Blackwell handbook of judgment and decision making (pp. 177–199). Malden: Blackwell Publishing Ltd.
Grubb, M. D. (2015). Overconfident consumers in the marketplace. Journal of Economic Perspectives, 29, 9–36.
Harrison, G. W., & Phillips, R. D. (2014). Subjective beliefs and statistical forecasts of financial risks: The chief risk officer project. In T. J. Andersen (Ed.), Contemporary challenges in risk management. New York: Palgrave Macmillan.
Herz, H., Schunk, D., & Zehnder, C. (2014). How do judgmental overconfidence and overoptimism shape innovative activity? Games and Economic Behavior, 83, 1–23.
Hoelzl, E., & Rustichini, A. (2005). Overconfident: Do you put your money on it? The Economic Journal, 115, 305–318.
Hollard, G., Massoni, S., & Vergnaud, J.C. (2015). In search of good probability assessors: An experimental comparison of elicitation rules for confidence judgments. Theory and Decision, forthcoming.
Isoni, A., Loomes, G., & Sugden, R. (2011). The willingness to pay—willingness to accept gap, the “endowment effect”, subject misconceptions, and experimental procedures for eliciting valuations: Comment. The American Economic Review, 101, 991–1011.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263–291.
Kent, D., & Hirshleifer, D. (2015). Overconfident investors, predictable returns, and excessive trading. Journal of Economic Perspectives, 29, 61–88.
Keren, G. (1991). Calibration and probability judgements: Conceptual and methodological issues. Acta Psychologica, 77, 217–273.
Kothiyal, A., Spinu, V., & Wakker, P. P. (2011). Comonotonic proper scoring rules to measure ambiguity and subjective beliefs. Journal of Multi-Criteria Decision Analysis, 17, 101–113.
Kruger, J., & Dunning, D. (1999). Unskilled and unaware of it: How difficulties in recognizing one’s own incompetence lead to inflated self-assessments. Journal of Personality and Social Psychology, 77, 1121–1134.
Lattimore, P. K., Baker, J. R., & Witte, A. D. (1992). The influence of probability on risky choice: A parametric examination. Journal of Economic Behavior & Organization, 17, 377–400.
Levene, H. (1960). Robust tests for equality of variances. In I. Olkin, S. G. Ghurye, W. Hoeffding, W. G. Madow, & H. B. Mann (Eds.), Contributions to probability and statistics: Essays in honor of Harold Hotelling (pp. 278–292). Menlo Park: Stanford University Press.
Liberman, V. (2004). Commentary: Local and global judgements of confidence. Journal of Experimental Psychology: Learning, Memory, and Cognition, 30, 729–732.
Lichtenstein, S., & Fischhoff, B. (1981). The effects of gender and instructions on calibration. Decision Research Technical Report 81–5, Decision Research, Eugene, OR.
Lichtenstein, S., Fischhoff, B., & Phillips, L. D. (1982). Calibration of probabilities: The state of the art to 1980. In D. Kahneman, P. Slovic, & A. Tversky (Eds.), Judgment under uncertainty: Heuristics and biases (pp. 306–334). Cambridge: Cambridge University Press.
Ludwig, S., Wichardt, P. C., & Wickhorst, H. (2011). Overconfidence can improve an agent’s relative and absolute performance in contests. Economics Letters, 110, 193–196.
Malmendier, U., & Tate, G. (2005). CEO overconfidence and corporate investment. Journal of Finance, 60, 2661–2700.
Malmendier, U., & Tate, G. (2015). Behavioral CEOs: The role of managerial overconfidence. Journal of Economic Perspectives, 29, 37–60.
Massoni, S., & Roux, N. (2012). Optimal group decision: A matter of confidence calibration. Working Paper, CES Paris.
Merkle, C., & Weber, M. (2011). True overconfidence: The inability of rational information processing to account for apparent overconfidence. Organizational Behaviour and Human Decision Processes, 116, 262–271.
Moore, D. A., & Cain, D. M. (2007). Overconfidence and underconfidence: When and why people underestimate (and overestimate) the competition. Organizational Behaviour and Human Decision Processes, 103, 197–213.
Moore, D., & Healy, P. J. (2008). The trouble with overconfidence. Psychological Review, 115, 502–517.
Niederle, M., & Vesterlund, L. (2007). Do women shy away from competition? Do men compete too much? Quarterly Journal of Economics, 122, 1067–1101.
Odean, T. (1999). Do investors trade too much? The American Economic Review, 89, 1279–1298.
Offerman, T., Sonnemans, J., van de Kuilen, G., & Wakker, P. (2009). A truth serum for non-Bayesians: Correcting proper scoring rules for risk attitudes. The Review of Economic Studies, 76, 1461–1489.
Olsson, H. (2014). Measuring overconfidence: Methodological problems and statistical artifacts. Journal of Business Research, 67, 1766–1770.
Rustichini, A., De Young, C.G., Anderson, J., & Burks, S.V. (2012). Towards the integration of personality theory in the explanation of economic and health behavior. IZA Discussion Paper Series No. 6750.
Schaefer, P. S., Williams, C. C., Goodie, A. S., & Campbell, W. K. (2004). Overconfidence and the big five. Journal of Research in Personality, 38, 473–480.
Starmer, C. (2000). Developments in non-expected utility theory: The hunt for a descriptive theory of choice under risk. Journal of Economic Literature, 38, 332–382.
Svenson, O. (1981). Are we all less risky and more skilful than our fellow drivers? Acta Psychologica, 47, 143–148.
Trautmann, S. T., & van de Kuilen, G. (2015). Belief elicitation: A horse race among truth serums. The Economic Journal, 125, 2116–2135.
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–323.
Urbig, D., Stauf, J., & Weitzel, U. (2009). What is your level of overconfidence? A strictly incentive compatible measurement of absolute and relative overconfidence. Discussion Paper Series 09–20, Utrecht School of Economics.
Wakker, P. P. (2010). Prospect theory: For risk and ambiguity. Cambridge: Cambridge University Press.
Wu, G., Zhang, J., & Gonzalez, R. (2004). Decision under risk. In D. Koehler & N. Harvey (Eds.), The Blackwell handbook of judgment and decision making (pp. 399–423). Oxford: Oxford University Press.
Acknowledgments
We are grateful to Thomas Epper for providing us with the data from their experiments and the R-code for the econometric estimation. We are also grateful for helpful comments from the editor and an anonymous referee, as well as Steve Burks, Robin Cubitt, Dirk Engelmann, Tobias Schmidt, Joep Sonnemans, Simone Quercia, Francesco Fallucchi and Antonio A. Arechar plus participants at: the CCC meeting, UEA (2012); the TIBER XI workshop, Tilburg; the Workshop on Human Decision Making in Birmingham; the NIBS 2014 workshop on financial decision making; and the Berlin Behavioral Economics Seminar, October 2014. Martin Sefton and Chris Starmer acknowledge the support of the ESRC funded Network for Integrated Behavioural Science (ES/K002201/1).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: City quiz questions


Appendix B: Post Study Questionnaire

Appendix C: Histograms of Average Reported Confidence and ConfEV (Subject Level)

Appendix D: Histograms of Risk Preference Parameters

Appendix E: Average Switch Point as an Alternative Risk Measure
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Murad, Z., Sefton, M. & Starmer, C. How do risk attitudes affect measured confidence?. J Risk Uncertain 52, 21–46 (2016). https://doi.org/10.1007/s11166-016-9231-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11166-016-9231-1