Social comparison and risky choices

Abstract

Theories (and experiments) on decision making under risk typically ignore (and exclude) a social context. We explore whether this omission is detrimental. To do so we experimentally investigate the simplest possible situation with both social comparison and risk: participants choose between two lotteries while a referent faces a fixed payoff. Participants are more risk averse when they can earn at most as much as their referent (loss situation) than when they are ensured they will earn at least as much as their referent (gain situation). Prospect theory with a social reference point would predict the exact opposite behavior. These results show that straightforward extensions of existing theories to allow for social comparison do not provide accurate predictions.

Using comparison to evaluate outcomes or possibilities is a regular feature of human decision making. We compare our own situation to those of others (e.g. Clark et al. 2008) and what is to what could have been (Loomes and Sugden 1982) or to what was (Kahneman and Tversky 1979) and these comparisons often affect our choices. The universal nature of comparison is emphasized by the importance of a reference point in two separate streams of research in behavioral economics: decision making under risk and social preferences. Reference points affect risk attitudes through loss aversion and probability weighting (Kahneman and Tversky 1979; Tversky and Kahneman 1992). People’s social preferences, their willingness to pay to raise or lower the payoff of others, are likewise reference dependent as they are influenced by the decision maker’s earnings relative to her social reference point, the earnings of a peer (Fehr and Schmidt 1999; Bolton and Ockenfels 2000).

Loss aversion features prominently both in the literature on decision making under risk and in social preference theories. In individual decision making “losses loom larger than gains” (Kahneman and Tversky 1979, p. 279) and, similarly, people care much more about being worse off than others than about being better off (e.g. Fehr and Schmidt 1999). This raises the question of whether a social reference point can also cause well-established behavioral effects of individual reference points, such as the reflection effect. This is not self evident; some studies have found that individual and social reference points have contrary effects. According to Bault et al. (2008), people may actually be gain seeking relative to a social reference point in some situations. Also, what little information there is about the effect of a social reference point on the shape of the utility function suggests that it is concave in both the gain and loss domain (Vendrik and Woltjer 2007) while for individual reference points utility is convex in the loss domain (Kahneman and Tversky 1979).

Although the previous paragraph refers to existing research that allows for some comparison between the effects of individual and social reference points, the extent of their similarity remains largely unexplored. A reason for this gap in understanding is the very different focus of the decision making under risk and social preference literatures. The focus of the first line of research on risk has led to theories that are concerned with the shape of the utility function and the effect of probabilities. Social preference researchers on the other hand are mainly concerned with factors that strengthen or weaken social preferences. Because of the different research agendas, there is not nearly enough empirical information to compare the behavioral effects of social and individual reference points.

In this paper we aim to fill some of this gap in empirical information. We explore whether a well known effect of a reference point, the reflection effect, is exhibited relative to a social reference point. The reflection effect is the behavioral regularity that when all outcomes are losses risk seeking is generally observed, while risk aversion is the norm when all outcomes are gains¹ (Kahneman and Tversky 1979). If a social reference point has this effect, participants will make risk seeking choices when they know they will earn at most as much as a peer and risk averse choices when they know they will earn at least as much as a peer.

In our experiment participants are presented with such situations. Participants choose between lotteries which always yield positive earnings for the decision maker, but we manipulate the earnings of a matched participant, the referent. Particularly, we compare choices between lotteries in a loss setting (the referent earns more), a gain setting (the referent earns less) and a neutral setting (the referent earns the same). Figure 1 gives an example of the three kinds of choice situations presented to participants. The decision maker can compare her own earnings to those of the referent but cannot affect her referent’s earnings, nor does she receive any information about the decisions of others.² However, the decision maker’s choice can be influenced by observing the earnings of another participant, her social reference point.

Fig. 1

Lottery screens. Each panel shows a decision situation. The blue bar represents the decision maker’s earnings, the red bar her referent’s earnings. Participants choose between option 1 displayed on the left and option 2 displayed on the right. Top panel: loss situation, the decision maker earns at most as much as her referent. Middle panel: gain situation, the decision maker earns at least as much as her referent. Bottom panel: neutral situation, the decision maker and her referent earn equal amounts

In order to make the referent more relevant, matched participants first play a Bertrand game and are shown each other’s picture. The nature of the interaction between participants in the Bertrand game may affect the way they perceive the other. Participants who cooperated are likely to have a different relationship than participants who competed. Different relationships may in turn lead to a different effect of social comparison. We therefore measure the social tie between a participant and her referent.

We find that participants chose the safe lottery more often in the loss situation than in the gain situation. This result provides a clear rejection of the hypothesized reflection effect with respect to a social reference point. In fact participants were on average risk averse in all (loss, neutral and gain) situations, but more so in the loss situation. Behavior in the neutral situation is in between that in the loss and gain situations. Neither social ties nor the type of interaction in the Bertrand game mediate the social comparison effect.

The rest of this paper is structured as follows. Section 1 discusses relevant empirical and theoretical literature on both individual and social decision making and related research where both social influences and risk play a role. Section 2 explains the design of our experiment, Section 3 introduces our research questions and Section 4 provides the results. Section 5 concludes.

1 Theoretical background and related empirical findings

1.1 Reference dependence

Although normatively appealing, the descriptive power of expected utility theory is challenged by a great host of observed deviations. Reference dependence is an important characteristic of many theories that try to explain these deviations. Although expected utility theory holds that only final wealth states matter, experiments show that it is important whether an outcome is coded as a gain or a loss.

Loss aversion is probably the most well known effect of reference dependence. It explains extreme risk aversion for gambles involving small losses and gains (Rabin 2000). Fishburn and Kochenberger (1979) were first to show that utility functions in terms of changes in wealth are steeper for losses than for gains. Numerous other studies have since confirmed loss aversion (e.g. Tversky and Kahneman (1992); Gneezy and Potters (1997); Abdellaoui et al. (2007)).

A second behavioral regularity that shows the importance of reference dependence is the reflection effect. Kahneman and Tversky (1979) found that a gamble framed in terms of either gains or losses by changing the initial endowment has a profound effect on risk preferences. For gains they observe risk aversion, but for losses risk seeking is the predominant choice. The most famous illustration of this effect is the “Asian disease” study (Tversky and Kahneman 1981). In this study participants exhibited a preference for relatively safe policies when outcomes were framed as saving lives (gains) and for relatively risky policies when outcomes were framed as prevented deaths (losses). A meta-analysis (Kühberger et al. 1999) corroborates the existence of the reflection effect.

Not surprisingly, reference dependence plays a vital role in the most successful theory on decision making under risk: cumulative prospect theory (CPT) (Tversky and Kahneman 1992).³ Loss aversion is directly incorporated in CPT’s utility function by a kink around the reference point.⁴ The reflection effect is explained mainly by (cumulative) probability weighting. Probabilities for outcomes far from the reference point are underweighted, if the probability is not too small (>1/3) (Prelec 1998; Wakker 2010).⁵ As a consequence the decision weight of the best gains and the worst losses is often smaller than their probability. These low decision weights in turn lead to risk aversion for gains and risk seeking for losses. The shape of the CPT utility function, concave for gains and convex for losses, strengthens this tendency.

As this discussion makes clear the reference point is a driving force for risk preferences. That makes the determination of the reference point very important. According to Kahneman and Tversky: “the reference state usually corresponds to the decision maker’s current position, [but] it can also be influenced by aspirations, expectations, norms and social comparisons” (Tversky and Kahneman 1991, pp. 1046, 1047). Most studies assume that the status quo (e.g. Rabin 2000; Samuelson and Zeckhauser 1988) or the lagged status quo (e.g. Thaler and Johnson 1990) is the relevant reference point. Expectations have, however, also received attention as a possible reference point (Köszegi and Rabin 2006). The reference point can also be another variable than wealth such as the purchasing price of an asset (Odean 1998). The use of many different reference points and the suggestion of Kahneman and Tversky raise the question whether the income of a peer may also play this role.

1.2 A social reference point

Although social comparison has received little attention as a driver of risk preferences, its effect on other types of decisions has received ample attention from economists.⁶ People are willing to raise the earnings of others in a disadvantageous position but lower that of others in an advantageous position (e.g. Fehr and Schmidt 1999). Kindness or unkindness of the other (e.g. Fehr and Gächter 2000) and social ties (Sonnemans et al. 2006), mediate social preferences. Fehr and Schmidt (2006) review much of the evidence in this field as well as models that incorporate the observed behavior.⁷

One important characteristic of a reference point, loss aversion, is also present with respect to the earnings of a peer and forms an important part of many influential theories. In the inequity aversion models of Fehr and Schmidt (1999) and Bolton and Ockenfels (2000) the influence of relative earnings on utility is stronger when others earn more than you than when others earn less. Fehr and Schmidt note that their model “essentially means that a subject is loss averse in social comparisons: negative deviations from the reference outcome count more than positive deviations” (Fehr and Schmidt 1999, p. 824).⁸

Loss aversion observed around the referent’s earnings suggests that the role of the social reference point is similar to that played by other reference points. This raises the question of whether we can also observe the reflection effect around a social reference point. As discussed above the prevailing explanation for the reflection effect depends on both the shape of the utility function and probability weighting. To date no research examines the effects of a social reference point on probability weighting. There is, however, some research that attempts to ascertain the shape of the social utility function.

Vendrik and Woltjer (2007) examined the effect of the difference between a household’s income and the average income of a likely reference group on reported satisfaction. Their finding is that utility is concave in income, independent of whether the difference between own and reference income is negative or positive. The level of concavity is not significantly different for negative or positive deviations between own and reference income. As these authors observe, this is not in accordance with prospect theory where convexity is expected in the loss domain.⁹ Because convexity in the loss domain is part of the explanation of the reflection effect, the finding that utility is concave in social losses makes a social reflection effect less likely. A utility function that is concave on both domains predicts risk aversion in both the loss and the gain domain, if we abstract from the possible effect of probability weighting.

The utility function found by Vendrik and Woltjer is steeper for negative deviations than for positive ones, confirming (social) loss aversion. As a result risk seeking choices would actually be less likely in the loss domain than in the gain domain. If an agent chooses between two lotteries (A and B) by comparing the expected utility (EU) of these lotteries but perceives the expected utility with error, she will choose lottery A if: $EU(A) - EU(B) + \varepsilon > 0$ where ε is an error with mean zero. If U is a concave function and EU(A) > EU(B) then EU(A)-EU(B) is bigger if the utility function is steeper. Therefore it is more likely that $EU(A) - EU(B) + \varepsilon > 0$. In general a steeper utility function with the same error makes mistakes less likely. Given that with a concave function risk seeking choices are always mistakes, such choices also become less likely.

1.3 Related research

Although most theories and empirical investigations concern either social comparison or decision making under risk, some recent studies have explored situations where both social concerns and risk are present. Such studies have, among other things, found that uncertainty caused by others—strategic uncertainty—leads to more risk averse behavior than other types of uncertainty (Bohnet and Zeckhauser 2004). Other studies show that combining ideas developed specifically for either social decisions or decisions under risk do not always predict decisions in situations where both are present. For example, although people are willing to pay to raise the (expected) earnings of others they will not pay to reduce others’ risk (Brennan et al. 2008).

Bault et al. (2008) cast doubt on the presence of loss aversion around a social reference point when people make decisions that affect only their own earnings. In their experiment people make choices over lotteries while observing the choices of another participant who faces the same choice situations.¹⁰ Inequity aversion models, which assume loss aversion around a social reference point, predict that participants try to match the other’s choices. Surprisingly, Bault et al. observe the opposite behavior: if participants face an opponent more likely to select the risky (safe) lottery, they are found to be more likely to select the safe (risky) lottery. These findings can only be rationalized by a model where (at least) advantageous inequality is valued positively. Furthermore the positive effect of advantageous inequality has to dominate the negative effect of disadvantageous inequality.

Most closely related to our experiment is an experiment preformed by Rohde and Rohde (2011). These authors also study risk taking in a social context where the decision maker has no influence on the payoff of the participants she is coupled with. Three aspects of this study make it difficult to link the observed decisions to a social reference point however. Firstly participants faced not one but ten referents, who may receive different amounts. Therefore it is hard to establish the outcome against which a decision maker could compare her own payoff. Secondly if the referents do get a single fixed amount, that amount is, in most periods, somewhere in between the possible lottery payoffs for the decision maker, making it impossible to classify lotteries as concerning gains or losses.¹¹ Thirdly, in their study participants did not interact with each other before making risky choices and anonymity was guaranteed, which may result in a less salient social reference point.

2 Design

Our experiment is designed to observe choices under risk in situations with one fixed social reference point, the simplest possible situation that includes both risk and social comparison. Table 1 shows the experimental tasks and the order in which they where presented. Task 4, the lottery choices, is of primary interest. In this task participants choose between two lotteries, one of which is clearly more risky than the other. Our main interest is in the behavioral difference between the loss and the gain lotteries (see Fig. 1). The other tasks are used to establish and measure social ties which can enhance the likelihood and importance of social comparison.

Table 1 The order of the experimental tasks

The experiment starts with a social value orientation test (the circle-test) with a randomly determined participant. After this first part participants are coupled with their social referent (labeled “Other”). A Bertrand game is played to make the social referent more salient and to allow participants to develop different social ties, which may influence the effect of the social reference point. After the Bertrand game a second circle-test is administered in which the participant is coupled with the Other. The second circle-test is followed by the main part of the experiment where participants choose between lotteries. After this a post-experimental questionnaire is administered. To make social comparison even more focal we present participants with a photograph of their Other. Photos are shown directly after the end of the Bertrand game and on every subsequent screen, including during the lottery part.¹²

Only one part of the experiment is paid out to ensure that earnings from an earlier part cannot influence behavior in the lottery part. With a probability of 50% the part where participants make choices over lotteries, with a probability of 30% the Bertrand game and with a probability of 10% each, one of the two circle-tests is paid. If the lottery part is paid, only one of the choices of one of the coupled participants is played out (determined randomly) and that choice determines the total payoff of both participants. This ensures that the decision makers perceive each lottery as independent. Participants answer control questions to confirm their understanding of this and other procedures.

An English translation of the experimental instructions is provided in Appendix B; the original Dutch instructions are available upon request. All parts of the experiment are computerized (using PHP/MYSQL). We will now discuss the different parts of the experiment in more detail.

2.1 Photograph (Enhancing social comparison)

A photograph is taken of each participant before he or she enters the laboratory.¹³ Participants are told that they will be matched with the same participant, the Other, during parts 2, 3 and 4 of the experiment and that they will see a photo of the Other after part 2 of the experiment. Participants who know each other are requested to sit together in our reception room. We then make sure that they will not be matched.¹⁴

2.2 Circle-tests (Part 1 and 3, measuring social value orientation and social ties)

Circle-tests (Sonnemans et al. 2006) are employed to measure the social value orientation of participants and their social tie towards the Other. In the circle-test the participant chooses a point on a circle with a radius of €15. Each point on the circle represents a combination of payoffs for herself and the participant she is matched with, the receiver. The circle-test is presented to the participant without any point selected or payoff combination displayed. When she clicks on a point on the circle’s perimeter the corresponding payoff combination is shown. The participant can try as many points as she wants before confirming a payoff combination.¹⁵

Selecting a point on the circle involves making a tradeoff between the participant’s own payoff and that of the receiver. As all payoff combinations lie on a circle the decision maker’s earnings (x) and those of the receiver (y) have to fulfill the condition ${x^2} + {y^2} = {15^2}$. The slope of the circle differs along the circle, which affects the rate of transformation between one’s own and the receiver’s earnings. At the point of the perfectly selfish (€15, €0) payoff combination the slope is infinitely steep while it becomes ever shallower as one moves away from this point. This allows even weak, positive or negative, feelings about the receiver’s payoff to influence the selected point.

A payoff combination can be represented by a vector from the origin to the point on the circle corresponding to that payoff combination. The angle between this vector and the vector representing the purely selfish payoff distribution measures the decision-maker’s relative concern for the receiver. When the decision maker chooses a negative amount for the other the angle is recorded as negative.

At the start of the experiment participants perform the first circle-test in which they are randomly matched to an anonymous other participant. They are informed that they will not be matched with this same participant later in the experiment. The second circle-test is administered after the completion of the Bertrand experiment. At this point participants see their own picture and that of their Other. Subjects only get feedback on either circle-test if this part of the experiment is selected to be paid out at the very end of the experiment. The total payoff to a participant is equal to the amount she allotted to herself plus the amount allotted to her by the matched participant.¹⁶

The outcome of this first circle-test is a measure of the participant’s concern for an anonymous other, her social value orientation. The second circle-test measures a participant’s attitude towards the Other. Finally, the difference in angle between the second and first test measures the social tie to the Other; the importance of the Other’s payoff relative to the payoff of an anonymous person (Sonnemans et al. 2006).¹⁷

2.3 Bertrand game (Part 2, creating social ties)

In the second part of the experiment participants play a Bertrand game with so-called box demand.¹⁸ In this game matched participants simultaneously choose an integer from {0,1,…,99,100} which represents a percentage. The participant who chooses the lowest percentage gets her percentage of €5.-. The participant with the highest percentage gets nothing. If both participants choose the same percentage they share that percentage of €5.-. The game is played ten rounds without re-matching. If the Bertrand game is paid out, a subject receives her accumulated earnings over all 10 rounds.

Assuming both participants are selfish, the Nash equilibriums for a one-shot version of this game are both participants choosing 0%,1% or 2%. In this (finitely) repeated version of the game, playing one of these equilibriums in each round is an equilibrium. Even if a pair plays the Pareto optimal of these equilibriums (2%) in all rounds both participants will earn no more than €0.50. Cooperation can increase earnings substantially. Full cooperation, both choosing 100% in all rounds, results in both participants earning €25.-.¹⁹

The preceding paragraph shows that cooperation is financially attractive in this game; however, defection can also be very lucrative. Choosing 99% instead of 100% when the other player chooses 100% raises earnings in that round from €2.50 to €4.95. The attractiveness of both cooperation and defection make it likely that participants will develop many different types of social ties, depending on how the game unfolds.²⁰ Different social ties allow us to explore the impact of social ties on the effect of social comparison on choices under risk.

Independent of the kind of social tie developed, the Bertrand game ensures that all participants have some meaningful interaction with their Other. This is likely to strengthen the effect of social comparison. Of course the bond between a participant and her Other is still less strong than that between peers, friends or foes to which the participant is likely to compare herself in real life. Also, even though different participants have different types of interaction in the Bertrand game, in some sense all participants share a similar history with their other in the sense that they have played the Bertrand game together.

2.4 Lotteries (Part 4, main experimental task)

In the lottery part of the experiment, participants face a total of 42 choice situations. In each of these they choose between two different lotteries that simultaneously determine their own payoff and that of the Other. All lotteries are so-called simple lotteries²¹ with two possible outcomes. The choice in each situation is between a safe and a risky lottery with the same probabilities but with a larger variance of the outcomes in the risky lottery. In about half of the choice situations, the risky lottery is presented on the left. To prevent order effects choice situations are presented to each participant in a different, random, order. The lotteries are displayed in Appendix A.

Thirty of the 42 choice situations are created by presenting five original lottery pairs in six different ways. These six presentations are based on modifications in two dimensions. The first dimension is the social reference point, the payoff of the Other. Three kinds of social reference points are used: in loss situations the Other’s payoff is equal to the highest possible payoff for the decision maker; in gain situations the Other’s payoff is equal to the lowest possible payoff for the decision maker and in neutral situations the Other’s payoff is equal to the decision maker’s payoff regardless of the choice and outcome of the lottery. Figure 1 shows an example of a loss, a gain and a neutral situation.

The second dimension is the expected payoff: either the safe or the risky lottery has a slightly higher expected value. The safe lottery in the original lottery pair is slightly perturbed to create two closely related lottery pairs for each original pair. This manipulation ensures that participants cannot be indifferent in both cases.

In the loss and gain situations subjects make choices that affect only their own outcome and cannot observe the choices of others. This eliminates the possibility of social learning, preferences for conformity and concerns about the other’s payoff or reciprocity (as the other cannot influence your payoff either) affecting behavior. Twelve other lottery pairs are added to the aforementioned thirty lottery pairs. These are included to obscure the intentions of the experimenters and are not directly related to the research questions at hand.

2.5 Questionnaire (Part 5)

Participants are presented with a post-experimental questionnaire in which they are asked to list their field of study, their gender and their age. In addition they are asked to guess the age and field of study of the Other, to characterize the Other’s personality (kindness, cheerfulness and helpfulness) and looks, and to indicate how similar they think the Other is to them. Personality, looks and similarity are all rated using a seven-point scale. Participants are further asked to report, using a seven-point scale, on the emotions they experienced during the Bertrand game (rage, irritation, envy, joy, surprise and disappointment) and how satisfied they are with the outcome, their own decision and the Other’s decisions. Likewise the importance of different aspects of the lotteries is rated.

3 Research questions

Our experiment is designed to answer two research questions: first, does a social reference point influence decisions under risk, and if so in what direction?; and second, do social ties or experiences in the Bertrand game influence this effect? We will now discuss these questions and how the observations in the experiment can answer them in detail.

3.1 Does a social reference point influence decisions under risk?

In the loss and gain situations the payoff of the referent is independent of the choice of the decision-maker or the outcome of the lottery. The decision of the participant only influences her own earnings. Assuming the decision maker maximizes expected utility, neither selfish preferences nor linear social preferences predict any difference in behavior between gain and loss situations. A social reference point on the other hand does predict a treatment difference. If the payoff of the Other is the decision maker’s reference point, all outcomes are gains in the gain situation and losses in the loss situation. According to the reflection effect this induces risk seeking choices in the loss situation and risk averse choices in the gain situations.²²,²³

This prediction is a natural extension of (cumulative) prospect theory to a social reference point, but it is doubtful whether such conjectures about behavior in social situations on the basis of theories based on observations of behavior in private settings hold. As Bault et al. (2008) and Brennan et al. (2008) show, behavior in settings that include both risk and social comparison is not easy to predict by straightforward extensions of models developed to account for either social preferences or risky choices. Furthermore the results of Vendrik and Woltjer (2007) suggest that at least one of the forces that drive the reflection effect according to prospect theory—the shape of the utility function—may not be present in a social setting. Vendrik and Woltjer’s utility function is concave for both gains and losses, relative to a social reference point. The level of concavity is equal for gains and losses but the slope is steeper for losses. As discussed above, this implies risk aversion in both loss and gain situations and fewer mistakes and therefore fewer risk seeking choices in loss situations.²⁴ As in all choice situations in our experiment both lotteries have almost equal expected earnings, a concave utility function without error would predict that participants almost exclusively choose the safer lottery. Errors would be the main explanation for participants choosing the risky lottery. Therefore the findings of Vendrik and Woltjer would predict fewer risky choices in the loss situations.

It is not obvious how the behavior in the neutral situations (where the payoff to decision maker and social referent will always be equal) will relate to the behavior in the gain and loss situations. In neutral situations the participant’s decision also influences the earnings of the referent. The decision maker may therefore take into account the assumed (risk) preferences of the referent. However, the findings in Brennan et al. (2008) suggest that the risks faced by others have little impact on decisions. The differences in expected value are small, so it is unlikely that care for the other’s expected payoff will influence choices. Consequently, if we accept the typical assumption of social preference theories that equal earnings is a neutral point, social comparison will not influence decisions in neutral situations. It thus seems plausible that in this case all outcomes will be coded as gains. According to (cumulative) prospect theory this means choices should be in line with those for gain lotteries. If the social reference point affects decisions through some other mechanism the effects of a high and a low social reference point are likely to run in opposite directions compared to a neutral situation. In that case the risk aversion in the neutral situation should be in between that observed in the loss and gain situations.

3.2 Do social ties or experiences in the Bertrand game influence the social comparison effect?

Besides determining whether a social reference point affects decision making under risk, our experiment allows us to explore factors that may determine the strength of the social comparison effect. In this section we describe these factors and the way in which they can influence social comparison.

A decision maker will only engage in social comparison when she finds her referent relevant. In the case of a positive or negative social tie, the Other is apparently not irrelevant. We therefore expect a greater effect of social comparison, resulting in a greater difference in behavior between loss and gain situations, for participants with a positive or negative social tie compared to participants with a neutral social tie. Furthermore a negative social tie may influence social comparison differently than a positive social tie. For example a referent with a positive (negative) social tie may be relatively more (less) concerned with social comparison in gain situations where the other earns less and relatively less (more) concerned with social comparison in the loss situations where the other earns more. Another possibility is that it is not so much the social tie to the specific Other, but the concern with the referent’s payoff as captured by the second circle-test that affects the extent of social comparison.

The tendency to engage in social comparison may also depend on individual characteristics of the decision maker. For practical reasons no personality questionnaires are administered, but participants who behave more pro-socially may have more attention for the payoffs of others compared with egoistic participants. Therefore we can expect that pro-social participants, as identified by the first circle-test, are more likely to engage in social comparison. It is also possible that a more pro-social person is more concerned with social comparison when the other earns less, but less concerned when the other earns more.

Although the experiences in the Bertrand game are likely to be expressed through the social tie, our experiment also allows us to explore the effects of these experiences more directly. In particular, the effect of social comparison may well be different for couples who cooperated (defined as both participants choosing 100 in a round) than for those who did not achieve cooperation. Moreover, when cooperation breaks down due to one participant being “betrayed” by the Other (defined as the participant chooses 100 while the Other chooses a lower percentage after the participants cooperated in the previous round) this yields yet another, distinctly different, experience. It is plausible that such different experiences lead to different social comparison effects. The self-reports on emotions experienced during the Bertrand game are also informative about how a participant views the Other. A person who experienced anger is likely to care for the Other’s outcomes in a different way than someone whose partner gave her cause for joy. This motivates the analysis of the correlations between the social comparison effects and the self-reported emotions.

Social comparison is known to depend on whether an individual considers the Other to be part of her in-group or her out-group (Mussweiler and Bodenhausen 2002). Our questionnaire allows for several measures of similarity between the decision maker and the Other. It is more likely that the participant considers the Other as a relevant peer if similarity is higher—therefore we expect a positive relation between similarity and the effect of the social reference point. We further expect that participants will be more likely to engage in social comparison when they perceive of the Other as a better person. We therefore expect that the effect of social comparison will be strengthened if a participant rates his or her Other higher on the positive attributes. It could also be that the earnings of a “better” person are more relevant when the Other earns less than when the Other earns more.

4 Results

4.1 Social reference point effect

Seven sessions of the experiment were run at the CREED laboratory in Amsterdam in December of 2008. 126 people participated in the experiment. Almost all of them were students from the University of Amsterdam; 46.8% of the participants were students of economics or business and 55.6% were male. A session lasted about 1.5 to 2 hours. All statistical tests in this section report two-sided p-values.

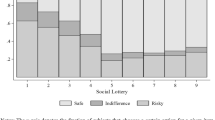
Figure 2 shows the average percentage of the time participants choose the safer lottery in the loss, gain and neutral situations. The safe lottery is chosen more often in the loss situation than in the gain situation. This difference is highly significant according to a Wilcoxon matched-pairs signed-rank test (p = .0001).

Fig. 2

Average percentage of safe choices in the loss, neutral and gain situations

For every loss/gain situation pair we compare choices. Of the 1,260 observations (126 participants and 10 loss/gain situation pairs) in 937 cases (74.4%) the choice was the same in loss and gain situations, in 203 cases (16.1%) more safe choices and in 120 cases (9.5%) fewer safe choices were made in the loss situation compared with the gain situation (binomial test p < .001²⁵). Studying each loss/gain situation pair separately we find that for 9 out of 10 pairs the safer lottery is chosen more often in the loss situation (binomial test p = .02). On the level of participants we find that for 38 participants (30.2%) the social comparison effect is neutral (no switches for 22 participants and the same number of switches in both directions for 16 participants), 61 participants (48.4%) made more safe choices and 27 (21.4%) made fewer safe choices in the loss situations (binomial test p < .001²⁶).

Given these tests the effect appears to be robust over situation pairs and participants: choices are more risk averse in situations where the social referent earns more (loss situations) than in situations where the social referent earns less (gain situations). This finding is opposite to the behavior predicted when the referent’s income is used as a reference point. It is, however, in line with the prediction made by the utility function of the shape found by Vendrik and Woltjer (2007).

It is difficult to assess the strength of the treatment effect. Most decisions are the same in the loss and gain treatment. That suggests the effect is not extremely large, but it is not possible to quantify the effect on an individual level. The fraction of participants for whom we find an effect in the predominant direction is twice as large as in the opposite direction even if it is not a majority of all participants.

In neutral situations the safer lottery was chosen 74.4% of the time. This is in between the percentage of safe choices in the loss and gain situations. Choices in the neutral situations are significantly different from those in the gain situations (Wilcoxon test p = .04) and marginally significantly different from those in the loss situations (Wilcoxon test p = .09).

• Result 1: Social comparison does matter for individual decision making: The risk-averse option is chosen more often in the gain situations than in the loss situations.

• Result 2: Behavior in the neutral situation is in between the behaviors in the loss and gain situations.

A bivariate logistic individual fixed effects regression confirms these findings and allows us to control for other factors. Table 2 reports on the regression’s results. Most importantly the main social comparison effects remain significant. Several other base variables have a significant effect on choices in the expected direction. Firstly, an increase in the difference in variance between the safe and the risky lottery made it more likely that a participant would choose the safe lottery. This is what is expected for risk averse individuals. Secondly, a higher probability of the best outcome in the risky lottery makes choosing the safe lottery more likely. The greater underweighting of larger probabilities, as specified by prospect theory, explains this effect. This finding strengthens the view that outcomes are coded as gains. Thirdly, the safe lottery is chosen more often when it has a higher expected value than the risky lottery. Fourthly, participants are also somewhat more risk averse in later periods.

Table 2 Logistic individual fixed effects regression withthe probability of choosing the safe lottery as dependent variable.^a

We also find two interesting interaction effects of the gain situation with the difference in variance and with the probability of the best outcome. In gain situations the difference in variance no longer has a significant effect, while the effect of the probability of the best outcome is stronger.²⁷ This could suggest a somewhat different decision process for gain lotteries. Possible participants made a less careful decision for gain lotteries, paying more attention to striking features like the probability of the best outcome and less to features that require a closer examination like the difference in variance.

4.2 The influence of social ties and Bertrand game

We now turn to the second research question: Do social ties or experiences in the Bertrand game influence the social comparison effect? We start by examining how the observed behavior relates to the social tie as measured by the circle-tests. If the difference between the angle chosen in the first and the second circle-tests is larger than 5°, we consider this as a positive or negative social tie (Sonnemans et al. 2006). The participants with no social tie can be divided in two equally large categories: those who choose relatively selfishly in both tests, or relatively cooperatively in both tests. Table 3 displays the average difference between the loss and gain situations for these four categories.

Table 3 The size of the experimental effect for different social ties

Interestingly, the social comparison effect seems to be smaller for selfish participants who are likely to have less attention for the earnings of others; however, this difference is not statistically significant. Spearman’s rank correlations between the experimental effect and the social tie, the first angle (the more general social attitude) or the second angle (the social attitude to the specific Other) are also not statistically significant at conventional levels (all p > .44).

Next we calculate Spearman’s rank correlations²⁸ (indicated by Rho in the remainder of this section) between the social comparison effect and measures obtained in the Bertrand game and questionnaire. Rough measures of the success of the interaction in the Bertrand game are a participant’s own earnings and the difference between her earnings and those of the Other. Neither of these is significantly correlated with the social comparison effect at conventional levels (p > .4). The average amount of cooperation in a pair (Rho = −.04 p = .68) or the occurrence of betrayal (Mann–Whitney test p = .85) are not significantly correlated with the social comparison effect either.

Participants report on negative emotions experienced during the Bertrand game. These emotions were rage, irritation, envy and disappointment and are combined into a single scale labeled anger.²⁹ Three questionnaire items related to the Bertrand game request participants to report their satisfaction with the outcome, their own decisions and the decisions of the Other. These are combined in a scale labeled satisfaction. Neither scale nor the reported joy is found to correlate significantly with the social comparison effect (p > .26).

Several questions relating to the participant’s perception of the Other are combined in a scale labeled attractiveness. These questions relate to looks, kindness, cheerfulness, helpfulness, openness and quality of the Other’s picture. Two other questions, about the intelligence of the Other and whether the Other is thought to be a thinker, are combined in a scale labeled perceived intellect.³⁰ Neither of these measures correlates significantly with the social comparison effect (p > .25).

The perceived general similarity between the participant and her referent and the perceived similarity regarding the age and field of study of the Other, as measured in the questionnaire, are not significantly related to the social comparison effect. Similarity between the players can also be measured objectively (same sex or different sex, difference in age and same or different field of study). None of these variables is correlated significantly with behavior in the lottery part.

• Result 3: No relationship is found between the size of the effect of the social reference point and

  • a. Social attitude or social ties as measured by the circle-tests

  • b. Experiences or experienced emotions in the Bertrand game

  • c. Perceived characteristics of the Other

  • d. Similarity, either perceived or objective.

4.3 Additional analyses

As none of our measures of the experience in the Bertrand game and the beliefs about and attitudes towards the Other are found to correlate with behaviour in the lottery part, it seems legitimate to question whether this is due to the reliability or relevance of these measures. We will therefore take a closer look at the relations between these measures.

As expected, the experiences in the Bertrand game are found to influence a participant’s social tie. The social tie is positively correlated with the differences in the earnings of matched participants in the Bertrand game (Rho = .21, p = .017). This effect is mainly caused by participants who earn less than their referent. The correlation between earnings in the Bertrand game and the social tie is found to be marginally significant (Rho = .17, p = .063). The mean social tie of participants who are betrayed in some period of the Bertrand game is significantly smaller than the social tie of non-betrayed participants (−3.19 < +3.28, Mann–Whitney test p = .02).

The anger and satisfaction scales, based on the reported emotions experienced during the Bertrand game, are found to be significantly correlated with earnings in the Bertrand game, as is the reported joy experienced during the Bertrand game³¹ (Rho is−.61, .67 and .51 respectively, all p < .001).³² Anger is negatively related with the social tie (Rho = −.32, p < .001).

Greater perceived attractiveness and perceived similarity are positively and significantly correlated to the social tie. (Rho is .27 (p = .008) and .24 (p = .01) respectively). Perceived intellect is not significantly correlated with the social tie. The Other is reported as both less attractive and less similar if the respondent experienced betrayal. (Mann–Whitney test p = .011 and p = .062 respectively.)

We conclude that the social tie is related to the experiences in the Bertrand game and the perception of the referent in expected ways; the failure to find a relation between the social tie and the social comparison effect cannot result from an ineffective measurement of the social tie.³³

Finally, in the questionnaire we also asked about the goals of participants in the lottery part. A competitive goal (“I found it important to earn more than the Other”) is negatively correlated with the attractiveness of the Other (Rho = −.31, p = .002) and correlates weakly with the social comparison effect (Rho = .16, p = .08). We find a somewhat stronger social comparison effect for participants who reported paying more attention to the amount of the Other (Rho = .169, p = .060).

5 Conclusion

Real life risky decisions are hardly ever made in social isolation: professional traders observe their colleagues, investors their neighbors, and athletes their competitors. The effect of social comparison on decisions has received ample attention in social preferences theories and experiments, but the social context is remarkably ignored in the field of decision making under risk. Our lottery choice task considers the simplest possible situation where both risky choices and social comparison are present; choosing between two lotteries while comparing one’s own payoffs to the fixed payoff of one social referent, the Other.³⁴ We find that participants are more risk averse when they can earn at most as much as the Other (loss situation) than when they are ensured they will earn at least as much as the social referent (gain situation).

It is well established that a non-social reference point (like present wealth) leads typically to risk seeking in the loss situation and risk aversion in the gain situation (the reflection effect), as predicted by prospect theory. Our results with a social reference point are the opposite of this prediction. We find that social comparison influences decision making under risk but that this effect cannot be explained by straightforward extensions of theories on decision making under risk to social situations.

The finding that this social reference point influences the behavior in another direction than the standard reference point is intriguing. It is, however, less surprising given the results of other recent studies which also find unexpected results in situations that include both social comparison and risk. Bault et al. (2008) show that while losses loom larger in individual decision making tasks, gains loom larger than losses in the social situation they study. Brennan et al. (2008) show that people aren’t willing to pay to reduce others’ risk despite their social preferences over expected outcomes. More directly related is the finding by Vendrik and Woltjer (2007) on the effect of social comparison on the utility function. These authors establish that both below and above the social reference point utility functions are concave, while other reference points lead to a convex utility function for losses. As the utility function is also steeper for losses, this implies fewer risk seeking choices in the loss domain, which provides a possible explanation for our findings.

Although this provides a possible explanation for our result, it is certainly early days to be definite about behavior in situations with risk and social comparison as the number of studies in this emerging field is very limited. However, our findings, together with research mentioned above, show the importance of studying such situations. It also shows that models will have to make great strides to incorporate the observed behavior.

Appendices

Appendix A: The Lottery Pairs

Table 4  

Appendix B: Translation of the Instructions

(original Dutch instruction available upon request)

General Instructions

This experiment consists of 4 parts. You will receive instructions on each part prior to the start of the part concerned.

If you have any questions during the experiment, raise your hand.

3.1 The OTHER

During each part you will be coupled with another person in this room who we will call the OTHER. In parts 2, 3 and 4 this is always the same person. The person to whom you are coupled in part 1 is a different person than the person you are coupled with in parts 2, 3 and 4.

3.1.1 Photo

Before the start of the experiment we made a photograph of all participants. After part 2 (and not before) you get to see a photo of the person you are coupled with in parts 2, 3 and 4.

When you get to see a photo of the OTHER he or she will also get to see a photo of you. When you are not yet seeing a picture of the OTHER, the OTHER will not see a photo of you either.

3.1.2 Payout

During this experiment you can make money. The earnings of only 1 of the 4 parts will be paid out. Which part this will be is determined after the end of the last part. With 10% chance this will be part 1, with 30% chance this will be part 2, with 10% chance this will be part 3 and with 50% chance this will be part 4. How much you earn in a specific part depends on the choices made by you and/or the OTHER. Besides their earnings in the experiment everyone will receive €10,-.

[Control questions: the participant had to answer questions concerning the matching process, the payout probabilities and the point in the experiment where photos would be displayed.]

Instructions for part 1

4.1 Choice

In this part you have to choose between combinations of earnings for yourself and the OTHER. All possible combinations are represented on a circle like the one shown above. Later you can click on any point on the circle. Which point you choose determines how much money you and the OTHER earn. You cannot click on the circle yet.

4.2 Earnings

The axes in the circle represent how much money you and the OTHER earn when you choose a certain point on the circle. The horizontal axis shows how much you earn: the more to the right, the more you will earn. The vertical axis shows how much the OTHER will earn: the more to the top, the more the OTHER earns. The distribution can also mean negative earnings for you and/or the OTHER. Points on the circle left of the middle mean negative earnings for you, points below the middle mean negative earnings for the OTHER. When you click on a point on the circle the corresponding combination of earnings, in cents, will be displayed in the table to the right of the circle. You can try different points by clicking on the circle using your mouse. Your choice will only become definite when you click on the “send” button.

The OTHER is presented with the same choice situation. Your total earnings in this part consist of the amount allotted by you to yourself and the amount allotted to you by the OTHER by his or her choice.

4.3 Payout

The OTHER’s chosen combination is only made public if this part is paid out (this happens with a chance of 10%, see the general instructions on the paper on the table).

After this part you will be coupled to a different participant for parts 2, 3 and 4. (See the general instructions on paper.)

[Control questions: the participant had to choose some specified distributions on the circle.]

Instructions for part 2

5.1 The OTHER

You are now coupled to a different person than in part 1. From now on you will be coupled to this person.

5.1.1 Decisions

This part consists of 10 rounds. Every round both you and the OTHER make a decision. This decision consists of choosing a percentage, at least 0 and at most 100. This percentage should be a whole number. The percentages chosen by you and the OTHER determine what you and the OTHER earn in a round.

5.1.2 Earnings

The earnings in each round are determined in the following way:

• If you and the OTHER choose the same percentage you both get half of €5,- multiplied by the percentage chosen by you.

• If the chosen percentages are different the one who chose the lowest percentage will get €5,- multiplied by that percentage. The person who chose the highest percentage will get nothing in that case.

Total earnings in this part are equal to the earnings over all 10 rounds added together.

5.1.3 Payout

This part is paid out with 30% chance; see the general instructions on the paper on the table.

[Control questions: participants had to calculate earnings of themselves and the OTHER resulting from specified percentages chosen by themselves and the OTHER]

Instructions for part 3

This part is the same as part 1 except that you are coupled to a different person, the person you were matched with in the previous part. So you again have to choose between combinations of earnings for yourself and an OTHER. The other is now the person you were coupled with in part 2.

6.1 Choice

In this part you have to choose between combinations of earnings for yourself and the OTHER. All possible combinations are represented on a circle like the one shown above. Later you can click on any point on the circle. Which point you choose determines how much money you and the OTHER earn. You cannot click on the circle yet.

6.2 Earnings

The axes in the circle represent how much money you and the OTHER earn when you choose a certain point on the circle. The horizontal axis shows how much you earn: the more to the right, the more you will earn. The vertical axis shows how much the OTHER will earn: the more to the top, the more the OTHER earns. The distribution can also mean negative earnings for you and/or the OTHER. Points on the circle left of the middle mean negative earnings for you, points below the middle mean negative earnings for the OTHER. When you click on a point on the circle the corresponding combination of earnings, in cents, will be displayed in the table to the right of the circle. You can try different points by clicking on the circle using your mouse. Your choice will only become definite when you click on the “send” button.

The OTHER is presented with the same choice situation. Your total earnings in this part consist of the amount allotted by you to yourself and the amount allotted to you by the OTHER by his or her choice.

6.3 Payout

The OTHER’s chosen combination is only made public if this part is paid out (this happens with a chance of 10%, see the general instructions on the paper on the table).

[Control questions: participants had to select a specified payoff combination and answer questions concerning payout probabilities and the matching process.]

Instructions for part 4

7.1 Choices

In this part you have to choose between 2 different lotteries on every screen. In total you will be presented with such a choice situation 42 times.

The lotteries in this part determine both your earnings and those of the OTHER. Below you can see an example of a screen like the screens you will get to see later. On the screen you can see two lotteries between which you can choose. One to the left of the line in the middle of the screen, the other to the right. The blue bar represents how much you will earn in the outcome concerned. The red bar how much the OTHER will earn. The amounts are also written below the bars. The chance of a certain outcome is represented by the circle below the bars. The dark colored part of the circle represents the chance of the outcome concerned. Below the circle the chance in percentages is written.

7.2 Choice situations

The choice situation below is only an example. You will not be asked to choose between the lotteries you see here.

In this example the earnings of the OTHER are equal, independent of your choice or the outcome. This may be the case in the choice situations you will be presented with later, but it will not be the case in all choice situations.

7.3 Earnings

If this part is selected to be paid out, it is first determined whether one of yours or one of the OTHER’s choice situations will be detrimental. Therefore there is just as much chance that it will be one of your choice situations as that it will be one of the choice situations of the OTHER. Then it will be determined which of the 42 choice situations of the selected person will be looked at. Each choice situation has an equal chance of being selected. The selected choice situation will then be looked at to determine which of the two lotteries was chosen by the selected person (you or the OTHER). This lottery is then played out and determines the total earnings of both you and the OTHER.

7.4 Payout

The chance that this part is paid out is 50% (see the general instructions on paper which are on your table).

If one of the choice situations presented to you is selected the payoff to you and the OTHER is determined only by the lottery chosen by you in that choice situation. That means that when you make a choice you can assume that only that choice determines the total earnings of you and the OTHER.

[Control questions: participants had to answer questions regarding their understanding of the payout probabilities and presentation of the lotteries.]