Learning Through Inquiry

Teaching science through inquiry is a long-standing practice, with broad agreement about the form it should take. Students are expected to investigate researchable questions; gather and analyse data; and develop and represent evidence-based claims. The role of the teacher is both complex, multifaceted and demanding (Dobber, et al., 2017). Teachers are expected to facilitate student inquiry using specific strategies such as questioning to guide student conceptual understanding during the inquiry process (Kawalkar & Vijapurkar, 2013), to focus on the development of student metacognitive thinking skills (Ben-David & Zohar, 2009) and to create a culture of inquiry in classrooms and schools (Uiterwijk-Luijk, et al., 2019). Authoritative teacher or textbook representations are generally used to guide this learning, with a strong focus on explicit teacher instruction (Buckley & Boulter, 2000; Bybee, 1997; Furtak et al., 2012; Sell et al., 2006).

Parallel to the use of canonical representations in supporting student inquiry learning, teachers have also guided students to construct, review and refine their own representations, leading to learning gains. However, this representation construction approach (RCA) poses new challenges for teachers. The teacher is expected to elicit and guide students’ reasoning about their own represented claims as an orientation to understanding and learning scientific forms of reasoning and their representation. This RCA raises questions about how and when these representations are introduced, and the role of teacher instruction in this form of inquiry.

In this paper, we aim to clarify further the rationale for this form of guided inquiry and the necessary teacher strategies and underlying purposes in key early stages of topic exploration. This paper addresses the following research questions:

  1. 1.

    What teacher strategies can be used to enact the initial stages of a representation construction approach to guided inquiry that integrates mathematics and science?

  2. 2.

    What are key challenges for teachers in this form of inquiry?

We first review warrants for this representation construction approach, followed by an analysis of teacher strategies during the enactment of key early stages of the RCA in the topics of chemistry and mathematics with a Grade 5 class. An interdisciplinary focus was used to guide students’ learning about the science concepts of states of matter, evaporation and the mathematical concepts of formal and informal measurement and data representation. Analysed data included video capture of the teacher’s guidance of tasks and classroom discussion, student artefacts and teacher and student interviews.

Literature Review

Learning in science and mathematics is increasingly recognised as students knowing how to reason about and apply these subjects’ concepts through using and integrating multiple semiotic modes or forms of representation, including talk, gesture, image, number and physical manipulations (Arzarello et al., 2009; Park et al., 2020; Prain & Waldrip, 2006). Many studies have focused on how multiple representations in different modes support this reasoning process, indicating the value of practical inquiry to anchor reasoning processes (e.g. Airey & Linder, 2009; Jaipal, 2010; Tytler et al., 2013). While many of these representations are informal, such as talk, gesture and object manipulation, authoritative teacher and textbook representations are generally used to induct students into the disciplinary norms for demonstrating and applying this reasoning. Many researchers have also noted the challenges for students in understanding the conventions and referents of these canonical representations and their underpinning reasoning, with an extensive literature on how to address this problem (e.g. Buckley and Boulter, 2000; Dyrvold, 2020).

The main proposed solution is explicit teacher explication of the rules of different sign systems, such as graphs and tables (Buckley and Boulter, 2000; Bybee, 1997; Furtak et al., 2012; Sell et al., 2006; Unsworth, 2001), and teacher demonstrations of how these systems and their grammars, and resultant canonical representations, can be applied to the particular topic of inquiry. Sometimes, researchers have advocated that these tools should be learnt before being applied to a problem (Metz, 1995), for example, as part of worked examples in science and mathematics (Atkinson et al., 2000) or introduced as expert examples of scientific and mathematical reasoning after practical work (Schwartz et al., 2012; Unsworth, 2001).

Parallel to using canonical representations and their underpinning grammars in inquiry, teachers have also guided students to construct, review and refine their own representations, producing strong learning outcomes in science (Manz et al., 2020; Tytler et al., 2013, 2021) and in mathematics (Lehrer & Schauble, 2006; Mulligan et al., 2018). However, this RCA clearly poses new challenges for teachers. The teacher is expected to elicit and guide students’ reasoning about their own representations as an orientation to understanding and learning scientific forms of reasoning and their representation. Practical work can give students a ‘feel’ for scientific activities, reasoning and meaning systems (Sutton, 1992, p. 79), but this inquiry needs to start with students’ own meaning-making resources including language and visual representation. By starting with, or supplementing these current representational resources and forms of reasoning, the teacher is potentially well-placed to guide students towards the reasoning moves and warrants entailed in scientific abstractions and their representation.

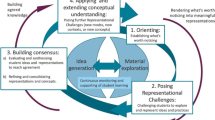
This representation construction approach logically extends Lemke’s (1990) persuasive claim that teachers need to encourage students to use everyday reasoning and talk to learn the reasoning processes and their representation in science, with RCA extending reasoning resources to include visual, graphical, actional and mathematical modes. In this paper, we draw on our initial account of this representation construction pedagogy to clarify how the teacher guides students’ reasoning (Tytler et al., 2021). In this four-stage pedagogical model, the teacher (1) orients students, (2) poses representational challenges, (3) evaluates and builds consensus about key concepts and (4) applies and extends conceptual understanding (Tytler et al., 2021). We recognise that this pedagogy increases the complexity of the teacher’s role in interpreting and guiding student representations, and we aim to explore and clarify the necessary teacher’s strategies and underlying purposes in the first three stages of topic exploration.

We consider that starting with students’ own representations in learning to reason in science is further warranted in terms of Peirce’s (1955) general theory of meaning-making. For Peirce (1955), all meaning-making entails interpreting referents (objects, processes, experiences, changes to phenomena, practices in the world) in signs, or representations, where signs stand in for their referents and enable sign-makers to reason in multiple ways. By focusing on students generating, discussing and refining their own represented claims, the teacher can engage students in reasoning about their own sign, meaning and referent relationships in inquiry as the bases for being supported to understand scientific ones. In coming to understand science’s abstracted meanings, students need to make meanings across modes in what Kress and van Leeuwen (2006, p. 39) labelled ‘transduction’. For example, to understand rate of change, students need to make sense of graphs from which this concept can be inferred, but also understand how this concept can be applied and represented in other contexts. To achieve transduction, or creative reasoning across modes, students need to reason about correspondences of meaning within and across their own sign systems, as well as coherence of meaning within and across science’s systems (Tytler et al., 2021; 2022).

As with using canonical representations in guided inquiry, the teacher in an RCA needs to ensure that students’ own representations go beyond unresolved exploration of topics or are merely dismissed and then replaced by canonical ones. Student tasks and challenges therefore need to contextualise target concepts and make them meaningful. Depending on student capabilities, teacher implicit and explicit instruction is needed to guide learning and its representation. Each stage of the inquiry can entail both individual and whole-class direct and implicit teacher instruction to set up topic foci, methods and processes of inquiry and guide student inference-making, clarify confusion, resolve debate and consolidate learning (Tytler et al., 2021; Lehrer, 2021).

An Interdisciplinary Mathematics and Science Pedagogical Model

In seeking to characterise how teachers can integrate science and mathematics learning through a representation construction process, we developed an inquiry-based, four-stage pedagogical model (IMS, Tytler et al., 2021).

The four stages of the model are as follows:

  • Orienting: The teacher interests students by pointing out puzzles in what is to be studied. She questions them to find out their current knowledge then explores their ideas to guide inquiry foci. Where appropriate, she introduces resources for later stages of the inquiry. In this initial stage, her representational challenges to students are mainly verbal, thus limiting transductive demands.

  • Posing representational challenges: The teacher challenges students to explore and represent their ideas and practices further, both verbally and in multimodal texts, often involving initial material investigative work. For instance, they may be challenged to represent gathered data or to represent a process, such as a microscopic account of evaporation, implying the need to support student meaning-making across modes.

  • Building consensus: First, the teacher uses student ideas and representations to compare, evaluate and then synthesise their ideas about which aspects of their representations effectively show patterns in data, or suggest explanations. Second, she guides refinement and consolidation of ideas to establish shared conceptual understanding and associated representations. Depending on student capabilities, she provides indirect instruction (such as task-framing, prompts and further questions) and direct instruction (such as explanations and modelling) to develop students’ knowledge of how representations enable and show learning.

  • Applying and extending conceptual understanding: The teacher creates new representational challenges to extend student knowledge and practices in related situations, or introduces further concepts through representational challenges, to repeat the cycle.

This paper explores and clarifies the necessary teacher’s strategies and underlying purposes in the first three stages of this model.

Methodology

The study reported in this paper is part of a longitudinal research project ‘Enriching mathematics and science learning through an interdisciplinary approach’ (IMS), funded by the Australian Research Council from 2018 to 2021 (https://imslearning.org/), that aims to investigate the effectiveness of an interdisciplinary learning approach to mathematics and science. The project employed a design-based approach (Cobb et al., 2003), where theoretical understandings are developed and refined through iterative cycles of design, enactment, evaluation and redesign of instructional interventions. Instructional interventions include collaborative design of the lesson sequences with participant teachers, and ongoing researcher support as teachers enacted the programmes. The study reported in this paper was conducted in 2019 in a private K-12 college in regional Victoria, Australia. One class of Grade 5 children (with an average age of 11 years old) participated in a 5-week lesson Chemistry sequence with their teacher Mike, with 6 students selected as focus students by Mike to represent a wide ability range. This is the third topic sequence that Mike enacted as part of the IMS project. The first two topics are optics and space.

The researchers observed the 5 lessons over a period of 5 weeks. The data analysed included video recordings of teacher guidance of tasks and classroom discussion; classroom artefacts and student work; and post-sequence semi-structured individual interviews with the teacher and 6 focus students. This paper focuses on illustrating the early stages of the IMS pedagogy through unpacking and interpreting what Mike did in guiding the students through the inquiry process. Our interpretation of the teacher intentions was informed by our classroom observations during the field work, repeated viewing of the video records of classroom activities and the teacher interview. The student work included in this analysis was intended to illustrate the variety of representations generated.

The Design of the Chemistry Sequence

The sequence was designed based on the Victorian Grades 5–6 science curriculum in chemical sciences: (1) ‘Solids, liquids and gases behave in different ways and have observable properties that help to classify them’ (VCSSU076), and (2) ‘Changes to materials can be reversible, including melting, freezing, evaporating, or irreversible, including burning and rusting’ (VCSSU077). The mathematics concepts include rate of change, measurement (length, area, volume and time) and data representation. We note that the concept of rate of evaporation is in the Grade 7 mathematics curriculum (VCMNA257), linking to ‘investigation, interpretation and analysis of graphs based on real life data’. In this sequence, instead of standard mathematics problems, the science provides a meaningful context for contextualised mathematical learning and for catering for a range of abilities. This interdisciplinary sequence was first designed by the research team, and then modified in consultation with the teacher during planning sessions. Ongoing modification occurred as the teacher enacted the sequence and conferred with the research team.

Similar to an optical sequence design, the mathematics and science tasks and activities in this sequence were developed based on shared forms of inquiry such as data representation and modelling of phenomena (see Table 1).

Table 1 Lesson sequence on chemistry
Full size table

Each lesson in the designed sequence has incorporated several IMS pedagogical stages. In this paper, our focus is on the first three stages of the pedagogy to illustrate how the teacher-oriented students towards a particular aspect of the phenomenon or concept and challenged them to represent aspects of the phenomenon in question.

Results

In this section, we illustrate possible ways the first three stages of the IMS pedagogy can be enacted through analysing two main tasks from the chemistry sequence: (1) exploring the rate of water evaporation and (2) the absorbency of paper towels. In identifying Mike’s strategies, we report on the context of the lesson sequence to clarify his intentions and illustrate effects on learners.

Exploring the Phenomenon of Evaporation

Over the three lessons, students were challenged to:

  • Represent where water exists on a map of the school

  • Represent changes from solid to liquid to gas as ice is heated

  • Represent the evaporation of water over a week from different-sized containers

The first three lessons were designed to develop students’ understanding of particle ideas and explain changes of state in water. The teacher provided several anchoring events to orient students’ attention to key aspects of the phenomenon and targeted concepts, such as spacing and motion of particles.

Orienting Students to Visualise the Phenomenon of Evaporation

In lesson 1, Mike aimed to focus on evaporation by discussing the forms of water around the school and introducing the word ‘molecules’ but left the definition open. In lesson 2, he took the class outside with a bucket of water and their notebooks, where they put their hands into the water, pressed them onto the concrete pavement, and then observed what happened. As handprints disappeared, the class noted down what they thought occurred. They were invited to reason using their current sense of referent, sign and meaning relationships, with possible inclusion of the new sign ‘molecules’. After a few attempts, involving testing, drawing with chalk around the wet handprints and timing their disappearance, everyone returned to class.

Student verbal explanations included ‘evaporation’ and ‘the water molecules evaporated because of the heat from the sun’. Mike turned to a beaker of water and asked ‘so with this water, I want you to think about what’s happening to the molecules of water as I’m heating it up’. He boiled the water to guide student reasoning about evaporation, and then asked the students to record in their workbooks what they thought water molecules in different states look like under a high-powered microscope. One student, Jenny, offered to share and represent her ideas for the class (Table 2).

Table 2 Jenny explaining her idea of molecule to the class
Full size table

After a class discussion, Mike demonstrated diffusion, asking the students to think about the motion of particles in an open space and when heated:

  1. 1)

    Air freshener: ‘if I spray here, why could you smell it there?’

  2. 2)

    Food dye in hot and cold water: ‘when we heat the molecules up, what do you think will happen?’

These demonstrations aimed to introduce dynamic aspects of the particle model not apparent in Jenny’s static whiteboard drawings, namely motion and spacing between molecules. Mike’s questions aimed to extend student understanding of what needed to be represented and prompt further student reasoning without direct explanation.

Challenge: Representing Changes of State in Water

Following the discussion of molecular motion and its link to temperature, based on the two demonstrations, Mike challenged the class to represent visually, and with annotation, the melting and evaporation processes at molecular level. Table 3 demonstrates Mike’s framing of the challenge by heating ice cubes to accelerate naturally occurring processes.

Table 3 Mike challenged students to represent changes of state
Full size table

In this transductive representational challenge, Mike invites the students to turn a perception-based set of verbal signs from the material experience (‘it’s evaporating’) into a multimodal visual and written sign system, and to make an explanatory claim about the process. This transduction is enabled by students’ prior knowledge, their guided experience of the phenomena, representational resources and reasoning from contextual clues. His prompts encourage student independent choices to represent the process, thus encouraging variety in the representations (see Fig. 1a and b).

Fig. 1
figure 1

Differences in how students represented space between and movement of particles. a Spacing between particles and movement of particles using arrows for the gas state, and b the particles escaping into liquid when ice was heated

Full size image

These examples show differences in how students represented space between and movement of particles. Figure 1a shows how this student invented a way to show spacing between particles and movement of particles using arrows for the gas state. Figure 1b depicts the particles escaping into liquid when ice was heated, as shown in the drawings and accompanying linguistic account. At this stage, student representations tend to be intuitive, revealing possible misconceptions for clarification.

Challenge: Mathematising the Rate of Water Evaporation in Different-Sized Containers

Mike then challenged the class to devise an experiment to test under what conditions water in different containers evaporates quickest, and to represent their claims. Groups of three and four students were provided with four different shaped beakers (Fig. 2). Mike used direct instruction to specify some conditions for the investigation by explaining that the students were to fill each beaker with 100 ml of water and then place the beakers in the room, leave them for a week and then measure remaining water. This left open questions of how to make precise measurements and how to represent them.

Fig. 2
figure 2

Experimental setup for one student group

Full size image

Mike was aware that the class knew how to calculate the surface area of square and rectangular shapes. For more complex shapes, circles and hexagons, he directed them to the internet to perform the calculations. In a subsequent interview, he commented that the open approach catered for mixed student ability: ‘It gave you the ability to scaffold it to different levels…. You had the kids who were just doing a cube compared to people who were doing a cylinder or a square based pyramid. You had different types of ability levels that you could cater to’. He indicated that ‘even though some of them probably didn’t get the full understanding they would have got a good level of understanding’.

Mike further challenged them to consider influences on the rate of evaporation and asked ‘how can we speed up its drying’ with a focus on heat, and moving air (wind) as factors. He brought together a range of experiences and ideas (e.g. conditions for drying clothes or puddle) to prompt students’ visual and verbal reasoning in their representations. To complete the lesson, he asked the class to generate a claim and reasons about which container will lose most water over 1 week. These claims were evaluated in the following week’s lesson based on the experimental results (lesson 3).

Building Consensus: Comparing and Synthesising Results to Develop Explanations

Mike started lesson three requesting students in groups measure the water left in their containers and compare results to their predictions. Through his interaction with a few groups, the connections between surface area and evaporation rate emerged. This was followed by all groups reporting back their results and a whole-class discussion where Mike guided discussion on volume-surface area ratio through using a variety of cones, cylinders and prisms. In the following episode, Mike provided explicit instruction as he brought together different student groups’ ideas by emphasising connections between the container’s surface area and the amount of evaporation.

T:So looking back last week, we made a prediction and we actually worked out the area of the water. So is the area of the water exposed to air, does that have an influence on how much it evaporates? Can you see a direct link between that?

S:Yeah.

T:The bigger the area, the more evaporation?

Ss:Yes

Stan:Our A had a 100cm of surface area and container A also lost the most.

T:So what about container C, what was its area?

Stan:C was 74.95 and lost 39.

Ss:And container D was our smallest and lost the least.

T:This one, it had the lowest surface area of water exposed to air and it lost the least, this one had the biggest area in contact to air and it has lost the most. Then it was this one lost the second most which is C and then D. The thing that was interesting is C has a surface area of 64.95 and the surface area of D was 56.25. So they are similar only 8 cm2 difference and the amount they evaporated was also very similar which is another little interesting point. So some good things to look at when you are getting those results.

In this challenge, the students coordinated two sets of quantities—surface area of the container and the changes in volume of water—to identify the rate of evaporation over a week. Because each group had different-sized containers, the teacher attempted to bring students ideas together in the discussion to focus on the mathematical relationships between surface area and volume of water. By asking each group to report their results and discussing the patterns across the student groups, Mike provided opportunities for students to transduce meanings across modes. Recognition of variation in visual data patterns (one set of sign-specific meanings) across different resources was remade into a verbal explanation for varying rates of evaporation (a new meaning expressed verbally and derived from the data representation, and now also an inferential claim drawing on model-based reasoning). While the students did not formally generate representations that precisely identified the mathematical relationship of the two variables, it appears that their verbal accounts indicate some conceptual understanding of evaporation. This was noted by the teacher:

Being able to come back a week later and then do the follow up where they measured how much water was left and to make the direct link between-- well I made the prediction that this one would evaporate more because it’s got the greatest surface area exposed and it was one of those lessons that you really saw your intention or what you hoped the kids would learn come to fruition. Because you got to see the before and after. Everything worked really well, the maths was strong.

Table 4 includes two student work samples and their interview reflections that show some student learning from this experience.

Table 4 Student work from the evaporation investigation task
Full size table

Students discussed the factors influencing the rate of evaporation: temperature and surface areas. Sally drew connections between the room temperature and the movement of molecules as the explanation for the different evaporation rates. Samantha attended to both the shape of the container (small or big opening of the containers) and the motion of molecules affected by temperature. In both cases, the students tried to incorporate their emerging understanding of molecules into their reasoning.

Exploring the Absorbency of Paper Towels Through Formal and Informal Measurement

In lesson 5, Mike’s aim was to build students’ understanding of different properties of materials. By testing paper towel water absorbency, they were expected to reason about absorbency using informal and formal measures. Different brands were used to determine efficiency for cleaning water spills or drying hands, with students expected to devise a fair experiment. Mike intended students to learn about measurement and scoring as mathematical concepts, setting them the challenge to estimate, measure and represent variability, as indicated in the interview:

Because there was that sense of how you are going to measure the absorbency of the paper towel as opposed to it is or it isn't, how are you going to decide which one is more absorbent than the other, which ones stronger. They actually had to come up with something that could quantify that … which again it keeps me thinking about that, the need to be more aware of trying to make those maths links really obvious and really clear.

Students were to use formal measures and convert between millilitres and litres, including use of decimal notation. They were expected to collect data and design, and represent and interpret their data display using representations. Mike led the discussion before groups determined their methods. Mike asked the students to consider key paper towel features and how to measure them scientifically. Through prompts, he challenged them to score these features and consider whether an overall score could be developed.

Orienting: Identifying Measures for Absorbency of Paper Towel

Mike held up to the class four different rolls of paper towel of varying appearance and cost, and asked them to identify: ‘Which paper towel would be the most effective?’ and ‘How do we decide what we mean by it being effective?’. The students then examined the towel qualities by sight and touch.

When challenged to show how to assess varying towel effectiveness, the students’ responses included looking at the thickness or ply of different brands. One student claimed that ‘we need to know how much water we are using’ and another asked ‘does the water temperature make a difference?’. To support students devise their own measures, Mike modelled one way to test absorbency by placing a sheet of towel over the beaker and dropping water onto the towel until it began to sag into the beaker (see Fig. 3).

Fig. 3
figure 3

Teacher modelling paper towel absorbency test

Full size image

Mike probed the students about other properties to test. He asked how they would test paper strength. One student suggested conducting the experiment in the same manner as the teacher demonstration in Fig. 4, but also placing a small weight on top of the towel then dropping water. ‘Great idea!’ Mike responded, and then posed a further question: ‘How are you going to make sure you have consistent results and that your results are fair?’ One student suggested an eye dropper for the water and for measurement. Mike then explained that they needed to account for the number of millilitres of water absorbed: ‘How many turns or drops were needed before the water started to leak into the beaker? If you are testing weight, how much weight would the towel hold?’.

Fig. 4
figure 4

One student group work on paper towel testing

Full size image

Challenge: Measuring Absorbency of Paper Towel

The students conducted the experiment by counting ‘drops’, an informal measurement. One group of girls, in conversation with Mike, were asked what they meant by ‘drops’ as a measure. The students demonstrated this physically, but Mike challenged the students to devise a way to convert ‘drops’ to ‘millilitres’. The group searched the lab for a measuring cylinder that would allow them to drop a millilitre of water into the cylinder and count the number of drops. They carried out this task three times and determined that 16 drops equalled one ml. Figure 4 shows the work in converting from informal to formal measurement and their determination to identify the most absorbent towel.

Our results indicate that the representation construction approach assumes that teachers have a strong understanding of quality inquiry processes, their warrants, and their representation, as shown by Mike, and can feed these productive constraints into what the students reason about, and how. In enacting IMS pedagogical principles, Mike used a number of strategies, including (1) eliciting and building on initial inputs from the students; (2) feeding in prompts as resources for reasoning; (3) encouraging creative reasoning through student-generated representations; and (4) building bridges to scientific explanations. Mike constantly sought to elicit, interpret and respond to students’ reasoning about everyday experience (e.g. water existing in different forms, drying hands using paper towel). This eliciting was often undertaken through teacher questioning with student verbal responses, in relation to an observed or experienced phenomenon. While inviting creative reasoning about the phenomenon of evaporation, he subtly prompted his students to consider additional information, for example the introduction of the term ‘molecules’, and to consider referents of terms in relation to the context of investigation without providing direct answers. He encouraged the students to represent their thinking using a variety of representational forms. In exploring paper towel absorbency, he actively prompted students to consider the notion of absorbency as a material property, contextualised through an extensive discussion of the methods of investigation and controlling of variables. In both examples, Mike constantly sought to link their everyday language and explanations (verbal, diagrammatic and tabular) to the more systematic reasoning processes entailed in science inquiry and representation, through anchoring student reasoning in material explorations and representational challenges.

The challenges for teachers using this form of guided inquiry include (a) providing sufficient experiential and symbolic support to provide clues for student transductive meaning-making across modes; (b) judicious timing of when and how to use indirect and direct instruction to set up, advance and consolidate student learning in the inquiry, based on need; and (c) supporting both science and mathematics learning.

Discussion

Integrating science with mathematics increased the complexity of tasks and posed further challenges for how the teacher elicited and prompted students’ everyday resources as the bases for meaning-making in science and mathematics. By implication, this means that the teacher needs to support students in developing fluency in concepts and representations across both subjects as part of the guided inquiry and facilitate student transductive meaning-making across a diverse range of modes and representational forms, including verbal, visual, embodied and mathematical representations. This inquiry needs to start with students’ own meaning-making resources as demonstrated by Mike in this short sequence. It also requires the teacher to constantly elicit and monitor new meanings as they emerge, using indirect and direct instruction, to guide and expand student reasoning. As noted in the case, when the teacher supported this process with carefully sequenced material inquiries and representational challenges, together with judicious prompting and explanations, it opened up opportunities for students to respond creatively and productively to this form of inquiry.

In this sequence, the mathematics learning is contextualised through science in real-life situations, different from the long-standing descriptive word problems or more recently depictive mathematics problems (Hoogland et al., 2018). The contextual nature of the problems raised both representational opportunities and challenges for student mathematics learning and for the teacher in catering for mixed abilities. Mike considered the links between maths and science authentic: ‘the kids were actually doing genuine maths in a scientific setting rather than just doing them in total isolation’. He considered the relationship between maths and science in the sequence: ‘You can sometimes get too tied up in the science content without thinking about that, the process of coming to that understanding is so important. Any time you can put a maths concept in a proper setting or in a setting that they can apply it, it’s much more beneficial’. He found the sequence was well-balanced: ‘there is always that question if you spend too much time on the maths does the science become the poor cousin and you find that nice balance between the two of them’. However, as noted by the teacher, there is always scope to extend student understanding beyond curricular prescription if there is a meaningful context. Mike considered that the links to mathematics can be made stronger: ‘You could easily just transfer that and put it straight into a maths class and it would have held up as a really good math class looking at volume looking at three dimensional shapes’. Mike also acknowledged the need to consolidate the learning in both science and mathematics from the sequence: ‘It would have been probably even nicer to have a little bit more time to follow that one up and take it from the concrete and apply it to the abstract which you could then do it in a math class if you had that division going properly’.

Implications for Future Research

While the IMS model provides a flexible approach to guided inquiry, our case study points to the need for more research on (a) productive representational challenges that contextualise key concepts in different topics at different year levels; (b) longitudinal studies of student learning outcomes from the IMS pedagogy; and (c) teacher understanding of the transductive demands of student multimodal reasoning and learning in science and mathematics, and how teachers can support this process. Our study highlights both the challenges and necessity for teachers to understand and support this reasoning across modes.