Search for Symbol Sense Behavior: Students in Upper Secondary Education Solving Algebraic Physics Problems

Abstract

Students in upper secondary education encounter difficulties in applying mathematics in physics. To improve our understanding of these difficulties, we examined symbol sense behavior of six grade 10 physics students solving algebraic physic problems. Our data confirmed that students did indeed struggle to apply algebra to physics, mainly because they lacked both sufficient symbol sense behavior and basic algebraic skills. They used ad hoc strategies instead of correct, systematic rule-based procedures involving insight. These ad hoc strategies included the cross-multiplication, the numbering, and the permutation strategy. They worked only for basic formulas containing few variables. In problems with more variables, students got stuck. The latter two strategies substitute numbers for variables. The permutation strategy randomly checks several permutations to guess which one is correct. The numbering strategy substitutes numbers to check algebraic manipulations. Our results indicate insufficient focus on conceptual understanding of algebra in some mathematics textbooks, leading to reliance on poorly understood ad hoc strategies. Effective teaching of algebraic skills should not focus on either basic algebraic skills or on symbol sense behavior. Instead, both aspects should be taught in an integrated manner. Our operationalization of symbol sense behavior turned out to be very useful for analysis. In contrast to earlier qualitative studies, it provided us the opportunity to measure symbol sense behavior quantitatively. This operationalization should also be applicable to other science subjects. Furthermore, we discussed some implications of our results for curricula, teachers, science teacher educators, and textbook publishers aiming at successful application of mathematics in physics.

Introduction

Mathematics plays a major role in science education (Karam 2014; Roorda et al. 2015). However, research has shown that students face difficulties when applying mathematics in science subjects (e.g., Quinn 2013; Redish and Kuo 2014). Such struggles can be persistent and concern students of all ages.

Even if students’ knowledge of mathematics is sufficient, its application in science subjects is not guaranteed. Except for a couple of studies (e.g., Cui 2006; Rebello et al. 2007), this phenomenon has hardly been researched. The pioneering study of Hudson and McIntire (1977) with pre-course tests of algebraic and trigonometric knowledge and skills taken by 200 students initiating a physics course has shown that a solid grasp of mathematics is not sufficient to guarantee the application of these in physics; although the student has those skills, the performance in physics can be poor.

Several researchers have shown that the main reason for the lack of application above is related to compartmentalized thinking (e.g., Nashon and Nielsen 2007; Quinn 2013; Turşucu et al. 2018b) in which students see mathematics and science as two different subjects. In many countries, teaching these subjects separately consolidates and intensifies this phenomenon (e.g., Netherlands institute for curriculum development 2018; The National Academies Press 2018; TIMMS and PIRLS 2018).

Berlin and White (2010; 2012, 2014) suggest a remedy for compartmentalized thinking may be coherent mathematics education (CME) that is of major importance for students. The idea behind CME is fostering connection between mathematics and science education through, e.g., alignment of notations. In addition, improvement of mathematical proficiency (Kilpatrick et al. 2001) including the five interwoven strands adaptive reasoning, conceptual understanding, procedural fluency, productive disposition, and strategic competence may also help improve the application of mathematics in science subjects. In algebra education, especially crucial are the second and third strands. Together, these strands form algebraic expertise, referring to algebraic skills with particular emphasis on procedural fluency in relation to conceptual understanding (Andrá et al. 2015; Arcavi 1994; Drijvers 2011). The algebraic skills involving conceptual understanding are called symbol sense, relating to the ability to first consider an algebraic expression carefully, to find its relevant aspects, and to choose a wise systematic problem-solving strategy based on these aspects. Symbol sense contains “an intuitive feel for when to call on symbols in the process of solving a problem, and conversely, when to abandon a symbolic treatment for better tools” (Arcavi 1994, p. 25). By means of examples, Arcavi described eight behaviors indicating symbol sense behavior. These examples demonstrated the intimate relationship between procedural skills and conceptual understanding as if they were two sides of the same coin of algebraic expertise.

Flexible manipulation skills (FMS) are regarded as a key behavior of symbol sense and deal with the ability to flexibly manipulate expressions (both technical and with insight) and being in control of the work. FMS consists of two intertwined concepts: showing sensitivity towards gestalt view on algebraic expressions and handling in a suitable way with their visual salience (Kirshner and Awtry 2004). The former concept includes “the ability to consider an algebraic expression as a whole, to recognize its global characteristics, to‘read through’ algebraic expressions and equations, and to foresee the effects of a manipulation strategy” (Bokhove and Drijvers 2010, p. 43). The latter deals with visual cues of algebraic expressions. As part of visual salience, Wenger (1987) distinguished between pattern salience (PS) that is related to sensitivity towards patterns in algebraic expressions, and local salience (LS) relating to sensitivity towards local algebraic symbols, i.e., visual attractors such as fractions, square root signs, and exponents. Hence, FMS plays an essential role in solving algebraic problems in physics class.

Bokhove and Drijvers (2010) extended the notion of gestalt view to the students’ strategic decision of what to do next. They studied mathematics tasks in a digital environment. These tasks caused crises, inviting the application of basic algebraic skills (BAS) and demonstration of symbol sense behavior (SSB), e.g., expanding brackets (LS) or canceling out common factors (PS) without coming any closer to the desired result.

Research Aim and Research Question

This study aims to report the findings of a qualitative study with a quantitative component on SSB of students in upper secondary education. The central research question is “To what extent do students in upper secondary education demonstrate symbol sense behaviour when solving algebraic physics problems?”

According to teachers in upper secondary education, among students encountering difficulties with applying mathematics in algebraic physics problems, grade 10 students face the biggest problems (Turşucu et al. 2017). Therefore, we selected grade 10 students to gain deeper insight in their algebraic problem-solving abilities, especially their basic algebraic skills and their symbol sense behavior.

For the operationalization of SSB, we follow the line of Bokhove and Drijvers (2010) in the sense that we examine students’ BAS and sensitivity towards LS and PS. Different from them, we investigate algebraic physics problems. We do not focus on the meaning or nature of physical concepts, because the emphasis is on algebraic skills learned in mathematics class and applied to physics problems.

For stylistic reasons, we will use the concepts procedural skills and procedural fluency (Kilpatrick et al. 2001) interchangeably to refer to the same basic algebraic skills. This also applies to conceptual understanding and insightful learning. Furthermore, our sample contained one male and five female students. Therefore, also the terms “the student” and “she” were used interchangeably to denote the same.

Relevance of This Study

Our extensive literature research with various web-search engines including Google Scholar and ProQuest on scholarly articles reveals the absence of studies investigating SSB in algebraic physics problems. Since we examine physics rather than mathematics, investigation of SSB may add to the evaluation of this concept. Our literature study also reveals that the mechanisms behind the lack of successful application of mathematics in science subjects are under researched. In addition, students having a solid grasp of mathematics, but facing difficulties in applying this subject in physics, is highly under researched. This study may offer insights in how students apply algebraic skills from mathematics in physics and provide insight in these underlying mechanisms that can be used by curriculum developers, mathematics and physics teachers, mathematics and science teacher educators, and textbook publishers aiming to improve the application of mathematics in physics, and strengthen students’ demonstration of CME (e.g., Alink et al. 2012; Berlin and White 2012, 2014). As to curriculum developers aiming at CME, it may provide design principles that connects the physics curriculum to that of mathematics. This may be a content standard dealing with the same pedagogical approach to using algebraic skills (Turşucu et al. 2018a). Whether students are in the mathematics or in the physics classroom, they may not be confused about different ways of how algebraic skills are applied. This may also impede compartmentalized thinking (Nashon and Nielsen 2007; Quinn 2013). Physics textbooks may contain, e.g., introduction paragraphs where physics formulas ($h=\frac{1}{2}\cdotp g\cdotp {t}^2$) are treated together with corresponding mathematical expressions (y = b·x²) that students learned in mathematics class. On the individual level, mathematics teachers may provide context to algebra by examining analogous physics problems. Even on the collaboration level, there are possibilities; for instance, the development of common problem-solving strategies where algebraic skills are used with insight in both subjects. Through professional teaching programs, mathematics and science teacher educators can make mathematics and physics teachers aware (Girvan et al. 2016) of the underlying mechanisms above and discuss remedies.

These issues above are of major importance for many countries aiming at enhancement of the application of algebraic skills from mathematics in physics class, especially improving SSB in algebraic physics problems.

Background

Mathematics in Dutch Upper Secondary Education (USE)

The researchers in this study were all affiliated with the academic science teacher education program in Delft in the Netherlands. Hence, we approached Dutch secondary schools rather than those from another country. In this regard, it may be worthwhile to discuss shortly the Dutch context in relation to education, especially that of secondary education (SE) that contains three lower years (LSE) and three upper years (USE).

According to the OECD (2018), the Netherlands is regarded as an advanced industrial nation where both mathematics and science education are high on the governmental agenda (Ministry of Education, Culture and Science 2018). Internationally, Dutch students in USE score accordingly on mathematics and science assessments, including assessments on physics (TIMMS and PIRLS 2018).

In the first year of USE, grade 10 students who follow physics have to choose between mathematics A and mathematics B. The latter puts more emphasis on algebra than the former. The content of these subjects is described in national curricula (Netherlands institute for curriculum development 2016). These curricula contain both the general educational core goals and the more specific standards, which are tested in national final examinations.

Because of the difference in emphasis on algebra in both mathematics subjects, some teachers think (Turşucu et al. 2017) that mathematics B should be compulsory for physics students. For this belief to be generalizable for the Dutch context, quantitative research is needed.

The algebraic skills in both curricula are mainly associated with algebraic activity (Netherlands institute for curriculum development 2016). Although it is hard to characterize the latter, it involves activities such as implicit or explicit generalizations, patterns of relationships between numbers, and mathematical operations with variables, formulas, and expressions (Drijvers 2011). As a working definition of the concept of formula, we used algebraic expressions with real measurable quantities (e.g., speed). An expression can be a formula involving physical quantities or an abstract algebraic expression with abstract mathematical variables (placeholders).

Mathematics curricula refer to algebraic skills to cover the entire set of mathematical activities above. These skills are divided into specific skills and general skills. The first concept deals with knowledge about algebra and manipulation skills, and hence is close to BAS (Kieran 2013; Wu 1993). General skills contain developing systematic problem-solving strategies and showing insight in the structure of expressions. We conclude that algebraic expertise is not mentioned in these curricula, but the description of using algebraic skills with insight is identical to that of symbol sense in earlier studies (e.g., Andrá et al. 2015; Arcavi 2005).

Algebraic techniques are part of algebraic skills and used to manipulate expressions (Drijvers 2011). Hence, they play a key role in this study. Some well-known techniques are “substitution” used to replace single variables in expressions, and “multiplication of both sides” where the left and right side of the equals sign is multiplied by the same variable. In the next section, we will discuss these techniques.

The application of algebra in mathematics A is mainly related to contexts from everyday life. To a lesser extent, this also holds for mathematics B that contains many more abstract problems requiring algebraic proof than mathematics A does.

Regarding the connection between these curricula with the physics curriculum, there is no explicit reference to alignment through compatible notations, concept descriptions, and pedagogy of mathematical approaches. Even though it is of major importance for students, also reference to the organization of the learning process in order to achieve a logical learning line across both subjects is absent. As a result, certain mathematical concepts are used in physics class before they were introduced in mathematics class (Turşucu et al. 2018b). Furthermore, the algebra used in mathematics curricula is considered to be sufficient to tackle algebraic problems in physics class (Netherlands institute for curriculum development 2018).

The connection above is of major importance in a very large number of countries, especially in secondary education (e.g., Alink et al. 2012; Berlin and White 2012, 2014). A lack of alignment across these subjects, may be confusing for students and impede both their application of algebraic skills in physics and CME. For instance, for the lens formula in geometrical optics, a mathematics teacher may write $\left(\mathcal{O}-f\right)\left(i-f\right)={f}^2$, while a physics teacher writes ${\mathcal{O}}^{-1}+{i}^{-1}={f}^{-1}$$\left(\mathcal{O}\ne 0,i\ne 0\right)$ (Turşucu et al. 2018a). Such mismatches may also hold for concept descriptions and the pedagogy of mathematical approaches above. Therefore, curriculum developers should explicate the importance of connection across both subjects.

Algebra in Physics

Dutch students in secondary school start with physics in their second year of LSE (grade 8). Quantities are introduced through a strong context-concept approach (e.g., van Bemmel et al. 2013). The number of formulas describing physical quantities in this year is negligible, let alone using algebraic skills to manipulate formulas. In the next year, formulas are used more frequently (e.g., Alkemade et al. 2014), but the algebraic skills level needed to manipulate them is low. This changes in grade 10, immediately after the transition from LSE to USE where the intended level of algebraic skills increases substantially (e.g., Ottink et al. 2014). Indeed, as mentioned above, among students in USE, grade 10 students face the biggest difficulties with applying mathematics in algebraic physics problems (Turşucu et al. 2017).

Most of the physics formulas are symbolic representations of proportionalities containing real, measurable quantities expressed in various symbols. For instance, whereas the potential energy E_pot. = m·g·h and the period of a spring-mass system $T=2\cdotp \pi \cdotp \sqrt{\frac{\boldsymbol{m}}{\boldsymbol{C}}}$ are proportional to h and $\sqrt{m}$ respectively, the attractive gravitational force ${F}_{\mathrm{G}}=G\cdotp \frac{m\cdotp M}{r^2}$ is inversely proportional to r². The formulas in algebraic physics problems and the algebraic skills needed to solve them are described in the Dutch physics curriculum Netherlands institute for curriculum development 2016). These formulas can also be found in BINAS, a natural sciences information booklet that students use during regular physics tests and the final examination.

In recent years, algebraic physics problems including algebraic curve straightening, e.g., the curve related to Boyle’s law P·V = c, derivation of formulas such as deriving the escape velocity ${v}_{\mathrm{escape}}=\sqrt{\frac{2\cdotp G\cdotp {M}_{\mathrm{sun}}}{r}}$ from our solar system, and dimensional analysis, for instance showing that the quantity acceleration due to gravity g in the free fall formula $h=\frac{1}{2}\cdotp g\cdotp {t}^2$ has the unit $\frac{m}{s^2}$, have become more important in USE. Solving them correctly, i.e., using mathematically correct procedures, requires sufficient algebraic expertise with BAS and demonstration of symbol sense behavior.

Mathematics and Physics Teaching

In many countries (Stein and Smith 2010) including the Netherlands (Turşucu et al. 2017; van Zanten and van den Heuvel-Panhuizen 2014), textbooks mediate between both the core goals and standards of education (the intended curriculum) and the actual teaching in classrooms (the implemented curriculum) Stein and Smith 2010. They are very closely followed by teachers, who teach their students from these books. Therefore, to a very large extent, textbooks shape classroom practice. As to algebra education, physics students apply mathematics and especially algebraic skills that they have learned in mathematics textbooks to solve algebraic physics problems in physics lessons.

Since explicit reference to connection in Dutch mathematics and physics curricula is absent, there is also no alignment between mathematics and physics textbooks. This impedes students’ successful application of mathematics in physics and demonstration of CME (e.g., Alink et al. 2012; Berlin and White 2012, 2014). Hence, the connection between these subjects mainly depends on individual efforts. For instance, physics teachers designing teaching materials that aim to align both subjects through content. Such individual attempts are also of major importance for countries without centralized curricula.

Algebraic Expertise in Detail

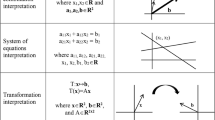
Similar to Arcavi (1994), Drijvers (2011) views algebraic expertise as a spectrum extending from basic algebraic skills (Kieran 2013; Wu 1993) to symbol sense involving conceptual understanding. This is illustrated in Fig. 1. Whereas basic algebraic skills deal with procedural work with a local focus and algebraic reasoning, symbol sense concerns strategic work with a global focus and emphasis on algebraic reasoning. In our case, strategic work refers to a physics student who is in control of the work and seeks for a different systematic approach when a strategy appears to be insufficient. Having a global focus is related to recognition of patterns in physics formulas and equations where these formulas are involved. Algebraic reasoning deals, for example, with extreme cases and symmetry considerations. Analogous to Bokhove and Drijvers (2010), we focus on the relationship between local and global, and procedural and strategic work.

Fig. 1

Algebraic expertise ranging from basic skills to symbol sense

Concerning the relationship between basic skills (Kieran 2013; Wu 1999) and conceptual understanding (Schoenfeld 2016), the last decades have been an arena for a long-standing debate called “Math Wars” related to how students best acquire algebraic expertise: by first practicing standard procedures or focusing on insightful learning? This pedagogical war led to conflicting ideas about designing curricula, content of textbooks, and effective teaching practice. In recent years, this discussion shifted towards the belief that both procedural skills and conceptual learning should be taught in an integrated manner (Rittle-Johnson et al. 2015). To improve algebraic expertise, one needs to view their relationship as bidirectional and continuous: “understanding of concepts makes basic skills understandable, and basic skills can reinforce conceptual understanding” (Bokhove and Drijvers 2010, p. 43). This view on algebraic expertise will also be our point of departure.

As for teaching practice, such an integrated approach may involve ideas for teaching algebraic skills in both mathematics and physics class. For instance, to show that g in the formula $h=\frac{1}{2}\cdotp g\cdotp {t}^2$ has the unit $\frac{m}{s^2}$, one may first isolate g. Solving for g requires insight in algebraic techniques. Physics textbooks may need introductory paragraphs summarizing prior mathematical knowledge that students learned in their mathematics textbooks. This idea is based on the importance of activation of pre-knowledge in the context of learning and instruction in relation to better students’ achievements (e.g., Hailikari et al. 2008; Turşucu et al. 2018a). For instance, solving the analogous mathematical expression y = b · x² for x gives $x=\sqrt{\frac{y}{b}}$. Next, g in $h=\frac{1}{2}\cdotp g\cdotp {t}^2$ is solved. Substitution of units in $g=\frac{2\cdotp h}{t^2}$ is regarded as basic algebraic skills. This integrated approach can be extended to mathematics, where physics formulas may be written next to mathematical expressions.

Systematic Algebraic Strategies Versus Ad hoc Strategies

In this study, we distinguish between “systematic algebraic strategies,” i.e., using algebraic skills with insight as described in the curriculum (Netherlands institute for curriculum development 2016), and the application of ad hoc strategies. For stylistic reasons, we use ad hoc strategies and ad hoc approach interchangeably to denote the same. This also holds for systematic algebraic strategies and systematic algebraic approach. As a working definition of systematic algebraic strategies, we use a systematic, rule-based problem-solving approach in which algebraic techniques are used with insight, where rule refers to the standard rules for multiplication and division of powers, such as x^a·x^b·x^a + b, which play the role of algebraic axioms in high school algebra. With ad hoc strategies, we refer to mathematical strategies that are not based on standard algebraic rules with insight, and only work for a specific case that may lead to fragmented knowledge, impeding generalization of algebra. Especially, in more sophisticated problems for which insight is needed rather than ad hoc strategies, students may get stuck. In addition, applying them depends on the approval of an authority. For instance, a student may be skillful in using the formula triangle of the form a = b·c, but gets stuck when solving for b in a = b·c·d. She only succeeds after a teacher, i.e., authority, introduces a new ad hoc approach. While such strategies may not always yield correct solutions, they can be useful as initial attempts to solve a problem (Roorda 2012). Thus, ad hoc strategies may be harmful for students’ application of algebraic skills in physics, mainly because of the lack of insight in algebraic skills.

Concrete examples of ad hoc strategies are the application of mnemonics such as the formula triangles above, substitution of numbers for variables to verify whether an operation will result in a valid outcome, or guessing a solution for a problem and then working backwards.

In this study, using algebraic skills with insight becomes visible through the application of algebraic techniques during procedures involving BAS and sensitivity towards gestalt view and the visual salient aspects LS and PS in expressions.

Methodology

Selection Criteria for Participants

To gain insight in students’ symbol sense behavior during algebraic problem-solving in physics, we needed two different groups, each containing three anonymized grade 10 physics students from a regular school. To this extent, we used convenience sampling (Bryman 2015) to find two physics teachers who together with their students were available and willing to participate in this study. Next, we used the “Interview Protocol Physics Teachers” in the third subsection of the Appendix to conduct an interview with them and select appropriate students. To ensure appropriate length and clearness, this protocol was redesigned several times and tested on different teachers and social scientists during the pilot-phase prior to this study. The physics teachers used “Magister,” a student monitoring system for secondary education (accounts.magister.net 2018) to select appropriate students based on their mathematics and physics grades. Based on the Dutch ten-point grading system, these students had a sufficient mathematics grade and an insufficient physics grade (< 5.5). This implies that students’ insufficient application of mathematics in physics is not due to their insufficient mathematics knowledge, but related to their inadequate application step in physics. To ensure that it was legitimate to compare the students’ individual results and that of both groups, the students should use the same mathematics and physics textbook and have a similar knowledge domain at the start of these interviews. These selection criteria were so strong, that we only found two schools satisfying these criteria. For group (I) of school (I), this yielded Aron (the only male student in this study), Beth, and Chloe with mathematics A, and for group (II) of school (II) Diana, Eve, and Fiona with mathematics B of group (II). They all used the physics textbook SysNat (Ottink et al. 2014a) and the same mathematics textbook series Getal and Ruimte: Reichard et al. (2014a) for group (I) and Reichard et al. (2014b) for group (II). The details are presented in Table 1. The physics grades range from 5.0 up to 5.4 and for mathematics from 6.4 up to 7.9.

Table 1 Mathematics and physics grades of the respondents

Design of the Tasks

The tasks were designed so that they should trigger students solving algebraic physics problems and provide insight in their algebraic expertise with BAS and SSB. Based on these design principles, we first selected four exercises from the physics textbook SysNat (Ottink et al. 2014) that we called “Ideal gas” (Task 1), “Falling stone” (Task 2), “Uniform circular motion” (Task 3), and “Spring-mass system” (Task 4). Only “Task 3” was identical to that of the physics textbook. The other exercises were adjusted into algebraic physics problems described in symbolic representations (Goldin 2000). Next, these tasks were solved by grade 10 students who did not participate in this study. This pilot phase provided us information about the appropriateness of these problems, such as clearness, length, and that these problems were doable by students. After analyzing their work, some of the tasks were slightly adjusted to meet our design principles. This resulted in “The Tasks” described in the Appendix. The “Systematic Solution Set to The Tasks” (solution set in short) are also presented in the Appendix. We focused on rewriting formulas and solving kinematic energy relations.

Design of Task-Based Interviews (TBIs)

The TBIs have their origin in clinical interviews that were used by Piaget (1954) to gain deeper understanding of students’ cognitive development. Such clinical studies are regarded as qualitative research. Conducting TBIs to gain insight in students’ problem-solving behaviors follow from gaining deeper understanding of students’ cognitive development. Therefore, TBIs are part of qualitative research (e.g., Bokhove and Drijvers 2010; Maher and Sigley 2014). This implies that our study can also be considered as a qualitative study. The quantitative component of this study is related to the quantization of BAS and SSB that we developed to compare the individual performance of students and that of group (I) and group (II), and will be discussed in the following subsections. Our interviews were carefully designed so that students had only interaction with the tasks and the interviewer. Therefore, the TBIs were conducted by two independent researchers (one per group) in an appropriate, quiet place. The TBIs took approximately 40 min and were based on a structured protocol consisting of two parts that was designed in such a way that the instructions were clear and students could easily work with it. Based on the feedback of the non-participating students above, some parts of this protocol were reorganized and rewritten. These adjustments led to “Interview Protocol for Students” in the fourth subsection of the Appendix. In the first part, students were asked questions about their background, the textbooks they used, and their mathematics and physics grades were double checked. In the second part, they solved “The Tasks” while thinking aloud (Charters 2003). The interviews were videotaped. Next, the audio part was transcribed ad verbatim, for which the students gave consent. The interviewer only interrupted when a procedure or reasoning was not clear enough or she remained silent for 1 min. We used stimulated recall techniques (Geiger et al. 2016) to get as much information as possible on the students’ solutions. If necessary, we provided small neutral hints.

Data Analysis: Phase 1–Phase 4

Data analysis of videotaped data comprises seven consecutive phases (Powell et al. 2003), not requiring a rigid order. Regarding this study, in “phase 1” (viewing attentively the video data), we acquired a first and general understanding of how the respondents solved the algebraic physics problems. Since their behavior was video recorded, we could easily identify the first interesting and relevant observations such as the application of ad hoc strategies.

“Phase 2” (describing the video data) was less important, because the relevant information in videotaped data was captured in detail by the interview transcripts. This process is described in “phase 4.”

In “phase 3” (identifying critical events), we identified critical events, i.e., students’ application of algebraic techniques, ad hoc approaches, and other relevant steps, during problem solving in which a mathematical explanation or argument was involved. These events are further described in “phase 5.”

In “phase 4” (transcribing), the audio part of videotaped data was transcribed ad verbatim.

Data Analysis: Phase 5

In “phase 5” (coding), we operationalized our central research question through the coding scheme (spread sheet) in Table 2. The coding process was based on analyzing physical episodes (to a lesser extent), the transcripts of the audio part of videotaped data, and the students’ written solution set to the tasks. Their solution set was compared to our systematic solution set in Appendix and coded afterwards using Table 2. The dots in the cells indicate that they are empty and should be filled in. This process is explained in the next subsection. Thus, Table 2 is complete.

Table 2 Coding scheme to analyze students’ SSB

Prior to the TBIs, we identified both the required algebraic technique (Drijvers 2011) and the needed BAS or symbol sense type in the systematic set. Later, this was compared to students’ written solution set and assigned to scores to gain insight in their SSB (Bokhove 2011). For instance, to solve sub task a) of “Task 1 Ideal gas” in Appendix systematically, procedure 1 requires the application of “multiplication of both sides” of $\frac{P\cdotp V}{T}=C$ by T which yields P · V = C · T, since $T\cdotp \frac{P\cdotp V}{T}={T}^{1-1}\cdotp P\cdotp V=P\cdotp V$. This implies that this procedure requires students’ sensitivity towards the exponent −1 in T⁻¹, and is associated with the symbol sense type LS.

Students may use seemingly different approaches than manipulating exponents above. For instance, canceling out variables $\underset{\_}{m}\bullet g\cdot h=\frac{1}{2}\cdot \underset{\_}{m}\cdot {\left({v}_{\mathrm{final}}\right)}^2$ that is mathematically equivalent to working with exponents. Such procedures are also correct and do not affect students’ SSB. This also holds for interchanging procedures.

How Was the Coding Scheme Used?

The first column “Time” in Table 2 refers to the interview timeline in which a critical event was observed.

The column “Subtask” refers to the subtasks in Appendix. Except for the columns “Time,” “Subtask,” and “ad hoc strategies,” the columns “AT” (Algebraic Technique) and “Trigger” contained drop-down boxes with each having different options. Based on the used algebraic technique during a procedure, one of the options “multiplication of both sides,” “division of both sides,” “substitution,” “taking the square root of both sides,” “squaring both sides,” and “subtraction from both sides” of the third column “AT” was selected (coded) in the spreadsheet. If instead of the latter, she applied ad hoc strategies, the details were thoroughly described in the column “ad hoc strategies.”

The last column “Trigger” contains the options “positive,” “negative,” or “missed opportunity.” A procedure was coded “positive” or “negative” when she chose the right procedure, thereby respectively executing correctly with score “1,” and incorrectly with score “0.5.” “Missed opportunity” refers to the third scenario in which the neutral student made no attempt to solve the task, e.g., when she overlooked a required procedure, or used ad hoc approaches. This led to SSB (%), the symbol sense behavior percentage per subtask. Other scores are OSSB (%), the overall symbol sense behavior percentage for the whole set of subtasks, and OBAS (%), the overall BAS percentage for the whole set of subtasks. These two scores are calculated by $\frac{\mathrm{sum}\ \mathrm{of}\ \mathrm{all}\ \mathrm{sub}\ \mathrm{task}\ \mathrm{scores}}{25}\bullet 100\%$ and $\frac{\mathrm{sum}\ \mathrm{of}\ \mathrm{all}\ \mathrm{sub}\ \mathrm{task}\ \mathrm{scores}\ \mathrm{requiring}\ \mathrm{BAS}\ \mathrm{only}}{5} \bullet 100\%$ respectively. As can be seen in the solution set of Appendix, the number “25” in OSSB (%) is the sum of 20 procedures involving LS and PS, and five involving BAS. Performing each procedure flawlessly yields the maximum score of 25.

Furthermore, a student was regarded procedurally fluent if OBAS (%)≥ 90.0% (4.5 out of 5 points). We regarded her OSSB (%) to be sufficient when OSSB (%) ≥ 80.0% (20 out of 25 points).

Data Analysis: Phases 6 and 7

In “phase 6” (constructing storyline), we identified the ad hoc strategies that were used, and then determined the students’ SSB (%) per subtask followed by OBAS (%) and OSSB (%). See the first three subsections of the next section.

As to “phase 7” (composing narrative), the transcripts, students’ written solution set, and the findings from “phase 6” were further integrated, leading to a narrative containing common findings. These are presented in the last two subsections of the next section.

To enhance reliability of our results (Bryman 2015), the two independent researchers crosschecked their results. Next, this was double checked by the first author, who found an overlap of approximately 95%. After discussing the remaining 5%, some adjustments were made which led to 100% agreement among them.

Results

Although each students’ work was analyzed in detail, we only present the results of Diana, Eve, and Chloe, because their combination of SSB (%), OBAS (%), OSSB (%), and problem-solving strategies varied a lot.

Diana

Diana has a 6.6 for mathematics B and a 5.2 for physics. She used the permutation strategy to solve task 1a and b, 3a, and task 4. With the tasks 3a and 4, she faced serious difficulties, and for tasks 2a and 3a, she needed hints, but she did not use ad hoc approaches. Consequently, her interview lasted long, i.e., circa 60 min.

Her SSB characteristics per subtask can be found in Table 3. The second (1a) up to the eighth column (4) of the first row, each represent a subtask. The second row “Missed opportunity” shows the sum of how many procedures per subtask she made no attempt to solve a task or used ad hoc strategies. For subtask 2b, this number is one. Furthermore, three procedures were correct (positive score 3) and one was not (negative score 0.5).

Table 3 Symbol sense behavior characteristics of Diana per subtask

We calculated her SSB (%) per subtask. For subtask 2b, this becomes $\frac{0.5+3}{5}\bullet 100\%=70.0\%$. Her total number of “Missed opportunity” corresponds to 11 (six ad hoc strategies and five overlooked procedures) including one BAS procedure, eight LS, and two PS procedures. This corresponds to a large 44.0% of the perfect score. Her lowest SSB (%) concerns the subtasks 1a and 1b (0% each) and her highest subtask 4 (75.0%). The latter corresponds to the well-performed first three procedures. For the last procedure, she substitutes numbers for variables and gets stuck. Diana’s OBAS (%) is $\frac{3.5}{5}\bullet 100\%=70.0\%$. Hence, she lacks a solid domain of BAS. Her OSSB (%) is $\frac{11.5}{25}\bullet 100\%=46.0\%.$ This score is mainly due to the application of ad hoc approaches, implying the absence of sensitivity towards systematic procedures with LS and PS. Instead of showing insight in the application of algebraic techniques, there is a focus on the permutation strategy. This is illustrated in Table 4.

Table 4 Diana’s permutation strategy to solve subtask 1a

Based on trial-and-error, she permutates numbers to discover the arrangement of valid outcomes for subtask 1a. Although this strategy provided right outcomes for subtask 1a, 1b, 3a, and 4, she made mistakes when the substituted number of variables became larger. Especially, when numbers are identical, but represent different variables. For instance, for subtask 3a, she substitutes numbers for $G\cdotp \frac{m\cdotp M}{r^2}=\frac{m\cdotp M}{r^2}$, but loses her overview and fails in making the next step and needs a hint. This process of using an ad hoc approach followed by failure and a hint also applies for subtask 4.

During the evaluation of her work, Diana indicated that the permutation strategy was “actually a residual technique acquired in mathematics class in grade 8”. This may imply that they learned ad hoc strategies, rather than the mathematics teacher putting emphasis on insight in why and how algebraic skills are used systematically.

Eve

Eve is a female student with a 7.1 for mathematics B and a 5.4 for physics. As to her TBI, she often used a combination of algebraic techniques with insight and the permutation strategy for task 1a and 1b and the numbering strategy for task 2a, 3a, and 4. The numbering strategy is different than the former strategy and aims at simplification of formulas or validation of solutions with insight. She frequently switched from systematic algebraic strategies to ad hoc strategies and only used a hint for 2b. Her interview took 67 min.

Eve’s symbol sense behavior characteristics are shown in Table 5. Her “Missed opportunity” corresponds to seven including one BAS procedure, five LS, and one PS procedure (six ad hoc approach and one overlooked procedure).

Table 5 Symbol sense behavior characteristics of Eve per sub task

This corresponds to 28.0% of the maximum OSSB (%), which is low compared to Diana. Her highest SSB (%) is both for subtask 2b (80.0%) and subtask 3b (80.0%), and her lowest subtask 1b (0%) where she used the numbering strategy to validate her answer. As Diana, this lower score is mainly related to using ad hoc strategies. Contrary to other subtasks, the algebraic techniques involved in 2b and 3b were used in a right manner and with insight.

Both her OBAS (%) of 70.0% (3.5 points) and her OSSB (%) with 64.0% (16 points) are insufficient, but her OSSB (%) is higher than that of Diana. Without the application of ad hoc strategies, especially in task 1 and 2a, both her OBAS (%) and OSSB (%) would have been sufficient. Eve’s numbering strategy for subtask 2a is depicted in Table 6. Even if this approach led to the correct solution, she does not understand why it is legitimate to cancel out the masses m in the square root sign. This is related to a lack of insight in algebraic skills.

Table 6 Eve’s numbering strategy to solve subtask 2a

After her TBI, Eve mentioned that both the numbering and the permutation strategy were learned in mathematics class in grade 8. This confirms Diana’s statement on the permutation strategy, since they are classmates since grade 8. Nevertheless, Diana did not use the numbering strategy.

Chloe

Chloe is a female student with a 6.4 for mathematics A and a 5.3 for physics. She worked much faster than Diana and Eve, and only used the cross-multiplication strategy to solve task 1a, 1b, and 3a. Chloe seems to have automated this approach that she performed smoothly for task 1. Hence, her TBI lasted 37 min.

Chloe’s symbol sense behavior characteristics are displayed in Table 7. Her “Missed opportunity” is 13 and contains one BAS procedure, eight LS, and nine PS procedures (five ad hoc approaches and eight overlooked procedures). This is equivalent to 52.0% of the maximum OSSB (%), implying a lack of SSB. Her highest SSB (%) is for subtask 2a (75.0%) where she lost points for the last two procedures. During the third procedure, she did not multiply the value 0.5 with 2. Her lowest SSB (%) is for task 1 (0%). Chloe’s insufficient OBAS (%) of 70.0% (3.5 points) is identical to that of Diana and Eve. Her OSSB (%) of 38.0% (9.5 points) is lower than them.

Table 7 Symbol sense behavior characteristics of Chloe per subtask

In Table 8, we show Chloe’s cross-multiplication strategy in subtask 3a. Although Chloe intended, she forgets to cross multiply and at the same time canceled out the masses m. Probably, she lost her overview.

Table 8 Chloe’s cross-multiplication strategy and cancelation of m’s to solve subtask 3a

For subtask 2b, she canceled out the masses in $m\cdotp g\cdotp h=\frac{1}{2}\cdotp m\cdotp {\left({v}_{\mathrm{final}}\right)}^2+{F}_{\mathrm{res}}\bullet h$. This procedure is forbidden and implies that the previous cancelation in subtask 3a was not based on understanding, but on routine based on ad hoc approaches. Indeed, during the evaluation, Chloe mentioned that she used ad hoc strategies, but did not understand why these were mathematically incorrect. For instance, for subtask 1 she writes $\frac{P\cdotp V}{T}=\frac{P\cdotp V}{T}$ and then cross-multiplies, yielding P·V = C·T. It turned out that she learned this approach from the mathematics A textbook. Furthermore, as for task 3b, Chloe mentioned that she lost her overview and got stuck because of the large number of variables.

OBAS (%) and OSSB (%)

In the previous section, OBAS (%) was incorporated into OSSB (%). To gain more insight in the relation between them, we placed OBAS (%) next to OSSB (%), see Fig. 2. Both Beth (A) with mathematics A and Fiona (B) with mathematics B have insufficient OSSB (%) and OBAS (%). Aron (A)’s OSSB (%) is sufficient (80.0%), but his OBAS (%) is not. Except for Aron, all students lacked both sufficient BAS and insight.

Fig. 2

OBAS (%) and OSSB (%) per student

We also calculated the ratio of $\frac{\mathrm{OBAS}\ \left(\%\right)\ }{\mathrm{OSSB}\ \left(\%\right)\ }$ per student. Except for Diana and Chloe, this number for the other students is roughly 1. For them, their OBAS (%) might be used as a reasonable predictor for their OSSB (%).

On the individual level, Aron has both the highest OSSB (%) (80.0%) and OBAS (%) (76.0%). The lowest OSSB (%) and OBAS (%) are respectively for Chloe (38.0%) and Fiona (50.0%). Furthermore, Chloe, Diana, and Eve have the same OBAS (%) (70.0%), but a different OSSB (%).

We also calculated 〈OBAS (%)⟩, i.e., the average of OBAS (%) for each mathematics group. This also applies for ⟨OSSB (%)⟩, i.e., the average of OSSB (%). For group (I), we found ⟨OBAS (%)⟩ = 70.0% and ⟨OSSB (%)⟩ ≈ 56.7%, and for group (II), ⟨OBAS (%)⟩ = 63.3% and ⟨OSSB (%)⟩ = 50.7%. Concerning ⟨OSSB (%)⟩, there is a difference of 6.7% between these groups. For ⟨OBAS (%)⟩, this is 6.0%. Although group I performed slightly better than II, these differences are reasonably small, and can be neglected. Furthermore, we found ⟨OBAS (%)⟩ = 70.0% and ⟨SSB (%)⟩ ≈ 55.3% for the average OSSB (%) of all students. These values converge to the findings above: none of the students have both sufficient procedural skills and SSB.

〈SSB (%)〉 per Subtask

Below in Fig. 3, we displayed ⟨SSB (%)⟩, i.e., the average SSB (%) per subtask among all students.

Fig. 3

⟨SSB (%)⟩ per subtask

Because of the criterion OSSB (%) ≥ 80.0%, ⟨SSB (%)⟩ ≥ 80.0% was regarded sufficient. None of the tasks met this criterion, which confirms students’ insufficient OSSB (%). Students’ average OBAS (%) was not incorporated in Fig 3, since subtask 1a, 1b, and 4 did not contain BAS procedures.

We may say that there are two regimes of scores. Subtasks 1a, 1b, and 3b belong to the very low (ranging from 33.3 up to 41.7%), and subtasks 2a, 2b, 3a, and 4 to the less higher scores (ranging from 52.8 up to 68.8%). For subtasks 1a (41.7%) and 1b (33.3%), Chloe, Diana, Eve, and Fiona used ad hoc approaches, which strongly impeded ⟨OSSB (%)⟩ of both subtasks.

Regarding subtask 2a, most students faced difficulties with procedure 2. They were required to think globally and demonstrate sensitivity towards the symbol sense type PS by dividing both sides by m. They performed well on the other procedures. Especially, the last procedure for which they achieved the maximum score. This contributed to a higher ⟨SSB (%)⟩, i.e., 68.8%.

With respect to subtask 2b, most students lost points in the first and fourth procedure. Only one student performed flawlessly on the first procedure involving BAS. For the fourth procedure, students encountered problems to cancel out the $\frac{1}{2}$ in $\frac{m\cdotp g\cdotp h-{F}_{\mathrm{res}.}\cdotp h}{m}=\frac{1}{2}\cdotp {\left({v}_{\mathrm{final}}\right)}^2$. After multiplying both sides with 2, they got rid of the $\frac{1}{2}$in the term $\frac{1}{2}\bullet {\left({v}_{\mathrm{final}}\right)}^2$. Still, they struggled with the meaning of 2 in the expression $2\cdotp \frac{m\cdotp g\cdotp h-{F}_{\mathrm{res}.}\cdotp h}{m}$. They often only multiplied m ∙ g ∙ h by 2, thereby ignoring $\frac{-{F}_{\mathrm{res}.}\cdotp h}{m}$.

As to 3b, most of the students faced problems with procedures 3, 4, and 5. Chloe, Aron, Beth, and Fiona explicitly mentioned that they lost their overview and were discouraged because of the large number of variables (the largest among all subtasks) in $G\cdotp \frac{M}{r}={\left(\frac{2\cdotp \pi \cdotp r}{T}\right)}^2$. The same applies, to a lesser extent, for 3a. Here, most students used ad hoc strategies to solve it, explaining the insufficient ⟨SSB (%)⟩ = 52.8% above.

Concerning task 4, students built upon insights acquired in the preceding subtasks, partially driven by hints. With ⟨OSSB⟩ = 64.6%, these insights resulted in a similar high score as 2a.

Discussion and Conclusion

The purpose of this study was to measure the extent to which upper secondary students demonstrate symbol sense behavior (SSB) when solving algebraic physics problems. The main difference with previous studies (e.g., Bokhove 2011; Drijvers 2015) is that these tasks contain expressions with variables relating to real, measurable physical quantities, and other studies to abstract mathematical variables without meaning in real life.

With regard to operationalization of SSB, we followed the line of Bokhove and Drijvers (2010) in the sense that we focused on students’ sensitivity towards gestalt view and visual salient aspects of algebraic expressions. While they used a digital environment to assess students’ work, we deployed traditional pen-and-paper settings involved in other studies (Arcavi 1994, 2005; Wenger 1987). Moreover, aforementioned studies have a predominantly qualitative character, whereas our coding scheme in combination with the systematic solution set including clearly worked out systematic procedures, provided us the opportunity to investigate SSB qualitatively with a quantitative component. This component should not be confused with quantitative research to generalize results from a larger sample population (Bryman 2015). Instead, beyond qualitative explanations, it provided us quantitative insight in students’ BAS and SSB.

We expect that our systematic algebraic approach can also be used in other science subjects, e.g., in algebraic manipulations involving the Hardy-Weinberg equation in biology p² + 2·p·q + q² = 1 or the Nernst equation in chemistry $E={E}^0+\frac{R\cdotp T}{n\cdotp F}\ln \left[\frac{\left[\mathrm{Ox}\right]}{\left[\mathrm{Red}\right]}\right]$. Furthermore, this study was based on a theoretical model (Powell et al. 2003) with detailed consecutive steps to analyze videotaped data, not present in earlier studies.

We selected tasks that should trigger students solving algebraic physics problems and provide insight in their procedural skills and SSB (Bokhove 2011). Indeed, this was the case, contributing to the internal validity of this study. In addition, the way we investigated basic algebraic skills (BAS) (Kieran 2013; Wu 1999) and symbol sense turned out to be helpful in analyzing both aspects. Overall, we observed that students lacked sufficient SSB and a solid domain of BAS, mainly due to the time-consuming, ad hoc strategies. These only worked for basic expressions containing fewer variables. In problems with more variables, students got stuck, and were unable to explain why operations with ad hoc strategies led to problems. On the subtask level, some students showed SSB.

The findings above corroborate and extend earlier studies, stating that using ad hoc strategies leads to fragmented knowledge, impedes generalization of algebra, and can be harmful for conceptual understanding. Instead of such strategies, students should learn systematic algebraic problem-solving strategies as in the solution set (see Appendix). This involves a rule-based problem-solving approach in which algebraic techniques are used with insight, where the term rule plays the role of algebraic axioms in high school algebra. Students should show sensitivity towards gestalt view and visual salience (FMS). This solution set should be considered and implemented by curriculum developers, textbooks and textbook publishers, teachers, and mathematics and science teacher educators aiming at successful application of mathematics in physics and strengthening students’ demonstration of CME. Regarding the first, we recommend physics curricula adopting content standards that refer to the importance of using algebraic skills to solve problems with insight as described in the mathematics curriculum (Netherlands institute for curriculum development 2016).

Concerning activation of prior mathematical knowledge, our research has shown that it is probably better to use the same pedagogy of algebraic skills, especially algebraic techniques as in mathematics curricula. The latter should emphasize the importance of science context, especially algebraic physics problems analogous to mathematics problems. For the science audience, regardless of whether these curricula are centralized and shaping the content of textbooks, we recommend physics textbooks to avoid the time-consuming ad hoc strategies such as the permutation strategy. With respect to algebraic problem-solving, mathematics textbooks should include systematic procedures with insight similar to that in the solution set in the Appendix, thereby paying attention to differentiation of algebraic techniques during procedures, e.g., “substitution” and “multiplication of both sides” of the equals sign. This may contribute to conceptual understanding of algebraic skills. Physics problems should be included to provide context for corresponding mathematics problems. We recommend physics textbooks adopting paragraphs where physics problems are introduced through corresponding mathematics problems that students have learned in mathematics class. Again, we emphasize the importance of activation of pre-knowledge (e.g., Hailikari et al. 2008) and using identical problem-solving pedagogies to that in mathematics textbooks. We note that such emphasis requires sufficient organization of the learning process. Otherwise, certain mathematical concepts are taught in physics class before they are explained in mathematics class (Alink et al. 2012; Turşucu et al. 2018b). These design principles have major implications for textbook publishers. In many countries, they are bound to one discipline, since each of them pursues different aims. Our study indicates that it is probably better that mathematics and physics publishers work together to develop textbook series in which these principles are incorporated.

With regard to mathematics and physics teachers, it is pivotal that they are able to explain basic mathematics. This should be a pre-requisite for pre-service teachers following science teacher education programs leading to a teaching qualification. Probably, this is the most important matter in improving the application of mathematics in physics. Furthermore, the issues, such as activation of prior-knowledge and using identical pedagogies in systematic problem-solving with insight, also apply for individual mathematics and physics teachers. In addition, even mentioning that physics formulas are rooted in mathematics class, writing mathematics and physics expressions next to each other, or relating physical quantities to the variables x and y used in mathematics can impede compartmentalized thinking (Turşucu et al. 2018a). Similar issues hold for mathematics teachers, e.g., mentioning that algebraic skills are used in science classes, especially in physics.

In many countries including the Netherlands (Turşucu et al. 2018b), physics teachers’ curricula are overloaded (e.g., Lyons 2006). As a consequence, teachers can lack time for sufficient collaboration with other departments. We recommend mathematics and physics teachers to systematically reserve some fixed amount of time in their school timetables. This may compel teachers to stick to their schedules. In addition, informal meetings may also offer a solution. Overall, we think that such collaborative efforts should focus on alignment of both subjects that is feasible to adopt in teaching practice.

Through professional teaching programs, science teacher educators can make teachers aware (Girvan et al. 2016) of the mechanisms underlying students’ difficulties when applying mathematics in science subjects, especially in physics. This also applies for providing solutions to combat these difficulties. Similarly, we recommend mathematics teacher educators to address these issues to their audience consisting of teachers and future teachers. Overall, both teacher educators should emphasize the importance of using systematic algebraic strategies, rather than ad hoc strategies lacking insight.

Our research has shown that the application of ad hoc strategies may help students to solve basic algebraic problems. However, there are risks for the longer term. Students can become dependent on an authority, i.e., a teacher or a textbook that tells them what is mathematically correct and what is not. In addition, mathematics can become a collection of incoherent and misunderstood strategies for them. Students often do not know the boundaries of such strategies, i.e., where they apply and where not. Especially, in new and more sophisticated situations, students encounter difficulties. We conclude that ad hoc approaches can be harmful for the application of algebraic skills with insight. Furthermore, with a rule-based problem-solving approach that becomes visible through the application of algebraic techniques with insight during procedures involving BAS and demonstration of SSB, students are flexible and able to handle such new and more sophisticated problems. These issues above are of major importance for many countries aiming at enhancement of the application of algebraic skills from mathematics in physics class, especially improving SSB in algebraic physics problems.

Observing SSB is not a straightforward affair (Bokhove and Drijvers 2010), for it is not easy to recognize whether students rely on procedural skills or demonstrate insight into expressions. Indeed, both concepts are intertwined, which is illustrated in Fig. 1 (Drijvers 2011). Nevertheless, we succeeded quite easily using the numerical criteria OSSB (%)≥ 80.0% and SSB (%)≥ 80.0%. Similarly, we used the criterion OBAS (%)≥ 90.0% for the observation of procedural fluency (BAS). Even though this might look as if we decoupled BAS and the symbol sense items LS and PS of OSSB (%), this is not the case. Investigation of OBAS (%) was helpful in gaining insight into the extent to which students demonstrated basic algebraic skills. In addition, OBAS (%) was already incorporated in OSSB (%), indicating the intertwinement above.

The comparable performance of both mathematics groups confirms that the algebra involved in both subjects is sufficient to tackle algebraic physics problems (Netherlands institute for curriculum development 2016). This contrasts with earlier teachers’ beliefs that students should choose mathematics B instead of mathematics A (Turşucu et al. 2017) , since the former puts more emphasis on algebra than the latter.

Our findings support earlier studies in which students encounter difficulties applying mathematics in physics (e.g., Roorda et al. 2015; Turşucu et al. 2017). This contributes to the relevance of this study.

Limitations of This Study and Further Recommendations

Even though we aimed at a 50%:50% gender ratio (Bryman 2015), our sample consisted of 1 male and 5 female students. This was due to strong selection principles needed to safeguard the quality of this study. Firstly, the respondents should be selected from two regular schools having a sufficient mathematics and an insufficient physics grade (< 5.5). They were required to follow the same mathematics and physics textbook series (Ottink et al. 2014; Reichard et al. 2014a) and have a similar knowledge domain in these subjects at the moment of interviews. Finally, they should be willing to participate in this study.

On the other hand, based on our aforementioned extended literature study, there are no indications that a sample with an equal number of male and female students would have generated fundamentally different results. Instead, they may be similar. Indeed, students’ performance in terms of OBAS (%) and OSSB (%) is mainly related to a combination of grades for both subjects and a similar knowledge domain, rather than on gender. Thus, it is very likely that male and female students with similar grades will show similar performance. As a result, the composition of our sample should not be seen as a limiting factor. Despite this, it is worthwhile to elaborate on this matter, since this may add to the internal validity (Bryman 2015) of this study.

The grade criterion above was to ensure that students’ difficulties with algebraic physics problems were mainly because of insufficient application of algebraic skills in physics and not related to a lack of basic mathematics (Kieran 2013; Wu 1999). In addition, the other criteria were essential to make sure that it was legitimate to compare the results of group I and group II. This also applies for comparing individual students in both groups. We note that students’ poor physics grades can also be the result of the absence of a variety of aspects, e.g., having a positive attitude towards physics or understanding physical concepts.

Since this study was based on a very small sample, the findings cannot be extended to the whole Dutch population. Neither is it representative for the Dutch context. The individual differences among mathematics A and mathematics B students’ grades and their SSB characteristics are too fundamental.

When stuck, students got hints to help them proceed. These hints were as unobstructive as possible. For instance, Aron got stuck in procedure 3 of subtask 2a and asked: “Is this okay?”. He was given the hint “Look carefully at $\mathrm{m}\cdotp \mathrm{g}\cdotp \mathrm{h}=\frac{1}{2}\bullet \mathrm{m}\cdotp {\left({\mathrm{v}}_{\mathrm{final}}\right)}^2$ and the next step”. He continued his work with correct procedures. Other hints in this study were also unobstructive as possible.

As to design principles, we recommend incorporation of two aspects in the interview protocol. It should explicate that students should reserve time reading the questions carefully, since they immediately started solving the tasks. Another problem was that half of the students worked fast and did not check their solutions after they finished their problems. These contained sloppy mistakes which may have been overcome if they had carefully re-examined their work. They would have benefited from a guideline emphasizing re-examination of their “finished” work, which is supported by earlier studies (Hattie and Timperley 2007; Shute 2008), and may add to their meta-cognitive skills.

The criteria OBAS (%)≥ 90.0% and OSSB (%) ≥ 80.0% are not chosen arbitrarily, but the result of consensus among all authors after a series of discussions. Firstly, physics students should have a solid foundation of BAS, irrespective of having mathematics A or mathematics B. This sheds light on the relatively high number of OBAS (%). However, meeting this criterion does not imply a similar high OSSB (%). Indeed, SSB also depends on talent (Drijvers 2011). Hence, we have chosen OSSB (%) ≥ 80.0% instead of, e.g., 90.0%.

Our findings have consequences for effective teaching practice. Should we focus on procedural skills, or pay attention on insightful learning? We have seen that students experienced difficulties because their basic procedures were not automated, the problem required unusual reasoning, or the automated procedures were insufficient to tackle unusual problems. Thus, both procedural skills and insight should be taught in an integrated manner, corroborating previous studies (Arcavi 2005; Bokhove 2011; Drijvers 2015). This also confirms our expectation. We conclude that this result should be used as a key principle by the “four school actors.”

Two mathematics A students learned the cross-multiplication strategy from their textbook Getal en Ruimte (Reichard et al. 2014a). We note that this textbook series has the largest market share in the Netherlands, influencing large number of highly textbook-driven teachers who teach them to their students (Stein and Smith 2010; van Zanten and van den Heuvel-Panhuizen 2014). In short, textbooks determine how and what students learn. As to the harmful ad hoc strategies, we strongly recommend conducting a textbook analysis of Getal en Ruimte in which different types of such strategies are mapped and analyzed. The findings should be communicated to the publisher.

Furthermore, all respondents were involved in grade 10. Their lack of BAS and SSB might indicate insufficient attention to algebraic skills in grade 9. This may also be examined through textbook analysis.

Appendix

The Tasks

Task 1 Ideal Gas

The formula for an enclosed ideal gas is given by $\frac{P\cdotp V}{T}=C$. Here, P is the pressure of the gas in Pa, V its the volume in m³, and T its temperature in K.

a) Solve for V in $\frac{P\cdotp V}{T}=C$.

b) Solve for T in $\frac{P\cdotp V}{T}=C$.

Task 2 Falling Stone

The potential energy of a stone is given by the formula E_pot. = m·g·h. Here, E_pot. is the potential energy of the stone in J, m its mass in kg, g its acceleration due to gravity in $\frac{m}{s^2}$, and h its height in meter. When the stone is dropped from a height h through a medium without air resistance the potential energy is only converted into kinetic energy. At the moment, the stone hits the ground; this energy is ${E}_{\mathrm{kin}.}=\frac{1}{2}\cdotp m\cdotp {\left({v}_{\mathrm{final}}\right)}^2$. Here, E_kin. is the kinetic energy of the stone in J, m its mass in kg, and v_final its final speed in m·s⁻¹.

a) Solve for v_final in E_pot. = E_kin.

Now, we add air resistance to the medium. As a consequence, when the falling stone hits the ground, its potential energy is converted into kinetic energy and heat. For the heat, we can write Q = F_res. ∙ s. Here, Q is the falling stone’s produced heat in J, F_res. the average air resistance in N, and h the height in m. At the moment the stone hits the ground, we can write E_pot. = E_kin. + Q.

b) Solve for F_wr in E_pot. = E_kin. + Q.

Task 3 Uniform Circular Motion

Imagine that the earth is orbiting around the Sun in uniform circular motion. In order to the earth remain in orbit, the attractive gravitational force F_G. between the earth and the Sun must equal the centripetal force F_C between these objects. Hence, we can write $G\cdotp \frac{m\cdotp M}{r^2}=\frac{m\cdotp {v}^2}{r}$. Here, G is the universal constant of gravitation in N ∙ m² ∙ kg⁻², m the earth’s mass in kg, M the Sun’s mass in kg, v the earth’s constant speed around the Sun in m ∙ s⁻¹, and r is the distance between the centers of the masses in m.

a) Solve for v² in F_G = F_C.

The earth’s speed around the Sun is given by $v=\frac{2\cdotp \pi \cdotp r}{T}$. Here, r is the distance between the mass centers in m, T the time it takes to complete one orbit around the Sun in s.

b) Derive the formula $\frac{r3}{T^2}=\frac{G\cdotp M}{4{\pi}^2}$ by using $G\cdotp \frac{m\cdotp M}{r^2}=\frac{m\cdotp M}{r^2}$ and $T=\frac{2\cdotp \pi \cdotp r}{v}$.

Task 4 Spring-Mass System

The period of a spring-mass system is given by $T=2\cdotp \pi \bullet \sqrt{\frac{\boldsymbol{m}}{\boldsymbol{C}}}$. Here, T is the period in seconds m the mass of the attached object in kg and C the spring constant in N ∙ m⁻¹. Solve for m in $T=2\bullet \pi \bullet \sqrt{\frac{\boldsymbol{m}}{\boldsymbol{C}}}$.

Systematic Solution Set to The Tasks

Task 1 Ideal Gas

• a) Procedure 1 (LS): multiplication of both sides of $\frac{P\bullet V}{T}=C$ with T. Result: P·V = C·T; procedure 2 (LS): dividing both sides of P·V = C·T through P. Result: $=\frac{C\cdotp T}{P}$ .

• b) Procedure 1 (LS): multiplication of both sides of $\frac{P\cdotp V}{T}=C$ with T. Result: P·V = C·T; procedure 2 (LS): dividing both sides of P·V = C·T through C. Result: $\frac{P\cdotp V}{C}=T$.

Task 2 Falling Stone

• a) Procedure 1 (BAS): substitution of E_pot. = m·g·h and ${E}_{kin.}=\frac{1}{2}\cdotp m\bullet {\left({v}_{\mathrm{final}}\right)}^2$ in E_pot. = E_kin.. Result: $m\cdotp g\cdotp h=\frac{1}{2}\cdotp m\cdotp {\left({v}_{\mathrm{final}}\right)}^2$; procedure 2 (PS): division of both sides of E_pot.·E_kin. through m. Result: $g\cdotp h=\frac{1}{2}\cdotp {\left({v}_{\mathrm{final}}\right)}^2$; procedure 3 (LS): multiplication of both sides of $g\cdotp h=\frac{1}{2}\cdotp {\left({v}_{\mathrm{final}}\right)}^2$ with 2). Result: 2·g·h = (v_final)²; procedure 4 (LS): taking the square root of 2·g·h = (v_final)²on both sides. Result: $\sqrt{2\cdotp g\cdotp h}={v}_{\mathrm{final}}$.

• b) Procedure 1 (BAS): substitution of E_pot. = m·g·h, ${E}_{\mathrm{kin}.}=\frac{1}{2}\cdotp m\cdotp {\left({v}_{\mathrm{final}}\right)}^2$ and Q = F_res.·h in E_pot. = E_kin. + Q. Result: $m\cdotp g\cdotp h=\frac{1}{2}\cdotp m\cdotp {\left({v}_{\mathrm{final}}\right)}^2+{F}_{\mathrm{res}.}\cdotp h$; procedure 2 (PS): substraction of F_res.·h from both sides of $m\cdotp g\cdotp h=\frac{1}{2}\cdotp m\cdotp {\left({v}_{\mathrm{final}}\right)}^2+{F}_{\mathrm{res}.}\cdotp h$. Result: $m\cdotp g\cdotp h-{F}_{\mathrm{res}.}\cdotp h=\frac{1}{2}\cdotp m\cdotp {\left({v}_{\mathrm{final}}\right)}^2$; procedure 3 (LS): division of both sides of $m\cdotp g\cdotp h-{F}_{\mathrm{res}.}\cdotp h=\frac{1}{2}\cdotp m\cdotp {\left({v}_{\mathrm{final}}\right)}^2$ through m. Result: $\frac{m\cdotp g\cdotp h-{F}_{\mathrm{res}.}\cdotp h}{m}=\frac{1}{2}\cdotp {\left({v}_{\mathrm{final}}\right)}^2$; procedure 4 (LS): multiplication of both sides of $\frac{m\cdotp g\cdotp h-{F}_{\mathrm{res}.}\cdotp h}{m}=\frac{1}{2}\cdotp {\left({v}_{\mathrm{final}}\right)}^2$with 2. Result: $2\cdotp \frac{m\cdotp g\cdotp h-{F}_{\mathrm{res}.}\cdotp h}{m}={\left({v}_{\mathrm{final}}\right)}^2$; procedure 5 (LS): taking the square root of $2\cdotp \frac{m\cdotp g\cdotp h-{F}_{\mathrm{res}.}\cdotp h}{m}={\left({v}_{\mathrm{final}}\right)}^2$on both sides. Result:$\sqrt{2\cdotp \frac{m\cdotp g\cdotp h-{F}_{\mathrm{res}.}\cdotp h}{m}}={v}_{\mathrm{final}}$.

Task 3 Uniform Circular Motion

• a) Procedure 1 (BAS): substitution of${F}_G=G\cdotp \frac{m\cdotp M}{r^2}$ and ${F}_G=\frac{m\cdotp {v}^2}{r}$ in F_G = F_C.Result: $G\cdotp \frac{m\cdotp M}{r^2}=\frac{m\cdotp {v}^2}{r}$; procedure 2 (PS): dividing both sides of $G\cdotp \frac{m\cdotp M}{r^2}=\frac{m\cdotp {v}^2}{r}$ through m. Result: $G\cdotp \frac{M}{r^2}=\frac{v^2}{r}$; procedure 3 (PS): multiplication of both sides of $G\cdotp \frac{m\cdotp M}{r^2}=\frac{m\cdotp {v}^2}{r}$ with r. Result: $G\cdotp \frac{M}{r}={v}^2$.

• b) Procedure 1 (BAS): substitution of $v=\frac{2\cdotp \pi \cdotp r}{T}$ in $G\cdotp \frac{M}{r}={v}^2$. Result: $G\cdotp \frac{M}{r}={\left(\frac{2\cdotp \pi \cdotp r}{T}\right)}^2$; procedure 2 (BAS): execution of previous procedure. Result: $G\cdotp \frac{M}{r}=\frac{4\cdotp {\pi}^2\cdotp {r}^2}{T^2}$; procedure 3 (LS): division of both sides of $G\cdotp \frac{M}{r}=\frac{4\cdotp {\pi}^2\cdotp {r}^2}{T^2}$ through 4. Result: $G\cdotp \frac{M}{4\cdotp r}=\frac{\pi^2\cdotp {r}^2}{T^2}$; procedure 4 (LS): division of both sides of$G\cdotp \frac{M}{4\cdotp r}=\frac{\pi^2\cdotp {r}^2}{T^2}$ through π². Result: $G\cdotp \frac{M}{4\cdotp {\pi}^2\cdotp r}=\frac{r^2}{T^2}$; procedure 5 (PS): multiplication of both sides of $G\cdotp \frac{M}{4\cdotp {\pi}^2\cdotp r}=\frac{r^2}{T^2}$ with r. Result: $r\cdotp G\cdotp \frac{M}{4\cdotp {\pi}^2\cdotp r}=r\cdotp \frac{r^2}{T^2}\to G\cdotp \frac{M}{4\cdotp {\pi}^2}=\frac{r^2}{T^2}$.

Task 4 Spring-Mass System

Procedure 1 (LS): division of both sides of $T=2\cdotp \pi \cdotp \sqrt{\frac{m}{C}}$ through 2. Result: $\frac{T}{2}=\frac{2\cdotp \pi \cdotp \sqrt{\frac{m}{c}}}{2}\to \frac{T}{2}=\pi \cdotp \sqrt{\frac{m}{c}}$; procedure 2 (LS): division of both sides of $\frac{T}{2}=\cdotp \pi \cdotp \sqrt{\frac{m}{c}}$ through π. Result: $\frac{T}{2\cdotp \pi }=\sqrt{\frac{m}{c}}$. procedure 3 (LS): squaring both sides of $\frac{T}{2\cdotp \pi }=\sqrt{\frac{m}{c}}$. Result: $\frac{T^2}{4\cdotp {\pi}^2}=\frac{m}{c}$; procedure 4 (LS): multiplication of both sides of $\frac{T^2}{4\cdotp {\pi}^2}=\frac{m}{c}$ with C. Result: $C\bullet \frac{T^2}{4\bullet {\pi}^2}=C\bullet \frac{m}{c}\to \frac{C\bullet {T}^2}{4\bullet {\pi}^2}=m$.

Interview Protocol Physics Teachers

Introduction

This interview will take approximately 15 min and is part of the PhD-study of the interviewer, Süleyman Turşucu. By means of a questionnaire, we will ask you to respond to questions about the background of some of your grade 10 physics students, and the mathematics and physics textbooks they use.

Purpose of This Interview

We aim to select three grade 10 physics students having a sufficient mathematics grade and an insufficient physics grade (< 5.5). Later, during an interview, these students will be asked to solve algebraic physics problems while being videotaped and thinking aloud (Charters 2003). We hope that these interviews will provide insight in how the application of algebraic skills from mathematics in physics may be improved.

Interview Approach

Would you please read aloud the questions of the questionnaire below one by one, and provide answers? This conversation can be audiotaped so that it can be listened back. Furthermore, the students’ names will be anonymized. Would you consent to your students participating in this study?

Questionnaire

• 1. Would you please provide us the names of your grade-10 physics students who have a sufficient mathematics grade and an insufficient physics grade (< 5,5)?

• 2. Would you please provide us insight in the attitude of these students towards learning?

• 3. Would you please tell us which physics textbook these students use, and why this textbook was chosen?

• 4. Would you please tell us which mathematics textbook these students use?

Interview Protocol Physics Students

Introduction

This interview contains two parts. In the first part, we ask you general questions about your background, and in the second part, we ask you to solve four tasks including algebraic physics problems while thinking aloud and being videotaped.

First Part: General Questions

• a. Would you please tell me why you chose mathematics and science subjects?

• b. Would you please tell me your opinion about mathematics and physics?

• c. Would you please provide me the grades for mathematics and physics?

Second Part: Solving Algebraic Physics Problems

Would you please solve these four tasks ‘Task 1: ideal gas’, ‘Task 2: falling stone’, ‘Task 3: uniform circular motion’ and ‘Task 4: spring-mass system’ below while thinking aloud. Please write down as many intermediate steps as possible. I will only interrupt you when a procedure or reasoning is not clear enough, or it remains silent for about one minute. The information that you provided in the first and second part of this interview will only be used for my PhD-research. Your name will be anonymized.