Abstract
Cronbach’s alpha is a statistic commonly quoted by authors to demonstrate that tests and scales that have been constructed or adopted for research projects are fit for purpose. Cronbach’s alpha is regularly adopted in studies in science education: it was referred to in 69 different papers published in 4 leading science education journals in a single year (2015)—usually as a measure of reliability. This article explores how this statistic is used in reporting science education research and what it represents. Authors often cite alpha values with little commentary to explain why they feel this statistic is relevant and seldom interpret the result for readers beyond citing an arbitrary threshold for an acceptable value. Those authors who do offer readers qualitative descriptors interpreting alpha values adopt a diverse and seemingly arbitrary terminology. More seriously, illustrative examples from the science education literature demonstrate that alpha may be acceptable even when there are recognised problems with the scales concerned. Alpha is also sometimes inappropriately used to claim an instrument is unidimensional. It is argued that a high value of alpha offers limited evidence of the reliability of a research instrument, and that indeed a very high value may actually be undesirable when developing a test of scientific knowledge or understanding. Guidance is offered to authors reporting, and readers evaluating, studies that present Cronbach’s alpha statistic as evidence of instrument quality.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Science education research often involves the adoption of existing, or the development of new, instruments to measure phenomena of interest. In the present paper, two particular types of instrument are considered, scales and tests. Scales are here considered to measure constructs in the affective domain, such as attitudes. Tests are here considered to measure cognitive features such as knowledge and understanding of science concepts and topics.
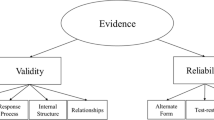
When choosing an instrument, or developing a new instrument, for a study, a researcher is expected to consider the relevance of the instrument to particular research questions (National Research Council Committee on Scientific Principles for Educational Research, 2002) as well as the quality of the instrument. Quality may traditionally be understood in terms of such notions as validity (the extent to which an instrument measures what it claims to measure, rather than something else) and reliability (the extent to which an instrument can be expected to give the same measured outcome when measurements are repeated) (Taber, 2013a).
In a physical sciences context, we might expect to be able to test reliability by taking repeated measurements to see how consistent the readings are. A high reliability does not ensure accuracy (for example, an ammeter which has not been properly calibrated may give very consistent repeat readings, without these being accurate) but does provide a basis for making inferences about changes (an increase in the reading on an ammeter which is poorly calibrated but has shown to give repeatable readings can be inferred to indicate an increased current). However, when an instrument does not give reliable readings, it may be difficult to distinguish genuine changes in what we are seeking to measure from changes in readings that are an artefact of the unreliability of the instrument.
In educational research, it may be quite difficult to test the reliability of an instrument such as an attitude scale or a knowledge test by simply undertaking repeated readings because human beings are constantly changing due to experiences between instrument administrations, and also because they may undergo changes due to the experience of the measurement process itself. So, a student may answer a set of questions, and that very activity may set in chain thinking processes that lead to new insights or further integration of knowledge. A day, week, or month later, the student may answer the same questions differently for no other reason than that responding to the original test provided a learning experience.
The present article takes the form of a methodological critique, focused on one measure commonly associated with instrument reliability in science education research (Cronbach’s alpha). The genesis of this study was dissatisfaction with the treatment of Cronbach’s alpha in some papers I was reading in relation to my own scholarship and—in particular—as a referee or editor. The impression developed was that although this statistic was often quoted by authors of science education studies submitted for publication, it was not always made clear what the statistic represented, or why it was relevant, or why some particular value was (or was not) desirable. This impression was tested, and reinforced, by looking to see how Cronbach’s alpha was applied in published studies in the field. An initial informal search suggested these concerns did not simply reflect the treatment of alpha in a few isolated papers but were more widespread and led to the identification of examples that illustrated points worthy of raising within the research community. A more systematic investigation of the use of the statistic in a sample of science education papers published in leading journals in the field in 2015 was then undertaken. This paper presents findings from that survey, to illustrate the extent and nature of the use of Cronbach’s alpha in published reports of science education in highly regarded journals in the field, as well as exploring identified issues of concern by discussing examples from the literature consulted.
The focus on science education here is not intended to suggest that studies in this field are more problematic in this regard than those in other fields (which were not examined for the present study). Rather, this methodological critique has been prepared from within the context of science education because it is believed that the issues identified will be relevant to others who engage with research in this field (as authors, as editors and reviewers, and as readers) and that recommendations could be developed which will be useful to colleagues in the field when preparing or evaluating research reports. It is hoped that by locating this critique within the substantive field, and by illustrating points with examples from the science education literature, the study will be visible and accessible to others engaging with this body of literature.
The present article is organised into three main parts. It begins by exploring current practice in science education by describing how Cronbach’s alpha is used within published studies in science education. Some illustrative examples that highlight particular issues relating to practice in reporting the alpha statistic are explored from studies reporting the development and/or use of instruments designed to measure affective constructs or aspects of cognition (such as student knowledge). This offers a context for discussing the nature of Cronbach’s alpha itself, and the reason this statistic was originally introduced, and so its potential role in instrument development and evaluation. This then provides a basis for critiquing some common practises used by authors reporting the statistic in their research reports in science education. In particular, some assumptions that are commonly explicit or implicit in research reports —that alpha should be as high as possible and that a high alpha can be taken as a sign of instrument quality—will be questioned, in particular in relation to the development of instruments to test science knowledge and understanding. This then leads to some recommendations for good practice for authors regarding how the statistic should be presented in studies reporting instrument development or application in science education and advice for those reading science education reports on identifying features of good and more questionable practice.
The Use of Cronbach’s Alpha in Science Education Studies
It is common to see the reliability of instruments used in published science education studies framed in terms of a statistic known as Cronbach’s alpha (Cronbach, 1951). Cronbach’s alpha has been described as ‘one of the most important and pervasive statistics in research involving test construction and use’ (Cortina, 1993, p. 98) to the extent that its use in research with multiple-item measurements is considered routine (Schmitt, 1996, p. 350). Alpha is commonly reported for the development of scales intended to measure attitudes and other affective constructs. However, the literature also includes reports of the development of tests of student knowledge and understanding that cite Cronbach’s alpha as an indicator of instrument quality.
The Frequency of Use of Cronbach’s Alpha in Science Education
To give an indication of the extent to which Cronbach’s alpha is used in science education research, a survey was undertaken of papers published in issues of four prestigious science education journals during one academic year. The 2015 volume of the journals were surveyed as this was the most recent year for which a full volume was available. The journals selected were those most widely considered to be high-status research journals and which routinely included reports of empirical work across science education. These are International Journal of Science Education (IJSE, Volume 37, comprising 18 issues), Journal of Research in Science Teaching (JRST, Volume 52, comprising 10 issues), Research in Science Education (RISE, Volume 45, comprising 6 issues—some articles in this volume are cited as 2014 according to the publisher’s metadata, reflecting their first publication on line) and Science Education (SE, Volume 99, comprising 6 issues). The choice of these journals was intended to ensure that all articles considered would have been subjected to rigorous peer review.
The on-line search facility provided by each journal publisher (Taylor & Francis for IJSE; Wiley for JRST and SE; Springer for RISE) was used to find articles listed as being published in the 2015 volume that included the word Cronbach in the text, in order to identify articles that made explicit reference to Cronbach’s alpha. Seventy articles were initially identified, although one of these did not explicitly refer to the alpha statistic (but appeared in the initial screen as it included a citation to a paper by Cronbach). There were therefore 69 explicit references to Cronbach’s alpha in papers published in the four science education journals in their volumes for 2015.
The figure of 69 explicit references to Cronbach’s alpha likely underestimates the actual level of reference to this statistic in the volumes surveyed as authors may refer to [Cronbach’s] alpha values without specifying the specific statistical test being used. For example, one paper in the IJSE volume surveyed (Bathgate, Crowell, Schunn, Cannady, & Dorph, 2015) made two references to an unspecified alpha statistic. Bathgate and colleagues describe developing “a measure of students’ ability to make effective arguments in science” (p.1596) for which “the overall instrument had acceptable reliability (alpha = .77),” and a “knowledge test administered before and after the 4-month classroom unit on weather and climate” which comprised “21 items, alpha = .78” (p.1600). It seems very likely that this statistic is the Cronbach alpha. Similarly, a paper in the 2015 volume of JRST described a post-test with items “designed expressly for the study” where they found that “two of the items did not discriminate understanding of the deep structure as intended, reducing the reliability statistic (Alpha) for the test. We discarded these two items. The remaining four post-test questions…were fairly reliable, α = 0.70” (Shemwell, Chase, & Schwartz, 2015, p. 68). Again, it seems likely from the context that the statistic referred to here is Cronbach’s alpha, although this was not explicitly stated.
As such examples can only be assumed to report the Cronbach alpha (as there are other statistics labelled alpha), they were not included in the survey, and no attempt was made to systematically identify such papers in the sampled volumes. It would seem to be good practice for authors citing statistical results to be unambiguous about the particular statistical tests they have carried out, rather than leaving readers to infer this from the context. Of the 69 articles that explicitly referred to Cronbach’s alpha, 64 cited values of alpha, including 61 which reported values of alpha as new results. These differences arise because some papers mentioned alpha in explaining the choices of statistics applied, but did not report values of alpha, and some papers cited alpha values from research reviewed, but did not report the statistic from new empirical work reported.
Describing the Significance of Alpha
Authors who report results for Cronbach’s alpha describe or explain the meaning of the alpha statistic in various ways—and some cite the statistic without any explanation at all. The articles identified in the 2015 volumes of the four research journals surveyed (IJSE, JRST, RISE, SE) were examined to see how authors who cited values of alpha (64 articles) described it. The most common descriptors were (separately or together) reliability or internal consistency. Twelve articles used both of these terms, including one paper that described alpha in terms of internal consistency, reliability, and also discriminating power,
In this study, Cronbach’s coefficient α was used to calculate the internal consistency coefficients of the items included in the questionnaire through a pilot study with 42 science teachers. Results of the reliability analysis showed that the items in the six scales had a satisfactory discriminating power. (Mansour, 2015, p. 1773)
As this quotation shows, authors considering reliability and internal consistency as equivalent may assume that this is understood by readers and does not need to be explicitly stated. In some cases, the shift between terms was clear enough. So, for example, in a study concerned with gender differences in motivation and engagement of senior secondary physics students (Abraham & Barker 2014), alpha is directly linked with both terms: “In preliminary analysis, we examined the Cronbach’s alpha estimate of internal consistency of each a priori scale… Specifically, support for the six-factor model requires (a) acceptable reliability for each scale (i.e. alpha = 0.70 or above)…” (p.63, emphases added). Sometimes, however, such explicit linking is absent, as in a study exploring biology undergraduates’ conceptions related to learning and their self-efficacy (Lin, Liang, & Tsai, 2015), which reported on a questionnaire drawing upon a previously published instrument. Lin and colleagues made explicit references to Cronbach’s alpha as a reliability coefficient in the context of discussing the source instrument and the new empirical results. However, it was left to readers to appreciate that internal consistency was being considered as synonymous to reliability:
For the overall reliability, the Cronbach’s alpha value was .80. The alpha values of the 2 subscales were .88 and .89… the revealed values of skewness (at least less than 2) and kurtosis (at least less than 7) … suggested normal distribution of the data. The results indicated the satisfactory level of construct validity and internal consistency of this modified questionnaire. Also, it was suitable to measure the university students’ conceptions of learning biology. (pp.454–455)
A reader who did not appreciate that the authors were using the two different terms interchangeably might find it difficult to unpack the logical thread (“overall reliability, the Cronbach’s alpha value was .80… The results indicated the satisfactory level of…internal consistency…”) from the wider textual context.
Most (44/64) of the articles reporting results including alpha values did refer to alpha as reliability—including one exploring perceptions related to global warming that suggested it should not necessarily be seen a measure of internal consistency as “while Cronbach’s alphas are the standard value reported for scale reliability, this value tends to underestimate the internal consistency of scales consisting of fewer than 10 items” (Herman, 2015, p. 8) and offered mean inter-item correlation values as an alternative measure of internal consistency.
Some of the articles in the sample qualified the term reliability or linked it to some other descriptor. One article referred to it as interrater reliability (and another paper in the sample used alpha in that way), one as reliability of separation and two as internal reliability. One paper equated alpha with both reliability and congruence. One of the papers that described alpha as reliability implied it related to items fitting on a single scale. Two other papers (that did not use the terms reliability or internal consistency) did specify that alpha was concerned with items being on a single scale or unidimensionality (as will be discussed later in this article, Cronbach’s alpha does not provide evidence of scale unidimensionality.)
One paper that referred to alpha as internal consistency also used the alternative term coherence (Wild, 2015). This study, that explored chemistry learners’ perceptions of learning environment and Science, Technology, Engineering and Mathematics (STEM) career expectations, modified a previously reported instrument. When discussing the previously published instrument, alpha was described as internal consistency (“Research using the CLES with American elementary, middle, and high school students has found high internal consistency (0.93 ≤ Cronbach’s α ≤ 0.94)”, p. 2290), but when discussing the new analysis undertaken, the alternative term was used (“The perception of a CLE item showed high coherence (Cronbach’s α = 0.90)”, p. 2290) albeit in a subsection titled “Internal consistency and factor analyses”.
Alpha was therefore found to be used as an indicator of reliability, interrater reliability, reliability of separation, internal reliability, internal consistency, congruence, unidimensionality and/or coherence. However, 8 of the 64 articles (i.e. 1 in 8) that cited values for alpha did so without offering any indication at all of what the statistic signified.
Characterising Values of Cronbach’s Alpha
Many, but not all, of the papers found to cite alpha values in the 2015 volumes of four science education journals (IJSE, JRST, RISE, SE) offered qualitative interpretations of the significance of the values calculated in relation to what was being measured (which, as discussed above, was usually considered as a form of reliability or internal consistency). Some papers also offered indications of alpha having a threshold or cut-off as an acceptable, sufficient or satisfactory level. This was normally seen as ≥0.70 (five instances) or >0.70 (three instances) although one article more vaguely referred to “the acceptable values of 0.7 or 0.6” (Griethuijsen et al., 2014).
A wide range of different qualitative descriptors was used by authors to interpret alpha values calculated. These descriptors are reported here (and represented graphically in Fig. 1) with the range (except where a descriptor was only applied to a single value in the sample) representing the highest and lowest values labelled that way in articles surveyed. So, alpha values were described as excellent (0.93–0.94), strong (0.91–0.93), reliable (0.84–0.90), robust (0.81), fairly high (0.76–0.95), high (0.73–0.95), good (0.71–0.91), relatively high (0.70–0.77), slightly low (0.68), reasonable (0.67–0.87), adequate (0.64–0.85), moderate (0.61–0.65), satisfactory (0.58–0.97), acceptable (0.45–0.98), sufficient (0.45–0.96), not satisfactory (0.4–0.55) and low (0.11). Figure 1 offers a visual indication of the wide range of values labelled by some of these descriptors (e.g. acceptable, sufficient) in the sampled studies. This diverse list of terms suggests that there is no clear consensus on the most appropriate labels to use to describe the values obtained when calculating alpha. Figure 1 also suggests there is no clear hierarchy within the range of terms (e.g. high cf. fairly high; not satisfactory overlapping with sufficient and acceptable) used across different scholars, so that terminology seems to be somewhat arbitrary.
The common notion of there being a threshold of acceptability for alpha values, if only as a rule of thumb (Plummer & Tanis Ozcelik, 2015), was not always seen as implying that lower values of alpha should be taken as indicating an unsatisfactory instrument. Griethuijsen et al. (2014) reported a cross-national study looking at student interests in science where “several of the values calculated for Cronbach’s alpha are below the acceptable values of 0.7 or 0.6” (p.588). For example, an “interest in school science” factor was based on a subset of five questionnaire items with Cronbach’s alpha of 0.502 (p.589), and the “interest in domestic activities” factor was based on a subset of three items with alpha of 0.446 (p.590). The authors justified continuing with their analysis using the data collected in these administrations by arguing that “slightly increasing the number of items would lead to acceptable values for Cronbach’s alpha” (p.589).
Examples of Alpha Cited in Measuring Affective Constructs
Many examples could be cited of studies where Cronbach’s alpha is used in characterising questionnaires aimed at measuring features in the affective domain (attitude, motivation and the like). Examples are presented here that have been selected to illustrate some key features of the use of this statistic in research in science education.
Tuan and colleagues (Tuan, Chin, & Shieh, 2005) report a study “to develop a questionnaire that measures students’ motivation toward science learning” (p.639). The questionnaire included items relating to six distinct scales—‘self-efficacy, active learning strategies, science learning value, performance goal, achievement goal and learning environment stimulation’, considered to reflect different “factors of motivation” (p.643). These distinct factors are described in the paper for readers. Tuan, Chin and Shieh report that “construct validity was verified by factor analysis”, and they present a table showing how each of the items in the questionnaire has a factor loading above 0.4 on one, and only one, of the scales. That is, in a well-designed instrument with several scales, the response patterns of an item intended to be part of a particular scale should be more similar to response patterns of the other items on that scale than the items on the other scales that are intended to be associated with a different construct or aspect.
The authors used the Cronbach alpha coefficient as a measure of “the internal consistency of the six scales”. They report that “the Cronbach alpha reliability coefficient for each scale, using an individual student as the unit of analysis, ranged between 0.87 and 0.70” which they considered “generally satisfactory” (p.644) (n.b. generally satisfactory is another variation on those descriptors found in the survey of 2015 studies, shown in Fig. 1). Tuan, Chin and Shieh also explored the degree of distinctness of the different scales, reporting that “the discriminative validity ranged from 0.09 to 0.51, showing the independence of each scale and also somewhat overlapping with other scales” (p.646). That is, they calculated the mean correlation for each of the scales with the five other scales and obtained (in ascending value) results of 0.09, 0.30, 0.31, 0.32, 0.39 and 0.51. It would be suspect if the correlations between these scales were very high, as that would suggest that the sets of items making up the different scales were not measuring different factors. What is of interest for the present discussion however is that the authors quote a value of Cronbach’s alpha for the instrument as a whole, again when taking the individual student as the unit of analysis, and this is reported as 0.91 (p.646). That is, the measure used for internal consistency across the whole questionnaire (0.91) is greater than any of the coefficients (0.70, 0.75, 0.80, 0.81, 0.82, 0.87) obtained for the six somewhat overlapping scales from which it was composed. This is a point returned to later in this paper.
There are many other examples of authors quoting high alpha values for multi-construct scales. In a study exploring self-regulation of biology learning, Eilam and Reiter (2014) adopted the Learning and Study Strategies Inventory, a 76-item instrument comprising of 10 scales. The authors report Cronbach alpha values for each scale and for the instrument overall, and again, the overall value is higher than that of the distinct scales (0.91 cf. 0.73, 0.75, 0.76, 0.79, 0.83, 0.84, 0.86, 0.87, 0.89, 0.89, p.716). These values are reported without any explanation, interpretation or comment, presumably because the authors (and one supposes the experts who peer reviewed the manuscript for the journal) consider their relevance self-evident and not requiring commentary.
Heddy and Sinatra (2013) report a study looking at both affect and conceptual change in learning about evolution. One of the instruments they used in this study was an Evolution Emotions Survey that they published in full in their paper. The instrument was used to explore a range of emotions: “enjoyment, hope, pride, anger, anxiety, shame, hopelessness, boredom” (p.729). Among the items included in the instrument were I enjoy being in class, I am full of hope, I feel frustrated in class, I feel nervous in class, I am ashamed, I have lost all hope of understanding this class and I find this class fairly dull, providing face validity at least that the items in the different scales were indeed eliciting responses based on different emotions. The authors did not report Cronbach’s alpha for the scales for these distinct emotions, but rather offered readers the statistic for the overall instrument as being 0.97. Their interpretation of this statistic was that “reliabilities for the emotions survey were excellent” (p.729). The desirability of such a high value of alpha, close to the theoretical limit of 1, seems to be assumed, but this will be questioned later in this article.
Another study that used Cronbach’s alpha in characterising an instrument developed for measuring affect in science education is “Developing attitude to science scales for use with children of ages from five to eleven years” (Pell & Jarvis, 2001) which “reports on the development stages of three attitudes to science and school scales for use with children aged from 5 to 11 years” (p,847). Pell and Jarvis report that ‘Attitude subscales measure “liking school”, “independent investigator”, “science enthusiasm”, the “social context” of science and “science as a difficult subject” with Cronbach Alpha reliabilities for the year groups varying from above 0.8 to below 0.7’ (p.847). That is, in common with many other authors (see above), Pell and Jarvis consider alpha to reflect the reliability of a scale of instrument.
Of particular interest here is that the alpha value obtained reflects the specific sample tested. Pell and Jarvis included different age pupils in their study and reported that a subscale they labelled liking school “is most reliable when measuring the attitudes of the youngest pupils. At year 1, reliability = 0.83, N = 41, whereas by year 6, reliability has progressively reduced to r = 0.66, N = 166” (p.853). They argued that some items in their scale were more associated with being in school by respondents in some age groups than others, such that those items were able to elicit the desired construct better with younger children. By contrast, Lamb, Akmal and Petrie (2015) in a study “to investigate content, cognitive and affective outcomes related to STEM integrated curriculum” (p.410) explain lower reliabilities of an instrument administered to kindergarten pupils (as compared to second and fifth grade pupils) as due to “the varying ability of kindergarteners to interpret questions and responses” (p.422). This reflects how Cronbach’s alpha cannot be seen as a measure of a scale or instrument per se but only of its application to a particular sample of respondents.
Examples of Alpha Cited in Measuring Cognitive Constructs
Cronbach’s alpha is also widely used by those designing tests of student knowledge and understanding, again as an indicator of instrument quality. Casanoves, González, Salvadó, Haro & Novo (2015) report a study of the attitudes towards and knowledge of biotechnology among Spanish university students’ preparing for teaching. The knowledge component was a 21-item instrument asking respondents to judge whether statements were true or false. This instrument was said to measure “knowledge level of biotechnology and genetics” and it was reported that “the reliability (Cronbach’s α) of the knowledge questionnaire was .721” (p.2930). In this example then, alpha was used to offer evidence of reliability of the 21 items collectively in assessing “knowledge level of biotechnology and genetics” implicitly treated as a unitary construct.
Other authors similarly suggest or imply that a high value of Cronbach’s alpha is desirable when a test of knowledge includes items testing across a range of different science concepts. Yang, Lin, She and Huang (2015, pp. 1572–1573) report using “a two-tier multiple-choice diagnostic instrument developed to measure the degree of students’ conceptual understanding in science (Cronbach’s α = 0.81…)” as a measure of prior knowledge across six diverse topics: “(1) the classification of substances, (2) fire prevention, (3) thermal convection, (4) chemical reaction rates, (5) sound waves and (6) mass conservation” (p.1571). Howe and colleagues report using knowledge tests each covering a range of concepts in the forces topic for which they considered values of Cronbach alpha offered grounds for regarding test scores as lying on single scale (Howe et al., 2014, p. 173), whilst Mumba and colleagues (Mumba, Mbewe, & Chabalengula, 2015) reported an alpha value of 0.83 for a wide-ranging conceptual knowledge test in the topic of light.
Some other studies reporting knowledge assessment instruments in areas of science recognise that the target knowledge has multiple aspects. One such study is “An analysis of 16–17-year-old students’ understanding of solution chemistry concepts using a two-tier diagnostic instrument’ (Adadan & Savasci, 2011) which ‘focused on the development of a two-tier multiple-choice diagnostic instrument, which was designed and then progressively modified and implemented to assess students’ understanding of solution chemistry concepts” (p.513). These authors developed an instrument that (in its final version) comprised 13 items that explored student understandings of aspects of solution chemistry “in multiple contexts with multiple modes and levels of representation”. Six aspects of solution chemistry were represented (p.519):
-
the nature of solutions and dissolving,
-
factors affecting the solubility of solids,
-
factors affecting the solubility of gases,
-
the types of solutions relative to the solubility of a solute,
-
the concentration of solutions, and
-
the electrical conductivity of solutions.
The authors provided information on how they understood each of these aspects.
Adadan and Savasci call upon the Cronbach alpha statistic and relate it to both the terms reliability and internal consistency:
The reliability of [the Nature of Solutions and Solubility—Diagnostic Instrument] was represented by using the Cronbach alpha coefficient. Cronbach alpha values of 0.7 or higher indicate acceptable internal consistency...The reliability coefficients for the content tier and both tiers were found to be 0.697 and 0.748, respectively (p.524).
In recommending their instrument for classroom use, the authors note that some of the items were found to be of high difficultly but claim that “the test is robust enough that even if...any two or three items considered to be difficult...are removed from the test, the Cronbach alpha reliability would not drop below the acceptable value of 0.70” (p.539). For Adadan and Savasci then, a critical value of alpha of 0.70 offers evidence of the reliability/internal consistency of an instrument that explores student understanding of six distinct aspects of a scientific topic area across different contexts, modes, and levels of representation.
A somewhat similar use was made of Cronbach alpha reliabilities by Arslan, Cigdemoglu and Moseley (2012), who report a “three-tier diagnostic test to assess pre-service teachers’ misconceptions about global warming, greenhouse effect, ozone layer depletion, and acid rain” through the development of the atmosphere-related environmental problems diagnostic test (AREPDiT). Their third tier asked students about their confidence in item responses to “differentiate a lack of knowledge from a misconception” (p.1667). The authors describe the development of their instrument and how “after the revision of the first version, the Cronbach alpha coefficient of the second version increased from 0.60 to 0.74, which can be considered acceptable according to criterion-referenced tests” (p.1677). However, Arslan and colleagues did not offer readers any guidance on the sense in which the instrument should be considered acceptable because of this statistical result.
It was reported above how Tuan, Chin and Shieh used factor analysis to confirm that the items associated with their different scales in their questionnaire did indeed load upon the intended scales. Arslan, Cigdemoglu and Moseley however reported that in the case of their three-tier instrument “although an exploratory factor analysis on pre-service teachers’ total score was conducted, reasonable factors were not obtained.” They suggested that “this could be because the items are loosely related to each other and do not measure either a single atmosphere related environmental concept or the three dimensions (nature, consequences, and solutions) of [global warming, greenhouse effect, ozone layer depletion, and acid rain]” (p.1679). So in this study, items that were considered to be “loosely related to each other,” and not to measure understanding of a single concept, collectively gave rise to an alpha value “considered acceptable”, providing a warrant for the authors to claim “The AREPDiT proved to be a valid and reliable diagnostic instrument to explore the knowledge and misconceptions of pre-service teachers” (p.1683).
Another recent study using alpha to characterise an instrument reported a “conceptual inventory of natural selection as a tool for measuring Greek university students’ evolution knowledge” (Athanasiou & Mavrikaki, 2013), which set out to “compare various groups of Greek university students for their level of knowledge of evolution by means of natural selection" (p.1269). The groups comprised of biology specialists at different stages of university study (post-graduate, final year undergraduates, other undergraduates) and non-specialists who either were or were not taking subsidiary biology courses. The authors here used an existing instrument, the Conceptual Inventory of Natural Selection (CNIS), originally published in English and translated it into Greek for use in their local context.
Athanasiou and Mavrikaki noted some problems with the instrument, reporting that “a principal components analysis revealed problems with the items designed to assess the concepts of population stability, differential survival and variation inheritable, therefore these items need to be reconsidered” (p.1262). They suggested that their analysis of how different items loaded upon different constructs “pose a question about the internal validity of the CINS” (p.1270). Despite this, the authors also reported that “the reliability of the Greek CINS was estimated as very good” (p.1269), a judgement which was based upon a value of Cronbach’s alpha of 0.877 for their complete sample. Values of Cronbach’s alpha were also quoted for the different groups of students (0.65, 0.78, 0.87, 0.88, 0.91), now described as offering “estimated coefficients of internal consistency” (p.1269). These were interpreted as “good” apart from the group with the lowest value (0.65—obtained for those non-biologists who did not attend any biology courses)—which was said to have “a poor but acceptable Cronbach’s alpha” (p.1270).
As suggested above, then, the values for Cronbach’s alpha apply to the particular sample responding on a particular occasion and should not be assumed to be a fixed feature of the scale or instrument. This is reinforced by a study undertaken to explore undergraduates’ understandings of acid strength. Bretz and McClary (2014) found that the alpha value obtained from repeated administrations of their diagnostic instrument to a group of 52 students shifted from 0.39 to 0.54 over a period of three months. Taken at face value, their diagnostic instrument—a fixed set of items—became more reliable, or more internally consistent, over time. Bretz and McClary report that the “students had three months additional instruction (including concepts about acid strength) between the pre/post-administrations” (p.214). It seems that the items in the instrument became more similar in terms of the responses they elicited from these particular learners after the students had experienced additional formal teaching about the canonical scientific concepts being tested: something to be both expected and welcomed (and a finding consistent with Athanasiou and Mavrikaki’s finding that reliability in their study was lowest for the group of students who had not been formally taught biology in higher education). A similar finding was reported by Berger and Hänze (2015) in a study of teaching physics through the jigsaw cooperative learning technique where internal consistency, as measured by alpha, increased from 0.45 before instruction to 0.60 after teaching. This underlines how the alpha statistic always relates to a particular administration of an instrument.
Abraham and Barker (2014) administered their Physics Motivation Questionnaire, a 22-item instrument “measuring six constructs” (p.62) in the context of a sequence of modules (waves, electricity, motion, the cosmic engine) studied by year 11 students in Sydney such that the same items (e.g. “I know I am able to do well in this module”) referred to different module contexts in different administrations, so that alpha might be expected to shift between administrations. Five of their six constructs were measured by subscales of three to five items (the sixth was represented by one item), and a distinct value of alpha was quoted for each subscale, for each of the modules. So, for example, alpha for the interest value subscale varied from 0.832 for the waves module to 0.909 for the cosmic engine module. As the sample size varied between administrations (n = 222–280), the differences in alpha could relate to the variation in respondents and/or to general shifts in attitude to the subject through the school year, as well as the module context. Abraham and Barker also cited an estimated value of alpha for their single item (“I do not want to continue physics to year 12”) subscale of 0.98, although they offered no indication of how they made the estimate or how alpha for a single-item subscale should be understood.
Key Findings Regarding the Use of Cronbach’s Alpha in Science Education Studies
Alpha is then widely used by authors in science education to represent the reliability, or the internal consistency, of an instrument or an instrument scale in relation to a particular sample or subsample of a population. These terms are often seen as synonymous in relation to alpha, and a number of alternative terms are also associated with alpha values cited in science education. A value of around 0.70 or greater is widely considered desirable (although characterisation of the qualitative merits of specific values seems highly variable between studies). The examples reviewed here show that alpha values of 0.7 or above can be achieved even when an instrument is exploring multiple constructs or testing for several different aspects of knowledge or understanding. As seen above, acceptable values of alpha may be reported even when an instrument includes items of high difficulty that few students can correctly answer, or items that are considered to be only loosely related to each other, or when items are found to be problematic in terms of their loading on factors associated with the particular constructs they are intended to elicit (that is, when items may not clearly belong in the scale or test section they are designated to be part of).
The Nature of the Alpha Statistic
Cronbach’s alpha is then commonly used in studies as an indicator of instrument or scale reliability or internal consistency. Alpha became widely used after being discussed by Cronbach (1951) who reasonably suggested that using the label α was more convenient than repeatedly referring to the “Kuder-Richardson Formula 20” (p.299).
What Does Alpha Actually Measure?
Cronbach was concerned with having a measure of reliability for a test or instrument which could be obtained from a single administration given the practical difficulties (referred to earlier) in obtaining test-retest data—and he distinguished the latter as a matter of test stability (lack of change over time) as opposed to tests like Cronbach’s alpha that offered measures of equivalence (whether different sets of test items would give the same measurement outcomes). The approach used to test equivalence was based on dividing the items in an instrument into two groups, and seeing whether analysis of the two parts gave comparable results.
Clearly, in using such an approach, there are many ways a large set of items could be divided. Consequently, the level of equivalence found might vary depending upon how the split is made and so can in practice lead to quite different split-half coefficients. However, if all possible splits were made (that is, in effect the process is repeated for each possible split), then it is possible to produce a statistic that reflects the overall pattern of coefficients. Cronbach’s alpha was such a statistic: a function of all the split-half coefficients for a test. Cronbach wrote that “if all the splits for a test were made, the mean of the coefficients obtained would be α” (p.306). So, alpha reflects the extent to which different subsets of test items would produce similar measures. Cronbach suggested that alpha “reports how much the test score depends upon general and group, rather than item specific, factors” (p.320).
Gardner (1995), writing in Research in Science Education about instruments to measure attitudes to science, discussed how “Cronbach’s alpha is the statistic which is most widely used today for estimating internal consistency” (p.285), explaining that “alpha is maximised when every item in a scale shares common variance with at least some other items in the scale” (p.286, emphasis in original). Gardner highlighted how when using a ratings scale where a total score was obtained by summing the responses across items it is important that all the items reflect the same construct. That is, that the scale needs to be unidimensional to provide an “interpretable” result, as ‘a score obtained from a measuring scale ought to indicate the “amount” of the construct being measured’. The study of Tuan, Chin and Shieh to measure students’ motivation towards science learning (discussed earlier) offers an example where an instrument (questionnaire) was developed with a number (there six) of distinct scales. Following Gardner’s advice, it would make sense to assign alpha scores on the specific scales (“self-efficacy, active learning strategies, science learning value, performance goal, achievement goal, and learning environment stimulation”), but calculating an alpha value across all items to give an overall measure of internal consistency of the overarching ‘motivation’ instrument is not justified.
It was mentioned above that Tuan, Chin and Shieh obtained a high value of alpha (0.91) for their overall questionnaire despite it being composed of six discrete scales measuring different constructs and therefore lacking unidimensionality. The Cronbach alpha calculated across Tuan, Chin and Shieh’s multi-scale instrument was higher than the values of any of the individual scales, showing that high value of alpha does not necessarily indicate a high level of consistency (or equivalence in Cronbach’s term) between the instrument items as a whole. The same was found in Eilam and Reiter’s study. Given that some authors choose to report cross-scale results, readers should be aware that the Cronbach alpha statistic is most valuable in relation to single-construct scales and less informative when reported for instruments measuring several constructs at once (Adams & Wieman, 2010).
The practice of reporting only an overall alpha value when an instrument is comprised of several discrete scales (as in the Heddy and Sinatra study discussed above) is less useful to readers. As Gardner pointed out, “a scale may be composed of several clusters of items each measuring a distinct factor; as long as every item correlates well with some other items, the scale will demonstrate internal consistency” (p.286). That is, any combination of different scales is likely to give a high overall alpha as long as the scales themselves have high internal consistency. In principle, one could pool sets of scale items intended to elicit (for example) mathematics confidence, enjoyment of field work, attitude to formal examinations, and motivation to complete homework, and demonstrate a high overall value of alpha as long as there are related items within the individual scales.
Gardner bemoaned that many researchers appeared to conflate internal consistency and unidimensionality and did not appreciate that a high value of alpha did not support an inference that all the items in an instrument were measuring the same thing. Rather, a high value of alpha simply meant that every item in the instrument was measuring something similar to some of the other items. Sijtsma (2009) has more recently made the point more bluntly: “both very low and very high alpha values can go either with unidimensionality or multidimensionality of the data” (p.119).
Sijtsma (2009) develops an argument explored in Cronbach’s (1951) seminal paper that alpha does not offer an accurate value for reliability as understood by psychometricians (but rather a lower bound, although Cronbach himself had argued in his 1951 paper that alpha was often a suitable proxy) and suggests that internal consistency is not a notion that has a clear and agreed meaning. Sijtsma argued that ‘all that alpha can reveal about the “interrelatedness of the items” is their average degree of “interrelatedness” provided there are no negative covariances and keeping in mind that alpha also depends on the number of items in the test’ (p.114, italics in original). Calculating alpha across multiple scales (where the total number of items is necessarily higher than in the individual scales) tends to inflate the value obtained. This may be relevant to why in the Tuan, Chin and Shieh (2005) study discussed earlier, the overall value of alpha for their instrument exceeded the individual alpha coefficients within the six ‘somewhat overlapping’ scales from which it was compiled: that is, the measure of internal consistency was higher across the pooled items from six distinct scales intended to elicit different constructs than it was within any one of those individually more homogeneous scales.
Mun, Mun and Kim (2015) published an account of their development of an instrument they call the Scientific Imagination Inventory, where they report alpha values for components of the instrument as well as the overall instrument. Mun and colleagues identified three components of scientific imagination (and two sub-dimensions of each, giving six factors overall), which they labelled as scientific sensitivity (comprising emotional understanding and the experience of imagination), scientific creatvity (comprising originality and diversity) and scientific productivity (comprising creation and reproduction and scientific sense of reality). The authors prepared an initial inventory of 29 items, which was vetted for content validity by a panel of science educators, before it was administered to a sample of 662 Korean school pupils.
The responses were examined and various tests were applied to the instrument, including the use of Cronbach’s alpha, where “Cronbach α scores greater than .70 were considered as indicative of acceptable reliability… After checking the reliability of each factor using the Cronbach α coefficient, items that decreased the reliability of each factor were removed” (pp.2099–2100). Factor analysis allowed six interpretable factors (considered to be the factors built into the design) to be identified, and items with low loadings on the relevant factors were removed. This left 20 items in the reduced instrument. Mun and colleagues provide the values of alpha for the refined instrument at three levels: the six factors, the three components and the overall instrument. These statistics are compiled here in Table 1. The use of factor analysis to confirm that items primarily load upon the expected factor suggests that the greatest degree of alignment should be between items within the specific factors. Despite this, alpha is higher for the scientific sensitivity component overall than separately for its two subordinate factors (0.67 > 0.572, 0.595). Moreover, “The internal consistency reliabilities using the Cronbach α coefficient was .79 for all items” (p.2100) and this overall measure of consistency was greater than that of any of the three components or their individual factors. Indeed, the overall statistic calculated for all 20 items pooled as if one scale was the only presented value of alpha which met the criterion of “acceptable reliability” cited by the authors themselves (p.2099).
Mun and colleagues’ value of alpha of 0.79 across their instrument was obtained despite items not all measuring the same thing and was in part a result of the composite instrument having more items than its (apparently less reliable) component individual factor subscales. In summary, Cronbach’s alpha is most valuable for indicating scale reliability in the sense of the equivalence of items within single-construct scales, but the statistic does not offer any indication that scales are actually unidimensional (which should be tested by other means).
What Value of Alpha Is Desirable?
In everyday terms, a high value of alpha offers a guard against specific items being unique in the particular sense of eliciting response patterns unlike any of the other items (Cortina, 1993). This is a sensible thing to wish to guard against if an instrument is intended to offer a range of items eliciting responses aligned with the same construct. Thus, the procedure, referred to above (Mun et al., 2015), of removing items that are found to reduce overall alpha values. However, that is clearly not equivalent to suggesting that it is desirable for all items in a scale to elicit precisely the same pattern of responses as this would imply a scale contains redundant items.
Cortina (1993) noted over 20 years ago that it was common for authors to assume that demonstrating that alpha was greater than 0.70 was sufficient to consider no further scale development was needed, leading to the statistic simply being presented in studies without further interpretation. This feature was found in some of the science education papers discussed above. Cortina describes this as an improper use of the statistic. For one thing, as alpha tends to increase with the size of an instrument (Cortina, 1993; Schmitt, 1996), it is generally possible to increase alpha to 0.70 by simply adding more items to a test as long as those items are not completely unlike the existing items. As was seen above, authors may sometimes simply make the argument that had they included more items, they would have reached an acceptable value of alpha as a justification for not considering a value below 0.7 as indicative of a problem with the instrument (Griethuijsen et al., 2014).
Cronbach (1951) had suggested that a high value of alpha was ‘desirable’ when an instrument was used to assign a score to an individual, but he argued that the key point should be that scores obtained when using an instrument had to be interpretable—and this was often possible without needing very high values of alpha. Although adding more items into an instrument can increase the value of alpha, Cronbach pointed out that adding additional items that measure the same thing as the existing items leads to a redundancy that is inefficient. Little additional useful information is obtained, but the instrument takes longer to administer (and analyse). From this perspective, Heddy and Sinatra’s (2013) claim (see above) that obtaining an alpha value of 0.97 for their multi-scale Evolution Emotions Survey represented "excellent" reliability is less convincing. Schmitt (1996) has suggested that there is no general level (such as 0.70) where alpha becomes acceptable, but rather that instruments with quite a low value of alpha can still prove useful in some circumstances.
Discussion
It seems then that despite many authors following a rule-of-thumb that alpha should reach 0.70 for an instrument to have an acceptable level of self-consistency, there are limited grounds for adopting such a heuristic. Moreover, it should not be assumed that a very high value of alpha is always a good thing. A high value certainly does not imply that an instrument or scale is unidimensional—and in some cases, a very high value may indicate an inefficient level of redundancy in items.
One particular issue raised above concerned the quoting of alpha values for overall instruments that are designed to incorporate several dimensions or scales. Not all papers reporting instruments include a listing of the final items included, but where authors do include the full list of items, it is possible for readers to consider for themselves the relationship between different items in a multi-scale instrument—to make a reader judgement of what might be called face equivalence, the extent to which items appear to be eliciting the same underlying knowledge facet, opinion or perception. To illustrate this, Mun, Mun and Kim’s (2015) account of their development of the Scientific Imagination Inventory (described above) provides the full list of items in the final version of their instrument. Mun and colleagues identified three components of scientific imagination (and two sub-dimensions of each, giving six factors overall) but found that the overall measure of consistency across the full set of instrument items was greater than that for any of the three components or their individual factors (see Table 1).
Mun et al., provide their final list of items (pp.2111–2112), and four of these are selected here to illustrate how a high overall alpha does not necessarily imply that all items are strongly related:
E2. Animals such as dogs and cats are able to feel emotions just like me
E3. I feel as if elements of nature, such as animals or plants, are my friends
D1. I try to find answers as often as possible
D2. When the problem is not easy to solve, I try to find a new way to solve it
A reader might well consider that E2 and E3 (both drawn from the emotional understanding factor) seem to be tapping into something similar, a sense of harmony with nature perhaps. Similarly, D1 and D2 (drawn from the diversity factor) both seem to be tapping a self perception about attitude to facing problems. It is less clear however that considering animals and plants as friends (E3) is strongly linked with seeing oneself as a creative problem-solver (D2) for example. The high value of overall internal consistency of the 20 items reflects how each item shares variance with at least some other items—so D2 does not have to share a high level of variance with E3, for example, as long as each of those items do share variance with some others.
At the outset of the paper, I distinguished between instruments that are intended to measure affective features such as attitudes and motivation from those exploring cognitive features. Instruments with an affective focus such as attitude scales play an important role in science education research and evaluation, and these instruments do need to identify clear constructs that are being measured, and instrument designers (or adapters) do need to demonstrate that items on a single scale are indeed measuring the same thing. Alpha is not sufficient for this but may well be used alongside other tools (such as factor analysis) to characterise such scales (as seen in some of the examples discussed above). It is at least as important that such scales measure what they claim to measure (that is, that they are valid) as that they can be shown to be unidimensional—so construct validity also needs to be demonstrated. As the example of the Athanasiou and Mavrikaki (2013) study considered above shows, an instrument may be found to have a high value of alpha, even when other indicators suggest there are problems with the instrument’s validity.
Alpha Used to Characterise Tests of Broad Knowledge Domains
Cronbach’s alpha is also regularly used in research in science education exploring aspects of the cognitive domain. Here, one aspect of validity is whether the phrasing of questions and the scoring of responses is considered to reflect what are judged scientifically acceptable answers for the student group concerned. Readers can only confirm this for themselves when the full instrument is available for scrutiny. This is certainly not something to be taken for granted. For example, a study by Nehring, Nowak, zu Belzen and Tiemann (2015) used a 90-item test (for which a Cronbach alpha value is reported), exemplified by a single sample question presented in the journal paper.
This item tells students that “A neutralisation is a chemical reaction in which an acid and a base react. In this process, the pH becomes neutral…” and asks students to use this information to determine which “assumption” someone could “prove” when “Jan and Laura add the same quantity of acid and base in a test tube.” One of the options is that “the pH becomes neutral” (p.1351). There are a number of points that might be questioned here. Leaving aside whether scientific enquiry should be said to “prove” anything, it might be quibbled that pH (a number) does not become neutral but rather indicates whether the substance or mixture tested is neutral (in a way that is temperature dependent) and also that the notion of “same quantity” is not explained. The same quantity could imply the same volume or the same mass or the same number of moles—none of which would necessarily ensure there would be no unreacted acid or base. Moreover, the question appears to encourage the alternative conception that neutralisation necessarily leads to a neutral product—something that is often, but certainly not generally, the case (Schmidt, 1991). A reader whom was not convinced about the validity of that item might wonder about the other 89 items that were not selected as exemplars in the published account.
Accounts of new tests of knowledge and understanding, such as diagnostic instruments in specific science topics, are often characterised by reporting a value for alpha. Yet, it is not always clear how authors intend this to be understood or what the statistic actually reflects. One might pose the question of how we are to understand a construct such as “students’ understanding of solution chemistry concepts” (Adadan & Savasci, 2011) or “knowledge of evolution” (Athanasiou & Mavrikaki, 2013) or “knowledge level of biotechnology and genetics” (Casanoves et al., 2015) or “conceptual knowledge of light” (Mumba et al., 2015).
Notions such as knowledge and understanding are ubiquitous in the discourse of science education, although usually taken-for-granted as part of a shared register of terms describing mental properties or events that are seldom operationally defined in research (Taber, 2013b). Yet it would generally be accepted that such research foci as understanding of solution chemistry concepts, or knowledge of evolution or knowledge of biotechnology and genetics or conceptual knowledge of light are likely to involve a range of related but somewhat discrete aspects.
Some studies in science education acknowledge that administration of instruments genuinely testing a range of distinct knowledge facets should not be expected to give high alphas. Bretz and McClary (2014) calculated and reported alpha for their administrations of an instrument used in a study of undergraduates’ understandings of the concept of acid strength but concluded that “the traditional threshold of 0.7 as indicative of acceptable reliability is actually a flawed metric when it comes to diagnostic assessments” (p.216). Berger and Hänze (2015) describe how for the knowledge test they used in their study of the jigsaw learning method, “the internal consistency as measured by Cronbach’s alpha coefficient was 0.45 for their pre-test and 0.60 for the post-test, which we considered acceptable given the limited number of test items and the broad range of tested knowledge” (p.303). That is, internal consistency (i.e. item equivalence) was not expected to be high here, because of the different physics concepts tested within the one instrument. Similarly, Nehring et al. (2015) report an alpha reliability of 0.55 for a conceptual knowledge test used in a study of learning about scientific enquiry drawing on a range of chemistry concepts. They explain this value in terms of how “conceptual knowledge may constitute a non-coherent latent construct across a multitude of students” (p.1351).
However, other authors present high values of alpha as indicators of quality of conceptual tests. Mumba and colleagues actually state that the “conceptual knowledge of light” test they used in their study (where Cronbach’s alpha was 0.83) probes “17 light concepts” (Mumba et al., 2015, p. 191), and these are quite a diverse set including, inter-alia, reflection, shadow formation, speed of light, refraction, vision, electromagnetic spectrum, filters, and the transverse nature of waves.
Casanoves et al. (2015) present the 21 items that made up their instrument for assessing knowledge of biotechnology, for which they reported “reliability (Cronbach’s α) of … .721” (p.2930). This instrument includes a wide range of items relating to such matters as applications of microorganisms in biotechnology (“bacteria are used in the elaboration of daily products (e.g. cheese, vinegar and vitamin C)”, affordances of biotechnology (“through genetic modification, foods with higher nutritional values can be achieved”), natural products (“the most powerful toxic substances are naturally occurring”), genetics and disease (“AIDS is a genetic disease”), hereditary (“children resemble their parents because they share the red blood cells”) and commonality of genetic material across species (“crocodiles have the same genetic material as ostriches”). Knowledge of biotechnology and genetics is clearly multifaceted, and the need for 21 items suggests that it was recognised that a measurement of knowledge level of biotechnology and genetics necessitated probing a number of more specific features of that knowledge. Despite this, the overall alpha value (here equated with reliability) suggests there is a fair degree of shared variance between items in the instrument.
Inspection of the items allows the reader to identify pairs of items that might be expected to elicit similar response patterns in relation to respondent knowledge: for example “Through genetic modification, foods with higher nutritional values can be achieved” with “It is possible to change the genetic characteristics of a plant to make it more resistant to a given plague”, (or “Bacteria are used in the elaboration of daily products (e.g. cheese, vinegar and vitamin C)” with “A yogurt is a biotechnological product”) (p.2931). Detailing instrument items within research reports supports readers in interpreting and evaluating those reports. An examination of the items included in the instrument reported by Casanoves et al. (2015) allows a reader to see both that a range of aspects of knowledge of biotechnology are being tested, and also that the instrument includes multiple items to elicit knowledge of specific concepts (such as genetic modification; food products) within the topic. This latter feature would be expected to lead to individual items having shared variance with some other items when the instrument is administered to a student group, providing the basis for a high value of alpha across the overall instrument.
Misuse of Alpha to Imply Unidimensionality
It seems that despite Gardner’s (1995) warning in this journal that researchers should not conflate internal consistency and unidimensionality and consider a high value of alpha as suggesting that the items in an instrument were all measuring the same thing, reports are still being published in prestige science education journals asking readers to make just this inference. Indeed, sometimes, the argument may be made explicitly. In a study exploring the assessment of student-generated graphs in science, Vitale, Lai and Linn (2015, p. 1438) suggested that “relatively high values of Cronbach’s α (six items, pre-test: α = 0.70; post-test: α = 0.77) suggest that these items all, at least partially, measured the same factor” (emphasis added). Depending on how the authors intend the qualifier “at least partially”, this claim is either misleading or trivial. In the context of a study exploring the impact of school chemistry classes organised as “collaborative participation”, Patchen and Smithenry (2014) refer to how “the extent to which the grouped items in [a] scale measured the same construct (i.e. internal consistency) was assessed by calculating a Cronbach’s alpha reliability coefficient” (emphasis added).
Howe and colleagues (2014) report the development and evaluation of a teaching module in the topic of forces for 11–12 years olds that covered the themes of balanced and unbalanced forces, measuring forces, stretching, flotation and density, surface friction, and stopping distance (p.166). Part of the evaluation of the module concerned the preparation of three structurally similar knowledge tests that “were specific to the Forces module” (p.168) and which were administered to the 16 school classes that were taught the module as well as 13 control classes. Despite the range of concepts included in the module and tests, the authors felt confident in claiming that “Cronbach α (.67 for pre-test, .74 for immediate post-test, .77 for deferred post-test) provided reasonable grounds for regarding test scores as lying on single scales” (p.173, emphasis added). So, published studies in science education may adopt the questionable assumption that conceptual knowledge across one (or more) school topics should be considered a single dimension and inappropriately offer a high value of alpha as evidence of such unidimensionality.
Other studies offer overall values of alpha as grounds for confidence in instruments even when they are acknowledged to be accessing manifold features of knowledge. Adadan and Savasci (2011) identified six aspects of solution chemistry in their study—each of which they described in relation to several features. As their final instrument comprised of 13 items, it is not obvious that having items that tested for different things (different features of student understanding)—as might be indicated by a low value of alpha—would reflect a problem with their instrument. Given that a high value of alpha simply means that every item in an instrument is measuring something similar to some of the other items, we might sometimes prefer a wide-ranging test instrument over a highly redundant one with a very high alpha value. Indeed, in a study such as that of Adadan and Savasci, where 13 items test for students’ understandings of “six aspects of solution chemistry,” each of which is complex in the sense of being made up of more than a single discrete knowledge feature, in “multiple contexts with multiple modes and levels of representation” (p.513), we might wonder how to best interpret an alpha value of approximately 0.70.
A high value of alpha obtained from administering an instrument to a sample of students could be understood as suggesting that the items are measuring some common factor(s) rather than unique features associated with individual test items. If redundancy has been deliberately built into the instrument, this is to be expected. However, in the case of a test of knowledge or understanding, if items are each meant to test for discrete aspects of understanding, or discrete knowledge elements, then it would not seem appropriate to consider understanding (e.g. of solution chemistry) or knowledge (e.g. of evolution) as homogenous constructs. If the topic being tested is considered to consist of distinct aspects, each presenting students with particular learning challenges, and separate items have been written to test for these distinct aspects, then finding that there is a high alpha coefficient across the test may perhaps indicate the test is not working as we intended.
Cronbach suggested alpha reflects “how much the test score depends upon general and group, rather than item-specific, factors” (p.320), but in a test of knowledge and/or understanding, we may wish to include very specific items to test different knowledge components. In such a situation, a high alpha value may suggest that a lot of the variance is due to general respondent-related factors (e.g. intelligence, study diligence, motivation in the subject) and that consequently, the instrument does not differentiate well between different features of the conceptual material being tested. This could explain why in Arslan, Cigdemoglu and Moseley’s (2012) study, items that were considered to be ‘loosely related to each other’, relating to four different concept areas, collectively gave rise to an alpha value of 0.74.
The argument made here is that whilst there is a logic in seeking a high alpha value for scales intended to measure foci that are conceptualised as single constructs, where a range of items are designed to elicit that single construct, it is less clear that the focus of a test of knowledge and/or understanding in a complex science topic is best conceptualised as a single coherent construct. In developing instruments of this kind—tests, diagnostic instruments, concept inventories—researchers should carefully consider whether seeking a high value of internal consistency in the sense measured by alpha (i.e., equivalence across the set of items) is actually desirable in terms of their research aims.
Conclusion
This study has surveyed how the application of Cronbach’s alpha has been presented in major science education journals over a single year and has reviewed some illustrative examples of research where Cronbach’s alpha is reported in studies in science education. The survey of recent studies (published in well-regarded journals) suggest that alpha is routinely being quoted, but often without its use being explained or the value quoted being fully interpreted for readers. The methodological literature cited above highlights known limitations of the use of alpha, yet it remains common practice in science education to consider alpha reaching the somewhat arbitrary value of 0.70 as a sufficient measure of reliability or internal consistency of an instrument. This suggests that the present study could act as a useful critique for colleagues working in science education and undertaking, evaluating, or looking to be informed by, studies developing or applying instruments such as scales, concept inventories and tests.
It is not argued here that alpha has no value in science education research nor that alpha should not be calculated and cited in research reports. However, it is suggested that authors need to do more than simply present the statistic without further comment. This is especially important in a field such as science education that is diverse and draws upon a wide range of research traditions (Taber, 2014). Whilst the reader should always engage with research reports critically and seek to test the assertions and knowledge claims of authors, it is inevitable that many readers of research papers will only have limited familiarly with the particular methods used. In an ideal world, all those working in science education would have a high literacy in statistical methods (as well as in other complementary approaches) but, given the diversity of the field, there is a responsibility on authors not to assume that all readers of their research are fully familiar with the strengths and weaknesses (or even the purposes) of the statistical techniques used.
A research report sets out the case for accepting specified new knowledge claims “by a careful, logical argument, drawing upon convincing evidence” (Taber 2013a: 320), and researchers are expected to “provide a coherent and explicit chain of reasoning” (National Research Council Committee on Scientific Principles for Educational Research, 2002, p. 4). They are also expected to select methods because of “their appropriateness and effectiveness in addressing a particular research question” (National Research Council Committee on Scientific Principles for Educational Research, 2002, p. 3). Where researchers are claiming that a particular instrument is fit for use in science education, they should then both; (i) select appropriate techniques to evaluate the instrument that has been developed (or adapted or adopted), and (ii) provide a clear and explicit argument for why any test statistics quoted should be considered to demonstrate the instrument is suitable for its intended purpose.
The discussion in this paper leads to the following recommendations:
-
When authors present values of Cronbach’s alpha in their published research, they should explain what they consider the statistic reflects (e.g. if internal consistency, how do they understand this) and why they feel this statistic is informative in relation to their research aims.
-
Authors should interpret the value of alpha reported in the context of their particular study, taking into account the expected dimensionally of what they are seeking to measure and the total number of items included in the instrument or scale discussed.
-
Authors should be clear about the limitations of alpha and present it alongside other complementary statistical measures (such as the outcomes of factor analyses) where appropriate.
-
Authors should offer readers sight of the items included in an instrument so they can make their own judgements of (what I have termed here) face equivalence—to what extent items within a particular scale or instrument seem to be targeted at the same underlying construct or knowledge facet.
The latter point also links to demonstrating face validity (e.g. see the comments about the study by Nehring and colleagues above) as a key feature of a research report in any field considered scientific is that it should be fully open to critique and detailed enough to iteratively support further research. The notion of replicability may not apply in educational research in the strict sense that it does in the physical sciences, as we cannot reproduce the conditions of previous research, and contextual differences between research samples complicate the generalisability of findings (Taber, 2014). This was seen, for example, in the study by Athanasiou and Mavrikaki (2013), where a Greek translation of the original English Conceptual Inventory of Natural Selection was administered. However, research that seeks to be considered scientific needs to be reported in sufficient detail to allow others to build on it—and that clearly requires the availability of full instruments rather than simply reporting sample items.
This present analysis also suggests some points that readers might use as a checklist when evaluating studies that cite values of Cronbach’s alpha:
-
As alpha does not offer any guide to the validity of a scale or instrument, do authors offer complementary evidence that the scale or instrument measures what it is claimed to measure?
-
Are high values of alpha a reflection of redundancy in a scale or instrument where a large number of items are used when fewer might suffice? (This might be indicated where the scale or instrument contains large numbers of items but may be better judged by inspection of the actual items where these are provided.)
-
As alpha does not offer evidence of dimensionality, do authors who claim that instruments include components that elicit distinct factors provide evidence of dimensionality (i.e. that subscales are supported by factor analysis)?
-
Where subscales are pooled and overall values of alpha reported, does a high overall value of alpha likely largely reflect the shared variance within the subsidiary subscales rather than across items between subscales? (Would a pooling of the subscales be expected to provide a composite set of highly related items if the subscales are intended to measure distinct constructs?)
-
Could a high overall alpha value that is quoted for the administration of an instrument intended to test knowledge and understanding across a science topic or concept area indicate that the main construct being elicited might be a more generic feature of the student response to items (e.g. intelligence) rather than indicating that learning across the particular topic or concept area should be considered as a single dimension?
-
Alternatively, could a high overall alpha value that is quoted for the administration of an instrument intended to test knowledge and understanding across a science topic or concept area indicate that the instrument may not sufficiently test the full range of learning objectives across the topic?
Clearly, readers will be better placed to judge issues such as these when the full set of items included in an instrument are available for scrutiny.
Whilst many researchers who use alpha may have a nuanced appreciation of its affordances and limitations, it is important both; (i) to avoid the impression that alpha is sometimes calculated simply because that is what is routinely done, and (ii) not to ask readers less familiar with the statistic to take on trust that a quoted value assures instrument quality simply because it reaches an arbitrary threshold level. Similar considerations should apply in relation to any specialised research methods applied in studies reported in science education journals. This paper has focused on Cronbach’s alpha because it is a commonly used technique that is recognised in the methodological literature as having major limitations. The recent studies cited here demonstrate that Cronbach’s alpha continues to be reported in science education research papers; (i) without commentary, and (ii) when it is not clear that the statistic offers relevant evidence of instrument quality. There are then particularly strong reasons to ask authors reporting alpha to take care to explain clearly why they have calculated the value and what the result indicates about their instrument.
References
Abraham, J., & Barker, K. (2014). Exploring gender difference in motivation, engagement and enrolment behaviour of senior secondary physics students in new South Wales. Research in Science Education, 45(1), 59–73. doi:10.1007/s11165-014-9413-2.
Adadan, E., & Savasci, F. (2011). An analysis of 16-17-year-old students’ understanding of solution chemistry concepts using a two-tier diagnostic instrument. International Journal of Science Education, 34(4), 513–544. doi:10.1080/09500693.2011.636084.
Adams, W. K., & Wieman, C. E. (2010). Development and validation of instruments to measure learning of expert-like thinking. International Journal of Science Education, 33(9), 1289–1312. doi:10.1080/09500693.2010.512369.
Arslan, H. O., Cigdemoglu, C., & Moseley, C. (2012). A three-tier diagnostic test to assess pre-service teachers’ misconceptions about global warming, greenhouse effect, ozone layer depletion, and acid rain. International Journal of Science Education, 34(11), 1667–1686. doi:10.1080/09500693.2012.680618.
Athanasiou, K., & Mavrikaki, E. (2013). Conceptual inventory of natural selection as a tool for measuring Greek university students’ evolution knowledge: differences between novice and advanced students. International Journal of Science Education, 36(8), 1262–1285. doi:10.1080/09500693.2013.856529.
Bathgate, M., Crowell, A., Schunn, C., Cannady, M., & Dorph, R. (2015). The learning benefits of being willing and able to engage in scientific argumentation. International Journal of Science Education, 37(10), 1590–1612. doi:10.1080/09500693.2015.1045958.
Berger, R., & Hänze, M. (2015). Impact of expert teaching quality on novice academic performance in the jigsaw cooperative learning method. International Journal of Science Education, 37(2), 294–320. doi:10.1080/09500693.2014.985757.
Bretz, S. L., & McClary, L. (2014). Students’ understandings of acid strength: how meaningful is reliability when measuring alternative conceptions? Journal of Chemical Education, 92(2), 212–219.
Casanoves, M., González, Á., Salvadó, Z., Haro, J., & Novo, M. (2015). Knowledge and attitudes towards biotechnology of elementary education preservice teachers: the first Spanish experience. International Journal of Science Education, 37(17), 2923–2941. doi:10.1080/09500693.2015.1116718.
Cortina, J. M. (1993). What is coefficient alpha? An examination of theory and applications. Journal of Applied Psychology, 78(1), 98–104. doi:10.1037/0021-9010.78.1.98.
Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16(3), 297–334. doi:10.1007/bf02310555.
Eilam, B., & Reiter, S. (2014). Long-term self-regulation of biology learning using standard junior high school science curriculum. Science Education, 98(4), 705–737. doi:10.1002/sce.21124.
Gardner, P. L. (1995). Measuring attitudes to science: unidimensionality and internal consistency revisited. Research in Science Education, 25(3), 283–289. doi:10.1007/bf02357402.
Griethuijsen, R. A. L. F., Eijck, M. W., Haste, H., Brok, P. J., Skinner, N. C., Mansour, N., et al. (2014). Global patterns in students’ views of science and interest in science. Research in Science Education, 45(4), 581–603. doi:10.1007/s11165-014-9438-6.
Herman, B. C. (2015). The influence of global warming science views and sociocultural factors on willingness to mitigate global warming. Science Education, 99(1), 1–38. doi:10.1002/sce.21136.
Howe, C., Ilie, S., Guardia, P., Hofmann, R., Mercer, N., & Riga, F. (2014). Principled improvement in science: forces and proportional relations in early secondary-school teaching. International Journal of Science Education, 37(1), 162–184. doi:10.1080/09500693.2014.975168.
Lamb, R., Akmal, T., & Petrie, K. (2015). Development of a cognition-priming model describing learning in a STEM classroom. Journal of Research in Science Teaching, 52(3), 410–437. doi:10.1002/tea.21200.
Lin, T.-C., Liang, J.-C., & Tsai, C.-C. (2015). Conceptions of memorizing and understanding in learning, and self-efficacy held by university biology majors. International Journal of Science Education, 37(3), 446–468. doi:10.1080/09500693.2014.992057.
Mansour, N. (2015). Science teachers’ views and stereotypes of religion, scientists and scientific research: a call for scientist–science teacher partnerships to promote inquiry-based learning. International Journal of Science Education, 37(11), 1767–1794. doi:10.1080/09500693.2015.1049575.
Mumba, F., Mbewe, S., & Chabalengula, V. M. (2015). Elementary school teachers’ familiarity, conceptual knowledge, and interest in light. International Journal of Science Education, 37(2), 185–209. doi:10.1080/09500693.2014.971906.
Mun, J., Mun, K., & Kim, S.-W. (2015). Exploration of Korean students’ scientific imagination using the scientific imagination inventory. International Journal of Science Education, 37(13), 2091–2112. doi:10.1080/09500693.2015.1067380.
National Research Council Committee on Scientific Principles for Educational Research. (2002). Scientific Research in Education. Washington DC: National Academies Press.
Nehring, A., Nowak, K. H., zu Belzen, A. U., & Tiemann, R. (2015). Predicting students’ skills in the context of scientific inquiry with cognitive, motivational, and sociodemographic variables. International Journal of Science Education, 37(9), 1343–1363. doi:10.1080/09500693.2015.1035358.
Patchen, T., & Smithenry, D. W. (2014). More than just chemistry: the impact of a collaborative participant structure on student perceptions of science. Research in Science Education, 45(1), 75–100. doi:10.1007/s11165-014-9414-1.
Pell, T., & Jarvis, T. (2001). Developing attitude to science scales for use with children of ages from five to eleven years. International Journal of Science Education, 23(8), 847–862. doi:10.1080/09500690010016111.
Plummer, J. D., & Tanis Ozcelik, A. (2015). Preservice teachers developing coherent inquiry investigations in elementary astronomy. Science Education, 99(5), 932–957. doi:10.1002/sce.21180.
Schmidt, H.-J. (1991). A label as a hidden persuader: chemists’ neutralization concept. International Journal of Science Education, 13(4), 459–471.
Schmitt, N. (1996). Uses and abuses of coefficient alpha. Psychological Assessment, 8(4), 350–353. doi:10.1037/1040-3590.8.4.350.
Shemwell, J. T., Chase, C. C., & Schwartz, D. L. (2015). Seeking the general explanation: a test of inductive activities for learning and transfer. Journal of Research in Science Teaching, 52(1), 58–83. doi:10.1002/tea.21185.
Sijtsma, K. (2009). On the use, the misuse, and the very limited usefulness of Cronbach’s alpha. Psychometrika, 74(1), 107–120. doi:10.1007/s11336-008-9101-0.
Taber, K. S. (2013a). Classroom-based research and evidence-based practice: an introduction (2nd ed.). London: Sage.
Taber, K. S. (2013b). Modelling learners and learning in science education: developing representations of concepts, conceptual structure and conceptual change to inform teaching and research. Dordrecht: Springer.
Taber, K. S. (2014). Methodological issues in science education research: a perspective from the philosophy of science. In M. R. Matthews (Ed.), International Handbook of Research in History, Philosophy and Science Teaching (Vol. 3, pp. 1839–1893). Dordrecht: Springer Netherlands.
Tuan, H.-L., Chin, C.-C., & Shieh, S.-H. (2005). The development of a questionnaire to measure students’ motivation towards science learning. International Journal of Science Education, 27(6), 639–654. doi:10.1080/0950069042000323737.
Vitale, J. M., Lai, K., & Linn, M. C. (2015). Taking advantage of automated assessment of student-constructed graphs in science. Journal of Research in Science Teaching, 52(10), 1426–1450. doi:10.1002/tea.21241.
Wild, A. (2015). Relationships between high school chemistry students’ perceptions of a constructivist learning environment and their STEM career expectations. International Journal of Science Education, 37(14), 2284–2305. doi:10.1080/09500693.2015.1076951.
Yang, W.-T., Lin, Y.-R., She, H.-C., & Huang, K.-Y. (2015). The effects of prior-knowledge and online learning approaches on students’ inquiry and argumentation abilities. International Journal of Science Education, 37(10), 1564–1589. doi:10.1080/09500693.2015.1045957.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Taber, K.S. The Use of Cronbach’s Alpha When Developing and Reporting Research Instruments in Science Education. Res Sci Educ 48, 1273–1296 (2018). https://doi.org/10.1007/s11165-016-9602-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11165-016-9602-2