A new PIN model with application of the change-point detection method

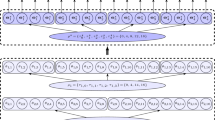
Abstract

The existing PIN models impose a restriction on the number of possible intensity pairs. However, our investigation shows that the number of empirical intensity pairs is significantly more than the one these models assume, and this number changes daily. Therefore, we propose a new model which, by using the change-point detection technique, can adjust this number according to the data. The model also considers autocorrelation, which is lacking in the existing PIN models. In addition, we show that the proposed model can examine how public information transfers to individual stock price and quantify transfer delay.

Appendix. Preliminary empirical studies in the introduction

In the introduction, we have motivated our studies by briefly presented that the empirical data contradicts what previous models assumed by having a considerably higher and diversified estimated number of mixture components. This is done by using the empirical data described in Sect. 3.3. For each day of each company, we assume the buy/sell order flows of that day follow the model as described in Sect. 3.1 with an unknown number of $I\left(m\right)$, which is the number of parameter pairs, or equivalently, the number of components of the model. We then use the change-point detection algorithm discussed in Sect. 3.2 to estimate this number, and also the parameter pairs for each of these components.

For example, based on the data of Apple stock in 28/12/2012, the change-point detection algorithm estimates a total of 32 components, with the parameter pair of each component presenting as a dot in Fig. 

Fig. 6

Scatter plot of estimated pairs of ${(\uplambda }_{\mathrm{B},\mathrm{j}},{\uplambda }_{\mathrm{S},\mathrm{j}})$ for Apple stock on 28/12/2012

6. We further summarize the estimated number of components for each single day of the Apple stock during the period, and present them through a histogram in Fig. 

Fig. 7

Histogram of the daily estimated J for Apple stock

7. Both of the figures confirm the argument of assumption contradiction claimed in the introduction. The other companies show similar behaviors.

The figure presents the estimated pairs of ${(\uplambda }_{\mathrm{B},\mathrm{j}},{\uplambda }_{\mathrm{S},\mathrm{j}})$ for Apple stock on 28/12/2012 assuming that the buy/sell order flows follow a mixture of joint Poisson distributions with parameters (${\uplambda }_{\mathrm{B},\mathrm{j}},{\uplambda }_{\mathrm{S},\mathrm{j}})$. The estimations are based on the algorithm provided by Du et al. (2016), which first estimated the number of components, J, and then estimated ${(\uplambda }_{\mathrm{B},\mathrm{j}},{\uplambda }_{\mathrm{S},\mathrm{j}})$ for $1\le j\le J$. The scatter plot presents all such estimated pairs ${(\uplambda }_{\mathrm{B},\mathrm{j}},{\uplambda }_{\mathrm{S},\mathrm{j}})$.

The figure presents the distribution of the daily estimated J for Apple stock from 3/1/2003 to 28/12/2012 using the same algorithm as in Fig. 6.