Competing to Sell the Reference Product

Abstract

In a sequential model of vertical product differentiation in which consumers are loss-averse, I analyse how firms compete to sell the reference product when they set prices. I find that there are two subgame perfect equilibria: one where the reference point for all consumers is the higher-quality product; and the other where the reference point is the lower-quality product. However, applying the risk-dominance criterion, I obtain that the sole risk-dominant equilibrium is for the higher-quality firm to sell the reference product. Since the hedonic price of the higher-quality product is the highest, consumers do not suffer any psychological disutility in the risk-dominant equilibrium.

1 Introduction

Selling the reference product implies that when consumers buy a product they compare the product of any rival firm with yours. Therefore, if the rival firm’s product is more expensive (inclusive of an hedonic adjustment), consumers who buy the rival product suffer a psychological loss; but if the reference product is more expensive, consumers who buy the reference product suffer no such loss. Thus, selling the reference product gives firms the advantage that their consumers do not bear any psychological loss, while those of competing firms bear such a loss when they set a higher price.

I develop a model in which firms compete to sell the reference product based on first-mover advantage, so the firm that sets the price first makes its product the reference point for all consumers. The mechanism behind this can be based on cognitive bias "anchoring" (Kahneman, 1992; Higgins & Liberman, 2018). I consider that firms compete on price,¹ so they prefer to be price followers rather than price leaders: There is a second-mover advantage (van Damme & Hurkens, 2004).² There is thus a trade-off between moving first (and selling the reference product) and moving second (and being a price follower).

I assume that consumers are loss-averse for both the price and the quality of products (Kahneman & Tversky, 1979; Tversky & Kahneman, 1991), so the degree of loss aversion is the same for both characteristics. This is supported empirically by Neumann and Böckenholt (2014), who find no general differences in the degree of loss aversion between the price dimension and the quality dimension. Thus, I consider that the utility of consumers is reference-dependent for the hedonic price of a product, where “ hedonic price” is defined as the price/quality ratio of a product.³

I find that there are two subgame perfect equilibria (SPE): one where the reference point is the higher-quality product; and the other where the reference points is the lower-quality product. Applying the risk-dominance criterion (Harsanyi & Selten, 1988),⁴ I obtain that the sole risk-dominant equilibrium is for the higher-quality firm to sell the reference product. Comparing the two SPEs from a welfare perspective, I find that the degree of loss-aversion is key to determining the social optimum.

The rest of the paper is organised as follows: Sect. 2 reviews the literature. Section 3 describes the model formally. Section 4 presents the equilibrium. Section 5 analyses welfare. Section 6 concludes.

2 Literature Review

The seminal paper on how loss aversion on the part of consumers affects price competition is Heidhues and Köszegi (2008).⁵ Following (Köszegi & Rabin, 2006), they consider that consumers are loss-averse in relation to a reference point, which is formed by their lagged rational expectations. Heidhues and Köszegi find that consumers’ loss aversion in terms of money increases the intensity of competition and reduces or eliminates price variation. Karle and Peitz (2014) modify that model to consider that firms commit to deterministic prices before consumers form their reference points.

The literature to date has considered that the reference product is formed by rational expectations lagged in the purchase (Heidhues & Köszegi, 2008) or by a weighted average of prices (Nasiry & Popescu, 2011). Ma et al. (2019) empirically find that the reference prices affect bid premia and target announcement-period returns in deals with greater uncertainty in acquirer valuation. Moreover, Lee and Yerramilli (2022) suggest that bidders use past values as reference points to choose announcement timing strategically. Thus, the timing of pricing could affect the reference point.

Unlike the papers cited above, in this paper the formation of the reference product here does not depend on expectations but on when firms set prices: The first product to have a price becomes the reference product. However, if the products are priced at the same time, I follow Zhou (2011) and consider that each product is the reference for some consumers. In a duopoly model, Zhou (2011) shows that loss aversion in price intensifies competition, while loss aversion in taste softens competition, as in Karle and Peitz (2014).

Previous papers develop models of horizontal product differentiation, but I consider that products differ vertically. In a monopoly model à la Mussa and Rosen (1978) with loss-averse consumers, Carbajal and Ely (2016) study optimal price discrimination when consumers have reference-dependent preferences for product quality. They consider that the reference point can be determined by past experiences or current aspirations. They find that optimal price discrimination may show efficiency gains relative to second-best contracts without loss aversion.

Hahn et al. (2018) also study price discrimination but consider that consumers have reference-dependent preferences for the quality and price of the product. They show that offering menus with a small number of bundles is consistent with profit-maximising firms. In the same framework, Courty and Nasiry (2018) apply loss aversion within a class of products of the same quality but not across quality classes. Courty and Nasiry show that uniform pricing can be optimal across quality classes up to a quality threshold.⁶

This paper is related to the price-leadership literature: In a vertically differentiated market in which firms choose quality and price, Lambertini (1996) finds that price leadership does not arise under partial market coverage. However, Li (2014) shows that the higher-quality firm leads the market when the price game takes place after the quality game. Li (2014) also shows that it is socially optimal for the lower-quality firm to be a price leader.

3 The Model

There are two firms –1 and 2– that produce a product of quality $q_{i}$ and sell at price $p_{i}$, where $i=1,2$. I normalise the product quality 1 to 1 – $q_{1}=1$– and I assume that $q_{2}\in \left( 0,1\right)$. Therefore, product 1 is a higher-quality product.

Firms compete on prices; but at an earlier stage they simultaneously choose when to set their prices, so the product that is priced first becomes the reference product. However, if both products are priced at the same time a proportion $\phi$ of consumers take product 1 as a reference while the rest take product 2 as a reference.

Selling the reference product is important because when a consumer goes to buy a product, he/she compares it with the reference product. He/she experiences a psychological disutility when buying a non-reference product whose hedonic price is higher than that of the reference product, where “hedonic price” is defined as the price/quality ratio of a product (p/q). Otherwise, consumers experience a psychological gain, the utility of which is normalised to zero, as in Zhou (2011).

I consider a continuum of consumers indexed by $\theta \in \left[ 0,1\right]$, where $\theta$ is assumed to follow a uniform distribution and represents consumers’ tastes for the quality of a product. Each consumer is assumed to buy either a single unit of the product or none at all.

There are two types of consumer when firms set prices simultaneously: those who take product 1 as a reference product; and those who take product 2 as a reference. If the reference product of a consumer $\theta$ is product 1, his/her reference-dependent utility is⁷:

$$\begin{aligned} U(\theta )=\left\{ \begin{array}{cl} \theta -p_{1} &{} \text {if he/she buys 1} \\ \theta q_{2}-p_{2}-\lambda \max \left\{ 0,\frac{p_{2}}{q_{2}}-p_{1}\right\} &{} \text {if he/she buys 2} \\ 0 &{} \text {if he/she does not buy,} \end{array} \right. \end{aligned}$$

(1)

but if the reference product is product 2, his/her utility is:

$$\begin{aligned} U(\theta )=\left\{ \begin{array}{cl} \theta -p_{1}-\lambda \max \left\{ 0,p_{1}-\frac{p_{2}}{q_{2}}\right\} &{} \text {if he/she buys 1} \\ \theta q_{2}-p_{2} &{} \text {if he/she buys 2} \\ 0 &{} \text {if he/she does not buy,} \end{array} \right. \end{aligned}$$

(2)

where $\lambda >0$ is the degree of loss aversion of a consumer, which represents the consumer’s sensitivity to the difference in hedonic price compared to the reference product. I assume that the degree of loss aversion is the same for all consumers, and that the degree of loss aversion is the same for the price and quality of a product.

To obtain the demand functions of each firm, I first define indifferent consumers. Among those consumers whose reference product is 1, let $\widehat{ \theta }_{i}$ be a consumer who is indifferent between buying product $i=1,2$ and not buying at all; and let ${\widehat{\theta }}$ be a consumer who is indifferent between buying products 1 and 2, where ${\widehat{\theta }} _{1}=p_{1}$,

$$\begin{aligned} \begin{array}{cc} {\widehat{\theta }}_{2}=\left\{ \begin{array}{cl} \frac{p_{2}}{q_{2}}+\frac{\lambda }{q_{2}}\left( \frac{p_{2}}{q_{2}} -p_{1}\right) &{} \text {if }p_{1}\le \frac{p_{2}}{q_{2}}\text {,} \\ \frac{p_{2}}{q_{2}} &{} \text {if }p_{1}\ge \frac{p_{2}}{q_{2}}\text {,} \end{array} \right. &{} {\widehat{\theta }}=\left\{ \begin{array}{cl} \frac{p_{1}-p_{2}}{1-q_{2}}+\frac{\lambda }{1-q_{2}}\left( p_{1}-\frac{p_{2} }{q_{2}}\right) &{} \text {if }p_{1}\le \frac{p_{2}}{q_{2}}\text {,} \\ \frac{p_{1}-p_{2}}{1-q_{2}} &{} \text {if }p_{1}\ge \frac{p_{2}}{q_{2}}\text {.} \end{array} \right. \end{array} \end{aligned}$$

Furthermore, among those consumers whose reference product is product 2, let ${\widetilde{\theta }}_{i}$ be a consumer who is indifferent between buying product $i=1,2$ and not buying at all; and let ${\widetilde{\theta }}$ be a consumer who is indifferent between buying products 1 and 2, where ${\widetilde{\theta }}_{2}=p_{2}/q_{2}$,

$$\begin{aligned} \begin{array}{cc} {\widetilde{\theta }}_{1}=\left\{ \begin{array}{cl} p_{1} &{} \text {if }p_{1}\le \frac{p_{2}}{q_{2}}\text {,} \\ p_{1}+\lambda \left( p_{1}-\frac{p_{2}}{q_{2}}\right) &{} \text {if }p_{1}\ge \frac{p_{2}}{q_{2}}\text {,} \end{array} \right. &{} {\widetilde{\theta }}=\left\{ \begin{array}{cl} \frac{p_{1}-p_{2}}{1-q_{2}} &{} \text {if }p_{1}\le \frac{p_{2}}{q_{2}}\text {,} \\ \frac{p_{1}-p_{2}}{1-q_{2}}+\frac{\lambda }{1-q_{2}}\left( p_{1}-\frac{p_{2} }{q_{2}}\right) &{} \text {if }p_{1}\ge \frac{p_{2}}{q_{2}}\text {.} \end{array} \right. \end{array} \end{aligned}$$

Given that $0<q_{2}<q_{1}=1$, if $p_{1}\le p_{2}/q_{2}$, the following inequalities are true:

$$\begin{aligned} \theta -p_{1}\ge \theta -p_{2}/q_{2}>q_{2}\left( \theta -p_{2}/q_{2}\right) =\theta q_{2}-p_{2}\ge \theta q_{2}-p_{2}-\lambda \left( \frac{p_{2}}{q_{2}} -p_{1}\right) \end{aligned}$$

This implies that all consumers prefer to buy product 1 rather than product 2 when $p_{1}\le p_{2}/q_{2}$. Therefore, the demand for product 2 is zero, so firm 2 has an incentive to deviate and set its (hedonically adjusted) price below $p_{1}$. Therefore, in equilibrium, $p_{1}>p_{2}/q_{2}$. This means that those consumers whose reference product is 1 will not experience a psychological disutility from buying product 2. Thus, if the reference product of all consumers is 1, no consumer experiences a psychological disutility. From this point forward I consider only the case in which $p_{1}>p_{2}/q_{2}$.

Demand for products 1 and 2 is defined as follows:

$$\begin{aligned} \begin{array}{cc} D_{1}=\phi \left( 1-{\widehat{\theta }}\right) +\left( 1-\phi \right) \left( 1- {\widetilde{\theta }}\right) ;&D_{2}=\phi \left( {\widehat{\theta }}-\widehat{ \theta }_{2}\right) +\left( 1-\phi \right) \left( {\widetilde{\theta }}- {\widetilde{\theta }}_{2}\right) \text {.} \end{array} \end{aligned}$$

(3)

I consider the costs that are incurred by firms in developing products as sunk costs and the marginal production costs (for both products) as zero. Thus, the profit of firm $i=1,2$ is $\pi _{i}=p_{i}D_{i}$.

As in Hamilton and Slutsky (1990), I develop a complete information game with observable delay, which is as follows: In the first stage, firms simultaneously decide when to set the price of their products. If they choose the same period, they set prices simultaneously; and a proportion $\phi$ of consumers take product 1 as a reference, while the rest take product 2. Otherwise, the firms set prices sequentially, so that the leader sells the reference product and the follower sells the non-reference product. In the second stage, they price their products accordingly. Finally, consumers make their purchase decision.

In the next section, I seek to find the subgame perfect equilibrium (SPE) of the game by backward induction.

4 Equilibrium

4.1 Second Stage

I now solve the three subgames that can arise after firms decide when to set the prices of their products. If they choose the same period, they set prices simultaneously. Otherwise, they set prices sequentially, and one firm (1 or 2) becomes the leader.

4.1.1 Simultaneous Price Subgame

In this subgame, the two firms set prices simultaneously. Thus, a proportion $\phi$ of consumers take product 1 as the reference product, while a proportion $1-\phi$ take product 2 as the reference product. By maximising the firms’ profits, I obtain the reaction function of each firm, which is:

$$\begin{aligned} p_{1}\left( p_{2}\right) =\frac{p_{2}\left( q_{2}+\lambda \left( 1-\phi \right) \right) +q_{2}\left( 1-q_{2}\right) }{2q_{2}\left( 1+\lambda \left( 1-\phi \right) \right) };p_{2}\left( p_{1}\right) =\frac{q_{2}}{2}p_{1}. \end{aligned}$$

From the intersection of these functions, I obtain the equilibrium prices and then the equilibrium demands and profits, which are⁸

$$\begin{aligned} \begin{array}{l} p_{1}^{S}=\frac{2\left( 1-q_{2}\right) }{4-q_{2}+3\lambda \left( 1-\phi \right) };D_{1}^{S}=\frac{2\left( 1+\lambda \left( 1-\phi \right) \right) }{ 4-q_{2}+3\lambda \left( 1-\phi \right) };\pi _{1}^{S}=\frac{4\left( 1-q_{2}\right) \left( 1+\lambda \left( 1-\phi \right) \right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{2}}; \\ p_{2}^{S}=\frac{q_{2}\left( 1-q_{2}\right) }{4-q_{2}+3\lambda \left( 1-\phi \right) };D_{2}^{S}=\frac{1+\lambda \left( 1-\phi \right) }{4-q_{2}+3\lambda \left( 1-\phi \right) };\pi _{2}^{S}=\frac{q_{2}\left( 1-q_{2}\right) \left( 1+\lambda \left( 1-\phi \right) \right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{2}}. \end{array} \end{aligned}$$

(4)

Loss aversion in the hedonic price dimension negatively affects those consumers whose reference product is 2 but who buy product 1 since $p_{1}^{S}>p_{2}^{S}/q_{2}$. Thus, when $\lambda$ increases, firm 1 sets lower prices to compensate those consumers, and since prices are strategic complements, firm 2 also sets lower prices, so demand for both products increases. As a result the profits of both firms decrease.

These results are summarised in Proposition 1:

Proposition 1

At the equilibrium when the two firms price simultaneously, greater loss aversion (a higher $\lambda$) means lower prices and profits for both products, but more demand.

Proof See Appendix.

Proposition 1 shows that loss aversion in the hedonic price is procompetitive because it increases the incentives of firms to reduce their prices. This is in line with the results obtained by Zhou (2011); Amaldoss and He (2018), though they consider prices and not hedonic prices.⁹

Recall that those consumers whose reference product is 1 do not experience a psychological disutility from buying product 2 because the price of product 1 is the highest. When the proportion of consumers whose reference product is 1 increases, there are proportionally fewer consumers who experience a psychological disutility. In this case, firms react by increasing prices because there are fewer consumers to be compensated for the psychological disutility. As a result, the demand for both products decreases; but the profits increase.

These results are summarised in Proposition 2:

Proposition 2

At the equilibrium when the two firms price simultaneously, a greater proportion of consumers who take product 1 as their reference product (a higher $\phi$) means higher prices and profits for both products, but lower demand.

Proof See Appendix.

4.1.2 Firm 1 is the Leader

In this subgame, firm 1 sets its price first and becomes the leader, so product 1 is the reference product and the utility function of all consumers is (1). Thus no consumer experiences loss aversion because the hedonic price of non-reference product 2 is lower than that of reference product 1: $p_{1}^{L1}\ge \frac{p_{2}^{L1}}{q_{2}}$. The equilibrium thus coincides with that obtained in a model without loss-averse consumers (see (Li, 2014)).

$$\begin{aligned} \begin{array}{ll} p_{1}^{L1}=\frac{1-q_{2}}{2-q_{2}};D_{1}^{L1}=\frac{1}{2};\pi _{1}^{L1}= \frac{1-q_{2}}{2\left( 2-q_{2}\right) };&p_{2}^{L1}=\frac{q_{2}\left( 1-q_{2}\right) }{2\left( 2-q_{2}\right) };D_{2}^{L1}=\frac{1}{2\left( 2-q_{2}\right) };\pi _{2}^{L1}=\frac{q_{2}\left( 1-q_{2}\right) }{4\left( 2-q_{2}\right) ^{2}}. \end{array} \end{aligned}$$

4.1.3 Firm 2 is the Leader

Firm 2 is now the leader, so it gets the first-mover advantage of selling the reference product. Thus, (2) represents the utility function of all consumers who may suffer psychological losses when buying from the rival firm 1. Taking into account that $p_{1}\ge \frac{p_{2}}{q_{2} }$ and maximising firm 1’s profit, its reaction function is obtained as:

$$\begin{aligned} p_{1}\left( p_{2}\right) =\frac{1-q_{2}}{2\left( \lambda +1\right) }+\frac{ \lambda +q_{2}}{2q_{2}\left( \lambda +1\right) }p_{2}. \end{aligned}$$

When firm 2 maximises its profit –$\pi _{2}\left( p_{1}\left( p_{2}\right) ,p_{2}\right)$– the price that firm 2 sets is:

$$\begin{aligned} p_{2}^{L2}=\frac{q_{2}\left( 1-q_{2}\right) }{2\left( \lambda +2-q_{2}\right) }. \end{aligned}$$

From $p_{2}^{L2}$, I obtain: the price that is set by firm 1; both firms’ demands; and both firms’ profits in this subgame¹⁰

$$\begin{aligned} \begin{array}{ll} p_{1}^{L2}=\frac{\left( 1-q_{2}\right) \left( 3\lambda +4-q_{2}\right) }{ 4\left( \lambda +1\right) \left( \lambda +2-q_{2}\right) };D_{1}^{L2}=\frac{ 3\lambda +4-q_{2}}{4\left( \lambda +2-q_{2}\right) };D_{2}^{L2}=\frac{1}{4};&\pi _{1}^{L2}=\frac{\left( 1-q_{2}\right) \left( 3\lambda +4-q_{2}\right) ^{2}}{16\left( \lambda +1\right) \left( \lambda +2-q_{2}\right) ^{2}};\pi _{2}^{L2}=\frac{q_{2}\left( 1-q_{2}\right) }{8\left( \lambda +2-q_{2}\right) }. \end{array} \end{aligned}$$

As in the subgame where both firms set prices simultaneously, I find that loss aversion in the hedonic price dimension negatively affects the prices of both products: The demand for product 1 increases; but the demand for product 2 is not affected. As a result the profits of both firms decrease.

Proposition 3 summarises these results:

Proposition 3

At the equilibrium when firm 2 is the leader, greater loss aversion (a higher $\lambda$) means lower prices and profits for both products, but more demand for product 1.

Proof See Appendix.

As in a model without loss-averse consumers, demand for product 2 is not affected, although its price decreases. This is because firm 2 is the price leader. Note that the equilibrium demand for product 1 is also constant when firm 1 is the price leader (as was shown above).

4.2 Comparative Statics

As is shown in the proposition below, both firms set higher prices when firm 1 is the leader. This is because the higher-quality product 1 is the reference in this case, so consumers experience no loss aversion when purchasing either product, and firms can set higher prices. However, when firm 2 is the leader or firms set prices simultaneously, consumers who buy product 1 suffer psychological disutility if their reference is the lower-quality product 2. Thus, firm 1 reacts by setting a lower price than when it is the leader. Prices are strategic complements, so firm 2 also reacts by setting a lower price:

Proposition 4

Given $\lambda >0$, $q_{2}\in \left( 0,1\right)$ and $\phi \in \left( 0,1\right)$, the following emerges:

• i) $p_{i}^{L1}>\max \left\{ p_{i}^{L2},p_{i}^{S}\right\}$ $i=1,2,$

• ii) $p_{1}^{L2}>p_{1}^{S}$ if $\phi <{\widehat{\phi }}=\frac{\lambda ^{2}+2\lambda q_{2}+q_{2}^{2}}{3\lambda \left( 3\lambda +4-q_{2}\right) }$; otherwise, $p_{1}^{L2}\le p_{1}^{S}$; and,

• iii) $p_{2}^{L2}>p_{2}^{S}$ if $\phi <\widehat{{\widehat{\phi }}}=\frac{ q_{2}}{3\lambda }+\frac{1}{3}$; otherwise, $p_{2}^{L2}\le p_{2}^{S}$.

Proof See Appendix.

As is shown in Proposition 4, competition is greater when firms set prices simultaneously if the proportion of consumers whose reference is product 1 is small enough, so prices are lowest.¹¹ An increase in that proportion means that there are fewer consumers who suffer a disutility when buying 1. Thus, firm 1 reacts by setting a higher price. Prices are strategic complements, so firm 2 also reacts by setting a higher price. Thus, when the proportion of consumers whose reference product is 1 is large enough, prices that are set simultaneously increase to the point where they are higher than those that are set when firm 2 is the leader.

4.3 First Stage: Timing Choices

In this stage firms decide when to set the prices of their products. They thus compete to sell the reference product, which is the one whose price is set first.

Table 1 summarises the game at this stage:

Table 1 Timing

Given that $\pi _{1}^{L1}>\pi _{1}^{S}$ and $\pi _{2}^{L1}>\pi _{2}^{S}$, I find that an SPE is an outcome in which firm 1 prices first and thus sells the reference product and firm 2 sells the non-reference product. As can be seen in Proposition 4, firms set higher prices when firm 1 is the leader because that firm sells the higher-quality product and consumers experience no psychological disutility in this outcome. Therefore, firms have no incentive to deviate from the outcome in which firm 1 is the leader, as is summarised in Proposition 5:

Proposition 5

Firm 1 as the leader is an SPE.

Proof See Appendix.

On the other hand, when firms set their prices simultaneously they take into account the proportion of consumers whose reference product is 2 – $1-\phi$ – because consumers suffer psychological disutility if they buy product 1. If that proportion is small enough (high $\phi$), they set prices higher than when firm 2 is the leader, as can be seen in Proposition 4.¹² Thus, firms deviate from the outcome in which firm 2 is the leader when $\phi$ is high enough. Otherwise, firms do not deviate; and the outcome in which firm 2 is the leader is an SPE, as is summarised in Proposition 6:

Proposition 6

Firm 2 as the leader is an SPE when $\lambda$ is very small or $\phi \le \phi ^{*}\left( q_{2},\lambda \right) \in \left( 0,1\right]$, where $\phi ^{*}\left( q_{2},\lambda \right)$ is the value of $\phi$ such that $\pi _{2}^{S}=\pi _{2}^{L2}$.

Proof See Appendix.

When the degree of loss aversion is very low, neither firm deviates from the SPE where firm 2 is the price leader (L2). Thus, there are two SPEs for any level of quality of firm 2. This coincides with the findings reported by Li (2014). This is because this model converges with the one developed by Li (2014) when consumers are not loss averse ($\lambda =0$).

Otherwise, when the degree of loss aversion is not too low, firm 2 as the price leader is still an SPE when the proportion of consumers whose reference product is 1 is sufficiently small. This is because firms continue to set higher prices when firm 2 is the leader (Proposition 4), even though prices have decreased (Proposition 3). However, when that proportion is sufficiently large, firms have an incentive to deviate and simultaneously set prices because their profits are higher (Proposition 4). Thus, firm 1 as the price leader is the only SPE when the proportion of consumers whose reference product is 1 is not sufficiently small.

To select an equilibrium I consider the refinement risk dominance equilibrium (Harsanyi & Selten, 1988), which selects the equilibrium that yields the greatest deviation losses, so that firms have less incentive to deviate.

These results are summarised in the following proposition:

Proposition 7

The sole risk-dominant equilibrium is firm 1 as the leader.

Proof See Appendix.

As can be seen in Proposition 7, the least risky outcome for firms is that in which firm 1 becomes the leader in prices. Thus, consumers experience no psychological disutility because the reference point is the product with the highest hedonic price.

5 Welfare Analysis

I focus on the sequential subgames in analysing welfare, because they are SPEs. But first I analyse the profits of the industry and the consumer surplus. Let $\Pi ^{i}=\pi _{1}^{i}+\pi _{2}^{i}$ be the industry profit at the SPE $i=L1,L2$. Consumer surplus in each SPE is defined as follows:

$$\begin{aligned} \begin{array}{l} CS^{L1}=\int _{{\widehat{\theta }}_{2}}^{{\widehat{\theta }}}\left( \theta q_{2}-p_{2}^{L1}\right) d\theta +\int _{{\widehat{\theta }}}^{1}\left( \theta -p_{1}^{L1}\right) d\theta , \\ CS^{L2}=\int _{{\widetilde{\theta }}_{2}}^{{\widetilde{\theta }}}\left( \theta q_{2}-p_{2}^{L2}\right) d\theta +\int _{{\widetilde{\theta }}}^{1}\left( \theta -p_{1}^{L2}-\lambda \left( p_{1}^{L2}-\frac{p_{2}^{L2}}{q_{2}}\right) \right) d\theta . \end{array} \end{aligned}$$

Let $W^{i}=\Pi ^{i}+CS^{i}$ be welfare at the SPE $i=L1,L2$. The industry profit, the consumer surplus, and the welfare in each SPE are shown below:

$$\begin{aligned} \begin{array}{l} \Pi ^{L1}=\frac{\left( 1-q_{2}\right) \left( 4-q_{2}\right) }{4\left( 2-q_{2}\right) ^{2}};CS^{L1}=\frac{4+q_{2}-q_{2}^{2}}{8\left( 2-q_{2}\right) ^{2}};W^{L1}=\frac{12-9q_{2}+q_{2}^{2}}{8\left( 2-q_{2}\right) ^{2}}; \\ \Pi ^{L2}=\frac{\left( 1-q_{2}\right) \left( 16-4q_{2}-q_{2}^{2}+\lambda \left( 24-2q_{2}^{2}+\lambda \left( 2q_{2}+9\right) \right) \right) }{ 16\left( \lambda +1\right) \left( \lambda +2-q_{2}\right) ^{2}}; \\ CS^{L2}=\frac{16+3q_{2}\left( 1-q_{2}\right) \left( 4-q_{2}\right) +\lambda \left( 24+2q_{2}\left( 9-5q_{2}\right) +\lambda \left( 9+7q_{2}\right) \right) }{32\left( \lambda +2-q_{2}\right) ^{2}}; \\ W^{L2}=\frac{48-28q_{2}-9q_{2}^{2}+5q_{2}^{3}+\lambda \left( 4-q_{2}\right) \left( 22+q_{2}-7q_{2}^{2}\right) +\lambda ^{2}\left( 51+11q_{2}-14q_{2}^{2}\right) +\lambda ^{3}\left( 9+7q_{2}\right) }{32\left( \lambda +1\right) \left( \lambda +2-q_{2}\right) ^{2}}. \end{array} \end{aligned}$$

As can be seen, the industry profit, the consumer surplus, and the welfare when the high-quality firm is the leader are independent of the degree of loss aversion. This is because in this SPE the leader sells the reference product, whose hedonic price is the highest. Thus, consumers suffer no psychological disutility.

However, when the higher-quality firm is the follower, the reference is the lower-quality product. Therefore, those consumers who buy the higher quality product, whose hedonic price is the highest, suffer a disutility. When the degree of loss aversion increases, firms react by setting lower prices so as to compensate these consumers, so industry profits decrease. On the other hand, consumer surplus increases because prices decrease and more consumers buy a product. However, the loss aversion negatively affects welfare because the negative effect on profits is higher.

Proposition 8 summarises these results:

Proposition 8

At the SPE when firm 2 is the leader, greater loss aversion (a higher $\lambda$) means lower industry profits and welfare, but a higher consumer surplus.

Proof See Appendix.

Firms compensate consumers who suffer disutility when the lower-quality firm is the leader, so the industry’s profit is greater when the leader is the higher-quality firm. On the other hand, consumers prefer the lower-quality firm as a leader because prices are lower and more consumers buy a product. Therefore, from a welfare perspective, it is preferable for the lower-quality firm to be the leader when the degree of loss aversion is low enough; otherwise, it is better for the higher-quality firm to be the leader to avoid psychological disutility for consumers.

These results are summarised in Proposition 9:

Proposition 9

Given that $q_{2}\in \left( 0,1\right)$ and $\lambda >0$:

• i) $\Pi ^{L1}>\Pi ^{L2}$,

• ii) $CS^{L2}>CS^{L1}$; and,

• iii) $W^{L1}\ge W^{L2}$ if $\lambda \ge \lambda ^{*}$, where $\lambda ^{*}\in \left[ 0,\frac{6}{5}\right]$; otherwise, $W^{L1}<W^{L2}$.

Proof See Appendix.

According to Proposition 9, the degree of loss-aversion of consumers is key to determining the social optimum. This is in line with the result obtained in a model of vertical product differentiation without loss-averse consumers by Li (2014), who shows that it is socially optimal for the lower-quality firm to be the price leader.

6 Conclusions

In a sequential model in which consumers are loss-averse, I study how firms compete to sell the reference product when they set prices, so that the leader sells the reference product but if firms choose simultaneously each product is the reference for some consumers. I assume that consumers are loss-averse for the hedonic price of the product; where "hedonic price" is defined as the price/quality ratio of a product. Thus, the degree of loss aversion is the same for the price and quality of a product. This is empirically supported by Neumann and Böckenholt (2014).

The results are the following: There are two subgame perfect equilibria (SPE): one where the reference point for all consumers is the higher-quality product; and the other where it is the lower-quality product. However, when the risk dominance criterion is applied, the sole risk-dominant equilibrium is for the higher-quality firm to sell the reference product. Since the hedonic price of the higher-quality product is highest, consumers suffer no psychological disutility in the risk-dominant equilibrium, while consumers in the other SPE do.

Comparing the two SPEs from a welfare perspective, I find that it is preferable for the lower-quality firm to sell the reference product when the degree of loss aversion is low enough; otherwise it is better for the higher-quality firm to sell the reference product, so as to avoid psychological disutility for consumers. Thus, the degree of loss-aversion is key to determining the social optimum.

Appendix

Proof of Proposition 1

Given $\lambda >0$, $q_{2}\in \left( 0,1\right)$, and $\phi \in \left( 0,1\right)$, the following emerges:

$$\begin{aligned} \begin{array}{l} \frac{\partial p_{1}^{S}}{\partial \lambda }=-\frac{6\left( 1-\phi \right) \left( 1-q_{2}\right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{2}}<0;\frac{\partial D_{1}^{S}}{\partial \lambda }=\frac{2\left( 1-\phi \right) \left( 1-q_{2}\right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{2}}>0;\frac{\partial \pi _{1}^{S}}{\partial \lambda }=- \frac{4\left( 1-\phi \right) \left( 1-q_{2}\right) \left( 2+q_{2}+3\lambda \left( 1-\phi \right) \right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{3}}<0; \\ \frac{\partial p_{2}^{S}}{\partial \lambda }=-\frac{3\left( 1-\phi \right) q_{2}\left( 1-q_{2}\right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{2}}<0;\frac{\partial D_{2}^{S}}{\partial \lambda }=\frac{\left( 1-\phi \right) \left( 1-q_{2}\right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{2}}>0;\frac{\partial \pi _{2}^{S}}{\partial \lambda }=- \frac{q_{2}\left( 1-\phi \right) \left( 1-q_{2}\right) \left( 2+q_{2}+3\lambda \left( 1-\phi \right) \right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{3}}<0. \end{array} \end{aligned}$$

$\square$

Proof of Proposition 2

Given $\lambda >0$, $q_{2}\in \left( 0,1\right)$, and $\phi \in \left( 0,1\right)$, the following emerges:

$$\begin{aligned} \begin{array}{c} \frac{\partial p_{1}^{S}}{\partial \phi }=\frac{6\lambda \left( 1-q_{2}\right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{2}}>0;\frac{\partial D_{1}^{S}}{\partial \phi }=-\frac{2\lambda \left( 1-q_{2}\right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{2}}<0;\frac{\partial \pi _{1}^{S}}{\partial \phi }=\frac{4\lambda \left( 1-q_{2}\right) \left( 2+q_{2}+3\lambda \left( 1-\phi \right) \right) }{ \left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{3}}>0; \\ \frac{\partial p_{2}^{S}}{\partial \phi }=\frac{3\lambda q_{2}\left( 1-q_{2}\right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{2}}>0;\frac{\partial D_{2}^{S}}{\partial \phi }=-\frac{\lambda \left( 1-q_{2}\right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{2}} <0;\frac{\partial \pi _{2}^{S}}{\partial \phi }=\frac{\lambda q_{2}\left( 1-q_{2}\right) \left( 2+q_{2}+3\lambda \left( 1-\phi \right) \right) }{ \left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{3}}>0. \end{array} \end{aligned}$$

$\square$

Proof of Proposition 3

Given $\lambda >0$, $q_{2}\in \left( 0,1\right)$, and $\phi \in \left( 0,1\right)$, the following emerges:

$$\begin{aligned} \begin{array}{l} \frac{\partial p_{1}^{L2}}{\partial \lambda }=-\frac{\left( 1-q_{2}\right) \left( \lambda \left( 3\lambda +8-2q_{2}\right) +q_{2}^{2}+6-4q_{2}\right) }{ 4\left( \lambda +1\right) ^{2}\left( \lambda +2-q_{2}\right) ^{2}}<0;\frac{ \partial \pi _{1}^{L2}}{\partial \lambda }=-\frac{\left( 1-q_{2}\right) \left( 3\lambda +4-q_{2}\right) \left( 4-2q_{2}+q_{2}^{2}+6\lambda +3\lambda ^{2}\right) }{16\left( \lambda +1\right) ^{2}\left( \lambda +2-q_{2}\right) ^{3}}<0. \\ \frac{\partial D_{1}^{L2}}{\partial \lambda }=\frac{1-q_{2}}{2\left( \lambda +2-q_{2}\right) ^{2}}>0;\frac{\partial p_{2}^{L2}}{\partial \lambda }=-\frac{ q_{2}\left( 1-q_{2}\right) }{2\left( \lambda +2-q_{2}\right) ^{2}}<0;\frac{ \partial D_{2}^{L2}}{\partial \lambda }=0;\frac{\partial \pi _{2}^{L2}}{ \partial \lambda }=-\frac{q_{2}\left( 1-q_{2}\right) }{8\left( \lambda +2-q_{2}\right) ^{2}}<0; \end{array} \end{aligned}$$

$\square$

Proof of Proposition 4

Given $\lambda >0$, $q_{2}\in \left( 0,1\right)$, and $\phi \in \left( 0,1\right)$, the following emerges:

$$\begin{aligned} \begin{array}{l} p_{1}^{L1}-p_{1}^{L2}=\frac{\left( 1-q_{2}\right) \left( \lambda \left( 4\lambda +6-q_{2}\right) +q_{2}\left( 2-q_{2}\right) \right) }{4\left( 2-q_{2}\right) \left( \lambda +1\right) \left( \lambda +2-q_{2}\right) }>0;p_{1}^{L1}-p_{1}^{S}=\frac{\left( 1-q_{2}\right) \left( q_{2}+3\lambda \left( 1-\phi \right) \right) }{\left( 2-q_{2}\right) \left( 3\lambda \left( 1-\phi \right) +4-q_{2}\right) }>0; \\ p_{1}^{L2}-p_{1}^{S}=\frac{\left( 1-q_{2}\right) \left( \lambda ^{2}+2\lambda q_{2}+q_{2}^{2}-3\lambda \phi \left( 3\lambda +4-q_{2}\right) \right) }{4\left( \lambda +1\right) \left( \lambda +2-q_{2}\right) \left( 3\lambda \left( 1-\phi \right) +4-q_{2}\right) }>0\longleftrightarrow \phi< {\widehat{\phi }}=\frac{\lambda ^{2}+2\lambda q_{2}+q_{2}^{2}}{3\lambda \left( 3\lambda +4-q_{2}\right) }; \\ p_{2}^{L1}-p_{2}^{L2}=\frac{\lambda q_{2}\left( 1-q_{2}\right) }{2\left( 2-q_{2}\right) \left( \lambda +2-q_{2}\right) }>0;p_{2}^{L1}-p_{2}^{S}=\frac{ q_{2}\left( 1-q_{2}\right) \left( q_{2}+3\lambda \left( 1-\phi \right) \right) }{2\left( 2-q_{2}\right) \left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) }>0 \\ p_{2}^{L2}-p_{2}^{S}=\frac{q_{2}\left( 1-q_{2}\right) \left( q_{2}+\lambda -3\lambda \phi \right) }{2\left( \lambda +2-q_{2}\right) \left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) }>0\longleftrightarrow \phi < \widehat{{\widehat{\phi }}}=\frac{q_{2}}{3\lambda }+\frac{1}{3} \end{array} \end{aligned}$$

$\square$

Proof of Proposition 5

Given $\lambda >0$, $q_{2}\in \left( 0,1\right)$, and $\phi \in \left( 0,1\right)$, the following emerges:

$\pi _{1}^{L1}-\pi _{1}^{S}=\frac{\left( 1-q_{2}\right) \left( 9\lambda ^{2}\left( 1-\phi \right) ^{2}+q_{2}^{2}+2\lambda \left( 1-\phi \right) \left( 4+q_{2}\right) \right) }{2\left( 2-q_{2}\right) \left( 3\lambda \left( 1-\phi \right) +4-q_{2}\right) ^{2}}>0,$

$\pi _{2}^{L1}-\pi _{2}^{S}=\frac{q_{2}\left( 1-q_{2}\right) \left( q_{2}\left( 8-3q_{2}\right) +\lambda \left( 1-\phi \right) \left( 8-4q_{2}^{2}+10q_{2}+9\lambda \left( 1-\phi \right) \right) \right) }{ 4\left( 2-q_{2}\right) ^{2}\left( 3\lambda \left( 1-\phi \right) +4-q_{2}\right) ^{2}}>0.$ $\square$

Proof of Proposition 6

Given $\lambda >0$, $q_{2}\in \left( 0,1\right)$, and $\phi \in \left( 0,1\right)$, I obtain the following:

$\frac{\partial \left( \pi _{2}^{S}-\pi _{2}^{L2}\right) }{\partial \phi }= \frac{\lambda q_{2}\left( 1-q_{2}\right) \left( 2+q_{2}+3\lambda \left( 1-\phi \right) \right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{3}}>0$,

$\left. \pi _{2}^{S}-\pi _{2}^{L2}\right| _{\phi =0}=-\frac{q_{2}\left( 1-q_{2}\right) \left( \lambda +q_{2}\right) ^{2}}{8\left( \lambda +2-q_{2}\right) \left( 3\lambda +4-q_{2}\right) ^{2}}<0$ and

$\left. \pi _{2}^{S}-\pi _{2}^{L2}\right| _{\phi =1}=\frac{q_{2}\left( 1-q_{2}\right) \left( 8\lambda -q_{2}^{2}\right) }{8\left( 4-q_{2}\right) ^{2}\left( \lambda +2-q_{2}\right) }\lesseqgtr 0\longleftrightarrow \lambda \lesseqgtr \frac{q_{2}^{2}}{8}$.

If $\lambda <q_{2}^{2}/8$, then $\pi _{2}^{S}<\pi _{2}^{L2}$. Thus, firm 2 does not deviate from L2 for any value of $\phi$. Otherwise, there is a $\phi ^{*}\left( q_{2},\lambda \right) \in \left( 0,1\right)$ such that:

$\pi _{2}^{S}-\pi _{2}^{L2}\left\{ \begin{array}{cc}<0 &{} \text {if }\phi <\phi ^{*}\left( q_{2},\lambda \right) \\ =0 &{} \text {if }\phi =\phi ^{*}\left( q_{2},\lambda \right) \\>0 &{} \text {if }\phi >\phi ^{*}\left( q_{2},\lambda \right) . \end{array} \right.$

Thus, firm 2 does not deviate from L2 for $\phi \le \phi ^{*}\left( q_{2},\lambda \right)$, but it deviates for $\phi >\phi ^{*}\left( q_{2},\lambda \right)$.

I analyse the incentives of firm 1 to deviate. Given $\lambda >0$, $q_{2}\in \left( 0,1\right)$, and $\phi \in \left( 0,1\right)$, I obtain the following:

$\frac{\partial \left( \pi _{1}^{S}-\pi _{1}^{L2}\right) }{\partial \phi }= \frac{4\lambda \left( 1-q_{2}\right) \left( 3\lambda \left( 1-\phi \right) +2+q_{2}\right) }{\left( 4-q_{2}+3\lambda \left( 1-\phi \right) \right) ^{3}} >0$ and

$\left. \pi _{1}^{S}-\pi _{1}^{L2}\right| _{\phi =0}=-\frac{\left( \lambda +q_{2}\right) ^{2}\left( 1-q_{2}\right) \left( 16\left( 2-q_{2}\right) +q_{2}^{2}+17\lambda ^{2}+2\lambda \left( 24-7q_{2}\right) \right) }{16\left( \lambda +1\right) \left( 3\lambda +4-q_{2}\right) ^{2}\left( \lambda +2-q_{2}\right) ^{2}}<0$.

$\left. \pi _{1}^{S}-\pi _{1}^{L2}\right| _{\phi =1}=\frac{\left( 1-q_{2}\right) \left( 16\lambda \left( 11\lambda +4\lambda ^{2}+8\right) -\lambda q_{2}\left( 56\lambda +8q_{2}-6q_{2}^{2}+9\lambda q_{2}+96\right) -q_{2}^{2}\left( 32-16q_{2}+q_{2}^{2}\right) \right) }{16\left( 4-q_{2}\right) ^{2}\left( \lambda +1\right) \left( \lambda +2-q_{2}\right) ^{2}}\lesseqgtr 0\longleftrightarrow \lambda \lesseqqgtr {\overline{\lambda }}$, where ${\overline{\lambda }}\in \left( 0,\frac{1}{2}\right]$,

$\frac{\partial \left( \left. \pi _{1}^{S}-\pi _{1}^{L2}\right| _{\phi =1}\right) }{\partial \lambda }=\frac{\left( 1-q_{2}\right) \left( 3\lambda +4-q_{2}\right) \left( 6\lambda +3\lambda ^{2}+4-2q_{2}+q_{2}^{2}\right) }{ 16\left( \lambda +1\right) ^{2}\left( \lambda +2-q_{2}\right) ^{3}}>0$.

If $\lambda <{\overline{\lambda }}$, then $\pi _{1}^{S}<\pi _{1}^{L2}$. Thus, firm 1 does not deviate from L2 for any value of $\phi$. Otherwise, there is a $\phi ^{\prime }\left( q_{2},\lambda \right) \in \left( 0,1\right)$ such that:

$\pi _{1}^{S}-\pi _{1}^{L2}\left\{ \begin{array}{cc}<0 &{} \text {if }\phi <\phi ^{\prime }\left( q_{2},\lambda \right) \\ =0 &{} \text {if }\phi =\phi ^{\prime }\left( q_{2},\lambda \right) \\>0 &{} \text {if }\phi >\phi ^{\prime }\left( q_{2},\lambda \right) . \end{array} \right.$

Thus, firm 1 does not deviate from L2 for $\phi \le \phi ^{\prime }\left( q_{2},\lambda \right)$, but it deviates for $\phi >\phi ^{\prime }\left( q_{2},\lambda \right)$.

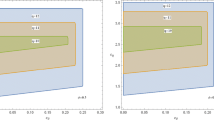
Figure 1a shows that $\phi ^{*}\left( q_{2},\lambda \right) <\phi ^{\prime }\left( q_{2},\lambda \right)$ for $\lambda =\left\{ \frac{1}{2},2,8\right\}$ and any $q_{2}\in \left( 0,1\right)$.¹³ Therefore, L2 is a SPE if $\phi \le \phi ^{*}\left( q_{2},\lambda \right)$ because neither firm deviates for these values of $\phi$.$\square$

Fig. 1

Proofs of Proposition 6 and 7

Proof of Proposition 7

Let $\pi _{i}^{S}-\pi _{i}^{L1}$ be the deviation losses from the equilibrium L1 by firm $i=1,2$, and let $\pi _{i}^{S}-\pi _{i}^{L2}$ be the deviation losses from the equilibrium L2 by firm $i=1,2$. The equilibrium L1 risk dominates L2 if: $\left( \pi _{1}^{S}-\pi _{1}^{L1}\right) \left( \pi _{2}^{S}-\pi _{2}^{L1}\right) >\left( \pi _{1}^{S}-\pi _{1}^{L2}\right) \left( \pi _{2}^{S}-\pi _{2}^{L2}\right)$.

Let $F\left( q_{2},\phi ,\lambda \right) =\left( \pi _{1}^{S}-\pi _{1}^{L1}\right) \left( \pi _{2}^{S}-\pi _{2}^{L1}\right) -\left( \pi _{1}^{S}-\pi _{1}^{L2}\right) \left( \pi _{2}^{S}-\pi _{2}^{L2}\right)$. Note that the equilibrium L1 risk dominates L2 if $F\left( q_{2},\phi ,\lambda \right) >0$. $F\left( q_{2},\phi ,\lambda \right)$ is continuous, decreasing in $\phi$ and positive when $\phi =0$.

$$\begin{aligned} \begin{array}{l} \frac{\partial F\left( q_{2},\phi ,\lambda \right) }{\partial \phi }=-\frac{ \lambda q_{2}\left( 3\lambda \left( 1-\phi \right) +q_{2}+2\right) \left( A+\lambda ^{2}\left( 92-36q_{2}-q_{2}^{2}\right) +8\lambda ^{3}\left( 4-q_{2}\right) +q_{2}\left( 8-q_{2}\right) \left( 2-q_{2}\right) ^{2}\right) \left( 1-q_{2}\right) ^{2}}{16\left( \lambda +1\right) \left( 2-q_{2}\right) ^{2}\left( \lambda +2-q_{2}\right) ^{2}\left( 3\lambda \left( 1-\phi \right) +4-q_{2}\right) ^{3}}<0 \\ F\left( q_{2},0,\lambda \right) =\frac{q_{2}\left( 1-q_{2}\right) ^{2}\left( B+C+D+\lambda ^{4}\left( 1880-164q_{2}-598q_{2}^{2}+137q_{2}^{3}\right) +16\lambda ^{5}\left( q_{2}+5\right) \left( 11-4q_{2}\right) +144\lambda ^{6}\right) }{128\left( 2-q_{2}\right) ^{3}\left( \lambda +1\right) \left( 3\lambda +4-q_{2}\right) ^{2}\left( \lambda +2-q_{2}\right) ^{3}}>0 \end{array} \end{aligned}$$

where $A=\lambda 2\left( 2-q_{2}\right) \left( 16+6q_{2}-3q_{2}^{2}\right)$, $B=q_{2}\left( 2-q_{2}\right) ^{2}\left( 4\lambda \left( 32-q_{2}^{3}\right) +\right.$ $\left. +q_{2}^{2}\left( 2-q_{2}\right) \left( 8-q_{2}\right) \right)$, $C=2\lambda ^{2}\left( 2-q_{2}\right) \left( 400q_{2}-276q_{2}^{2}+32q_{2}^{3}+q_{2}^{4}+128\right)$ and $D=4\lambda ^{3}\left( 416+192q_{2}-456q_{2}^{2}+156q_{2}^{3}-13q_{2}^{4}\right)$. Therefore, there is a $\phi ^{**}\left( q_{2},\lambda \right)$ such that:

$F\left( q_{2},\phi ,\lambda \right) \left\{ \begin{array}{cc}>0 &{} \text {if }\phi<\phi ^{**}\left( q_{2},\lambda \right) \\ =0 &{} \text {if }\phi =\phi ^{**}\left( q_{2},\lambda \right) \\ <0 &{} \text {if }\phi >\phi ^{**}\left( q_{2},\lambda \right) \end{array} \right.$

Therefore, L1 risk dominates L2 if $\phi <\phi ^{**}\left( q_{2},\lambda \right)$. Note that L1 is an equilibrium for every $\phi$, but L2 is an equilibrium when $\phi <\phi ^{*}\left( q_{2},\lambda \right)$. Thus, L1 and L2 coexist when $\phi <\phi ^{*}\left( q_{2},\lambda \right)$. Figure 1b shows that $\phi ^{*}\left( q_{2},\lambda \right) <\phi ^{**}\left( q_{2},\lambda \right)$ for $\lambda =\left\{ \frac{1}{2},2,8\right\}$ and any $q_{2}\in \left( 0,1\right)$.¹⁴ Therefore, L1 risk dominates L2 for every $\phi$ in which L2 exists. $\square$

Proof of Proposition 8

Given that $q_{2}\in \left( 0,1\right)$ and $\lambda >0$, I obtain:

$$\begin{aligned} \begin{array}{l} \frac{\partial \Pi ^{L2}}{\partial \lambda }=-\frac{\left( 1-q_{2}\right) \left( \lambda \left( 36-2q_{2}-q_{2}^{2}\right) +\lambda ^{2}\left( 30+5q_{2}-2q_{2}^{2}\right) +\lambda ^{3}\left( 2q_{2}+9\right) +16-8q_{2}+4q_{2}^{2}-q_{2}^{3}\right) }{16\left( \lambda +1\right) ^{2}\left( \lambda +2-q_{2}\right) ^{3}}<0; \\ \frac{\partial CS^{L2}}{\partial \lambda }=\frac{\left( 1-q_{2}\right) \left( 3\lambda +q_{2}+\lambda q_{2}+4-q_{2}^{2}\right) }{8\left( \lambda +2-q_{2}\right) ^{3}}>0;\frac{\partial W^{L2}}{\partial \lambda }=-\frac{ \left( 1-q_{2}\right) \left( 3\lambda +4-q_{2}\right) \left( 2\lambda +\lambda ^{2}+q_{2}^{2}+2-2q_{2}\right) }{16\left( \lambda +1\right) ^{2}\left( \lambda +2-q_{2}\right) ^{3}}<0. \end{array} \end{aligned}$$

$\square$

Proof of Proposition 9

Given that $q_{2}\in \left( 0,1\right)$ and $\lambda >0$, I obtain:

$$\begin{aligned} \begin{array}{l} \Pi ^{L1}-\Pi ^{L2}=\frac{\left( 1-q_{2}\right) \left( 4\lambda ^{3}\left( 4-q_{2}\right) +\lambda ^{2}\left( 44-24q_{2}+7q_{2}^{2}-2q_{2}^{3}\right) +2\lambda \left( 2-q_{2}\right) \left( 8-4q_{2}+q_{2}^{2}\left( 4-q_{2}\right) \right) +q_{2}^{2}\left( 2-q_{2}\right) ^{2}\right) }{ 16\left( 2-q_{2}\right) ^{2}\left( \lambda +1\right) \left( \lambda +2-q_{2}\right) ^{2}}>0 \\ CS^{L2}-CS^{L1}=\frac{\left( 1-q_{2}\right) \left( 10\lambda q_{2}^{3}+\lambda ^{2}\left( 20+8q_{2}-7q_{2}^{2}\right) +8\lambda \left( 4+3q_{2}-5q_{2}^{2}\right) +q_{2}\left( 8-3q_{2}\right) \left( 2-q_{2}\right) ^{2}\right) }{32\left( 2-q_{2}\right) ^{2}\left( \lambda +2-q_{2}\right) ^{2}}>0 \\ \left. W^{L1}-W^{L2}\right| _{\lambda =0}=-\frac{q_{2}\left( 1-q_{2}\right) \left( 8-5q_{2}\right) }{32\left( 2-q_{2}\right) ^{2}}<0 \\ \left. W^{L1}-W^{L2}\right| _{\lambda =\frac{6}{5}}=\frac{\left( 1-q_{2}\right) \left( 13\,872-39\,856q_{2}+38\,792q_{2}^{2}-14\,120q_{2}^{3}+1675q_{2}^{4}\right) }{352\left( 2-q_{2}\right) ^{2}\left( 16-5q_{2}\right) ^{2}}>0 \end{array} \end{aligned}$$

Given that $W^{L1}$ does not depend on $\lambda$ and $W^{L2}$ is decreasing on $\lambda$, the difference $W^{L1}-W^{L2}$ is increasing on $\lambda$. Therefore, there is a $\lambda ^{*}\in \left[ 0,\frac{6}{5}\right]$ such that $W^{L1}-W^{L2}=0$, so that it is negative when $\lambda <\lambda ^{*}$ and positive when $\lambda >\lambda ^{*}$. $\square$