1 Introduction

We investigate the innovation diffusion incentives in the presence of bargaining between an upstream (U) input innovator and two downstream (D) firms. We consider two ex-ante identical D firms producing and selling a final output to heterogeneous consumers, and two differentiated inputs in the U market: a low-quality input that is provided by competitive firms and a high-quality patented input that is provided by an independent innovator. The quality of the final good depends on the quality of the input.

In such a framework, under simultaneous bargaining, opportunistic behavior on the part of the monopolist arise (e.g., Rey and Tirole, 2007): The upstream monopolist has the incentive to behave opportunistically during the separated negotiations by discounting to selected D firms. Anticipating this opportunistic behavior, each D firm will never agree on a per-unit royalty that is higher than the marginal cost of production of the new input.

As a result, the patent holder is in a disadvantaged position when selling two licenses. The implication, in most cases, is that exclusive licensing prevails over nonexclusive licensing. Another consequence is the inefficiency of the bargaining process: The negotiators’ joint profits are not maximized. A way out of this opportunism problem is sequential bargaining (see, among others, de Fontenay and Gans, 2005; Do and Miklós-Thal, 2022; Stole and Zwiebel, 1996). These contributions, however, assume a zero outside option for the negotiators, which is not very realistic.Footnote 1

We argue that this is relevant from a theoretical point of view as well as for the empirical evidence. In several industries (such as computers and electrical appliances), we observe that new (intermediate) products (such as an Intel chip or a software package) co-exist with older and lower qualities substitutes. For instance, in the negotiation for a new software package, the D firms can produce the output (such as a computer) with the new software; but they could also stay with the old software (at least from a short-term perspective).

As a result of the competition that the input supplier may face, when negotiating a nonexclusive licensing contract for a new input, the D firms’ outside options are strategic: They depend on the control variables of the negotiation problem. This implies a deviation from the maxi-mization of the negotiators’ joint profit. Recently, this has been pointed out by Inderst and Shaffer (2018) in a context with no-bargaining.

Our contribution is to study the role of the strategic outside option in determining technology diffusion and efficiency of the bargaining process. We show that, under certain conditions, the option for the D firms of purchasing an alternative (low quality) input at marginal cost makes it unprofitable for the innovator to maximize the negotiators’ surplus. This, in turn, affects innovation diffusion incentives. Interestingly, this has important implications on the social desirability of vertical integration between the U innovator and either D firm.

In the spirit of Bedre-Defolie (2012), we analyse a sequential bargaining game between the U firm and two D firms; we assume, in turn, that renegotiation is and is not allowed. The order of negotiation is endogenous. We consider observable two-part tariff contracts where fixed fees are not paid upfront, but only after learning about contract terms of others. Indeed, the U monopolist may have the incentive to offer a two-part tariff contract with a fixed fee that is optional, which thus provides a means for the D firms to withdraw from the contracts in case of opportunistic behavior (see de Fontenay and Gans, 2005).

In a somewhat similar vein, Marx and Shaffer (2010) consider break-up fees that are paid ex-post in a sequential bargaining frame. As they show, such an option eliminates the incentive to opportunistic behaviors.

As for the per-unit royalties, we also consider the possibility of negative per-unit royalties. Although subsidies are rarely observed, there is empirical evidence in terms of transmission of know-how and technical assistance to the licensee (see, among others, (Gawer and Henderson, 2007; Liao and Sen, 2005). Moreover, theoretical contributions point out that neither a negative fee, nor a negative per-unit royalty, can, a priori, be considered welfare detrimental (e.g., Filippini and Vergari, 2017; Liao and Sen, 2005; Milliou and Petrakis, 2007; Sudhir and Rao, 2006).

Our main results are as follow:

In the absence of renegotiation, the U innovator and the first negotiator cannot renegotiate their contract in the event of disagreement between U and the second negotiator, so that there is a commitment to the first contract (commitment scenario). The sequential bargaining that leads to nonexclusive licensing implies that most of the surplus is produced by the second D firm: Setting a large per-unit royalty in the first contract represents a commitment device that allows the first two negotiators to limit the quantity produced in the market. Clearly, this is incentive compatible as long as the second D firm is not very powerful, so that the first two negotiators can appropriate enough of the surplus. This explains why the innovator prefers to start negotiating with the more powerful firm.

Equilibrium results crucially depend on the possibility for the negotiators to set negative royalties. In particular, if negative royalties are allowed, the presence of the second D firm’s strategic outside option prevents the monopoly outcome from being implemented: There is an incentive to subsidize the second D firm. As a consequence, the bargaining is inefficient, and complete technology diffusion prevails over exclusive licensing only for relatively low bargaining power of the second D firm. If instead negative royalties are not allowed, the constrained sequential bargaining implies that the outside option of the second D firm is not strategic anymore: Nonexclusive licensing leads to the monopoly outcome.

In the presence of renegotiation, instead, the U innovator and the first negotiator will renegotiate an exclusive licensing contract in case of disagreement between U and the second D firm, so that there is no commitment to the first contract (no-commitment scenario). The consequence is that the outside option of the second D firm is positive but not strategic anymore. This allows the first two negotiators to maximize industry profit. This is profitable as long as the bargaining power of the second D firm is low enough. Indeed, if the second D firm is very powerful, the monopoly outcome is not profitable anymore because a too large part of the surplus should be left to this firm. In this case, the innovator prefers to negotiate an exclusive licensing contract with the less powerful firm.

We extend our analysis to assess the profitability for the U innovator to integrate vertically with either D firm, thus becoming an internal patent holder. The vertically integrated firm always has the incentive to sell the new input to the rival non-affiliate: By partially co-opting the rival via a per-unit royalty that is larger than the marginal cost, it is able to implement a quasi-monopoly outcome. This ability increases with its bargaining position vis-á-vis the non-affiliate firm. This explains why the innovator prefers to integrate vertically with the more powerful D firm.

Comparing vertical separation (VS) with vertical integration (VI), we find that the latter is always privately profitable in the absence of renegotiation. The private profitability of VI, however, is reduced in the presence of renegotiation. Indeed, the bargaining position of the second D firm becomes weaker as its outside option is not strategic anymore. This implies that, under VS, now the U innovator and the first D firm are able to obtain a larger part of the producer surplus, which makes, in some cases, their merger unprofitable.

As for social profitability, VI is also welfare-improving whenever it replaces the exclusive licensing outcome. Although VI implies some anti-competitive effects, it also allows the diffusion of the new input and the resulting increase of the average quality.


Related Literature

On top of the literature on vertical bargaining (that we mentioned above), our paper is related to a growing literature that analyzes optimal patent licensing under bargaining. Tauman and Watanabe (2007) and Watanabe and Muto (2008) consider bargaining among the patent holder and firms by games with side payments, then negotiating a fixed fee. Kishimoto and Muto (2012) compare fixed fee versus royalties under Nash bargaining when there is an internal patent holder in a Cournot duopoly. They find that royalty licensing always prevails.

Mauleon et al. (2013) consider instead an external patent holder and find that under complete information, the patent holder prefers to license by means of up-front fixed fees regardless of the degree of product differentiation, the innovation size, and the level of bargaining power. Under private information about the relative bargaining power of the parties, instead, royalty licensing prevails.

More recently, Stamatopoulos (2021) considers an external patent holder bargaining, with two asymmetric Cournot duopolists, an innovation that would allow the less efficient firm to reduce its production cost. We somewhat extend this literature, by analyzing, although in a complete information framework and ex-ante symmetric firms, the optimal licensing mode for both an external and internal patent holder and non-linear contracts.

Finally, there is a vast literature on the competitive effects of vertical integration. In particular, Rey and Tirole (2007) show that vertical integration is always profitable as the U producer can protect its monopoly power through input foreclosure, but vertical integration is anticompetitive. Reisinger and Tarantino (2013), in contrast, show that vertical integration can be privately unprofitable in the presence of complementary input producers. In our framework, both the private and the social profitability of VI depend on the type of bargaining process, and on the distribution of the bargaining power among negotiators, as well as on the innovation size.

The remainder of the paper is structured as follows. In Sect. 2, we set up the ex ante-innovation model and we then introduce the product innovation. In Sect. 3, we study the optimal licensing of an external innovator (vertical separation). In Sects. 4 and 5, we consider the incentives of an internal patent holder and assess the profitability of vertical integration.

2 Model

2.1 Status Quo

We consider two firms—\(D_{1}\) and \(D_{2}\)—that produce a homogeneous good and that compete à la Cournot. Final output production requires an essential input that is provided by a competitive upstream market.

There is a continuum of consumers indexed by \(\theta\) who are uniformly distributed in the interval \(\left[ 0,1\right]\). Parameter \(\theta\) is proportional to the willingness to pay for intrinsic quality. Each consumer has a unit demand and buys either one unit of a good of quality s at price p or buys nothing at all. Formally, the indirect utility of consumer type \(\theta\) is:

$$\begin{aligned} U(\theta )=\left\{ \begin{array}{ll} \theta s-p,&\text { if consumer type }\theta \, \text { buys} \\ 0,&\text { if does not buy} \end{array} \right. \end{aligned}$$

The demand for the good is then

$$\begin{aligned} Q\left( p\right) =1-\left( \frac{p}{s}\right) \iff p\left( Q\right) =s\left( 1-Q\right) , \end{aligned}$$

where \(Q=q_{1}+q_{2}\) and p/s is the fraction of consumers with a taste parameter that is less than \(\theta\); the fraction of consumers who do not buy the good.Footnote 2

As for the supply side, the essential input of quality s is produced at zero cost and it is sold at the competitive price \(w=0\). There is perfect vertical complementarity, and quality is connected to the input. The downstream (D) firm i profit function is: \(\pi _{i}=pq_{i}\). D firms compete in quantities; thus the Cournot duopoly profits and social welfare are:

$$\begin{aligned} & \pi _{i}=\frac{s}{9}, \\ & SW=\frac{4}{9}s. \end{aligned}$$

2.2 Innovation

An independent input producer develops a patented product innovation which allows the D firms to improve the final product quality from s to \(\psi s\) with \(\psi >1\) measuring the innovation size. Production costs are set to zero.Footnote 3

We study the licensing incentives of this external patent holder in the presence of bargaining. The U firm negotiates a two-part licensing contract \(\left( r,F\right)\) with either one or both D firms. We consider the set of possible contracts such that \(r\in {\mathbb {R}}\) and \(F\in {\mathbb {R}}\).

2.3 Timing

The timing of the interaction between the U innovator and the D firms is as follows.

  1. (1)

    First, U decides whether to negotiate with either one (exclusive licensing) or both D firms (nonexclusive licensing) as well as deciding the order of negotiation.

  2. (2)

    Second, bargaining takes place.Footnote 4

  3. (3)

    Third, the D firms compete in the market à la Cournot and transfers are made according to the signed vertical contracts.

3 Sequential Bargaining (Vertical Separation)

The U innovator negotiates sequentially bilateral contracts with \(D_{i}\) and/or \(D_{j}\).

The timing is as follows. In stage 1, U and \(D_{1}\) negotiate a (two-part tariff) contract that is a function of the quantity purchased:

$$\begin{aligned} T_{1}\left( q_{1}\right) =\left\{ \begin{array}{ll} F_{1}+r_{1}q_{1},&\text {if }q_{1}>0 \\ F_{01}\le 0,&\text {if }q_{1}=0 \end{array} \right. . \end{aligned}$$

This contract specifies a (positive) payment if the D firm buys a positive input quantity, and a (non positive) payment if it does not purchase. In stage 2, \(D_{2}\) observes \(T_{1}\) if it is signed, and then negotiates the contract

$$\begin{aligned} T_{2}\left( q_{2}\right) =\left\{ \begin{array}{ll} F_{2}+r_{2}q_{2},&\text { if }q_{2}>0 \\ F_{02}\le 0,&\text { if }q_{2}=0 \end{array} \right. . \end{aligned}$$

In stage 3, \(D_{1}\) observes \(T_{2}\) if it is signed. In words, fixed fees are not paid upfront, but only after learning about the contract terms of others [this is in line with de Fontenay and Gans (2005)]. They can also take the form of break-up fees [in line with Marx and Shaffer (2010)].Footnote 5

Clearly, there exists a mutually beneficial agreement as long as there are gains from trade; positive joint extra-profits (JEP, henceforth). JEP are defined as the difference between the two negotiators’ joint profits if there is an agreement and their joint profits if their negotiation fails, in which case each party gets its disagreement payoff.

Let \(\alpha _{i}\in \left[ 0,1\right]\) be the bargaining power of firm \(D_{i}\) vis à vis U. We apply the asymmetric Nash bargaining solution to each bilateral negotiation: It involves the determination of payoffs for each negotiator derived from the maximization of the asymmetric Nash product: the product of each party’s gain over the disagreement payoff raised to their bargaining power. As was pointed out in Muthoo (1999, pp. 35–36), the maximization of the asymmetric Nash product implies that each negotiator obtains a share (corresponding to its bargaining power) of the JEP that is generated by the bargaining plus its disagreement payoff.Footnote 6

We solve the game by backward induction, and we find the Nash equilibrium for the external patent holder. According to the U innovator licensing incentives, two possible subgames follow:

  1. 1.

    Exclusive licensing: Only one of the D firms adopts the new input. The non-innovating firm, say firm 1, produces the low quality good at zero production costs and sells it at price \(p_{1}\); the innovating firm 2 adopts the new input and sells the high quality good at price \(p_{2}\). This is the standard vertical differentiation scenario with an uncovered market, where the demand functions, in the region of prices where both firms are active, are easily derived as:

    $$\begin{aligned} q_{1}& = \frac{p_{2}-p_{1}}{s\left( \psi -1\right) }-\frac{p_{1}}{s} \iff p_1=\frac{p_2}{\psi }+\frac{q_1 s (1 - \psi )}{psi},\\ q_{2}& = 1-\frac{p_{2}-p_{1}}{s\left( \psi -1\right) } \iff p_2=p_1 + s ( \psi -1) (1 - q_2). \end{aligned}$$

    Firm 1 gains \(\pi _{1}\left( 0,r_{2};s,s\psi \right)\); while the innovating firm 2 gets \(\pi _{2}\left( r_{2},0;s\psi ,s\right) -F_2\).

  2. 2.

    Nonexclusive licensing (which corresponds to complete technology diffusion): All D firms adopt the new input and they sell a homogeneous final good of quality \(s\psi >s\) at price \(p^{\psi }\). The inverse demand for the good is:

    $$\begin{aligned} p^{\psi }=s \psi (1-Q^{\psi }). \end{aligned}$$

    The D firms’ profits \(\pi _{i}\left( r_{i},r_{j};s\psi ,s\psi \right) -F_i\) depend on the two part-tariff contracts \(c_{i}=\left( r_{i},F_{i}\right)\) with \(i=1,2\) and \(i\ne j\).

Before proceeding with the analysis, we make the following assumption.

Assumption:

$$\begin{aligned} \alpha _1 \ge \alpha _2. \end{aligned}$$
(1)

In words, the first negotiating D firm is at least as powerful as the second negotiating D firm. As we will see, this assumption is without loss of generality as the order of negotiation is endogenous and the innovator, in case of nonexclusive licensing, always has a weak preference to start negotiating with the more powerful firm.

Finally, for notational purposes, we indicate with \(CTD_i\) the non-exclusive licensing deal that occurs as a result of sequential bargaining starting with firm \(D_i\); and we indicate with \(EL_i\) the exclusive licensing deal with firm \(D_i\), where \(i={1,2}\).Footnote 7

3.1 Exclusive Licensing (EL)

Consider first the EL subgame, in which U and \(D_{1}\) have not reached an agreement. Standard Cournot competition leads to the third stage equilibrium quantities that we plug into the profit functions and solve for the bargaining stage.Footnote 8

The JEP of U and \(D_{2}\) is:

$$\begin{aligned} JEP^{EL}\left( U-D_{2}\right) =p_{2}q_{2}\left( r^{EL},0;s\psi ,s\right) - \frac{s}{9}. \end{aligned}$$

They maximize \(JEP^{EL}\left( U-D_{2}\right)\) with respect to \(r^{EL}\).Footnote 9 The unconstrained maximization problem leads to the following optimal contract:

$$\begin{aligned} r^{ELneg}=-\frac{s}{4}; F^{ELneg}\left( \alpha _2 \right) =\frac{s\left( 18\psi -17\right) \left( 1-\alpha _2 \right) }{72}+\frac{s}{8}. \end{aligned}$$
(2)

The U innovator subsidizes the licensee so as to make the licensee more aggressive in the Cournot market; and U reaps a higher profit via the fixed fee. As a result, the firms’ payoffs and industry profit (producer surplus, PS) are:

$$\begin{aligned} \pi _{1}\left( 0,r^{ELneg};s,s\psi \right) =\frac{s}{16}; \pi _{2}\left( r^{ELneg},0;s\psi ,s\right) -F^{ELneg} =\frac{s}{72}\left( 18\alpha _2 \psi -17\alpha _2 +8\right) ; \end{aligned}$$
$$\begin{aligned} \Pi _U^{ELneg}\left( \alpha _2 \right)& = \frac{s}{72}\left( 1-\alpha _2 \right) \left( 18\psi -17\right) ; \end{aligned}$$
(3)
$$\begin{aligned} PS^{ELneg}=\frac{s(4 \psi -1)}{16}. \end{aligned}$$
(4)

If instead negative royalties are not allowed, the optimal contract isFootnote 10:

$$\begin{aligned} r^{EL}=0; F^{EL}\left( \alpha _2 \right) =\left( 1-\alpha _2 \right) s\left( \psi -1\right) \frac{36\psi ^{2}-16\psi +1}{9\left( 4\psi -1\right) ^{2}}. \end{aligned}$$
(5)

Firms’ payoffs are then:

$$\begin{aligned} \pi _{1}\left( 0,r^{EL};s,s\psi \right)& = s\frac{\psi ^{2}}{\left( 4\psi -1\right) ^{2}};\pi _{2}\left( r^{EL},0;s\psi ,s\right) =\psi s\frac{\left( 2\psi -1\right) ^{2}}{\left( 4\psi -1\right) ^{2}}, \nonumber \\ \Pi _U^{EL} (\alpha _2)& = F_{EL}\left( \alpha _2 \right) =\left( 1-\alpha _2 \right) s\left( \psi -1\right) \frac{36\psi ^{2}-16\psi +1}{9\left( 4\psi -1\right) ^{2}}. \end{aligned}$$
(6)

From the innovator’s profit (both expressions 3 and 6), it can be easily verified that they decrease with the bargaining power of the licensing firm. We can thus conclude the following:

Lemma 1

For the case of exclusive licensing, the innovator chooses to negotiate with the less powerful D firm.

Given our assumption \(\alpha _1 \ge \alpha _2\), this implies that, for the case of exclusive licensing, the innovator chooses \(EL_2\).

3.2 Nonexclusive Licensing (CTD)

Suppose next that U negotiates with both D firms.Footnote 11

The JEP that is generated by the bargaining \(U-D_{i}\) is:

$$\begin{aligned} & JEP\left( U-D_{i}\right) =\left[ \pi _{i}\left( r_{i},r_{j};s\psi ,s\psi \right) -\pi _{i}\left( 0,r_{j};s,s\psi \right) \right] \\ & \quad+ \left[ r_{i}q_{i}\left( r_{i},r_{j};s\psi ,s\psi \right) + F_i +r_{j}q_{j}\left( r_{j},r_{i};s\psi ,s\psi \right) -r_{j}q_{j}\left( r_{j},0;s\psi ,s\right) \right] . \end{aligned}$$

If both negotiations succeed, both firms produce the high quality \(s\psi\) and the industry profit is \(PS=\sum _{i=1,2}p_{i}q_{i}\left( r_{i},r_{j}\right)\). This is the nonexclusive licensing subgame, whose last stage equilibrium variables are defined in Appendix Complete Technology Diffusion.

At the last stage, U and \(D_2\) negotiate the optimal contract to maximize their joint extra profit. These are defined once the negotiators’ outside options are specified. We consider two possibilities in turn:

  1. 1.

    In the absence of renegotiation, the U disagreement payoff is \(r_{1}q_{1}\left( r_{1},0;s\psi ,s\right) + F_1\), whereas the \(D_{2}\) disagreement payoff is \(\pi _{2}\left( 0,r_{1};s,s\psi \right)\).

  2. 2.

    If instead renegotiation is allowed, then U disagreement payoff is \(\Pi _U^{EL}(\alpha _1)\) (or \(\Pi _U^{ELneg}(\alpha _1)\) if negative royalties are possible), whereas the \(D_{2}\) disagreement payoff is \(\pi _{2}\left( 0,r^{EL};s,s\psi \right)\).

3.2.1 No Renegotiation (Commitment Scenario)

In the absence of renegotiation, given the contract \(\left( r_{1},F_{1}\right)\), U and \(D_{2}\) maximize their \(JEP_2\)Footnote 12

$$\begin{aligned} & \max _{r_{2}}\left( r_{1}q_{1}\left( r_{1},r_{2};s\psi ,s\psi \right) +pq_{2}\left( r_{2},r_{1};s\psi ,s\psi \right) \right. \nonumber \\ & \quad \left. -r_{1}q_{1}\left( r_{1},0;s\psi ,s\right) -\pi _{2}\left( 0,r_{1};s,s\psi \right) \right) \ge 0. \end{aligned}$$
(7)

Solving backwards, assuming an unconstrained maximization, we maximize condition (7) with respect to \(r_{2}\), and we find the last stage equilibrium royalty \(r_{2}\) for a given \(r_{1}\):

$$\begin{aligned} r_{2}\left( r_{1}\right) =\frac{2r_{1}-s\psi }{4}. \end{aligned}$$
(8)

Note that \(r_2\) increases in \(r_1\) and it always holds that \(r_1>r_2\). Moving backward, U and \(D_{1}\) maximize their \(JEP_1\) that is computed in \(r_{2}\left( r_{1}\right)\). Formally, their objective is:

$$\begin{aligned} & JEP_1 =\Pi _{U} \left( r_{1},r_{2}\right) +\pi _{1}\left( r_{1},r_{2}; s \psi , a \psi \right) -\pi _{1}\left( 0,r^{ELneg};s,s\psi \right) \\ & \quad-r^{ELneg}q_{2}\left( r^{ELneg},0;s\psi ,s\right) \text {.} \end{aligned}$$

Maximizing \(JEP_1\) with respect to \(r_{1}\) is equivalent to maximizing their joint profit: \(JP_1\)

$$\begin{aligned} & JP_1=\sum _{i=1,2} p q_{i}\left( r_{i},r_{j}\right) -\pi _{2}\left( 0,r_{1};s,s\psi \right) \nonumber \\ & \quad-\alpha _{2}\left( r_{1}q_{1}\left( r_{1},r_{2};s\psi ,s\psi \right) +pq_{2}\left( r_{2},r_{1};s\psi ,s\psi \right) -r_{1}q_{1}\left( r_{1},0;s\psi ,s\right) -\pi _{2}\left( 0,r_{1};s,s\psi \right) \right) . \end{aligned}$$
(9)

Note that when \(\alpha _{2}=0\), their joint profit becomes \(\sum _{i=1,2}p q_{i}\left( r_{i},r_{j}\right) -\pi _{2}\left( 0,r_{1};s,s\psi \right)\): Even if \(D_2\) has no bargaining power, their objective is lower than the industry profit, and we move away from the industry profit maximization because firm 2’s outside option \(\pi _{2}\left( 0,r_{1};s,s\psi \right)\) is strategic: It depends on the control variable \(r_{1}\). The optimal \(r_{1}\) as a function of \(\alpha _{2}\) is thenFootnote 13:

$$\begin{aligned} r_{1}^{N}\left( \alpha _{2},\psi \right) =\frac{s\psi \left( -16\psi +2\alpha _{2}+16\psi ^{2}+1\right) }{2\left( 16\psi ^{2}-4\psi +2\alpha _{2}\left( 2\psi -1\right) +1\right) }. \end{aligned}$$
(10)

Substituting \(r_{1}^N\left( \alpha _{2},\psi \right)\) into (8), we find:

$$\begin{aligned} r_{2}^{N}\left( \alpha _{2},\psi \right) =s\psi \frac{3\psi +\alpha _{2}\left( \psi -1\right) }{\left( 2-4\psi \right) \alpha _{2}+\left( 4\psi -16\psi ^{2}-1\right) }<0. \end{aligned}$$
(11)

The unconstrained sequential bargaining leads U to subsidize firm \(D_2\); \(r_{1}\), and, in turn, the equilibrium variables only depend on \(\alpha _{2}\): how much U has to give to \(D_{2}\). The result is a Stackelberg-like equilibrium with \(q_{2}^{N}\left( \alpha _{2},\psi \right) =1/2>q_{1}^{N}\left( \alpha _{2},\psi \right)\): The leader role, in terms of quantity produced, is undertaken by firm \(D_2\). Firms’ payoffs and industry profit areFootnote 14:

$$\begin{aligned} & \pi _{1}^{N}-F_{1}^{N}=\frac{1}{16}s+\alpha _{1}JEP^{N}\left( U-D_{1}\right) , \\ & \pi _{2}^{N}-F_{2}^{N}=s\psi ^{2}\tfrac{\left( 12\psi +2\alpha _{2}-3\right) ^{2}}{4\left( -4\psi -2\alpha _{2}+16\psi ^{2}+4\psi \alpha _{2}+1\right) ^{2}}+\alpha _{2}JEP^{N}\left( U-D_{2}\right) . \end{aligned}$$
$$\begin{aligned} PS^{N}\left( \alpha _{2} \right) =s\psi \tfrac{\left( 2\psi -4\alpha _{2}+16\psi ^{2}+6\psi \alpha _{2}+1\right) \left( -10\psi +16\psi ^{2}+2\psi \alpha _{2}+1\right) }{4\left( -4\psi -2\alpha _{2}+16\psi ^{2}+4\psi \alpha _{2}+1\right) ^{2}}. \end{aligned}$$
(12)
$$\begin{aligned} \Pi _{U}^{N}(\alpha _1,\alpha _2)=PS^{N}\left( \alpha _{2},\psi \right) -\left( \pi _{1}^{N}-F_{1}^{N}\right) -\left( \pi _{2}^{N}-F_{2}^{N}\right) . \end{aligned}$$

Although complete technology diffusion does not allow the negotiators to implement the monopoly outcome because of the presence of the strategic outside option of \(D_{2}\), industry profit is larger than under exclusive licensing. Indeed, it is straightforward to verify that \(PS^{N}-PS^{ELneg}>0\). Having two contracts rather than one allows the U innovator to gain a better control over the quantity that is produced in the downstream market.

The above contracts entail a negative royalty for firm \(D_2\). We next analyze what happens if negative royalties are not allowed. The reasoning is similar to the one developed above: As we proceed backwards, the best response of U and \(D_2\) to \(r_1\) that is set in the first stage stays the same: \(r_{2}\left( r_{1}\right) =\frac{2r_{1}-s\psi }{4}\). U and \(D_1\) incorporate this best response in their objective but now they solve a constrained maximization problem as \(r_{2}\left( r_{1}\right) =\frac{2r_{1}-s\psi }{4} \ge 0 \iff r_1 \ge s \psi /2\). The solution to this problem implies the corner royaltiesFootnote 15:

$$\begin{aligned} r_1^C = s \psi /2; r_2^C=0. \end{aligned}$$
(13)

Interestingly, this constrained sequential bargaining results in the monopoly outcome, as at equilibrium the following holds:

$$\begin{aligned} q_1(r_1^C,r_2^C)=0; q_2(r_2^C,r_1^C)=1/2, PS^C=\frac{s \psi }{4}. \end{aligned}$$

The reason for this outcome comes from the binding constraint that is imposed on \(r_1\) that, in turn, makes non-strategic the outside option of \(D_2\) when U and \(D_1\) set their contract maximizing objective (9).

The negotiators’ payoffs are then:

$$\begin{aligned} & \pi _1^C-F_1^C=\frac{s \psi ^2}{(4 \psi - 1)^2}+\alpha _{1}JEP^{C}\left( U-D_{1}\right) , \\ & \pi _2^C-F_2^C=\frac{(r_1^C+s \psi )^2}{s(4 \psi - 1)^2}+\alpha _{2}JEP^{C}\left( U-D_{2}\right) , \\ & \Pi _U^C (\alpha _1,\alpha _2) =PS^C-(\pi _1^C-F_1^C)-(\pi _2^C-F_2^C). \end{aligned}$$

It is worth noting that, however, the constrained sequential bargaining is not always implementable. In particular, the contracts that are defined in (13) are equilibrium contracts if and only ifFootnote 16

$$\begin{aligned} \alpha _2>\alpha _2^{NN} (\psi )\equiv \frac{-4 + 59 \psi - 19 \psi ^2}{(-1 + \psi ) (4 + \psi (-73 + 72 \psi ))}. \end{aligned}$$
(14)

Whenever \(\alpha _2<\alpha _2^{NN}(\psi )\), the bargaining at the first stage fails because \(JEP_1<0\); whereas for \(\alpha _2>\alpha _2^{NN}(\psi )\) it holds that \(JEP_1>0\). Indeed, on one hand, \(JEP_1\) decreases in \(\alpha _2\): The larger is \(\alpha _2\) the larger is the share of surplus that U and \(D_1\) have to give to \(D_2\); on the other hand, as \(\alpha _2\) increases there is a positive effect on \(JEP_1\) because the outside option of U decreases (whereas the outside option of \(D_1\) stays constant). At equilibrium, the overall effect is positive: \(JEP_1\) is increasing in \(\alpha _2\).

Under CTD, the role of the two D firms is asymmetric because sequential bargaining is such that most of the surplus is produced by the second negotiating firm, \(D_2\): We show in Appendix Sequential Bargaining Without Renegotiation that \(\Pi _{U}^{N}(\alpha _1,\alpha _2)-\Pi _{U}^{N}(\alpha _2,\alpha _1) \ge 0 \iff \alpha _1 \ge \alpha _2\). We can thus conclude the following.

Lemma 2

For the case of nonexclusive licensing, in the commitment scenario, the innovator chooses to start negotiating with the most powerful firm.

Given our assumption \(\alpha _1 \ge \alpha _2\), this implies that the innovator chooses \(CTD_1\).

Optimal licensing in the commitment scenario We are now in the position to compare exclusive and nonexclusive licensing in the absence of renegotiation. We remark that if negative royalties are allowed, although the sequential bargaining is not efficient, in terms of the surplus that is produced it is more efficient than exclusive licensing. In contrast, if negative royalties are not allowed, the constrained sequential bargaining is efficient as it maximizes the negotiators’ (industry) profit. This result contrasts with Bedre-Defolie (2012) where efficiency is restored only under renegotiation. As we show in the following proposition, however, the preference of the U innovator depends on the two D firms bargaining powers.

Proposition 3

(i) If negative royalties are allowed, \(CTD_1\) always prevails over \(EL_2\); if negative royalties are not allowed, as long as \(CTD_1\) is implementable—if \(\alpha _2>\alpha _2^{NN}(\psi )\)—it prevails over \(EL_2\); \(EL_2\), instead, prevails if \(\alpha _2<\alpha _2^{NN}(\psi )\).

Proof

See Appendix Sequential Bargaining Without Renegotiation. \(\square\)

For the case of negative royalties, \(EL_2\) is never profitable as compared with nonexclusive licensing because in both cases the U innovator has an incentive to subsidize the downstream production of \(D_2\) (as in both cases the equilibrium royalty \(r_2\) is negative); but with \(CTD_1\) the U firm can also manipulate (control) to a certain extent the quantity produced by \(D_1\). Figure 1 illustrates this result for the particular but representative case of \(\psi =2\).

For the case of non-negative royalties, whenever \(D_2\) has weak enough bargaining power (\(\alpha _2<\alpha _2^{NN}\)), the negotiators have no incentives to enter the constrained sequential bargaining as there are no gains from trade. Note that this always holds for low levels of the innovation.Footnote 17 This is the reason why exclusive licensing with the less powerful D firm prevails.

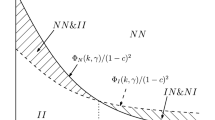
When instead the innovation size is large enough but not particularly high so that \(CTD_1\) is implementable, although industry profit is maximized with sequential bargaining, this is not always the profit maximizing strategy of the U firm. Figure 2 illustrates this result for the particular but representative case of \(\psi =2\).

Recalling that firm \(D_2\) produces most of the surplus and that \(\alpha _1 \ge \alpha _2\), we find that \(EL_2\) is profitable only as long as \(CTD_1\) is not implementable. Indeed, otherwise, \(CTD_1\) is always preferred over \(EL_2\) because in this case, industry profit is maximized and U is able to appropriate most of the surplus because the share of surplus that is allocated to \(D_2\) is sufficiently low. Finally, when \(\psi\) is particularly high, so that \(CTD_1\) is always implementable, nonexclusive licensing always prevails.Footnote 18

Fig. 1
figure 1

Innovation diffusion without renegotiation when negative royalties are allowed, \(\alpha _1 \ge \alpha _2\), and \(\psi =2\)

Full size image
Fig. 2
figure 2

Innovation diffusion without renegotiation when negative royalties are not allowed, \(\alpha _1 \ge \alpha _2\) and the innovation size is intermediate, e.g., \(\psi =2 \iff \alpha _2^{NN}=0.26\)

Full size image

3.2.2 With Renegotiation (Non-commitment Scenario)

Consider next the case with renegotiation from scratch. In this case, firms’ outside options change. When negative royalties are allowed, \(JEP\left( U-D_{2}\right)\) are then:

$$\begin{aligned} & JEP_R\left( U-D_{2}\right) = r_{1}q_{1}\left( r_{1},r_{2};s\psi ,s\psi \right) + F_1 + p q_{2}\left( r_{2},r_{1};s\psi ,s\psi \right) \nonumber \\ & \quad - \Pi _U^{ELneg} (\alpha _1) -\pi _{2}\left( 0,r^{ELneg};s,s\psi \right) . \end{aligned}$$
(15)

At the last stage, U and \(D_{2}\) maximize \(JEP_R\left( U-D_{2}\right)\) with respect to \(r_{2}\). The outside options are independent of \(r_{2}\), so that this maximization problem coincides with the previous case (without renegotiation), and \(r_{2}\left( r_{1}\right) =\frac{2r_{1}-s\psi }{4}\).

As for the joint profit of U and \(D_{1}\), they are:

$$\begin{aligned} & \pi _{U}+\pi _{1}= \sum _{i=1,2}p q_{i}\left( r_{i},r_{j}\right) -\pi _{2}\left( 0,r^{ELneg};s,s\psi \right) \nonumber \\ & \quad -\alpha _{2} JEP_R\left( U-D_{2}\right) . \end{aligned}$$
(16)

Anticipating the second stage, U and \(D_{1}\) maximize this objective computed in \(r_{2}\left( r_{1}\right)\) subject to the non-negativity of their gains from trade. Substituting \(r^{ELneg}=-s/4\) into the objective (16), the solution leads to the following. When negative royalties are allowed, CTD is implementable only for \(\alpha _2<1/2\) and the equilibrium contract is: \(r_{1}^{R}=\frac{s\psi }{2}\), \(r_{2}^{R}=0\).Footnote 19 Sequential bargaining with renegotiation results in the monopoly outcome, as at equilibrium the following holds:

$$\begin{aligned} q_1(r_1^R,r_2^R)=0; q_2(r_R^C,r_1^R)=1/2; PS^R=\frac{s \psi }{4}. \end{aligned}$$

The U innovator gets profit:

$$\begin{aligned} & \Pi _U^R (\alpha _1,\alpha _2)\nonumber \\ & \quad =\frac{s (9 + \alpha _1 (8 - 59 \alpha _2) + 8 \alpha _2 + 17 \alpha _1 \alpha _2 (\alpha _1 + \alpha _2) - 18 \psi (1 + \alpha _1 \alpha _2 (\alpha _1 + \alpha _2-3 )))}{72 (-1 + \alpha _1 \alpha _2)}. \end{aligned}$$
(17)

The efficiency of the bargaining is due to the fact that \(D_2\)’s outside option is not strategic anymore. In particular, note that the two D firms have now the same outside option: \(\pi _{i}\left( 0,r^{ELneg};s,s\psi \right) =s/16\). At equilibrium, they play a symmetric role in the negotiation: \(\Pi _U^{R}(\alpha _1,\alpha _2)=\Pi _U^{R}(\alpha _2,\alpha _1)\). Thus, the order of negotiation is not relevant, it is neutral.

When negative royalties are not allowed, although the firms’ outside options change,Footnote 20 nonexclusive licensing is implementable only for \(\alpha _2<1/2\), and the equilibrium contract stays the same as under negative royalties.

Examining the innovator’s equilibrium profit, we can conclude the following.

Lemma 4

For the case of nonexclusive licensing, in the non-commitment scenario, the innovator is indifferent with respect to the choice of the order of negotiation.

Optimal licensing in the non-commitment scenario Assume that, given the irrelevance of the order of negotiations, under nonexclusive licensing, U chooses to start negotiating with firm \(D_1\), that is \(CTD_1\). We find the following.

Proposition 5

Under renegotiation: (i) if \(\alpha _{2}<\frac{1}{2}\), \(CTD_1\) always prevails over \(EL_2\) and it leads to the monopoly outcome; (ii) if \(\alpha _{2}>\frac{1}{2}\), \(EL_2\) prevails over \(CTD_1\).

Proof

See the Appendix Sequential Bargaining with Renegotiation. \(\square\)

When introducing renegotiation, nonexclusive licensing prevails as long as it is implementable. Figure 3 illustrates this result for the particular but representative case of \(\psi =2\). In particular, for \(\alpha _2<1/2\), \(CTD_1\) prevails and leads to the monopoly outcome. The intuition for why we need a condition on \(\alpha _2\) to be low enough is similar to the no-renegotiation scenario: as under complete technology diffusion all of the surplus is produced by \(D_2\), for this contract to be profitable for all negotiators, \(D_2\)’s share of the pie cannot be too high.

Fig. 3
figure 3

Innovation diffusion with renegotiation, \(\alpha _1 \ge \alpha _2\), and \(\psi =2\)

Full size image

Non-negative fees and royalties As a final remark, we point out that optimal contracts, under nonexclusive licensing, entail either negative royalties and/or negative fees. This is shown in Table 1, which summarizes the optimal contracts for the case of an external patent holder.

Let us briefly discuss the case in which neither negative royalties nor negative fixed fees - side payments among the three negotiators - are allowed. The second-stage bargaining game (\(U-D_2\)) would imply again that \(r_2(r_1)=\frac{2 r_1-s \psi }{4}>0 \iff r_1> \frac{s \psi }{2}\). This leads to a quantity that is produced by \(D_2\) that is equal to 1/2 (which corresponds to the monopoly level of output) independently of \(r_1\). Clearly, given \(r_2(r_1)\) and \(q_2=1/2\), at the first stage the incentive is to induce firm \(D_1\) to produce a quantity that is as low as possible. Indeed, as we analyzed, given the possibility to use side payments, \(r_1\) is chosen such that \(D_1\) produces a nil quantity and it is compensated by a negative fee.

If negative fee is not allowed, we impose \(F_1 \ge 0\): Considering the binding constraint at equilibrium, we can set \(F_1=0\) and find \(r_1\) such that \(D_1\) is indifferent with respect to reaching the agreement with U. Note, however, that \(r_2(r_1)=\frac{2 r_1-s \psi }{4}\) also implies that the quantity that is produced by \(D_1\) is equal to \(q_1(r_1)=\frac{s \psi -2 r_1}{2}>0 \iff r_1< \frac{s \psi }{2}\). The incentives to reach an agreement on nonexclusive licensing would not be compatible: \(r_2(r_1), q_1(r_1) \ge 0\) cannot hold simultaneously. Consequently, exclusive licensing would prevail.

Table 1 Synthesis of optimal contracts in case of external patent holder
Full size table

4 Vertical Integration

Suppose now that the U producer and, say, firm \(D_{1}\) merge. We label this integration \(VI_1\). The vertically integrated firm is an internal patent holder and its profit consists of two parts: the profit from selling the new input to the rival \(D_{2}\) (if it decides to license) and the profit from selling the high quality good 1. The patent holder and \(D_{2}\) bargain over \(\left( r_{2},F_{2}\right)\). Their joint extra-profit is:

$$\begin{aligned} JEP(VI - D_{2} ) = & \pi _{{VI}} \left( {0,r_{2} ;s\psi ,s\psi } \right) + \pi _{2} \left( {r_{2} ,0;s\psi ,s\psi } \right) \\ - & \pi _{{VI}} \left( {0,0;s\psi ,s} \right) - \pi _{2} \left( {0,0;s,s\psi } \right). \\ \end{aligned}$$

With regard to the optimal royalty, if negative fees are allowed, the VI firm would implement the monopoly outcome by inducing the non-affiliate firm to produce a zero quantity and by compensating it through a fixed fee that is equal to its outside option plus a share \(\alpha _{2}\) of \(JEP(VI-D_{2})\). The optimal contract would be:

$$\begin{aligned} r^{VIn}=\frac{s\psi }{2};\;q_{2}\left( r^{VIn},0;s\psi ,s\psi \right) =0;F^{VIn}\left( r^{VIn}\right) <0. \end{aligned}$$

The non-affiliate firm then obtains \(\pi _{2}\left( \frac{s\psi }{2},0;s\psi ,s\psi \right) -F_{2}\left( \frac{s\psi }{2}\right) =\frac{1}{4} s\psi \frac{\left( 4\psi -3\right) \alpha _{2}+4\psi }{\left( 4\psi -1\right) ^{2}}\), and the VI entity obtains:

$$\begin{aligned} \Pi ^{VIn}=\frac{1}{4}s\psi \frac{\left( 3-4\psi \right) \alpha _{2}+\left( 16\psi ^{2}-12\psi +1\right) }{\left( 4\psi -1\right) ^{2}}. \end{aligned}$$
(18)

In many antitrust jurisdiction, such a use of negative fees would be illegal. In essence, the VI firm would be paying \(D_2\) to refrain from producing, in return for a share of VI’s monopoly profits.

If the VI firm is constrained to nonnegative fees, it will optimally let the non-affiliate firm to produce a positive quantity that is as low as possible: The licensee has to be compensated through a market profit not only for its outside option but also for a share of the joint extra-profit generated in the licensing process. Therefore, the optimal quantity \(q_{2}\left( r_{2}\right)\) is such that \(\pi _{2}\left( r_{2}\right) =\frac{ \psi ^{2}s}{\left( 4\psi -1\right) ^{2}}+\alpha _2 JEP(VI-D_{2})\).

Solving for \(r_{2}\), we find the following optimal contract:

$$\begin{aligned} r^{VI}\left( \alpha _2 \right) =s\psi \tfrac{\left( \left( \alpha _2 +4\right) \left( 4\psi -1\right) -3\sqrt{\left( \alpha _2 +4\right) \left( -3\alpha _2 +4\psi +4\alpha _2 \psi \right) }\right) }{2\left( 4\psi -1\right) \left( \alpha _2 +4\right) }; F^{VI}(r^{VI})=0. \end{aligned}$$

As expected \(r^{VI}\left( \alpha _2 \right)\) decreases with \(\alpha _2\). The equilibrium inventor’s profit and social welfare areFootnote 21:

$$\begin{aligned} & \Pi _{VI}\left( \alpha _2 \right) =s\psi \frac{5\left( 2\psi -1\right) ^{2}-\left( 4\psi ^{2}-7\psi +4\right) \left( 1-\alpha _2 \right) }{\left( 4\psi -1\right) ^{2}\left( 4+\alpha _2 \right) }-f; \end{aligned}$$
(19)
$$\begin{aligned} & SW_{VI}\left( \alpha _2 \right) =s\psi \tfrac{-3\left( 1-\alpha _2 \right) -64\psi +120\psi ^{2}+14\left( 1-\alpha _2 \right) \psi +9-24\left( 1-\alpha _2 \right) \psi ^{2}+\left( 4\psi -1\right) \sqrt{\left( 4\psi +4\alpha _2 \psi -3\alpha _2 \right) \left( \alpha _2 +4\right) }}{4\left( 4\psi -1\right) ^{2}\left( \alpha _2 +4\right) }. \end{aligned}$$
(20)

For the cases of both negative and non-negative fees, equilibrium profits from vertical integration—expressions 18 and 19—are positive; they increase in \(\psi\); and they decrease in \(\alpha _2\). This implies that U prefers to merge with the more powerful firm, which means that \(VI_1\) occurs. Moreover, for non-negative fees, social welfare decreases with the internal patent holder’s bargaining power: The lower is \(\alpha _2\), the more the monopoly outcome is approached.

Concerning the licensing incentives, as proved above, we conclude the following:

Proposition 6

For the case of non-negative fees, the internal patent holder always sells the innovation to the rival firm.

Indeed, if the VI firm does not license the innovation to \(D_2\), then \(D_2\)’s best option is simply to produce the low quality product. Consequently, for this non-licensing scenario, VI’s and \(D_2\)’s profits will be the outcome of a vertically differentiated Cournot game: the VI firm produces the high quality product and compete with \(D_2\) that produces the low quality product. Each firm gains the profit on its Cournot quantity.Footnote 22 The VI firm can do better than this by licensing the new input to \(D_2\) and by charging a sufficiently high per-unit royalty so that \(D_2\) is only “epsilon” better off than if it produces the low quality product. This way, the VI firm induces a milder competition in the market (the total quantity decreases and the producer surplus increases), and it gets the royalty revenues from \(D_2\)’s production and sales of the improved product, in addition to the profit on its quantity.Footnote 23

5 Profitability of VI

We can now assess the merger profitability by comparing the profit of the VI entity with the sum of the profit of the inventor and the potential merging firm under VS: an internal versus external patent holder.

Private profitability of VI

Proposition 7

(i) In the absence of renegotiation, \(VI_1\) is always privately profitable. (ii) In the presence of renegotiation, when \(\alpha _2 < 1/2\), \(VI_1\) is privately profitable as long as the bargaining power of the non - affiliate firm and the innovation size are large enough; when \(\alpha _2 > 1/2\), \(VI_1\) is privately profitable.

Proof

See Appendix Proof of Proposition 7. \(\square\)

In the absence of renegotiation and negative royalties, under VS, (Stackelberg-like) non exclusive licensing prevails (Fig. 1): Firm \(D_2\) has the role of the leader in terms of quantity produced. This explains why the merger between firms U and \(D_1\) yields a larger profit than under VS where \(D_1\) would be the follower.

With non-negative royalties, under VS, either exclusive licensing (\(EL_2\)) or non exclusive licensing (\(CTD_1\), monopoly) prevails (Fig. 2). VI is clearly profitable with respect to (constrained) exclusive licensing. As for the monopoly-like result under VS, recall that it is implemented for \(\alpha _2\) sufficiently low by letting firm \(D_2\) produce the monopoly outcome, this explains why the merger between firms U and \(D_1\) yields a larger profit than under VS where \(D_1\) produces a nil quality.

Consider finally the case of renegotiation. Under VS, for \(\alpha _2>1/2\), \(EL_2\) prevails (Fig. 3): The profitability of VI with respect to \(EL_2\) stays the same as it is not affected by renegotiation. For \(\alpha _2<1/2\), under VS the monopoly is implemented again by letting firm \(D_2\) produce the monopoly outcome. Under VI, instead, given the positive outside option of the non-affiliate \(D_{2}\), it is never possible to reach the monopoly outcome under VI unless the VI entity can compensate the non-affiliate via a negative fee.

In any case, VI is not always profitable. Consider the case in which, also under VI, negative fees are allowed so that the monopoly is implemented and the merger can reach its maximal profit. To assess the profitability of VI it is, then, relevant to compare the part of producer surplus that is to be given to \(D_2\) under VI and under VS: if this is larger under VI, then the merger between U and \(D_1\) is not profitable.

Consider the limiting case in which the bargaining power of the non-affiliate is very close to zero: this surplus coincides with the outside option in the event of disagreement. If negative royalties are allowed, this is equal to \(\pi _2(0,0;\;s, s \psi )=\frac{s \psi ^2}{(4 \psi -1)^2}\) under VI, and it is equal to \(\pi _2(0,r^{ELneg};\;s, s \psi )=\frac{s}{16}\) under VS: firm \(D_2\)’s outside option is larger under VI than under VS. Indeed, under VI the rival firm produces the high quality at zero marginal cost, whereas under VS, the rival firm is subsidized via negative royalty to produce the high quality. This explains why VI is not profitable.Footnote 24

As the bargaining power of \(D_2\) increases, however, the surplus to be given to this firm increases faster under VS than under VI, so that VI becomes relatively more profitable.

A similar reasoning applies when considering the effect of the innovation size: For low values of \(\psi\) the part of producer surplus to be given to \(D_2\) under VI is larger than under VS. As \(\psi\) increases, however, this surplus increases faster under VS than under VI, with the result that VI is profitable for large innovations. The idea is that as \(\psi\) and \(\alpha _2\) increase, the bargaining position of \(D_2\) becomes stronger under VS than under VI where the surplus has to be shared between two negotiators rather than three.

Social desirability of VI With respect to social profitability, under both VS and VI the monopoly can be implemented under certain conditions that were analyzed above. Clearly, as long as under vertical separation the monopoly outcome can be implemented, VI is not welfare improving.

For the social desirability comparison, we thus focus on the cases in which under VS the monopoly cannot be implemented and negative fixed fees are not allowed, so that under VI a quasi-monopoly arises. We find the following results.

Proposition 8

(i) In the absence of renegotiation, when negative royalties are allowed, VI is welfare improving whenever \(\psi\) is sufficiently high; when negative royalties are not allowed, VI is welfare improving whenever it replaces exclusive licensing: for \(\alpha _2 < \alpha _2^{NN}\).

(ii) In the presence of renegotiation, for \(\alpha _2 > 1/2\): when negative royalties are allowed, VI is welfare improving whenever \(\psi\) is sufficiently high; when negative royalties are not allowed, VI is always welfare-improving.

Proof

See Appendix Proof of Proposition 8. \(\square\)

Under VI a quasi-monopoly is implemented, and both firms produce the high quality product. Their quantities depend on \(\psi\) in such a way that the quantity that is produced by the non-affiliate is decreased, whereas the quantity that is produced by the VI entity is increased,Footnote 25 In the absence of renegotiation, when negative royalties are allowed, under VS nonexclusive licensing with a Stackelberg-like equilibrium takes place (see Fig. 1): Firm \(D_2\) produces a quantity equal to 1/2, whereas firm \(D_1\) produces a lower quantity that decreases in \(\psi\). Thus, in both cases of VI and VS a homogeneous high-quality duopoly is implemented.

The social profitability depends on the total quantities. For the limit case in which \(\psi\) is close to one (very small innovation), total quantity is larger under VS than under VI. As \(\psi\) increases, both total quantities decreaseFootnote 26; however total quantity under VI decreases less than total quantity under VS, so that for \(\psi\) high enough total quantity is larger under VI than under VS.

When instead negative royalties are not allowed, we focus on the case \(\alpha _2 < \alpha _2^{NN}\) where exclusive licensing takes place under VS: A vertically differentiated duopoly arises. Social welfare comparison shows that VI is more desirable than \(EL_2\) because it allows an increase in the average quality in the market that offsets the anti-competitive effect of VI.

In the presence of renegotiation, if we focus on \(\alpha _2 > 1/2\), exclusive licensing takes place under VS. If negative royalties are not allowed, VI is welfare-improving because, again, it allows an increase in the average quality in the market that offsets the anti-competitive effect of the merger. If instead, negative royalties are allowed, the comparison is ambiguous, as in this case, although the innovation is not completely diffused, downstream production is subsidized.

We can conclude that some profitable mergers are welfare-improving, as we point out in the following remark:

Remark 9

Regardless of the commitment scenario: When negative royalties are allowed, vertical integration is privately profitable and socially desirable whenever the innovation size is large enough; when negative royalties are not allowed, vertical integration is both privately profitable and socially desirable as long as it prevents exclusive licensing.

6 Conclusion

We have analyzed the incentives of an upstream input innovator to diffuse its product innovation in a duopoly market in the presence of bargaining. More precisely, we have developed a sequential bargaining game where the second negotiating firm’s outside option can be strategic. This occurs when the U innovator can commit to the first contract and negative royalties are allowed: in this case the bargaining is inefficient; however, nonexclusive licensing prevails over exclusive licensing. The outside option stops being strategic when negative royalties are not allowed as well as when renegotiation of the first contract can take place. In this case, sequential bargaining leads to the monopoly outcome. This implies that the bargaining is efficient; however, it is not always implementable so that in some cases the innovation is not completely diffused: exclusive licensing prevails over nonexclusive licensing.

We have also evaluated the profitability for this upstream firm to enter the market via vertical integration, endogenizing the patent holder’s choice to stay outside or inside the market. We find that the upstream innovator prefers merging with the more powerful firm and the vertically integrated entity always sells the new input to the rival non-affiliate. This implies a positive quality improving effect of vertical integration as compared with vertical separation when exclusive licensing occurs.