Price Competition in a Vertizontally Differentiated Duopoly

Abstract

This paper develops a price competition duopoly model in which products are both horizontally and vertically differentiated. Firms each offer a standard and a premium product to buyers—some of whom are brand loyal. We establish the existence of a unique and symmetric competitive pricing equilibrium. Equilibrium prices are increasing in the degree of horizontal differentiation and the number of brand-loyal customers. The equilibrium price of the standard (premium) good is decreasing (increasing) in the quality difference and profits can increase in costs when this difference is large enough. If the pricing decision is taken at the product (division) level, then there is again a unique (and symmetric) competitive pricing equilibrium. Equilibrium prices and profits are lower than in the centralized case and demand for the standard product is higher when the quality difference is sufficiently large. Welfare is unambiguously lower with decentralized pricing.

1 Introduction

In the period mid 2017 until mid 2018, U.S. citizens spent over $5 billion on dry dog food.¹ The table below lists the four leading dry dog food brands in the period mid 2017 until mid 2018.² These four brands are produced by the two major firms in the dog food market: Nestlé (39% market share) and Mars (24% market share). The last column of the table presents the price per pound at Walmart for a large-sized bag.³ Notice that both manufacturers offer a ‘standard’ and a ‘premium’ brand and that segment prices are (approximately) the same.

Rank	Brand	Dollar sales (million)	Manufacturer	$/lb
1	Pedigree	$603	Mars, Inc.	0.52
2	Purina dog chow	$457	Nestlé Purina Petcare Co.	0.45
3	Purina one smartblend	$346	Nestlé Purina Petcare Co.	1.08
4	Iams proactive health	$265	Mars, Inc.	1.08

There are many industries that consist of a few firms that compete in multiple market segments that are characterized by product quality.⁴ A critical feature of such quality-segmented markets is that competition has both a horizontal and a vertical dimension. For instance, if a firm raises the price of its premium product, then it is likely to ‘lose’ customers to rival brands as well as to its own lower quality division(s). Likewise, if a firm cuts its premium product price, then ceteris paribus it steals customers from comparable quality competitors while cannibalizing the sales of its other items. The fact that multi-product firms are partly in competition with themselves makes the design of an optimal pricing policy far from trivial.

The purpose of this paper is to study strategic pricing by sellers that are competing ‘head-to-head’ in several quality segments simultaneously. Toward that end, we develop a price-setting duopoly model of vertizontal product differentiation in which firms offer both a standard and a premium product. Demand for these product types comes from two different sorts of customers: those who are brand-anchored; and those who are quality-anchored. Brand-anchored buyers choose only between the standard and premium product of their preferred supplier; by contrast, quality-anchored buyers have a preference for a particular quality level and choose between brands only.⁵ The model contains no less than nine distinct demand- and supply-side parameters, which enables us to study separately the impact of these ‘horizontal’ and ‘vertical’ forces on firms’ pricing decisions.

To summarize some of our main findings: We establish the existence of a unique (and symmetric) competitive pricing equilibrium and perform a series of comparative statics exercises on this equilibrium outcome. With regard to the ‘horizontal forces’, we find that equilibrium prices are increasing in the extent of brand differentiation and decreasing in the number of quality-anchored buyers. With regard to the ‘vertical forces’, we establish that equilibrium prices are increasing in the number of brand-anchored buyers and show that the price of the standard (premium) product is decreasing (increasing) in the quality difference. Interestingly, we find that equilibrium profits may rise when there is a segment-wide increase in production costs.

We then use these results as a basis of comparison to explore the effect of decentralized pricing. If pricing decisions are taken at the product (division) level, then there is again a unique (and symmetric) competitive pricing equilibrium. The equilibrium outcome is such that both prices and profits are lower than in the centralized case. If the quality difference between the standard and premium product is substantial and the costs of producing additional quality are sufficiently small, then a switch from centralized to decentralized pricing leads to an increase of the standard good’s sales. By contrast, the premium product’s market share increases when the quality difference is limited and the marginal costs of producing extra quality are high enough. Last, we find that societal welfare is unambiguously lower with decentralized pricing.

The next section provides a brief literature review. Section 3 introduces the vertizontal differentiation model. The symmetric version of this model is analyzed in Sect. 4. Sections 5 and 6 consider the impact of asymmetry in consumer preferences, unit costs and organizational structure. Section 7 concludes. All proofs are relegated to the Appendix.

2 Literature Review

This research is at the intersection of three strands of literature: First, it is naturally related to other works that consider vertizontal product differentiation. Vertizontal differentiation models have been employed to study a variety of economic questions: Di Comite et al. (2014), for instance, introduces a quadratic representative consumer model with vertizontal preferences to assess empirically firm performance in export markets. Building on Neven and Thisse (1990); Ribeiro (2015) analyzes price competition between two platforms (e.g., media outlets, clubs) that are vertizontally differentiated. Li and Peeters (2017) examine a vertizontal differentiation setting to study strategic quality information disclosure. None of this research considers multi-product competition, however.

Second, our work contributes to the growing literature on strategic firm behavior in multi-product oligopolies. Nocke and Schutz (2018) provides a framework to study multi-product pricing when these goods are horizontally differentiated. With regard to quality differentiation, Champsaur and Rochet (1989) examines what range of qualities profit-maximizing duopolists prefer to offer. More recently, Jing and Zhang (2011) and Johnson and Myatt (2003, 2006, 2015) also study competition among firms that sell multiple quality-differentiated products to address questions that are related to price promotions, entry, and product-line configurations. These works consider heterogeneity either in taste or in quality—but not both.

Perhaps closest to our work are Gilbert and Matutes (1993) and Desai (2001); both articles analyze strategic product line choices by multi-product firms in a vertizontally differentiated spatial setting. A key difference for our model is the presence of brand-loyal customers. Furthermore, our focus is on strategic pricing with vertizontal product differentiation and on how this pricing is affected by demand and supply side factors, such as consumer preferences, degree of differentiation, and production costs.

Third, and last, our analysis sheds light on the potential impact of delegating pricing authority. Stephenson et al. (1979), for example, use a sample of medical supplies and equipment sellers to compare central pricing authority with delegated pricing authority to the sales force. Among other things, they establish that gross margins and return on assets are lower with decentralized pricing. As argued by Lal (1986), however, delegating pricing responsibility to salespersons can be profitable when they have superior information about the selling environment. Frenzen et al. (2010) provide some empirical support for this. They establish a positive relation between pricing authority delegation and firm performance and this effect is strengthened in the presence of information asymmetry and market-related uncertainty.

More generally, there is an extensive literature that addresses the question of who should be granted pricing authority within an organization. Major contributions include Moorthy (1988), Bhardwaj (2001), Joseph (2001), McGuire and Staelin (2008), and Homburg et al. (2012), amongst many others. This literature presents conditions under which (de-)centralized pricing is optimal from a company’s perspective.

We compare the situation where price decisions are taken at the firm level (centralized pricing) with the situation where price decisions are taken at the product-quality-type level (decentralized pricing). Within our vertizontal differentiation setting, prices and profits are higher under centralized pricing. A main difference with the existing literature on the locus of pricing authority is that we consider the impact of (de-)centralized pricing on the demand for quality and welfare.

3 A Model of Vertizontal Product Differentiation

Consider a simultaneous-move price-setting duopoly with a low- (standard) and a high- (premium) quality market segment. Along the lines of Hotelling (1929), let both of these submarkets be represented by a unit interval. Quality is homogeneous within each segment and is indicated by the quality indices $\beta >0$ and $\beta +\delta >0$ for the standard and the premium product, respectively. The additional (perceived) quality of the premium product is therefore given by $\delta >0$. Products are positioned at the extremes of their respective segment and, without loss of generality, we assume that firm 1 is located at ‘0’ and firm 2 is located at ‘1’.

Firms’ cost structures are identical, and the low- and the high-quality varieties are respectively produced at constant marginal costs $c_{\ell }$ and $c_h$, with $c_h>c_{\ell }\ge 0$. It is further assumed that $\delta >c_h-c_{\ell }$: The difference in product quality exceeds the additional costs of producing the premium product. Both the quality indices and cost parameters are exogenously given.

The demand side comprises two types of consumers: There is a mass of $2\mu >0$ buyers who are brand-anchored and equally divided between both firms. These customers choose between buying a low- and a high-quality item from a particular brand: firm 1 or firm 2. They are characterized by a taste parameter y, which is uniformly distributed on the unit interval [0, 1] and which reflects the willingness to pay for extra quality. Thus, a consumer at the lower bound does not derive utility from more quality, whereas it is maximally valued at the upper extreme.

The remaining consumers are quality-anchored: They have a strict preference for a given quality and only choose between buying from firm 1 or firm 2. Both the standard and the premium quality-anchored buyers are uniformly distributed on the unit interval [0, 1] with mass $\mu _{\ell }>0$ and $\mu _h>0$, respectively. A customer who is ‘located’ at $x_j$ experiences a disutility of $\tau _j\cdot x_j$ when buying from firm 1 and $\tau _j\cdot (1-x_j)$ when buying from firm 2, where $\tau _j>0$ for $j=\ell ,h$.⁶

Our categorisation of customers is in part motivated by some recent findings in the consumer search literature. For example, it has been argued that consumers only search a small part of the attribute space and that state-dependence in search behavior is strong (Kim et al., 2011; Bronnenberg et al., 2016). This limits consumers’ consideration set (Mehta et al., 2003; De los Santos et al., 2012) and makes for insufficient comparisons across products and services (Simonson et al., 2013; Sela & LeBoeuf, 2017). With regard to the presence of quality-anchored buyers, note that this may partly result from differences in income. Indeed, an alternative interpretation is that consumers have the same valuation for quality, but different spending budgets (Gabszewicz & Thisse, 1979; Shaked & Sutton, 1982; Klumpp & Su, 2019).

As is well-known, in these types of spatial settings one can distinguish three cases depending on the set prices: (i) local monopolies; (ii) single monopoly; and (iii) competition.⁷ In the following, we confine ourselves to situations in which the products compete. Case (i) is ruled out by assuming that all consumers buy the good—the market is ‘covered’—which effectively requires the quality index $\beta$ to be sufficiently high. Specifically, each customer is assumed to purchase one unit of the product so that total market demand is given by $2\mu +\mu _{\ell }+\mu _h>0$.

To exclude Case (ii), we employ the notion of ‘social equilibrium’ as introduced by Debreu (1952).⁸ The distinctive feature of this concept is that the sets of feasible strategies depend on the strategies that are chosen by others. Within the context of our model this means that a firm’s feasible prices are effectively determined by its rival’s price. In particular, for some given segment price of the competitor, a seller cannot set its price so low that it gains the complete segment. Likewise, it cannot pick a price so high that it loses the entire segment. Price differences are thus restricted in such a way that all product types have a positive market share.

Let us now derive demand for each product type. Consider a brand i-anchored buyer ‘located’ at $y_i$. This consumer is indifferent between buying the low-quality and buying the high-quality variety when:

$$\begin{aligned} \textstyle \beta +\delta y_i-p_{ih}=\beta -p_{i\ell } \quad \Longleftrightarrow \quad y_i=\frac{p_{ih}-p_{i\ell }}{\delta }, \end{aligned}$$

where $p_{ih}$ and $p_{i\ell }$ are the prices of firm i’s high- and low-quality product, respectively. Note that the degree to which the premium product is valued more than the standard product is determined by the combination of the ‘objective’ quality measure $\delta$ and the ‘subjective’ quality measure $y_i$.

As an illustrative example, consider the choice between buying a software package with and without a supporting service package. At equal prices, virtually everyone would value the bundle more than the stand-alone software package. This difference in quality is captured by the parameter $\delta$. Yet, some customers may have poor computer skills and highly appreciate the additional support, whereas others may be IT experts who require little to no help. This heterogeneity in the ‘valuation of quality’ is captured by the parameter $y_i$.

Similarly, a quality j-anchored customer ‘located’ at $x_j$ in the segment $j=\ell ,h$ is indifferent between buying from firm 1 and buying from firm 2 when:

$$\begin{aligned} \textstyle p_{1j}+\tau _jx_j=p_{2j}+\tau _j(1-x_j) \quad \Longleftrightarrow \quad x_j=\frac{p_{2j}-p_{1j}+\tau _j}{2\tau _j}. \end{aligned}$$

Taken together, this gives the following demand for the firms’ high- and low-quality product:

$$\begin{aligned} \begin{array}{ll} d_{1h}=\mu \cdot (1-{\widehat{y}}_1)+\mu _h\cdot {\widehat{x}}_h &{} d_{2h}=\mu \cdot (1- {\widehat{y}}_2)+\mu _h\cdot (1-{\widehat{x}}_h) \\ *[0.5em] d_{1\ell }=\mu \cdot {\widehat{y}}_1+\mu _{\ell }\cdot {\widehat{x}}_{\ell } &{} d_{2\ell }=\mu \cdot {\widehat{y}}_2+\mu _{\ell }\cdot (1-{\widehat{x}}_{\ell }), \end{array} \end{aligned}$$

where ${\widehat{y}}_i\equiv \max \big \{\min \big \{\frac{p_{ih}-p_{i\ell }}{\delta },1\big \},0\big \}$, $i=1,2$ and ${\widehat{x}}_j\equiv \max \big \{\min \big \{\frac{p_{2j}-p_{1j}+\tau _j}{2\tau _j},1\big \},0\big \}$, $j=\ell ,h$.

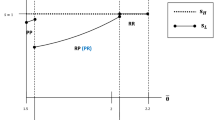
Figure 1 provides a graphical illustration of this model.

Fig. 1

A stylized illustration of a vertizontally differentiated duopoly with brand-anchored consumers who are located on the dashed vertical segments and quality-anchored consumers who are located on the solid horizontal segments

In the following, we focus on cases in which each product type is bought by both brand- and quality-anchored buyers: ${\widehat{x}}_j\in (0,1)$, $j=\ell ,h$; and ${\widehat{y}}_i\in (0,1)$, $i=1,2$ (see Fig. 1). These conditions depend on price differences and are satisfied as long as the differences are not too large. Given that the competitor charges $p_{kh}$ and $p_{k\ell }$, the condition ${\widehat{x}}_j\in (0,1)$ holds when firm i picks prices $p_{ij}\in (p_{kj}-\tau _j,p_{kj}+\tau _j)$. Similarly, ${\widehat{y}}_i\in (0,1)$ requires that $p_{i\ell }$ and $p_{ih}$ are chosen such that $0<p_{ih}-p_{i\ell }<\delta$. Note, however, that for the latter both prices are selected by the same seller. To ensure that ${\widehat{y}}_i$ remains in the interior, we impose the following assumption which effectively provides an upper bound on the difference between competition intensity in both quality segments.⁹

Assumption 1

$-(c_h-c_{\ell })<\tau _h-\tau _{\ell }<\delta -(c_h-c_{\ell })$.

In the following analysis, we solve for a Nash equilibrium of this game—which we refer to as competitive pricing equilibrium.

4 Equilibrium Pricing and Analysis

In this section, we explore the nature of price competition between the two firms. Under the assumption that both simultaneously pick prices from their (relative) strategy sets as specified above, firm 1 chooses $p_{1\ell }$ and $p_{1h}$ to maximize

$$\begin{aligned} \pi _1(p_{1\ell },p_{1h},p_{2\ell },p_{2h})=\, & {} (p_{1\ell }-c_{\ell })\cdot d_{1\ell } + (p_{1h}-c_h)\cdot d_{1h} \\=\, & {} \textstyle (p_{1\ell }-c_{\ell })\cdot \big (\mu \cdot (\frac{ p_{1h}-p_{1\ell }}{\delta })+\mu _{\ell }\cdot (\frac{p_{2\ell }-p_{1\ell }+\tau _{ \ell }}{2\tau _{\ell }})\big ) \\{} & {} \qquad \textstyle + (p_{1h}-c_h)\cdot \big (\mu \cdot (1-\frac{ p_{1h}-p_{1\ell }}{\delta })+\mu _h\cdot (\frac{p_{2h}-p_{1h}+\tau _h}{2\tau _h}) \big ), \end{aligned}$$

whereas firm 2 selects $p_{2\ell }$ and $p_{2h}$ to maximize

$$\begin{aligned} \pi _2(p_{1\ell },p_{1h},p_{2\ell },p_{2h})=\, & {} (p_{2\ell }-c_{\ell })\cdot d_{2\ell } + (p_{2h}-c_h)\cdot d_{2h} \\=\, & {} \textstyle (p_{2\ell }-c_{\ell })\cdot \big (\mu \cdot (\frac{ p_{2h}-p_{2\ell }}{\delta })+\mu _{\ell }\cdot (1-\frac{p_{2\ell }-p_{1\ell }+ \tau _{\ell }}{2\tau _{\ell }})\big ) \\{} & {} \qquad \textstyle + (p_{2h}-c_h)\cdot \big (\mu \cdot (1-\frac{ p_{2h}-p_{2\ell }}{\delta })+\mu _h\cdot (1-\frac{p_{2h}-p_{1h}+\tau _h}{2\tau _h}) \big ). \end{aligned}$$

The next result shows that there is a unique competitive pricing equilibrium and that this equilibrium is symmetric. Moreover, the equilibrium price of the premium product exceeds that of the standard product:

Proposition 1

Under Assumption 1, there is a unique competitive pricing equilibrium. In this equilibrium, firms set prices symmetrically at:

$$\begin{aligned} \textstyle p_{\ell }^* = c_{\ell }+\tau _{\ell }+\frac{2\tau _{\ell }\mu }{ 4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h} [(c_h-c_{\ell })\mu _h+2(\tau _h-\tau _{\ell })\mu _h+4\tau _h\mu ] \end{aligned}$$

and

$$\begin{aligned} \textstyle p_h^* = c_h+\tau _h+\frac{2\tau _h\mu }{4\mu (\tau _{\ell }\mu _h+\tau _h \mu _{\ell })+\delta \mu _{\ell }\mu _h}[\delta \mu _{\ell }-(c_h-c_{\ell })\mu _{ \ell }-2(\tau _h-\tau _{\ell })\mu _{\ell }+4\tau _{\ell }\mu ]. \end{aligned}$$

Furthermore, $0<p_h^*-p_{\ell }^*<\delta$.¹⁰

The way in which equilibrium prices are presented here is reminiscent of the equilibrium outcome in a standard version of Hotelling’s model of horizontal product differentiation: $p_j^*=c_j+\tau _j$, $j=\ell ,h$. In fact, notice that both prices coincide when the number of brand-anchored buyers becomes negligible: $\mu \downarrow 0$.

Even though one might a priori expect firms to set higher prices in the presence of brand-anchored buyers, Proposition 1 reveals that vertizontal equilibrium prices may actually be lower than those in the corresponding horizontal version without brand-loyal customers: when $\mu \downarrow 0$. The price of the standard product is, for example, lower than $c_{\ell }+\tau _{\ell }$ when there is severe price competition in the premium segment ($\tau _h\downarrow 0$) and relatively low competitive pressure in the other submarket ($\tau _{\ell }\uparrow c_h-c_{\ell }$).

Likewise, the premium price is lower than $c_h+\tau _h$ when there is strong price competition in the standard-quality product market ($\tau _{\ell }\downarrow 0$) and relatively low competitive pressure in the premium segment ($\tau _h\uparrow \delta -(c_h-c_{\ell })$). Intense price competition in one segment therefore puts downward pressure on prices in the adjacent segment and this ‘negative vertical price effect’ can dominate the ‘positive horizontal price effect’: The presence of brand-anchored buyers can lead to more competitive prices in the segment where price competition is otherwise less severe.

We now proceed by studying comparative statics of the equilibrium prices. The next proposition shows that both prices are increasing in both unit production costs:

Proposition 2

Under Assumption 1, the equilibrium prices $p_{\ell }^*$ and $p_h^*$ are increasing in the unit production costs $c_{\ell }$ and $c_h$.

The firms’ standard and premium prices are naturally increasing in their own production costs. Demand for the adjacent quality then rises with a subsequent price increase in that segment. It can, moreover, be shown that the direct effect dominates the indirect effect, so that an increase in $c_h$ ceteris paribus boosts low-quality product sales. An increase in $c_{\ell }$ likewise leads to a rising premium product market share, all else equal.

The impact on prices of a change in the (perceived) quality difference ($\delta$), horizontal competitive pressure ($\tau _{\ell }$ and $\tau _h$), and the number of brand- and quality-anchored buyers ($\mu$, $\mu _{\ell }$ and $\mu _h$) is less clear. To explore this in more detail, we impose the following condition:

Assumption 2

$-\frac{c_h-c_{\ell }}{2}<\tau _h-\tau _{\ell }<\frac{\delta -(c_h-c_{\ell })}{2}$.

This assumption is directly comparable to Assumption 1 and restricts the range within which the horizontal differentiation parameters are allowed to vary.

Let us start by exploring the effect of changes in the horizontal dimension of the model. The following result gives the price impact of changes in the horizontal differentiation parameters and the number of low- and high-quality-anchored consumers.

Proposition 3

Under Assumption 2, the equilibrium prices $p_{\ell }^*$ and $p_h^*$ are increasing in the horizontal differentiation parameters $\tau _{\ell }$ and $\tau _h$ and decreasing in the number of low and high quality-anchored buyers $\mu _{\ell }$ and $\mu _h$.¹¹

An increase in the horizontal differentiation parameter $\tau _j$, $j=\ell ,h$, leads ceteris paribus to an increase of prices in segment j. This, in turn, generates more demand in the other segment with a subsequent price increase.

With regard to the number of quality-anchored buyers, more customers in, say, the premium segment intensifies competition in that part of the market with lower premium prices resulting. More brand-anchored buyers are therefore willing to switch to the high-quality product, which in turn makes it less costly to cut prices in the lower segment. As before, the direct effect dominates the indirect effect so that an increase in the number of high (low) quality-anchored buyers results in more high (low) quality product sales. Notice that it is the presence of brand-anchored consumers that drives this effect: Absent a brand-loyal customer base, equilibrium prices would be independent of the mass of quality-oriented consumers.

Next, let us turn to the vertical sphere. The following result shows how the equilibrium prices are affected by changes in the number of brand-anchored customers and the quality difference:

Proposition 4

Under Assumption 2, the equilibrium prices $p_{\ell }^*$ and $p_h^*$ are increasing in the number of brand-anchored consumers $\mu$. Furthermore, $p_{\ell }^*$ is decreasing and $p_h^*$ is increasing in the quality difference $\delta$.

A growing number of brand-anchored buyers naturally enhances the incentive to exploit their loyalty through raising prices.

The price effect of a change in quality difference is more subtle. As one would expect, an immediate effect of an increase in $\delta$ is that more buyers prefer the high-quality product. The resulting premium price rise does not fully offset this effect, which is partly due to the presence of competition in the high-quality segment. The subsequent loss in brand-anchored consumers who buy the standard product makes it less costly to cut the standard good price and steal some business in the low-quality segment. Overall, however, premium product sales are increasing in the quality difference.

Let us now turn to equilibrium profits: Profits are not trivial to analyze within the current framework, which is particularly due to the richness in the parameters that describe the demand side. By imposing symmetry across quality segments, however, we can establish the following supply-side effect.

Proposition 5

Assume $\mu _h=\mu _{\ell }$ and $\tau _h=\tau _{\ell }$.

• (i) If $\delta >2(c_h-c_{\ell })$, then equilibrium profits $\pi _1^*$ and $\pi _2^*$ are increasing in $c_{\ell }$ and decreasing in $c_h$.

• (ii) If $\delta <2(c_h-c_{\ell })$, then equilibrium profits $\pi _1^*$ and $\pi _2^*$ are decreasing in $c_{\ell }$ and increasing in $c_h$.

This result reveals that equilibrium profits can decrease, but may also increase in unit production costs. If the quality difference between the standard and premium product is sufficiently large, then profits are decreasing in $c_{h}$ and increasing in $c_{\ell }$. The reason is as follows: If $\delta >2(c_{h}-c_{\ell })$, then the majority of brand-anchored buyers opts for the premium product: ${\widehat{y}}_{i}^{*}=\frac{p_{ih}^{*}-p_{i\ell }^{*}}{\delta }<\frac{1}{2}$ is relatively low.¹² The reduced price-cost margin $p_{ih}^{*}-c_{h}$ would therefore result in relatively large losses. This negative direct effect is only partly offset by the positive indirect effect: the rise in the price of the standard good. The latter effect is smaller since only a modest part of the brand-anchored buyers prefers the low-quality product when the quality difference is high.

In a similar fashion, equilibrium profits increase in $c_{\ell }$. The direct effect is again negative, but relatively small since few brand-anchored consumers choose the standard good. By contrast, the positive indirect effect that comes from the increase in the premium price is comparably big because of the large share of brand-anchored buyers that picks the high-quality product. The combined effect is positive when $\delta$ is sufficiently high. A similar logic applies when the difference in quality is sufficiently low, meaning that the majority of brand-anchored buyers opts for the standard good: ${\widehat{y}}_{i}^{*}=\frac{p_{ih}^{*}-p_{i\ell }^{*}}{\delta }>\frac{1}{2}$ is relatively high. In that case, profits are decreasing in $c_{\ell }$ and increasing in $c_{h}$.

In sum, firms benefit from a segment-wide cost decrease in the most popular submarket. Strikingly, however, they also benefit from a segment-wide cost increase in the least popular submarket. The negative direct effect of the cost increase is more than compensated for by the resulting price increase in the adjacent popular segment.¹³

5 Asymmetries

In this section and in Sect. 6, we consider price competition in the vertizontally differentiated duopoly when there is some asymmetry between the sellers. We examine two types of asymmetries: asymmetry in demand- and supply-side parameters; and (in Sect. 6) asymmetry in organizational structure. To maintain tractability, it is assumed throughout this section that $\mu _{h}=\mu _{\ell }$, $\tau _{h}=\tau _{\ell }$, and $c_{\ell }=0$.¹⁴

5.1 Demand- and Supply-side Parameters

We discuss two possible demand-side asymmetries that relate to consumer preferences: (1) the number of brand-anchored consumers in the vertical segments; and (2) the product taste of quality-anchored consumers in the horizontal segments. We also consider a possible supply-side asymmetry: unit cost of producing the premium product.

To begin, suppose there is a difference in brand-loyal customer bases. In that case, we find that the firm with more brand-anchored buyers ceteris paribus charges a higher price for both the standard and the premium product. Being the higher-priced firm, this seller consequently captures a smaller share of the quality-anchored buyers. However, the implied lower market share is more than compensated for by the higher mark-up so that the firm with the larger brand-loyal customer base is the one making more profit.

Let us now turn to the possibility that quality-oriented buyers have different tastes for both brands. Specifically, it is assumed that $\tau _{\ell }$ ($=\tau _{h}$) are different for the two firms. In this case, we find that the favorite firm—the seller with the lower $\tau$—sets the higher price for both product varieties. Taking a comparative statics perspective, this firm is able to harvest its brand-loyal customer base without losing too much share in the two quality segments. In fact, the equilibrium is such that it still has the higher market share in each horizontal submarket. Since there are no differences in the vertical segments, this implies that the firm with the lower $\tau$ earns the highest profits.

Third, suppose that one of the sellers faces higher costs when producing its premium product. This firm then charges a higher price for its high-quality good, which implies a smaller market share in the premium segment. Interestingly, this high-cost supplier becomes the lower-priced firm in the standard segment. The implied larger market share in the low-quality segment does not make up for its disadvantageous position in the premium segment, however. Overall, therefore, it is the low-cost supplier that makes more profit.

6 Organizational Structure

A different type of asymmetry that can affect the competitive pricing equilibrium concerns the allocation of pricing authority. In the preceding analysis, we have assumed pricing decisions to be taken at the firm level. Yet, and as already touched upon in Sect. 2, companies sometimes choose to delegate such decisions to lower-level management or sales departments. Within the context of our model, decentralized pricing means that pricing decisions are taken at the product quality type level.

The issue of (de-)centralized pricing has been addressed by McGuire and Staelin (2008) within the context of a vertical production chain. Amongst others, they show that decentralized decision-making is a Nash equilibrium when products are sufficiently close substitutes. Moorthy (1988) offers conditions under which (de-)centralized pricing emerges as an equilibrium. Bhardwaj (2001) extends these analyses by explicitly taking account of sales agents’ effort. He finds that firms prefer centralized pricing when there is sufficiently intense effort competition.

Under the parameter restrictions that we impose to maintain tractability—$\mu _{h}=\mu _{\ell }$, $\tau _{h}=\tau _{\ell }$, and $c_{\ell }=0$—we find that centralized pricing is an equilibrium and decentralized pricing is not.¹⁵ Yet, when firms adopt a different organizational structure, it is the seller that delegates pricing authority that makes more profits. If we take a Darwinian dynamic perspective as in Alchian (1950) and Vega-Redondo (1997), this suggest that decentralized pricing may become the dominant organizational mode. In the next section, we explore the possibility that both sellers delegate pricing decisions to the product division level in more detail.

6.1 Centralized Versus Decentralized Pricing

We now direct attention to the case in which both firms have delegated pricing authority and compare this with the centralized pricing results presented in Sect. 4. Since prices are determined at the product quality type level, these quality divisions effectively operate as distinct firms: With decentralized pricing there is competition among four rather than two vertizontally differentiated market entities. In what follows, we show that with decentralized pricing: (i) consumers are better off; (ii) firms are worse off; and (iii) society as a whole is worse off. Moreover, the market share of the standard product is shown to increase (decrease) with decentralized pricing when the marginal costs of quality is sufficiently low (high).

The next result is directly comparable to Proposition 1 and shows that there is again a unique (and symmetric) competitive pricing equilibrium when prices are set at the product type level. Akin to the centralized pricing case, the equilibrium price of the premium product exceeds that of the standard good.

Proposition 6

Under Assumption 1 and $\delta \ge \max \{\tau _{\ell },\tau _h\}$, there is a unique competitive pricing equilibrium. In this equilibrium, firms set prices symmetrically at:

$$\begin{aligned} \textstyle p_{\ell }^{\circ } = c_{\ell }+\frac{(2\tau _h\mu +\delta \mu _h)(\delta \mu _{\ell }+2\mu (c_h-c_{\ell }))+2\delta \tau _h\mu (\mu _{\ell }+\mu _h+2\mu )}{ (4\tau _{\ell }\mu +\delta \mu _{\ell })(4\tau _h\mu +\delta \mu _h)-4\tau _{\ell } \tau _h\mu ^2}\tau _{\ell } \end{aligned}$$

and

$$\begin{aligned} \textstyle p_h^{\circ } = c_h+\frac{(2\tau _{\ell }\mu +\delta \mu _{\ell })(\delta \mu _h+2\mu [\delta -(c_h-c_{\ell })])+2\delta \tau _{\ell }\mu (\mu _{\ell }+\mu _h+2 \mu )}{(4\tau _{\ell }\mu +\delta \mu _{\ell })(4\tau _h\mu +\delta \mu _h)-4\tau _{ \ell }\tau _h\mu ^2}\tau _h. \end{aligned}$$

Furthermore, $0<p_h^{\circ }-p_{\ell }^{\circ }<\delta$.

To avoid complex expressions, but without renouncing any factor that is crucial to the understanding of the mechanic forces when comparing decentralized pricing with centralized pricing in the context of the vertizontally differentiated market, we restrict the parameters to $\mu _h=\mu _{\ell }=\mu =1$ and $\tau _h=\tau _{\ell }$ and assume $\delta \ge \max \{\tau _{\ell },\tau _h\}$ (such that ${\widehat{y}}^{\circ }\in (0,1)$). Doing so, we obtain the following result.

Proposition 7

Prices and profits are lower under decentralized pricing than under centralized pricing. Moreover,

• (i) If $\delta >2(c_h-c_{\ell })$, then there is greater demand for low quality under decentralized pricing than under centralized pricing.

• (ii) If $\delta <2(c_h-c_{\ell })$, then there is greater demand for high quality under decentralized pricing than under centralized pricing.

This proposition shows that producer surplus—which is defined as the sum of profits—is lower when pricing authority is delegated. This is a direct consequence of increased competition. By contrast, consumers benefit from decentralized pricing. Indeed, each non-switching customer benefits from a lower price, and those who do switch benefit even more.

Notice that whether demand shifts from the standard to the premium segment or vice versa depends on the marginal cost of quality. If $\delta >2(c_{h}-c_{\ell })$, then the amount of premium products that are sold under centralized pricing exceeds the amount of standard products that are sold. A transition to decentralized pricing results in a price reduction for all products. However, since the premium product has the bigger market share, the corresponding marginal revenue is lower: It is ceteris paribus more costly to reduce the price of the premium product than that of the standard good. Delegating pricing authority in this case consequently leads to an increase in the equilibrium price difference, which implies an increase in the standard good’s market share (Proposition 7(i)). As Proposition 7(ii) shows, the opposite occurs when $\delta <2(c_{h}-c_{\ell })$.

To determine the net welfare effect, first note that the market is covered under both centralized and decentralized pricing. As long as customers do not switch between product types, therefore, a change in the locus of pricing authority would only cause a redistribution of welfare. Consequently, any change in total surplus should come from those who switch between the low- and high-quality product type. Proposition 7(i) shows that if $\delta >2(c_{h}-c_{\ell })$, then for each brand there is an interval Y of brand-anchored buyers who switch from the high- to the low-quality product. Likewise, Proposition 7(ii) shows that when $\delta <2(c_{h}-c_{\ell })$, there is an interval Y of brand-anchored buyers who switch in the opposite direction.

These switching consumers $y\in Y$ create a welfare gain (loss) by a reduction (increase) in $c_{h}-c_{\ell }$ and a welfare loss (gain) of $\delta y$. Aggregating these differences over all switching consumers gives the change in overall welfare,

$$\begin{aligned} 2\int _{Y}\delta y-(c_{h}-c_{\ell })\>\text {d}y, \end{aligned}$$

which leads to the following conclusion:

Proposition 8

Decentralized pricing unambiguously yields a welfare loss.

The logic behind this result is as follows: Suppose that $\delta >2(c_{h}-c_{\ell })$, so that the market share of the standard product increases when moving from a centralized to a decentralized pricing system (Proposition 7(i)). Since part of the premium products are replaced with standard products, there is a saving in production costs. This has a positive effect on societal welfare. There is, however, a counter effect: First, the switching customers lose the benefit of having a higher-quality product $\delta$; this is an effect that is relatively substantial in this case. Second, those who switch have a relatively high valuation for quality: y is relatively high. Together, this implies that the loss $\delta y$ of a switching customer with valuation y is large and, in fact, so large that it outweighs the positive cost-saving effect.

Now suppose that $\delta <2(c_{h}-c_{\ell })$, so that the market share of the premium product increases when moving from a centralized to a decentralized pricing system (Proposition 7(ii)). This results in an increase in production costs, which negatively affects social welfare. There is also a positive effect $\delta y$, because a switching customer with valuation y now consumes the premium product. Notice, however, that in this case switching customers have a fairly low valuation for quality—y is ‘small’—and that the extra quality of a premium product is limited: $\delta$ is ‘small’. As Proposition 8 reveals, the additional gain from an increase in the premium product’s market share is insufficient to compensate for the additional costs of producing the high-quality good.

7 Concluding Remarks

In this paper, we consider strategic pricing by sellers that supply multiple quality variants of their product and simultaneously compete ‘head-to-head’ in the corresponding quality-segments. Specifically, we analyzed a duopoly model of vertizontal product differentiation in which firms offer a standard and a premium good. Under the assumption that demand includes both brand- and quality-anchored buyers, we established the existence of a unique (and symmetric) competitive pricing equilibrium. These equilibrium prices are increasing in the degree of brand differentiation as well as in the number of brand-anchored buyers. Moreover, equilibrium profits may increase in production costs and the equilibrium price of the standard (premium) product is decreasing (increasing) in the quality difference.

We contrasted these findings with the possibility that pricing decisions are taken decentrally at the product type level. We prove there is again a unique (and symmetric) competitive pricing equilibrium in which both prices and profits are lower than in the centralized case. We furthermore find that demand for the standard product is higher when the quality difference is sufficiently large and show that welfare is unambiguously lower with decentralized pricing.

There are several natural avenues for future research: One is to extend the dimensions of the model: the number of firms or of quality segments. This, however, is likely to prove challenging in terms of deriving explicit and meaningful expressions. Another is to use this framework to analyze competition among multi-product and single-product, niche, firms. Finally, it is worth exploring what type of vertizontally differentiated markets may emerge endogenously. The interesting question is then under what conditions firms would position themselves ‘head-to-head’ along the quality spectrum when engaging in price competition.

Appendix: Proofs

Proof of Proposition 1

The first-order conditions for the two simultaneous maximization problems yield the following system of linear equations:

$$\begin{aligned} \begin{pmatrix} 4\tau _{\ell }\mu +2\delta \mu _{\ell } &{} -4\tau _{\ell }\mu &{} -\delta \mu _{\ell } &{} 0 \\ -4\tau _h\mu &{} 4\tau _h\mu +2\delta \mu _h &{} 0 &{} -\delta \mu _h \\ -\delta \mu _{\ell } &{} 0 &{} 4\tau _{\ell }\mu +2\delta \mu _{\ell } &{} -4\tau _{\ell }\mu \\ 0 &{} -\delta \mu _h &{} -4\tau _h\mu &{} 4\tau _h\mu +2\delta \mu _h \end{pmatrix} \begin{pmatrix} p_{1\ell } \\ p_{1h} \\ p_{2\ell } \\ p_{2h} \end{pmatrix} \quad \\ = \begin{pmatrix} (2\tau _{\ell }\mu +\delta \mu _{\ell })c_{\ell }-2\tau _{\ell }\mu c_h+\delta \tau _{\ell }\mu _{\ell } \\ (2\tau _h\mu +\delta \mu _h)c_h-2\tau _h\mu c_{\ell }+\delta \tau _h(2\mu +\mu _h) \\ (2\tau _{\ell }\mu +\delta \mu _{\ell })c_{\ell }-2\tau _{\ell }\mu c_h+\delta \tau _{\ell }\mu _{\ell } \\ (2\tau _h\mu +\delta \mu _h)c_h-2\tau _h\mu c_{\ell }+\delta \tau _h(2\mu +\mu _h) \end{pmatrix} . \end{aligned}$$

For both firms, solutions being maxima of their respective maximization problem is guaranteed by the negative definite Hessians:

$$\begin{aligned} \begin{pmatrix} -(4\tau _{\ell }\mu +2\delta \mu _{\ell }) &{} 4\tau _{\ell }\mu \\ 4\tau _h\mu &{} -(4\tau _h\mu +2\delta \mu _h) \end{pmatrix} . \end{aligned}$$

Since the matrix of coefficients in the system of linear equations is non-singular, we know that this system has one real solution. Moreover, given that asymmetric equilibria need to come in pairs, this solution must be symmetric. Exploiting this symmetry (that is, assuming $p_{1\ell }=p_{2\ell }=p_{\ell }$ and $p_{1h}=p_{2h}=p_h$), the above system reduces to

$$\begin{aligned} \begin{pmatrix} 4\tau _{\ell }\mu +\delta \mu _{\ell } &{} -4\tau _{\ell }\mu \\ -4\tau _h\mu &{} 4\tau _h\mu +\delta \mu _h \end{pmatrix} \begin{pmatrix} p_{\ell } \\ p_h \end{pmatrix} = \begin{pmatrix} (2\tau _{\ell }\mu +\delta \mu _{\ell })c_{\ell }-2\tau _{\ell }\mu c_h+\delta \tau _{\ell }\mu _{\ell } \\ (2\tau _h\mu +\delta \mu _h)c_h-2\tau _h\mu c_{\ell }+\delta \tau _h(2\mu +\mu _h) \end{pmatrix} . \end{aligned}$$

Solving this system gives the solution $(p_{\ell }^*,p_h^*)$ as specified in the proposition. Finally, feasibility conditions for the demand being well-specified (i.e., ${\widehat{y}}_1,{\widehat{y}}_2\in (0,1)$ at prices $p_{\ell }^*$ and $p_h^*$) requires $p_h^*>p_{\ell }^*$ and $p_h^*-p_{\ell }^*<\delta$. As one can easily verify, Assumption 1 is a sufficient condition for $p_h^*>p_{\ell }^*$ and $p_h^*-p_{\ell }^*<\delta$.

$\square$

Proof of Proposition 2

The first derivative of $p_{\ell }^*$ with respect to $c_{\ell }$ and $c_h$ is respectively given by:

$$\begin{aligned} \textstyle \frac{\partial p_{\ell }^*}{\partial c_{\ell }} = \frac{ 2\mu (\tau _{\ell }\mu _h+2\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h}{ 4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h}> 0 \quad \text {and}\quad \frac{\partial p_{\ell }^*}{\partial c_h} = \frac{ 2\tau _{\ell }\mu _h\mu }{4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{ \ell }\mu _h} > 0, \end{aligned}$$

and the first derivative of $p_h^*$ with respect to $c_{\ell }$ and $c_h$ is respectively given by:

$$\begin{aligned} \textstyle \frac{\partial p_h^*}{\partial c_{\ell }} = \frac{ 2\tau _h\mu _{\ell }\mu }{4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{ \ell }\mu _h}> 0 \quad \text {and}\quad \frac{\partial p_h^*}{\partial c_h} = \frac{2\mu (2\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h}{ 4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h} > 0. \end{aligned}$$

$\square$

Proof of Proposition 3

The first derivative of $p_{\ell }^*$ with respect to $\tau _{\ell }$, $\tau _h$, $\mu _{\ell }$ and $\mu _h$ is respectively given by:

$$\begin{aligned} \textstyle \frac{\partial p_{\ell }^*}{\partial \tau _{\ell }} = (4\mu \tau _h\mu _{\ell }+\delta \mu _{\ell }\mu _h)\cdot \frac{4\mu (\tau _{\ell } \mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h+2\mu ([(c_h-c_{\ell })+2(\tau _h- \tau _{\ell })]\mu _h+4\tau _h\mu )}{(4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+ \delta \mu _{\ell }\mu _h)^2}> 0, \\ \textstyle \frac{\partial p_{\ell }^*}{\partial \tau _h} = 4\tau _{\ell }\mu _h\mu \cdot \frac{4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+ \delta \mu _{\ell }\mu _h+2\mu ([\delta -(c_h-c_{\ell })-2(\tau _h-\tau _{\ell })] \mu _{\ell }+4\tau _{\ell }\mu )}{(4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h)^2} > 0, \\ \textstyle \frac{\partial p_{\ell }^*}{\partial \mu _{\ell }} = -2\tau _{\ell }\mu (4\tau _h\mu +\delta \mu _h)\cdot \frac{[(c_h-c_{\ell })+2(\tau _h- \tau _{\ell })]\mu _h+4\tau _h\mu }{(4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+ \delta \mu _{\ell }\mu _h)^2} < 0, \end{aligned}$$

and

$$\begin{aligned} \textstyle \frac{\partial p_{\ell }^*}{\partial \mu _h} = -8\tau _{\ell }\tau _h\mu ^2\cdot \frac{[\delta -(c_h-c_{\ell }-2(\tau _h-\tau _{\ell })]\mu _{\ell }+4\tau _{\ell }\mu }{ (4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h)^2} < 0. \end{aligned}$$

The first derivative of $p_h^*$ with respect to $\tau _{\ell }$, $\tau _h$, $\mu _{\ell }$ and $\mu _h$ is respectively given by:

$$\begin{aligned} \textstyle \frac{\partial p_h^*}{\partial \tau _{\ell }} = 4\tau _h\mu _{\ell }\mu \cdot \frac{4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+ \delta \mu _{\ell }\mu _h+2\mu ([(c_h-c_{\ell })+2(\tau _h-\tau _{\ell })]\mu _h+4 \tau _h\mu )}{(4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h)^2 }> 0, \\ \textstyle \frac{\partial p_h^*}{\partial \tau _h} = \left( 4\tau _{\ell }\mu _h\mu +\delta \mu _{\ell }\mu _h\right) \cdot \frac{ 4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h+2\mu ([ \delta -(c_h-c_{\ell })-2(\tau _h-\tau _{\ell })]\mu _{\ell }+4\tau _{\ell }\mu )}{ (4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h)^2} > 0, \\ \textstyle \frac{\partial p_h^*}{\partial \mu _{\ell }} = -8\tau _{\ell }\tau _h\mu ^2\cdot \frac{[(c_h-c_{\ell })+2(\tau _h-\tau _{\ell })] \mu _h+4\mu \tau _h}{(4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell } \mu _h)^2} < 0, \end{aligned}$$

and

$$\begin{aligned} \textstyle \frac{\partial p_h*}{\partial \mu _h} = -2\tau _h\mu (4\tau _{\ell }\mu +\delta \mu _{\ell })\cdot \frac{[\delta -(c_h-c_{ \ell })-2(\tau _h-\tau _{\ell })]\mu _{\ell }+4\tau _{\ell }\mu }{(4\mu (\tau _{\ell } \mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h)^2} < 0. \end{aligned}$$

The terms in squared brackets in the numerator are positive by Assumption 2.

$\square$

Proof of Proposition 4

The first derivative of $p_{\ell }^*$ with respect to $\mu$ and $\delta$ is respectively given by:

$$\begin{aligned} \textstyle \frac{\partial p_{\ell }^*}{\partial \mu } = 2\tau _{\ell }\cdot \frac{\delta \mu _{\ell }\mu _h([(c_h-c_{\ell })+2(\tau _h-\tau _{\ell })]\mu _h+8 \tau _h\mu )+16\tau _h\mu ^2(\tau _{\ell }\mu _h+\tau _h\mu _{\ell })}{ (4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h)^2} > 0 \end{aligned}$$

and

$$\begin{aligned} \textstyle \frac{\partial p_{\ell }^*}{\partial \delta } = -\tau _{\ell }\mu _h\cdot \frac{2\mu _{\ell }\mu ([(c_h-c_{\ell })+2(\tau _h-\tau _{ \ell })]\mu _h+4\tau _h\mu )}{(4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h)^2} < 0. \end{aligned}$$

The first derivative of $p_h^*$ with respect to $\mu$ and $\delta$ is respectively given by:

$$\begin{aligned} \textstyle \frac{\partial p_h^*}{\partial \mu } = 2\tau _h\cdot \frac{ \delta \mu _{\ell }\mu _h([\delta -(c_h-c_{\ell })-2(\tau _h-\tau _{\ell })]\mu _{ \ell }+8\tau _{\ell }\mu )+16\tau _{\ell }\mu ^2(\tau _{\ell }\mu _h+\tau _h\mu _{\ell }) }{(4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h)^2} > 0 \end{aligned}$$

and

$$\begin{aligned} \textstyle \frac{\partial p_h^*}{\partial \delta } = \tau _h\mu _{\ell }\cdot \frac{2\mu _{\ell }\mu ([(c_h-c_{\ell })+2(\tau _h-\tau _{\ell })]\mu _h+4\tau _h\mu ) }{(4\mu (\tau _{\ell }\mu _h+\tau _h\mu _{\ell })+\delta \mu _{\ell }\mu _h)^2} < 0. \end{aligned}$$

In determining the sign of these derivatives, notice that the term in squared brackets in the numerators is positive by Assumption 2.

$\square$

Proof of Proposition 5

Setting $\mu _{\ell }=\mu _h$ and $\tau _{\ell }=\tau _h$, the first derivative of $\pi ^*$ with respect to $c_{\ell }$ and $c_h$ is given by:

$$\begin{aligned} \textstyle \frac{\partial \pi ^*}{\partial c_{\ell }} = -\frac{\partial \pi ^*}{ \partial c_h} = \frac{4\tau _h\mu ^2(\delta \mu _h+4\tau _h\mu )[\delta -2(c_h-c_{ \ell })]}{\delta (\delta \mu _h+8\tau _h\mu )^2}. \end{aligned}$$

The term in the squared brackets determines the sign of the derivatives.

$\square$

Proof of Proposition 6

The first-order conditions for the four simultaneous maximization problems yield the following system of linear equations

$$\begin{aligned} \begin{pmatrix} 4\tau _{\ell }\mu +2\delta \mu _{\ell } &{} -2\tau _{\ell }\mu &{} -\delta \mu _{\ell } &{} 0 \\ -2\tau _h\mu &{} 4\tau _h\mu +2\delta \mu _h &{} 0 &{} -\delta \mu _h \\ -\delta \mu _{\ell } &{} 0 &{} 4\tau _{\ell }\mu +2\delta \mu _{\ell } &{} -2\tau _{\ell }\mu \\ 0 &{} -\delta \mu _h &{} -2\tau _h\mu &{} 4\tau _h\mu +2\delta \mu _h \end{pmatrix} \begin{pmatrix} p_{1\ell } \\ p_{1h} \\ p_{2\ell } \\ p_{2h} \end{pmatrix} \quad \\ = \begin{pmatrix} (2\tau _{\ell }\mu +\delta \mu _{\ell })c_{\ell }+\delta \tau _{\ell }\mu _{\ell } \\ (2\tau _h\mu +\delta \mu _h)c_h+\delta \tau _h(2\mu +\mu _h) \\ (2\tau _{\ell }\mu +\delta \mu _{\ell })c_{\ell }+\delta \tau _{\ell }\mu _{\ell } \\ (2\tau _h\mu +\delta \mu _h)c_h+\delta \tau _h(2\mu +\mu _h) \end{pmatrix} . \end{aligned}$$

Since the matrix of coefficients in the system of linear equations is non-singular, we know that this system has one real solution. Moreover, given that asymmetric equilibria need to come in pairs, this solution must be symmetric. Exploiting this symmetry—assuming $p_{1\ell }=p_{2\ell }=p_{\ell }$ and $p_{1h}=p_{2h}=p_h$—the above system reduces to

$$\begin{aligned} \begin{pmatrix} 4\tau _{\ell }\mu +\delta \mu _{\ell } &{} -2\tau _{\ell }\mu \\ -2\tau _h\mu &{} 4\tau _h\mu +\delta \mu _h \end{pmatrix} \begin{pmatrix} p_{\ell } \\ p_h \end{pmatrix} = \begin{pmatrix} (2\tau _{\ell }\mu +\delta \mu _{\ell })c_{\ell }+\delta \tau _{\ell }\mu _{\ell } \\ (2\tau _h\mu +\delta \mu _h)c_h+\delta \tau _h(2\mu +\mu _h) \end{pmatrix} . \end{aligned}$$

Solving this system gives the solution $(p_{\ell }^{\circ },p_h^{\circ },)$ as specified in the proposition. Finally, feasibility conditions for the demand being well-specified (i.e., ${\widehat{y}}_1,{\widehat{y}}_2\in (0,1)$ at prices $p_{\ell }^{\circ }$ and $p_h^{\circ }$) requires $p_h^{\circ }>p_{\ell }^{\circ }$ and $p_h^{\circ }-p_{\ell }^{\circ }<\delta$. It can be verified that Assumption 1 and $\delta \ge \max \{\tau _{\ell },\tau _h\}$ are a sufficient condition for $p_h^{\circ }>p_{\ell }^{\circ }$ and $p_h^{\circ }-p_{\ell }^{\circ }<\delta$.

$\square$

Proof of Proposition 7

For $\mu _h=\mu _{\ell }=\mu =1$ and $\tau _h=\tau _{\ell }=\tau$, we have:

$$\begin{aligned} \begin{array}{ll} p_{\ell }^*=c_{\ell }+2\tau -\frac{[\delta -2(c_h-c_{\ell })]\tau }{\delta +8\tau } &{} p_h^*=c_h+2\tau +\frac{[\delta -2(c_h-c_{\ell })]\tau }{\delta +8\tau } \\ *[0.5em] p_{\ell }^{\circ }=c_{\ell }+2\frac{\delta }{\delta +2\tau }\tau -\frac{ [\delta -2(c_h-c_{\ell })]\tau }{\delta +6\tau } &{} p_h^{\circ }=c_h+2\frac{\delta }{ \delta +2\tau }\tau +\frac{[\delta -2(c_h-c_{\ell })]\tau }{\delta +6\tau } \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{ll} {\widehat{y}}^*=\frac{1}{\delta }\Big \{(c_h-c_{\ell })+\frac{2[\delta -2(c_h-c_{ \ell })]\tau }{\delta +8\tau }\Big \}&{\widehat{y}}^{\circ }=\frac{1}{\delta }\Big \{ (c_h-c_{\ell })+\frac{2[\delta -2(c_h-c_{\ell })]\tau }{\delta +6\tau }\Big \}. \end{array} \end{aligned}$$

From this, we obtain the profits

$$\begin{aligned} \begin{array}{ll} \pi ^*=4\tau +\frac{(\delta +4\tau )[\delta -2(c_h-c_{\ell })]^2\tau }{ \delta (\delta +8\tau )^2}&\pi ^{\circ }=4\frac{\delta }{\delta +2\tau }\tau +\frac{ (\delta +2\tau )[\delta -2(c_h-c_{\ell })]^2\tau }{\delta (\delta +6\tau )^2}. \end{array} \end{aligned}$$

The statement in the proposition follows from a comparison of these values.

$\square$

Proof of Proposition 8

If $\delta >2(c_h-c_{\ell })$, then $Y=[{\widehat{y}}^*,{\widehat{y}}^{\circ }]$ and the change in welfare is given by

$$\begin{aligned} 2\int _{{\widehat{y}}^*}^{{\widehat{y}}^{\circ }}(c_h-c_{\ell })-\delta y\>\text {d} y =-[\delta ({\widehat{y}}^*+{\widehat{y}}^{\circ })-2(c_h-c_{\ell })]\cdot ( {\widehat{y}}^{\circ }-{\widehat{y}}^*). \end{aligned}$$

Alternatively, if $\delta <2(c_h-c_{\ell })$, then $Y=[{\widehat{y}} ^{\circ },{\widehat{y}}^*]$ and the change in welfare is given by

$$\begin{aligned} 2\int _{{\widehat{y}}^{\circ }}^{{\widehat{y}}^*}\delta y-(c_h-c_{\ell })\>\text {d} y =[\delta ({\widehat{y}}^*+{\widehat{y}}^{\circ })-2(c_h-c_{\ell })]\cdot (\widehat{ y}^*-{\widehat{y}}^{\circ }). \end{aligned}$$

Both expressions lead to

$$\begin{aligned} \textstyle -\frac{16\tau ^3(\delta +7\tau )[\delta -(c_h-c_{\ell })]^2}{ \delta (\delta +6\tau )^2(\delta +8\tau )^2}, \end{aligned}$$

which is negative.

$\square$