Abstract
When knowledge sharing is non-contractible, we show that competing downstream firms may prefer to help improve an inefficient alternative supply source than help to improve the technology of the efficient actual supplier—even if this is costless. A downstream firm can have incentives to decrease the efficiency of the actual supplier in order to improve its outside options. Non-controlling partial backward ownership can—through the participation of the downstream firm(s) in the upstream profits—align the incentives of the supplier and its competing customers. This improves industry performance while simultaneously benefiting consumers. Partial backward ownership has similar effects as strengthening a downstream firm’s bargaining power and making knowledge sharing contractible.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Knowledge sharing among suppliers and buyers can reduce inefficiencies and improve the production process.Footnote 1 For example, a downstream firm might gain knowledge on how to produce an input that it purchases from its upstream supplier more efficiently through either its experience or its own research and development activities.Footnote 2 In such situations, it is crucial that there are incentives to share knowledge as these relationships are often tacit and non-contractible.Footnote 3
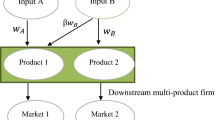
In this article, we study non-contractible knowledge sharing and non-controlling partial ownership in a vertical relations framework. The model features upstream an efficient, strategic supplier and a less efficient upstream competitive fringe. The strategic supplier offers secret two-part tariffs to the competing downstream firms that feature a fixed fee and a unit input price at marginal cost. Sourcing from the fringe determines a downstream firm’s outside option and thus the level of the fixed fee. A downstream firm can share knowledge that makes the upstream production less costly.
We first show that when knowledge sharing is not contractible, a downstream firm may not share knowledge with the actual supplier—even when it is costless and increases both supplier efficiency and industry profits. The reason is that a more efficient supplier is also better placed to serve rivals at lower costs, and the rivals consequently will sell more at lower prices. This worsens the downstream firm’s threat point of obtaining the input alternatively if no agreement with the efficient supplier is reached. The incentives of downstream firms are thus not aligned with the objective of (integrated) industry profit maximization. Instead, a downstream firm may prefer to invest in improving the inefficient alternative supply source to improve its bargaining position with the supplier.
In a second step, we show that partial backward ownership can encourage knowledge sharing. With sufficiently high ownership shares, the gains from improving the actual supply chain’s efficiency outweigh the incentive to improve the outside option (the inefficient alternative supplier). Allowing a downstream firm to have a backward passive ownership position in its supplier thus has a similar effect as making the potential improvements in essence contractible. Thus, partial backward ownership can increase efficiency, industry profit, and consumer welfare at the same time.
One may argue that a vertical merger also aligns the incentive of the upstream and downstream entity and should be conducive to the sharing of knowledge. However, vertical mergers often face stricter scrutiny from anti-trust authorities and are often a long, drawn-out, costly process with substantial uncertainty.Footnote 4 We show that one does not need corporate control to align the knowledge-sharing incentives, but that a sufficiently high participation in the gains from efficient trade is enough (through non-controlling partial ownership). Moreover, different from a vertical merger, partial ownership can solve the incentive problem between the upstream firm and several downstream firms simultaneously—without distorting competition.
The remainder of this article is structured as follows: The next section covers the related literature and Sect. 3 sets up the model. Section 4 studies a downstream firm’s technology sharing incentives without partial ownership. In Sect. 5, we discuss how partial backward ownership encourages downstream firms to increase the supplier’s efficiency. Section 6 contains extensions. We show that our main results—which we derive for Cournot competition in the downstream market—can also arise under differentiated Bertrand competition. Moreover, we also demonstrate that the initial incentive problem of knowledge sharing is caused by a lack of downstream bargaining power. Partial backward ownership is similar to improving the bargaining power of the downstream firms in this context. We also generalize the results to different wholesale tariffs and study ownership acquisitions. Section 7 concludes.
2 Related Literature
The starting point of our analysis is the observation that a downstream firm may be in a position to help its supplier improve its production but may not have the incentive to do so. The merits of sharing technology with suppliers have been discussed by Kotabe et al. (2003) and Dyer and Hatch (2004) in the context of Japanese firms.Footnote 5 Bönte and Keilbach (2005) find that when downstream firms cannot protect knowledge, their knowledge-sharing incentives are not aligned with the other parts of the supply chain. Similarly, Hughes and Kao (2001) argue that retailers might be less willing to share knowledge when the supplier has its own downstream business. Bönte and Wiethaus (2007) conclude that knowledge sharing with a supplier that also strengthens its downstream rivals discourages such knowledge sharing. In a complementary article, Wiethaus (2005) shows that competing firms choose identical R&D approaches in order to maximize knowledge flows between each other. These articles do not consider partial ownership.
In a horizontal setting, Ghosh and Morita (2017) show that sharing efficiency-enhancing knowledge with a competitor has the disadvantage that the competitor obtains a competitive advantage.Footnote 6 They show that horizontal ownership can overcome this obstacle. In the current article we find that, even in a vertical setting, a retailer does not have the incentive to share cost-reducing technology with a common supplier. This is because sharing cost-reducing technology with a common supplier makes rivals better off as well. This reduces the bargaining position of the retailer vis-a-vis the supplier. We show that partial ownership helps align technology-sharing incentives to maximize industry profit.
Another stream of literature has studied how supply contracts affect supply chain coordination. Cachon and Lariviere (2005) and Wang and Shin (2015) show that revenue-sharing contracts can induce supply-chain coordination. These contracts are set to maximize the industry supply-chain profit; consequently, coordination in the strategic decisions of firms at different levels of the supply chain is ensured. Instead, we focus on partial ownerships that do not allow control over the strategic decisions of other firms in the supply chain. We show that such control is not necessary to allow coordination.
Lin et al. (2014) find that a vertical merger allows the manufacturer to control the investment process and hence invest efficiently. Instead, we show that full integration may not be necessary to align innovation incentives with the industry. Non-controlling partial backward ownership is sufficient to align a firm’s incentives to share technology with its supplier.
The present article is related to two strands of literature that study partial vertical ownership. The first strand focuses on the competitive effects of partial vertical ownership.Footnote 7 The second strand focuses on the effects on investments in a supply chain.
Dasgupta and Tao (2000) show that a supplier has a greater incentive to produce relationship-specific inputs when the customer holds a non-controlling ownership share in the supplier.Footnote 8 Similarly, Choi et al. (2014) consider a setting where an upstream firm can sell exactly one indivisible unit of input to one of two different customers that do not compete. They find that partial ownership can increase investment incentives.Footnote 9 In their setting, partial backward ownership is not a solution if the supplier makes take-it-or-leave-it (TIOLI) offers, or if each customer can buy a unit of the input, or if both customers have symmetric investment capabilities. Instead, we consider a setting where a supplier sells inputs to different—and possibly competing—downstream firms and show that partial ownership can be helpful.
Allen and Phillips (2000) empirically study partial ownership held by corporations in US firms and identify many instances where downstream firms hold ownership stakes in upstream firms. They find that such partial ownership combined with product market relationships in R&D-intensive industries is associated with improvements in operating performance. Their findings are consistent with our theory that partial backward ownership facilitates cooperation and, in particular, technology transfer to the target firm. More generally, their findings underline the importance of understanding the relationship between partial ownership and supply chain cooperation.
3 Model
There are \(n>1\) symmetric downstream firms that produce a homogeneous product and compete in quantities.Footnote 10 Input is supplied either by an efficient supplier—which is denoted as U—with marginal cost \(c^{U}={\tilde{c}}>0\) or an alternative inefficient supply source (denoted I) with marginal costs \(c^{I}={\tilde{c}}+c\), where \(c>0\).Footnote 11 An example of such alternative supply sources could be private labels in the retail market.Footnote 12
We start with the case without ownership links between the firms. The game has three stages:
-
1.
A downstream firm—for instance, firm 1—decides whether to help innovate either only U or only I, or both U and I. If a supplier innovates, its marginal cost decreases by \(k\in (0,\ c)\).Footnote 13 The resulting marginal costs are public knowledge.
-
2.
Supplier U offers secret two-part contracts \(\{f_{i},\ w_{i}\}\) to each downstream firm with \(w_{i}\) and \(f_{i}\) as the linear and fixed parts of the tariff, respectively.Footnote 14 The downstream firms simultaneously decide to accept or reject the contract that is offered. The acceptance decisions become public—but not the contract terms.Footnote 15
-
3.
Downstream firms simultaneously source input quantities \(x_{i}^{U}\) from U and \(x_{i}^{I}\) from I, produce output quantities \(q_{i}\), and sell them.Footnote 16
We employ secret contracts, which limit the ability of a supplier to exert market power due to the opportunism problem; see Hart and Tirole (1990).Footnote 17 Intuitively, after negotiating contracts with a customer, the suppliers has the incentive to renegotiate contracts with a rival customer. As a consequence, no customer will accept a contract above the bilateral contracting level. This opportunism problem does not arise in public contracts as the supplier is unable to secretly renegotiate contracts with a rival to the detriment of a customer. The benchmark case discusses results under secret contracts. In Sect. 6.3, we show that our main results can also arise when firms offer public contracts.
As regards stage 1, we mainly analyze how profits before any innovation costs change with such innovations. At this point, we abstract away from costs of innovation. We first focus on the case that only one downstream firm can induce an innovation. Our leading example for inducing an innovation is knowledge sharing.Footnote 18 We consider the case that all firms can do so in Sect. 5.2. In stage 2, U has all the bargaining power and makes TIOLI offers. We show in Sect. 6 that our analysis also extends to cases with more balanced bargaining power.
Supplier U’s profit if all downstream firms accept its contract offer is given by
Absent partial ownership and if it accepts the contract of U, a downstream firm i’s profit before the fixed fee \(f_{i}\) is given by
where P(Q) is the downstream price, which decreases in total output \(Q=\sum _{i=1}^{n}q_{i}\).
In stage 3, contract acceptance or rejection decisions of the downstream firms become public, but the contracts remain secret. A breakdown in negotiations between U and a customer is observable but not verifiable (in court), and therefore cannot be contracted upon.Footnote 19 It seems plausible that an industry insider can infer the supplier of a competitor, while the exact contract terms are hard to ascertain. The secrecy of contracts is not crucial: We show in the extension section that our main results hold when the contract terms are observable.
We study symmetric Perfect Bayesian Equilibria where downstream firms have passive beliefs.Footnote 20 For what follows, we assume that the profit functions satisfy standard regularity conditions.Footnote 21
Assumption 1
Denote by \(\pi (y,z)\) the resulting equilibrium flow profit \(\left( P(Q)-y\right) q_{i}\) when firm i has marginal costs of y and its rivals have marginal costs of z. The profit \(\pi (y,z)\) decreases when all costs increase uniformly from the same level: \(\partial \pi (s,s)/\partial s<0\); decreases in the own costs: \(\partial \pi (y,z)/\partial y<0\); and increases by a finite amount when the competitors’ marginal costs increase: \(\infty>\partial \pi (y,z)/\partial z>0\).
4 Innovation Without Partial Ownership
4.1 Market Prices and Quantities
With passive beliefs, upon receiving a contract offer each downstream firm anticipates that its rivals will stick to the anticipated equilibrium quantity \(Q_{-i}^{*}\). Moreover, the profit that U obtains from other downstream firms is unaffected by a change in the marginal price that U charges downstream firm i. This is because the price deviation is unobserved by the rivals—who can thus not condition their output decisions on it.
As a result, U chooses the tariff for downstream firm i as if U and i were an integrated entity—as in Hart and Tirole (1990) and Rey and Vergé (2004). The equilibrium contracts are presented below.
Lemma 1
Without partial ownership, supplier U charges tariffs with marginal prices \(w_{i}\) that are equal to marginal costs \(c^{U}\).
Proof
See “Appendix 1”. \(\square\)
Total output equals the output of a Cournot oligopoly with n firms with marginal costs of \(c^{U}\). The flow profit of a downstream firm is thus \(\pi (c^{U},\ c^{U}).\) U extracts the downstream profits through the fixed fees that leave each firm i just its outside option \(\pi (c^{I},\ c^{U})\).Footnote 22
Lemma 2
In equilibrium, all downstream firms accept the wholesale contract \(\{w^{*}=c^{U},\ f^{*}=\pi (c^{U},\ c^{U})-\pi (c^{I},\ c^{U})\}\). Supplier U’s profit is \(\pi ^{U}=n\cdot f^{*}=n\left[ \pi (c^{U},\ c^{U})-\pi (c^{I},\ c^{U})\right]\), and a downstream firm’s profit is \(\pi (c^{I},\ c^{U})\).
Our results do not rely on the assumption of secret two-part tariffs. Analogous results can be obtained for observable two-part tariffs and also for the case that the supplier does not sell inputs on a per-unit basis, but can sell to each downstream firm a machine that allows it to produce inputs at marginal costs of \(c^{U}\) instead of \(c^{I}\).
4.2 Innovation Incentives
Let us now turn to the innovation incentives in stage 1. We consider innovations that reduce the marginal input costs. Our main assumption is that the supplier and customer cannot contract upon the innovation.Footnote 23
We analyze the incentives of a downstream firm to induce innovations. For simplicity, we assume that inducing the innovation—for instance, through knowledge transfer—is costless for the downstream firm, as is the innovation itself. This generalizes to the case where there is a cost, as long as this is not too large. We assume for now that the supplier can serve all downstream firms equally at the lower costs in the case of innovation.Footnote 24
The following proposition characterizes the incentive of a downstream firm to share information.
Proposition 1
Without backward ownership, a downstream firm has no incentive to help with innovation which reduces its supplier’s marginal costs \(c^{U}\). A downstream firm has an incentive to help reduce only the alternative sourcing costs \(c^{I}\).
Recall from Lemma 2 that the profit of a downstream firm is just its outside option profit \(\pi (c^{I},c^{U})\). This is because the supplier has all the bargaining power and makes TIOLI offers.Footnote 25 This downstream profit—\(\pi (c^{I},c^{U})\)—decreases in the own costs \(c^{I}\). Thus, there are incentives to decrease \(c^{I}\). This is the case even if it is certain that I remains the less efficient supply source that will ultimately not be used for production. This implies that technology development that is focused on I is just a means for a downstream firm to extract rents from its supplier. It improves the threat point in negotiations, with no actual effects on industry profits and consumer surplus.Footnote 26 This can lead to inefficient innovation activities.
The downstream firm does not obtain any of the benefits from sharing cost-reducing knowledge with U. Instead, sharing such knowledge with U only reduces its profits as the rivals are served more efficiently. Formally, the downstream profit \(\pi (c^{I},c^{U})\) increases in \(c^{U}\). Consequently, the downstream firm benefits from increasing the efficient supplier’s costs \(c^{U}\). This incentive prevails until the costs equal the alternative sourcing costs of \(c^{I}\). This could induce a downstream to interfere with U’s supply processes and thus increase U’s marginal costs. In a real world case, such sabotage would likely need to be secret in order to sustain a healthy business relationship.Footnote 27
In summary, the technology sharing incentives of the customer are inefficient from an integrated industry standpoint. This is the case even if innovations and knowledge sharing are costless. In the next section, we examine partial ownership as a tool for firms to commit credibly to sharing the gains from such informal technology spillovers and thus aligning the incentives of firms with the integrated industry. This is relevant when fully contracting upon the innovation activities is not feasible, as we explain in the next paragraph.
Contracting upon innovations
For reference, assume that the supplier and customer can contract upon the success of the innovations that lead to lower upstream production costs.
The joint profit of a downstream firm and supplier U is
As \(\pi (c^{U},c^{U})\) decreases in \(c^{U}\) and \(\pi (c^{I},c^{U})\) increase in \(c^{U}\), the joint profit clearly increases as \(c^{U}\) decreases. This means that it is profitable for supplier U and the downstream firm to write an enforceable contract that rewards the downstream firm with a transfer \(t\ge \pi (c^{I},{\tilde{c}})-\pi (c^{I},{\tilde{c}}-k)\) for conducting the cost-decreasing innovation. However, it might be hard to write an enforceable contract for tacit information sharing.
5 Innovation with Partial Backward Ownership
We now analyze how pricing and the incentives to induce innovations change when there is backward ownership:Footnote 28 Each downstream firm \(i\in \{1,2..n\}\) may now have a partial non-controlling ownership share of supplier U, which we denote by \(\delta _{i}\in [0,1)\) \(\forall i\). Partial ownership refers to an ownership share that is strictly below one. Non-controlling refers to ownership that does not involve control over the target firm’s pricing strategy: e.g., pure financial interests, non-voting shares. In the following analysis ownership is non-controlling.Footnote 29
5.1 Equilibrium Prices and Quantities
The net profit of a downstream firm is \(\Pi _{i}=\pi _{i}-f_{i}+\delta _{i}\pi ^{U}\), which one can write as
where \(q_{i}^{BR}\) is the optimal quantity that is set by firm i given its input costs and the anticipated output of its rivals: \(Q_{-i}^{*}=\sum _{j\ne i}^{n}q_{j}^{*}\). Note that for a positive ownership share—\(\delta _{i}\)—firm i gets a discount of \(\delta _{i}\) on the upstream margin \(w_{i}-c^{U}\) and on the fixed fee \(f_{i}\).
U offers each downstream firm i a contract \(\{w_{i},\ f_{i}\}\) that maximizes
where the outside profit of a downstream firm when it sources alternatively at cost \(c^{I}\) is
where \(q_{j}^{*\text {DEV}}\) are the the anticipated quantities that are set by firm \(j\ne i\) as the breakdown in negotiations is observable. This is the optimal quantity for firm j when the input costs of firm i are \(c^{I}\) and anticipating that everyone else obtains equilibrium prices \(w_{k}^{*}\) for \(k\ne i\). Further, we define \(Q_{-i}^{*\text {DEV}}:=\sum _{j\ne i}q_{j}^{*DEV}.\)
We find that it is still optimal for supplier U to offer a downstream firm a contract with a marginal price that is equal to U’s marginal costs: \(c^{U}\). As a result, partial backward ownership does not affect the equilibrium quantities. This implies that partial ownership \(\delta _{i}\) affects the downstream profit only through the fixed fee.
Lemma 3
For any structure of non-controlling backward ownership shares \(\delta _{i}\in [0,1),\) U offers contracts that are characterized by \(w_{i}=c^{U}\) and \(f_{i}=\left[ \pi (c^{U},c^{U})-\pi (c^{I},c^{U})\right] /(1-\delta _{i})\). The downstream profit is given by
Proof
See “Appendix 1”. \(\square\)
5.2 Innovation Incentives
We now study how partial backward ownership affects the innovation incentives. For a profit share \(\delta _{i}>0\) that firm i obtains in U, the equilibrium downstream profit is a weighted sum of the outside option flow profit—\(\pi (c^{I},c^{U})\)—and the equilibrium flow profits: \(\pi (c^{U},c^{U})\)—see Eq. (4). Recall that when \(c^{U}\) decreases, the deviation profit \(\pi (c^{I},c^{U})\) decreases, but the actual flow profit \(\pi (c^{U},c^{U})\) increases. As \(\delta _{i}\) increases, the weight on \(\pi (c^{I},c^{U})\) decreases, and the weight on \(\pi (c^{U},c^{U})\) increases.
To understand better the knowledge-sharing incentives, we take the derivative of the downstream firms i’s profit, Eq. (4), with respect to \(c^{U}\) and solve for the critical level of partial ownership that ensures that \(\partial (\pi _{i}-f_{i}+\delta _{i}\cdot \pi ^{U})/\partial c^{U}>0\). This yields that for any partial ownership level
technology sharing with U is profitable. The critical level \({\widetilde{\delta }}\) lies in the feasible range of (0, 1) as \(\partial \pi (c^{I},c^{U})/\partial c^{U}>0\) and \(\partial \pi (c^{U},c^{U})/\partial c^{U}<0\). We summarize the results in the following proposition.
Proposition 2
For a sufficiently high backward ownership share—\(\delta _{i}>{\widetilde{\delta }}\)—downstream firm i benefits from a decrease in the costs \(c^{U}\) of supplier U and thus has an incentive to help reduce these costs if doing so is costless or not too costly.
Proposition 2 shows that a large enough backward ownership share—a share close to 100% is always sufficient—makes the sharing of cost-reducing technology with U incentive-compatible for the downstream firm. This is because partial ownership allows participation in the upstream flow profits and thus the gains from a reduction in \(c^{U}\). Participation in upstream profits can also be achieved through bargaining over tariffs. In Sect. 6.1, we show that large enough downstream bargaining power can also align knowledge sharing incentives.
It is important to note that this critical threshold of partial ownership falls in the ownership shares of its rivals. This implies that as i’s rivals increase their ownership stake in U, the ownership requirement is less stringent for i to share knowledge of cost-reducing technology. To provide intuition, we rewrite the profit of downstream firm i expressed in Eq. (4), as
An increase in the ownership stake of a rival downstream firm increases the fixed fee of the rival firm (see Lemma 3). This increases the supplier’s profits which also benefits firm i through its ownership stake \(\delta _{i}\). In particular, the relative weight of \(\pi (c^{U},c^{U})\) in the profit of firm i increases (see Eq. 5). As a result, a smaller ownership stake \(\delta _{i}\) is needed to ensure that knowledge sharing by firm i occurs.
Technology sharing with U does not imply that there is no incentive for technology sharing with I. Instead, it is clear from Eq. (4) that sharing cost-reducing technology with I increases the profit of a downstream firm and it therefore always shares technology with I. Moreover, we show that for \(\delta _{i}>{\widetilde{\delta }},\) downstream firm i shares cost-reducing knowledge with U as well under the threat that in the event of a contractual breakdown, it sources its input from I. This way the downstream firm maximizes the profit that it obtains through its supply relationship with U. This is summarized below.
Corollary 1
For \(\delta _{i}>{\widetilde{\delta }}\), the technology allocation that maximizes downstream firm \(i's\) profit is to share the technology with both U and I. This allocation improves productive efficiency and social welfare.
Even if a downstream firm’s incentives are to share cost-reducing knowledge with U, it still wants to maximize the surplus extraction for a given ownership level. Increasing the outside option profit \(\pi (c^{I},c^{U})\) increases the downstream firm’s equilibrium profit, as can be observed in Eq. (4). This profit increases if the cost-reducing technology is shared with I. Therefore, even with partial ownership, downstream firm i induces innovation in the alternative supplier to maximize its profits.
We do not consider the case of a vertical merger (which involves \(\delta _{i}=100\%\)) as it allows full control of firm U. In this article, we are interested in aligning the incentives of a downstream firm i with the industry incentives without endowing full control to the downstream firms.Footnote 30 Moreover, a vertical merger might not be feasible, either due to financial constraints or anti-trust concerns. Anti-trust concerns can arise as the merged entity can prevent any cost-reducing knowledge spillover to rivals. This implies that the knowledge is now used to improve the production process for the benefit of the downstream entity and to the detriment of its rivals. With a large enough ownership share, knowledge sharing occurs and is used to improve the total production process. This leads to an industry efficiency enhancement while a vertical merger improves the production process only for the merged entity. This result is valid due to the assumption in our paper that technology transfer is costless.
Instead, if the technology transfer is costly, then transferring technology to the inefficient supplier implies a waste of resources. This is an example of burning resources to improve the terms of trade.Footnote 31 Depending on the technology and the process of technology transfer, it might not be feasible to share knowledge with a second firm. Formally, the costs of knowledge transfer could be convex so that it is prohibitively costly to share knowledge with a second supplier.Footnote 32 In this case, partial backward ownership can induce the downstream firm(s) to redirect the technology transfer from the inefficient to the efficient supply source. To further fix ideas, we discuss how partial ownership affects the amount of knowledge sharing.
Relationship between backward ownership and the amount of knowledge sharing
Suppose that downstream firm i can share information that decreases the cost \(c^{U}\) of the efficient supplier. Sharing more information decreases the cost more but sharing information is increasingly costly. Suppose that the cost for downstream firm i of reducing the cost \(c^{U}\) is given by \(\phi (k)\) with \(\phi (0)=0\), \(\phi '(k)>0\) and \(\phi ''(k)>0\). The profit of the downstream firm thus becomes \(\pi _{i}-f_{i}+\delta _{i}\cdot \pi ^{U}-\phi (\Delta )\), which equals
Recall that the profit of i increases when \(\Delta\) increases through the term \(\pi (c^{U}-\Delta ,c^{U}-\Delta )\) but decreases through \(\pi (c^{I},c^{U}-\Delta )\) and \(\phi (\Delta )\). As the relative weight of \(\pi (c^{U}-\Delta ,c^{U}-\Delta )\) increases in \(\delta _{i}\), the optimal choice of \(\Delta\) increases in \(\delta _{i}\) as well. In other words, more cost reductions at U through knowledge sharing occurs when the ownership share is higher.
Consequently, other things equal, a downstream firm tends to share more (or, more costly) information if the backward ownership share is higher.
Knowledge sharing by several downstream firms
It might be that all downstream firms could potentially induce cost-reducing innovations at the common supplier. For instance, each downstream firm could, with certainty or some probability, induce a different innovation, such that the cost reductions add up. One could also imagine that there is complementarity across downstream firms such that each firm needs to have incentives to cooperate in order to achieve an upstream innovation.Footnote 33 In this case, it is desirable to align the incentives of all downstream firms. Suppose that all downstream firms have the same ownership share \(\delta\). The profit of a downstream firm stated in Eq. (4) decreases to
We observe that, at \(\delta =0\), the downstream firm’s profit on the right-hand side of Eq. (6) equals \(\pi (c^{I},c^{U})\), whereas for \(\delta =1/n\), it equals \(\pi (c^{U},c^{U})\).Footnote 34 Recall that the derivative of \(\pi (c^{I},c^{U})\) with respect to \(c^{U}\) is positive, whereas the derivative of \(\pi (c^{U},c^{U})\) with respect to \(c^{U}\) is negative. While a share of 1/n perfectly aligns the incentives with respect to industry profits, a smaller share is sufficient for downstream profits to increase when supplier U becomes more efficient—when \(c^{U}\) decreases—and thus for efficient innovations to occur. Therefore, we can conclude that there exists a threshold \(\underline{{\delta }}\) with \(0<\underline{{\delta }}<1/n\), such that for any \(\delta \in ({{\underline{{\delta }}},1/n})\) each downstream firm’s profit increases when the efficient supplier’s cost \(c^{U}\) decreases.
To further fix ideas, suppose that each downstream firm has a symmetric non-controlling backward ownership share of 1/n. A downstream firm’s equilibrium profit is \(\pi (c^{U},c^{U})\) and each downstream firm is willing to induce innovations that reduce the costs \(c^{U}\) of supplier U, while no downstream firm has an incentive to reduce the production costs \(c^{I}\) of the alternative supply source.
We abstract here from the question of corporate control of U—which is not central to our main arguments, but is a natural question when the n downstream firms together have all the profit rights of U. In principle, it may still be the case that an outside investor with no or hardly any profit rights holds a “golden share” or has other rights of control.Footnote 35
6 Further Analyses
6.1 Bargaining Over Wholesale Tariffs
We have so far assumed that supplier U makes TIOLI offers. In this subsection, we relax this assumption and examine the case when the downstream firms have bargaining power. We ask whether downstream bargaining power induces a knowledge sharing by downstream firms that is similar to partial ownership.
We find that there exists a critical level of downstream bargaining power below which there is no sharing of technology and our result of inefficient-vertical-innovation-incentives-absent-partial-ownership holds. For higher levels of downstream bargaining power, firms have incentives to reduce the costs of U even without partial ownership.
Suppose each downstream firm has a bargaining power of \(\beta \in [0,1]\), so that U’s bargaining power is \(1-\beta\). These power shares determine the split of the additional rents from trading between the parties. We maintain the assumption of secret wholesale contracts with passive beliefs as before. The equilibrium tariffs solve the corresponding Nash bargaining problem
The anticipated upstream profit in the case of a breakdown in negotiation with i is
where \(q_{j}^{DEV}\) is the quantity of i’s rivals in the case of a breakdown in negotiations with firm i. The equilibrium wholesale contracts are characterized below.
Lemma 4
Bilateral bargaining between U and each downstream firm yields \(w_{i}^{*}=c^{U}\) and \(f_{i}^{*}=(1-\beta )\left( \pi (c^{U},c^{U})-\pi (c^{I},c^{U})\right)\). The downstream profit is \(\pi _{i}-f_{i}^{*}=\beta \ \pi (c^{U},c^{U})+(1-\beta )\ \pi (c^{I},c^{U})\).
Proof
See “Appendix 1”. \(\square\)
The intuition for the marginal cost pricing result is as before: As the contracts are secret, the actual marginal wholesale price does not affect the output choices of the other downstream firms. The upstream and the downstream firm act like an integrated entity when setting wholesale prices. Only the fixed fees differ and depend on the bargaining power of the supplier. One can see that the fixed fee decreases as the bargaining power \(\beta\) of the downstream firm increases. The fixed fees are always weakly positive.
The net downstream profit is a weighted sum of the equilibrium flow profit and the outside option profit. If a downstream firm has no bargaining power with respect to the supplier (\(\beta =0\)), it obtains just the outside option flow profit—which decreases as \(c^{U}\) falls. Instead, when the downstream firm has all the bargaining power (\(\beta =1\)), it obtains the full flow profit \(\pi (c^{U},c^{U})\) and thus benefits from cost reductions. As \(\beta\) increases, the downstream firm cares more about the equilibrium flow profits than it does about its outside option. As the downstream profit in equation is continuous in the bargaining power \(\beta\), there exists a threshold \({\tilde{\beta }}\in (0,1)\), such that for all \(\beta >{\tilde{\beta }}\), it holds that \(\partial \left( \pi _{i}-f_{i}\right) /\partial c^{U}<0\). We summarize the result below.
Proposition 3
A downstream firm has an incentive to foster cost-reducing innovations of the efficient supplier U if the downstream firm has sufficient bargaining power.
It is important to note that the mere fact that a downstream firm has some level of bargaining power (\(\beta >0\)) does not ensure that a downstream firm has incentives to reduce the costs of the efficient supplier. Its bargaining power needs to be high enough. The next corollary generalizes Proposition 2 to show that partial backward ownership also helps to align the incentives if a downstream firm does not have enough bargaining power.
Corollary 2
Suppose that the bargaining power of a downstream firm is not sufficient to incentivize cost-reducing innovations of the efficient supplier U. Endowing the downstream firm with a sufficiently high partial ownership share of supplier U aligns the incentives of the downstream firm.
Proof
See “Appendix 1”. \(\square\)
In general, bargaining power is the ability of an economic agent to obtain rents from a trade. In view of noncontractible supply chain cooperation, such as knowledge sharing, it might be beneficial for an upstream firm to endow the downstream firms with some bargaining power. The question is how can a firm commit to “fair” supply terms in the future. One possibility could be long-term framework agreements, but these may not be renegotiation proof.
Another solution is backward ownership which—similar to downstream bargaining power—can align the incentives of downstream firms. An obvious advantage of ownership shares is that they are structural arrangements, which are in place independent of supply contracts. For example, a customer might disregard a promise of a supplier to “fair” terms of trade as “cheap talk.” Instead, ownership shares are contractual rights, which the supplier (or its initial owner) can sell to a downstream firm. These contractible ownership rights encourage noncontractible actions—such as knowledge sharing—as they allow for participation in upstream gains that is similar to the effect of bargaining power.
6.2 Limited Innovation Spillovers to Rivals
So far, we have assumed that when a downstream firm induces an innovation at U, this reduces the marginal production costs for all downstream firms equally. We relax this assumption and assume that the rivals can benefit only from a proportion \(\sigma \in [0,1)\) of the cost reduction.Footnote 36 It is straightforward to show that for any \(\sigma\) the wholesale prices (\(w_{i}\)) are equal to marginal costs and the profit of a downstream firm without backward ownership is the outside option value
For any \(\sigma >0\), the downstream profit decreases in the case of an innovation by supplier U absent partial ownership. For \(\sigma =0\), the downstream profit, which is given by Eq. (7), does not change, and a downstream firm is indifferent between sharing and not sharing the technology with U. We know that, even for \(\sigma =1\), partial ownership can align the incentives of the downstream firm with supplier U and induce cooperation. Consequently, for any \(\sigma \in [0,1)\) it is possible to find a level of backward ownership such that technology sharing is induced. As argued above, our results follow through.
6.3 Public Wholesale Tariffs
As the results of models with vertical relations can depend on the contracting assumption, we show that our main results also hold with public two-part tariffs. In what follows, we demonstrate that our main results can also be obtained with public wholesale tariffs.
With secret contracts, an upstream firm faces an opportunism problem and, under common assumptions, typically cannot charge prices above marginal costs (see Hart and Tirole (1990) ). In particular, with secret contracts and passive beliefs, upon receiving a contract offer, each downstream firm anticipates that its rivals will stick to the anticipated equilibrium quantity. Thus, contracts are set as if U and i were an integrated entity with marginal cost pricing as the outcome.
Suppose that an unconstrained monopolist offers observable two-part tariffs to competing downstream firms with marginal prices that are above marginal costs. The alternative assumption is that all downstream firms can observe the supplier’s contract offers before they accept or reject the offers. This is, for instance, effectively the case if the supplier is limited by regulation to offering each downstream firm the same tariff. The well-known opportunism problem is eliminated and the supplier can sustain unit wholesale prices above marginal costs.
Interestingly, when U competes against a competitive upstream fringe, it can be optimal for the constrained monopolist to charge marginal wholesale prices that are below the alternative sourcing costs \(c^{I}\). The intuition is that the supplier decreases the equilibrium marginal prices to reduce the outside option of the competing downstream firms. This way it extracts more profits through the fixed fees.Footnote 37
We assume that marginal prices cannot be below marginal costs (\(w_{i}\ge c^{U}\)) and show that there exists a level of \(c^{I}\) below which the marginal price \(w_{i}\) that is equal to \(c^{U}\) is optimal for U.Footnote 38 One motivation for the modeling choice of excluding the possibility of \(w_{i}<c^{U}\) is that a firm that offers a linear tariff that is below marginal costs is vulnerable to accusations of predatory pricing behavior.Footnote 39 The assumption is fairly standard in the literature. This implies that one obtains the same results with respect to innovation incentives and partial backward ownership with observable as with secret wholesale tariffs. To show that the main results can also be obtained with public contracts, we focus in this extension on the case where marginal cost pricing results.
No partial ownership
If all downstream firms source from supplier U, the downstream firm sets quantities that solve
The solution to the n first-order conditions gives us equilibrium quantities and profits for given marginal input prices denoted by \(q_{i}^{*}(w_{i},{\varvec{w}}_{\varvec{-i}})\), \(Q^{*}(w_{i},{\varvec{w}}_{\varvec{-i}})\) and \(\pi ^{*}(w_{i},{\varvec{w}}_{\varvec{-i}})\). Here, \({\varvec{w}}_{\varvec{-i}}\) is the vector of the wholesale prices charged to \(i'\)s rivals. As the contracts are public, the equilibrium quantities and profits of each downstream firm depend on all the actual marginal wholesale prices set by U. The outside option profit of firm i is \(\pi _{i}^{*}(c^{I},{\varvec{w}}_{\varvec{-i}}).\) The fixed fees are \(f_{i}=\pi ^{*}(w_{i},{\varvec{w}}_{\varvec{-i}})-\pi _{i}^{*}(w_{i}=c^{I},{\varvec{w}}_{\varvec{-i}}).\)
The supplier solves
subject to \(w_{i}\ge c^{U}\ \forall i\). The following lemma characterizes the parameter range in which marginal cost pricing also occurs with public contracts.
Lemma 5
There exists a cost level \(c^{I}={\hat{c}}\), such that for all \(c^{I}<{\hat{c}},\) the supplier sets public wholesale prices that are equal to marginal costs. These tariffs are the same as for the case of secret contracting. Hence, a downstream firm has no incentive to induce an innovation that reduces the marginal costs of the efficient supplier U absent partial ownership.
Proof
See “Appendix 1”. \(\square\)
Partial ownership
We now show that partial ownership aligns the incentives of the downstream firms with industry surplus also in the case of public wholesale contracts. For expositional purposes, let us assume there are two firms (\(n=2\)) that both have partial ownership \(\delta _{i}=\delta\) in the supplier. Consequently, the profit of firm i is
Let us denote the equilibrium quantities as \((q_{1}^{*},\ q_{2}^{*})\) and the total quantity in the market as \(Q^{*}=q_{1}^{*}+q_{2}^{*}.\)
The outside option of firm i is to source alternatively, which yields a profit of
If we move on to the contracting stage, the supplier sets \((w_{i},\ f_{i})\) for \(i\in {1,2}\). The supplier’s problem is to
The fixed fees are set such that the participation constraint of the downstream firms are binding, which yields \(f_{i}=\frac{\pi _{i}-\pi _{i}^{I}(c^{I},w_{j})}{1-\delta }\) \(\forall i\).Footnote 40 The supplier’s maximization problem becomes
The following proposition characterizes the parameter space when the supplier uses marginal cost pricing in a wholesale pricing strategy.
Proposition 4
For \(c^{I}<{\hat{c}}\), the supplier sets wholesale prices that are equal to marginal costs. For sufficiently large partial ownership shares, each downstream firm’s equilibrium profit is \(\pi (c^{U},c^{U})\) and each downstream firm is willing to induce innovations that reduce the costs \(c^{U}\) of supplier U as well as the costs of the alternative supplier (\(c^{I}\)).
Proof
See “Appendix 1”. \(\square\)
For \(c^{I}<{\hat{c}},\) the supplier charges marginal prices that are equal to its marginal cost. Under this parameter restriction, the results are as in the case with secret contracts. Downstream firms are the residual claimants of a proportion of the industry profit and hence would like to reduce the costs of U. For larger alternative sourcing costs, one can obtain similar results. We explain the intuition below:
Suppose that \(c^{I}>\hat{c,}\) then it is expected that the wholesale prices are symmetric and are in the range \(c^{I}>w>c^{U}\). The upper bound on w arises because the efficient supplier is still constrained by the alternative supply option. Without partial ownership—and for a given equilibrium wholesale price that is charged to each downstream firm—the profit of each downstream firm is its outside option, which is given by \(\pi (c^{I},w)\). It is straightforward to see that this is analogous to the outside option of a downstream firm in the benchmark case where rivals source from U. This outside option is falling as w falls and as a result our benchmark knowledge-sharing result holds for the case without partial ownership.
Now, suppose without any loss of generality that firm 1 holds an ownership stake \(\delta _{1}\) in U. The ensuing profit would again then be a linear combination of the outside option flow profit and the on-equilibrium flow profit as given below
For a large enough partial ownership stake, the downstream firm has an incentive to share cost-reducing technology with U. Thus, our benchmark results still hold for \(w>c^{U}\).
6.4 Linear Upstream Prices and Partial Ownership
So far, we have considered that U offers two-part tariffs. Let us now look at the case of linear tariffs. For simplicity, suppose that the marginal wholesale prices are observable. We find that wholesale prices (\(w_{i}\)) are above marginal costs \(c^{U}\). Absent partial backward ownership and if the alternative supply source is sufficiently competitive, it is optimal for U to charge \(w_{i}=c^{I}\).Footnote 41 With input costs of \(c^{I}\) when sourcing from U, the profit of a downstream firm is just the outside option profit \(\pi (c^{I},c^{I})\).
As with two-part tariffs, the profit of a downstream firm does not increase as its supplier’s costs (\(c^{U}\)) decrease.Footnote 42 This means that there is no profitable incentive for the downstream firm to help to reduce the input costs of U. There is, however, again an incentive to reduce the alternative sourcing costs \(c^{I}\) as a lower input cost level for all downstream firms leads to higher profits.
With partial ownership of firm i, its downstream profit when all firms source from U is given by
Its marginal profit is
Firm i receives a per-unit discount of \((w_{i}-c^{U})\) on each unit bought. As a consequence, supplier U can raise \(w_{i}\) until the effective input price is again \(c^{I}\). If the supply source is sufficiently attractive, this means that \(c^{I}-c^{U}\) is not too large, and it is optimal for U to charge \(w_{i}=\frac{c^{I}-c^{U}\delta _{i}}{1-\delta _{i}}\,\forall i\).Footnote 43 An increase of the (nominal) linear wholesale price in the backward ownership share has also been shown by, for instance, Flath (1989), Greenlee and Raskovich (2006); as well as Hunold and Stahl (2016). This result is consistent with empirical evidence. Gans and Wolak (2013) study the passive backward integration of a large Australian electricity retailer into a baseload electricity generation plant and report a significant increase in the wholesale price.Footnote 44
Note that the input prices for other firms do not affect the marginal profit of firm i. The resulting downstream quantities are thus the same as without partial ownership. The resulting equilibrium downstream profit of firm i is
In equilibrium, the per-firm output equals 1/n times the total Cournot output when all downstream firms have effective input costs of \(c^{I}\).
With partial ownership, the profit of a downstream firm as stated in Eq. (8) increases as the supplier’s costs (\(c^{U}\)) decrease. A downstream firm thus has an incentive to reduce the supplier’s costs when \(\delta _{i}>0\) and \(n>1\). This would not be the case if there were no other downstream firms as long as supplier U charges an input price of \(c^{I}\), similar to the case of non-linear tariffs—although in the latter case a sufficiently higher partial backward ownership share would be necessary to create an incentive to decrease \(c^{U}\).
6.5 Downstream Bertrand Competition and Partial Ownership
The result that a downstream firm may have no incentive to help improve supplier U’s efficiency also holds under differentiated Bertrand competition. Backward ownership has an additional effect of relaxing downstream competition. To keep the exposition simple, we focus on linear tariffs. This is because—as is discussed in Rey and Vergé (2004)—passive beliefs are often not a plausible equilibrium concept in the case of two-part tariffs and price competition downstream.
The demand of a downstream firm is now given by \(q_{i}\): with \(q_{i}\) decreasing in the own price \(p_{i}\) and increasing in the competitors’ prices \(p_{j},\,j\ne i\). We assume that firms are differentiated and compete in prices, such that we obtain smooth best response functions and interior optima with prices above marginal costs. The profit of a downstream firm that has an ownership share \(\delta _{i}\) of the efficient supplier U and sources all of its inputs from U is given by
Differentiating this profit with respect to \(p_{i}\) yields the first-order condition
U still has an incentive to charge the highest possible price of \(w_{i}=\frac{c^{I}-c^{U}\delta _{i}}{1-\delta _{i}}\,\forall i\) under the assumption of effective upstream competition (\(c^{I}-c^{U}\) not too large). Condition (10) thus becomes
and the downstream profit of firm i is given by
Under downstream Cournot competition, the profit of downstream firm i is affected only by the supplier’s actual costs \(c^{U}\) if firm i has partial ownership (\(\delta _{i}>0\)). In this case, the downstream firm has incentives to reduce U’s costs.
With price competition there is the additional effect that the marginal profit increases with partial ownership as \(\partial q_{j}/\partial p_{i}>0\) for \(i\ne j\), which typically leads to higher final prices in the industry. See Hunold and Stahl (2016) for a complete analysis of this additional effect.
6.6 Ownership Acquisitions
Let us briefly discuss how ownership acquisitions could materialize. Let us start from a situation of complete independence where each firm is owned by a different owner. Suppose that the owners of firm U and downstream firm 1 consider transferring a non-controlling ownership share \(\delta >0\) of U from the initial owner of firm U to firm 1 at a transfer price of t. With the use of a slightly ad hoc notation, the initial owner of U benefits from the transfer if
which yields the minimum transfer level t that the supplier accepts for an ownership share \(\delta\). Similarly, the condition for the initial owner of firm 1 is
which yields the maximum transfer level that the owner of firm 1 is willing to pay for a share \(\delta\) in U.
Joint gains from the trade exist when the sum of the left hand sides of the above two equations is larger than the sum of the right-hand-sides:
Gains from trade exist if the ownership transfer induces firm 1 to help decrease the cost \(c^{U}\) of the upstream firm and thereby increase their joint profits. Recall from Proposition 2 that this is the case for \(\delta _{1}>{\widetilde{\delta }}\). In this case, there is a range of transfer prices \(({\underline{t}},{\overline{t}})\) in which both owners gain from the transfer. Moreover, as \(\delta\) rises, this price range rises as now the acquiring firm obtains a bigger share of a more efficient U. Thereby, the transfer price increases as the ownership stake increases.
Alternatively, for \(\delta _{1}<{\widetilde{\delta }}\), the left-hand-side of Eq. (14) equals the right hand side and no gains from trade exist. Here, an equity transfer is a zero sum game and would only materialize at a transfer price per share of \(t/\delta =\Pi ^{U}(\delta _{1}=\delta )=\Pi ^{U}(\delta _{1}=0)\).
7 Conclusion
We studied the incentives of competing downstream firms to foster supply chain innovations that increase supplier efficiency. Our leading example is knowledge about how the supplier could produce the inputs more efficiently, which a downstream firm has gained when using the inputs. Knowledge sharing might involve exploratory discussions and collaborations of the engineers of the downstream firm and its supplier. Such knowledge sharing might be implicit, and its success might be difficult to measure. We have therefore focused on the case in which firms cannot contract upon these actions and outcomes.
We first showed that a downstream firm with little or no bargaining power may have no incentive to induce an innovation that reduces its supplier’s marginal costs. Instead, a downstream firm has incentives to help improve the inefficient alternative supply source. These incentives can induce costly and socially wasteful investments in, for instance, in-house production facilities or inefficient independent suppliers.
The distorted incentives arise because a powerful efficient supplier offers the downstream firm just its outside option of buying from the inefficient alternative supplier. This outside option value falls when the efficient supplier’s costs decrease and rises if the alternative supply costs fall. This results in technologies being shared with the inefficient supplier to improve the outside option rather than the actual supply process. This technology allocation is inefficient from a social and industrial standpoint.
Non-controlling backward ownership shares can solve this problem and induce efficient innovation incentives. With a sufficiently high ownership share, a downstream firm benefits from a decrease in the costs of the powerful efficient supplier and thus has an incentive to foster such innovations. This increases industry performance and profits.
In summary, the argument that non-controlling backward ownership induces efficient supply chain innovations applies to markets with the following characteristics: First, one or several downstream firms are potentially capable of supporting the supplier in improving its efficiency. For instance, by using the inputs they gain knowledge on how to improve production of the inputs in a better way. Second, it may be difficult to write complete contracts in return for fostering upstream innovation appropriately. Third, downstream firms may have limited bargaining power.
Both firms and competition authorities can benefit from a deeper understanding of the incentives to foster supply chain innovations and the positive role of non-controlling ownership in this respect. For upstream firms, it is important to recognize that their industrial customers may have no incentive to help improve their supplier’s efficiency, but may instead have an incentive to worsen it. At the same time, industrial customers may have strong incentives to invest inefficiently even in inferior alternative sourcing options. This may also include sharing the trade secrets of their supplier with its (potential) upstream competitors.
For such situations, a management implication is to consider equity transactions that endow the downstream firms with financial interests in their suppliers. This can align the supply chain incentives and in this way foster supply chain cooperation and boost efficiency. This clearly improves industry performance and profits. In principle, it should be possible to find an agreeable price for such an equity transaction and, if necessary, convince competition authorities of its social benefits.
Assessing the pro- and anti-competitive effects of ownership acquisitions is also important for merger control. While there are jurisdictions that already control minority acquisitions, it is not yet the case at the European level, but it is an ongoing discussion.Footnote 45 Both for assessing the relevance of controlling partial vertical ownership and for assessing individual cases, it is important to understand its effects better. The present article complements the growing literature on the anti-competitive effects of vertical partial ownership. We discuss its pro-competitive effects that include fostering supply chain innovations through vertical knowledge spillovers and other forms of not contractible but essential vertical collaborations.
Notes
Hartley (2000) and Kwon and Suh (2004) show that information sharing between firms builds stronger supply chain relationships. Lee et al. (1997) suggest that information sharing by downstream firms with upstream firms can mitigate the “bullwhip" effect which is defined as the amplification in demand order variabilities when moving up the supply chain.
For example, executives and engineers who work for Toyota and for its suppliers meet under the direction of a Toyota sensei (teacher) to improve the suppliers’ processes (Liker & Choi, 2004). Similarly, Honda of America sent an engineer to spend a year with a Cleveland-based company, Atlantic Tool and Die. The engineer offered suggestions that led to marked improvements on the shop floors (Liker & Choi, 2004).
See the non-horizontal merger guidelines of the European Commission.https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:C:2008:265:0006:0025:en:PDF.
Similarly, the authorities view controlling backward ownerships suspiciously. See EC WHITE PAPER Towards more effective EU merger control, para 36. https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52014DC0449&rid=2.
For instance, Toyota has around 24 percent share in its suppliers Denso and Aisin, with whom it also has a strategic partnership (https://www.denso.com/global/en/investors/stock/overview/, http://www.aisin.com/investors/stock/, last access June 2018).
When producing general inputs, the supplier has the outside option of selling these in other markets. However, the supplier’s bargaining position toward the customer is worse as with backward ownership the customer also benefits from these sales in the event of a negotiation breakdown. In particular, the customer’s outside option in the case of general inputs is not zero, but positive, which reduces the gains from trade with the supplier and thus leads to a more favorable Nash-bargaining outcome for the customer.
They assume that one customer values the input more than the other and can additionally make a costly investment that increases the value of the input for both customers. The assumption that the input price equals the value for the lower-value customer implies that the high-value customer has reduced investment incentives. With partial backward ownership, this customer effectively pays less because it gets part of the price back through the profit participation, which can increase the investment incentive.
The results in this article also hold when the firms produce a differentiated product. For the case of price competition with differentiated products, see Sect. 6.5.
The alternative supply can be an in-house production facility or a fringe supplier. A potential difference between an alternative supplier and in-house production arises only if a downstream firm induces innovations at only its in-house supply or a fringe that is also used by others, but this is not essential for our main arguments.
It has been well documented that private labels in the retail industry present a strong competitive constraint on established brands. This improves the bargaining position of retailers vis-a-vis established brands. See Inderst and Mazzarotto (2008).
We assume that \({\tilde{c}}\) is sufficiently large such that \(c^{U}\) and \(v^{I}\) remain non-negative.
Our results go through when acceptance decisions are not public. See “Appendix 2”.
Non-controlling ownership stakes that downstream firms hold in upstream firms (backward ownership) tend to have no effect on downstream prices when there is an upstream monopolist (Greenlee & Raskovich, 2006). They can lead to higher prices when downstream firms compete in price as they internalize each other’s demand through the margin on input sales (Hunold & Stahl, 2016). To abstract from these pricing effects, we use downstream Cournot competition as a benchmark in the main part.
See Sect. 4.2 for details.
See Caprice (2006) for a similar set-up. Our results are qualitatively the same if the contract acceptance is not observable. See “Appendix 2”.
Under this belief structure, downstream firms do not revise their beliefs about the offers that have been made to rivals when receiving an out-of-equilibrium offer. See Nocke and Rey (2014), as well as: Hart and Tirole (1990), O’Brien and Shaffer (1992), McAfee and Schwartz (1994), Caprice (2006), Rey and Tirole (2007), Arya and Mittendorf (2011).
These assumptions ensure that the equilibrium is characterized by first-order conditions and downstream quantities are strategic substitutes. It is sufficient that profits are strictly concave in own quantities and the cross-derivatives are negative: \(\partial ^{2}\pi _{i}/(\partial q_{i}\partial q_{-i})<0\) for \(i\ne -i\).
U must leave each downstream firm the profit it could earn when sourcing from I while its rivals have marginal costs \(c^{U}\).
Our leading example is the knowledge that a downstream firm has gained when using the inputs in its production process. This could be knowledge about how the input can be produced in a more efficient way. Transferring this knowledge to the supplier might involve exploratory discussions and collaborations between the customer’s engineers and its supplier, and the causal success of these might be difficult to measure. Consequently, such knowledge might be rather implicit and difficult to contract upon.
We generalize this in Sect. 6.2.
In Sect. 6.1, we study the case where downstream firms also have bargaining power. In this case, for low levels of downstream bargaining power the downstream firms have similar incentives to those here.
At least as long as the alternate supply source production remains less efficient than supplier U. Even if it becomes more efficient, this remains a suboptimal investment if the alternative would have been to reduce further the costs of the more efficient supplier U.
While evidence on improving one’s own outside options is easy to find, we are not aware of direct evidence of such sabotage activities.
Backward means that a downstream firm holds shares in an upstream firm.
This avoids the discussion with respect to the level of shareholdings at which control arises—which depends on corporate law, the shareholder agreement, and the distribution of ownership share holdings in the target firm.
In this article, we do not strive to change the control over the strategic decisions of firms at different levels of the supply chain as is seen in older articles. We show that profit participation (without control of the supply chain) is enough to align the firms’ incentives at different levels of the supply chain.
For example, the engineer who is necessary for transferring the technology might have limited time.
Instead, if the downstream firms have perfectly substitutable knowledge—or similar inputs for upstream innovation—it might be sufficient to incentivize one downstream firm in order to achieve an improvement in supplier U. However, this leaves potentially inefficient investments in inferior supply sources, which alter the outside options and thus the terms of trade.
If the term in the first bracket is zero, only the second summand remains. This is the case for \(1-(n-1)\frac{\delta }{1-\delta }=0\implies \delta =\frac{1}{n}.\)
See Hunold and Schlütter (2018) for a discussion of the effects of profit and control rights that are due to partial vertical ownership.
The case assumed so far is \(\sigma =1\).
See Inderst and Shaffer (2011) for a detailed analysis.
This is because for a low enough \(c^{I}\) we obtain a corner solution of \(w_{i}=c^{U}\). This is the case both with and without partial backward ownership.
For instance, the European Commission (EC) presumes that pricing below average variable costs by a dominant firm in the market is considered abusive. See https://ec.europa.eu/dgs/competition/economist/pred_art82.pdf.
Note here that in the term \(\pi _{i}-\pi _{i}^{I}(c^{I},w_{j})\), the fixed fees \(f_{j}\) cancel out.
This is the case when the cost difference \(c^{I}-c^{U}\) is not too large.
At least as long as the change is not so large that the supplier becomes an unconstrained monopolist.
This follows from \(c^{I}=w_{i}-\delta _{i}(w_{i}-c^{U}).\)
Gans and Wolak (2013) build their theory using a model of fixed-price forward contracting. Nevertheless, their empirical finding of a price increase is also consistent with the theory presented here.
See Appendix II “Non-controlling minority shareholdings and EU merger control” of the European Commission Staff Working Document “Towards more effective EU merger control” of 2013 (last accessed February 2019).
This can be seen as \((\frac{\partial q_{i}^{*}}{\partial w_{i}}+\frac{\partial Q_{-i}^{*}}{\partial w_{i}})<0\) and \(P'(Q^{*})<0.\)
Note here that in the term \(\pi _{i}-\pi _{i}^{I}(c^{I},w_{j})\), the fixed fees \(f_{j}\) cancel out.
Threshold \({\hat{c}}\) is such that \(\frac{\partial \pi ^{U}}{\partial w_{1}}=(P'(Q^{*})q_{2}-\frac{\partial \pi _{2}^{*}(w_{2}={\hat{c}},w_{1})}{\partial w_{1}}=0\) and \(w_{1}=w_{2}=c^{U}\) is optimal.
References
Allen, J. W., & Phillips, G. M. (2000). Corporate equity ownership, strategic alliances, and product market relationships. The Journal of Finance, 55(6), 2791–2815.
Arya, A., & Mittendorf, B. (2011). Disclosure standards for vertical contracts. The RAND Journal of Economics, 42(3), 595–617.
Baumol, W. J., & Ordover, J. A. (1994). On the perils of vertical control by a partial owner of a downstream enterprise. Revue d’Économie Industrielle, 69(1), 7–20.
Benoit, J.-P. (1984). Financially constrained entry in a game with incomplete information. The RAND Journal of Economics, 490–499.
Bonnet, C., & Dubois, P. (2010). Inference on vertical contracts between manufacturers and retailers allowing for nonlinear pricing and resale price maintenance. The RAND Journal of Economics, 41(1), 139–164.
Bönte, W., & Keilbach, M. (2005). Concubinage or marriage? Informal and formal cooperations for innovation. International Journal of Industrial Organization, 23(3–4), 279–302.
Bönte, W., & Wiethaus, L. (2007). Knowledge disclosure and transmission in buyer-supplier relationships. Review of Industrial Organization, 31(4), 275–288.
Cachon, G. P., & Lariviere, M. A. (2005). Supply chain coordination with revenue-sharing contracts: Strengths and limitations. Management Science, 51(1), 30–44.
Caprice, S. (2006). Multilateral vertical contracting with an alternative supply: The welfare effects of a ban on price discrimination. Review of Industrial Organization, 28(1), 63–80.
Cavusgil, S Tamer, Calantone, Roger J., & Zhao, Yushan. (2003). Tacit knowledge transfer and firm innovation capability. The Journal of Business and Industrial Marketing, 18(1), 6–21.
Choi, J. P., Ghosh, A., Niu, S., & Moritam, H. (2014). Vertical learning alliances and partial equity ownership in the presence of performance spillovers. Working paper.
Dasgupta, S., & Tao, Z. (2000). Bargaining, bonding, and partial ownership. International Economic Review, 41(3), 609–635.
Deneckere, R. J., & Preston McAfee, R. (1996). Damaged goods. Journal of Economics and Management Strategy, 5(2), 149–174.
Dyer, J. H., & Hatch, N. W. (2004). Using supplier networks to learn faster. MIT Sloan Management Review, 45(3), 57–63.
Fiocco, R. (2016). The strategic value of partial vertical integration. European Economic Review, 89, 284–302.
Flath, D. (1989). Vertical integration by means of shareholding interlocks. International Journal of Industrial Organization, 7(3), 369–380.
Fudenberg, D., & Tirole, J. (1986). A theory of predation. The RAND Journal of Economics, 366–376.
Gans, J. S., & Wolak, F. (2013). A comparison of ex ante versus ex post vertical market power: evidence from the electricity supply industry. SSRN Working paper No. 1288245.
Ghosh, A., & Morita, H. (2017). Knowledge transfer and partial equity ownership. The RAND Journal of Economics, 48(4), 1044–1067.
Greenlee, P., & Raskovich, A. (2006). Partial vertical ownership. European Economic Review, 50(4), 1017–1041.
Hamel, Gary. (1991). Competition for competence and interpartner learning within international alliances. Strategic Management Journal, 12(S1), 83–103.
Hart, O., & Tirole, J. (1990). Vertical integration and market foreclosure. Brookings Papers on Economic Activity. Microeconomics. (pp. 205–286).
Hartley, J. L. (2000). Collaborative value analysis: Experiences from the automotive industry. Journal of Supply Chain Management, 36(3), 27–32.
Hughes, J. S., & Kao, J. L. (2001). Vertical integration and proprietary information transfers. Journal of Economics & Management Strategy, 10(2), 277–299.
Hunold, M., & Schlütter, F. (2018). Vertical financial interest and control. Working paper.
Hunold, M., & Stahl, K. (2016). Passive vertical integration and strategic delegation. The RAND Journal of Economics, 47(4), 891–913.
Hunold, Matthias. (2020). Non-discriminatory pricing, partial backward ownership, and entry Deterrence. International Journal of Industrial Organization, 70, 102615.
Inderst, R., & Mazzarotto, N. (2008). Buyer power in distribution. In ABA Antitrust Section Handbook, Issues in Competition Law and Policy (Vol. 3, pp. 1953–1978). ABA.
Inderst, Roman, & Shaffer, Greg (2011). Wholesale price determination under the threat of demand-side substitution. Available at SSRN 2395274 .
Kotabe, M., Martin, X., & Domoto, H. (2003). Gaining from vertical partnerships: Knowledge transfer, relationship duration, and supplier performance improvement in the US and Japanese automotive industries. Strategic Management Journal, 24(4), 293–316.
Kwon, I.-W.G., & Suh, T. (2004). Factors affecting the level of trust and commitment in supply chain relationships. Journal of Supply Chain Management, 40(1), 4–14.
Lee, H. L., Padmanabhan, V., & Whang, S. (1997). Information distortion in a supply chain: The bullwhip effect. Management Science, 43(4), 546–558.
Levy, N., Spiegel, Y., & Gilo, D. (2018). Partial vertical integration, ownership structure, and foreclosure. American Economic Journal: Microeconomics, 10(1), 132–80.
Liker, Jeffrey K., & Choi, Thomas Y. (2004). Building deep supplier relationships. Harvard Business Review, 82(12), 104–113.
Lin, Y.-T., Parlaktürk, A. K., & Swaminathan, J. M. (2014). Vertical integration under competition: Forward, backward, or no integration? Production and Operations Management, 23(1), 19–35.
Mathews, R. D. (2006). Strategic alliances, equity stakes, and entry deterrence. Journal of Financial Economics, 80(1), 35–79.
McAfee, R. P., & Schwartz, M. (1994). Opportunism in multilateral vertical contracting: Nondiscrimination, exclusivity, and uniformity. The American Economic Review, 84(1), 210–230.
Mowery, D. C., Oxley, J. E., & Silverman, B. S. (1996). Strategic alliances and interfirm knowledge transfer. Strategic Management Journal, 17(S2), 77–91.
Nocke, V., & Rey, P. (2014). Exclusive dealing and vertical integration in interlocking relationships. SSRN Working paper No. 2503427.
Nonaka, I. (1994). A dynamic theory of organizational knowledge creation. Organization Science, 5(1), 14–37.
O’Brien, D. P., & Shaffer, G. (1992). Vertical control with bilateral contracts. The RAND Journal of Economics, 23(3), 299–308.
Rey, P., & Tirole, J. (2007). A primer on foreclosure. Handbook of Industrial Organization, 3, 2145–2220.
Rey, P., & Vergé, T. (2004). Bilateral control with vertical contracts. RAND Journal of Economics, 35(4), 728–746.
Spiegel, Y. (2013). Backward integration, forward integration, and vertical foreclosure. CEPR Discussion Paper DP9617.
Villas-Boas, S. B. (2007). Vertical relationships between manufacturers and retailers: Inference with limited data. The Review of Economic Studies, 74(2), 625–652.
Wang, J., & Shin, H. (2015). The impact of contracts and competition on upstream innovation in a supply chain. Production and Operations Management, 24(1), 134–146.
Wiethaus, L. (2005). Absorptive capacity and connectedness: Why competing firms also adopt identical R&D approaches. International Journal of Industrial Organization, 23(5), 467–481.
Yildirim, H. (2007). Proposal power and majority rule in multilateral bargaining with costly recognition. Journal of Economic Theory, 136(1), 167–196.
Acknowledgements
We thank Toker Doganoglu, Paul Heidhues, Ismael Martínez-Martínez, Daniel Müller, Hans-Theo Normann, Frank Schlütter, Yossi Spiegel, Tim Thomes, Christian Wey, Lawrence White, two anonymous referees, as well as seminar participants at CORE, DICE, the University of Würzburg, and participants of the IIOC 2018 and the MaCCI 2018 annual conference for helpful comments and discussions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Proofs
Proof of Lemma 1
Suppose that each firm believes that the equilibrium contracts that are given to all firms \(j\in \{1,2..n\}\) are \((w_{j}^{*},f_{j}^{*})\) and the corresponding quantities that are demanded by each firm j as \(q_{j}^{*}.\) Let \({\varvec{w}}_{\varvec{-j}}^{*}\) be the vector of the wholesale prices that are charged to all of the firms other than j. With passive beliefs, a firm’s conjecture on the contracts that are offered to its rivals does not change when it is offered an off-equilibrium contract. Hence, as a result, firm i chooses the quantity \(q_{i}^{BR}\) that solves the FOC
where \(Q_{-i}^{*}\) is the sum of the expected quantity of the other downstream firms when they believe the equilibrium contracts \((w_{j}^{*},f_{j}^{*})\) for \(j\ne i\in \{1..n\}\) are being offered. The profit of firm i is given as
If i rejects the contract offer, its profit is given as
where \(Q_{-i}^{*\text {DEV}}\)are the quantities of the rivals when the wholesale prices are \((w_{i}^{*}=c^{I},{\varvec{w}}_{\varvec{-i}}^{*})\). This is because a breakdown in negotiations is observable after the contracting stage. U sets the fixed fee for a given marginal price such that a downstream firm’s profit equals its outside option. This implies
The supplier’s profits are then given as
Differentiating with respect to \(w_{i}\) yields the FOC
Using the FOC (15) of downstream firm i yields
This implies \(w_{i}^{*}=c^{U}\)for all i. \(\square\)
Proof of Lemma 3
It is common knowledge when prices are determined that each firm holds a non-controlling share \(\delta _{i}\in [0,1)\) of the upstream firm U. Apart from this, the setting is the same as without vertical ownership. We therefore build on the proof of Lemma 1 and focus on differences from the previous case. As we can maintain the assumption of passive beliefs, for any contract received by firm i, it expects that all of the other firms \(j\ne i\in \{1...n\}\) choose the quantity \(q_{j}^{*}.\) In turn, firm i chooses the best-response quantity \(q_{i}^{BR}\) which now solves the expression
A downstream firm takes into account that it obtains a “rebate” \(\delta _{i}\) on the upstream margin of U.
The profit of firm i when it accepts \(U'\)s contract is given as
If i rejects the contract offer, its profit is given as
Supplier U sets the fixed fee for a given marginal price such that a downstream firm’s profit equals its outside option. This yields
The resulting upstream profit is
which can be reduced to
Differentiating with respect to \(w_{i}\) yields
Using the FOC (16) yields
Hence, we again obtain \(w_{i}^{*}=c^{U}\) for all downstream firms.
If all of the other downstream firms source from supplier U at marginal costs of \(c^{U}\), the profit of downstream firm i—which sources inputs alternatively at marginal costs \(c^{I}\) and has an ownership share \(\delta _{i}\)—is
If firm i sources from U at the tariff \(\{w_{i}=c^{U},\ f_{i}\}\), its profit is
Supplier U can raise \(f_{i}\) until \(\pi _{i}-f_{i}=\Pi _{i}^{\text {I}}:\)
The resulting profit of downstream firm i is obtained by noting that
This yields
\(\square\)
Proof of Lemma 4
Downstream firm i chooses the quantity \(q_{i}^{BR}\) that solves the FOC
where \(Q_{-i}^{*}={\displaystyle \sum _{j\ne i}q_{j}^{*}}\) is the expected quantity of the other downstream firms when they believe the equilibrium contracts \((w_{j}^{*},f_{j}^{*})\) are offered. The profit of firm i is given by
If i rejects the contract offer, its profit is given as
where \(Q_{-i}^{*\text {DEV}}\)are the quantities that are demanded by the rival firms when the set of wholesale prices are \((w_{i}^{*}=c^{I},{\varvec{w}}_{\varvec{-i}}^{*})\). This is because of our assumption that a breakdown in negotiations is observable after the contracting stage. Supplier U and firm i set the fixed fee and marginal wholesale prices to maximize the Nash bargaining solution:
where \(\pi ^{U,DEV}=\sum _{j\ne i}[(w_{j}^{*}-c^{U})\ q_{j}^{DEV}+f_{j}^{*}]\). The first-order condition of the Nash bargaining game with respect to \(f_{i}\) gives us
Substituting this into the maximization problem and simplifying gives us the program
Only the first and third term in the long parentheses of the above expression are a function of \(w_{i}\). This is the bilateral profit of supplier U and firm i from sales of i. Taking first-order conditions with respect to \(w_{i}\), we get the familiar expression
This implies \(w_{i}^{*}=c^{U}.\) By symmetry, supplier U offers contracts to all downstream firms in which the marginal price \(w_{i}\) equals its marginal costs \(c^{U}\). The fixed fees are given as
\(\square\)
Proof of Lemma 5
The supplier solves the program
subject to \(w_{i}>c^{U}\ \forall i\). The optimal wholesale price solves the first-order conditions
Focusing on A, we notice that it maximizes industry profit. A can be rewritten as \((P'(Q^{*})Q_{-i}^{*}+w_{i}-c^{U})(\frac{\partial q_{i}^{*}}{\partial w_{i}}+\frac{\partial Q_{-i}^{*}}{\partial w_{i}})\) by substituting the first-order conditions of the downstream firm i. We can clearly notice then that when \(w_{i}=c^{U}\), \(A|_{\{w_{i}=c^{U}\}}>0\).Footnote 46 As a result, we show that industry surplus-maximizing wholesale prices are higher than marginal costs. Let us denote the industry profit-maximizing wholesale prices \(w_{i}^{*}=w_{-i}^{*}:=w^{M}\). The expression \(B=\sum _{j\ne i}^{n}P'(Q^{*}({\varvec{w}}_{\varvec{-j}},w_{j}=c^{I}))\ \frac{\partial Q_{-j}^{*}({\varvec{w}}_{\varvec{-j}},w_{j}=c^{I})}{\partial w_{i}}\ q_{j}^{*}(w_{j}=c^{I},{\varvec{w}}_{\varvec{-j}})>0\) as \(\frac{\partial Q_{-j}^{*}({\varvec{w}}_{\varvec{-j}},w_{j}=c^{I})}{\partial w_{i}}<0\). It is easy to see that \(\frac{\partial \pi ^{U}}{\partial w_{i}}|_{\{w_{i}=w_{j}=w^{M}\}}<0\), which implies that in the presence of an outside option or buyer power, the wholesale prices are lower. Due to symmetry downstream, we will obtain symmetric wholesale prices, and hence, we denote the optimal wholesale price as \(w^{*}\). One can then show that as \(c^{I}\) falls, the wholesale prices also fall. When \(c^{I}\) is large enough such that \(q_{i}^{*}(w_{i}=c^{I},{\varvec{w}}_{\varvec{-i}})\le 0,\) the outside option is set at zero and \(\frac{\partial \pi ^{U}}{\partial w_{i}}|_{\{w_{i}=w_{j}=c^{U}\}}=((P'(Q^{*})Q_{-i}^{*}+w_{i}-c^{U})(\frac{\partial q_{i}^{*}}{\partial w_{i}}+\frac{\partial Q_{-i}^{*}}{\partial w_{i}})>0\), which implies that \(w^{*}>c^{U}.\) At the other extreme case, when \(c^{I}=c^{U}\), and \(w=c^{U}\), \(\frac{\partial \pi ^{U}}{\partial w_{i}}|_{\{w_{i}=w_{j}=c^{U},c^{I}=c^{U}\}}=(P'(Q^{*})\ q_{i}(w_{i},{\varvec{w}}_{\varvec{-i}})\ (\frac{\partial Q_{-i}^{*}(c^{U},c^{U})}{\partial w_{i}}))<0\), which implies that the optimal wholesale prices have to be lower. As the wholesale prices cannot be below marginal costs, there will be a corner solution. We now show the existence of a threshold \({\hat{c}}\), such that for all \(c^{I}\le {\hat{c}}\), there exists a corner solution where \(w^{*}=c^{U}.\) Using the intermediate value theorem and the fact that \(\frac{\partial \pi ^{U}}{\partial w_{i}}\) is continuous in \(c^{I}\), we can say that there exists a \(c^{I}={\hat{c}}\), such that \(\frac{\partial \pi ^{U}}{\partial w_{i}}|_{\{w_{i}=w_{j}=c^{U},c^{I}={\hat{c}}\}}=0\). Hence, for all \(c^{I}<{\hat{c}},\) the wholesale prices are set at \(w^{*}=c^{U}.\) \(\square\)
Proof of Corollary 2
We assume that a downstream firm i has bargaining power denoted by \(\beta\) vis-a-vis U, whose bargaining power is \(1-\beta\). For simplicity, we assume each downstream firm \(i\in \{1..n\}\) has the same bargaining power irrespective of the partial ownership share \(\delta _{i}\) in U.
We maintain the assumption of passive beliefs, for any contract received by firm i, it expects that all the other firms \(j\ne i\in \{1 \ldots n\}\) choose the quantity \(q_{j}^{*}.\) In turn, firm i chooses the best-response quantity \(q_{i}^{BR}\) which now solves the expression
A downstream firm takes into account that it obtains a “rebate” \(\delta _{i}\) on the upstream margin of U. The profit of firm i when accepting \(U'\)s contract is given as
If i rejects the contract offer, its profit is given as
where \(Q_{-i}^{*\text {DEV}}\)is the quantity that demanded by all the rival firms when the set of wholesale prices are \((w_{i}^{*}=c^{I},{\varvec{w}}_{\varvec{-i}}^{*})\). This is because of our assumption that a breakdown in negotiations is observable. To simplify notation, let us define the following:
where \(\pi ^{U,DEV}=\sum _{j\ne i}[(w_{j}^{*}-c^{U})\ q_{j}^{DEV}+f_{j}^{*}]\). Note that A is the surplus of i before the effective fixed fee from trade with U and C is the surplus of U before the fixed fee.
U and firm i set the fixed fee and marginal wholesale prices to maximize the Nash bargaining solution:
The first-order condition of the Nash bargaining game with respect to \(f_{i}\) gives us
Substituting this into the above maximization problem and simplifying yields
Substituting back for A and C yields
Only the underlined expression is a function of \(w_{i}\). It consists of the bilateral joint profit which is maximized at \(w_{i}=c^{U}\). In particular, simplifying the above equation, we get the FOC \((w_{i}-c^{U})(1-\delta _{i})\frac{\partial q_{i}^{BR}}{\partial w_{i}}=0\), which \(w_{i}=c^{U}\)solves.
The optimal fixed fees are then given as
The equilibrium profit of firm i is given as
Taking the derivative of the above expression with respect to \(c^{U}\), we get
The above expression is negative for \(\beta =1\), whereas for \(\beta =0\) the sign is ambiguous. Suppose that the partial ownership share \(\delta _{i}\) is sufficiently small such that the sign of the above expression is positive at \(\beta =0\): for instance, \(\delta _{i}=0\).
Let us define the critical bargaining power such that the above expression is zero at \({\hat{\beta }}\). Taking the total derivative of the expression at \({\hat{\beta }}\) with respect to \(\delta _{i}\), we get
The critical bargaining power that is necessary to allow the sharing of technology and partial ownership are substitutes. Hence, the higher is the ownership share \(\delta _{i}\) by a downstream firm, the lower its bargaining power needs to be for it to benefit from cost-reducing innovations of the efficient supplier. \(\square\)
Proof of Proposition 4
For expositional purposes, let us assume that the two downstream firms have symmetric partial ownership shares \(\delta _{i}=\delta\) of U. The profit of firm i is then given as
Rearranging yields
The first-order conditions with respect to \(q_{i}\) is \(\frac{\partial \pi _{i}}{\partial q_{i}}=(P(Q)-w_{i})+P'(Q)\ q_{i}+\delta (w_{i}-c^{U})=0\). Let us denote the equilibrium quantities as \((q_{1}^{*}(w_{1},\ w_{2}),\ q_{2}^{*}(w_{2},\ w_{1}))\) and the total quantity in the market as \(Q^{*}(w_{1},\ w_{2})=q_{1}^{*}+q_{2}^{*}.\) The alternative sourcing profit of firm i with a partial ownership \(\delta\) is given as
Let us move on to the upstream contracting stage, where the supplier sets \((w_{i},\ f_{i})\) for \(i\in {1,2}\). The supplier’s problem is given by
The fixed fees are set such that the participation constraints of the downstream firms are binding and are hence given as \(f_{i}=\frac{\pi _{i}-\pi _{i}^{I}(c^{I},w_{j})}{1-\delta }\) \(\forall i\).Footnote 47 The supplier’s maximization problem then becomes
Taking the first derivative with respect to \(w_{i}\) gives the following first-order conditions:
Rearranging and substituting from the first-order condition of \(q_{i},\) we get
The comparative statics of total quantity with a change in \(w_{i}\) as well as the change in \(q_{1}^{*}\) and \(q_{2}^{*}\) are given as
where \(a:=\frac{\partial ^{2}\pi _{i}}{\partial q_{i}^{2}}=2P'(Q^{*})+P''(Q^{*})q_{1}\), \(b:=\frac{\partial ^{2}\pi _{i}}{\partial q_{i}\partial q_{j}}=P'(Q^{*})+P''(Q)q_{i}\) . It is easy to verify that \((a+b)<0\) and \(a-b<0\).
Due to symmetry, \(\frac{\partial q_{1}}{\partial w_{1}}=\frac{\partial q_{2}}{\partial w_{2}}\) and \(\frac{\partial q_{1}}{\partial w_{2}}=\frac{\partial q_{2}}{\partial w_{1}}\forall i\ne j\in {1,2}\). Moreover, we can then write the change in total quantity with a change in \(w_{i}\) as \(\frac{\partial Q^{*}}{\partial w_{1}}=\frac{(1-\delta )}{(2(P'(Q^{*})+P''(Q^{*})q_{1}^{*})+P'(Q^{*}))}<0\) where \(P'(Q^{*})+P''(Q^{*})q_{1}<0\).
When the alternative input source is not a credible supply substitution threat—\(c^{I}\) is large enough such that \(q_{1}^{*}(w_{1}=c^{I},w_{2})\le 0\)—the alternative profit equals only the profit from partial ownership. This profit is given as
where \(q_{2}^{M}\) is the quantity that is offered when only firm 2 is active downstream off equilibrium and firm 1 is absent from the downstream market. Hence, the derivative of the supply profit with respect to \(w_{1}\) is given as
Substituting the above expression with \(\frac{\partial \pi _{2}^{I}(w_{2}=c^{I},w_{1}=c^{U})}{\partial w_{1}}=\delta q_{1}^{M}\) and rearranging, we get
The above expression utilizes the fact that for symmetric wholesale prices the quantities demanded by each firm are equal in equilibrium and hence \(q_{1}^{*}=q_{2}^{*}\). It is easy to see that the above derivative is positive.
We now look at the sign of the above equation at \(c^{I}=c^{U}\) where the alternative supply source is as efficient as the incumbent supplier. This is the case where the downstream firms have the largest buyer power. Evaluating the above derivative at \(w_{1}^{*}=w_{2}^{*}=c^{U}\) yields
Rearranging yields
The intermediate value theorem and the fact that \(\frac{\partial \pi ^{U}}{\partial w_{i}}\) is continuous on \(c^{I}\) imply that there exists a \(c^{I}={\hat{c}}\) such that \(w_{i}^{*}=w_{j}^{*}=c^{U}\).Footnote 48 By assumption, the wholesale prices cannot be below cost. Hence, for all \(c^{I}<{\hat{c}},\) the wholesale prices are set at \(w^{*}=c^{U}.\) We therefore show the existence of marginal cost pricing in a public contract setting. \(\square\)
Appendix 2: Non-observable Contract Acceptance
We first study the case when there is no partial ownership and show that there is no incentive to foster upstream innovation. We then move on to the case in which downstream firms have partial ownership and look at the innovation incentives.
The only difference to our previous case is the non-observability of the contract acceptance. This implies that the profit of firm i off-equilibrium when i rejects the contract offer is given as
One can see that due to non-observability of the acceptance or rejection decision, the belief firm i has in the equilibrium quantity choice of its rivals does not change. As the outside option is constant in \(w_{i}\) and is only a function of \(w_{-i}^{*}\), the value of the choice variable \(w_{i}\) on equilibrium does not change and is equal to \(c^{U}\). Only the fixed fee changes and is given by \(f^{*}=\pi (c^{U},c^{U})-\Pi _{i}^{\text {I}}\). Non-observability of contract acceptance only redistributes rents. As \(\frac{\partial \Pi _{i}^{\text {I}}}{\partial c^{U}}>0\), the firm i has no incentive to share a cost-reducing technology with the efficient supplier U and instead wants to share it with the alternative supply source.
Similarly, we can obtain the equilibrium contracts for the case when firm i has partial ownership \(\delta _{i}\) in U. Using the idea that the alternative sourcing profit of firm i is independent of \(w_{i}\), we again obtain that the wholesale prices are equal to marginal costs \(c^{U}\). Only the fixed fees are different. This redistribution of rents arises because the profits in the case of a contractual breakdown and alternative sourcing are different. Hence, the profit of a firm with partial ownership \(\delta _{i}\) is given as
where \({\tilde{\pi }}\) is the off-equilibrium flow profit of firm i which deviates and obtains \(w_{i}=c^{I}\), while the other firms cannot observe that a firm i is not supplied by the efficient supplier. As the flow profits \(\pi (c^{U},\ c^{U})\) increase when \(c^{U}\) decreases, for a sufficiently large weight \(\delta _{i}\), firm i has incentives to offer cost-reducing technology to the efficient supplier.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hunold, M., Shekhar, S. Supply Chain Innovations and Partial Ownership. Rev Ind Organ 60, 109–145 (2022). https://doi.org/10.1007/s11151-021-09836-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11151-021-09836-9