Upstream Competition with Complex and Unobservable Contracts

Abstract

This paper examines situations where two vertically integrated firms consider supplying an input to an independent downstream competitor via privately observed contracts. We identify equilibria where competition in the upstream market emerges—the downstream competitor gets supplied—as well as when the downstream firm does not receive the input and is excluded from the market. The likelihood of the outcome in which the downstream firm does not get supplied depends not only on demand parameters, but also on contractual flexibility and observability. We show that when contracts are unobservable, downstream entry will occur less often. Furthermore, our results suggest that permitting contracts that enable the contracting parties to coordinate their behavior in the downstream market may improve welfare by increasing the likelihood that the downstream firm is supplied.

1 Introduction

A lack of upstream competition may arise in a variety of contexts. For example, in several of the European mobile telecommunications markets the mobile network operators (MNOs) refused to supply wholesale airtime to rival mobile virtual network operators (MVNOs). In the allocation of spectrum, the possibility that firms acquire and hoard excess spectrum to prevent access by competitors raised concerns of a collective refusal to supply.¹ While regulatory and competition policy approaches have implicitly assumed that this situation is likely to emerge as a result of coordination, recent research has established that a lack of upstream competition may arise as the equilibrium of a static oligopoly game.

This literature, which is discussed at length in Sect. 1, investigates the incentives of vertically integrated firms (VIFs) to provide access to independent downstream competitors and mainly assumes that contracts are observable to all parties.² Additionally, they focus on a given restricted contractual form: e.g. a linear wholesale price. However, the degree of sophistication of contracts and their observability have significant empirical and practical relevance.³ In line with these facts, we consider contracts which are: (i) private; and (ii) are “complex” or “sophisticated” in that they allow the contracting parties to maximize their joint profits.

Our model consists of two VIFs that compete to supply an input to an independent competitor in the downstream market, where products are differentiated. We show that the unobservability of contracts makes it more likely that the independent competitor is foreclosed. Furthermore, upstream competition emerges—or, equivalently in our context, the downstream firm gets supplied—for a larger region of parameters, when more sophisticated contracts are allowed. We also provide practically relevant and permissible examples of such contracts.

Our results imply interesting complications for competition policy. Some examples of sufficiently sophisticated contracts envisage a high degree of coordination among contracting parties. Hence they may raise competition concerns and may be frowned upon by anti-trust authorities. However, we show that there are situations where anti-trust oriented restrictions on contract complexity may actually make upstream competition less likely to emerge, and therby result in lower welfare.

In the next section, we discuss related literature. The basic model is introduced in Sect. 3. In Sect. 4, we describe the set of equilibria that obtain with linear unobservable wholesale contracts. In Sect. 5, we relax this restriction and characterize equilibria when joint profit maximizing contracts are available and present the welfare implications of permitting more complex contractual forms. Sect. 6 concludes.

2 Related Literature

The earliest paper of note is Dewenter and Haucap (2006). They employ fixed-fee contracts: Neither VIF can alter the marginal cost of a downstream competitor and all downstream competitors are symmetric. With a model of differentiated-product price competition in the downstream market, they investigate the incentives of one VIF—among M active VIFs—to invite a downstream competitor and show that no downstream competitor will be invited if products are close substitutes to one another.

Höffler and Schmidt (2008) analyze a setup that is similar to ours but do not consider the possibility that the upstream firms choose not to supply a downstream rival, and they allow for only observable linear wholesale contracts. They show that entry by a new downstream competitor need not reduce downstream prices. However, their result only holds true when one of the VIFs is exogenously assigned to supply the downstream firm and/or when downstream competition is spatial. When the VIFs compete in the upstream market, the equilibrium that they derive in a model with linear demands entails marginal cost wholesale prices.⁴

Bourreau et al. (2011) also examine the nature of competition between VIFs and non-integrated downstream competitors. They show that an equilibrium where both VIFs refuse to supply the input—“complete foreclosure”—is a possibility when all of the firms in the downstream market are symmetric. The existence of this type of equilibrium depends on the degree of substitutability between downstream products. In deriving their results, Bourreau et al. (2011) employ linear wholesale price contracts that are observable to all parties.

Hombert et al. (2019) study vertical merger waves that may result in insufficient upstream competition for supplying inputs to the remaining unintegrated downstream firms. The most relevant part of their paper is an extension of their model where they consider private linear wholesale price contracts. They focus on monopoly-like equilibria in which one upstream firm supplies the independent downstream competitor while all other integrated firms do not make competing offers; this is a situation that results in partial foreclosure. For this result to obtain however, they require that the integrated firms are more efficient in the downstream market.

Ordover and Shaffer (2007) study how two VIFs respond to demand for access to their upstream products by a non-integrated downstream rival. They focus on observable linear wholesale price contracts. They demonstrate by numerical simulations that there may be equilibria where neither VIF offers the input for sale. However, the underlying mechanism that yields this equilibrium in their model involves asymmetric cannibalization of the downstream products of the two VIFs.⁵

Calcagno and Giardino-Karlinger (2019) study a model where two VIFs collude on the upstream and downstream markets and decide whether to supply a more efficient independent downstream competitor. Foreclosure of the downstream competitor arises because the VIFs cannot commit not to undercut the downstream competitor after the upstream wholesale contract is signed. They point out that certain contractual provisions may alleviate this hold-up problem and lead to downstream entry. This result is similar to one of the main points of our paper—more complex contractual arrangements can lead to downstream entry—but the underlying mechanism is different.

Horstmann et al. (2017) conduct an experiment where downstream foreclosure arises even though the parameter range that is chosen for the experiment predicts competition at the upstream segment as a unique equilibrium when contracts are observable. The setup of their experiment uses real-time moves, which more accurately describes a scenario in which upstream agreements are not (immediately) observable. In this respect, their findings confirm our hypothesis that unobservability of upstream contracts makes foreclosure more likely.

Our paper is also related to the literature on the implications of observability of contracts in vertical relationships. The seminal work by Hart and Tirole (1990) examines the incentives of upstream input suppliers to integrate with downstream firms under the assumption of private contracts. McAfee and Schwartz (1994; see also Rey and Tirole (2007)) examine an upstream monopolist that supplies an input to downstream firms and show the importance of different off-equilibrium beliefs on equilibrium predictions.

In our analysis, we adopt off-equilibrium beliefs that are similar to the wary beliefs that are introduced by McAfee and Schwartz (1994) and are studied later in more detail in Rey and Vergé (2004). Pagnozzi and Piccolo (2012) examine the effect of contract observability on manufacturers’ incentives to sell through independent agents, rather than selling to the public directly.

To our knowledge, ours is the first paper to examine the effects of unobservable contracts and their complexity on the incentives of vertically integrated firms to supply to an independent downstream competitor.⁶

3 The Model

Consider an industry with two vertically integrated firms (VIFs): $i=1,2$. The VIFs produce a homogenous input that is needed for the production of a downstream product. There is a third downstream competitor—$i=3$—that can compete with the VIFs if it can obtain the input. Furthermore, both VIFs produce the homogeneous input at a marginal cost of $c_{I}$. One unit of the input is then used in producing one unit of the final good at a marginal cost of $c_{O}$, which is assumed to be the same for all three firms.⁷

We assume that the products in the downstream market are differentiated. This implies that an additional variant in the downstream market not only increases competition but also the surplus as consumers value variety. In turn, the VIFs will have incentives to offer contracts to a potential downstream competitor with the hopes of appropriating some of this additional surplus. It turns out that the characterization of the resulting equilibria is not easily achieved in a general setting. We will, therefore, introduce a commonly used linear demand formulation that is due to Shubik and Levitan (1980).

Let a representative consumer of the downstream products have the following quasi-linear utility function:⁸

$$\begin{aligned} U(q_1,q_2,q_3,y;\beta )=\sum _{j=1}^3 q_j-\frac{1}{2}\left( \sum _{j=1}^3 q_j\right) ^2-\frac{3}{2(1+\beta )}\left[ \sum _{j=1}^3 q_j^2 - \frac{ \left( \sum _{j=1}^3 q_j \right) ^2}{3}\right] +y \end{aligned}$$

(1)

where $q_j$, $j=1,2,3$, are the quantities of the three downstream products consumed and y is a composite good whose price is normalized to unity. It is straightforward to derive the corresponding demand functions:

$$\begin{aligned} q_j(p_1,p_2,p_3)= & {} \frac{1}{3}\bigg [1 -p_j-\beta \bigg (p_j-\frac{1}{3} (p_1+p_2+p_3)\bigg )\bigg ] \quad j=1,2,3. \end{aligned}$$

(2)

The smaller is the value of $\beta$, the more differentiated are the products. When $\beta =0$, the products are independent of one another and each firm becomes a monopoly in its downstream product market; as $\beta \rightarrow \infty$ the products become perfect substitutes.

In the event that only the two VIFs are active in the downstream market, the demand functions that they face are derived by maximizing the utility given in equation (1) with the constraint that $q_3=0$:

$$\begin{aligned} q_i(p_1,p_2)=\frac{1+\beta }{3+2\beta }\bigg [1-p_i-\frac{\beta }{3}(p_i-p_j) \bigg ] \qquad i\ne j\in \{1,2\}. \end{aligned}$$

(3)

Given these demand functions, it is necessary that we have $1-c_I-c_O>0$ so that production takes place; this is an assumption that we make for the rest of the paper. We assume that the VIFs make take-it-or-leave-it contract offers which contain an exclusivity clause.⁹

The sequence of actions in our model is as follows:

• Stage 1: The VIFs offer privately observed exclusive upstream sales contracts to firm 3.

• Stage 2: Firm 3 decides which, if any, offer to accept. The acceptance decision is publicly observed—although the terms of the contract remain private information of the contracting parties.

• Stage 3: All firms that have/obtain the input compete in the downstream product market in prices.

The fact that upstream contracts are only privately observed plays an important role: With an observable upstream contract the contracting parties (one VIF and firm 3) can influence the behavior of the outsider VIF—which is akin to the first-mover advantage of a Stackelberg leader: Observability allows the contracting parties to use the contents of the contract as a commitment device.

By contrast, with a private contract this device is no longer available and the outsider VIF needs to form a belief with regard to the features of the contract; thus its behavior is independent of the actual contents of the contract. As we will also see in the specific cases later on, unobservability weakens the commitment power of an upstream contract and makes supplying the input less attractive for a VIF.

Given that we focus on unobservable contract offers, we will use Perfect Bayesian Equilibrium (PBE) as our solution concept. The set of PBE is potentially large due to the latitude one has in specifying off-equilibrium beliefs. We adopt a version of wary beliefs in our setting. Wary beliefs were first introduced by McAfee and Schwartz (1994) and developed further by Rey and Vergé (2004).

In our setup, off-equilibrium beliefs need to be specified only following a deviation where the identity of the contracting VIF changes. Following such a deviation, the VIF that finds itself being the outsider—contrary to the expected equilibrium outcome—needs to form a belief about the agreed-upon contract by the other two firms in order to formulate its downstream response. We assume that the outsider VIF believes that the other two firms have agreed upon a contract that maximizes the payoff of the contracting VIF conditional on being acceptable for firm 3. Moreover, the two contracting firms believe that the outsider VIF forms its beliefs in this fashion.

Note that this setup and the corresponding information structure differs from those in McAfee and Schwartz (1994). However, the underlying idea that agents base their off-equilibrium beliefs on the expectation that the deviating parties design a new contract to the latter’s maximum benefit remains the same. Because of this, we will still call these “wary beliefs”. We explicitly derive and demonstrate the implications of this specification of off-equilibrium beliefs in each case that we study below.

4 Upstream Competition with Linear Wholesale Prices

In this section, we follow most of the literature that studies competition between VIFs by using linear observable contracts to supply a downstream competitor. However, we focus on linear private contracts.¹⁰

We start our analysis by investigating possible equilibria in which firm 3 is completely foreclosed. In such an equilibrium, both VIFs are expected to make unacceptably high wholesale price offers to firm 3 and will earn duopoly profits. In all of the cases that we investigate later on, this outcome represents the outside option of a VIF that contemplates making a contract offer to firm 3 when its rival is expected to make an unacceptable offer. The derivation of the equilibrium prices and profits for this case—based on the model that we presented in Sect. 3 and denoted by $\{{{\hat{p}}}_1, {{\hat{p}}}_2\}$ and ${\hat{\varPi }}_1({{\hat{p}}}_1,{{\hat{p}}}_2)={\hat{\varPi }}_2({{\hat{p}}}_1,{{\hat{p}}}_2)= \varPi ^D$, respectively—is straightforward and is provided in the Appendix.

For foreclosure to arise in equilibrium, neither VIF should have an incentive to deviate unilaterally and make an acceptable offer to firm 3. Suppose, in contrast to the equilibrium expectations, VIF i has made an acceptable offer. In the continuation game that follows this deviation, the three firms compete downstream. The fact that VIF i and firm 3 signed a contract is observed by VIF j, $j\ne i$.

Let us start by computing the optimal wholesale price from the perspective of VIF i that results in the highest deviation profits when VIF j is expected to respond to this deviation by a downstream price given by $\tilde{ p}_{j}$. For a given value of the linear wholesale price w and a belief with regard to ${\tilde{p}}_{j}$ and the retail price of firm 3—${\tilde{p}} _{3}$—the profit function of VIF i is given by

$$\begin{aligned} \pi _{i}(p_{i},{\tilde{p}}_{j},{\tilde{p}} _{3},w)=(p_{i}-c_{I}-c_{O})q_{i}(p_{i}, {\tilde{p}}_{j},{\tilde{p}} _{3})+(w-c_{I})q_{3}(p_{i},{\tilde{p}}_{j},{\tilde{p}} _{3}). \end{aligned}$$

The best response of VIF i in downstream competition is given by¹¹

$$\begin{aligned} p_{i}({\tilde{p}}_{j},{\tilde{p}}_{3},w)={\mathop {{\mathrm{argmax}}}\limits _{p_{i}}}\ \pi _{i}(p_{i},{\tilde{p}} _{j},{\tilde{p}}_{3},w). \end{aligned}$$

At the same time, firm 3’s best response price—given w, ${\tilde{p}}_{j}$, and its belief as to the retail price of VIF i—${\tilde{p}}_{i}$ is determined by

$$\begin{aligned} p_{3}({\tilde{p}}_{i},{\tilde{p}}_{j},w)={\mathop {{\mathrm{argmax}}}\limits _{p_{3}}}\ \pi _{3}({\tilde{p}}_{i}, {\tilde{p}}_{j},p_{3},w)\equiv {\mathop {{\mathrm{argmax}}}\limits _{p_{3}}} \ (p_{3}-w-c_{O})q_{3}( {\tilde{p}} _{i},{\tilde{p}}_{j},p_3). \end{aligned}$$

One can solve these two best responses—$p_{i}=p_{i}( {\tilde{p}}_{j},p_{3}(p_{i},{\tilde{p}}_{j},w),w)$ and $p_{3}=p_{3}(p_{i}({\tilde{p}}_{j},p_{3},w),{\tilde{p}}_{j},w)$—to obtain the prices that VIF i and firm 3 would charge as functions of w and ${\tilde{p}} _{j}$ only, which result in $p_{i}({\tilde{p}}_{j},w)$ and $p_{3}({\tilde{p}}_{j},w)$. Suppose that at these prices, firm 3 obtains a non-negative profit: $\pi _{3}(p_{i}({\tilde{p}}_{j},w),{\tilde{p}}_{j},p_{3}({\tilde{p}} _{j},w),w)\ge 0$, so that firm 3 finds the offered wholesale price w acceptable. VIF i will choose w to maximize

$$\begin{aligned} {\bar{\pi }}_{i}({\tilde{p}}_{j},w)=(p_{i}({\tilde{p}} _{j},w)-c_{I}-c_{O})q_{i}(p_{i}({\tilde{p}}_{j},w),{\tilde{p}}_{j},p_{3}(\tilde{ p }_{j},w))+(w-c_{I})q_{3}(p_{i}({\tilde{p}}_{j},w),{\tilde{p}}_{j},p_{3}(\tilde{ p}_{j},w)), \end{aligned}$$

subject to the constraint that firm 3 accepts it, which yields the optimal wholesale price: $w({\tilde{p}}_{j})$.

Let us turn to the pricing decision of VIF j. In order to formulate its retail price, VIF j needs to form a belief with regard to the linear wholesale price that has been negotiated by the contracting parties. Given this belief as to the wholesale price, ${{\tilde{w}}}$, VIF j is in a position to find the best response prices of VIF i and firm 3 as a function of their belief about VIF j’s retail price, ${{\tilde{p}}}_j$. Accordingly, VIF j chooses its price $p_j$ to maximize

$$\begin{aligned} \pi _j ( p_i({{\tilde{p}}}_j, {{\tilde{w}}}), p_j, p_3({{\tilde{p}}}_j, \tilde{w}))=(p_j-c_I-c_O)q_j(p_i({{\tilde{p}}}_j, {{\tilde{w}}}), p_j, p_3({{\tilde{p}}}_j, \tilde{w})). \end{aligned}$$

Note that here VIF j incorporates the information that a linear contract is signed between VIF i and firm 3 in formulating its beliefs with regard to the downstream retail prices of its rivals, $p_i({{\tilde{p}}}_j, {{\tilde{w}}})$ and $p_3({{\tilde{p}}}_j, {{\tilde{w}}})$. Maximizing $\pi _j ( p_i({{\tilde{p}}}_j, {{\tilde{w}}}), p_j, p_3({{\tilde{p}}}_j, {{\tilde{w}}}))$ with respect to $p_j$ results in the best response price of VIF j, $p_j({{\tilde{p}}}_j,{{\tilde{w}}})$—when it expects the rival firms to agree upon a wholesale price of ${{\tilde{w}}}$ and when they expect VIF j to charge ${{\tilde{p}}}_j$.

Denote the equilibrium prices of the continuation game that starts with a deviating offer of $w^{d}$ with $(p_{i}^{d},p_{j}^{d},p_{3}^{d})$. In this equilibrium, it must be that $w^{d}=w(p_{j}^{d})$, $p_{i}^{d}=p_{i}(p_{j}^{d},w^{d})$, $p_{j}^{d}=p_{j}(p_{j}^{d},w^{d})$ and $p_{3}^{d}=p_{3}(p_{j}^{d},w^{d})$. The deviation profit for VIF i is given by $\pi _{i}(p_{i}^{d},p_{j}^{d},p_{3}^{d},w^{d})$. A deviation is not profitable whenever $\pi _{i}(p_{i}^{d},p_{j}^{d},p_{3}^{d},w^{d})<{\varPi }^{D}$, which we show to hold whenever the substitutability between the downstream products is sufficiently large; specifically, whenever $\beta >15.09$. As a result, whenever downstream products are close substitutes, there exists a perfect Bayesian Nash equilibrium with wary beliefs, in which neither VIF makes an acceptable offer to firm 3, which is thereby foreclosed.

Next, we consider equilibria in which firm 3 receives acceptable offers. From the discussion above, it is clear that when the downstream products are sufficiently differentiated—for $\beta <15.09$—a firm will have incentives to extend an offer to firm 3 when its rival does not make an acceptable offer. Regardless of the level of substitution in the downstream market, the firm whose offer is accepted ends up with a higher profit than its rival VIF. Thus, expecting the other VIF to make an offer, each VIF has an incentive to make a competing offer to firm 3 for all possible values of downstream substitutability.

In such a situation, firm 3 faces two wholesale price offers—$w_{1}$ and $w_{2}$—in the beginning of stage 2. With wary beliefs, it is always optimal for firm 3 to accept the lower wholesale price offer. When VIFs make the same wholesale price offer, we break the tie in favor of VIF 1 and assume that firm 3 patronizes VIF 1. Given this decision rule and the fact that the contracting VIF earns at least as much as the outsider VIF, in equilibrium, both VIFs undercut one another until they no longer can do so. Both VIFs make contract offers with wholesale prices that are equal to the marginal cost of producing the input good, $c_{I}$, and firm 3 then accepts the offer of VIF 1. We summarize these results in the next proposition.

Proposition 1

(Linear unobservable wholesale contracts) Under differentiated goods price competition, with linear unobservable contracts:

• (i) For all $\beta <\infty$, there exists an equilibrium in which both VIFs make a contract offer to firm 3 at a wholesale price that is equal to the marginal cost of producing the input, $c_I$.

• (ii) For all $\beta >15.09$, there exists another equilibrium where both VIFs refuse to make an acceptable offer to firm 3, and firm 3 thereby is foreclosed.

Proof

Straightforward algebraic calculations that prove these statements are provided in the Appendix. $\square$

Part (i) of Proposition 1 is intuitive. Given the homogeneity of the input good, and with each VIF expecting the other VIF to make an acceptable offer, both VIFs compete fiercely and set a wholesale price that is equal to the marginal cost of producing the input. Proposition 1 implies that, in our setting, the emergence of upstream (wholesale) competition and the downstream competitor’s being supplied are equivalent events.¹²

The intuition that underlies the foreclosure equilibrium is more subtle. Consider a situation where no VIF offers an acceptable contract and examine a VIF’s incentives to deviate and make an acceptable offer. When a VIF can earn higher profits by making an acceptable offer, then foreclosure cannot occur in equilibrium. Conversely, when upon such a deviation a VIF cannot earn higher profits, foreclosure is an equilibrium.

A deviating VIF faces the following trade-off: On the one hand, deviating and making an acceptable offer to firm 3 increases the number of firms in the downstream market from two to three, which in turn results in a large reduction in downstream prices as well as in the deviating VIF’s downstream profits. However, at the same time, the deviating VIF also obtains positive profits in the upstream market. A VIF will not deviate—and therefore a foreclosure equilibrium is possible—when the gain in profits in the upstream market is smaller than the loss in profits in the downstream market.

When downstream products are close substitutes, the loss in downstream profits is large, and the gain in upstream profits cannot compensate for this loss, which makes a deviation unprofitable. Similarly, when downstream products are poor substitutes, the reduction in downstream profits is relatively smaller and the gain in upstream profits more than offsets the loss in downstream profits, which makes a deviation profitable. Hence, the foreclosure equilibrium only exists when downstream products are sufficiently close substitutes.

Note that this intuition is not inconsistent with a well-established result that an increase in substitutability in models of product differentiation generally raises the degree of competition. Also in our model, downstream competition intensifies when products are closer substitutes. However, here the VIFs have the additional option of not supplying the input to the independent firm. When the downstream market is characterized by tougher competition—higher substitutability—the VIFs have weaker incentives to supply the independent firm and stronger incentives to foreclose.

One may wonder whether the cutoff value of $\beta =15.09$ implies a high or low substitutability between downstream products. As will be discussed in detail in Sect. 4.1, the various cutoff points that are identified in this paper can be considered to be quite common based on recent studies on actual markups in various industries. They correspond to a degree of substitutability where firms would have moderate market power.

We next investigate the role of unobservability of contracts in the emergence of the foreclosure equilibrium. With linear observable contracts, Höffler and Schmidt (2008) establish an equilibrium outcome in which both VIFs set wholesale prices that are equal to marginal cost. Although they do not consider the issue of a refusal to supply in their paper, it is straightforward to show in their model that, for $\beta >26.77$, both firms refusing to supply is also a Nash equilibrium. Comparing the levels of substitutability that are required to sustain a foreclosure equilibrium—15.09 versus 26.77—we can see that when contracts are unobservable (which we argue is the more realistic assumption) a foreclosure equilibrium is more likely.

The reason is straightforward: Consider again an outcome where neither VIF makes an offer to firm 3 and examine the incentives of a VIF to deviate and make an acceptable offer. As we noted above, the crucial tradeoff that this VIF faces is between the gain in profits in the upstream market and the loss in profits in the downstream market: The higher is the degree of competition in the downstream market, the less likely it is that the VIF will deviate, and, hence, the more likely is the foreclosure equilibrium.

We will now argue that—compared to the case where contracts are observable—unobservability makes the downstream market more competitive.

When contracts are observable, the deviating VIF is able to commit to a wholesale price before downstream prices are set in the continuation game. This first-mover advantage allows the VIF to set a relatively high wholesale price and soften downstream competition. By contrast when contracts are not observable, the deviating VIF loses this commitment mechanism and offers a lower wholesale price. As this is expected in equilibrium, when contracts are not observable, equilibrium wholesale as well as downstream prices are lower. Therefore, under unobservability a deviating VIF faces tougher competition and deviation profits are lower.

Now consider again the tradeoff that is faced by the deviating VIF. Because under unobservable contracts downstream competition is tougher, the loss in downstream markets is higher. As a result, compared to the observable case, a VIF will be willing to deviate only if substitutability between downstream products is lower. Hence, the critical $\beta$ below which a VIF deviates is lower when contracts are unobservable (15.09) compared to when they are observable (26.77). With unobservable contracts, foreclosure is possible for a wider range of substitutability.

To summarize: Relative to the case with unobservable contracts, the availability of a commitment mechanism under observable contracts makes a deviation from the foreclosure outcome more profitable. Interestingly, this commitment mechanism makes the foreclosure outcome less likely, and results in a higher likelihood of upstream competition between the VIFs.

5 Joint Profit Maximization Through Upstream Contracts

We now drop the assumption of linear wholesale prices and consider the case where contracts between the VIFs and firm 3 are unrestricted. More specifically, we assume that firms have access to sufficiently sophisticated contracts: Contracts that allow the contracting parties to implement the outcome that maximizes their joint profits. In essence, a sophisticated unobservable contract is capable of delivering the profits that would result if the contracting parties were to merge. We further assume that such contracts have an available instrument that allows the contracting parties to share this profit.

In order formally to define a sufficiently sophisticated unobservable contract, let us assume that C—which can depend on any relevant variable such as quantities, prices etc.¹³—represents the contract that VIF i and firm 3 sign. Let T(C) denote the corresponding payment from firm 3 to VIF i. Then, the profit function of the contracting VIF can be written as

$$\begin{aligned} \pi _{i}^C(p_{i},p_{j},p_{3})=\underbrace{(p_i-c_I-c_O)q_i(p_{i},p_{j},p_{3}) }_{\mathrm{Downstream profits of VIF }i}+ \underbrace{ T(C)-c_Iq_3(p_{i},p_{j},p_{3})}_{\mathrm{Upstream profits of VIF }i} \end{aligned}$$

while the profit of firm 3 is given by

$$\begin{aligned} \pi _{3}^C(p_{i},p_{j},p_{3})=(p_3-c_O)q_3(p_{i},p_{j},p_{3}) -T(C). \end{aligned}$$

In this scenario, the profit function of the non-contracting firm remains as before and consequently we have $\pi _{j}^C(p_{i},p_{j},p_{3})=\pi _{j}(p_{i},p_{j},p_{3})$.

For a given contract, C, and a belief about the price of VIF j, ${{\tilde{p}}}_j$, firms i and 3 non-cooperatively choose their prices as $p_i({{\tilde{p}}}_j,C)$ and $p_3({{\tilde{p}}}_j,C)$. In this case, the contract that is offered by firm i will maximize the joint profits of firms i and 3:

$$\begin{aligned} C^*({{\tilde{p}}}_j) ={\mathop {{\mathrm{argmax}}}\limits _{C}} \ \pi _i^C(p_i({{\tilde{p}}}_j,C),{{\tilde{p}}}_j,p_3(\tilde{p}_j,C))+\pi _3^C(p_i({{\tilde{p}}}_j,C),{{\tilde{p}}}_j,p_3({{\tilde{p}}}_j,C))) \end{aligned}$$

with the corresponding profits of

$$\begin{aligned} \pi ^C({{\tilde{p}}}_j)= \pi _i^C(p_i({{\tilde{p}}}_j,C^*({{\tilde{p}}}_j)),\tilde{p}_j,p_3({{\tilde{p}}}_j,C^*({{\tilde{p}}}_j)))+\pi _3^C(p_i({{\tilde{p}}}_j,C^*(\tilde{p}_j)),{{\tilde{p}}}_j,p_3({{\tilde{p}}}_j,C^*({{\tilde{p}}}_j))). \end{aligned}$$

The maximum profit that a decision maker can achieve by jointly choosing $p_i$ and $p_3$—conditional on a belief about the price of VIF j, ${{\tilde{p}}}_j$, and when these choices cannot be observed by firm j—is simply the maximum joint profit against this belief and is given by

$$\begin{aligned} \pi ^M({{\tilde{p}}}_j)=\max _{p_i,p_3} \pi _i^C(p_i,\tilde{p}_j,p_3)+\pi _3^C(p_i,{{\tilde{p}}}_j,p_3). \end{aligned}$$

Definition 1

(Sufficiently Sophisticated Unobservable Contracts) A contract, $C^*({{\tilde{p}}}_j)$—when its details are unobservable to firm j but its existence is known before all firms choose their prices—is considered to be sufficiently sophisticated if for all expected prices of VIF j, ${{\tilde{p}}}_j$,

$$\begin{aligned} \pi ^C({{\tilde{p}}}_j)=\pi ^M({{\tilde{p}}}_j). \end{aligned}$$

Such contracts trivially exist. The simplest example is a contract that sets the prices of the contracting parties as a best response to the price of the non-contracting VIF, and by means of a fixed payment distributes the resulting profit between the two contracting firms. Although the coordination that such a contract enables might be seen as a violation of competition laws, there are other contractual forms that are used in practice without legal consequences and that can be shown to be sufficiently sophisticated. We argue in Sect. 5.2 that a resale price maintenance (RPM) contract with a maximum price restriction is sufficiently sophisticated.

Sufficiently sophisticated contracts will lead to higher joint profits for the contracting firms as they eliminate the double marginalization problem that appears with linear wholesale prices, and furthermore allow the coordination of the downstream prices of the contracting parties. The resulting higher profits provide stronger incentives to deviate from a foreclosure outcome and thereby induce more upstream competition. Thus, we can show that even explicit agreements between a VIF and the downstream competitor that coordinate their downstream prices via a vertical contract can result in higher welfare.

We now proceed with the analysis in support of this claim.

5.1 Equilibrium with Unobservable Sufficiently Sophisticated Contracts

Consider first the equilibrium when firm 3 does not receive any acceptable offers. The outcome in this situation is the duopoly outcome that we described in the preceding section where both VIFs obtain $\varPi ^D$ in equilibrium.

In all other possible continuation games, firm 3 accepts an offer from one of the VIFs. Naturally, such a continuation game can be part of an equilibrium or it arises as a result of a deviation in the first stage where the VIFs make their offers. Either way, the contracting parties that use sufficiently sophisticated contracts will maximize their joint profits. When the contracting VIF i and firm 3 believe that VIF j will set set a price, ${{\tilde{p}}}_j$, they will agree on a contract that induces them to set their prices such that

$$\begin{aligned} \{p_i({{\tilde{p}}}_j), p_3({{\tilde{p}}}_j)\}={\mathop {{\mathrm{argmax}}}\limits _{p_i,p_3}}\ \pi _i^C(p_i,\tilde{p}_j,p_3)+\pi _3^C(p_i,{{\tilde{p}}}_j,p_3). \end{aligned}$$

Similarly, expecting the contracting parties to charge ${{\tilde{p}}}_i$ and ${{\tilde{p}}}_3$, the non-contracting VIF j selects its price such that

$$\begin{aligned} p_j({{\tilde{p}}}_i, {{\tilde{p}}}_3)={\mathop {{\mathrm{argmax}}}\limits _{p_j}} \ \pi _j^C({{\tilde{p}}}_i, p_j,\tilde{p}_3). \end{aligned}$$

Let $\{p_i^e, p_j^e, p_3^e\}$ denote the equilibrium prices. Then, these prices simultaneously solve $p_i^e=p_i(p_j^e)$, $p_j^e=p_j(p_i^e, p_3^e)$ and $p_3^e=p_3(p_j^e)$. Note that the mechanism by which the downstream prices are set is the same regardless of whether the continuation game is part of an equilibrium or not. As long as sufficiently sophisticated contracts can be used, the downstream equilibrium prices will be the same in all possible continuation games where firm 3 contracts with one of the VIFs.

Given the characterization of the equilibria of the continuation games in the downstream market, the decision problem that is faced by firm 3 in the second stage is straightforward. When both VIFs make offers, it will accept the offer that results in the highest payoff—provided that at least one offer yields a non-negative profit. On the other hand, when it faces only a single offer it will be in favor of accepting it as long as the offer yields a non-negative profit as its outside option is simply zero.

We can now turn our attention to the first stage competition between the VIFs in making offers to firm 3. To streamline the discussion, let $\varPi ^C=\pi _{i}^C(p_1^e, p_2^e, p_3^e )+\pi _{3}^C( p_i^e, p_j^e,p_3^e )$ denote the joint profits of the contracting parties and $\varPi ^O= \pi _{j}^C(p_1^e,p_2^e, p_3^e )$ denote the equilibrium profit of the non-contracting VIF. One key point we establish in the Appendix is that for all values of $\beta$, we have $\varPi ^C>\varPi ^O$ : The joint profit of the contracting parties is greater than that of the outsider VIF in any continuation game.

Consider first the outcome where both VIFs believe that they will make unacceptable offers to firm 3 and compete as duopolists in the downstream market. Suppose that VIF 1 deviates by making an acceptable offer. VIF 1 can extract a profit that is almost equal to $\varPi ^C$ by means of a sufficiently sophisticated contract.¹⁴ In such a case, VIF 2 will observe that an agreement has taken place between VIF 1 and firm 3 and formulate its downstream response based on the belief that they have agreed on a contract that maximizes their joint profits. On the other hand, by making an unacceptable offer, VIF 1 will obtain the duopoly profit $\varPi ^D$. A simple comparison reveals that $\varPi ^D>\varPi ^C$ for $\beta >32.89$.

For a sufficiently high substitutability of the downstream products, VIF 1 is better off refraining from supplying the input to firm 3, when it expects VIF 2 not to make an offer as well. An analogous argument applies for VIF 2. As a result, when downstream products are sufficiently close substitutes, there is a PBE with wary beliefs where both firms find it in their interest not to make an acceptable offer to firm 3 and upstream competition fails to emerge.

Now consider the remaining possibility. Suppose in equilibrium both VIFs make acceptable offers but the offer of VIF 2 is expected to be accepted and the contracting firms earn $\pi _3^C=\varPi ^C-T$ and $\pi _2^C=T$, where T is the payment used to share the joint profits. In the postulated equilibrium VIF 1 earns $\varPi ^O$. As long as $T>\varPi ^O$, VIF 1 will have an incentive to make a slightly more attractive offer and earn slightly less than T. The two VIFs, then, expecting the other to undercut any acceptable offer, will compete until neither can offer a higher payment to firm 3 in the first stage.

In equilibrium both VIFs will make offers that deliver a payoff of $\pi _3^C=\varPi ^C-\varPi ^O$ to firm 3 and earn $\pi _1^C= \pi _2^C=\varPi ^O$ in equilibrium. Given that $\varPi ^C>\varPi ^O$ for all possible values of $\beta$, such an equilibrium where the VIFs compete to supply firm 3 always exists.

Before proceeding further, let us summarize our findings in the next proposition.

Proposition 2

(Equilibrium Outcomes with Sufficiently Sophisticated Contracts) Under differentiated goods price competition, when VIFs 1 and 2 can make sufficiently sophisticated contract offers to firm 3:

• (i) For all $\beta <\infty$ there exists a PBE with wary beliefs in which both VIFs make identical competing offers to firm 3. In this equilibrium the VIFs each earn $\varPi ^O$ and firm 3 earns $\pi _3^C=\varPi ^C-\varPi ^O>0$.

• (ii) For all $\beta >32.89$ there exists a PBE with wary beliefs in which both VIFs refuse to make an acceptable offer to firm 3. In this equilibrium the VIFs each earn $\varPi ^D$, while firm 3 is foreclosed and earns a profit of zero.

Furthermore, for all $\beta >32.89$ both VIFs find it better to coordinate on the outcome where firm 3 is not supplied, as $\varPi ^D>\varPi ^O$.

Proof

The proof of the proposition follows from the above discussion and straightforward algebraic calculations that are provided in the Appendix. $\square$

The takeaway from Proposition 2 is that when downstream products are close substitutes, vertically integrated firms prefer not to supply a downstream rival.¹⁵ However, there is another equilibrium where both VIFs make competing offers. When multiple equilibria exist, from the point of view of the VIFs, the foreclosure equilibrium dominates the equilibrium where they compete with each other to supply firm 3. As we discuss below, in contrast, a utilitarian social planner would prefer the equilibrium where upstream wholesale competition to supply the downstream firm emerges. On the other hand, when downstream products are sufficiently poor substitutes, upstream wholesale competition should naturally emerge.¹⁶

The equilibrium outcomes in Proposition 2 are similar to those of Proposition 1. In order to compare the two cases, we present in Table 1 the critical values of the substitutability parameter $\beta$, above which the VIFs do not supply the downstream competitor. As can be seen, when compared with observable contracts, the critical substitutability level is lower for both types of unobservable contracts. On the other hand, a comparison of the substitutability parameters along the contract complexity dimension shows that in both cases complex contracts increase the possibility that upstream wholesale competition emerges. Thus, there may be a procompetitive role for complex contracts when contracts are unobservable.

Whenever $15.09<\beta \le 32.89$, upstream wholesale competition arises as a unique equilibrium if firms have access to sufficiently sophisticated contracts, while there is an equilibrium in which neither VIF supplies the input to the downstream firm when contracts are restricted to linear tariffs.

For moderate substitutability between downstream products, allowing sophisticated contracts—even those that coordinate the downstream prices of the contracting parties—may lead to competition in the upstream market, which results in higher welfare when compared with the foreclosure outcome, as we show below.¹⁷

Table 1 The value of the substitutability parameter, $\beta$, above which the VIFs refuse to supply the downstream competitor

Indeed, a simple comparison of the equilibrium prices under the duopoly and the three-firm oligopoly structures reveals that—for moderate substitutability between downstream products—consumers are unambiguously better-off when downstream entry occurs.

The next proposition sums up our findings.

Proposition 3

(Welfare comparison) Assume that when there are multiple equilibria, the VIFs coordinate on the foreclosure equilibrium that results in higher profits. When we compare the outcomes between linear tariffs and sophisticated contracts, for “moderate levels of substitutability”—for $15.09\le \beta <32.89$—downstream entry occurs only under the latter. Furthermore, downstream entry leads to lower prices for all products and leads to higher consumer and total welfare.

Proof

Straightforward algebraic calculations that prove these statements are provided in the Appendix. $\square$

Proposition 3 indicates that for moderate levels of substitutability foreclosure is an equilibrium when contracts are linear, but not when contracts are complex. For this range of substitutability, starting at a situation where neither VIF makes an acceptable contract offer, a profitable deviation exists when contracts are sufficiently sophisticated, but not with linear contracts. We now try to provide the intuition for this result.

Compared to the case with linear contracts, three factors make a deviation from a foreclosure outcome profitable under complex contracts (remember that these contracts allow the contracting parties to behave as if they have merged): First, this eliminates the double marginalization problem that arises with linear contracts. Second, acting as a merged entity reduces the competition between the contracting VIF and firm 3 in the downstream market. These two factors increase the joint profits of the deviating VIF and firm 3. Third, the deviating VIF is able to capture the downstream profits of firm 3 by means of a fixed transfer. Such opportunities do not exist when contracts are linear.

Since a VIF that deviates can increase its profits by making an acceptable offer to firm 3, foreclosure cannot be an equilibrium for these moderate levels of substitutability when sufficiently sophisticated contracts are available. The only possible equilibrium is one where both VIFs make acceptable offers to firm 3, and firm 3 enters. The resulting higher level of competition in the downstream market increases consumer welfare, as compared to the case where upstream competition to supply the downstream firm does not emerge due to linear contracts.

Do sophisticated contracts always lead to higher consumer welfare compared to the case where only linear contracts are allowed? The answer is no. Specifically when $0<\beta <15.09$, moving from linear to sophisticated contracts actually reduces consumer welfare.¹⁸ To see why, we have to compare the equilibria under linear and sophisticated contracts. In both cases, the only possible equilibrium is one where upstream wholesale competition obtains. Under linear contracts, the wholesale prices are equal to marginal cost, as shown in Proposition 1.¹⁹ Equilibrium downstream prices replicate those that would arise under competition between three symmetric firms.

By contrast, under sophisticated contracts, because the contracting VIF and firm 3 act as merged entities, they coordinate their prices in the downstream market, which leads to higher prices. Due to strategic complementarity the outsider VIF responds with a price increase as well, which results in higher downstream equilibrium prices when compared with equilibrium prices under linear contracts. As a result, for low levels of substitutability, compared to the case of linear contracts, equilibrium under sophisticated contracts leads to higher prices and lower consumer welfare.

To summarize: Whenever upstream competition to supply the downstream firm will occur in any event, a switch from linear to sophisticated contracts reduces consumer surplus and welfare. However, for moderate levels of substitutability, there are two equilibria and it is reasonable to assume that the VIFs favor the foreclosure equilibrium. In this case, the downstream competitor cannot enter absent sophisticated contracts. We can, therefore, conclude that allowing complex contractual agreements works to the favor of consumers and social welfare only when, in their absence, an independent downstream firm is unable to obtain the upstream input and enter the downstream market.

The range of $\beta$ values where sufficiently sophisticated contracts result in higher welfare is arguably relevant. Given the stylized nature of our model, it is impossible to report direct evidence in support of our claim. We can, however, provide some indirect evidence that shows that the range of $\beta$-values that are considered in Proposition 3 correspond to a moderate degree of market power. In a recent paper De Loecker et al. (2020) measure the markups in a wide range of industries and report that in 2016 the markups—defined as the ratio of price to marginal cost—ranged between roughly 0.93 and 2.64. Clearly, this measure is not independent of marginal costs.

Fig. 1

Markups defined as $\dfrac{{\mathrm{Price}}}{\mathrm{Marginal Cost}}$. The left panel presents duopoly markups, the right panel presents markups when three firms compete downstream with sophisticated contracts

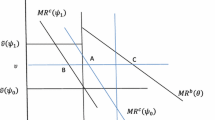
In Fig. 1, we present the markups that are generated by our model for $\beta \in [15.09,32.89]$—the relevant range for Proposition 3—and for several possible values of marginal costs. The left panel presents markups that would arise in a duopoly (foreclosure equilibrium); the right panel presents the markups of the contracting VIF that correspond to the equilibrium with sufficiently sophisticated contracts and downstream entry.

As can be seen in the figure, markups decline with $\beta$ and the level of marginal costs as expected. More important: For both types of equlibria and for all values of the marginal costs that we consider, our model generates markup levels that are comparable to those found in De Loecker et al. (2020). Therefore, we presume that the range of the $\beta$-values that are considered in Proposition 3 to be quite common in practice. Furthermore, given that the markups that we have computed are all larger than 1.2, for the $\beta$ values that are in consideration, firms have moderate market power. In turn, this indicates that the $\beta$ values where Proposition 3 applies can be considered to be moderate.

5.2 Sufficiently Sophisticated Contracts in Practice

The use of sufficiently sophisticated contracts allows close coordination of behavior among the contractual partners. As we have shown above, while such contracts are often frowned upon by competition authorities, allowing them may be welfare-enhancing. Nevertheless, similar joint profit-maximizing outcomes can also be implemented by contracts that are deemed acceptable by competition authorities. As an example, we present an informal discussion showing that maximum RPM contracts are sufficiently sophisticated. A formal proof is provided in the Appendix.

$\blacksquare$ Maximum RPM Contracts: Maximum RPM contracts are not considered to be harmful per se and are part of a block exemption in Europe,²⁰ while in the US they are evaluated on a rule-of-reason basis.²¹ A maximum RPM contract in our context specifies a maximum price—$p_{3}^{max}$—that firm 3 can charge in the downstream market, together with a per-unit wholesale price $w_{3}$ and a fixed fee $f_{3}$.

With a maximum RPM contract, the contracting VIF—say VIF 2—has an additional instrument: By setting the price ceiling for the downstream price of firm 3 equal to $p_3^e$ and choosing the wholesale price to capture all of firm 3’s downstream margin—$p_3^e-c_O$—VIF 2 can fully internalize the effects of its own downstream price choice on its upstream profits. As a result, it optimally selects the joint profit-maximizing price for its downstream product—$p_2^e$—as well.

Given this wholesale price and the maximum price restriction, firm 3 would actually prefer to charge a higher downstream price than $p_3^e$, but is unable to do so. The maximum price limit induces firm 3 to charge the downstream price that the integrated firm would prefer. In addition, the choice of the wholesale price allows VIF 2 to commit to a downstream price as if VIF 2 and firm 3 are integrated. The two instruments—maximum price and the wholesale price—therefore play a crucial role in implementing the prices that would be chosen by an integrated firm. Absent one of these instruments—as is the case with a two-part tariff contract—this outcome cannot be implemented.

The implication of the preceding argument is that—by using a maximum RPM contract—although VIF 2 and firm 3 make their downstream decisions independently, they will set downstream prices that are equal to those that would be set by an integrated firm. VIF 1—correctly anticipating that VIF 2 and firm 3 will enter a joint profit-maximizing contractual relationship—responds to these prices. Therefore, the equilibrium outcome when firm 3 enters into a contractual arrangement that is based on RPM with one of the VIFs is equivalent to the outcome where the contracting parties merge. Hence, maximum RPM contracts are sufficiently sophisticated and our results from Propositions 2 and 3 apply.

One policy implication of this result is that when products are sufficiently close substitutes—in our model, when $\beta <15.09$—maximum RPM contracts will reduce consumer welfare. Given that competition authorities usually regard maximum RPM contracts favorably, it seems important to make a distinction for when the upstream firm is also active in the downstream market.²²

6 Conclusion

We study competition between two VIFs in an upstream market and extend the existing literature in two directions: First, we focus on unobservable contracts. Second, we allow for more sophisticated contracts, which, we argue, would arise naturally when two parties negotiate in secret. Regardless of contract complexity, we find that there always exists an equilibrium in which upstream competition emerges. When downstream products are close substitutes, there is another equilibrium where the VIFs refuse to sell the input. This latter equilibrium yields higher profits to both VIFs, so it is natural to expect that the VIFs coordinate on this outcome.

This characterization of equilibrium outcomes resembles qualitatively those found in the literature that focus on observable and linear wholesale contracts. However, with unobservable contracts, the foreclosure outcome obtains for a wider set of parameters. In a world where contracts are negotiated in private, an outcome where VIFs collectively refuse to sell to a downstream competitor can arise more often. Furthermore, we show that when firms can use contracts that maximize the joint profits of the contracting parties, it is more likely that upstream competition to supply the downstream firm emerges.

Our findings have some implications for competition and regulatory policy: Basing regulation on a logic that relates observed collective refusal to supply to repeated interactions is incomplete in that a collective refusal to supply may occur as a result of non-collusive coordination in a static game that has multiple equilibria. Absent a requirement of an obligation to deal, competition policy should be careful in evaluating contractual relationships between VIFs and independent downstream competitors. Our results indicate that permitting agreements between contracting parties—which are outcome-equivalent to those where contracting parties coordinate their behavior in the downstream market—may be welfare-improving.

Appendix

1.1 Duopoly Equilibrium

When neither VIF supplies the input, they compete in the downstream market as duopolists. They both earn

$$\begin{aligned} {\hat{\varPi }}_{i}(p_1,p_2)=(p_i-c_I-c_O)q_i(p_1,p_2) \qquad i\in \{1,2\}. \end{aligned}$$

The equilibrium of the price competition game is symmetric and yields the following equilibrium prices

$$\begin{aligned} {{\hat{p}}}_1={{\hat{p}}}_2=c_I+c_O+\frac{3(1-c_I-c_O)}{\beta +6}, \end{aligned}$$

which in turn yield equilibrium profits of

$$\begin{aligned} {\hat{\varPi }}_1({{\hat{p}}}_1,{{\hat{p}}}_2)={\hat{\varPi }}_2({{\hat{p}}}_1,{{\hat{p}}}_2)={\hat{\varPi }}^D=\frac{ 3(1+\beta )(3+\beta )(1-c_I-c_O)^2}{(6+\beta )^2(2+3\beta )}. \end{aligned}$$

Proof of Proposition 1

Let us start by deriving the equilibrium choices that the contracting VIF i and the downstream competitor, firm 3, would make when they have agreed upon a wholesale price w, and they believe VIF j will set a downstream price of ${{\tilde{p}}}_j$. In this case, firm 3 maximizes $\pi _3 ({{\tilde{p}}}_i,{{\tilde{p}}}_j, p_3, w)$, while VIF i maximizes $\pi _i(p_i,{{\tilde{p}}}_j,{{\tilde{p}}}_3, w)$. Solving the first-order conditions of the two firms simultaneously, we find

$$\begin{aligned} p_i({{\tilde{p}}}_j,w)=\frac{1}{2+\beta }+\frac{1}{3}{\frac{ \left( 3+2\beta \right) }{2+\beta }}(c_I+c_O)+{\frac{\beta \left( 3+2\beta \right) }{ \left( 2+\beta \right) \left( 6+ 5\beta \right) }}(w-c_I)+\frac{1}{3}\frac{\beta { {{\tilde{p}}}_j}}{ \left( 2+\beta \right) }, \end{aligned}$$

(4)

and

$$\begin{aligned} p_3({{\tilde{p}}}_j,w)=\frac{1}{2+\beta }+\frac{1}{3}{\frac{ \left( 3+2\beta \right) }{2+\beta }}(c_I+c_O)+\frac{6+8\beta +3\beta ^2}{(2+\beta )(6+5\beta )} (w-c_I)+\frac{1}{3}\frac{\beta {{{\tilde{p}}}_j}}{ \left( 2+\beta \right) }. \end{aligned}$$

(5)

Substituting $p_i=p_i({{\tilde{p}}}_j,w)$ and ${{\tilde{p}}}_3=p_3({{\tilde{p}}}_j,w)$ in $\pi _i(p_i,{{\tilde{p}}}_j,{{\tilde{p}}}_3,w)$ and maximizing with respect to w, yields the optimal choice of w conditional on ${{\tilde{p}}}_j$ and the acceptance decision by firm 3. Formally, $w({{\tilde{p}}}_j)$ solves $\tfrac{ \partial }{\partial w} \pi _i(p_i({{\tilde{p}}}_j,w),{{\tilde{p}}}_j,p_3(\tilde{p}_j,w),w)=0$ and yields

$$\begin{aligned} w({{\tilde{p}}}_j)= & {} c_I-\frac{1}{6}\frac{(6+5\beta )(36+42\beta +13\beta ^2)}{ (24+32\beta +11\beta ^2)(3+2\beta )}\left( c_I+c_O-\frac{3+ \beta {{\tilde{p}}}_j}{ 3+\beta }\right) . \end{aligned}$$

On the other hand, VIF j maximizes $\pi _j ({{\tilde{p}}}_i, p_j, {{\tilde{p}}}_3, {{\tilde{w}}})$; however, given the fact that it is aware of the process $\tilde{p}_i$ and ${{\tilde{p}}}_3$ will be set, it incorporates (4) and ( 5) into its maximization problem. Consequently, the optimal choice for VIF j solves,

$$\begin{aligned} \frac{\partial }{\partial p_j}\pi _j ({{\tilde{p}}}_i, p_j, {{\tilde{p}}}_3, {{\tilde{w}}}) \bigg |_{{{\tilde{p}}}_i=p_i({{\tilde{p}}}_j, {{\tilde{w}}}), \ {{\tilde{p}}}_3=p_3(\tilde{p}_j, {{\tilde{w}}})}=0 \end{aligned}$$

and is given by

$$\begin{aligned} p_j({{\tilde{p}}}_j, {{\tilde{w}}})=\frac{6+5\beta }{2(2+\beta )(3+2\beta )}+\frac{ 6+5\beta }{6(2+\beta )}(c_I+c_O)+\frac{\beta (1+\beta )}{2(2+\beta )(3+2\beta )} (w-c_I)+\frac{\beta ^2 {{\tilde{p}}}_j}{3(2+\beta )(3+2\beta )}. \end{aligned}$$

We are now in a position to derive various equilibrium conditions when firms are restricted to contracts that are based on linear wholesale prices. First consider the equilibrium where both VIFs are expected to make unacceptable offers to firm 3. Consider the deviation by VIF i to $w^d$, which is then accepted by firm 3. Given that we have derived above the optimal choice of w for VIF i conditional on ${{\tilde{p}}}_j$, and since we assume VIF j holds wary beliefs, in the equilibrium of this continuation game we must have $w^d=w(p_j^d)$ and $p_j^d=p_j(p_j^d,w^d)$. Solving these conditions we find the optimal wholesale price in case VIF i deviates as

$$\begin{aligned} w^d=c_I+\frac{(6+5\beta )(36+42\beta +13\beta ^2)}{432+936\beta +732 \beta ^2+237\beta ^3+25\beta ^4}(1-c_I-c_O) \end{aligned}$$

and the downstream equilibrium price that is charged by the non-contracting VIF that holds wary beliefs in the continuation game is given by

$$\begin{aligned} p_j^d=c_I+c_O+\frac{3(2+\beta )(36+51\beta +19\beta ^2)}{432+936\beta +732 \beta ^2+237\beta ^3+25\beta ^4}(1-c_I-c_O). \end{aligned}$$

Substituting these values in equilibrium price policies of VIF i and of firm 3 results in $p_i(p_j^d,w^d)$ and $p_3(p_j^d,w^d)$. Substituting all of the equilibrium values in the profit function of VIF i results in equilibrium profits in the continuation game that follows a deviation:

$$\begin{aligned} \pi _i(p_i^d, p_j^d,p_3^d, w^d)=\frac{1}{3}\frac{(3+2\beta )(6+5\beta )(3+ \beta )(11\beta ^2+32\beta +24)(23\beta ^2+69\beta +54)}{({432+936\beta +732 \beta ^2+237\beta ^3+25\beta ^4})^2}(1-c_I-c_O)^2. \end{aligned}$$

It is then straightforward to verify that $\pi _i(p_i^d, p_j^d,p_3^d, w^d)<\varPi ^D$ whenever $\beta >15.09$, which implies that for sufficiently high values of substitutability between the downstream products, the decision by both VIFs not not supply firm 3 is a PBE with wary beliefs.

Now consider the situation where VIFs 1 and 2 make competing offers. Suppose $w_1\le w_2$ is a PBE and the offer of VIF 1 is accepted in this equilibrium. This implies that all firms when they choose their downstream prices know that firm 3 will face a wholesale price given by $w_1$. In this case, the Nash equilibrium downstream prices of all three firms are

$$\begin{aligned} p_1(w_1)= & {} \frac{3}{2(3+\beta )}+\frac{1}{2}\frac{3+2\beta }{3+\beta }c_O+\frac{ 1}{2}\frac{18+18\beta +5\beta ^2}{(6+5\beta )(3+\beta )}c_I+\frac{1}{2}\frac{ \beta (9+5\beta )}{(6+5\beta )(3+\beta )}w_1, \\ p_2(w_1)= & {} \frac{3}{2(3+\beta )}+\frac{1}{2}\frac{3+2\beta }{3+\beta }c_O+\frac{ 1}{2}\frac{18+24\beta +7\beta ^2}{(6+5\beta )(3+\beta )}c_I+\frac{1}{2}\frac{ \beta (1+\beta )}{(6+5\beta )(3+\beta +3)}w_1, \\ p_3(w_1)= & {} \frac{3}{2(3+\beta )}+\frac{1}{2}\frac{3+2\beta }{3+\beta }c_O+\frac{ 3}{2}\frac{\beta (2+\beta )}{(6+5\beta )(3+\beta )}c_I+\frac{1}{2}\frac{ 18+21\beta +7\beta ^2 }{(6+5\beta )(3+\beta )}w_1. \end{aligned}$$

At these prices $\pi _3(p_1(w_1),p_2(w_1),p_3(w_1),w_1)$ is a positive-valued quadratic convex function of $w_1$ and achieves its minimum value of zero when

$$\begin{aligned} w_1={\bar{w}}_{acc} \equiv c_I+\frac{5+5\beta }{(6+\beta )(1+\beta )}(1-c_I-c_O). \end{aligned}$$

For $w_1 \le {\bar{w}}_{acc}$, $\pi _3(p_1(w_1),p_2(w_1),p_3(w_1))$ is decreasing; moreover, only in this case is the demand that is faced by firm 3 positive. Thus, firm 3 finds the offer acceptable as long as the linear wholesale price is less than ${\bar{w}}_{acc}$. Furthermore, when firm 3 is faced with two acceptable offers, it earns more when it contracts with the VIF that offers the lower wholesale price.

If the identity of the firm that makes the accepted offer changes, the equilibrium prices that the VIFs charge in the downstream market will be as we have written above with changing the identities of the VIFs. Therefore, firm 3 will accept the lower offer, as long as $w<{\bar{w}}_{acc}$.

Next, we can compute the difference in equilibrium profits of the contracting VIF and its rival VIF. In the case we are considering, this is

$$\begin{aligned} \pi _1(p_1(w_1),p_2(w_1),p_3(w_1),w_1)-\pi _2(p_1(w_1),p_2(w_1),p_3(w_1))= \frac{(w_1-c_I)(1+\beta )\varDelta (w_1)}{(6+5\beta )^2 (3+\beta )}, \end{aligned}$$

where $\varDelta (w_1)=9(2+\beta )(6+5\beta )(1-c_O-w_1)-\beta (36+48\beta +13 \beta ^2)(w_1-c_I)$. Since $\varDelta (w_1)$ is a decreasing function of $w_1$, this difference is quadratic concave, and positive whenever $c_I\le w_1 \le w_{max}$ where $w_ {max}$ is defined by $\varDelta (w_{max})=0$. It is easy to verify that

$$\begin{aligned} w_{max}=c_I+\frac{9(2+\beta )(6+5\beta )}{108+180\beta +93\beta ^2+13\beta ^3} (1-c_O-c_I). \end{aligned}$$

Note that $w_{max}>w^d$ since

$$\begin{aligned} w_{max}-w^d=\frac{(3+\beta )(3+2\beta )(6+5\beta )(108+162\beta +72\beta ^2+7 \beta ^3)(1-c_O-c_I)}{(108+180\beta +93\beta ^2+13\beta ^3)(432+936\beta +732 \beta ^2+237\beta ^3+25\beta ^4)}. \end{aligned}$$

Moreover, it is also easy to show that

$$\begin{aligned} w_{acc}-w_{max}={\frac{4{\beta }^{2} \left( \beta +3 \right) \left( 5\,\beta +6 \right) \left( 1-{c_I}-{c_O} \right) }{ \left( \beta +6 \right) \left( \beta +1 \right) \left( 13\,{\beta }^{3}+93\,{\beta }^{ 2}+180\,\beta +108 \right) }}>0. \end{aligned}$$

Let us start by establishing that there is no equilibrium in which both VIFs compete and the accepted wholesale price offer w satisfies $w_{max}<w<w_{acc}$. Without loss of generality, let us continue with the proposed equilibrium above in which $w_1\le w_2$ and the offer of VIF 1—$w_1$—is accepted by firm 3. When $w_{max}<w_1<w_{acc}$, VIF 2 will not have an incentive to undercut, VIF 1. However, given that VIF 2 is expected to react with $p_2(w_1)$ in this proposed equilibrium, one needs to check whether VIF 1 and firm 3 have incentives to deviate. Given that such a deviation does not change the identity of the VIF that serves firm 3, there is no need for VIF 2 to change its downstream price. We have derived the optimal wholesale price above in the event that VIF 2’s offer is unacceptable, conditional on the expected price of VIF 2: $w({{\tilde{p}}}_2)$. Whenever $w_1>w^d$, we have $w_1>w(p_2(w_1))$. Hence VIF 1 has an interest to reduce the wholesale price that it offers below $w_1$, thus upsetting the proposed equilibrium. Therefore, in our setting, a PBE with partial foreclosure as is found in Hombert et al. (2019) cannot exist. These arguments imply that wholesale prices that satisfy $w_{max}<w<w_{acc}$ cannot be part of an equilibrium.

Next consider wholesale prices in the range $w^d\le w_1 \le w_{max}$. When $w_2>w_1$ in equilibrium, VIF 1 earns a higher profit than VIF 2. Thus, VIF 2 has an incentive to make a competing offer and the identity of the firm supplying firm 3 will change. This will affect the equilibrium prices that the firms will charge in the downstream market. First, we need to pin down the beliefs of VIF 1 after it observes that the offer of VIF 2 is accepted. It believes that VIF 2 deviates in a fashion to maximize its profits and that VIF 2 and firm 3 believe that it will form its beliefs in this fashion. Given that firm 3 accepts offers with lower wholesale prices, and $w^d<w_1$, the optimal deviation by VIF 2 will be to set its wholesale price such that $w_2=w^d$, and make the sales to firm 3. Moreover, VIF 1, having wary beliefs, will consequently set its downstream price equal to $p_1=p_j^d$, which we derived above. These arguments suggest that $w^d<w<w_{max}$ cannot be part of a PBE in which two VIFs make competing offers.

Finally, consider the wholesale prices in the range $c_I< w\le w^d$. Let us start again from a proposed equilibrium in which VIF 1 charges $c\le w_1<w^d$ and VIF 2 charges $w_2>w_1$. Whenever $w_1>c_I$, we have established above that VIF 1 earns a higher profit than does VIF 2 in the proposed equilibrium. This implies that VIF 2 will have an incentive to deviate; but given the value of $w_1$, the optimal deviation will be to undercut VIF 1’s offer slightly. In the equilibrium of the continuation game following such a deviation, firm 3 will earn almost the same as in the proposed equilibrium, while VIFs 1 and 2 will switch roles, meaning that in the continuation game VIF 2 will earn more than VIF 1. Hence, whenever $w_1>c_I$, such a deviation is profitable. Therefore, the proposed equilibrium where wholesale prices exceed the marginal cost of producing the input good cannot exist.

The only remaining possibility is that both firms make competing offers with wholesale prices equal to the marginal cost of producing the input, namely $w=c_I$. As a result, all firms compete in the downstream market with a per unit cost of $c_I+c_O$ and the downstream equilibrium is symmetric with equilibrium prices given by

$$\begin{aligned} p_1^l=p_2^l=p_3^l=c_I+c_O+\frac{3}{2}\frac{1-c_I-c_O}{3+\beta }. \end{aligned}$$

Notice that, for this equilibrium to exist we do not need to make a restriction on the substitutability between the downstream products. Thus, such an equilibrium in which both VIFs make competing offers with marginal cost wholesale prices always exists, as is stated in Proposition 1.

Proof of Proposition 2

When firm i supplies the input to firm 3 while firm $j\ne i$, $i,j \in \{1,2\}$, does not, and firm i and 3 are able to select joint profit maximizing prices downstream, it is as if firm i and 3 have merged. Sufficiently sophisticated contracts emulate this outcome and the downstream equilibrium prices in a continuation game are independent of the nature of these contracts.

Expecting firm j to charge $p_j$, the resulting equilibrium prices of VIF i and firm 3 are given by

$$\begin{aligned} \{p_i(p_j),p_3(p_j)\} = {\mathop {{\mathrm{argmax}}}\limits _{p_i,p_3}}\ \pi _i( p_i,p_j,p_3)+\pi _3(p_i,p_j,p_3). \end{aligned}$$

Expecting its rivals to charge $p_i$ and $p_3$, VIF j sets its price equal to

$$\begin{aligned} p_j(p_i,p_3)={\mathop {{\mathrm{argmax}}}\limits _{p_j}}\ \pi _j(p_i,p_j,p_3). \end{aligned}$$

It is useful to derive the best response functions for these problems. Given our demand and cost structure, it is easy to verify that firms i and 3 respond to an expected price of their rival by setting

$$\begin{aligned} p_i(p_j)=p_3(p_j)=\frac{c_I+c_O}{2}+\frac{3+\beta p_j}{2(3+\beta )} \end{aligned}$$

while firm j’s best response is given by

$$\begin{aligned} p_j(p_j,p_3)=\frac{c_I+c_O}{2}+\frac{3+\beta (p_i+p_3)}{2(3+2\beta )}. \end{aligned}$$

It is easy to verify that the resulting Nash equilibrium prices are given by

$$\begin{aligned} p_j^e= & {} c_I+c_O+\frac{3+2\beta }{(3+\beta )^2-3}(1-c_I-c_O) \\ p_i^e = p_3^e= & {} c_I+c_O+\frac{6+5\beta }{2((3+\beta )^2-3)}(1-c_I-c_O) \end{aligned}$$

with the corresponding profits of

$$\begin{aligned} \varPi ^O=\pi _j^e( p_1^e, p_2^e, p_3^e)= & {} \frac{(3+2\beta )^3}{ 9((3+\beta )^2-3)^2 }(1-c_I-c_O)^2, \\ \varPi ^C=\pi _i^e( p_1^e, p_2^e,p_3^e)+\pi _3^e( p_1^e, p_2^e,p_3^e)= & {} \frac{ (6+5\beta )^2(3+\beta ) }{18((3+\beta )^2-3)^2}(1-c_I-c_O)^2, \end{aligned}$$

to the outsider firm and the contracting parties, respectively.

In the absence of an acceptable offer from VIF j, VIF i can capture all of $\varPi ^C$ by means of a fixed payment. Assuming this is the case, VIF i will extend an offer to firm 3 only when by doing so it can earn higher than the duopoly profits $\varPi ^D$. A comparison of $\varPi ^C$ and $\varPi ^D$ indicates that $\varPi ^D\ge \varPi ^C$ whenever $\beta \ge 32.89$. Thus, for sufficiently high values of $\beta$, it is a best response for a VIF not to make an offer to firm 3, when it expects that its rival also does not make an offer. Therefore, there exists an equilibrium in which firm 3 is foreclosed whenever the downstream products are sufficiently close substitutes, as is stated in Proposition 2.

Note that

$$\begin{aligned} \varPi ^C-\varPi ^O=\frac{(1+\beta )(1-c_I-c_O)^2}{2(6+6\beta +\beta ^2)}>0 \qquad \text{ for } \text{ all } \beta >0, \end{aligned}$$

thus, regardless of the value of $\beta$, if a VIF believes that the rival VIF will make an offer, it has an incentive to make a competing offer. Suppose VIF i makes an offer that transfers $\varPi ^C-T$ to firm 3, and keeps $\pi _i=T$ for itself. Suppose in equilibrium it is expected that VIF i’s offer is accepted. So long as $\varPi ^O<T$, firm j has an incentive to change its offer by providing firm 3 with a profit that is slightly higher than $\varPi ^C-T$. This offer will be accepted. Moreover, following this deviation VIF i also believes that VIF j and firm 3 will select the downstream prices in order to maximize their joint profits. Therefore, the downstream outcome is exactly the same as in the proposed equilibrium, only the roles played by VIFs i and j are changed.

Given this undercutting incentive, both VIFs will compete with one another until they no longer can do so: When they both earn $\varPi ^O$ in equilibrium. This gives another equilibrium: Both VIFs compete by making sufficiently sophisticated contract offers to firm 3.

Comparing the duopoly profits with the profits when VIFs compete to supply firm 3 implies that duopoly profits are always higher:

$$\begin{aligned} \varPi ^D-\varPi ^O=\frac{\beta (972+2187\beta +1836\beta ^2+729\beta ^3+144\beta ^4+11 \beta ^5)(1-c_I+c_O)^2}{9(6+\beta )^2(3+2\beta )(6+6\beta +\beta ^2)^2}>0. \end{aligned}$$

Thus it is Pareto superior for both VIFs to coordinate on the duopoly outcome that forecloses firm 3 when both outcomes can be supported in equilibrium.

Proof of Proposition 3

Whenever $15.09<\beta <32.89$, upstream competition to supply the downstream firm does not arise when the VIFs are restricted to linear tariffs, while it is the unique equilibrium outcome when firms can sign sufficiently sophisticated contracts. We compute the welfare in both cases as the sum of the consumer surplus and profits. With linear contracts, the favored equilibrium outcome from the perspective of the VIFs is the one where firm 3 is foreclosed and the two VIFs compete as duopolists. The corresponding welfare given by

$$\begin{aligned} W^D={\frac{ \left( 1 -{c_O}-{\ c_I}\right) ^2 \left( 1+\beta \right) \left( 3+\beta \right) \left( 9+\beta \right) }{ \left( 6+\beta \right) ^{2} \left( 3+2\beta \right) }}. \end{aligned}$$

In contrast, the welfare when both VIFs compete to supply the downstream firm by sufficiently sophisticated contracts is given by

$$\begin{aligned} W^C=\frac{ \left( 1- {\ c_I}-{\ c_O} \right) ^{2} \left( 18{\ \beta }^{4}+215{ \beta }^{3}+765{\beta }^{2}+1044\beta +486 \right) }{ 9( {\beta }^{2}+6\beta +6 ) ^{2}}. \end{aligned}$$

It is straightforward to show that the difference between the welfare measures under the two different outcomes is positive for all values of $\beta$. Therefore, from a welfare perspective, a downstream market with three active firms is better than one where only the two VIFs compete as duopolists.

The statement with regard to prices is straightforward to verify by comparing ${{\hat{p}}}_i$, $i=1,2$ with $p_i^e$ and $p_j^e$. The statement sith regard to $p_3$ is obvious as this price is very high (infinitely high) when firm 3 is foreclosed and much lower when firm 3 has access to the input good.

1.2 Competition with Two-Part Tariff Unobservable Contracts

Each VIF can offer a per unit wholesale price $w_k$ together with a fixed payment, $f_k$, $k=1,2$. It is useful once again to start our analysis with the case where in equilibrium neither VIF makes an acceptable contract offer to firm 3. Thus, in equilibrium both VIFs expect to earn $\varPi ^D$.

Now consider the deviation by VIF i that uses a two-part tariff in which it makes firm 3 an acceptable offer; and after VIF j, with $j\ne i$ and $i,j \in \{1,2\}$, learns the existence of a contract, they all compete in the downstream market by choosing their retail prices. Let ${{\tilde{p}}}_j^t$ denote the price that VIF j is expected to charge in equilibrium in the continuation game that follows the deviation.

When VIF i and firm 3 expect VIF j to charge ${{\tilde{p}}}_j^t$ and they have agreed upon a per unit fee of w, their equilibrium responses, $p_i({{\tilde{p}}}_j^t,w)$ and $p_3(\tilde{p}_j^t,w)$, will be as given in Eqs. (4) and (5) since the fixed transfers will not have an effect on the pricing decisions. VIF i can extract all of the downstream profits of firm 3 by means of a fixed payment.

Thus, in turn, when selecting the per-unit wholesale price w, VIF i maximizes the sum of its own and firm 3’s downstream profits taking into account the equilibrium responses in the subsequent price competition stage: The optimal wholesale price choice $w^t(p_j^t)$ of VIF i when VIF j is expected to charge ${{\tilde{p}}}_j^t$ is given by

$$\begin{aligned} w^t({{\tilde{p}}}_j^t)={\mathop {{\mathrm{argmax}}}\limits _{w}}\ \pi _i(p_i({{\tilde{p}}}_j^t, w), {{\tilde{p}}}_j^t, p_3({{\tilde{p}}}_j^t, w))+\pi _3(p_i({{\tilde{p}}}_j^t, w), {{\tilde{p}}}_j^t, p_3(\tilde{p}_j^t, w)). \end{aligned}$$

The solution in our setting to this problem is given by

$$\begin{aligned} w^t({{\tilde{p}}}_j^t)={c_I}-\frac{1}{6} \frac{\left( 6+ 5\beta \right) ^{2}\beta \left( {\ c_I}+{\ c_O}-{\frac{3+\beta {{{\tilde{p}}}_j^t}}{3+\beta }} \right) }{ \left( 12+16\beta +7{\beta }^{2} \right) \left( 3+2\beta \right) }. \end{aligned}$$

Facing this wholesale price offer together with a fixed fee that extracts all of its downstream profits, firm 3 is indifferent between accepting the offer or not. We break this tie in favor of firm 3’s accepting the offer of VIF i. VIF j—observing that a contract materialized between VIF i and firm 3 and having wary beliefs—expects VIF i and firm 3 to agree on a wholesale price that is given by $w^t({{\tilde{p}}}_j^t)$ and to charge prices of $p_i({{\tilde{p}}}_j^t,w^t({{\tilde{p}}}_j^t))$ and $p_3({{\tilde{p}}}_j^t,w^t({{\tilde{p}}}_j^t))$. It formulates its equilibrium price $p_j^t=p_j(p_i(\tilde{p}_j^t,w^t({{\tilde{p}}}_j^t)),p_3({{\tilde{p}}}_j^t,w^t({{\tilde{p}}}_j^t)))$ as a best response.

The equilibrium of the game that follows an optimal deviation is then established when $w^t=w(p_j^t)$ and $p_j^t=p_j(p_i(p_j^t,w^t( p_j^t)),p_3( p_j^t,w^t(p_j^t)))$. Substituting $w^t$ and $p_j^t$ in the pricing policies of VIF i and firm 3 in (4) and (5) yields the prices that these firms will charge in the continuation game that follows the optimal deviation: $p_i^t$ and $p_3^t$, respectively. For any other acceptable contract with a wholesale price of w, VIF j—not observing this value—continues to charge $p_j^t$, and VIF i and firm 3 expect this. In such a continuation game VIF i and firm 3 charge $p_i(p_j^t,w)$ and $p_3(p_j^t,w)$.

With this characterization of the behavior in the continuation game that follows an agreement between VIF i and firm 3, we are in a position to check whether—expecting its rival to not make a contract offer—VIF i will indeed deviate and thereby upset the proposed equilibrium. Note that when VIF i deviates optimally, it earns

$$\begin{aligned} \varPi ^t= & {} \pi _i(p_i^t,p_j^t,p_3^t)+\pi _3(p_i^t,p_j^t,p_3^t)\\= & {} \frac{ (3+\beta )(3+2\beta )(12+16\beta +7\beta ^2)(216+432\beta +315\beta ^2+83\beta ^3)}{ 3(216+468\beta +296\beta ^2145\beta ^3+17\beta ^4)}. \end{aligned}$$

A deviation is profitable whenever $\varPi ^t>\varPi ^D$, which is the case whenever $\beta <22.13$. This implies that—similar to other cases we studied above—as long as the substitutability between the downstream products is sufficiently high—$\beta \ge 22.13$—both VIFs in equilibrium will refuse to sell the input to a downstream competitor. Notice that this threshold is between the one with linear contracts and the one with sufficiently sophisticated contracts. This finding further demonstrates that the likelihood of a foreclosure equilibrium decreases with contract complexity.

Next consider the case where both VIFs make two-part tariff contract offers. Let $(f_i,w_i)$ and $(f_j,w_j)$ denote VIF i and VIF j’s offers, respectively, in a PBE and suppose in equilibrium the offer of VIF j is accepted. This implies that

$$\begin{aligned} \pi _3(p_i(w_j),p_j(w_j),p_3(w_j),w_j)-f_j> \pi _3(p_i(w_i),p_j(w_i),p_3(w_i),w_i)-f_i, \end{aligned}$$

as only under this circumstance would firm 3 be better off accepting VIF j’s offer.

Provided that in this proposed equilibrium,

$$\begin{aligned} \pi _j(p_i(w_j),p_j(w_j),p_3(w_j),w_j)+ \pi _3(p_i(w_j),p_j(w_j),p_3(w_j),w_j)\le \varPi ^t, \end{aligned}$$

VIF i can profitably deviate by making an offer with a wholesale price equal to $w^t$, and maximize the joint profits of itself and firm 3. Inducing firm 3 to accept this offer is a matter of transferring a share T of the maximum joint profits $\varPi ^t$ that exceeds the profits of firm 3 in the proposed equilibrium. Since the joint profits $\varPi ^t$ exceed the joint profits in the proposed equilibrium, finding such a transfer should always be possible, which upsets the proposed equilibrium.

Hence, in any equilibrium the contracting parties must earn $\varPi ^t$ collectively. Let $\bar{\pi }^t=\pi _j(p_i^t,p_j^t,p_3^t)$ denote the profit of the outsider VIF when the contracting VIF sets its per unit wholesale price to its joint profit maximizing level—$w^t$—in equilibrium. This implies that—like the case with sufficiently sophisticated contracts—the two VIFs will extend contract offers with $w^t$, and in fact pay the downstream competitor as much as $\varPi ^t-{{\bar{\pi }}}^t$ to take this offer, and earn ${{\bar{\pi }}}^t$ in equilibrium.

Therefore, there always exists an equilibrium in which two VIFs make competing offers with a wholesale price that is equal to $w^t$, which in turn induces downstream equilibrium prices of $(p_i^t,p_j^t, p_3^t)$ for all values of the substitutability parameter $\beta$.

1.3 Maximum RPM Contracts are Sufficiently Sophisticated

Consider an equilibrium where the offer of VIF 2 is accepted. With a maximum RPM contract we first solve the problem that is faced by VIF 2. Suppose that firms 1 and 3 are expected to charge $p_1^e$ and $p_3^e$ in the downstream market. In this scenario, firm 2 maximizes

$$\begin{aligned}&\max _{p_2} \varPi _2(p_1^e,p_2, p_3^e) \\&\quad = (p_2-c_I-c_O)q_2(p_1^e, p_2,p_3^e)+(w_3-c_I)q_3(p_1^e, p_2,p_3^e)+f_3. \end{aligned}$$

The first-order condition for firm 2 is given by

$$\begin{aligned} \frac{\partial }{\partial p_2}\varPi _2(p_1^e,p_2, p_3^e )= & {} q_2(p_1^e, p_2, p_3^e)+(p_2-c_I-c_O)\frac{\partial }{\partial p_2}q_2(p_1^e,p_2, p_3^e) \nonumber \\&+(w_3-c_I)\frac{\partial }{\partial p_2}q_3(p_1^e,p_2, p_3^e)=0. \end{aligned}$$

(6)

By selecting $w_3^e=p_3^e -c_O$, VIF 2 can commit to charging $p_2^e$ in equilibrium when firms 1 and 3 charge $p_1^e$ and $p_3^e$, respectively. This is because the choice of $p_2^e$—coupled with the per unit wholesale price choice of $w_3^e$—will replicate the first order condition of the maximization of the profits of an integrated firm with respect to $p_2$.

With regard to the problem that is faced by firm 3, suppose that firms 1 and 2 are expected to charge $p_1^e$ and $p_2^e$, respectively. In addition, assume that the per-unit wholesale price in the maximum RPM contract is set at $w_3^e= p_3^e-c_O$. Moreover, suppose that the maximum price that firm 3 can charge is given by $p_3^{max}=p_3^e$. Firm 3 is restricted to charge a price that is no larger than it would charge for product 3 when firms 2 and 3 integrate.

Under these conditions, firm 3 solves the following profit maximization problem:

$$\begin{aligned} \max _{p_3\le p_3^e} \pi _3( p_1^e, p_2^e,p_3)=(p_3-\underbrace{( p_3^e-c_O)} _{ w_3^e}-c_O)q_3(p_1^e, p_2^e,p_3))-f_3 \end{aligned}$$

The first derivative of this profit function is given by

$$\begin{aligned} \frac{\partial }{\partial p_3}\pi _3(p_1^e, p_2^e, p_3)=q_3(p_1^e, p_2^e, p_3)+(p_3-( p_3^e-c_O)-c_O)\frac{\partial }{\partial p_3}q_3( p_1^e, p_2^e, p_3). \end{aligned}$$

(7)

Evaluating the expression in (7) at $p_3=p_3^e$ yields

$$\begin{aligned} \frac{\partial }{\partial p_3}\pi _3( p_1^e , p_2^e, p_3) \bigg |_{p_3= p_3^e} \bigg . =q_3( p_1^e, p_2^e, p_3^e)>0. \end{aligned}$$

Firm 3 wishes to charge a price that exceeds $p_3^e$; however, given the constraint of the contract it will choose $p_3= p_3^e$.

From the perspective of VIF 1, the problem is no different from the case when firms 2 and 3 integrate. Expecting its two rivals to charge $p_2^e$ and $p_3^e$, VIF 1 will set its price at $p_1^e$ in equilibrium.

In an environment where the two VIFs compete by offering maximum RPM contracts, note that the two VIFs compete by adjusting their fixed fee offers, and the per-unit wholesale price will be set at $w_2^e= w_3^e= w^e=p_3^e -c_O$.

Thus we can state the following corollary to Proposition 2.

Corollary 1

When the two VIFs compete upstream by offering maximum RPM contracts:

• i) For all $\beta <\infty$ there exists an equilibrium with both VIFs making identical competitive offers to firm 3. In these offers, the maximum price that firm 3 can charge is set to $p_3^{max}= p_3^e$, and the per-unit wholesale price is set to $w^e=p_3^e-c_O$.

• ii) For all $\beta >32.89$ there exists an equilibrium with both VIFs’ refusing to make an offer to firm 3.