Endogenous Horizontal Product Differentiation in a Mixed Duopoly

Abstract

This paper studies endogenous horizontal product differentiation in a mixed duopoly. In the basic model in which firms have symmetric costs, we find that (i) product differentiation arises provided differentiation costs are sufficiently low; (ii) under Cournot competition, the welfare maximizing public firm always obtains more incentive for product differentiation, and the products are more differentiated in the mixed duopoly than in the private duopoly; and (iii) under Bertrand competition, the private firm invests in product differentiation when differentiation costs are at moderate levels while the public firm does so when differentiation costs are sufficiently low. The products may be more or less differentiated in the mixed duopoly depending on the differentiation costs. Two extensions of the basic model are also examined: one with a foreign private firm and the other with asymmetric costs.

Appendix: Proofs

1.1 Proof of Lemma 2

From (10) and (11), we obtain that ${\partial V_2^C}/{\partial s}=-2(a-c)^2(1-s)(2-2s+s^2)/(2-s^2)^3<0$, and ${\partial SW^C}/{\partial s}=-(a-c)^2(6-10s+3s^2+2s^3-s^4)/(2-s^2)^3<0$.

1.2 Derivations of (14) and (16)

By (13), we obtain that ${\partial W}/{\partial k_1}={\partial SW^C(s)}/{\partial s} \cdot {\partial s}/{\partial k_1}-1=\beta (a-c)^2 g_1(s)-1$, where $g_1(s)={s(6-10s+3s^2+2s^3-s^4)}/{(2-s^2)^3}$.

By (15), we obtain that ${\partial \pi _2}/{\partial k_2}={\partial V_2^C(s)}/{\partial s} \cdot {\partial s}/{\partial k_2}-1=\beta (a-c)^2g_2(s)-1$, where $g_2(s)={2s(1-s)(2-2s+s^2)}/{(2-s^2)^3}$.

1.3 Proof of Lemma 3

We have that $g_1(s)-g_2(s)=s(1-s)^2(2+2 s- s^2))/(2-s^2)^3>0$ for $s \in (0, 1)$. Furthermore, it is obvious from the expression that $g_2(s)>0$ for $s \in (0, 1)$.

1.4 Proof of Proposition 1

The threshold value, $\hat{\beta }$, for firm 1 to invest must satisfy the following two conditions

$$\begin{aligned} \left\{ \begin{array}{l} {\partial W}/{\partial k_1}=\beta (a-c)^2 g_1(s^*)-1=0, \\ SW^C(s^*)-k_1^*= SW^C(s=1). \end{array}\right. \end{aligned}$$

The first condition implies that firm 1 continues to invest in product differentiation until ${\partial W}/{\partial k_1}=0$ if it decides to undertake the investment. The second condition requires that investing $k_1$ is at least the same as zero investment. Note that $s^*=e^{-\beta k_1^*}$, which yields that $k_1^*=-\ln s^*/\beta$.

The above two equations can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} \beta (a-c)^2 g_1(s^*)-1=0, \\ {(7-6s^*-2{s^*}^2+2{s^*}^3)(a-c)^2}/{2(2-{s^*}^2)^2}+{\ln s^*}/{\beta }= {(a-c)^2}/{2}. \end{array}\right. \end{aligned}$$

By solving the two equations, we obtain that $s^*=0.3945$ and $\hat{\beta }=6.07/(a-c)^2$.¹⁸ Furthermore, it follows from $\beta (a-c)^2 g_2(s^*)-1=0$ that $s^*$ deceases with $\beta$. As a result, we have the results in Proposition 1.

1.5 Proof of Proposition 2

For ${6.07}/{(a-c)^2}<\beta \le {13.5}/{(a-c)^2}$, the products are differentiated in our model but are homogeneous in Brander and Spencer (2015a). For $\beta >{13.5}/{(a-c)^2}$, in Brander and Spencer (2015a, b) firms will differentiate their products from rival’s till $\beta (a-c)^2 g_3(s)-1=0$, where $g_3(s)=2s/(2+s)^3$. Hence, the equilibrium degree of substitutability $s^*_{B \& S}$ satisfies $g_3(s)=1/\left( \beta (a-c)^2\right)$. In our model, firm 1 chooses to differentiate its products from firm 2, and in equilibrium $s^*$ satisfies $g_1(s)=1/\left( \beta (a-c)^2\right)$ by (14). Thus, $g_3(s^*_{B \& S})=g_1(s^*)<1/13.5$. It is easy to show that $g_3(s)$ increases in s and in the considered range $g_1(s)>g_3(s)$. As a result, $g_3(s^*_{B \& S})=g_1(s^*)$ yields that $s^*_{B \& S}>s^*$, which implies that the products are more differentiated in our model.

1.6 Proof of Lemma 5

From (22) and (23), simple calculations yield that ${\partial SW^B}/{\partial s}=-(a-c)^2(6-9s^2-s^3+5s^4+s^5-s^6)/\left( (1+s)^2(2-s^2)^3\right) <0$, and ${\partial V_2^B}/{\partial s}=-2(a-c)^2(2-2s-s^2+2s^3)/\left( (1+s)^2(2-s^2)^3\right) <0$.

1.7 Proof of Lemma 6

Differentiating both $f_1(s)$ and $f_2(s)$ with respect to s yields that $f_1'(s)= (12 - 12 s - 24 s^2 + 16 s^3 + 19 s^4 - 5 s^5 - 5 s^6 + 5 s^7 + 3 s^8 - s^9)/((1 + s)^3 (-2 + s^2)^4)>0$ and $f_2'(s)= 2(4-12s+4s^2+20s^3-7s^4-s^5+8s^6)/((1 + s)^3 (2 - s^2)^4)>0$. Hence, both $f_1(s)$ and $f_2(s)$ are increasing functions of s, which proves part (i).

With the expressions of $f_1(s)$ and $f_2(s)$, we obtain that $s> 0.84$ by setting $f_1(s)<f_2(s)$. Similarly, we easily obtain that $f_1(s)>f_2(s)$ when $s< 0.84$, and $f_1(s)=f_2(s)$ when $s= 0.84$.

1.8 Proof of Proposition 3

Since both $f_1(s)$ and $f_2(s)$ increase in s, we have that ${\partial W}/{\partial k_1}\le \beta (a-c)^2/4-1$ and ${\partial \pi _2}/{\partial k_2}\le \beta (a-c)^2/2-1$ by setting $s=1$. Hence, if $\beta \le {2}/{(a-c)^2}$, both ${\partial W}/{\partial k_1}$ and ${\partial \pi _2}/{\partial k_2}$ are non-positive, which implies that neither firm 1 nor firm 2 will undertake the differentiation investment in equilibrium. So we have the result in part (i).

Next, we prove parts (ii) and (iii). From the above analysis, when ${2}/{(a-c)^2}<\beta \le {4}/{(a-c)^2}$, firm 2 invests while firm 1 does not. For $\beta > {4}/{(a-c)^2}$, both ${\partial W}/{\partial k_1}$ and ${\partial \pi _2}/{\partial k_2}$ are positive at $s=1$, which implies that both firms favor product differentiation. The remaining question here is which firm invests in equilibrium.

(1).:

Suppose that both firms make the investments. We have that $K^*=k_1^*+k_2^*$, and $s^*=e^{-\beta K^*}$ such that

$$\begin{aligned} \left\{ \begin{array}{l} {\partial W}/{\partial k_1}\mid _{s=s^*}=\beta (a-c)^2 f_1(s^*)-1=0,\\ {\partial \pi _2}/{\partial k_2}\mid _{s=s^*}=\beta (a-c)^2 f_2(s^*)-1=0. \end{array}\right. \end{aligned}$$

To satisfy the above two equations, we need that $f_1(s^*)=f_2(s^*)={1}/{\beta (a-c)^2}$. Incorporating $s^*= 0.84$ into the equation yields that $\beta =5.41/(a-c)^2$.

(2).:

Suppose that firm 2 makes the investment but firm 1 does not. We have that $k_1^*=0,$$K^*=k_2^*$, and $s^*=e^{-\beta K^*}$. It occurs if and only if

$$\begin{aligned} \left\{ \begin{array}{l} {\partial W}/{\partial k_1}\mid _{s=s^*}=\beta (a-c)^2 f_1(s^*)-1<0,\\ {\partial \pi _2}/{\partial k_2}\mid _{s=s^*}=\beta (a-c)^2 f_2(s^*)-1=0. \end{array}\right. \end{aligned}$$

To satisfy the above two conditions, we need that $f_1(s^*)<f_2(s^*)$ and $\beta ={1}/{(a-c)^2f_2(s^*)}$. By setting $f_1(s^*)<f_2(s^*)$, we obtain that $s^*> 0.84$, which yields that $f_2(s^*)>0.1847$. Thus, we have that $\beta <5.41/(a-c)^2$.

(3).:

Similarly, firm 1 makes the investment if and only if

$$\begin{aligned} \left\{ \begin{array}{l} {\partial W}/{\partial k_1}\mid _{s=s^*}=\beta (a-c)^2 f_1(s^*)-1=0,\\ {\partial \pi _2}/{\partial k_2}\mid _{s=s^*}=\beta (a-c)^2 f_2(s^*)-1<0, \end{array}\right. \end{aligned}$$

where $s^*=e^{-\beta K^*}$ and $K^*=k_1^*$. Simple calculations show that we need $\beta >5.41/(a-c)^2$ for the above two conditions to hold.

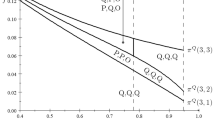
To summarize, if $\beta <5.41/(a-c)^2$, firm 2 invests but firm 1 does not; if $\beta \ge 5.41/(a-c)^2$, firm 1 invests but firm 2 does not. Hence, we have the results in part (ii) and (iii).

To show that v increases with $\beta$, we examine $s^*$ in equilibrium instead. When firm 2 invests, $s^*$ is determined by $\beta (a-c)^2 f_2(s^*)-1=0$; when firm 1 invests, $s^*$ is determined by $\beta (a-c)^2 f_1(s^*)-1=0$. With the properties of $f_1(s)$ and $f_2(s)$ in Lemma 6, it is straightforward that $s^*$ decreases with $\beta$. Hence, we have the result.¹⁹

1.9 Proof of Proposition 4

Products are differentiated for $\beta > 2/{(a-c)^2}$ for both models. In Brander and Spencer (2015a) firms will differentiate their products from rival’s product until $\beta (a-c)^2 f_3(s)-1=0$, where $f_3(s)=2s(1-s+s^2)/\left( (2-s)^3(1+s^2\right)$. Hence, in equilibrium $s^*_{B \& S}$ satisfies $f_3(s)=1/\left( \beta (a-c)^2\right)$. In our model, firm 2 invests until $\beta (a-c)^2 f_2(s)-1=0$ when $2/{(a-c)^2}<\beta <5.41/{(a-c)^2}$ and firm 1 invests until $\beta (a-c)^2 f_1(s)-1=0$ when $\beta \ge 5.41/{(a-c)^2}$. From the proof of Lemma 6, we know that $f_1(s)>f_2(s)$ when $s< 0.84$ and otherwise $f_1(s)<f_2(s)$. It is easy to show that $f_3(s)$ increases in s. Furthermore, we have that $f_3(s)<f_1(s)$ when $s< 0.70$ and otherwise $f_3(s)>\max \{f_1(s), f_2(s)\}$. The corresponding $\beta$ for $s=0.70$ in equilibrium is $\beta =5.74/{(a-c)^2}$. As a result, it follows that the products are more differentiated in our model for $\beta >5.74/{(a-c)^2}$. Otherwise, for $2/{(a-c)^2}<\beta \le 5.74/{(a-c)^2}$ products are more differentiated in the Brander and Spencer (2015a) model.

1.10 Proof of Proposition 5

We next show that $v^C>v^B>0$. Denote $s^C=1-v^C$, $s^B=1-v^B$. Then $s^B$ satisfies $\beta (a-c)^2 f_1(s)-1=0$, and $s^C$ satisfies $\beta (a-c)^2 g_1(s)-1=0$, where $s^C\in (0,0.3945]$. Case 1: If $s^B>0.3945$, there must be $s^B>s^C$: i.e., $v^C>v^B>0$. Case 2: If $s^B\le 0.3945$, we have that $f_1(s^B)= g_1(s^C)=1/\beta (a-c)^2$. The two functions—$f_1(s)$ and $g_1(s)$—increase in $s\in [0,0.3945]$, and furthermore $f_1(s)\le g_1(s)$ on this interval. It follows that $s^B>s^C$.

1.11 Proof of Proposition 6

Consider part (i) first. By (28), we obtain that ${\partial W}/{\partial k_1}= {\partial SW^C}/{\partial s} \cdot {\partial s}/{\partial k_1}-1=\beta (a-c)^2 g_{11}(s)-1$ and ${\partial \pi _2}/{\partial k_2}={\partial V_2^C}/{\partial s} \cdot {\partial s}/{\partial k_2}-1=\beta (a-c)^2 g_{21}(s)-1$, where $g_{11}(s)=s(1-s)/4$ and $g_{21}(s)=s(1-s)/2$. It is easy to show that both $g_{11}(s)$ and $g_{21}(s)$ are concave functions and that $g_{11}(s)\le g_{21}(s)$. Hence, firm 2 has more incentives to invest. As we did in the proof of Proposition 1, we are able to calculate the threshold value $\hat{\beta }$ for firm 2 to undertake the investment as $\hat{\beta }=9.82/(a-c)^2$. As a result, firm 2 makes the investment if and only if $\beta >9.82/(a-c)^2$.

Consider now part (ii): The products are differentiated in a private duopoly when $\beta >{13.5}/{(a-c)^2}$ as in Brander and Spencer (2015b). In a mixed duopoly, firm 2 invests until ${\partial \pi _2}/{\partial k_2}=\beta (a-c)^2g_{21}(s)-1=0$, while in a private duopoly the firms will differentiate their products from rival’s until $\beta (a-c)^2 g_3(s)-1=0$. It is easy to show that in the considered range $g_{21}(s)>g_3(s)$, which implies that the products are more differentiated in a mixed duopoly.

1.12 Proof of Proposition 7

Consider first part (i): By (30), we obtain that ${\partial W}/{\partial k_1}= {\partial SW^B}/{\partial s} \cdot {\partial s}/{\partial k_1}-1=\beta (a-c)^2 f_{11}-1$, and ${\partial \pi _2}/{\partial k_2}={\partial V_2^B}/{\partial s} \cdot {\partial s}/{\partial k_2}-1=\beta (a-c)^2 f_{21}-1$, where $f_{11}(s)=s/(4(1+s)^2)$ and $f_{21}(s)=s/(2(1+s)^2)$. It is easy to show that both $f_{11}(s)$ and $f_{21}(s)$ increase in s and $f_{11}(s)\le f_{21}(s)$, which yield that ${\partial W}/{\partial k_1} \le {\partial \pi _2}/{\partial k_2}$. As a result, firm 2 always has a greater incentive to undertake product differentiation. Firm 2 will make the investment as long as ${\partial \pi _2}/{\partial k_2}\mid _{s=1}=\beta (a-c)^2 f_{21}(s=1)-1>0$, which can be reduced to $\beta > 8/(a-c)^2$.

Consider now part (ii): The products are differentiated in a private duopoly when $\beta >{2}/{(a-c)^2}$ as in Brander and Spencer (2015b). In a mixed duopoly, firm 2 invests until ${\partial \pi _2}/{\partial k_2}=\beta (a-c)^2 f_{21}-1=0$, while in a private duopoly the firms will differentiate their products from rival’s till $\beta (a-c)^2 f_3(s)-1=0$. It is easy to show that in the considered range $f_{21}(s)<f_3(s)$, which implies that the products are less differentiated in a mixed duopoly.

1.13 Proof of Proposition 8

Consider first part (i): We have that ${\partial W}/{\partial k_1}=\beta (a-c_2)^2 \tilde{g}_1(s)-1,$ and ${\partial \pi _2}/{\partial k_2}=\beta (a-c_2)^2 \tilde{g}_2(s)-1,$ where $\tilde{g}_1(s)={s\left( (1-t)^2(s^3-6s)-(1-t)(s^4-3s^2-6)+(s^3-4s)\right) }/{(2-s^2)^3},$ and $\tilde{g}_2(s)={-2s\left( (1-t)^2(s^3+2s)-(1-t)(3s^2+2)+2s\right) }/{(2-s^2)^3}.$ It can be shown that $\tilde{g}_1(s)\ge \tilde{g}_2(s)$. As a result, the public firm has stronger incentives to undertake product differentiation investment. For any value of $t(<1/2)$, there exists $\beta _{1C}^*(t)$ such that firm 1 differentiates products for $\beta >\beta _{1C}^*(t)$, and otherwise the two firms produce homogeneous products (refer to the equilibrium quantities).

Consider next part (ii): In the basic model, the public firm invests when $\beta \ge 6.07/(a-c)^2$, and the equilibrium $s^*\le 0.3945$. With asymmetric costs, it is also that the public firm invests. Furthermore, we have that $\tilde{g}_1(s)\le g_1(s)$ for $s\le 0.3945$. Thus, the equilibrium product substitutability in the basic model is smaller, which implies greater product differentiation.

1.14 Proof of Proposition 9

Consider first part (i): We have that ${\partial W}/{\partial k_1}=\beta (a-c_2)^2 \tilde{f}_1(s)-1,$ and ${\partial \pi _2}/{\partial k_2}=\beta (a-c_2)^2 \tilde{f}_2(s)-1,$ where $\tilde{f}_1(s)={s(1-s+st)H(s)}/{\left( (2-s^2)^3(1-s^2)^2\right) },$ and $\tilde{f}_2(s)={2s(1-s+st)(2-4s+s^2+3s^3-2s^4-2t-s^2t+2s^4t)}/{\left( (2-s^2)^3(1-s^2)^2\right) },$$H(s)=6-6s-9s^2+8s^3+6s^4-4s^5-2s^6+s^7-6t+9s^2t-6s^4t+2s^6t.$ It can be shown that $\tilde{f}_1(s)\ge \tilde{f}_2(s)$ for $t\ge 0.03$. As a result, the public firm obtains stronger incentives to undertake product differentiation investments. There exists $\beta _{1B}^*(t)$ such that firm 1 differentiates products for $\beta >\beta _{1B}^*(t)$. Otherwise, neither firm invests and the private firm monopolizes the market. For $t<0.03$, $\tilde{f}_1(s)\ge \tilde{f}_2(s)$ does not always hold for $s\in [0,1].$ Using Matlab, we observe that in a very small range where the cost difference is relatively negligible ($t<0.015$), the investment behaviors of the two firms are approximately the same as that in the basic model. Otherwise, the public firm has stronger incentives to undertake product differentiation investments.

Consider next part (ii): It is easy to show that $\tilde{f}_1(s)<\max \{f_1(s), f_2(s)\}$. Thus, the equilibrium product substitutability in the basic model is smaller, which implies greater product differentiation.