Abstract
This paper examines the welfare implications of input price discrimination in a vertically-related market, which is composed of a monopolistic upstream market and a duopolistic downstream market. The downstream duopolists produce quality-differentiated products at different marginal costs. We show that the equilibrium input prices are closely related to the downstream quality gap and cost difference. When the monopolist simply charges a unit wholesale price for its input product, discriminatory pricing could be socially desirable even though the aggregate output remains unchanged. Nevertheless, if a two-part tariff is feasible, then banning price discrimination could increase the aggregate output and social welfare.


Similar content being viewed by others
Notes
For example, both the Robinson-Patman Act of 1936 in the United States and the Article 102(c) of the Treaty on the Functioning of the European Union (TFEU) conditionally prohibit price discrimination in input markets. See Schwartz (1986) for the legal issues of the Robinson-Patman Act and Geradin and Petit (2006) for comprehensive discussions of price discrimination under TFEU competition law.
See also Valletti (2003) for an analysis of a general demand model under a Cournot oligopoly.
Chen et al. (2011) consider both firm-specific heterogeneity and market-specific heterogeneity in their model and find that permitting input price discrimination is allocatively efficient in terms of the output distribution among consumers.
The low-wholesale-price result also arises when downstream firms have bargaining powers—e.g., O’Brien (2014)—or when the monopolist adopts sequential contracting (e.g., Kim and Sim 2015). Two papers are also related to the model of Herweg and Müller (2012): Dertwinkel-Kalt et al. (2016) complement the analysis of Herweg and Müller (2012) and gain the same conclusion that price discrimination in input markets is pro-competitive; they also examine pro-competitive price discrimination in a dynamic setting in which downstream firms choose their cost-reduction innovations. Kao and Peng (2012) allow the downstream market structure to be endogenously determined and find a similar welfare result to Herweg and Müller (2012).
Arya and Mittendorf (2010) also consider a two-part tariff and present the same welfare result.
With information asymmetry, Herweg and Müller (2014) also conclude that non-linear price discrimination is welfare harming if it does not increase expected aggregate output.
The marginal consumer \(\theta_{12}\) is indifferent between buying either product, whereas the marginal consumer \(\theta_{20}\) is indifferent between buying the low-quality product and not buying.
As compared to Inderst and Valletti’s (2009) demand functions that differ only in vertical intercepts, in our quality differentiation model the derived demands of the downstream firms differ in both the intercept and the slope. Hence, our specification of vertical differentiation allows for various derived demands for inputs.
The condition is derived from Assumption 1 (2). Given the condition, Assumption 1 (1) is met as \(s - c > 0\). On the other hand, the discriminatory monopolist’s profit is: \(\Omega \left( {w_{1}^{d} ,w_{2}^{d} } \right) = \left[ {(2s - 1)c^{2} - (4s^{2} - 4s)c + 2s^{3} - s^{2} - s} \right]/[4(4s - 1)(s - 1)].\) It also shows that Assumption 1 (3) is met as \(\Omega \left( {w_{1}^{d} ,w_{2}^{d} } \right) > \hbox{max} \{ \Omega_{1} ,\Omega_{2} \}\), where \(\Omega_{1} = (s - c)^{2} /(8s)\) and \(\Omega_{2} = {1 \mathord{\left/ {\vphantom {1 8}} \right. \kern-0pt} 8}\).
The upper and lower bounds are calculated from Assumption 1 (2). If \(c < \bar{c}\) (\(c > \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c}\)), then \(q_{1} (w_{u} ) > 0\) (\(q_{2} (w_{u} ) > 0\)). On the other hand, the monopolist’s profit is: \(\Omega (w^{u} ) = \left( {3s - c} \right)^{2} /\left[ {4(4s - 1)(2s + 1)} \right].\) Furthermore, if \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} < c < \bar{c}\), then Assumption 1 (3) is met as \(\Omega (w^{u} ) > \hbox{max} \{ \Omega_{1} ,\Omega_{2} \}\), where \(\Omega_{1} = (s - c)^{2} /8s\) and \(\Omega_{2} = 1/8\).
This result follows directly from the symmetric cross-price effects in the system of the derived demand functions. See also Layson (1998) for a detailed demonstration.
The inverse demand functions are derived by solving \(p_{1}\) and \(p_{2}\) in (1).
A two-part tariff itself is a form of block tariff, whereby the monopolist can implement second-degree price discrimination. Hence, in the regime of non-linear pricing, when we refer to the term price discrimination (or discriminatory pricing), it is not clear whether this means second-degree or third-degree price discrimination. To avoid confusion, in our paper the term “price discrimination” exclusively refers to third-degree price discrimination.
The proofs for the Bertrand results are available upon request.
We thank an anonymous referee for suggesting this.
Siebert (2015) demonstrates that if the marginal cost is zero, then a monopolist will not sell both the high-quality and low-quality product, but rather only the former due to the cannibalization effect. We assume that the high-quality product is more costly to produce than the low-quality one; i.e., \(c > 0\). Due to the cost advantage, the integrated monopolist always offers the low-quality product. However, if c is sufficiently large such that \(c > s - 1\), then the monopolist will not offer the costly high-quality product in order to avoid cannibalizing the demand for the low-quality (low-cost) product. Hence, we assume here that \(c < s - 1\).
The second-order conditions are always satisfied as \({{\partial \Omega } \mathord{\left/ {\vphantom {{\partial \Omega } {\partial p_{1} }}} \right. \kern-0pt} {\partial p_{1} }} = {{ - 2} \mathord{\left/ {\vphantom {{ - 2} {(s - 1)}}} \right. \kern-0pt} {(s - 1)}} < 0\) and \({{\partial \Omega } \mathord{\left/ {\vphantom {{\partial \Omega } {\partial p_{2} }}} \right. \kern-0pt} {\partial p_{2} }} = {{ - 2s} \mathord{\left/ {\vphantom {{ - 2s} {(s - 1)}}} \right. \kern-0pt} {(s - 1)}} < 0\).
Given a specific contract (\(w,F\)), the high-quality firm’s profit is lower than the low-quality firm’s profit when the cost difference is sufficiently large, and vice versa.
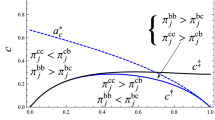
If the value of \(s\) is sufficiently large, then the uniform unit wholesale price may be negative in some of the three regimes. In order to encompass more realistic results, we therefore assume that \(s < 1.97\). Please refer to the proof of Lemma 2 in the “Appendix 1” section for the detailed calculations of the threshold quality gap and the upper and lower bounds for the cost difference.
Note in Lemma 2 that the ranking of the threshold levels of cost difference, \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} < c^{\prime} < c^{\prime\prime} < \bar{c}\), always holds true if \(s < 1.97\).
In the figures, the values of the relevant cost differences are: \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} \approx 0. 3 1 8 5\), \(\bar{c} \approx 0. 4 3 6 8\), \(c^{\prime} \approx 0. 3 5 8 6\), and \(c^{\prime\prime} \approx 0. 4 2 5 3\).
This incentive becomes even stronger when the cost difference increases, thereby making the unit wholesale price move downward as shown in the figure.
It also worth noting from Fig. 2 that if \(c > c^{\prime}\), then for cost differences close to \(c^{\prime}\) the aggregate output is still relatively large under uniform pricing. This implies that within the cost range \(c^{\prime} < c < c^{\prime\prime}\) in the figure, there exists a threshold cost difference below which the previous welfare conclusion applies. As the intuition for this result is the same as previously noted, instead of providing a formal proof with tedious calculations, we merely present this possibility through the numerical example of Fig. 2.
References
Arya, A., & Mittendorf, B. (2010). Input price discrimination when buyers operate in multiple markets. Journal of Industrial Economics, 58(4), 846–867.
Chen, C.-S., & Hwang, H. (2014). Spatial price discrimination in input markets with an endogenous market boundary. Review of Industrial Organization, 45(2), 139–152.
Chen, C.-S., Hwang, H., & Peng, C.-H. (2011). Welfare, output allocation and price discrimination in input markets. Academia Economic Papers, 39(4), 535–560.
Choi, C. J., & Shin, H. S. (1992). A comment on a model of vertical product differentiation. The Journal of Industrial Economics, 40(2), 229–231.
Coloma, G. (2003). Price discrimination and price dispersion in the Argentine gasoline market. International Journal of the Economics of Business, 10(2), 169–178.
DeGraba, P. (1990). Input market price discrimination and the choice of technology. American Economic Review, 80(5), 1246–1253.
Dertwinkel-Kalt, M., Haucap, J., & Wey, C. (2016). Procompetitive dual pricing. European Journal of Law and Economics, 41(3), 537–557.
Geradin, D., & Petit, N. (2006). Price discrimination under EC competition law: Another antitrust doctrine in search of limiting principles? Journal of Competition Law and Economics, 2(3), 479–531.
Herweg, F., & Müller, D. (2012). Price discrimination in input markets: Downstream entry and efficiency. Journal of Economics & Management Strategy, 21(3), 773–799.
Herweg, F., & Müller, D. (2014). Price discrimination in input markets: Quantity discounts and private information. Economic Journal, 124(577), 776–804.
Herweg, F., & Müller, D. (2016). Discriminatory nonlinear pricing, fixed costs, and welfare in intermediate-goods markets. International Journal of Industrial Organization, 46, 107–136.
Inderst, R., & Shaffer, G. (2009). Market power, price discrimination, and allocative efficiency in intermediate-goods markets. RAND Journal of Economics, 40(4), 658–672.
Inderst, R., & Valletti, T. (2009). Price discrimination in input markets. RAND Journal of Economics, 40(1), 1–19.
Kao, K.-F., & Peng, C.-H. (2012). Production efficiency, input price discrimination, and social welfare. Asia-Pacific Journal of Accounting & Economics, 19(2), 227–237.
Katz, M. L. (1987). The welfare effects of third-degree price discrimination in intermediate good markets. American Economic Review, 77(1), 154–167.
Kim, H., & Sim, S. (2015). Price discrimination and sequential contracting in monopolistic input markets. Economics Letters, 128, 39–42.
Layson, S. K. (1998). Third-degree price discrimination with interdependent demand. Journal of Industrial Economics, 46(4), 511–524.
Motta, M. (1993). Endogenous quality choice: Price versus quantity competition. Journal of Industrial Economics, 41(2), 113–131.
O’Brien, D. P. (2014). The welfare effects of third-degree price discrimination in intermediate good markets: the case of bargaining. RAND Journal of Economics, 45(1), 92–115.
Robinson, J. (1933). The economics of imperfect competition. London: Macmillan.
Schmalensee, R. (1981). Output and welfare implications of monopolistic third-degree price discrimination. American Economic Review, 71(1), 242–247.
Schwartz, M. (1986). The perverse effects of the Robinson-Patman Act. Antitrust Bulletin, 31(3), 733–757.
Siebert, R. (2015). Entering new markets in the presence of competition: Price discrimination versus cannibalization. Journal of Economics & Management Strategy, 24(2), 369–389.
Valletti, T. (2003). Input price discrimination with downstream Cournot competitors. International Journal of Industrial Organization, 21, 969–988.
Varian, H. R. (1985). Price discrimination and social welfare. American Economic Review, 75(4), 870–875.
Villas-Boas, S. B. (2009). An empirical investigation of the welfare effects of banning wholesale price discrimination. RAND Journal of Economics, 40(1), 20–46.
Wauthy, X. (1996). Quality choice in models of vertical differentiation. Journal of Industrial Economics, 44(3), 345–353.
Yoshida, Y. (2000). Third-degree price discrimination in input markets: Output and welfare. American Economic Review, 90(1), 240–246.
Acknowledgments
The author is very grateful to Lawrence J. White (the Editor) and two anonymous referees for very helpful comments. The financial support from the National Science Council of Taiwan (NSC 102-2410-H-034-065) is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Proof of Lemma 2
When solving the unit wholesale price under uniform pricing, we need to check the monopolist’s incentive for serving both downstream firms and the participation constraint for each downstream firm. If the monopolist serves only firm 1 or firm 2, then its profits are respectively:
Given a unit wholesale price, downstream firms’ profits gross of fixed fees are:
Note that Eqs. (29) and (30) are used to derive the relevant parameter ranges for the equilibrium uniform wholesale prices.
We shall derive the optimal uniform wholesale price in three regimes: First, if firm 2’s participation constraint is binding, then the monopolist solves:
From the first-order condition for profit maximization, the optimal wholesale price is:
The second-order condition is satisfied as: \(\partial^{2} \Omega /\partial w^{2} = - 4(3s - 1)/(4s - 1)^{2} < 0.\) The optimal fixed fee is \(F = \pi_{2} (w)\).
By substituting (32) into (31) and rearranging, the monopolist profit is specified as follows:
To ensure that the monopolist will serve both downstream firms—i.e., the profit in (33) is larger than that in (29)—the cost disadvantage must be larger than the threshold level:
Substituting (32) into (30) and rearranging yield:
From (35), to ensure that firm 1’s participation constraint is satisfied (i.e., \(\pi_{1} - \pi_{2} > 0\)), the cost difference must be smaller than the threshold level:
A comparison of (34) and (36) shows that \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} < c^{\prime}\). Hence, if \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} < c < c^{\prime}\), then (32) is the optimal unit wholesale price under uniform pricing. Note that in this case the uniform wholesale price may turn to be negative under some parameter combinations. The equilibrium wholesale price is positive only if: \(c < \tilde{c} = {{(4s^{2} - 3s + 1)} \mathord{\left/ {\vphantom {{(4s^{2} - 3s + 1)} {(12s - 5)}}} \right. \kern-0pt} {(12s - 5)}}\). However, if \(s > \tilde{s} \approx 1.97\), then \(\tilde{c} < c^{\prime}\) and (32) is negative for \(\tilde{c} < c < c^{\prime}\). Hence, to ensure that the equilibrium wholesale price is always positive, we further assume that \(s < 1.97\).
Second, if firm 1’s participation constraint is binding, then the monopolist’s objective function is: \(\Omega \text{ }(w) = \text{ }w\left( {q_{1} (w) + q_{2} (w)} \right) + 2\pi_{ 1} (w ).\) Proceeding as previously, we can respectively solve for the unit wholesale price, the monopolist’s profit, and the downstream firms’ profits as follows:
The fixed fee is \(\pi_{ 1} (w )\). The second-order condition satisfies: \({{\partial^{2} \Omega } \mathord{\left/ {\vphantom {{\partial^{2} \Omega } {\partial w^{2} }}} \right. \kern-0pt} {\partial w^{2} }} = {{ - 8s(2s - 1)} \mathord{\left/ {\vphantom {{ - 8s(2s - 1)} {(4s - 1)^{2} }}} \right. \kern-0pt} {(4s - 1)^{2} }} < 0.\)
From (29) and (38), the monopolist serves both downstream firms only if:
On the other hand, from (39), firm 2’s participation constraint is satisfied (i.e., \(\pi_{2} - \pi_{1} > 0\)) only if:
As \(c^{\prime\prime} < \bar{c}\), we thus conclude that given a quality level, if \(c^{\prime\prime} < c < \bar{c}\), then (37) is the optimal unit wholesale price.
Note that if \(c^{\prime} < c < c^{\prime\prime}\), then neither (32) nor (37) meet all of the downstream participation constraints. Under such circumstances, the equilibrium unit wholesale price is determined by the profit-equalization condition: \(\pi_{1} (w ) { = }\pi_{2} (w )\). By substituting the profits in (30) into the condition and solving for w, we obtain:
The optimal fixed fee is \(F = \pi_{1} (w ) { = }\pi_{2} (w )\). The monopolist’s profit is: \(\, \Omega \text{ } = {{\left[ {(s - c - 1)(\varPsi - \varUpsilon )} \right]} \mathord{\left/ {\vphantom {{\left[ {(s - c - 1)(\varPsi - \varUpsilon )} \right]} {\left[ {(s - 1)(4s - 1)} \right]}}} \right. \kern-0pt} {\left[ {(s - 1)(4s - 1)} \right]}}^{2}\), where \(\varPsi = - 4s^{3} + (6 + 16c)s^{2} - (2 + 9c)s + c\), and \(\varUpsilon = \left[ {4s^{3} - (7 + 12c)s^{2} + (4 + 5c)s - c - 1} \right]s^{1/2}\). Given \(s < 1.97\), in the cost range the uniform wholesale price is positive, and the monopolist’s profit \(\Omega \text{ }\) is larger than \(\, \Omega_{1}\) and \(\, \Omega_{2}\) in (29).
By summarizing the results in (32), (37), and (40), we obtain Lemma 2.
Appendix 2: Proof of Proposition 5
By substituting the corresponding marginal consumers from (23) and (28) into the social welfare function in (14), we can calculate the equilibrium welfare under either pricing policy as follows:
where \(\alpha = - 36s^{2} + 111s - 31\), \(\beta = 24s^{3} - 154s^{2} + 144s - 30\), and \(\gamma = - 4s^{4} + 87s^{3} - 37s^{2} + s + 1\).
The welfare difference (\(\Delta SW = \text{ }SW^{d} - SW^{u}\)) is then specified as follows:
where \(\tilde{\alpha } = 36s^{3} - 39s^{2} + 70s - 19\), \(\tilde{\beta } = - 2(s - 1)(3s + 1)(4s^{2} + 9s - 3)\), and \(\tilde{\gamma } = (s - 1)^{2} (4s^{3} + 25s^{2} - 10s + 1)\).
Letting \(\Delta SW\) equal zero and solving for the threshold levels of cost difference, we obtain:
This shows that the welfare difference is negative for \(\tilde{c}^{ - } < c < \tilde{c}^{ + }\); otherwise, it is positive. If \(s < 1.97\), then the cost ranking \(\tilde{c}^{ - } < \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} < c^{\prime} < \tilde{c}^{ + }\) always holds true. Hence, if \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} < c < c^{\prime}\), then \(\Delta SW < 0\), which completes the proof of Proposition 5.
Rights and permissions
About this article
Cite this article
Chen, CS. Price Discrimination in Input Markets and Quality Differentiation. Rev Ind Organ 50, 367–388 (2017). https://doi.org/10.1007/s11151-016-9537-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11151-016-9537-9
Keywords
- Input price discrimination
- Wholesale price discrimination
- Quality differentiation
- Two-part tariffs
- Social welfare