Task specialization and cognitive skills: evidence from PIAAC and IALS

Abstract

We study how the tasks conducted on the job relate to measures of cognitive skills using data from 18 countries participating in the Programme for the International Assessment of Adult Competences (PIAAC) and from 13 countries that also participate in the International Adult Literacy Study (IALS). We document two main findings. Firstly, individual-fixed effect models suggest that low-educated workers specializing in a particular set of basic tasks -say, in numeric relative to reading or ICT tasks- obtain 10% of one standard deviation higher scores in the domain of the PIAAC assessment most related to those tasks than in the rest -say, numeracy relative to literacy or problem-solving scores. Secondly, a synthetic cohort analysis using repeated literacy assessments in IALS and PIAAC indicates that, among the low-educated, long-run increases in the reading task component of jobs correlate positively with increases in cohort-level literacy scores. The results are stronger among low-skilled workers with less working experience or females -i.e., the set of workers who have had less time to sort in the labor market. An interpretation of our findings is that tasks conducted on the job help in building human capital but are imperfect substitutes of formal schooling.

1 Introduction

Workers obtain skills both in the formal education system and by learning on-the-job.¹ While there is a substantial literature on how schooling raises cognitive skills and, in turn, wages, much less is known about how skills are formed by learning on the job.² In particular, previous literature has documented a heterogeneity in experience profiles that could be due to search frictions, increased competition for jobs or differences in human capital accumulation -like the task content of jobs.

Our study uses data on actual tasks conducted on the job and on measures of cognitive skills to study the link between tasks and cognitive skills. We rely on measures of cognitive ability of representative samples of the population of 18 countries participating in PIAAC, an OECD-coordinated effort to measure the skills of the population between 16 and 65 years of age. We measure human capital through three cognitive measures in standardized tests: numeracy, literacy and problem-solving skills. The availability of three different measures is important, as it allows us to relate specific tasks to skills while holding constant an individual-fixed effect.

Measures of cognitive skills are an important source of information because of two main reasons. The first is that measures of cognitive abilities are available for representative samples of the population that include the long-term unemployed.³ Conceptually this is important, as the accumulation of human capital by low-skilled is an important policy parameter that may be difficult to measure using wages -as that group is more likely to be affected by non-employment -see Charles, Hurst and Notowidigdo (2016). By proxying human capital with measures of cognitive skills, we avoid econometric problems related to modeling labor market participation. Furthermore, the literature has documented that the skill measures we use are indeed related to wages.⁴

Our empirical strategy draws from the literature that estimates education production functions by using multiple measures of skills. In particular, we estimate the contribution of on-the-job learning on human capital by exploiting the availability of multiple measures of cognitive skills for the same individual and the fact that jobs vary in their task content.⁵ For example, we estimate the effect of the relative intensity of numeric (relative to reading) tasks on the job on the relative score in numeracy (versus literacy) tests, using a specification that absorbs any individual-level characteristic that is constant across human capital measures.⁶ We do similar exercises to test if workers in ICT intensive jobs perform better in the problem solving part of the test than on the literacy part.

The above mentioned estimates control for a fixed-effect that is common across all cognitive measures but also captures sorting components. For example, workers may invest in specific skills at the beginning of their working life anticipating higher monetary returns in future jobs (Lazear (2009)). Alternatively, tasks may have an amenity component, and workers may sort into jobs with those tasks according to their preferences.⁷ To get a sense of the magnitude of that sorting component, we use various methods. The first method assumes that very basic tasks like using a calculator or reading emails are unlikely to increase the cognitive skills of workers with high levels of schooling -we provide some evidence on this regard. As a result, any differential performance in numeracy tests relative to literacy or problem-solving tests associated to specialization in basic numeric tasks among college or high-school workers may reflect sorting across jobs, allowing us to assess to what extent our estimates reflect biases due to selection. A second method combines information from the literacy assessments in the 1994 International Adult Literacy Survey (IALS) and in PIAAC as well as information about the reading and numeric component on jobs to construct synthetic life-cycle profiles of reading tasks and literacy scores -see Barrett & Riddell (2016). We then regress cohort-level changes in literacy scores on the cohort-level changes in the reading content of jobs.⁸

Our results can be summarized as follows. Individuals with compulsory schooling and working in jobs with a relatively higher intensity of basic numeracy tasks perform relatively better in numeracy tests than in literacy or problem solving tests (and viceversa). Namely, respondents with basic schooling who fully specialize in basic numerical tasks on their jobs obtain between 7% and 10.8% of one standard deviation higher scores in the numeracy test than in the literacy test. On the other hand, in our preferred sample of individuals with less than 10 years of experience, the association between specialization in numerical tasks and relative performance in the numerical test is much weaker among individuals with a high school or a college degree. The relationship is also stronger among females. We interpret from the methods outlined above that sorting, despite of being an important mechanism on its own, is unlikely to drive all of our results.⁹

An interpretation of our findings is that on-the-job learning by conducting basic numerical, reading or ICT tasks is an imperfect substitute for formal education for workers with compulsory schooling. We draw on evidence in previous studies to obtain a tentative estimate of the degree of substitution between of one year of formal education and between two and four years of skill acquisition on the job. The rest of the paper is organized as follows. Section 2 describes the empirical method. Section 3 describes the datasets. Section 4 discusses the link between between tasks on-the-job and numeracy and literacy scores and the main results. Section 5 presents the main conclusions.

2 Empirical methods

We assume that human capital C_i is acquired by an individual i through the formal education system (that we denote as S_i) and by the task-content of his or her job, denoted by J_i. Individuals may also vary in their initial endowment of human capital, C_0,i, a measure that summarizes factors related to the innate ability of a worker.

$${C}_{i}={\alpha }_{0}+{\alpha }_{1}{S}_{i}+{\alpha }_{2}{J}_{i}+{\alpha }_{3}{J}_{i}* \ {S}_{i}+{C}_{0,i}+{\epsilon }_{i}$$

(1)

We use three different proxies of human capital, C_i, measured through numeracy, literacy and problem-solving scores in standardized tests (C_n,i, C_l,i and C_p,i respectively) and three different measures of tasks performed on each respondent’s current or last job: ICT-related (J_i = p_i) reading-related (J_i = l_i), numeracy-related (J_i = n_i). That means that we observe:

$${C}_{m,i}={\alpha }_{0,m}+{\alpha }_{1,m}{S}_{i}+{\alpha }_{2,m}{J}_{i}+{\alpha }_{3,m}{J}_{i}* {S}_{i}+{C}_{0,i}+{\epsilon }_{mi},\,\,m=n,l,p$$

(2)

where C_0,i absorbs initial skills that affect equally all sorts of cognitive skills (problem-solving, reading or numeracy-related). Also, as PIAAC is a cross-section, note that C_0,i is effectively a worker-time fixed effect. For that reason, C_0,i also absorbs any characteristic of the employer-employee match (like possible mismatches between the employee qualifications and those required by the job) or, in the case of non-employed individuals,¹⁰ any depreciation of their human capital that is constant across all cognitive measures. ϵ_mi is a mean-zero unobserved factor reflecting the initial endowment of domain-specific human capital, uncorrelated with the initial amount of general human capital C_0,i.¹¹

We focus on α_2,m, the impact of domain-specific tasks done on the job (reading, numeric and ICT) on domain-specific cognitive skills C_m,i.¹²

2.1 On the job learning vs sorting on the job

A problem when estimating model (2) is that the failure to hold pre-labour market ability constant, C_0,i, is likely to result in an upward bias of OLS estimates of α_2,m in Model (2).¹³ We exploit multiple measures of human capital for the same individual to control for C_0,i. In particular, under the assumption that the impact of conducting reading tasks on literacy scores equals the impact of mathematical tasks on numeracy scores (i.e. α_2,n = α_2,l = α_2,p and that α_3,n = α_3,l = α_3,p), one can take the difference between any pair of skills (say, numeracy vs literacy):

$${C}_{n}-{C}_{l}=[{\alpha }_{0,n}-{\alpha }_{0,l}]+[{\alpha }_{1,n}-{\alpha }_{1,l}]S+{\alpha }_{2}[n-l]+{\alpha }_{3}[n-l]* S+{\epsilon }_{n}-{\epsilon }_{l}$$

(3)

Model (3) identifies the impact of tasks performed on-the-job on particular forms of human capital (numeracy vs literacy) by comparing individuals who have different degrees of specialization in the tasks they perform in their jobs (in the example, numeric vs reading tasks, or n − l, but we can also estimate the impact on cognitive skills of n − p and l − p).¹⁴

A second consideration in Model (2) is that workers sort in the labour market according to their initial endowment of domain-specific human capital. For example, workers with an initial ability for numeracy-related jobs may sort into numeracy-intensive jobs. Alternatively, workers may decide to invest in a set of skills at the beginning of their careers in anticipation of obtaining a better job in the future if the current match dissolves (Lazear (2009)). In other words, workers with a higher value of ϵ_n − ϵ_l (or a comparative advantage in numeracy tasks) are likely to sort into a relatively math-intensive work environment -i.e., with a higher level of [n -l]. Sorting would generate a positive correlation between the numeracy content of a job and initial endowment of numerical human capital.

One way to see this bias is a model along the lines of Roy (1951). Assume that jobs are bundles of monetary and non-monetary aspects, the latter being related to the type of tasks they involve (either numeracy or reading- related tasks).¹⁵ Assuming that jobs involve either numeric tasks (n = 1, as we show below, a salesperson) or reading tasks (n = 0, as we discuss below, a personal care worker), conditional on choosing a numeric job, the gap in cognitive skills in math and, say, numeracy can be written as the sum of the return to skills and a selection term:

$$E({C}_{n}-{C}_{l}| n=1)={\alpha }_{2}n+E\{{\epsilon }_{n}-{\epsilon }_{l}| {\epsilon }_{n}-{\epsilon }_{l} \, > \, k\}$$

(4)

That is, the gap between measured numeracy and literacy skills may arise either because workers acquire numeracy skills in their jobs by performing relatively more numeric tasks (α₂) or because of a sorting process that arises both from initial comparative advantage in numeracy skills and for taste for jobs that involve numeracy tasks. While separating the sorting and the productivity components is very difficult we can obtain estimates of α₂ among groups of workers for whom (a) the ability to sort is limited and (b) the ability to learn from a certain tasks is higher than the rest. If α₂ is highest among such groups, we can infer that sorting does not account for the relationship between task specialization and human capital accumulation¹⁶¹⁷

For example consider the case of workers with a college degree, who are arguably more mobile than workers with basic schooling (see Charles et al. (2016)).¹⁸ Those workers may end up with higher numeracy skill levels -relative to literacy or problem-solving ones- due to their initial endowment of numeracy or because their choice of electives.¹⁹ Within that group of workers with a college degree, simple numeric tasks like using a calculator are unlikely to increase their skills but they may still be statistically associated to gaps between the numeracy and literacy or problem-solving skills because of sorting. Hence, the correlation between the numeracy vs reading or problem solving scores and the presence of simple numeracy tasks for those workers may simply capture preferences towards jobs with numeracy content.

Our strategy proceeds as follows. We first estimate for basic school workers a regression of the difference between the (normalized) numeracy vs literacy score on the presence of simple numeric tasks -relative to reading or ICT tasks. That estimate measures the causal impact of performing numeric tasks on the normalized numeracy score plus a sorting component. The second step is to estimate the same regression for a sample of individuals with either a high school or a college degree, with a higher ability to sort. If α₂ is largest among workers with basic schooling than among the rest, we infer that the link between tasks and human capital captures learning on the job. We repeat those exercises for numeracy vs problem-solving skills (by comparing scores in numeric jobs vs ICT intensive ones) and literacy vs ICT.²⁰

In addition, we use an alternative method to control for initial human capital endowments is to use repeated measures of cognitive abilities over time. For example, using several realizations for the same individual, we could control for C_0,i by taking differences over time. Unfortunately, repeated observations on cognitive skills are not available at the individual-level. Nevertheless, the repeated country-specific assessments in IALS (1994) and PIAAC (2012) make it possible to track cohort-level changes in the evolution of literacy skills and the task content of jobs over the life-cycle in thirteen countries. In particular, taking cohort-specific averages in Model (3):

$${\overline{C}}_{l,c,t}={\alpha }_{0,l,t}+{\alpha }_{l}{\overline{J}}_{l,c,t}+{\overline{C}}_{0,c}+{\overline{\epsilon }}_{l,c}$$

(5)

A hat over a variable denotes its cohort-specific mean (i.e., ${\overline{C}}_{l,c,t}={\sum }_{i}\frac{{C}_{l,i,t}}{{N}_{c}}$ is the cohort-specific average of the literacy score and ${\overline{J}}_{l,c,t}={\sum }_{i}\frac{{J}_{l,i,t}}{{N}_{c}}$ the cohort-level mean of tasks). We define cohorts as groups of respondents sharing (10-year) date-of birth, country, education level and gender. Drawing on multiple observations for the same cohort over time, one can take within-group differences and estimate α_(2, l) as follows:

$${\overline{C}}_{l,c,2012}-{\overline{C}}_{l,c,1994}={{\Delta }}{\alpha }_{0}+{\alpha }_{l}[{\overline{J}}_{l,c,2012}-{\overline{J}}_{l,c,1994}]+{\overline{\epsilon }}_{l,c,2012}-{\overline{\epsilon }}_{l,c,1994}$$

(6)

${\overline{J}}_{l,c,2012}-{\overline{J}}_{l,c,1994}$ reflects changes in the reading requirements of jobs over time. Unlike Model 2, changes in ${\overline{{{\mbox{}}}J}}_{l,c,2012}-{\overline{J}}_{l,c,1994}$ are unlikely to reflect sorting of individuals across jobs, as it is unlikely that members of a cohort systematically look for the same type of jobs. Still, to test for the presence of sorting due to correlation between ${\overline{\epsilon }}_{l,c,2012}-{\overline{\epsilon }}_{l,c,1994}$ and ${\overline{J}}_{l,c,2012}-{\overline{J}}_{l,c,1994}$ we control for changes in numeracy requirements of tasks on the job measured both in IALS (1994) and in PIAAC (2012). Under the assumption that α_l mainly picks up the reading content of jobs, it should not be affected by whether or not we introduce other indicators of the task contents of jobs, such as the numeracy intensity. Thus we run an alternative model and test if the numeracy content of jobs explains the increase in literacy. In addition, the initial use of tasks by a cohort could be an indicator of future cognitive skills (through learning) and sorting (if a cohort faces exceptionally low use of a skill, by convergence its use may increase). To verify the extent to which initial conditions are driving our results we introduce controls for the mean reading task use in 1994.

3 Database

The main data source is the Programme for the International Assessment of Adult Competencies (PIAAC), provided by the OECD and collected between August 2011 and March 2012. PIAAC includes an internationally comparable data on literacy and numeracy proficiency, as well as on the tasks performed at work by adults aged 16-65. We use 18 countries: Belgium, Canada, Czech Republic, Denmark, Estonia, Finland, France, Germany, Ireland, Italy, Korea, Netherlands, Norway, Slovak Republic, Spain, Sweden, USA and the United Kingdom (namely, England and Northern Ireland).²¹

In each country a representative sample of adults between 16 and 65 years took a direct assessment of their proficiency in numeracy, literacy and problem-solving. Numeracy measures the ability of “managing a situation or solving a problem in a real context by responding to mathematical information and content represented in multiple ways”. The “literacy” assessment excludes the ability to write, but goes beyond reading ability by measuring “the range of cognitive strategies (...) that adults must bring into play to respond appropriately to a variety of texts of different formats”.²² The “problem solving” assessment measures the ability of individuals to solve problems that arise using ICTs (...), where problems are a consequence of the availability of new technologies (...) and require the use of computer-based artifacts (...)”. Of the countries surveyed, France, Italy and Spain did not include that assessment, so we omit those countries in any model including problem-solving scores (but not in the rest). The survey was implemented either by computer or on paper and pencil.²³

In addition, PIAAC contains internationally comparable information about the educational attainment of individuals as well as about the tasks performed in the current or last job.

Tasks. The survey asks each employed respondent about how many times he or she conducted a particular task during the last month. In addition, non-employed respondents with previous labour market experience are also asked about the tasks done in their last job. The number of tasks listed in the survey is large, and we have classified them as either numeracy, reading or ICT related. Numeracy-related tasks include elaborating a budget, using a calculator, reading bills, using fractions or percentages, reading diagrams, elaborating graphs or using algebra. We classify as literacy-related tasks reading email, reading guides, reading manuals, writing emails, writing reports, reading articles, reading academic journals, reading books and writing articles. Finally, ICT tasks involve using email, using internet, processing texts, conducting transactions over internet, programming and using spreadsheets.

We also distinguish between basic and advanced tasks using principal component analysis, as their impact on human capital accumulation is likely to vary across educational groups. Regarding numerical tasks, we classify tasks into advanced and basic, and identified elaborating a budget, using a calculator, reading bills, using fractions or percentages and reading diagrams as basic tasks. Conversely, we classify elaborating graphs or using algebra as advanced tasks.²⁴ Similarly, we classified reading email, reading guides, reading manuals, writing emails, writing reports and reading articles as simple literacy tasks, while reading academic journals, reading books and writing articles were classified as advanced literacy tasks. Regarding ICT tasks, we classify using email, using internet and conducting transactions over internet as basic, and programming, processing texts and using spreadsheets as advanced tasks.²⁵

We measure the numeric task intensity of a job computing the number of math related tasks reported. If a worker reports performing all basic numeric tasks on her job (i.e. if at least once a month she elaborates a budget, reads bills, reads a diagram, uses a calculator, and computes a fraction or percentage in her current or last job) we grant her 1(=5/5) in “Basic math tasks”. If she conducts only one of the five tasks, we grant her 0.20 = (1/5).²⁶ For example, around 15% of low educated workers in the overall sample are granted one. We define “Basic literacy tasks” and “Basic ICT tasks” in a similar fashion. The degree of specialization is defined as the difference between “Basic math tasks”, “Basic literacy tasks” or “Basic ICT tasks”. The resulting distribution of numeracy, literacy and ICT content across 2-digit occupations is shown for individuals with basic schooling in Table 7. Note that the OECD also provides a measure of task intensity, which we introduce alternatively in results of Table 3.²⁷ However, the reason why we use our own measure is that to be able to get a scope of the relative magnitude of sorting and on-the-job learning components we draw on the distinction between basic and advanced tasks. The available measure in PIAAC does not allow for that distinction.²⁸²⁹

Formal education. We group individuals in three schooling levels, following a classification elaborated by the OECD. The first is primary education or less. The second is composed of individuals having completed either baccalaureate studies or forms of Vocational Training that, according to the ISCED classification, do not constitute university education. The third group is composed of individuals with any type of university education, including those forms of Vocational Training that ISCED considers equivalent to college.

Sample selection. To obtain a large sample of individuals from different countries we pool employed and unemployed individuals as well as females and males between 16 and 55 years of age. We decided to stop at 55 because at that age the fraction of retired workers jumps to 30%. As there is evidence pointing at retirement as being associated to a sharp cognitive decline and we focus on workers in the labor force, we chose that age range. Finally, we exclude from the sample respondents without labour market experience. The resulting sample contains 83,811 individuals in those 18 countries. Sample sizes per country vary between 19,566 in Canada and 2,737 in Sweden.

3.1 Summary statistics in PIAAC

Table 1 shows summary statistics for the 18 countries that conducted the numeric and literacy scores. The fraction of prime workers with basic schooling is 19% in the full sample, being highest in Spain (43%) and lowest in the Czech Republic (6%). The average number of years worked does not change much across countries, in contrast.

Table 1 Summary statistics, by country

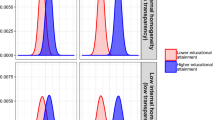
Figure 1 shows the fraction of individuals who report having performed in their current or last job one of the basic tasks, by schooling group. Figure 1b replicates Fig. 1 by schooling group but for advanced tasks. As expected, the fraction of individuals who report having performed a basic task is larger among those with basic schooling than among those with college. Excluding Finland, Czech and Slovak Republic, between one quarter and one third of individuals with basic schooling perform at least one of the simplest numeric (reading) tasks. That similarity may be surprising, given the large cross-country differences in the fraction of individuals with basic schooling or in the industrial composition.³⁰ Thus, the statistics in Figure 1 suggest that, in most of the countries we consider, a nontrivial share of individuals with basic schooling perform simple tasks at their jobs, thus having at least the possibility of acquiring some skills.³¹

Fig. 1

a Percentage of individuals performing advanced tasks by country and level of education. Source: PIAAC (2012). Sample of respondents of 16–55 years of age. The figure shows the percentage of individuals of the sample performing at least once a month a basic numeracy, literacy or ICT task according to their country and level of education. Basic numeracy tasks are elaborate budgets, use calculator, use fractions, read diagrams and bills. Basic literacy tasks are read emails, guides, manuals and articles and write emails and reports. Basic ICT tasks are using email, internet and processing texts and conducting transactions. The classification is based following Principal Component Analysis on Table 7. b Percentage of individuals performing advanced tasks by country and level of education. Source: PIAAC (2012). Sample of respondents of 16–55 years of age. The figure shows the percentage of individuals of the sample performing at least once a month a advanced numeracy, literacy or ICT task according to their country and level of education. Advanced numeracy tasks are elaborate charts and using algebra. Advanced literacy tasks are read academic journals, read books and write papers. Advanced ICT tasks are using spreadsheets, coding and programming, and discussing at internet. The classification is based following Principal Component Analysis on Table 7

3.2 Evidence from the International Adult Literacy Survey (IALS)

To implement the synthetic cohort analysis, we combine information from two assessments on Literacy: the 1994 International Adult Literacy Survey (IALS) and the already mentioned PIAAC.³² We use thirteen countries that are present both in IALS and PIAAC: Belgium, Canada, Czech Republic, Denmark, Finland, Germany, Ireland, Italy, Netherlands, Norway, Sweden, United Kingdom and the United States. The rescaled version of IALS has been designed so that measures of literacy cognitive skills (the only ones available in IALS) are comparable to those in subsequent assessments (in particular, ALL and PIAAC). All measures are in a 0–500 scale.

IALS also asks to respondents who have been employed for the last twelve months about how frequently they perform certain tasks in their jobs in a manner that is comparable to the questions posed in PIAAC. In particular, we use the following reading or writing-related tasks: reading letters or memos, reading reports, articles or manuals, writing letters and writing reports or articles. IALS also includes tasks that we classify as numerical, such as reading bills, reading diagrams or using math to compute costs or budgets.

We use individuals born between 1950 and 1969, as they would still be below 65 years of age eighteen years after the IALS assessment, once PIAAC is conducted. We aggregate observations in cells defined by 10-year birth cohorts, schooling level,³³ gender and country. For shorthand, we assign the IALS and PIAAC measurements of the 1950–1959 cohort to 40 and 55, respectively. Abusing notation, we assign the ages to the 1960–1969 cohort to 25 years in PIAAC (the average would be 30) and 55 in IALS (the average age would be 47). In Figure 3 we document the heterogeneity in life-cycle profiles across cohorts that we exploit to identify the response of literacy scores to the use of reading skills. The sample contains 50 cells of about 150 individuals in each of them (on average).³⁴

4 Results

4.1 Task specialization by occupation

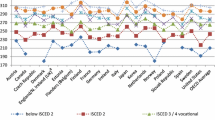
Figure 2 provides a visual test of the variation that identifies the parameter of interest α₂ by showing the different task intensity of 2-digit occupations that employ low-educated individuals. We compute the (frequency unweighted) relative basic task specialization and the difference in test scores and plot one against the other. The relationship is positive: workers with compulsory schooling working in occupations specialized in math-oriented tasks perform relatively better in the numeracy test than in the literacy one.³⁵

Fig. 2

Relative specialization in numeric tasks vs differential performance in the numeracy test. a Sample includes respondents in PIAAC database with basic schooling. b The differential grade between numeric test and literacy test is presented in the Y axis, while the X axis presents the difference between the proportion of numeric tasks done at least once a month over all numeric tasks considered and the proportion of literacy tasks done at least once a month over the all reading tasks considered. c Each dot is the average task intensity within each two-digit occupation and across all countries in the sample. d The OLS slope of the fitted line in the numeracy-literacy plot is .26 and the standard error is .17. The R-squared is 20%

Consider two cases. The first are personal care workers (occupation number 53), who constitute 9% of all individuals with basic schooling in the full sample. Workers in that occupation are comparatively specialized in reading tasks, as the frequency-adjusted difference between their numerical vs reading tasks is negative. The tasks conducted by the average person in the occupation give clues about the rationale for that ranking. Personal care workers elaborate budgets, read diagrams or use calculators with an intensity that is half the sample mean (i.e. the corresponding entry under each of those numeracy tasks is well below 1 in Table 7). Conversely, personal care workers read guides or emails and write emails more frequently than the average worker does (i.e. the frequency of those literacy tasks is well beyond 1 in Table 7). In that sense, personal care workers are specialized in reading tasks. On the other part, sales workers (occupation number 52), account for 7% of all individuals with basic schooling in the full sample. Those workers specialize in numerical tasks. Namely, the frequency-adjusted difference between intensity in numerical and reading tasks is generally beyond 1 in Table 7 (i.e., they devote more of their time to numerical tasks than to reading ones).

4.2 Regression analysis

Table 2 implements a version of Model (3) on a pooled sample of the 15 countries conducting the three assessments (columns 1–9) and on the full sample (columns 10–12). The numeracy, literacy and problem-solving scores are normalized by the country-specific standard deviation. The first set of regressions uses a sample of workers with at most 10 years of potential working experience, the second set uses workers with more than 10 years of working experience and finally the full sample of workers (between 16 and 55 years of age). Table 2 does not distinguish between simple and advanced tasks. All models control for a quadratic polynomial of the number of years of potential working experience, two indicators of the educational level of the respondent (high school and college), the interaction between education and years of working experience, and age dummies (grouped in 5 year bands). We also include nine 1-digit occupation dummies, 22 industry dummies and country dummies. In addition, we include intercepts for female, foreign born, whether the respondent lives with his or her couple, whether he or she does not work, whether the exam was done in paper, two dummies with self-assessed health status and two intercepts denoting if the respondent enjoys learning new things -the latter to control for the possible influence of non-cognitive skills.³⁶

Table 2 The impact of task specialization on relative performance in numeracy, literacy and problem solving scores^abc

We start with the sample of workers with a potentially shorter labor market history. The coefficient of n − l in the first row, first column of Table 2 is 0.16, implying that, relative to workers whose jobs have a similar incidence of numeric and literacy tasks, workers with basic schooling in jobs that fully specialize in numerical tasks perform 16% of one standard deviation better in the numeracy test than in the literacy one. The impact of full specialization in numeric tasks among workers with a high school degree is obtained by adding the estimate in column 1 row 5 of Table 2 to that in column 1, row 1, and amounts to 9.9% = (0.16–0.061) of one standard deviation -about 60% of the return for workers with basic schooling.

When we measure the relationship between ICT specialization and problem solving skills, the results for workers with a basic schooling degree are qualitatively similar. Relative to workers in jobs with a similar share of numeric and ICT tasks, those who fully specialize in numeric tasks obtain 24.8% of one standard deviation higher score in the numeracy test than in the problem-solving one -see column 2, row 2 of Table 2. Finally, basic schooling workers in jobs intensive in reading tasks (and no ICT tasks) obtain in the literacy assessment an score 33.6% of one standard deviation higher than in the problem solving assessment -see column 3, row 3 of Table 2.

In sum, the estimates across columns 1, 2 and 3 (rows 1, 2 and 3, respectively) suggest that specialization in one type of tasks (say, numeric) increases scores in the skill domain related to that type of tasks relative to the other two.

A second result to note is that task specialization results in lower differences in the relative score among workers with either a high school or a college degree. For example, among workers with a high school degree, those who fully specialize in numeric tasks (as opposed to ICT ones) obtain a score in the numeracy assessment that is 11.6% of one standard deviation higher than that in the problem solving one (0.116 is the difference between the 0.248 estimate in Table 2, row 2, column 2 and the 0.132 estimate in Table 2, row 6, column 2). The estimate is half that estimated among workers with basic education (0.248% of one standard deviation).

Heterogeneity by potential experience. We compare the previous results to those in the sample of respondents with more than 10 years of working experience in 2012. The rationale is that on-the-job learning and investments are typically more productive in the earlier stages of the working life. The link between specialization in numerical tasks and the relative score in the numerical test is larger for workers at the beginning of the working experience life with basic schooling: full specialization in numeracy tasks (as opposed to reading ones) increases the relative numeracy score by 16.0% of one standard deviation for workers with at most 10 years of work experience (Table 2, column 1, row 1) and 11.3% of one standard deviation in the sample for more than 10 years of working experience (Table 2, column 5, row 1). However, the differences across assessments numeracy relative to problem solving and literacy vs problem solving do not vary much with potential experience.³⁷

Table 3 conducts various sensitivity analyses of the results in Table 2. Firstly, we consider the possibility that workers may have qualifications above those required by their job. The second robustness check examines if the link between task specialization and cognitive skills is higher among workers in more stable jobs, who presumably have been doing the reported tasks for a longer period. The third robustness check excludes the unemployed at the time of the survey to test whether skill deterioration during non-employment periods affects the results. The fourth robustness check uses the alternative OECD index of task intensity.

Table 3 Robustness checks on the impact of task specialization on relative performance in numeracy, literacy and problem solving scores (individuals with 10 or lower than 10 years of working experience)^abc

While controlling for overqualification or considering samples of only individuals employed does not substantially vary the results, it is worth noting that the link between specialization in numerical tasks and a better performance in the numeracy test is stronger among low-skilled workers with tenures above the mean (the estimate is 12.8% of one standard deviation for workers with shorter tenures and 19.3% among those with longer ones). That finding is consistent with the notion that more time practicing a task increases cognitive skills more. However, tenure varies across workers in ways that depend on their unobserved ability, so other interpretations are possible.

4.3 Simple vs advanced tasks

As mentioned above, low-skilled workers conduct mainly simple tasks, so those are likely to drive the relationship with cognitive skills. Furthermore, under our assumptions, for workers with higher levels of schooling, the link may be informative about the degree of sorting in the labor market.

The differential skill return to specialization in basic tasks. Table 4 introduces individual fixed-effects to examine the relation between specialization in a set of basic tasks on the job and differential cognitive skills related to that domain. The results imply that respondents without either a high school or a college degree who fully specialize in basic numerical tasks score 10.5% of one standard deviation higher in the numeracy assessment than workers who are equally specialized in numeric and reading tasks (first column, first row). When we measure the impact of specialization in numeracy vs ICT tasks on numeracy scores (relative to problem-solving), the impact is somewhat smaller: 2.8% of one standard deviation, but it is imprecisely estimated. Finally, workers with basic schooling who specialize in reading vs ICT tasks obtain a higher score in the reading score than in the problem solving score (9.8% of one standard deviation, close to the 10.5% estimate in column 1, row 1). The estimate of the impact of specialization in basic tasks on relative scores varies then between 2.8 and 10.5% among workers with primary schooling, but taking into account standard errors, we cannot reject the hypothesis that the three estimates presented in Table 4 are equal in size. This similarity of coefficients among pairs of skills serves as a check of the implicit assumption that the impact of numeric tasks on numeracy is similar to the impact of literacy tasks on literacy (see Lavy (2015), or Martínez-Matute and Villanueva (2020), for a discussion).

Table 4 The impact of task specialization on relative scores (10 or lower than 10 years of working experience)^ab

To gain precision, column 4 in Table 4 stacks all the previous regressions. That is, each individual contributes up to three observations: one for each pair of assessments. The coefficient of each pair of tasks on their correspondent assessments are constrained to be the same, and standard errors are clustered at the individual level to take into account that observations from the same individual may be correlated. The coefficient in Table 4, column 4, row 4 is 0.108. This suggests that low-skill workers in jobs that specialize in one domain of basic tasks (for example, reading vs ICT) obtain a 10.8% of one standard deviation higher score in the related assessment (for example, literacy) than in the rest (for example, problem solving).

Impacts by school level. Next, we compare the impact of conducting basic tasks on the job on groups with higher educational levels. In practice, we subtract the estimate for respondents with high school from that for respondents with basic school, yielding the impact of specialization in basic tasks on the relative performance in the corresponding test for respondents with high school. We do this exercise using the estimates in Table 4, and using the sample where respondents have had less time to sort (individuals with less than 10 years of working experience). The impact of basic tasks on cognitive skills is smaller for high school graduates than for workers with basic schooling. When we measure specialization in basic tasks using the three measures as a benchmark (fourth column of Table 4) the impact of among high school graduates is 3.8% (0.038 = 0.108–0.070), subtracting the estimate in row 8, column 4, from that in row 4, column 4, in Table 4.

Overall, although point estimates vary with the definition of specialization, Table 3 suggests that the cognitive skill returns to specializing in basic tasks for workers with either high school or college degree are between non-significant and 40% of those we find among respondents with basic schooling. The result is consistent with the notion that learning through basic tasks on the job increases the skills of respondents with basic schooling.

4.4 Gender

We analyze in Table 5 separate impacts by gender.³⁸ To achieve precision, we proceed as in Table 4, column 4, and stack the three measures for each individual (the three pairwise differences between numeracy, literacy and problem solving scores) and regress them on the corresponding pairwise difference in the associated tasks. Interestingly, the patterns we detected in Table 4 are more pronounced for females than for males.

Table 5 The impact of task specialization on relative numeracy, literacy and problem solving, by gender

Firstly, among low-skill men, those who specialize in basic tasks obtain a relative score in that domain 7% of one standard deviation higher than low-skill males in jobs with an even distribution of tasks. The standard error is 5% of one standard deviation, so the estimate is not significantly different from zero. The corresponding estimate for low-skill females is twice as large: 14.7% of one standard deviation (standard error: 4.8%).

Secondly, and as it was the case in Table 4, the response of differential scores to the variation in specializing in basic tasks is stronger for low-skill females than for women with a high school or a college degree. Among females with a high school degree, those who work in jobs where they fully specialize in a basic task (say, numeric) obtain a score in that domain (numeracy) 2.9% higher than females in jobs with a balanced set of tasks. The estimate is five times smaller that of low skill females.

The finding that the relationship between task specialization and scores is stronger for low-skill females than for low-skill males suggests that all our results cannot be entirely driven by sorting. Men tend to accumulate more working experience in the labor market. Hence, they might be more exposed to selection.

4.5 The magnitude of the estimates

The estimates become larger when we focus on the low working experience sample. This sample is specially interesting as workers with 10 or less than 10 years of potential experience have had less time to select into jobs more akin to their characteristics. The raw estimate of full specialization on the relative performance in the numeracy test among basic schooling respondents is 10.8% of one standard deviation (fourth row of column 4 in Table 4). For respondents with a high school degree, the impact of specialization in basic tasks is 3.8% (obtained by subtracting the 0.07 differential impact among respondents with a high school degree in column 4, row 8, in Table 4 from the main impact of 10.8 in column 4, row 4). The return to specialization in basic tasks on their jobs for respondents with a college degree is 2.8% of one standard deviation (obtained by subtracting the 0.078 impact in column 4, row 12, in Table 3 from the main impact of 10.8).

Hence, under the assumption that the return to specializing in basic tasks for respondents with a high school or college degree basically measures sorting, we can apply equation (4) obtaining that workers with basic schooling who fully specialize in a set of basic tasks on a job perform around a 7% of one standard deviation better on the assessment relative to a worker with a balanced set of tasks. The remaining 3.8% (i.e., the difference between 10.8% shown in Table 4, row 4, and 7% shown in Table 4, row 8) would measure sorting in the labor market. We conduct now some back of the envelope calculations comparing our estimates to existing work analyzing how cognitive skills vary with formal education.

We do not have information on all tasks performed in all jobs during the working history of a worker, so we cannot establish if workers conducted numerical or other tasks in their current job only or during their complete working lives. Hence, we make the assumption that workers conducted numerical or literacy tasks during 4.8 years of experience, i.e. the average number of years worked among respondents with less than 10 years of potential experience. That conservative assumption implies that one year of conducting basic numeric tasks increases numeracy skills by between 1.46% (=7/4.8) and 2.25% (=10.8/4.8) of one standard deviation.

A caveat is that less than half of the workers with basic schooling conduct basic tasks (see Figure 1a). Assuming that 30% of workers with basic schooling conduct basic tasks on their jobs, the estimate of the impact of one year of experience on numeracy skills would be between 0.44% (=1.46*0.3) and 0.75%(=2.25*0.3) of one standard deviation.

To provide some sort of a benchmark, Hanushek et al. (2015) estimate that, in the United States, increasing compulsory education by one year increases skills by between 2.7% and 2.9% of one standard deviation. Hence, one extra year of schooling would be equivalent to between 1.3 (=2.9/2.25) and 2 years (=2.9/1.46) of on-the-job learning. If one takes into account that not all workers with basic schooling end up in a job involving basic tasks, one extra year of schooling would be equivalent to between 3.9 (=2.9/0.75) and 5.2 (=2.9/0.44) years of experience.

4.6 Evidence from synthetic cohorts

An alternative way of controlling for possible sorting in the labor market examines how cohort-level changes in the reading content of jobs relate to cohort level changes in literacy. As mentioned above, cohort-level changes in the reading content of a job are unlikely the result of individual sorting across jobs.

Figure 3 present cohort-level measures of the use of literacy tasks on the job in both assessments. This is shown for non-college workers in selected countries in the sample. The (frequency-adjusted) use of reading skills either increases to or stays constant around 40% between ages 25 and 40 (there are mild decreases in Canada and Finland). Between the ages 40 and 55, there is a great deal of heterogeneity, but typically the increase in the use of reading skills was milder between those ages than between 25 and 40 (see for example, Canada, Denmark, Sweden or Norway). We use that heterogeneity in life-cycle profiles across cohorts to identify the response of literacy scores to the use of reading skills.

Fig. 3

Fraction of time using reading tasks over the life cycle, evidence from IALS and PIAAC. Source: combined IALS (1994) and PIAAC (2012) samples of workers without a college degree. IALS asks respondents who worked in the last 12 months if they read letters or memos, reports, articles or manuals, wrote letters and reports or articles. We select a similar sample of individuals working in the last 12 months in PIAAC. The Figure includes cohorts born between 1940 and 1979, as they would still be below 65 years of age eighteen years at the time of the PIAAC assessment (2012). We aggregate observations in cells defined by 10-year birth cohorts,schooling level, gender and country. We assign the IALS and PIAAC measurements of the 1940-1947 cohort to 55 and 65, respectively (shown for completeness, not used in regresssions). We assign to the 1950–1959 cohort the ages of 40 and 55, respectively. We assign the ages to the 1960–1969 cohort to 25 years in PIAAC (the average would be 30) and 55 in IALS (the average age would be 47). The 1970–1979 cohort is available in PIAAC only

The first row in Panel A of Table 6 shows that, among cohorts with basic education, an increase of 100% in the time devoted to reading tasks on the job increases scores in the literacy assessment by 80% of one standard deviation (standard error: 32% of one standard deviation). Once we account for the initial level of tasks performed on the job by the cohort in 1994, the estimate increases slightly to 83.4% of one standard deviation. Finally, controlling for the increase between 1994 and 2012 in the time devoted to math tasks the estimate stays stable at about 78% of one standard deviation (column 3). The latter result is reassuring, as it implies that it is precisely the increase in time devoted to reading tasks the factor behind the life-cycle increase in literacy tasks. The time devoted to numeracy tasks has little explanatory power.

Table 6 The impact of cohort-level changes in reading tasks on cohort-level changes in literacy scores

On the other hand, it could be expected that the amount of time devoted to reading tasks in 1994 would explain cohort-level growth in literacy scores. The results do not support the view, as the coefficient is small and not statistically significant. A possible explanation is that reading tasks have increased substantially over the life cycle, diminishing the role of initial value.

The estimates in columns 2 and 3 of Table 6 imply that workers with primary schooling who increased their time to reading- or writing-related tasks on the job over the period increased their literacy scores by between 73% (Table 6, first row, column 3) and 83% of one standard deviation (Table 6, first row, column 1). Dividing by 18 years of experience results in an estimate of 80/18=4% of one standard deviation per year.

We can compare those estimates to those in the Table 4, row 4, column 4, that are about 10.8%. The average actual experience of individuals with 10 years of experience at most is 4.8 years. Hence the fixed-effect estimate suggests about 2.25 (=10.8/4.8) percent of one standard deviation per year. While estimates using synthetic cohorts are larger than those using worker-fixed effects is larger than the worker-fixed effect one, both estimates are not incompatible -specially if one takes into account that we do not know in PIAAC during how long were reading tasks acquired on the job.

Overall, the evidence from the synthetic cohort analysis is broadly consistent with the one found in PIAAC. We find this remarkable, given the very different set of assumptions involved in each procedure.

5 Conclusions

Cognitive skills account for a substantial share of the variation in labour market outcomes. This paper studies how on-the-job learning contributes to the acquisition of numeracy, literacy and problem-solving skills in eighteen OECD countries that implemented the PIAAC survey, focusing on individuals with low levels of schooling.

We use two empirical strategies. Firstly, we control for individual fixed effects by analyzing how the relative performance in numeracy, literacy and problem solving assessment vary with the differential exposure to numeracy, literacy and problem-solving tasks on-the-job. Our preferred estimates suggest that, among individuals with at most compulsory schooling, full specialization in basic numerical tasks increases the relative numeracy score by between 7% and 11% of one standard deviation. A second strategy uses repeated cross-sections of cognitive assessments to study how cohort-level changes in the reading content of jobs correlate with literacy scores. An interpretation of our results is that formal schooling and on-the-job learning are imperfect inputs in human capital production for workers with low levels of education.

Our findings have some implications for the design of active labour market policies. Firstly, cognitive test scores could be a good predictor of human capital that could indeed be easily checked for all unemployed. Secondly, specific tasks on-the-job might contribute to increase cognitive skills for low educated individuals. While the tentative rate of return to on-the-job training that we have estimated is between half and a fourth of that of formal schooling, the costs of increasing school attendance for prime aged workers may be substantial. Thirdly, the amount of on-the-job learning is determined by jobs requirements, which vary greatly across sectors.

Compliance with ethical standards Conflict of interest The authors declare that they have no conflict of interest. Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

 Table 7

Table 7 Frequency of numeracy, literacy and ICT tasks (basic schooling)^ab