Abstract
I propose a noncooperative marriage model that explicitly accommodates the possibility of endogenous exit and remarriage, and where marriages are of variable quality. The fundamental innovation is that the remarriage decision is infinitely repeated and the problem is fully stationary, reflecting the contemporary reality in marriage markets. I show that cooperative behavior within marriage is possible in subgame perfect equilibrium both in a setting where marriage quality is independently drawn and in a setting with persistent spouse-specific characteristics and an evolving marriage market quality. I show that spouses engage in cooperative behavior most easily when they have intermediate patience levels, which is a non-standard but intuitive game theoretic result in this setting. This model also contributes to the game theory literature by proposing another avenue for sustained cooperation in a repeated prisoner’s dilemma with endogenous exit: randomness in payoff streams.




Similar content being viewed by others
Notes
Throughout the paper, “marriage” is interpreted loosely to include any long-term partnership with an expectation of commitment. Indeed, according to the US Census Bureau (2003), 9.1% of households in the 2000 census were couples living together, unmarried but involved in a “close personal relationship.”
Divorce is terminal in this model.
The former note that, by an application of the folk theorem, any payoff that is feasible and individually rational is a possible subgame perfect equilibrium payoff of the repeated game.
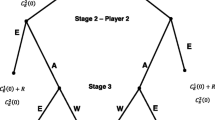
The problem with incorporating endogenous exit is that any player could defect against a cooperating partner, collect the corresponding deviation payoff, then begin the cooperative path with his next match, by assumption that the strategy is stationary. This constitutes a profitable deviation. Mailath and Samuelson (2006) give a proof.
Women, for example, bear child-rearing costs disproportionately, lowering their share of the marital surplus all else equal. There is a significant literature on the mechanism by which surplus is split within marriage; for example, this is discussed extensively by Chiappori et al. (2009a, b). I allow here for flexibility in the choice of a since whether there is a unique rule for sharing the marital surplus is an open question in the literature; Iyigun and Walsh (2007) assert that there is after allowing for pre-marital investments.
Otherwise, the pool would dwindle to empty since some matches will not return to the pool in equilibrium. The probability p does allow for the possibility that one side of the market may have more difficulty locating a partner.
The continuous measure of spouses guarantees zero probability of a rematch with one’s ex-spouse. Further, the information available when the match takes place (e.g. previous marriage history) is strategically irrelevant since the payoff structure is independently drawn for each match and there are no player-specific characteristics.
This is a geometric discount factor, so if we assume annualized periods δ = 1/(1 + r), where r is the interest rate.
Without loss of generality, we set the cooperative payoff at (2 + a)x. Simply set a = −a to generalize the calculation to the low-surplus partner.
The one shot deviation principle has an obvious interpretation in our setting. If one is going to divorce a partner, it certainly makes sense to do so immediately to allow for the possibility that future positive payoffs begin as close as possible to the present (i.e. with the least discounting). Now, a “period” may be quite long, but given our setup, the most profitable deviation is always in the first period of a match.
Other kinds of deviations are possible. For example, at the opposite end of the kind of deviation presented here, a player could defect in every period ad infinitum, collecting 3 when his spouse is called upon to cooperate in equilibrium and collecting 0 otherwise. A simple calculation shows that this is less profitable in expectation than a single defection followed by the cooperative equilibrium. Essentially, what is presented here is the most profitable possible defection, so guarding against it is sufficient to guard against any other type of defection.
This is obviously a subgame perfect equilibrium since mutual defection is a Nash Equilibrium of the stage game.
There is also a technical reason. Discount rates lower than 1/3 do not allow for cooperation using a grim-trigger strategy, under our parameterization of the prisoner’s dilemma, even without allowing for endogenous exit.
Reservation values are also monotonic in the discount factor in the McCall job search model, which is not game-theoretic, but which shares some features with our model.
Indeed, as one referee pointed out, men tend to marry younger women, so older women may face more difficulty locating partners than younger women, and vice versa for men.
Consider pregnancy and asymmetric child-rearing costs, as pointed out by a referee. Another point is that women initiate more divorces than men, which seems inconsistent with this result. On the other hand, women may face lower separation costs and may have a higher probability of rematching, at least early on in the marriage when most divorces tend to occur. If large enough, these effects can swamp the effects from the unequal distribution of surplus such that women initiate more divorces than men.
There may be cooperative equilibria with lower reservation values if, for example, the players expect to never remarry. But these change the fundamental nature of the problem, which is repeated access to the same remarriage market.
They model the “bad” players as endowed with a discount rate of 0, and thus always defecting. The import is the same in our model, in the sense that being matched with a bad player always yields a payoff of 0. This quality is endowed exogenously, meaning that spouses cannot make pre-marital investments to change their characteristics.
One might imagine a nonrandom matching process where good spouses are more likely to encounter other good spouses. However, if quality takes time and investment to discover and is not immediately self-evident, then the matching itself may be close to random. Also, as long as there is some possibility of encountering a bad spouse, and as long as this probability rises when there are more bad spouses in the pool, the salient feature of the matching process for purposes of our model still holds. Also, assortative matching is typically on only one element, so there will always be some hidden information upon matching.
Notice that the death probability is over matches and not over individuals. In this assumption, we also follow Ghosh and Ray (1996). It is nonsubstantive in that it does not change the qualitative nature of the results, but it facilitates accounting substantially.
This keeps the measure of the population at 1. Otherwise, the only steady state would be the trivial one where the pool consists only of bad players.
Notice that there is no death within marriage (or alternatively that it is already incorporated into the discount factor). As in Ghosh and Ray, the death probability given here is interpreted as match destruction.
While the solution here is for a steady state, as is typical in this literature, the steady state itself cannot be derived without laying out the dynamics of the process that converge to a steady state.
This is for two reasons. Players are staying married more easily since the reservation draw of x is lower, so fewer good spouses return to the pool. Furthermore, genetic replacements for marriages and exogenously destroyed matches are less likely to be of high quality.
References
Andaluz, J., & Molina, J. A. (2007). On the sustainability of bargaining solutions in family decision models. Review of Economics of the Household, 5, 405–418.
Becker, G. S. (1973). A theory of marriage: Part I. The Journal of Political Economy, 81, 813–846.
Becker, G. S. (1981). A treatise on the family. Cambridge: Harvard University Press.
Bourguignon, F., Browning, M., Cciappori, P.-A., & Lechene, V. (1993). Intra-household allocation of consumption: A model and some evidence from french data. Annales d’Economie et de Statistique, 29, 138–156.
Brinig, M., & Allen, D. (2000). These boots are made for walking: Why most divorce filers are women. American Law and Economics Review, 2, 126–129.
Carmichael, L., & Macleod, B. (1997). Gift giving and the evolution of cooperation. International Economic Review, 38, 485–510.
Chiappori, P.-A, Iyigun, M., & Weiss, Y. (2009). Spousal matching with children, careers and divorce. Working paper.
Chiappori, P.-A, Iyigun, M., & Weiss, Y. (2009). Divorce laws, remarriage and spousal welfare. Working paper.
Chiappori, P.-A., & Weiss, Y. (2006). Divorce, remarriage and welfare: A general equilibrium approach. Journal of the European Economic Association, 4, 415–426.
Datta, S. (1996). Building trust. STICERD Theoretical Economics Paper Series.
Flinn, C. J. (2000). Models of interaction between divorced parents. International Economic Review, 41, 545–578.
Ghosh, P., & Ray, D. (1996). Cooperation in community interactions without information flows. Review of Economic Studies, 63, 491–519.
Hauk, E. (2001). Leaving the prison: Permitting partner choice and refusal in prisoner’s dilemma games. Computational Economics, 18, 65–87.
Hoddinott, J., & Adam, C. (1998). Testing nash bargaining household models with time series data. Food Consumption and Nutrition Division.
Isen, A., & Stevenson, B. (2008). Women’s education and family behavior: Trends in marriage, divorce and fertility. Working paper.
Iyigun, M., & Walsh, R. P. (2007). Building the family nest: Pre-marital investments, marriage markets and spousal allocations. Review of Economic Studies, 74, 507–535.
Konrad, K. A., & Lommerud, K. E. (1995). Family policy with non-cooperative families. The Scandinavian Journal of Economics, 97, 581–601.
Lundberg, S., & Pollak, R. A. (1994). Noncooperative bargaining models of marriage. The American Economic Review, 84, 132–137.
Lundberg, S., & Pollak, R. A. (2003). Efficiency in marriage. Review of Economics of the Household, 1, 153–168.
Lundberg, S., & Pollak, R. A. (2007). The American family and family economics. Journal of Economic Perspectives, 21, 3–26.
Mailath, G. J., & Samuelson, L. (2006). Repeated games and reputations. New York: Oxford University Press.
Manser, M., & Brown, M. (1980). Marriage and household decision making: A bargaining analysis. International Economic Review, 21, 31–44.
McCall, J. J. (1970). Economics of information and job search. The Quarterly Journal of Economics, 84, 113–126.
Nixon, L. (1997). The effect of child support enforcement on marital dissolution. The Journal of Human Resources, 32, 159–181.
Schluessler, R. (1989). Exit threats and cooperation under anonymity. Journal of Conflict Resolution, 33, 728–749.
Stevenson, B. (2007). The impact of divorce laws on marriage-specific capital. Journal of Labor Economics, 25, 75–94.
Stevenson, B., & Wolfers, J. (2007). Marriage and divorce: Changes and their driving forces. Journal of Economic Perspectives, 21, 27–52.
Tauchen, H. V., Witte, A. D., & Long, S. K. (1991). Domestic violence: A nonrandom affair. International Economic Review, 32, 491–511.
Ulph, D. (1988). A general noncooperative nash model of household behaviour. Mimeo: University of Bristol.
US Census Bureau. (2003). Married-couple and unmarried-partner households: 2000. Census 2000 special reports.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Proof of inequalities (3)–(5) from Sect. 3
When each spouse unilaterally maximizes utility, the decision problem from (1) and (2) is:
Each spouse i’s level of contribution to the public good solves:
By contrast, the Pareto optimal collective solution is:
In contrast to (25), the optimal level of contribution to the public good for each spouse i solves:
The concavity of f(·) implies that public good provision is higher for the (C,C) outcome given in (26) than for the (D,D) outcome given in (24). With this established, the inequality in (3) is trivial since (26) maximizes U CC1 + U CC2 by definition, and the solutions in (24) and (26) are distinct. Finally, by definition each spouse i always earns his highest utility for a fixed value of g j by choosing the level of contribution given in (24), which establishes the inequalities in (4) and (5).
Appendix 2: Numerical solutions from Sect. 4
δ = .999 | δ = .99 | δ = .9 | δ = .8 | δ = .7 | δ = .6 | |
|---|---|---|---|---|---|---|
θ = .99 | ||||||
λ = .999 | \( \begin{gathered} \bar{x}^{*} = .862 \hfill \\ \pi^{*} = .986 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .831 \hfill \\ \pi^{*} = .983 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .738 \hfill \\ \pi^{*} = .974 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .731 \hfill \\ \pi^{*} = .973 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .757 \hfill \\ \pi^{*} = .976 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .800 \hfill \\ \pi^{*} = .980 \hfill \\ \end{gathered} \) |
λ = .99 | \( \begin{gathered} \bar{x}^{*} = .855 \hfill \\ \pi^{*} = .879 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .819 \hfill \\ \pi^{*} = .858 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .711 \hfill \\ \pi^{*} = .805 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .704 \hfill \\ \pi^{*} = .802 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .735 \hfill \\ \pi^{*} = .815 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .786 \hfill \\ \pi^{*} = .840 \hfill \\ \end{gathered} \) |
λ = .9 | \( \begin{gathered} \bar{x}^{*} = .807 \hfill \\ \pi^{*} = .473 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .752 \hfill \\ \pi^{*} = .435 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .587 \hfill \\ \pi^{*} = .362 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .588 \hfill \\ \pi^{*} = .363 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .644 \hfill \\ \pi^{*} = .383 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .725 \hfill \\ \pi^{*} = .420 \hfill \\ \end{gathered} \) |
λ = .8 | \( \begin{gathered} \bar{x}^{*} = .772 \hfill \\ \pi^{*} = .324 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .706 \hfill \\ \pi^{*} = .295 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .520 \hfill \\ \pi^{*} = .242 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .533 \hfill \\ \pi^{*} = .245 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .602 \hfill \\ \pi^{*} = .262 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .697 \hfill \\ \pi^{*} = .291 \hfill \\ \end{gathered} \) |
λ = .5 | \( \begin{gathered} \bar{x}^{*} = .683 \hfill \\ \pi^{*} = .149 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .676 \hfill \\ \pi^{*} = .233 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .401 \hfill \\ \pi^{*} = .114 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .444 \hfill \\ \pi^{*} = .118 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .540 \hfill \\ \pi^{*} = .127 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .656 \hfill \\ \pi^{*} = .145 \hfill \\ \end{gathered} \) |
δ = .999 | δ = .99 | δ = .9 | δ = .8 | δ = .7 | δ = .6 | |
|---|---|---|---|---|---|---|
θ = .9 | ||||||
λ = .999 | \( \begin{gathered} \bar{x}^{*} = .626 \hfill \\ \pi^{*} = .996 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .627 \hfill \\ \pi^{*} = .996 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .645 \hfill \\ \pi^{*} = .996 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .679 \hfill \\ \pi^{*} = .996 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .725 \hfill \\ \pi^{*} = .997 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .781 \hfill \\ \pi^{*} = .997 \hfill \\ \end{gathered} \) |
λ = .99 | \( \begin{gathered} \bar{x}^{*} = .621 \hfill \\ \pi^{*} = .959 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .621 \hfill \\ \pi^{*} = .959 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .639 \hfill \\ \pi^{*} = .960 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .674 \hfill \\ \pi^{*} = .963 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .721 \hfill \\ \pi^{*} = .967 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .779 \hfill \\ \pi^{*} = .971 \hfill \\ \end{gathered} \) |
λ = .9 | \( \begin{gathered} \bar{x}^{*} = .575 \hfill \\ \pi^{*} = .708 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .575 \hfill \\ \pi^{*} = .708 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .591 \hfill \\ \pi^{*} = .713 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .632 \hfill \\ \pi^{*} = .726 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .689 \hfill \\ \pi^{*} = .745 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .758 \hfill \\ \pi^{*} = .771 \hfill \\ \end{gathered} \) |
λ = .8 | \( \begin{gathered} \bar{x}^{*} = .534 \hfill \\ \pi^{*} = .548 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .534 \hfill \\ \pi^{*} = .548 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .549 \hfill \\ \pi^{*} = .552 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .596 \hfill \\ \pi^{*} = .566 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .661 \hfill \\ \pi^{*} = .588 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .739 \hfill \\ \pi^{*} = .620 \hfill \\ \end{gathered} \) |
λ = .5 | \( \begin{gathered} \bar{x}^{*} = .426 \hfill \\ \pi^{*} = .287 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .424 \hfill \\ \pi^{*} = .287 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .444 \hfill \\ \pi^{*} = .290 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .508 \hfill \\ \pi^{*} = .300 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .593 \hfill \\ \pi^{*} = .317 \hfill \\ \end{gathered} \) | \( \begin{gathered} \bar{x}^{*} = .693 \hfill \\ \pi^{*} = .340 \hfill \\ \end{gathered} \) |
Rights and permissions
About this article
Cite this article
Malcolm, M. A noncooperative marriage model with remarriage. Rev Econ Household 10, 133–151 (2012). https://doi.org/10.1007/s11150-010-9110-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11150-010-9110-5