Demand response in adjustment markets for electricity

Abstract

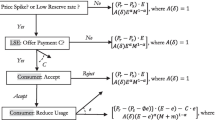
This article examines the participation of consumers in adjustment markets for electricity, which enable participants to respond to random supply shocks occurring after quantities have been contracted. If markets were perfect, opening the adjustment market to consumers would always increase ex post efficiency, hence welfare, as expected. In reality, some consumers hold private information on their value for electricity. We prove that under such information asymmetry, allowing consumers to participate in the adjustment market may reduce welfare. This arises because electricity suppliers in the model propose inefficient ex ante retail contracts to make them incentive compatible and to limit the information rents they must leave on the table for consumers to prevent them from misreporting their private information. If the value of ex post efficiency gains due to consumers’ participation in adjustment markets is low, whereas the information distortion is high, the overall net effect is a welfare decrease.

Appendices

Appendix 1: No demand participation in adjustment

Denote $q^{*}\left( \theta ,\mu \right)$ the ex post efficient production, defined by equality of marginal value and marginal cost

$$\begin{aligned} P\left( q^{*}\left( \theta ,\mu \right) ,\theta \right) =c\left( q^{*}\left( \theta ,\mu \right) +\mu \right) . \end{aligned}$$

Full differentiation of the above condition yields

$$\begin{aligned} \frac{\partial q^{*}}{\partial \mu }=\frac{c^{\prime }}{P_{q}-c^{\prime }} <0\Leftrightarrow 1+\frac{\partial q^{*}}{\partial \mu }=\frac{P_{q}}{ P_{q}-c^{\prime }}>0 \end{aligned}$$

since $P_{q}<0$ and $c^{\prime }\ge 0$. The optimal production decreases with the size of the shock $\mu$. However, $\left( q^{*}\left( \theta ,\mu \right) +\mu \right)$ increases with the shock $\mu$.

Define $\hat{\mu }$ the production shock such that $c\left( q^{*}\left( \theta ,\hat{\mu }\right) +\hat{\mu }\right) ={\mathbb {E}}_{\mu }\left[ c\left( q\left( \theta \right) +\mu \right) \right]$. For $\mu \le \hat{\mu }$, $c\left( q^{*}\left( \theta ,\mu \right) +\mu \right) \le c\left( q^{*}\left( \theta ,\hat{\mu }\right) +\hat{\mu }\right)$ since $\left( q^{*}\left( \theta ,\mu \right) +\mu \right)$ and $c\left( .\right)$ are increasing. Thus

$$\begin{aligned} P\left( q^{*}\left( \theta ,\mu \right) ,\theta \right)&=c\left( q^{*}\left( \theta ,\mu \right) +\mu \right) \le c\left( q^{*}\left( \theta ,\hat{\mu }\right) +\hat{\mu }\right) \\&={\mathbb {E}}_{\mu }\left[ c\left( q\left( \theta \right) +\mu \right) \right] =P\left( q\left( \theta \right) ,\theta \right) \end{aligned}$$

$\Leftrightarrow$

$$\begin{aligned} q\left( \theta \right) \le q^{*}\left( \theta ,\mu \right) . \end{aligned}$$

Appendix 2: Comparative statics on the adjustment market

Equilibrium:

$$\begin{aligned} p_{a}-S_{q}^{\prime }\left( q-q_{a}^{c},\theta \right)= & {} 0 \\ p_{a}-C^{\prime }\left( q+q_{a}^{s}\right)= & {} 0 \\ q_{a}^{c}+q_{a}^{s}= & {} \mu \end{aligned}$$

Total differentiation:

$$\begin{aligned} dp_{a}-S_{qq}^{^{\prime \prime }}dq+S_{qq}^{^{\prime \prime }}dq_{a}^{c}-S_{q\theta }^{^{\prime \prime }}d\theta= & {} 0 \\ dp_{a}-C^{\prime \prime }dq-C^{\prime \prime }dq_{a}^{s}= & {} 0 \\ dq_{a}^{c}+dq_{a}^{s}= & {} d\mu \end{aligned}$$

or

$$\begin{aligned} \left[ \begin{array}{ccc} 1 &{} S_{qq}^{^{\prime \prime }} &{} 0 \\ 1 &{} 0 &{} -C^{\prime \prime } \\ 0 &{} 1 &{} 1 \end{array} \right] \times \left[ \begin{array}{c} dp_{a} \\ dq_{a}^{c} \\ dq_{a}^{s} \end{array} \right] =\left[ \begin{array}{c} S_{qq}^{^{\prime \prime }}dq+S_{q\theta }^{^{\prime \prime }}d\theta \\ C^{\prime \prime }dq \\ d\mu \end{array} \right] \end{aligned}$$

Determinant of the full system:

$$\begin{aligned} \Delta =C^{\prime \prime }-S_{qq}^{^{\prime \prime }}>0 \end{aligned}$$

Effects on $p_{a}$:

$$\begin{aligned}&\displaystyle dp_{a}=\frac{\left| \begin{array}{ccc} S_{qq}^{^{\prime \prime }}dq+S_{q\theta }^{^{\prime \prime }}d\theta &{} S_{qq}^{^{\prime \prime }} &{} 0 \\ C^{\prime \prime }dq &{} 0 &{} -C^{\prime \prime } \\ d\mu &{} 1 &{} 1 \end{array} \right| }{\Delta }=\frac{-S_{qq}^{^{\prime \prime }}C^{\prime \prime }d\mu +C^{\prime \prime }\left( S_{qq}^{^{\prime \prime }}dq+S_{q\theta }^{^{\prime \prime }}d\theta \right) -C^{\prime \prime }S_{qq}^{^{\prime \prime }}dq}{\Delta }\\&\displaystyle \frac{\partial p_{a}}{\partial \mu }=\frac{-S_{qq}^{^{\prime \prime }}C^{\prime \prime }}{\Delta }>0\\&\displaystyle \frac{\partial p_{a}}{\partial \theta }=\frac{C^{\prime \prime }S_{q\theta }^{^{\prime \prime }}}{\Delta }>0\\&\displaystyle \frac{\partial p_{a}}{\partial q}=0 \end{aligned}$$

Effects on $q_{a}^{c}$:

$$\begin{aligned}&\displaystyle dq_{a}^{c}=\frac{\left| \begin{array}{ccc} 1 &{} S_{qq}^{^{\prime \prime }}dq+S_{q\theta }^{^{\prime \prime }}d\theta &{} 0 \\ 1 &{} C^{\prime \prime }dq &{} -C^{\prime \prime } \\ 0 &{} d\mu &{} 1 \end{array} \right| }{\Delta }=\frac{C^{\prime \prime }dq+C^{\prime \prime }d\mu -\left( S_{qq}^{^{\prime \prime }}dq+S_{q\theta }^{^{\prime \prime }}d\theta \right) }{\Delta }\\&\displaystyle \frac{\partial q_{a}^{c}}{\partial \mu }=\frac{C^{\prime \prime }}{\Delta }>0\\&\displaystyle \frac{\partial q_{a}^{c}}{\partial \theta }=-\frac{S_{q\theta }^{^{\prime \prime }}}{\Delta }<0\\&\displaystyle \frac{\partial q_{a}^{c}}{\partial q}=1 \end{aligned}$$

Effects on $q_{a}^{s}$:

$$\begin{aligned}&\displaystyle dq_{a}^{s}=\frac{\left| \begin{array}{ccc} 1 &{} S_{qq}^{^{\prime \prime }} &{} S_{qq}^{^{\prime \prime }}dq+S_{q\theta }^{^{\prime \prime }}d\theta \\ 1 &{} 0 &{} C^{\prime \prime }dq \\ 0 &{} 1 &{} d\mu \end{array} \right| }{\Delta }=\frac{S_{qq}^{^{\prime \prime }}dq+S_{q\theta }^{^{\prime \prime }}d\theta -C^{\prime \prime }dq-S_{qq}^{^{\prime \prime }}d\mu }{\Delta }\\&\displaystyle \frac{\partial q_{a}^{s}}{\partial \mu }=\frac{-S_{qq}^{^{\prime \prime }}}{ \Delta }>0\\&\displaystyle \frac{\partial q_{a}^{s}}{\partial \theta }=\frac{S_{q\theta }^{^{\prime \prime }}}{\Delta }>0\\&\displaystyle \frac{\partial q_{a}^{s}}{\partial q}=-1 \end{aligned}$$

Appendix 3: Welfare comparison in the linear case

Start from

$$\begin{aligned} 2\left( b+c\right) \left( W^{a}-W^{na}\right) =c^{2}var\left( \mu \right) -x\left( 1-\alpha \right) a\left( \underline{\theta }\right) ^{2}\left[ \left( 1-\beta \right) \left( 1+\lambda \right) -1+y\right] . \end{aligned}$$

Suppose the shock $\mu$ is distributed according to a Bernoulli distribution: $\mu =0$ with probability $\left( 1-\beta \right)$, and $\mu = \bar{\mu }$ with probability $\beta$, hence ${\mathbb {E}}\left[ \mu \right] =\beta \bar{\mu }$. Then,

$$\begin{aligned} c^{2}\frac{var\left( \mu \right) }{a\left( \underline{\theta }\right) ^{2}} =c^{2}\frac{\beta \left( 1-\beta \right) \bar{\mu }^{2}}{a\left( \underline{ \theta }\right) ^{2}}=\frac{1-\beta }{\beta }\left( c\frac{{\mathbb {E}}\left[ \mu \right] }{a\left( \underline{\theta }\right) }\right) ^{2}=\frac{1-\beta }{\beta }y^{2}. \end{aligned}$$

Introduce $\gamma =\frac{b}{c}$ and $\delta =\frac{\gamma }{1+\gamma }=\frac{ b}{b+c}\in \left( 0,1\right)$. Then, $\lambda =\frac{\beta }{1-\beta }\frac{ c}{c+b}=\frac{\beta }{1-\beta }\frac{1}{1+\gamma }=\frac{\beta }{1-\beta } \left( 1-\delta \right)$, and $1+\lambda =\frac{1-\delta \beta }{1-\beta }$ . Thus,

$$\begin{aligned} \left( 1-\beta \right) \left( 1+\lambda \right) -1=-\delta \beta , \end{aligned}$$

and

$$\begin{aligned} \Delta W\left( x,y\right) \overset{def}{=}\frac{2\left( b+c\right) \left( W^{a}-W^{na}\right) }{a\left( \underline{\theta }\right) ^{2}}=\frac{1-\beta }{\beta }y^{2}-x\left( 1-\alpha \right) y+x\left( 1-\alpha \right) \delta \beta . \end{aligned}$$

Opening the adjustment market reduces welfare if and only if $\Delta W\left( x,y\right) <0$. Thus, we examine the sign of $\Delta W\left( x,y\right)$. Consider $\Delta W=0$ as a quadratic equation in y. Its discriminant is

$$\begin{aligned} D\left( x\right)= & {} x^{2}\left( 1-\alpha \right) ^{2}-4x\left( 1-\alpha \right) \delta \left( 1-\beta \right) \\= & {} x\left( 1-\alpha \right) \left[ x\left( 1-\alpha \right) -4\delta \left( 1-\beta \right) \right] \\= & {} x\left( 1-\alpha \right) ^{2}\left[ x-x_{0}\right] , \end{aligned}$$

where $x_{0}=\frac{4\delta \left( 1-\beta \right) }{1-\alpha }$. If the information distortion is lower than $x_{0}$, $D\left( x\right) <0$, hence $\Delta W\left( x,y\right) >0$: opening the adjustment market to load curtailment always improves welfare.

On the other hand, if $x-x_{0}$ then $D\left( x\right) >0$, $\Delta W\left( x,y\right) =0$ admits two positive roots in y. Denote $y_{1}\left( x\right)$ the smallest one, defined by

$$\begin{aligned} y_{1}\left( x\right)= & {} \frac{\beta }{2\left( 1-\beta \right) }\left( x\left( 1-\alpha \right) -x\left( 1-\alpha \right) \sqrt{1-\frac{x_{0}}{x}} \right) \\= & {} \frac{\beta x\left( 1-\alpha \right) }{2\left( 1-\beta \right) }\left( 1- \sqrt{1-\frac{x_{0}}{x}}\right) =2\delta \beta \frac{x}{x_{0}}\left( 1-\sqrt{ 1-\frac{x_{0}}{x}}\right) . \end{aligned}$$

The largest root is

$$\begin{aligned} y_{2}\left( x\right) =2\delta \beta \frac{x}{x_{0}}\left( 1+\sqrt{1-\frac{ x_{0}}{x}}\right) . \end{aligned}$$

Thus, $\Delta W\left( x,y\right) <0$ for $x\ge x_{0}$ and $y\in \left( y_{1},y_{2}\right)$, provided $\left( 1+\lambda \right) x\le 1\$and $x+y\le 1$.

A necessary condition is

$$\begin{aligned} \left( 1+\lambda \right) x_{0}<1\Leftrightarrow \frac{4\delta \left( 1-\beta \right) }{1-\alpha }\frac{1-\delta \beta }{1-\beta }\le 1\Leftrightarrow \left( 1-\alpha \right) >4\delta \left( 1-\delta \beta \right) , \end{aligned}$$

which is condition (14).

If condition (14) is met, a sufficient condition for the existence of ${\mathcal {H}}$ is that $f\left( x_{0}\right) =x_{0}+y_{1}\left( x_{0}\right) -1<0$. Then, by continuity, for $x\ge x_{0}$ and close to $x_{0}$, and $y\ge y_{1}\left( x\right)$ and close to $y_{1}\left( x\right)$, $\Delta W\left( x,y\right) <0$, $\left( 1+\lambda \right) x\le 1$,  and $x+y\le 1$.

We have

$$\begin{aligned} f\left( x_{0}\right) =2\delta \beta +x_{0}-1=2\delta \beta +\frac{4\delta \left( 1-\beta \right) }{1-\alpha }-1, \end{aligned}$$

hence

$$\begin{aligned} f\left( x_{0}\right) <0\Leftrightarrow \frac{4\delta \left( 1-\beta \right) }{1-\alpha }<1-2\delta \beta . \end{aligned}$$

This requires $\left( 1-2\delta \beta \right) >0$ since the left-hand side is positive. Thus, if $\left( 1-2\delta \beta \right) >0$,

$$\begin{aligned} f\left( x_{0}\right) <0\Leftrightarrow 1-\alpha >\frac{4\delta \left( 1-\beta \right) }{1-2\delta \beta }, \end{aligned}$$

which is condition (15).

Both conditions (14) and (15) place lower bounds on $\left( 1-\alpha \right)$. Functional analysis proves that condition (14) is the binding one for low values of $\delta$, then condition (15) becomes the binding one for higher values of $\delta$.