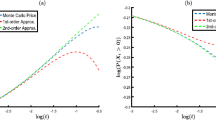Abstract
We show that the VIX Index structurally underestimates model-free implied volatility because its implementation omits extrapolation of the volatility smile in the tails. We use the asymptotic behavior of the volatility surface to construct a correction term that is model-independent and only requires option prices at the two outermost strikes. We show how to apply this correction to the VIX Index ex-post as well as how to modify its implementation accordingly. Furthermore, we show that the degree of underestimation varies over time. For the S&P 500 Index and the DJIA Index the error is larger in periods of sustained low volatility. This cannot be observed for the Volatility-of-VIX Index.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The CBOE VIX Index is the one of the most commonly used indicators for investor fear. It implements the static replication approach to variance swap pricing by Carr and Madan (1998), who show how to replicate the future realized variance of an assets’ return process between today and a future date T using the prices of options expiring at T. Britten-Jones and Neuberger (2000) coin the term model-free implied variance (MFIV), as the replication strategy does not depend on the assumption of a stochastic model for the underlying. The replication portfolio requires a continuous set of strikes from 0 to infinity. Since in practice option strikes are discrete and only actively traded in a relatively narrow range around the current price of the underlying, systematic errors are introduced.
Specifically, the methodology behind the VIX Index as outlined in CBOE (2018) truncates the tails completely, and makes no effort to compensate for this. This leads to structural underestimation of MFIV in the VIX Index implementation. Option trading activity varies over time with changing market regimes. When interest in far-from-the-money options wanes during calm market periods, the observable area of the volatility smile is truncated further than in more volatile periods. As the width of the observable option strike grid changes, the underestimation varies over time. Many hedging strategies reduce their risk exposure when the VIX Index is elevated. The structural underestimation therefore implies that these strategies underestimate market risk, and are systematically overinvested or underhedged. The goal of this paper is to examine this truncation error and to understand its dynamics over time. The truncation error term can compensate for the time-varying structural underestimation in the VIX Index by systematically accounting for grid width, and make values from different market regimes or underlyings comparable.
To compensate for truncation, we apply a result by Lee (2004) on the asymptotic behaviour of the volatility smile. By deconstructing the main integral of Britten-Jones and Neuberger (2000), which is based on Carr and Madan (1998), we isolate the tails of the volatility smile and compute them using asymptotic option prices. This yields a very simple truncation error correction term that is completely independent of model assumptions. The only required observations are the option prices at the outermost strike to parameterize each tail. The calculation is demonstrated using the reference data by CBOE (2018).
We calculate the truncation error for volatility indices of both the S&P 500 Index and the Dow Jones Industrial Average Index, and show how the truncation error varies depending on market conditions. As a counterexample, we show that the Volatility-of-VIX Index does not exhibit this pattern.
Our findings have implications for the analysis of the volatility premium as well as VIX Index futures. The volatility premium refers to the positive expected return that sellers of options capture. In the literature, it is commonly defined as the difference between the volatility of the underlying price and the VIX Index. For example, Eraker (2021) presents a general equilibrium model based on long-run risk that is able to capture the volatility premium as well as the negative correlation between prices of the underlying. Gruber et al. (2020) construct a state-based volatility process to model the term structure of the volatility premium in periods of low and high volatility separately. The structural underestimation of the VIX Index might explain a small portion of this premium. Bardgett et al. (2018) examine the information content of options on VIX Index futures and document a that it varies over time. Cheng (2019) studies the volatility premium embedded in VIX futures and finds a lower than expected response to rising market risk. Bakshi et al. (2021) show that VIX futures are in contango when jumps in volatility exist, and are correlated with jumps in the price of the underlying. This implies that the volatility premium compensates the option seller for the risk of large jumps. Eraker and Yang (2020) construct a sophisticated consumption-based equilibrium framework to integrate the pricing VIX and SPX options as well as equity and variance premium. The structural underestimation in the VIX Index is likely priced into VIX futures, and the described patterns might distort the VIX Index futures term structure.
To begin our analysis, we review the related literature. Next, we examine the construction of the VIX Index in detail to identify its structural bias. We then investigate the asymptotic behaviour of the volatility smile and show how to correct for truncation. Finally, historical option prices are used to calculate the truncation error over time, revealing its dependence on market volatility.
1.1 Notation
Markets are assumed to be free of arbitrage opportunities and complete. This implies the existence of an equivalent martingale measure (EMM) which is uniquely characterised by the risk neutral density \(\varPhi ^{\mathbb {Q}}\) of the stochastic process ruling the underlying. The fair value of a derivative is given by the expected value of its payoff under \({\mathbb {Q}}\).
Contracts live from time 0 to time T, which is specified in years. The current time is \(t \in [0,T]\). The time to maturity is \(\tau = T-t\). For discrete returns, actual trading days per year are used for annualization; for continuous cases, 365.25 calendar days and 252 trading days are assumed.
The price of an underlying at t is \(S_t\), its forward price at time t is \(F_t = S_te^{r\tau }\). Option strikes in absolute (dollar) terms are denoted K, while the strike in terms of log-moneyness against the forward price is denoted \(k = \log \left( \frac{K}{F_0}\right)\). Capitalized option prices \(C(K, \tau )\) and \(P(K, \tau )\) are quoted in dollar value, their counterparts in log-moneyness terms, such that \(C(K, \tau ) = F_0c(k, \tau )\) and \(P(K, \tau ) = F_0p(k, \tau )\). Unless explicitly specified, prices refer to the average of the bid and ask quotes. \(Q(K, \tau )\) and \(q(k, \tau )\) denote the price of the out-of-the-money option in dollar and log-moneyness, respectively.
The term implied volatility (IV) refers to the Black-Scholes implied volatility (BSIV) \(\sigma _{BSIV}\) that solves
uniquely, where \(C_{observed}(K, \tau )\) is an observed call price at strike K and \(C_{Black\text {-}Scholes}(K, \tau , \sigma _{BSIV})\) is the Black-Scholes price at strike K and volatility \(\sigma _{BSIV}\). The term volatility smile describes the set of BSIVs that is produced by all options on an underlying asset with the same expiration date. The term volatility surface refers to the collection of volatility smiles of all available expiration dates at a certain point in time.
Unless explicitly specified, all options are of European style, and dividends and interest rate r are assumed to be zero and omitted for clarity.
1.2 Literature review
Some fundamental results in the literature provide insight into the relationship between observed option prices and forward variance of the underlying. Breeden and Litzenberger (1978) show that the risk neutral price probability distribution of an underlying at expiration is uniquely determined by the complete set of options without assumption of a parametric model for the underlying. Neuberger (1994) introduces the concept of futures contracts that pay the natural logarithm of an underlying future at expiration and shows that the payoff of a delta-hedged log-contract depends purely on volatility of the underlying, provided its variance is constant over time. Independently, Dupire (1994) shows that a unique risk-neutral density \(\varPhi ^{\mathbb {Q}}\) can be recovered from market prices, if all prices are compatible with no arbitrage conditions and the underlying is governed by a diffusion process.
Carr and Madan (1998) show that a volatility swap whose payoff is the realized volatility of the underlying can be fairly priced by statically replicating log-contracts using the result of Breeden and Litzenberger (1978) and delta-hedging them as suggested by Neuberger (1994). Specifically, they show that a \(\frac{1}{K^2}\)-weighted portfolio of out-of-the-money options has virtually constant sensitivity to changes in variance, and construct a portfolio that perfectly replicates forward variance of a continuous underlying.Footnote 1 Furthermore, it is only based on the assumption of risk-neutrality, and does not rely on a specific stochastic model for the underlying process, except that it follows a diffusion. Britten-Jones and Neuberger (2000) extend their analysis and show that this result holds in the case of stochastic volatility in the underlying as well. Demeterfi et al. (1999) explore the effect of skewness on the price of variance and volatility swaps for continuously moving underlyings. Based on Carr and Madan (1998), Britten-Jones and Neuberger (2000) define MFIV as
with K being a strike from the set of all observable strikes, and, since the expectation is taken under \({\mathbb {Q}}\), \(C(K,\tau ) = {{\,\mathrm{{\mathbb {E}}}\,}}^{\mathbb {Q}}_t[max(F_t-K,0)]\).
Jiang and Tian (2005) show that Eq. 2 holds for price processes with jumps. They find evidence that the MFIV is a more accurate predictor of future realized variance than historical variance or Black-Scholes ATM implied variance.
Even though the result by Carr and Madan (1998) has been thoroughly investigated, the discrete and truncated nature of option markets still presents challenges in practical applications. The VIX Index was originally introduced by the Chicago Board Options Exchange (CBOE) in 1993 to measure market-expected 30-day volatility of the S &P 100 Index. In its original formulation as suggested by Fleming et al. (1995) it was defined as at-the-money Black-Scholes implied volatility, and computed by solving Eq. 1 with the current 30-day at-the-money option. In 2003, the VIX Index was updated to reflect the advances in option pricing theory laid out above, in conjunction with a change of the underlying to the S &P 500 Index. CBOE (2018) provide details on the updated calculation and Sect. 2 discusses its shortcomings. CBOE (2011) introduced a single-stock variant of the VIX Index for a handful of stocks whose options are very liquid. In 2012, CBOE (2012) introduced the Volatility-of-VIX Index, which applies the methodology of the VIX Index to options on the VIX Index itself. Jiang and Tian (2005) examine the practicality of 2 and identify two distinct sources of implementation error: discretization due to the fact that observed strikes of options are naturally discrete, but Eq. 2 is based on a continuous integral in K; and truncation because Eq. 2 requires integration along \(K \in [0, \infty )\). They state theoretical upper bounds for the truncation and discretization errors. Jiang and Tian (2007) examine the implementation of Eq. 2 by CBOE (2018) and find it to be systematically flawed. They show that, depending on the volatility environment, the magnitude of the implementation error is predictable. This paper partially extends their analysis. They suggest a numerical scheme to overcome the issues using cubic splines for interpolation, and linear extrapolation in log-moneyness space k beyond the outermost strikes. Benaim et al. (2009) investigate the concept of model-based interpolation and extrapolation, where a stochastic process is calibrated to fit option prices, which is used to generate a synthetic option price surface that overcomes the issues of truncation and discretization. They find that this approach introduces systematic errors in the tails. They suggest supplementing a model-based interpolation with numerical extrapolation. Broadie and Jain (2008) analyze the effect of discretization on the pricing of variance swaps using a variety of stochastic processes for the underlying and find that errors due to discretization are usually small, but the effect of jumps – which manifest in the tails of the smile – can be large. Carr and Wu (2009) and Jiang and Tian (2005) extrapolate with constant BSIV beyond the outermost strikes. While simple, this approach has several drawbacks. First, it satisfies the conditions set forth by Benaim and Friz (2009) if and only if we limit the underlying process to be log-normally distributed (the Black-Scholes case). For this specific case, the approach outlined in this paper can be adapted using the distribution-specific dynamics of Benaim and Friz (2009) to achieve an equivalent result. Second, it introduces dependency on the observed cutoff point: a cutoff point at a larger |k| has, under the described growth dynamics, necessarily a equal or larger BSIV, such that constant extrapolation leads to similar, albeit lower, structural underestimation as the implementation by CBOE (2018). Jiang and Tian (2007) furthermore criticise the introduction of kinks into the volatility smile, which violate no-arbitrage conditions. They interpolate with natural cubic splines and extrapolate BSIV linearly in log-moneyness, with the slope of the extrapolation function matching the first derivative of the spline at the outermost strike. Except for a Black-Scholes world where a constant extrapolation would be exact, any linear growth violates the no-arbitrage bounds set forth by Lee (2004).Footnote 2 Carr and Wu (2009) utilize MFIV to estimate variance risk premia for indices and single stocks. They also provide a detailed interpolation and extrapolation procedure, which differs from Jiang and Tian (2007) in that they use linear interpolation between strikes and constant extrapolation beyond the outermost strikes.
The relationship of the distribution of the underlying and the shape of the volatility surface permits analysis of the asymptotic behaviour of BSIV in the tails. Hodges (1996) establishes that the no-arbitrage bounds set forth by Merton (1973) can be expressed by quoting option prices in terms of their BSIV, where a positive BSIV prevents arbitrage of between options and the underlying plus cash, and having a single BSIV per strike and T enforces Put-Call parity. Furthermore, he provides bounds for the slope of implied volatility in the tails. Lee (2005) describes the static and dynamic characteristics of the volatility smile, and shows how the volatility smile can be interpreted as probabilistic density. Carr and Wu (2016) provide insights into the dynamic evolution of the volatility surface and derive no-arbitrage constraints based on those dynamics. Lee (2004) examines the asymptotic behaviour of BSIV in the strike domain. He finds that under absence of arbitrage the growth of BSIV is bound from above by \(\sqrt{\frac{\beta }{T}|k|}\), where \(\beta \in \left[ 0,2\right]\) being specific to either the left or right wing. Benaim and Friz (2009) expand and refine this result and show that the asymptotics of the volatility smile are a non-linear transform of the asymptotics of the underlyings’ return distribution. They show that the result of Lee (2004), under some mild technical conditions, precisely determines tail behaviour. Furthermore, they show how to explicitly derive the asymptotic behaviour of the BSIV for a variety of stochastic models. Benaim et al. (2012) examine the relationship between the moment-generating function and the moment formula. They suggest using it to extrapolate the implied volatility surface in the strike domain. In a preceding analysis, Drǎgulescu and Yakovenko (2002) come to agreeing results for the special case of distributions with stochastic variance. Gulisashvili (2010) provides asymptotic formulas for call options, as well as error estimates, based on Lee (2004) and Benaim and Friz (2009).
2 Structural shortcomings of the VIX index
The calculation of the VIX Index is laid out in detail in CBOE (2018). An overview is provided in Appendix 1.
CBOE (2018) implement Eq. 2 as a weighted Riemann sum based on Demeterfi et al. (1999) using the midpoint rule as
with \(N\in {\mathbb {N}}^+\) being the number of observed option prices, \(K_i\) being a strike price with \(K_i<K_{i+1} \forall i\in {\mathbb {N}}^+\), \(K^*\) being the at-the-money strike price, \(Q_{K_i}\) being the observed price of an out-of-the-money option at \(K_i\), \(\varDelta K_i = \frac{K_{i+1}-K_{i-1}}{2} \forall 1<i<N\) for all strikes between endpoints, and \(\varDelta K_1 = K_2-K_1\) and \(\varDelta K_N = K_N-K_{N-1}\) for the strikes at the endpoints.
Equation 3 implies that the tails of the volatility smile are cut off, leading to a systematic underestimation of forward variance. The truncation error becomes larger when the strike price grid becomes narrower in k. It also grows after large price movements in the underlying, specifically in the time between large price drops in the underlying, and the creation of new options by market makers.
Between strikes, each observation is weighted by half of the difference of the surrounding strikes. This is akin to a constant level interpolation symmetrically around each observation. The errors of this interpolation between strikes tend to be approximately self-cancelling, leading to a small error from interpolation. This does not happen in the region around the strike with the smallest Black-Scholes implied variance, leading to a fluctuating error sign. Some discussion on this can be found in Jiang and Tian (2005).Footnote 3 The extend of this depends on the shape of the smile around its minimum. Higher skewness in the underlying implied distribution tend to increase the fluctuation.
3 Asymptotic extrapolation and construction of the truncation error
The implementation of the VIX Index by CBOE (2018) does not compensate for truncation. By deconstructing Eq. 2, we compensate for the missing tails. We then examine the required strike grid width as well as convergence behaviour of the truncation error.
3.1 Construction of the truncation error
To compensate for truncation we utilize the asymptotic behaviour of BSIV by computing the respective Black-Scholes option prices and calculating the partial MFIV contribution of each tail.
Extrapolating with constant BSIV of the outermost option price would make the truncation error compensation highly dependent on only the price of these options, without taking the varying strikes into account. We utilize Gulisashvili (2010), who shows that Lee (2004)’s formula can be used to extrapolate option prices in the strike domain.
If we where to assume knowledge of the underlying distribution, we could use the precise tail behaviour based on Benaim and Friz (2009), as suggested by Gulisashvili (2010). The specific case of a Black-Scholes-compliant underlying would then result in constant extrapolation. While the boundary condition of Lee (2004) does not necessarily apply close to the money, it allows us to find the non-parametric asymptotic truncation error of MFIV, provided \(k_{min} \le 0 \le k_{max}\) and both \(k_{min}\) and \(k_{max}\) have sufficient distance from 0. Section 3.2 examines this issue in greater detail.
To compute the truncation error compensation, we first deconstruct MFIV into three segments: the observed center segment, and two tails. For the tails, we derive the Black-Scholes option price as a function of k and a tail-specific parameter \(\beta\). After calculating \(\beta\) for each tail to fit the outermost option price, we substitute the option price within the tail segments of the deconstructed MFIV. The center segment is left unchanged. The two tails compensate the missing MFIV contribution of Eq. 3.
By rewriting Eq. 2 in log-moneyness terms, we get
Appendix 2 provides a detailed derivation.
Since the asymptotic BSIV depends exclusively on k and \(\beta\) as \(k\longrightarrow \pm \infty\), we can define the extrapolated price of a far-out-of-the-money call option \({\tilde{c}}(k, \tau , \beta )\) as
where \(\varPsi\) is the Normal CDF.Footnote 4
As suggested by Benaim et al. (2012), \(\beta\) is chosen according to the outermost observed option for each tail individually. Since
we fix the outermost strike for each tail, and compute the respective \(\beta _{left, right}\) as
First, we derive the right side truncation error where \(k>0\). The observation farthest to the right is located at \(k_{max}\). Hence, \(max(0, 1-e^k) = 0\). The truncation error to the right side is a function of only \(k_{max}\) and \(\beta _{right}\) given by
The left side truncation error follows in similar fashion, using the asymptotic price of a far-out-of-the-money put option such that
The total truncation error is the sum of both sides given by
In comparison to Jiang and Tian (2005), who provide parametric as well as non-parametric upper bounds for the truncation error, this result provides an asymptotic value for the total truncation error. Provided \(k_{min}\) and \(k_{max}\) are sufficiently far from 0, this yields a correction term that can be added to MFIV without relying on numerical methods, and instead only relying on asymptotic properties of the volatility surface.
To calculate this truncation error, the uncorrected MFIV value, the observed minimum and maximum option prices, and their strikes are required. Beyond absence of arbitrage, no further parametric assumptions are required.
Illustration of the extrapolation approach. Simulated volatility smile generated with a Merton-model with \(\varOmega =\{\sigma =0.3, \alpha =0.5, \delta =0.5, \lambda =0.1 \}\). Left wing cutoff point \(k_{min}=-0.6\) with \(\beta _{left}=0.0646\), and right wing cutoff point \(k_{max}=0.6\) with \(\beta _{right}=0.2185\). Note that the extrapolation extends beyond the shown range and the extrapolation is only limited by machine precision
Figure 1 illustrates the extrapolation approach on a simulated volatility smile. The dotted line shows the volatility smile of a Merton-model with the specified parameters. The cutoff points are chosen to be \(k_{min}=-0.6\) and \(k_{max}=0.6\), and we calculate \(\beta _{left}\) and \(\beta _{right}\) as described above. The extrapolated wings are shown as a solid line. In the implementation described by CBOE (2018), the extrapolated wings are considered to be 0.
To apply the correction to an observed volatility index VI, square it to convert to variance, add the error correction from 14, and take its square root
3.2 Minimum requirements for strike grid width
The result of Lee (2004) only holds asymptotically, therefore the suggested truncation error may lead to overestimation when the observable strike grid is too narrow.
Top panel shows the dynamics of Lee (2004)’s tail parameter \(\beta\) as a function of k for various expiration times. Computation based on a Merton jump-diffusion model with parameter set \(\varOmega _{Merton}=\{\sigma =0.2,\alpha =-0.15, \delta =0.05, \lambda =0.5\}\) (Calibration parameters for the S &P-500 Index from Gatheral (2006, p. 63)). Bottom panel shows the frequency of daily cutoff strikes of the SPX Index with a time-to-maturity between 28 and 32 days (approximately \(\tau =0.083\)) between January 1996 and April 2016. Data extends beyond the shown range, but is hidden for visual clarity. Results for different models and parameterizations are provided in Appendix 4
To confirm the applicability of the extrapolation, we analyse the behaviour of the tail-parameters \(\beta _{left}\) and \(\beta _{right}\) as \(|k|\rightarrow \infty\) and show that the observed strike grid tends to be wide enough to admit extrapolation. A reasonable minimum cutoff strike can be found be found by calculating \(\beta\) for every possible cutoff strike of the volatility smile. By definition, \(\beta\) will level off further out-of-the-money, where the extrapolation will be in agreement with the smile. Since the observed volatility smile is truncated, this requires modelling the underlying explicitly. Gulisashvili (2010) provides explicit error estimates for the extrapolation term if the model is known. By imposing a minimum cutoff strike for each wing, this uncertainty of the extrapolation can be reduced.
The VIX Index has a time-to-expiration of 30 days. For short expirations, the jumps tend to be a more important feature than stochastic volatility. Therefore the Merton jump-diffusion model has been chosen as illustrative benchmark.Footnote 5
The top panel of Fig. 2 shows the dynamics of \(\beta _{Left}\) and \(\beta _{Right}\) as the cutoff strike is shifted outwards for multiple expirations. With increasing time to maturity, leveling off happens slower and the grid width requirement widens. Depending on data availability, the approach by Lee (2004) might not be sufficient. The model-specific approach by Benaim and Friz (2009) may help alleviate some uncertainty of the estimators, however one would be left with model risk.
The bottom panel of Fig. 2 shows a histogram of cutoff strikes for both left and right wing for SPX Index. Based on this data, taking the intended \(\tau =0.083\) into consideration, a minimum cutoff strike of \(k=\pm 0.05\) appears to provide a reasonable compromise between data availability and resulting uncertainty for our application. For the SPX Index, this condition is satisfied for \(99.8\%\) of data points in the left wing, and for \(97.8\%\) of data points in the right wing.Footnote 6
3.3 Convergence of \(TE_{Left}\) and \(TE_{Right}\)
Note that the integral in Eq. 2 is well-defined. By the substitution rule, the integral in Eq. 4 is also well-defined. In particular, we have
and the same is true for the integral from \(-\infty\) to \(-{\tilde{k}}\).
By definition of \({\tilde{c}}(k, \tau , \beta )\) and \({\tilde{p}}(k, \tau , \beta )\) and the asymptotic behaviour of \(\sigma _k\) by Lee (2004), we can approximate \(TE_{Total}\) to any given degree by moving the boundary for the approximating proper integral further out, and are limited only by machine precision.Footnote 7
4 Applying the truncation error term to the VIX index
To apply the truncation error to the VIX Index we must either modify the VIX Index to remove the extrapolation described above or calculate the actual cutoff points for the truncation error. Using the sample data provided by CBOE (2018) we show how to practically apply the truncation error.
4.1 Preliminary modifications
By construction, the VIX Index implements a very short extrapolation through the definition of \(\varDelta K_1\) and \(\varDelta K_N\) in Eq. 3. To deal with this modification, we can either shift the cutoff-strikes outward, or modify the underlying price weights at the endpoints.
4.1.1 Ex-post approach
When applying our correction term to the VIX Index (and similar indices with this protruding extrapolation), the outermost strikes need to be shifted outwards as
4.1.2 Direct approach
A slight modification to Eq. 3 can make the outward shift of the cutoff point superfluous. It is then straightforward to include the extrapolation. By redefining \(\varDelta K_{min}\) and \(\varDelta K_{max}\), we can avoid the shift described above.
In the original form, the observation at \(K_{i}\) is weighted with \(\varDelta K_{i} = \frac{K_{i+1}-K_{i-1}}{2}\), i.e. half of the distance between the surrounding strikes. This implies a constant option price for an interval with length \(\varDelta K_{i}\), centered around \(K_i\). At the outermost strikes, \(\varDelta K_{min, max}\) is defined as the distance to the adjacent strike, e.g. \(\varDelta K_{min} = K_{min+1}-K_{min}\) (CBOE, 2018, p.8).
To simplify the extrapolation, we redefine \(\varDelta K_{min, max}\) to represent half of the distance to the adjacent strike as
This modification alleviates the implicit extrapolation, but requires computing the center part of the MFIV implementation.
4.2 Step-by-step example
We will illustrate the approach using the dateset provided by CBOE (2018, Appendix 1 and 2). The original document provides two option chains, one 25 days from expiration (“near term”), a second chain 32 days from expiration (“next term”). We will show the calculations based on the near term set, and provide results the next term.
We calculate the individual strike contributions as \(\frac{\varDelta K_i}{K^2_i}e^{rT}q_i\) based on the modified \(\varDelta K\) values as shown in Table 1. The contributions of the two outermost strikes are halved. We compute the implied variance as
Next, we compute single-sided truncation error corrections using Eqs. 13 and 11 and add both to the computed variance. Finally, we compute the time-weighed average of the near-term and the far-term variance, and annualise to find the final extrapolated index value. Table 2 provides intermediary results.
CBOE (2018) reports a VIX level of 13.69. After the adjustment and compensation for truncation errors on both tails, we find a level of 14.07. In this specific example, truncation leads to an underestimation of variance of approximately 0.38 percentage points.
This adjustment simplifies the extrapolation significantly. The drawback is that it cannot be applied to a precomputed or observed volatility index value, and is therefore mostly useful where MFIV is to be computed from scratch.
5 Historical analysis
The truncation error is larger when the observed option strike grid is narrower. Following demand of market participants, market makers create new contracts. This changes the width of the strike grid over time. In this section, we analyze how the availability of observable option prices affects the truncation error over time. In periods of high market volatility, the strike grid of observable option prices tends to be wide, which implies a low total truncation error. As volatility levels quiet down after periods of steady growth, the strike grid shrinks, and the truncation error grows larger. In effect, the VIX Index is typically precise in turbulent market phases, but underestimates MFIV when it is low. This effect is shown for the S &P 500 Index (SPX Index) and the associated VIX Index, as well as the Dow Jones Industrial Average (DJIA Index) with its respective volatility index. The Volatility-of-VIX-Index (VVIX Index) does not exhibit this pattern.
5.1 Dataset and computation
The dataset consists of options traded on the CBOE Options Exchange between January 1st, 1996 and April 29th, 2016, spanning 5118 trading days. It contains daily bid and ask prices for 233186 option contract on the SPX Index, the DJIA Index, and the VVIX Index. The options have been selected to have a remaining lifetime between 23 and 37 days. The same liquidity requirements as laid out in CBOE (2018) are applied. Contracts that have not been traded on a given day (and thus have a “stale price”) are excluded for that day. For each day and maturity, once two contracts with neighbouring strikes and stale prices are encountered, all contracts further away from the money are discarded as well. These constraints leave around 2.73 million observations, 1.57 million of which for contracts on the SPX Index. The option price data is matched to price data of the underlying price and to linearly interpolated U.S. treasury rates.
Since the choice of each wings’ \(\beta\) depends on the respective outside strike, we require a minimum log-moneyness of \(\pm 0.05\). If the strike grid is narrower than this, the truncation error might grow unreasonably large. Based on the analysis in Sect. 3.2 and the intended time-to-expiration of 30 days, \(\pm 0.05\) appears to provide sufficient space for the \(\beta\) to level out.
For each day with sufficient option price data, the volatility index is calculated in two ways. First, we follow the reference implementation by CBOE (2018). Second, the truncation error is calculated and added to the strike-adjusted reference implementation. \(\beta _{Left}\) and \(\beta _{Right}\) are computed for the left and right wing based on the price with the lowest (highest) available strike after applying liquidity requirements. This is done for each trading day with available and admissible data.
5.2 Analysis
As strike price grid width changes over time, the total truncation error fluctuates. From day to day, fluctuations are due to the discrete nature of strikes and the fact that stale prices are not considered in the calculation. Using smoothed data reveals the structural effect on the volatility index. The truncation error grows in calm market phases, and contracts during correction phases. As market volatility spikes during a correction, high implied volatility levels and option delta create short-term spikes in the truncation error, which level off quickly. The daily log changes of the corrected volatility indices exhibit lower standard deviation and higher kurtosis than their uncorrected counterparts.
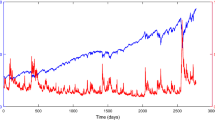
Observable option strikes and the effect on the truncation error over time. Top panel shows the S&P 500 Index level and the outermost observable strikes of each respective date. Middle panel shows the VIX Index and the VIX Index after adding the correction. Bottom panel shows the total truncation error and its 25-day rolling mean
Figure 3 shows the behaviour of the truncation error over time. The top panel illustrates the configuration of the option market in relationship to the underlying SPX Index over time. Each dot represents the outermost option strike observable at each point in time, with the options being subject to the liquidity constraints of CBOE (2018). The middle panel compares the VIX Index implementation as described in Sect. 2 with the amended implementation as described in Sect. 4.1.2. The bottom panel provides the relative error size and its 25-day rolling mean. The overall average truncation error is 1.13%.
In broad strokes, four distinct periods can be identified from Fig. 3. From 1996 to 2004, the SPX Index shows a large correction. The VIX Index is generally above 20%. The truncation error is fluctuating heavily, but its 25-day rolling mean mostly remains below its global average. Between 2004 and 2007 the SPX Index developed positively. The VIX Index mostly remaines below 20%. The truncation error fluctuates less, and its rolling mean rises to 2% and remains on this level. From 2007 to late 2012, the multiple large corrections in the SPX Index take place. The VIX Index spikes during the corrections, and remains above 20%. In this period, the truncation error falls below 1%, where it remains for most of the time. After 2012 until the end of the dataset in 2016, the SPX Index develops positively, and the VIX Index again remains around or below 20%. The truncation error grows to 2% and remains on this relatively high level. In the last few months of the dataset, a slight increase in the VIX Index coincides with a drop in the truncation error.
Overall, the truncation error appears negatively related to the VIX Index. In periods of high volatility, the truncation error fluctuates, but its rolling mean remains below the overall average truncation error. As the VIX Index remains on low levels, the truncation error is consistently elevated.
Observable option strikes and the effect on the truncation error over time. Top panel shows the DJIA Index level and the outermost observable strikes, subject to liquidity requirements. Middle panel shows the DJIA VIX Index and the DJIA VIX Index after adding the correction. Bottom panel shows the total truncation error and its 25-day rolling mean
Figure 4 shows the results of the historical calculation for the DJIA Index. Strike price grids, after applying liquidity requirements, for the DJIA Index tend to be narrower than for the SPX Index. The truncation error has an overall average of 2.72%, which is higher than the truncation error of the SPX Index.
The observation period can again be divided into four distinct periods. From the 1996 to 2004, the DJIA Index moves roughly sideways and exhibits elevated levels of volatility including several sharp spikes. The truncation error fluctuates strongly and its rolling mean fluctuates between 1 and 5%, but remains mostly below its overall average. From 2005 to 2007, the DJIA Index exhibits positive performance, and volatility levels remain consistently below 20%. The truncation error in this period is consistently elevated between 2.5% and 4.3%. In the period from 2008 to 2013, coinciding with negative returns, three large volatility spikes can be observed. The truncation error spikes during periods of negative market returns, and falls quickly below its overall average. From 2013 to 2016, DJIA Index returns are positive, and volatility levels are low. The rolling mean of the truncation error remains above its overall average for almost the entire time.
This behaviour is consistent with the analysis of the SPX Index. In periods with low DJIA VIX Index levels, the truncation error tends to be on a higher level. However, immediately after strong market corrections with corresponding volatility spikes, the truncation error spikes as well. This pattern is only very faintly visible in the analysis of the SPX Index.
Observable option strikes and the effect on the truncation error over time. Top panel shows the VIX Index level and the outermost observable strikes, subject to liquidity requirements. Middle panel shows the VVIX Index and the VVIX Index after adding the correction. Bottom panel shows the total truncation error and its 25-day rolling mean
Figure 5 shows the truncation error of the VVIX Index over time, the option-implied forward volatility of the VIX Index. The VVIX Index, detailed in CBOE (2012), applies the same methodology as CBOE (2018) to options on the VIX Index. The VIX Index is governed by a return distribution that is fundamentally different from a stock price index, with the most prominent difference being its mean reversion property in combination with a positive expected jump size. Furthermore, its negative correlation with the SPX Index makes it possible to use options on the VIX Index as hedging instruments for SPX Index-related delta risks. Fernandes et al. (2014) attempt to model the underlying process of the VIX Index directly and confirm both properties.
The dynamics of the VIX Index and the related VVIX Index appear very stable. While there are large spikes in the VIX Index during market corrections in the SPX Index, the VVIX Index exhibits much higher levels than the VIX Index, and fluctuates much more. The fluctuations are smaller in magnitude than those of the VIX Index, thus its range tends to be more localized over time. The individual trajectories appear more erratic than in the VIX Index, where spikes can often be linked with SPX Index corrections. Spikes in the VVIX Index occur but are less extensive.
Considering the truncation error, the available timeseries can be split into two periods. From 2006 to 2010, the truncation error starts on a very high level, but quickly shrinks to below the overall average level of 2.04%. The market correction in 2009 leads to a spike in the VIX Index, and to a spike in the truncation error levels. In the period after 2010, the truncation error remains mostly below its overall average, even as the VIX Index spikes.
The VVIX Index was introduced in 2012 (CBOE, 2012), but options on the VIX Index begin to be available from 2006, which extends the period for analysis. In the period shortly after introduction of VIX options to the market in 2006, a relatively large truncation error hints at a not-yet-developed market for VIX options.
In general, several patterns emerge from the analysis. For both equity indices, low levels of their volatility indices coincide with higher truncation errors than average. This is consistent for both the SPX Index and the DJIA Index, as well as over time. A possible explanation for this is that the width of the strike price grid with sufficient liquidity shrinks as volatility contracts. This implies that options are becoming cheaper and market participants can afford to purchase protection with higher delta. Another pattern which is consistent for both equity indices is that the truncation error sharply increases during market corrections. This can be explained by the spot price moving beyond the liquid strike grid, which creates large single-sided truncation errors on the left side. The truncation error of the VIX Index behaves completely different. This is fundamentally caused by the different stochastic processes that rule the underlying dynamics.
6 Conclusion
This paper examines the methodology behind the VIX Index and finds that it structurally underestimates MFIV because it ignores the unobservable tails of the volatility surface. Insights by Lee (2004) into the behaviour of the volatility surface at extreme strikes enable us to derive a compensation term that can correct the structural underestimation in the VIX Index. Historical analysis shows that the underestimation due to truncation fluctuates over time, as option trading activity in the tails varies.
Our approach does not require any assumptions about the underlying process, beyond those laid out by Lee (2004). The estimation of the extrapolation parameter \(\beta\) for each tail does however add an additional layer of uncertainty to the calculation. It is ultimately the shape of the volatility smile which determines the point where the \(\beta\)-parameters stabilize. Therefore, underlying dynamics and data availability must both be considered carefully when choosing a minimum strike grid width. It is straightforward to extend the suggested approach to incorporate specific model assumptions in scenarios with little available data or long maturities.
Analysis of historical truncation errors has revealed consistent patterns, where the truncation error grows in calm market phases. This implies that volatility indices underestimate forward volatility in calm market phases.
Analysing risk aversion in the market should account for these patterns, as risk appetite of market participants might be overestimated otherwise. The analysis of the term structure of variance can also be improved by this approach. Option chains tend do become less liquid with longer expirations, implying a possible systematic downward bias. The behaviour of the extrapolation factors \(\beta _{Left}\) and \(\beta _{Right}\) as time-to-maturity is increased must therefore be carefully considered.
VIX-like single-stock indices, such as introduced by CBOE (2011), can be based on underlyings with significantly less option trading activity. Compensating for this makes MFIV-estimates comparable between indices and stocks, independently of market conditions. The different market conditions, especially in the single-stock option market, also require further investigation. As strike grid width can be expected to be narrower, the validity of asymptotic extrapolation on heavily truncated volatility surfaces should be examined closely.
Notes
Specifically, see figure 2 in Jiang and Tian (2005).
See Appendix 3 for derivation.
Other models and parameterizations are provided in Appendix 4.
The results of the SPX Index analysis for different minimum cutoff strikes are provided in Appendix 5.
Our analysis is implemented in Python 3.9 x64 and appears to be stable to approximately \(k=\pm 30\), which should suffice for any practical application.
References
Bakshi, G., Crosby, J., Gao, X., & Xue, J. (2021). Volatility uncertainty, disasters, and VIX futures Contango. SMU Cox School of Business Research Paper 21–19:46.
Bardgett, C., Gourier, E., & Leippold, M. (2018). Inferring volatility dynamics and risk premia from the S &P 500 and VIX markets. Journal of Financial Economics, 131(3), 593–618. https://doi.org/10.1016/j.jfineco.2018.09.008
Benaim, S., & Friz, P. (2009). Regular variation and smile asymptotics. Mathematical Finance, 19(1), 1–12 arXiv:math/0603146.
Benaim, S., Dodgson, M., & Kainth, D. (2009). An arbitrage-free method for smile extrapolation. Royal Bank of Scotland, Technical Report.
Benaim, S., Friz, P., & Lee, R. (2012). On Black-Scholes implied volatility at extreme strikes. In R. Cont (Ed.) Frontiers in Quantitative Finance (pp. 19–45). Wiley, Hoboken. https://doi.org/10.1002/9781118266915.ch2
Breeden, D. T., & Litzenberger, R. H. (1978). Prices of state-contingent claims implicit in option prices. The Journal of Business, 51(4), 621–651.
Britten-Jones, M., & Neuberger, A. (2000). Option prices, implied price processes, and stochastic volatility. The Journal of Finance, 55(2), 839–866. https://doi.org/10.1111/0022-1082.00228.
Broadie, M., & Jain, A. (2008). The effect of jumps and discrete sampling on volatility and variance swaps. International Journal of Theoretical and Applied Finance, 11(8), 761–797. https://doi.org/10.1142/S0219024908005032.
Carr, P., & Madan, D. B. (1998). Towards a theory of volatility trading. In R. A. Jarrow (Ed.), Volatility: new estimation techniques for pricing derivatives (pp. 417–427). London: RISK Books.
Carr, P., & Wu, L. (2009). Variance risk premiums. Review of Financial Studies, 22(3), 1311–1341. https://doi.org/10.1093/rfs/hhn038.
Carr, P., & Wu, L. (2016). Analyzing volatility risk and risk premium in option contracts: A new theory. Journal of Financial Economics, 120(1), 1–20. https://doi.org/10.1016/j.jfineco.2016.01.004.
CBOE. (2011). CBOE to apply VIX methodology to individual equity options. https://ir.cboe.com/news-and-events/2011/01-05-2011/cboe-apply-vix-methodology-individual-equity-options
CBOE. (2012). Double the fun with CBOE’s VVIX index. https://cdn.cboe.com/resources/indices/documents/vvix-termstructure.pdf
CBOE. (2018). Cboe VIX whitepaper - Cboe volatility index. https://cdn.cboe.com/resources/futures/vixwhite.pdf
Cheng, I. H. (2019). The VIX premium. The Review of Financial Studies, 32(1), 180–227. https://doi.org/10.1093/rfs/hhy062.
Demeterfi, K., Derman, E., Kamal, M., & Zou, J. (1999). More than you ever wanted to know about volatility swaps. Goldman Sachs Quantitative Strategies Research Notes.
Derman, E., & Miller, M. B. (2016). The volatility smile: An introduction for students and practitioners. The Wiley finance series. Hoboken, New Jersey: Wiley.
Drǎgulescu, A. A., & Yakovenko, V. M. (2002). Probability distribution of returns in the Heston model with stochastic volatility. Quantitative Finance, 2(6), 443–453. https://doi.org/10.1080/14697688.2002.0000011
Dupire, B. (1994). Pricing with a smile. RISK 7.
Eraker, B. (2021). The volatility premium. The Quarterly Journal of Finance, 11(03), 2150014. https://doi.org/10.1142/S2010139221500142.
Eraker, B., & Yang, A. (2020). The price of higher order catastrophe insurance: The case of VIX options. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.3520256.
Fernandes, M., Medeiros, M. C., & Scharth, M. (2014). Modeling and predicting the CBOE market volatility index. Journal of Banking & Finance, 40, 1–10. https://doi.org/10.1016/j.jbankfin.2013.11.004
Fleming, J., Ostdiek, B., & Whaley, R. E. (1995). Predicting stock market volatility: A new measure. Journal of Futures Markets, 15(3), 265–302. https://doi.org/10.1002/fut.3990150303
Gatheral, J. (2006). The volatility surface: A practitioner’s guide. Wiley finance series. Hoboken, New Jersey: Wiley.
Gruber, P. H., Tebaldi, C., & Trojani, F. (2020). The price of the smile and variance risk premia. Management Science, 67(7), 4056–4074. https://doi.org/10.1287/mnsc.2020.3689.
Gulisashvili, A. (2010). Asymptotic formulas with error estimates for call pricing functions and the implied volatility at extreme strikes. SIAM Journal on Financial Mathematics, 1(1), 609–641. https://doi.org/10.1137/090762713.
Hodges, H. M. (1996). Arbitrage bounds of the implied volatility strike and term structures of European-style options. The Journal of Derivatives, 3(4), 23–35. https://doi.org/10.3905/jod.1996.407950.
Jiang, G. J., & Tian, Y. S. (2005). The model-free implied volatility and its information content. Review of Financial Studies, 18(4), 1305–1342. https://doi.org/10.1093/rfs/hhi027.
Jiang, G. J., & Tian, Y. S. (2007). Extracting model-free volatility from option prices: An examination of the Vix index. Journal of Derivatives, 14(3). https://doi.org/10.2139/ssrn.880459.
Lee, R. (2004). The moment formula for implied volatility at extreme strikes. Mathematical Finance, 14(3), 469–480. https://doi.org/10.1111/j.0960-1627.2004.00200.x.
Lee, R. (2005). Implied volatility: Statics, dynamics, and probabilistic interpretation. In R. Baeza-Yates, J. Glaz, H. Gzyl, J. Hüsler, & J. L. Palacios (Eds.), Recent advances in applied probability (pp. 241–268). Boston: Kluwer Academic Publishers.
Merton, R. C. (1973). Theory of rational option pricing. The Bell Journal of Economics and Management Science, 4(1), 141. https://doi.org/10.2307/3003143.
Neuberger, A. (1994). The log contract. Journal of Portfolio Management, 20(2), 74–80.
Acknowledgements
I am indebted to Philipp Rindler and Jérôme Blauth for many interesting discussions and valuable suggestions. I thank the participants of the IQ Kap Research Seminar on May 21, 2021 for insightful comments. My gratitude goes to Deka Investment for continuous support of this project and providing the data. Finally, I would like to thank the anonymous referee for a detailed review of this paper and for suggesting many improvements. Any remaining errors are my own.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Calculation of the VIX index
CBOE (2018) lays out the methodology of the VIX Index in detail. It fundamentally consists of the following steps:
-
1.
The two maturities closest to the 30 days-to-expiration mark are selected and all relevant options are chosen.
-
2.
Of those options, options with zero-bids are removed; If two options with adjacent strikes have zero-bids, all options further from the money are removed as well.
-
3.
The MFIV is computed for both maturities.
-
4.
The two resulting volatility estimates are linearly interpolated to match the desired time-to-expiration of 30 days.
Appendix 2: MFIV in terms of log-forward moneyness
We begin with the definition by Britten-Jones and Neuberger (2000), Eq. 2 as
By definition, we have
and thus \(\sigma _K = \sigma _k\) to shorten notation.
The price of an option in log-forward moneyness is quoted in relative terms, thus
Substitute and simplify to
Appendix 3: Derivation of the extrapolated Black-Scholes call price
In the standard Black-Scholes model, the price of a call option is given by
where \(\varPsi\) is the normal cumulative distribution function (CDF).
By Lee (2004), as \(k\longrightarrow \pm \infty\), \(\sigma _{BSIV}\longrightarrow \sqrt{\frac{\beta }{\tau }|k|}\), where \(\beta \in \left[ 0,2\right]\) being specific to either the left or right wing. To extrapolate c in the tails, compute \(\beta\) from the outermost option price, then substitute \(\sigma\) to get the price of a far-out-of-the-money call option in line with no-arbitrage limits as
Repeat for the price of a put option.
Appendix 4: Dynamics of Lee (2004)’s tail parameter
Figure 6 shows the \(\beta\)-curves for six different models to illustrate the general stability of the tail parameter dynamics. With short time-to-expiration, the tail parameters level out quickly. For longer time-to-expiration the specific model properties and parameters become more important.
\(\beta\)-curves in comparison. The top row shows the results for the Merton-model with \(\varOmega _{Merton1} = \{\sigma =0.2,\alpha =0.5, \delta =0.5,\lambda =0.02 \}\) and \(\varOmega _{Merton2} = \{\sigma =0.2,\alpha =0.3, \delta =0.7,\lambda =0.04 \}\). The middle row shows the results for the Heston-model with \(\varOmega _{Heston1} = \{v_0=0.0225, {\bar{v}}=0.0225, \kappa =3, \eta =0.25, \rho =0 \}\) and \(\varOmega _{Heston2} = \{v_0=0.09, {\bar{v}}=0.09, \kappa =3, \eta =0.25, \rho =0 \}\). The bottom row shows the results for the Stochastic Volatility with Jumps (SVJ)-model with \(\varOmega _{Svj1} = \{\varOmega _{Merton1}, \varOmega _{Heston1} \}\) and \(\varOmega _{Svj2} = \{\varOmega _{Merton2}, \varOmega _{Heston2} \}\)
Appendix 5: Truncation error under different cutoff strikes
Figure 7 provides the bottom plot of Fig. 3 for the minimum cutoff strikes \(\pm 0.05\), \(\pm 0.075\), and \(\pm 0.1\). While there are some visible differences, the general result appears to hold.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stahl, P. Asymptotic extrapolation of model-free implied variance: exploring structural underestimation in the VIX Index. Rev Deriv Res 25, 315–339 (2022). https://doi.org/10.1007/s11147-022-09190-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11147-022-09190-2