Abstract
Many financial contracts are equipped with exercise rights or other features enabling the parties to actively shape the contract’s payoff. These decisions pose a great challenge for the pricing and hedging of such contracts. The existing literature deals with these decisions by providing methods for specific contracts that are not easily transferable to other models. In this paper we present a framework that allows us to separate the treatment of the decisions from the pricing problem and derive a general pricing principle for the price of an option with decisions by both parties. To accomplish this, we present a general version of the duality between acceptance sets and pricing functions, and use it to translate the pricing problem into the language of acceptance. Expressing certain aspects of economic behavior in this language is sufficient to fully eliminate the decisions from the problem. Further, we demonstrate why time consistent pricing functions are crucial when dealing with options with embedded decisions and how the pricing functions used in many contributions can be derived if time consistency is added to our minimal set of assumptions.

Similar content being viewed by others
References
Ahn, H., Penaud, A., & Wilmott, P. (1999). Various passport options and their valuation. Applied Mathematical Finance, 6(4), 275–292.
Artzner, P., Delbaen, F., Eber, J.-M., & Heath, D. (1999). Coherent measures of risk. Mathematical Finance, 9(3), 203–228.
Artzner, P., Delbaen, F., Eber, J.-M., Heath, D., & Ku, H. (2007). Coherent multiperiod risk adjusted values and Bellman’s principle. Annals of Operations Research, 152(1), 5–22.
Boda, K., & Filar, J. A. (2006). Time consistent dynamic risk measures. Mathematical Methods of Operations Research, 63(1), 169–186.
Brennan, M., & Schwartz, E. (1977). The valuation of American put options. Journal of Finance, 32(2), 449–462.
Carr, P., Geman, H., & Madan, D. B. (2001). Pricing and hedging in incomplete markets. Journal of Financial Economics, 62(1), 131–167.
Chen, A. (1970). A model of warrant pricing in a dynamic market. The Journal of Finance, 25(5), 1041–1059.
Cheridito, P., Delbaen, F., & Kupper, M. (2006). Dynamic monetary risk measures for bounded discrete-time processes. Electronic Journal of Probability, 11(3), 57–106.
Cheridito, P., & Kupper, M. (2011). Composition of time-consistent dynamic monetary risk measures in discrete time. International Journal of Theoretical and Applied Finance, 14(01), 137–162.
Delbaen, F., & Schachermayer, W. (1994). A general version of the fundamental theorem of asset pricing. Mathematische Annalen, 300(1), 463–520.
Delbaen, F., & Schachermayer, W. (1998). The fundamental theorem of asset pricing for unbounded stochastic processes. Mathematische Annalen, 312(2), 215–250.
Detlefsen, K., & Scandolo, G. (2005). Conditional and dynamic convex risk measures. Finance and Stochastics, 9(4), 539–561.
Doob, J. (1994). Measure theory, volume 143 of graduate texts in mathematics series. Berlin: Springer.
Ekström, E. (2006). Properties of game options. Mathematical Methods of Operations Research, 63(2), 221–238.
Föllmer, H., & Schied, A. (2002). Convex measures of risk and trading constraints. Finance and Stochastics, 6(4), 429–447.
Gerer, J., & Dorfleitner, G. (2018). Optimal discrete hedging of American options using an integrated approach to options with complex embedded decisions. Review of Derivatives Research, 21, 175–199.
Geske, R., & Johnson, H. E. (1984). The American put option valued analytically. Journal of Finance, 39(5), 1511–1524.
Henderson, V. (2001). Passport options outside the black scholes world. In M. Kohlmann & S. Tang (Eds.), Mathematical finance, Basel (pp. 181–193). Basel: Birkhäuser.
Hyer, T., Lipton-Lifschitz, A., & Pugachevsky, D. (1997). Passport to success: Unveiling a new class of options that offer principal protection to actively managed funds. Risk Magazine, 10, 127–132.
Karatzas, I. (1988). On the pricing of American options. Applied Mathematics and Optimization, 17(1), 37–60.
Karatzas, I. (1989). Optimization problems in the theory of continuous trading. SIAM Journal on Control and Optimization, 27(6), 1221–1259.
Kifer, Y. (2000). Game options. Finance and Stochastics, 4, 443–463.
McKean, H. P. (1965). Appendix: A free-boundary problem for the heat-equation arising from a problem of mathematical economics. Industrial Management Review, 6(2), 32–39.
Merton, R. C. (1973). Theory of rational option pricing. Bell Journal of Economics and Management Science, 4(1), 141–183.
Myneni, R. (1992). The pricing of the American option. Annals of Applied Probability, 2(1), 1–23.
Pham, H. (2009). Continuous-time stochastic control and optimization with financial applications (Vol. 61). Berlin: Springer Science & Business Media.
Rockafellar, R. T. (1970). Convex analysis. Princeton: Princeton University Press.
Samuelson, P. A. (1965). Rational theory of warrant pricing. Industrial Management Review, 6(2), 13–31.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A Proofs
Definition A.1
(Timet-acceptable premiums) .
.
1.1 A.1 Proof of Corollary 3.1
Proof
Equation (3.2) from Definition 3.1 follows directly from Axiom 3.1 and the definition of \(\mathcal {A}\).
To prove t-compatibility assume \(\mathbb {P}{\left( \alpha _{t}\left( {f_n}\right) \right) }=1\) and therefore \(\mathbb {P}{\left( \alpha _{t}\left( {f_n}\right) \big |B_n\right) }=1\) for all \(n\in \mathbb {N}\). Take any \(x\in V_{t}\) and define \(h\equiv x+\sum _n f_n\mathbb {1}_{B_n}\). Due to \(B_n\)’s disjointness we have \(h{\mathop {=}\limits ^{B_n}} f_n+x\) and thus by the “\(\Longrightarrow \)” direction of Axiom 3.1, \(\mathbb {P}{\left( \alpha _{t}\left( {h}\right) \big |B_n\right) }=1\) and furthermore by Corollary B.2.3 \(\mathbb {P}{\left( \alpha _{t}\left( {h}\right) \right) }=1\). Using the “\(\Longleftarrow \)” direction of Axiom 3.1 yields \(\mathbb {P}{\left( \alpha _{t}\left( {\sum _nf_n\mathbb {1}_{B_n}}\right) \right) }=1\). \(\square \)
1.2 A.2 Proof of Theorem 3.1
This proof requires the following lemmata:
Lemma A.1
Given \(h\in \mathcal {X}_{}^t\), \(C\in \mathcal {F}_{\infty }\) and a non-empty set of payoffs \(Y\subset \mathcal {X}_{\mathcal {T}}^t\), such that \(h{\mathop {<}\limits ^{C}}\sup Y\), a sequence \((g_n)\subseteq Y\) exists as well as mutually disjoint events \(\{B_n\}\in \mathcal {F}_{t}\), such that \(B_n\subseteq \{g_n>h\}\cup {\overline{C}}\) and \(\mathbb {P}{\left( \bigcup _n B_n\right) }=1\).
Proof
By Theorem B.1 and \(Y\ne \varnothing \) a sequence \((g_n)\subseteq Y\) exists with pointwise supremum \(g(\omega )\equiv \sup _n g_n(\omega )\) such that \(g=\sup Y\). Define \(D_n\equiv \{h<g_n\}\cup {\overline{C}}\) and \(B_n\equiv D_n\setminus \bigcup _{m=1}^{n-1} B_m\). Disjointedness and \(B_n\subseteq \{h<g_n\}\cup {\overline{C}}\) follow trivially. Next, show:
The fourth from the least upper bound property of the supremum. By the hypothesis of the lemma we have \(\mathbb {P}{\left( \{h<g\}\cap C\right) }=\mathbb {P}{\left( C\right) }\). Together with \(\mathbb {P}\)’s additivity for disjoint events, Eq. (A.1) proves \(\mathbb {P}{\left( \bigcup _n B_n\right) }=1\). \(\square \)
Lemma A.2
\(\infty \in \mathcal {A}\) and  for any proper t-acceptance set \(\mathcal {A}\) and \(f\in \mathcal {X}_{[{t},\infty \rangle }\).
for any proper t-acceptance set \(\mathcal {A}\) and \(f\in \mathcal {X}_{[{t},\infty \rangle }\).
Proof
Due to \(\mathcal {A}\)’s t-compatibility some \(g\in \mathcal {A}\) exists. By Eq. (3.2) from Definition 3.1 and \(\infty \in V_{t}\) we can follow \(g+\infty =\infty =f-(-\infty )\in \mathcal {A}\). i.e.  . \(\square \)
. \(\square \)
Lemma A.3
For any proper t-acceptance set \(\mathcal {A}\) and \(f\in \mathcal {X}_{[{t},\infty \rangle }\):
Proof
By Lemma A.2 we can apply Lemma A.1 with \(h=0\),  and \(C=\Omega \) and get a sequence
and \(C=\Omega \) and get a sequence  and a sequence \((B_n)\) with \(B_n\subseteq \{0<g_n<\infty \}\) for any \(n\in \mathbb {N}\). Define \(x=\sum _n g_n \mathbb {1}_{B_n}\). By \(f-g_n\in \mathcal {A}\), the other properties of \(B_n\) and t-compatibility we have \(\sum _n (f-g_n) \mathbb {1}_{B_n}=f-x\in \mathcal {A}\). Furthermore, due to \(x>0\) and \(x\in L_{t}\), we have \(f=(f-x)+x\) and thus by Eq. (3.2) from Definition 3.1: \(f\in \mathcal {A}\). \(\square \)
and a sequence \((B_n)\) with \(B_n\subseteq \{0<g_n<\infty \}\) for any \(n\in \mathbb {N}\). Define \(x=\sum _n g_n \mathbb {1}_{B_n}\). By \(f-g_n\in \mathcal {A}\), the other properties of \(B_n\) and t-compatibility we have \(\sum _n (f-g_n) \mathbb {1}_{B_n}=f-x\in \mathcal {A}\). Furthermore, due to \(x>0\) and \(x\in L_{t}\), we have \(f=(f-x)+x\) and thus by Eq. (3.2) from Definition 3.1: \(f\in \mathcal {A}\). \(\square \)
Lemma A.4
For every cash invariant t-pricing function \(\pi \) and \(B\in \mathcal {F}_{t}\), it holds:
Proof
The second and fourth equation follow from cash invariance (Definition 3.5) and \(\infty \cdot \mathbb {1}_{\overline{B}}\in L^+_{t}\). \(\square \)
Proof of Theorem 3.1.1
First we show t-compatibility. \(A\left[ \pi \right] \) is not empty due to \(\pi _{}{\left( {\infty }\right) }\ge 0\), which follows from \(0\in \mathcal {X}_{[{t},\infty \rangle }\), \(\infty \in L^+_{t}\), cash invariance of \(\pi \) and the convention from Definition 2.1: \(\pi _{}{\left( {\infty }\right) }=\pi _{}{\left( {0}\right) }+\infty =\infty \ge 0\).
For t-compatibility, take a sequence \(f_n\) with \(\pi _{}{\left( {f_n}\right) }\ge 0\), mutually disjoint \(\{B_n\}\subseteq \mathcal {F}_{t}\) with \(\mathbb {P}{\left( \bigcup _n B_n\right) }=1\) and define \(g\equiv \sum _n^\infty f_n \mathbb {1}_{B_n}\). We need to prove \(\pi _{}{\left( {g}\right) }\ge 0\). Using Corollary B.1.2 it remains to show \(\pi _{}{\left( {g}\right) }{\mathop {\ge }\limits ^{B_n}} 0\) for any n: The two functions \(f_n+\infty \cdot \mathbb {1}_{\overline{B_n}}\) and \(g+\infty \cdot \mathbb {1}_{\overline{B_n}}\) are identical and thus Lemma A.4 can be applied to prove \(\pi _{}{\left( {g}\right) }{\mathop {=}\limits ^{B_n}}\pi _{}{\left( {f_n}\right) }\ge 0\).
Now prove the “\(\subseteq \)”-direction in Eq. (3.2) from Definition 3.1. For any f with \(0\le \pi _{}{\left( {f}\right) }\), \(g\in \mathcal {X}_{[{t},\infty \rangle }\) and \(x\in V_{t}\) with \(g= f+x\) (pointwise) it holds:
The first equality uses \(\pi \)’s cash invariance (Definition 3.5).
For the “\(\supseteq \)”-direction: Assume for each \(n\in \mathbb {N}\) it holds \(f+\frac{1}{n}\in A\left[ \pi \right] \), thus \( 0\le \pi _{}{\left( {f+\frac{1}{n}}\right) }\) and by \(\pi \)’s cash invariance \(0\le \pi _{}{\left( {f}\right) }+\frac{1}{n}\). By taking the limit \(n\rightarrow \infty \) yields the result: \(f\in A\left[ \pi \right] \). \(\square \)
Proof of Theorem 3.1.2
Take any \(f\in \mathcal {X}_{[{t},\infty \rangle }\) and show:
The first two equations are A’s and P’s definitions and the second uses cash invariance (Definition 3.5) of \(\pi \) and the convention from Definition 2.1. The last equation: The upper bound property of \(\pi _{t}{\left( {f}\right) }\) is trivial and to prove the least upper bound property, assume \(h\in \mathcal {X}_{[{t},\infty \rangle }\) is another upper bound and define the sequence \(g_n\equiv \min (n,\pi _{}{\left( {f}\right) })\). By definition of a t-pricing function, we have \(\pi _{}{\left( {f}\right) }\in L^\pm _{t}\) and thus \(g_n\in L^-_{t}\) and furthermore \(\pi _{}{\left( {f}\right) }\ge g_n\) for any \(n\in \mathbb {N}\). As an upper bound h fulfills \(h\ge g_n\), which in the limit \(n\rightarrow \infty \) proves that \(h \ge \pi _{}{\left( {f}\right) }\). \(\square \)
Proof of Theorem 3.1.3
It is a t-pricing function by Theorem B.1. It remains to show cash invariance.
Due to Lemma A.2 the following proof can ignore the case of empty sets. Take any \(x\in L^+_{t}\) and define  ,
,  , and the set \(B\equiv \{x=\infty \}\).
, and the set \(B\equiv \{x=\infty \}\).
- 1)
\(h+x{\mathop {\le }\limits ^{B}}g\): By taking into account the convention from Definition 2.1, it is easy to see that for any \(n\in \mathbb {N}\) it holds \(f+x-(n-\infty \cdot \mathbb {1}_{\overline{B}})=\infty \), which is element of \(\mathcal {A}\) by Lemma A.2. Consequently,
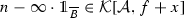 and the upper bound property of the supremum g directly implies \(n{\mathop {\le }\limits ^{B}}g\) and in the limit \(g{\mathop {=}\limits ^{B}}\infty {\mathop {\ge }\limits ^{B}}h+x\).
and the upper bound property of the supremum g directly implies \(n{\mathop {\le }\limits ^{B}}g\) and in the limit \(g{\mathop {=}\limits ^{B}}\infty {\mathop {\ge }\limits ^{B}}h+x\). - 2)
\(h+x{\mathop {\le }\limits ^{\overline{B}}} g\): Take any
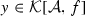 and define \(z\equiv y+x\cdot \mathbb {1}_{{\overline{B}}}\in L^-_{t}\), such that \(f+x-z=(f-y)\cdot \mathbb {1}_{{\overline{B}}}+\infty \cdot \mathbb {1}_{B}\). From \(f-y\in \mathcal {A}\), \(\infty \in \mathcal {A}\) (by Lemma A.2) and t-compatibility we derive \(f+x-z\in \mathcal {A}\), i.e.
and define \(z\equiv y+x\cdot \mathbb {1}_{{\overline{B}}}\in L^-_{t}\), such that \(f+x-z=(f-y)\cdot \mathbb {1}_{{\overline{B}}}+\infty \cdot \mathbb {1}_{B}\). From \(f-y\in \mathcal {A}\), \(\infty \in \mathcal {A}\) (by Lemma A.2) and t-compatibility we derive \(f+x-z\in \mathcal {A}\), i.e.  . The upper bound property of the supremum g and z’s definition yield \(g-x{\mathop {\ge }\limits ^{\overline{B}}} y\). Together with the previous result \(g{\mathop {=}\limits ^{B}}\infty \) we get \(g-x\ge y\) and thus \(g-x\) is an upper bound of
. The upper bound property of the supremum g and z’s definition yield \(g-x{\mathop {\ge }\limits ^{\overline{B}}} y\). Together with the previous result \(g{\mathop {=}\limits ^{B}}\infty \) we get \(g-x\ge y\) and thus \(g-x\) is an upper bound of 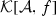 . By its definition, h has to be the least upper bound of this set, thus \(h\le g-x\), which proves the remaining \(h+x{\mathop {\le }\limits ^{\overline{B}}}g\).
. By its definition, h has to be the least upper bound of this set, thus \(h\le g-x\), which proves the remaining \(h+x{\mathop {\le }\limits ^{\overline{B}}}g\). - 3)
\(g\le h+x\): For any
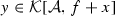 it holds \(f-(y-x)= f+x-y\) (taking into account the convention from Definition 2.1). Thus due to \(f+x-y\in \mathcal {A}\) we have
it holds \(f-(y-x)= f+x-y\) (taking into account the convention from Definition 2.1). Thus due to \(f+x-y\in \mathcal {A}\) we have 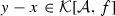 . The upper bound property of the supremum h entails \(y-x\le h\). Or in other words, \(h+x\) is an upper bound of the set
. The upper bound property of the supremum h entails \(y-x\le h\). Or in other words, \(h+x\) is an upper bound of the set 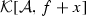 . By its definition, g has to be the least upper bound of the assertion follows. \(\square \)
. By its definition, g has to be the least upper bound of the assertion follows. \(\square \)
Proof of “\(\supseteq \)” in Theorem 3.1.4. Take any \(f\in \mathcal {A}\). It directly follows that  , and by the upper bound property of the supremum we have \({P{[\mathcal {A}]}}_{}(f)\ge 0\). The assertion follows from Definition 3.6 of \(A\left[ {P{[\mathcal {A}]}}\right] \). \(\square \)
, and by the upper bound property of the supremum we have \({P{[\mathcal {A}]}}_{}(f)\ge 0\). The assertion follows from Definition 3.6 of \(A\left[ {P{[\mathcal {A}]}}\right] \). \(\square \)
Proof of “\(\subseteq \)” in Theorem 3.1.4. Take any \(f\in A\left[ {P{[\mathcal {A}]}}\right] \). By Definition 3.6 this implies \(0\le {P{[\mathcal {A}]}}_{}(f)\). For any \(x\in V_{t}\), \({P{[\mathcal {A}]}}\)’s cash invariance ensures \( 0< x \le x+{P{[\mathcal {A}]}}_{}(f)={P{[\mathcal {A}]}}_{}(f+x)\). Now, Lemma A.3 implies \(f+x\in \mathcal {A}\). Using Eq. (3.2) from Definition 3.1 we arrive at \(f\in \mathcal {A}\). \(\square \)
1.3 A.3 Proof of Corollary 3.2
Proof
Define \(\pi \equiv {P{[\mathcal {A}]}}\). We have to show that  , i.e. \(\pi _{}{\left( {f}\right) }\in L^-_{t}\) and \(f- \pi _{}{\left( {f}\right) }\in \mathcal {A}\). The first statements follows from Theorem B.1 and the hypotheses \(\pi _{}{\left( {f}\right) }<\infty \). Now, prove the second statement using
, i.e. \(\pi _{}{\left( {f}\right) }\in L^-_{t}\) and \(f- \pi _{}{\left( {f}\right) }\in \mathcal {A}\). The first statements follows from Theorem B.1 and the hypotheses \(\pi _{}{\left( {f}\right) }<\infty \). Now, prove the second statement using
which follows from cash invariance, Definition 3.6 and Theorem 3.1.4. \(\square \)
1.4 A.4 Proof of Corollary 3.3
Proof
Assume \(B\in \mathcal {F}_{t}\), \(f,g\in \mathcal {X}_{}\) and \(f{\mathop {=}\limits ^{B}}g\) and define \(f'=f+\infty \cdot \mathbb {1}_{\overline{B}}\) and \(g'=g+\infty \cdot \mathbb {1}_{\overline{B}}\). By Lemma A.4 it remains to show \(\pi _{}{\left( {f'}\right) }=\pi _{}{\left( {g'}\right) }\), which by cash invariance and Theorem 3.1.2 follows from
We prove the “\(\Rightarrow \)”-direction of this equation, the other follows analogously. Assume \(f'-x\in A\left[ \pi \right] \). It holds for every \(y\in V_{t}\) and \(h=(g'-x)+y\), that \(h=(f'-x)+y\) and thus by Theorem 3.1.1 and Eq. (3.2) from Definition 3.1, \(h\in A\left[ \pi \right] \), which by the other direction of Eq. (3.2) from Definition 3.1 proves \(g'-x\in A\left[ \pi \right] \). \(\square \)
1.5 A.5 Properties of \(\inf \) and \(\sup \)
Lemma A.5
The following two mappings inherit \(\pi \)’s cash invariance:
Proof of the\(\sup \)-version. By Definition 3.5, we need to show for any \(x\in L^+_{t}\) and \(f\in \mathcal {X}_{[{t},\infty \rangle }\):
The first equation follows from the facts that fixation commutes with addition (trivially by Definition 2.3), \({x\big [\varphi _{}\big ]}=x\) (by Remark 2.4), and finally from cash invariance of \(\pi \).
For the second equation we need \(S\ne \varnothing \) and Theorem B.1, together ensuring the existence of a sequence \((\varphi _{n})_{n\in \mathbb {N}}\subseteq S\), such that \(g(\omega )\equiv \sup _{\varphi _{}\in S}\left( \pi _{}{\left( {{f\big [\varphi _{}\big ]}}\right) }(\omega ) +x(\omega )\right) \) and \(g=\sup _{n\in \mathbb {N}}(\pi _{}{\left( {{f\big [\varphi _{n}\big ]}}\right) }+x)\). It remains to show for all \(\omega \in \Omega \):
For all \(\omega \) with \(x(\omega )=\infty \), this follows directly from the convention introduced in Definition 2.1. For all other \(\omega \)’s, we have \(x(\omega )-x(\omega )=0\) and thus Eq. (A.2) follows from translational invariance of the supremum. \(\square \)
Proof of the\(\inf \)-version This prove is completely analogous with the only difference being that the S can be empty. However, in this case the assertion follows directly from the convention \(\inf \varnothing =\infty \) and the one introduced in Definition 2.1. \(\square \)
Lemma A.6
For any \(f\in \mathcal {X}_{[{t},\infty \rangle }\), \(h,g\in L^\pm _{t}\), local (Corollary 3.3) t-pricing function \(\pi \), t-compatible S and \(x\in V_{t}\) it holds:
If \(h<\infty \) and \(h\le \sup _{\varphi _{}\in {S_{}}}\pi _{}{\left( {{f\big [\varphi _{}\big ]}}\right) }\), then a \(\psi _{}\in S\) exists with \(h\le \pi _{}{\left( {{f\big [\psi _{}\big ]}}\right) }+x\).
If \(-\infty <g\) and \(\inf _{\varphi _{}\in {S_{}}}\pi _{}{\left( {{f\big [\varphi _{}\big ]}}\right) }\le g\), then a \(\psi _{}\in S\) exists with \(\pi _{}{\left( {{f\big [\psi _{}\big ]}}\right) }\le g+x\).
Proof of the\(\inf \)-version. As locality is invariant under a \(\pi \mapsto -\pi \) substitution an \(\inf \)-version of Lemma A.6 can be derived from it using the \(\inf /\sup \)-duality, \(-\sup A=\inf (-A)\). This derivation also relies on \(x\in L^+_{t}\). \(\square \)
Proof of the\(\sup \)-version. Using cash invariance (Lemma A.5) and \(h<\infty \) we have \(h{\mathop {<}\limits ^{C}}\sup _{\varphi _{}\in {S_{}}}\pi _{}{\left( {{(f+x)\big [\varphi _{}\big ]}}\right) }\) with \(C\equiv \{-\infty <h\}\). Let \(\{B_n\}\) be as in Lemma A.1 with \(g_n=\pi _{}{\left( {f[a_n]+x}\right) }\) for some sequence \(\{a_n\}_{n\in \mathbb {N}} \subseteq S\).
Define \(b=\sum _n^\infty a_n \mathbb {1}_{B_n}\). By the hypothesis of our lemma that S is t-compatible (Definition 3.2) and \(B_n\)’s properties we have \(b\in S\). By \(\sum _n^\infty a_n \mathbb {1}_{B_n}{\mathop {=}\limits ^{B_n}}a_n\) and Definitions 2.2 and 2.3 we have \(f[b]{\mathop {=}\limits ^{B_n}} f[a_n]\) and locality yields \(g_n{\mathop {=}\limits ^{B_n}}\pi _{}{\left( {{f\big [b\big ]}+x}\right) }\). From \(B_n\subseteq \{g_n>h\}\cup \{h=-\infty \} \) and cash invariance we obtain \(h{\mathop {\le }\limits ^{B_n}}\pi _{}{\left( {{f\big [b\big ]}}\right) }+x\) and the lemma now follows from \(\mathbb {P}{\left( \bigcup _n B_n\right) }=1\) and Corollary B.1.2. \(\square \)
1.6 A.6 Proof of Theorem 4.1
Proof
Define \(\pi \equiv {P{[\mathcal {A}]}}\) and prove for any \(f\in \mathcal {X}_{[{t},\infty \rangle }\):
The first equality follows from the infimum’s defining greatest lower bound property and the second from Theorem 3.1.4 and \(\mathcal {A}\)’s properness.
Furthermore, by Theorem 3.1.3 we follow that \(\pi \) is cash invariant and thus by Lemma A.5 (Section A.5) the \(\inf \)-pricing function is also cash invariant. Equation (A.3) shows that its dual acceptance set, which is automatically proper by Theorem 3.1.1, equals \(\mathcal {A}^{\forall S}_{}\).
The first sentence of the second paragraph follows directly from the lower bound property of the supremum and the last sentence from Lemma A.6 (with \(g\rightarrow \inf _{\varphi _{}\in {S_{}}}\pi _{}{\left( {{f\big [\varphi _{}\big ]}}\right) }\)). \(\square \)
1.7 A.7 Proof of Theorem 4.2
Proof of Theorem 4.2
The proof follows in analogy to the proof of Theorem 4.1 (Section A.6). We are required to show for any \(f\in \mathcal {X}_{[{t},\infty \rangle }\):
To prove “\(\Longleftarrow \)”, note that for any \(n\in \mathbb {N}\) an \(a_n\in S\) with \({f\big [a_n\big ]}+\frac{1}{n}\in \mathcal {A}\) exists. Theorem 3.1.4, \(\pi \)’s cash invariance (by Theorem 3.1.3) and the upper bound property of the supremum imply \(0\le \pi _{}{\left( {{f\big [a_n\big ]}+\frac{1}{n}}\right) }\le \frac{1}{n}+\sup _{\varphi _{}\in {S_{}}}\pi _{}{\left( {{f\big [\varphi _{}\big ]}}\right) }\). The assertion then follows after taking the limit \(n\rightarrow \infty \).
For the other direction, due to cash invariance and locality (Corollary 3.3) we can apply Lemma A.6 with \(h=0\). It shows that for any \(x\in V_{t}\) an \(a\in S\) such that \(0\le \pi _{}{\left( {{f\big [a\big ]}}\right) }+x\) exists and thus by cash invariance and Theorem 3.1.4 we have \({f\big [a\big ]}+x\in \mathcal {A}\).
If the supremum is finite, the upper bound property of the supremum and Lemma A.6 (with \(h\rightarrow \sup _{\varphi _{}\in {S_{}}}\pi _{}{\left( {{f\big [\varphi _{}\big ]}}\right) }\)) ensure, that for any finite \(x\in V_{t}\), there exists some \(\psi _{}\in S\) with:
This proves the last statement of the theorem. \(\square \)
1.8 A.8 Proof of Theorem 4.3
This proof requires the following lemma.
Lemma A.7
Given a proper \(\mathcal {A}^0\) with its dual pricing function \(\pi ^0\), it holds for all \(f\in \mathcal {X}_{\varnothing }\) and t-acceptance sets \(\mathcal {A}\) with \(\mathcal {A}\cap \mathcal {X}_{\varnothing }=\mathcal {A}^0\)
Proof
By Definition 3.3 and \(\mathcal {A}\cap \mathcal {X}_{\varnothing }=\mathcal {A}^0\) it remains to show  for any \(f\in \mathcal {X}_{\varnothing }\), which follows from
for any \(f\in \mathcal {X}_{\varnothing }\), which follows from
\(\square \)
Proof of Theorem 4.3
By Theorems 4.1 and 4.2 it holds for any i with \(\tau _{i}\in \mathbf {T}_c\) and \(f\in \mathcal {X}_{[{t},\infty \rangle }\):

We can use this relation recursively until we reach \( {P{[\mathcal {D}_{n+1}]}}\left( g\right) = {P{[\mathcal {A}^0]}}\left( g\right) \), with \(g\equiv f[a_1]\dots [a_n]\). By Definition 2.3 it is easy to see that \(g\in \mathcal {X}_{\varnothing }\) and thus using \(\mathcal {A}^0\subseteq \mathcal {X}_{\varnothing }\) and Lemma A.7 we have \({P{[\mathcal {A}^0]}}(g)=\pi ^0_{}{\left( {g}\right) }\). \(\square \)
1.9 A.9 Proof of Corollary 5.1
Proof of the “if”
Define  and
and  (\(B=\{g>-\infty \}\) due to
(\(B=\{g>-\infty \}\) due to  ). Assuming Eq. (5.2) we can prove Definition 5.2 by showing
). Assuming Eq. (5.2) we can prove Definition 5.2 by showing

1) We have

The first equation uses locality (by Corollary 3.3), the second cash invariance and \(g \cdot \mathbb {1}_{B}\in L^+_{t}\) and the third  .
.
2)  is trivial.
is trivial.
3) Note that \(g\le \infty \cdot \mathbb {1}_{B}-n\) for all \(n\in \mathbb {N}\). Using monotonicity and cash invariance we have  for any n and therefore due to
for any n and therefore due to  :
:  \(\square \)
\(\square \)
Proof of the “only if”
Assume  satisfies Definition 5.2 and show
satisfies Definition 5.2 and show

The first implication follows from monotonicity of  and the second from time consistency. \(\square \)
and the second from time consistency. \(\square \)
1.10 A.10 Proof of Lemma 5.1
Proof
The first statement follows directly from the lemma below. To prove Eq. (5.1), take any \(\varphi _{}\in \Phi _{}\) and show:
The second equality follows from cash invariance of \(\pi \), \(g\in \mathcal {X}_{\langle -\infty , {t} \rangle }\) and \(g(\varphi _{})\in L^+_{t}\). \(\square \)
Lemma A.8
For any \(f\in \mathcal {X}_{\mathbf {T}}\) and cash invariant t-pricing function \(\pi \), the mapping \(\varphi _{}\mapsto \pi _{}{\left( {{f\big [ {\varphi _{}}\big |_{\langle -\infty , {t} \rangle }\big ]}}\right) }\) is an element of \(\mathcal {X}_{\mathbf {T}\cap \langle -\infty , {t} \rangle }^t\).
Proof
That \(\pi _{}{\left( {{f\big [ {\varphi _{}}\big |_{\langle -\infty , {t} \rangle }\big ]}}\right) }\) is well-defined an \(\mathcal {F}_{t}\)-measurable, follows from the definition of a t-pricing function in Sect. 3.2.
To prove the remaining properties in Definition 2.2 take \(B\in \mathcal {F}_{t}\) and \(\varphi _{},\psi _{}\in \Phi _{}\) with \(\psi _{s}{\mathop {=}\limits ^{B}}\varphi _{s}\) for all \(s\in \mathbf {T}\cap \langle -\infty , {t} \rangle \cap \mathbf {T}_d\). The required equation
follows directly from locality (Corollary 3.3) and
which in turn follows from \(f\in \mathcal {X}_{\mathbf {T}}\) and Definitions 2.3 and 2.2. \(\square \)
1.11 A.11 Proof of Theorem 5.1
Proof of time consistency of . Define
. Define  . By Lemma A.8 we have \(\pi _{s}{\left( {f}\right) }\in \mathcal {X}_{[t, s\rangle }\subseteq \mathcal {X}_{[{t},\infty \rangle }\) and thus by Definition 3.3 it remains to show
. By Lemma A.8 we have \(\pi _{s}{\left( {f}\right) }\in \mathcal {X}_{[t, s\rangle }\subseteq \mathcal {X}_{[{t},\infty \rangle }\) and thus by Definition 3.3 it remains to show  . Take any \(x\in L^-_{t}\) and prove:
. Take any \(x\in L^-_{t}\) and prove:

The two equivalences follow from Eq. (5.3) and cash invariance (Theorem 3.1.3 and Definition 3.5). \(\square \)
Proof of time consistency of . Define
. Define  and show:
and show:

The first and third equivalences follow from Definition 3.6. The second from \(\pi \)’s time consistency. \(\square \)
1.12 A.12 Proof of Theorem 5.2
This proof requires the following lemma
Lemma A.9
Take a proper  with dual
with dual  and some
and some  with dual
with dual  that satisfies
that satisfies  . Taking into account Lemma 5.1, it holds \(\pi _{t}{\left( {f}\right) }=\pi ^0_{t}{\left( {f}\right) }\) for any payoff with no decisions at or after time t.
. Taking into account Lemma 5.1, it holds \(\pi _{t}{\left( {f}\right) }=\pi ^0_{t}{\left( {f}\right) }\) for any payoff with no decisions at or after time t.
Proof
This follows directly from Lemmas A.7 and 5.1 and \({f\big [ {\varphi _{}}\big |_{\langle -\infty , {t} \rangle }\big ]}\in \mathcal {X}_{\varnothing }\) for all \(\varphi _{}\in \Phi _{}\). \(\square \)
Proof of Theorem 5.2
Define  . Show for all \(j\in \{i,\dots ,n\}\) with \(\tau _{j}\in \mathbf {T}_a\), \(\tau _{j-1}< s\le \tau _{j}\) and \(g\in \mathcal {X}_{}\) or \(s=\tau _{j-1}\) and \(g\in \mathcal {X}_{\mathcal {T}\setminus \{s\}}\):
. Show for all \(j\in \{i,\dots ,n\}\) with \(\tau _{j}\in \mathbf {T}_a\), \(\tau _{j-1}< s\le \tau _{j}\) and \(g\in \mathcal {X}_{}\) or \(s=\tau _{j-1}\) and \(g\in \mathcal {X}_{\mathcal {T}\setminus \{s\}}\):

The first equation follows from  ’s time consistency,
’s time consistency,  ’s normalization and Theorem 5.1. The second follows from Lemma A.9 with \(\pi _{\tau _{j}}{\left( {g}\right) }\in \mathcal {X}_{\langle -\infty , {s} \rangle }\) (by Lemma A.8). And the third from Remark 2.5, Eq. (5.4) and Theorem 4.2.
’s normalization and Theorem 5.1. The second follows from Lemma A.9 with \(\pi _{\tau _{j}}{\left( {g}\right) }\in \mathcal {X}_{\langle -\infty , {s} \rangle }\) (by Lemma A.8). And the third from Remark 2.5, Eq. (5.4) and Theorem 4.2.
For j with \(\tau _{j}\in \mathbf {T}_c\), Theorem 4.1 would be needed instead of Theorem 4.2 and \(\inf \) instead of \(\sup \).
To prove the theorem we start with \(s\rightarrow t\) and \(g\rightarrow f\). Then we can apply this equation recursively with \(j\rightarrow j+1\), \(s\rightarrow \tau _{j}\) due to \({g\big [a_j\big ]}\in \mathcal {X}_{\mathcal {T}\setminus \{\tau _{j}\}}\). \(\square \)
1.13 A.13 Proof of Theorem 6.1
This proof uses the abbreviation \({\varphi _{}}\cdot X=\int _0^{\infty } \varphi _{t} \cdot \mathrm {d}X_t\).
Proof
Take any \(f\in L_{\infty }\) bounded from above by some \(z\in \mathbb {R}\), define  (Definition A.1) and show:
(Definition A.1) and show:
The first equation follows from the definition of \(\mathcal {A}\). The second uses Definition 4.2 and H’s definition.
Now, define \(\mathcal {D}= {}\left\{ {x\in L^-_{0}}\;\big |\; {\exists \varphi _{}\in S: f+{\varphi _{}}\cdot X\ge x}\right\} \) and show
The “\(\le \)” inequality follows directly from the trivial \(\mathcal {D}\subseteq \mathcal {C}\). To prove the reverse equality by \(\sup \mathcal {C}\)’s least upper bound property, it remains shown that \(\sup \mathcal {D}\) is an upper bound of \(\mathcal {C}\): For any \(x\in \mathcal {C}\) and \(n\in \mathbb {N}\) it follows from Eq. (A.4) that there exists a \(\varphi _{}\) in S, such that \(f+{\varphi _{}}\cdot X\ge x-\frac{1}{n}\). Consequently, \(x-\frac{1}{n}\in \mathcal {D}\) and thus \(x-\frac{1}{n}\le \sup \mathcal {D}\), which also holds in the limit \(n\rightarrow \infty \).
We can complete the proof through: \(\pi _{}{\left( {f}\right) } = \sup \mathcal {C}= \sup \mathcal {D}=\inf _{Q\in \mathcal {M}} \mathbb {E}_{Q}\left[ f\right] \), where the first equation uses Definition 3.3 of the pricing function, the second uses Eq. (A.5), and the thrid Theorem 5.12 of Delbaen and Schachermayer (1998, p. 246) with the substitution \(g\rightarrow -f\) and the infimum-supremum duality. \(\square \)
1.14 A.14 Proof of Theorem 6.3
Proof of Theorem 6.3
As the market is complete there is a unique sigma-martingale measure \(\mathcal {M}=\{Q\}\), which removes the second supremum in Eq. (6.3).
Define the vector of portfolio weights at time t using the component-wise product of two vectors: \(q_t\equiv \psi _{t}\text {*}X_t/Y_{t}(\psi _{})\). The option’s specifications restrict the set of allowed weights to
We will need the following trivial properties of \(dY_{t}\):
Results on stochastic control (e.g. Pham 2009) entail that there exists a value function v, with \(v(0,Y_{0})= \sup _{\psi _{}\in R}\mathbb {E}_{Q}\left[ (Y_T(\psi _{})-M)^+\right] \), that satisfies the following Hamilton-Jacobi-Bellman equation. For all \(t\in [0,T\rangle \) and \(y\in [{0},\infty \rangle \),
To prove the first statement of the theorem, we show that

satisfies the HJB equation. The terminal condition is trivial. To prove the differential equation, we subtract from it the Feynman-Kac equation for v, yielding:
The covariance matrix \(\Sigma \) is positive semi-definite and due to the convexity of the call price, it holds \(0\le \frac{\partial ^2 v}{\partial y^2}\). Therefore, the quadratic form on the l.h.s is convex (Rockafellar 1970, Theorem 4.5) and bounded on any bounded set. By Rockafellar (1970, Corollary 32.3.4 and Theorem 19.1) the supremum is attained at one of \(J\)’s extreme points. Consequently, it is given by the largest diagonal element of \(\Sigma \), i.e. \(\Sigma ^{kk}\). This also proves the second statement of the theorem.
For the third statement it is enough to look at the random part of the differential of the price:

\(\square \)
1.15 A.15 Proof of Theorem 6.4
Proof of Theorem 6.4
Let \(u_i\equiv \sup _{\psi _{}\in S_{i-1}} -{\eta _{\tau _{i}}{\left( {-f}\right) }\big [\psi _{}\big ]}\) denote the ask price at time \(s_{i-1}\) and show:

The first two equations follow from Theorem 6.2 and Eq. (6.2). The third follows from the \(\inf /\sup \)-duality and the definition of \(u_{i+1}\). After applying Lemma 4.1 of Gerer and Dorfleitner (2018) to both decisions in Eq. (A.8), it can be easily checked by comparing the right hand sides of Eqs. (A.7) and (A.8) with Eqs. (6.5) and (6.6) that \(g_i(h ,X_{\tau _{i}},Y_{\tau _{i}}(\psi _{}))= {u_i\big [\tau _{i-1}\mapsto h\big ]}(\psi _{})\). \(\square \)
Appendix B Mathematical theorems
Theorem B.1
(Existence of the essential supremum) Suppose that the measure space \((\Omega , {\mathcal {F}},\mu )\) is \(\sigma \)-finite. Then the essential supremum of a collection \({\mathcal {S}}\) of measurable functions into the set \(\overline{\mathbb {R}}\) exists. Furthermore, if \({\mathcal {S}}\) is nonempty then a sequence \((f_n)_{n\in \mathbb {N}}\) in \({\mathcal {S}}\) exists such that its pointwise supremum equals (almost surely) the essential supremum of \({\mathcal {S}}\).
Proof
See Chapter V.18 in Doob (1994). \(\square \)
Corollary B.1
(Properties of conditionally almost sure). Let \({\mathbf {D}}\) be a countable collection of sets with positive probability and \(A,B\in {\mathbf {D}}\).
- (1)
\( \mathbb {P}{\left( B\setminus C\right) }=0 \Longleftrightarrow \mathbb {P}{\left( C \big |B\right) }=1\)
- (2)
\( \left( \forall A\in {\mathbf {D}}: \mathbb {P}{\left( C \big |A\right) }=1 \right) \Longrightarrow \mathbb {P}{\left( C \big |\bigcup {\mathbf {D}}\right) }=1\)
- (3)
\(\mathbb {P}{\left( B \big |A\right) }=\mathbb {P}{\left( C \big |B\right) }=1 \Longrightarrow \mathbb {P}{\left( C \big |A\right) }=1\)
Proof of Corollary B.1.1
The statement follows from:
Using Corollaries B.2.1 and B.2.2, additivity of \(\mathbb {P}\) for disjoint sets and the definition of conditional probability. \(\square \)
Proof of Corollary B.1.2
By Corollary B.1.1 it follows from the antecedent for any \(A\in {\mathbf {D}}\): \(\mathbb {P}{\left( A\setminus C\right) }=0\). By using Corollary B.2.3 with subadditivity of \(\mathbb {P}\) we can follow \(\mathbb {P}{\left( \left( \bigcup {\mathbf {D}}\right) \setminus C\right) }=0\), which again with Corollary B.1.1 yields the result. \(\square \)
Proof of Corollary B.1.3
Using Corollary B.1.1 we can follow from the assumption: \(\mathbb {P}{\left( A\setminus B\right) }=\mathbb {P}{\left( B\setminus C\right) }=0\). By using Corollary B.2.4 with monotonicity and subadditivity of \(\mathbb {P}\), it follows \(\mathbb {P}{\left( A\setminus C\right) }=0\), which again with Corollary B.1.1 yields the result. \(\square \)
Corollary B.2
(Properties of sets). For all sets A, B, C and collections of sets \({\mathbf {D}}\), it holds: (1) \((A\setminus B)\cap (A\cap B)=\varnothing \), (2) \((A\setminus B)\cup (A\cap B)=A\), (3) \(\bigcup _{E\in {\mathbf {D}}}(E\setminus A) = \left( \bigcup {\mathbf {D}} \right) \setminus A\), and (4) \(A\setminus C\subseteq (A\setminus B) \cup (B\setminus C)\).
The proofs are left to the reader \(\square \)
Corollary B.3
(Convergence in probability preserves equality almost surely). For any set \(B\in \mathcal {F}_{\infty }\) and two sequences of random variables \((f_n)_{n\in \mathbb {N}}\) and \((g_n)_{n\in \mathbb {N}}\) that converge in probability to f and g, respectively, it holds \(f{\mathop {=}\limits ^{B}}g\), if \(B\subseteq \{f_n= g_n\}\).
Proof
Simple set manipulations yield:
Consequently, by Corollary B.1.1 and monotonicity of \(\mathbb {P}\), \(f{\mathop {=}\limits ^{B}}g\) is equivalent to
We prove Eq. (B.1) in two steps. First show for any \(m,n\in \mathbb {N}\):
The first “\(\subseteq \)” uses \(B\subseteq \{f-g=(f-f_n)-(g-g_n)\}\), together with the triangle inequality. By definition of convergence in probability we can then prove:
\(\square \)
Corollary B.4
(Integration preserves equality almost surely). For any set \(B\in \mathcal {F}_{\infty }\), integrator X and integrands \(a_1,b_2\), it holds \(\int a_1\; \mathrm {d}X{\mathop {=}\limits ^{B}}\int a_2\; \mathrm {d}X\), if \(B\subseteq \{a_1=a_2\}\).
Proof
Let \((a_i^n)_{n<\infty }\) be a sequence of simple integrands approximating \(a_i\). We can choose them such that \(a_1^n=a_2^n\) on B for all n. Define \(A_i\equiv \int _t^T a_i\mathrm {d}X\equiv \text {p}\lim _{n\rightarrow \infty } A^n_i\) (limit in probability) with \(A^n_i\equiv \int _t^T a^n_i \mathrm {d}X\). These integrals of simple integrands are defined path-wise and thus \(B\subseteq \{A_1^n=A_2^n\}\) for each n. By Corollary B.3 it holds \(P(A_1=A_2|B)=1\). \(\square \)
Rights and permissions
About this article
Cite this article
Dorfleitner, G., Gerer, J. Time consistent pricing of options with embedded decisions. Rev Deriv Res 23, 85–119 (2020). https://doi.org/10.1007/s11147-019-09158-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11147-019-09158-9



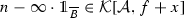 and the upper bound property of the supremum g directly implies
and the upper bound property of the supremum g directly implies 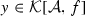 and define
and define  . The upper bound property of the supremum g and z’s definition yield
. The upper bound property of the supremum g and z’s definition yield 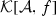 . By its definition, h has to be the least upper bound of this set, thus
. By its definition, h has to be the least upper bound of this set, thus 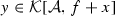 it holds
it holds 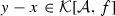 . The upper bound property of the supremum h entails
. The upper bound property of the supremum h entails 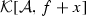 . By its definition, g has to be the least upper bound of the assertion follows.
. By its definition, g has to be the least upper bound of the assertion follows.