Abstract
We consider the valuation of collateralized derivative contracts such as interest rate swaps or forward FX contracts. We allow for posting securities or cash in different currencies. In the latter case, we focus on using overnight index rates on the interbank market. Using time varying haircuts, we provide an intuitive way to derive the basic discounting results, keeping in line with the most standard theoretical and market views. In a number of cases associated with margining with major central counterparties, pricing rules for collateralized trades remain linear, thus the use of (multiple) discount curves. We also show how to deal with partial collateralization, involving haircuts, asymmetric CSA, counterparty risk and funding costs. We therefore intend to provide a unified view. Mathematical or legal details are not dealt with and we privilege financial insights and easy to grasp concepts and tools.
Similar content being viewed by others
Notes
One could think of Treasury GC as a proxy.
In such a framework, the claim on default for a repo contract would differ from the claim associated with other OTC trades, such as interest rate swaps. We may relate cancellation to fails-to-deliver without penalty.
Default times of the counterparties are then assumed to be totally inaccessible. \(\lambda (t)\) is here the intensity of the first to default-time.
If the bond \(A\) is special, the corresponding repo rate is lower.
\(\frac{V(s)}{A(s)}\times A\left( {s+ds} \right) \) can be seen as the value of the collateral account, prior to the variation margin payment.
Define \(\zeta (s)=V(s)e^{-\int \nolimits _t^s {r(u)du} }\). \(d\zeta (s)=e^{-\int \nolimits _t^s {r(u)du} }dV(s)-r(s)\zeta (s)ds\). Thus, the present value of the collateral cash-flows equals: \(E_t^{Q^{\beta }} \left[ {\zeta (t)+\int \nolimits _t^T {d\zeta (s)+\left( {r(s)ds-\frac{dA(s)}{A(s)}} \right) \zeta (s)ds} -\zeta (T)} \right] \), which can be simplified as: \(E_t^{Q^{\beta }} \left[ {\int \nolimits _t^T {\left( {r(s)ds-\frac{dA(s)}{A(s)}} \right) V(s)e^{-\int \nolimits _t^s {r(u)du} }} } \right] \), which leads to the stated expression.
This illustrative example, where
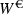 is a Brownian term independent of other involved quantities and the volatility is assumed to be constant can readily be extended.
is a Brownian term independent of other involved quantities and the volatility is assumed to be constant can readily be extended.“Risk-free” means that an uncollateralized swap curve or overnight rates in the interbank market are to be used in the discounting process. While this can be understood from an historical perspective, when the default component in effective fed funds rates or EONIA was neglected or when swaps contracts were deemed default-free and CVA/DVA effects could be neglected, the market terminology is misleading. “Recovery of swap”, similarly to “recovery of Treasury” would be more explicit.
Actually, if \(R+\lambda (1-\delta )\ge r_A \), the generator is super-additive and the price functional, associated with an asymmetric CSA, too. Conversely, if \(R+\lambda (1-\delta )\le r_A \), the generator is sub-additive and the price functional is sub-additive and thus convex, thanks to positive homogeneity. Concavity or convexity are useful properties, since when the price functional is not differentiable with respect to terminal payoff, we can still consider a non-empty subdifferential and deal with left and right Gâteaux derivatives, which stills allows for simple one-sided first order expansions.
When \(p=0\), the first-order expansion is readily derived and leads to different left and right derivatives.
References
Afonso, G., Kovner, A., & Schoar, A. (2011). Stressed not frozen: The federal funds market in the financial crisis. Journal of Finance, 66(4), 1109–1139.
Barden, P. (2009). Equity forward prices in the presence of funding spreads. In ICBI conference, Rome.
Bergman, Y. (1995). Option pricing with differential interest rates. Review of Financial Studies, 8(2), 475–500.
Bianchetti, M. (2010). Two curves, one price. Risk magazine, 23(8), 66–72.
Bielecki, T., Cialenco, I., & Iyigunler, I. (2011). Counterparty risk and the impact of collateralization in CDS contracts, working paper, Illinois Institute of Management.
Brigo, D., & Morini, M. (2010). Dangers of bilateral counterparty risk: The fundamental impact of closeout conventions, working paper, department of mathematics, King’s College.
Brigo, D., Capponi, A., Pallavicini, A., & Papatheodorou, V. (2011). Collateral margining in arbitrage-free counterparty valuation adjustment including re-hypothecation and netting, working paper, department of mathematics, King’s College.
Burgard, C., & Kjaer, M. (2011). Partial differential equation representations of derivatives with bilateral counterparty risk and funding costs. The Journal of Credit Risk, 7(3), 75–93.
Castagna, A. (2011). Funding, liquidity, credit and counterparty risk: Links and implications, working paper.
Castagna, A. (2012). Pricing of collateralized derivatives contracts when more than one currency are involved: Liquidity and funding value adjustments, working paper.
Castagna, A. (2013). Pricing of derivatives contracts under collateral agreements: Liquidity and funding value adjustments, working paper.
Cesari, G., Aquilina, J., Charpillon, N., Filipovic, Z., Lee, G., & Manda, I. (2010). Modelling, pricing, and hedging counterparty credit exposure, a technical guide. Springer.
Cox, J. C., Ingersoll, J, Jr, & Ross, S. A. (1981). The relation between forward prices and futures prices. Journal of Financial Economics, 9(4), 321–346.
Crépey, S. (2011). A BSDE approach to counterparty risk under funding constraints, working paper, University of Evry.
Crépey, S. (2012a). Bilateral counterparty risk under funding constraints part I: Pricing. Mathematical Finance. doi:10.1111/mafi.12004.
Crépey, S. (2012b). Bilateral counterparty risk under funding constraints part II: CVA. Mathematical Finance. doi:10.1111/mafi.12005.
Cvitanić, J., & Karatzas, I. (1993). Hedging contingent claims with constrained portfolios. Annals of Applied Probability, 3, 652–681.
Duffie, D. (1989). Futures markets. Englewood Cliffs: Prentice Hall.
Duffie, D., & Huang, M. (1996). Swaps rates and credit quality. Journal of Finance, 51(3), 921–948.
Duffie, D., Schroder, M., & Skiadas, C. (1996). Recursive valuation of defaultable securities and the timing of resolution of uncertainty. Annals of Applied Probability, 6(4), 1075–1090.
El Karoui, N., Peng, S., & Quenez, M.-C. (1997). Backward stochastic differential equations in finance. Mathematical Finance, 7(1), 1–71.
Fries, C. P. (2010). Discounting revisited. Valuation under funding costs, counterparty risk and collateralization, working paper.
Fujii, M., Shimada, Y., & Takahashi, A. (2009). A survey on modeling and analysis of basis spreads, CARF working paper.
Fujii, M., Shimada, Y., & Takahashi, A. (2009). A market model of interest rates with dynamic basis spreads in the presence of collateral and multiple currencies, CIRJE discussion paper.
Fujii, M., Shimada, Y., & Takahashi, A. (2010). A note on construction of multiple swap curves with and without collateral, working paper, University of Tokyo.
Fujii, M., & Takahashi, A. (2011). Choice of collateral currency. Risk, 24(1), 120–125.
Fujii, M., & Takahashi, A. (2011). Collateralized CDS and default dependence, working paper, University of Tokyo.
Fujii, M., & Takahashi, A. (2012). Perturbative expansion techniques for non-linear FBSDEs with interacting particle method, working paper, University of Tokyo.
Fujii, M., & Takahashi, A. (2013). Derivative pricing under asymmetric and imperfect collateralization and CVA. Quantitative Finance, 13(5), 749–768.
Geman, H., El Karoui, N., & Rochet, J.-C. (1995). Changes of numéraire, changes of probability measure and option pricing. Journal of Applied Probability, 32(2), 443–458.
Henrard, M. (2009). The irony in the derivatives discounting part II: The crisis, working paper, Dexia Bank, Brussels.
Henry-Labordère, P. (2012). Cutting CVA’s complexity. RISK, 25(7), 67–73.
Hull, J., & White, A. (2012). The FVA debate. Risk 25th anniversary issue, July 2012.
ISDA - International Swap and Derivatives Association (2010). Best practices for the OTC derivatives collateral process, technical document, June 30, 2010.
Johannes, M., & Sundaresan, S. (2007). The impact of collateralization on swap rates. Journal of Finance, 62(1), 383–410.
Kan, Y. H. & Pedersen, C. (2011). The impact of margin interest on the valuation of credit default swaps, working paper, Columbia University and Barclays Capital.
Kenyon, C. (2010). Post-shock short rate pricing. Risk, 23(11), 83–87.
Kijima, M., Tanaka, K., & Wong, T. (2009). A multi-quality model of interest rates. Quantitative Finance, 9(2), 133–145.
Korn, R. (1992). Option pricing in a model with a higher interest rate for borrowing than for lending, working paper.
Macey, G. (2011). Pricing with standard CSA defined by currency buckets, working paper, HSBC.
Mercurio, F. (2009). Interest rates and the credit crunch: New formulas and market models, working paper.
Mercurio, F. (2010a). Modern LIBOR market models: Using different curves for projecting rates and for discounting. International Journal of Theoretical and Applied Finance, 13, 1–25.
Mercurio, F. (2010b). A LIBOR market model with stochastic basis. Available at http://ssrn.com/abstract=1583081.
Morini, M., & Prampolini, A. (2010). Risky funding: A unified framework for counterparty and liquidity charges, working paper, Banca IMI.
Pallavicini, A., Perini, D., & Brigo, D. (2012). Funding, collateral and hedging: Uncovering the mechanics and the subtleties of funding valuation adjustments, working paper.
Peng, S. (2004). Nonlinear expectations, nonlinear evaluations and risk measures. Stochastic methods in finance. Lecture notes in mathematics, vol. 1856. Springer (pp. 243–256).
Peng, S. (2006). Modelling derivatives pricing mechanisms with their generating function, working paper.
Piterbarg, V. (2010). Funding beyond discounting: Collateral agreements and derivatives pricing. Risk Magazine, 23(2), 97–102.
Piterbarg, V. (2012). Cooking with collateral. Risk, 25(8), 58–63.
Schroder, M. (1999). Change of numeraire for pricing futures, forwards, and options. The Review of Financial Studies, 12(5), 1143–1163.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors are indebted to many people within the Fixed Income, Treasury and ALM departments of BNP Paribas. They thank participants to the FEBS—Labex RéFi conference on Financial Regulation & Systemic Risk, The French Banking Association “Rencontre des Chaires” and the Sorbonne Finance seminars in Paris and to the French Finance Association conference in Lyon for helpful comments. They also thank the referee for numerous and helpful remarks. The authors take the sole responsibility for any error within this document. Jean-Paul Laurent acknowledges support from the Fixed Income and Research Strategies Team (FIRST) of BNP Paribas and from the BNP Paribas Cardif chair “management de la modélisation”. The views expressed in this paper are authors own.
Appendix: Convexity adjustments
Appendix: Convexity adjustments
\(E_t^{Q_T^B } \left[ {X(T)} \right] ={E_t^{Q_T^A } \left[ {\frac{dQ_T^B }{dQ_T^A }X(T)} \right] }/{E_t^{Q_T^A } \left[ {\frac{dQ_T^B }{dQ_T^A }} \right] }\). Thus,
It can easily be shown that: \(E_t^{Q_T^A } \left[ {\exp \left( {-\int \limits _t^T {\left( {r_B -r_A } \right) (s)ds} } \right) } \right] =\frac{B_B \left( {t,T} \right) }{B_A \left( {t,T} \right) }\). Thus,
which involves a covariance term between the payoff \(X(T)\) and the stochastic spread terms \(r_B -r_A \).
Let us consider the special case associated with a Brownian filtration. Since \(\xi _T^A \) is a positive \(Q^{\beta }\)- martingale, we have: \(\frac{d\xi _T^A (t)}{\xi _T^A (t)}=\sigma _A \left( {t,T} \right) dW_A^\beta (t),\, \xi _T^A (t)=\varepsilon \left( {\int \nolimits _0^t {\sigma _A \left( {s,T} \right) dW_A^\beta (s)} } \right) \) where \(W_A^\beta \) is a \(Q^{\beta }\)- Brownian motion. Since \(\xi _T^{B,A} \left( t \right) =\frac{\xi _T^B \left( t \right) }{\xi _T^A \left( t \right) }\) is a \(Q_T^A \) - martingale and using Girsanov theorem, we have:
where \(W_B^{A,T},W_A^{A,T} \) are \(Q_T^A \) - Brownian motions.
\(\sigma _A \left( {t,T} \right) \) is related to collateralized discount bond prices since from \(B_A \left( {t,T} \right) =B_A \left( {0,T} \right) \xi _T^A \left( t \right) \exp \left( {\int \limits _0^t {r_A (s)ds} } \right) \), we get \(\frac{dB_A (t,T)}{B_A (t,T)}=r_A (t)dt+\sigma _A \left( {t,T} \right) dW_A^\beta (t)\).
Let us assume that \(X(T)>0\), thus \(p_{A,T} (t)>0\). \(\frac{dp_{A,T} (t)}{p_{A,T} (t)}=\sigma _X \left( {t,T} \right) dW_A^{X,T} (t)\), where \(W_A^{X,T}\) is a \(Q_T^A \)- martingale and \(X(T)\!=\!E_t^{Q_T^A } \left[ {X(T)} \right] \varepsilon \left( {\int \limits _t^T \!{\sigma _X \left( {s,T} \right) dW_A^{X,T} (s)} } \right) \). This leads to the following relation between forward prices under collaterals \(A,B\):
Rights and permissions
About this article
Cite this article
Laurent, JP., Amzelek, P. & Bonnaud, J. An overview of the valuation of collateralized derivative contracts. Rev Deriv Res 17, 261–286 (2014). https://doi.org/10.1007/s11147-014-9098-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11147-014-9098-8





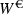 is a Brownian term independent of other involved quantities and the volatility is assumed to be constant can readily be extended.
is a Brownian term independent of other involved quantities and the volatility is assumed to be constant can readily be extended.