Estimating Census Tract House Price Indexes: A New Spatial Dynamic Factor Approach

Abstract

Geographically and temporally granular housing price indexes are difficult to construct. Data sparseness, in particular, is a limiting factor in their construction. A novel application of a spatial dynamic factor model allows for the construction of census tract level indexes on a quarterly basis while accommodating sparse data. Specifically, we augment the repeat sales model with a spatial dynamic factor model where loadings on latent trends are allowed to follow a spatial random walk thus capturing useful information from similar neighboring markets. The resulting indexes display less noise than similarly constructed non-spatial indexes and replicate indexes from the traditional repeat sales model in tracts where sufficient numbers of repeat sales pairs are available. The granularity and frequency of our indexes is highly useful for policymakers, homeowners, banks and investors.

Introduction

The most accessible and dominant way to track real estate market movements is through geographically coarse indexes. Both publicly available and proprietary indexes range in sub-national geographies from the zip code level to Core Based Statistical Area (CBSA).¹ Recently, the Federal Housing Finance Agency (FHFA) began publishing census tract level housing price indexes (Bogin et al., 2019; FHFA, 2022). These indexes—currently the smallest geography publicly available—provide researchers, policymakers, and investors a better understanding of an integral component of housing price: within-city location. The very nature of a building’s relationship with the local environment implies that coarse indexes at larger geographies may aggregate over high levels of local spatial variation. Indexes that better account for local spatial heterogeneity provide a more accurate representation of the space and asset market the properties are traded in. Thus, they are potentially more informative. The cost of this information gain, however, is an index prone to noise given the reduction in observations (Bogin et al., 2019; Constantinescu & Francke, 2013; Ren et al., 2017).

What kind of information do we lose when constructing indexes at higher levels of geography? Even indexes at the zip code level are at risk of aggregation bias when important and potentially highly variable local nonmarket interactions are spatially aggregated. Local nonmarket interactions are predominately concerned with access—access to employment locations, consumption amenities, natural amenities/green space—and perceived quality and desirability of nearby housing and neighbor characteristics. A household’s willingness to pay for access to these ‘housing externalities’ or ‘neighborhood consumption externalities’ is capitalized into land values and thus reflected in transaction prices (Guerrieri et al., 2013; Rossi-Hansberg et al., 2010). Rossi-Hansberg et al. (2010), among others, demonstrate that the influence of such externalities declines with distance, further emphasizing the importance of understanding the local spatial context.

The production of indexes over fine geographies is highly desirable from both a policy and investment perspective. For policy, spatially and temporally disaggregated house price indexes are an important component in the identification of neighborhoods at risk of decline or gentrification. Existing measures of gentrification in particular tend to rely on census data or surveys with limited geographic coverage (Ellen & O’Regan, 2011). These sources cannot provide fine geographic data at desirable temporal intervals. Thus, measures constructed from such datasets may fail to provide a timely or spatially accurate understanding of changing housing and resident characteristics. From the investment perspective, granular indexes can contribute to more well-informed real estate investment decisions and portfolio diversification strategies. Differences in price dynamics across geographic areas can come from both the capital and space markets, with the latter being more important (Geltner & Mei, 1995; Geltner et al., 2014).

Subsequently, there has been an increased interest in producing indexes that track real estate market movements on a more granular level. Zillow and Case-Shiller both produce zip code level indexes with Zillow also producing an index at a ‘neighborhood’ level.² As Bogin et al. (2019) point out, the Zillow index is a smoothed value-based index that by construction confounds price and quantity changes unless one assumes the quantity of housing services remains unchanged over time. While the Zillow index is publicly available, the Case-Shiller index is a repeat-sales based proprietary index making it costly to obtain and thus limits its usefulness for policymakers and researchers. Further, the Case-Shiller index only considers the single-family submarket and combines both purchases and refinances. As mentioned, FHFA provides the only publicly available census tract level index using the methodology outlined in Bogin et al. (2019). It is constructed using a weighted repeat sales model based on purchases and refinance transactions obtained from a set of proprietary mortgage transactions. This index is limited to the single-family submarket and to tracts with 100 or more repeat sales. It is reported on an annual basis.

In this paper, we propose a novel application of a spatial dynamic factor model in the construction of census tract level housing price indexes (Gamerman et al., 2008; Lopes et al., 2011; Strickland et al., 2011). The use of this method improves upon a number of shortcomings of existing public and proprietary indexes. Namely, we demonstrate the ability to construct a spatially and temporally granular index in the presence of sparse data. Construction of such granular indexes is not straightforward. Real properties are infrequently traded and tend to be heterogeneous (Bhattacharjee et al., 2016; Deng et al., 2012; Schwann, 1998). These characteristics produce a trade-off: higher granularity is more informative, but ceteris paribus also more noisy, and thus less useful (Geltner & Ling, 2006). Reducing noise via the common solution of ‘smoothing’ indexes ex-post introduces new issues which can be especially detrimental when indexes are used for portfolio allocation purposes (Geltner, 1991, 1993). Naive ex-post smoothing procedures like moving averages, considerably reduce the volatility of index returns and thus underestimate real estate risk. Moreover, ex-post smoothing does not take into account the variances and co-variances of estimated price indexes. The variance differs over time as the number of sales is time-varying, specifically in small samples. If this is not taken into account, index returns in periods with few observations are given too much weight in the smoothing procedure. Additionally, geographically granular indexes may also require a trade-off in the time dimension, i.e. constructing higher time dimension indexes in order to capture a sufficient number of observations (Bogin et al., 2019). From a policy and investor perspective, this may be undesirable.

As an alternative to ex-post smoothing, extant literature on real estate price indexing focuses on structural time series models. In structural time series models, time fixed effects from repeat sales and/or hedonic models are replaced with a stochastic trend. In general, the structural time series model consists of two sets of equations. In the repeat sales model, the first equation (called the ‘measurement equation’) relates the individual property log returns to changes in unobserved log price index levels. The second equation is the transition equation which specifies the structure of unobserved time trends (indexes). Early structural time series work assumes price innovations follow a random walk with drift (Goetzmann, 1992). Even though such structural time series models can quite easily handle low frequency data (for example, Bollerslev et al. (2016) and Francke and Van de Minne (2022) estimate daily real estate indexes), it is unclear how effectively they can be used to estimate spatially correlated indexes. Later contributions to the methodology that consider a spatial element augment the hedonic and repeat sales models with sub-cluster trends (Francke & De Vos, 2000; Francke & van de Minne, 2017). Ren et al. (2017) add information via neighborhood cluster to deal with low observations counts. Specifically, neighborhoods are clustered based on similarities in the neighborhood price dynamics and indexes depend on the cluster to which they are a part of.

Our use of a spatial dynamic factor model in the construction of housing price indexes allows for efficient and reliable estimation in the face of data sparseness. To carry out this methodology, we assume that every submarket (census tract, m = 1,…,M) index is a linear combination of K latent (sub)trends, where K <  < M. The latent trends (K × T), and the loadings for each submarket on said latent trends (M × K) are estimated from the data. Identification of such a dynamic factor model is challenging but also well established in extant literature (see for example Geweke & Zhou, 1996; Stock & Watson, 2002, 2005; Bernanke et al., 2005).

The methodology demonstrated here makes a number of distinct contributions to existing price indexing literature. To our knowledge, this is the first paper to use a linear combination of dynamic factors and loadings to estimate price indexes and the first paper to use a dynamic factor model on cross-sectional (micro) data. We also allow loadings on indexes to be spatially related via a spatial random walk as we expect that the index of submarket m is similar to the index of neighboring submarkets (Francke & Van de Minne, 2021). This provides a parsimonious decomposition of the spatio-temporal dynamics: the spatial structure is modeled by the loading matrix and the temporal dynamics by the factors. Even though such spatial dynamic factor models have existed since Gamerman et al. (2008), this is the first paper that uses this structure to estimate indexes. Our motivation for using such a setup is that real estate markets tend to co-move (Geltner et al., 2014; van de Minne et al., 2020). Additionally, the modelling flexibility gained via the use of a spatial random walk improves on previous, more ad hoc, methodologies (Larson & Contat, 2022).

Using 15 thousand condominium repeat sales in Manhattan between 2006 and 2019, we estimate 218 census tract level indexes on a quarterly basis. The average number of repeat sales per tract is less than 70, with some tracts having only one observation. Results indicate that our methodology produces realistic and robust indexes for both small and large sample size tracts. Robustness checks compare the proposed methodology against a number of existing methodologies within three sample size settings—low, medium, and high count. We compare against a standard repeat sales model (Bailey et al., 1963), locally weighted repeat sales model (McMillen, 2003), a standard repeat sales model with a random walk, and a standard repeat sales model with a local linear trend (Francke, 2010). In tracts with high counts of transactions, all indexes coalesce to a large degree and indicate our methodology is not mis-specified. However, we see the benefits of spatial dynamic factor repeat sales model in the construction of tracts without a substantial amount of observations. Notably, and as expected (Francke, 2010), the spatial dynamic factor model (SFDM) repeat sales indexes are less noisy and stable for different values of K latent trends, especially for K > 2.

This paper speaks to multiple strands in existing literature. These strands include the growing field of structural time-series repeat sales and hedonic price models, where time fixed effects are replaced by a stochastic trend specification (Bollerslev et al., 2016; Francke & van de Minne, 2017, among others) and the literature of spatial dependencies in real estate prices. For example, Bailey et al. (2016), Bhattacharjee et al. (2016), Pace et al. (1998), and Francke and Van de Minne (2021) use spatial relations to improve the efficiency of hedonic models. Larson and Contat (2022), in their construction of submarket level housing price indexes, aggregate low observation count census tracts with neighboring tracts to create supertracts. A related literature uses Kriging as a tool for imputing missing price data (Basu & Thibodeau, 1998), where granular indexes can be constructed from the imputed values (Davis et al., 2021; Hill & Melser, 2008).

The paper is structured as follows. Section 2 provides the methodology, which is followed by a discussion of the data and descriptive statistics in Sect. 3. The results are given in Sect. 4 with conclusions provided in Sect. 5.

Methodology

Hedonic and Repeat Sales Methodology

Real estate price indexing evolved around two related methodologies: hedonics (Haas, 1922) and repeat sales (Bailey et al., 1963). The hedonic pricing model assumes that the price of a commodity is composed by aggregating the individual contributions of each of its characteristics (Malpezzi, 2002). Formally:

$$\mathrm{ln}{P}_{it}={\upmu }_{t}+{x}_{it}^{^{\prime}}\upbeta +{\upepsilon }_{it}$$

(1)

where P are transaction prices of property i = 1,…,N at time t = 1,…,T (quarters), with characteristics x.³ The coefficients of the covariates on prices are denoted by β and are estimated from the data. The (log) price index is found by estimating a set of time fixed effects, denoted by µ_t in Eq. (1). The residuals are provided by ϵ, which is typically assumed to be an independent normally distributed random variable with mean zero and variance σ_ϵ².

In the repeat sales methodology we replace the covariates with a property fixed effect. This has two benefits—the first being a practical one. Some datasets simply do not contain (enough) characteristics to run a basic hedonic model. Secondly, property fixed effects account for time-invariant unobserved heterogeneity (Francke and Van de Minne, 2021). However, there are also downsides to the repeat sales model. First, (repeat) sales can be a non-random selection of the entire property stock which can generate sample selection bias, see Gatzlaff and Haurin (1997) and Hwang and Quigley (2004). Only properties that sell more than once can be used to identify the property fixed effects. ‘Winners’ tend to sell more often as compared to ‘losers’, meaning that repeat sales might overestimate returns. Second, an assumption that the property did not change between the buy and sale must be made.⁴ The repeat sales model is as follows:

$$\mathrm{ln}{P}_{it}={\upmu }_{t}+{\updelta }_{i}+{\upepsilon }_{it}$$

(2)

where δ_i is the aforementioned property level fixed effect. It should be noted that the repeat sales model is typically estimated in ‘differences’, see Francke and van de Minne (2017). By subtracting the (log) price of the sell with the (log) price of the buy (and differencing the time dummies), the property fixed effect cancels out. This is given by (Bailey et al., 1963)

$$\mathrm{ln}{P}_{it}-\mathrm{ln}{P}_{is}={\upmu }_{t}-{\upmu }_{s}+{\upepsilon }_{it}-{\upepsilon }_{is}$$

(3)

where t is the time of sale and s is the time of buy, and µ₁ = 0 for identification reasons. Thus, P_it is the price at the time of sale and P_is is the price at the time of buy. Both the standard hedonic and repeat sales model can be estimated using ordinary least squares (OLS). We focus on the repeat sales methodology in this paper. The main reason for this is the earlier mentioned practical one: we do not observe the necessary covariates for a hedonic model within our dataset (Sect. 3). More crucially, however, it should be noted that our proposed time series structure can be applied to both methodologies and thus allows for the consideration of time-varying characteristics.

Spatial Dynamic Factor Model

The standard repeat sales methodology is not suited for small granular markets, see Guo et al. (2014) and van de Minne et al. (2020) among others. The estimate of µ_t is sensitive to cross-sectional transaction price noise, in particular in small samples when the number of transactions per period is low. This happens, for example, with highly granular price indexes, high frequency indexes, and/or in the case of severe outliers. The resulting price indexes may then become very volatile (Francke, 2010), and/or are subject to heavy revisions (Wang & Zorn, 1997). As a result, research has opted to lower the frequency of the indexes (for example yearly instead of quarterly, Geltner & Ling, 2006; Wang & Zorn, 1997), or group multiple areas into one (Larson & Contat, 2022). However, in doing so, resulting indexes become less informative in many applications.

One solution is found via structural time series models where the time fixed effects (µ_t) are replaced by a stochastic trend specification. Within a structural time series model relevant unobserved components like trend, cyclical and seasonal components are specified explicitly. In contrast to the time fixed effects approach, the structural time series model estimates the price index level or return for period t on information in this period, as well as on information in preceding and subsequent periods. This means that even for particular time periods where few observations are available, an estimate of the price level can be obtained. For example, one can assume that prices evolve around a random walk, given by

$${\upmu }_{t}\sim \mathcal{N}\left({\upmu }_{t-1},{\upsigma }_{\upmu }^{2}\right),\hspace{0.17em}t=2,\dots ,T,\hspace{0.17em}{\upmu }_{1}=0$$

(4)

If the estimated hyperparameter ${\upsigma }_{\upmu }^{2}\to$ ∞, the model is similar to a standard time fixed effects setup but will result in smoother indexes otherwise. This simple model can be estimated using empirical Bayesian methods (Francke, 2010; Goetzmann, 1992), or by full Bayesian inference (Francke & van de Minne, 2017; van de Minne et al., 2020). Such indexes are not impacted by the choice of frequency as much as the traditional fixed effects approach is. In fact, recent research has shown how to estimate daily real estate indexes using such models (Bollerslev et al., 2016; Francke & Van de Minne, 2022). In this paper, we consider a quarterly frequency as this time dimension is more relevant for housing (buying and selling homes takes multiple months), and for computational efficiency reasons.⁵

Instead of estimating such models per market, it is more efficient to pool all data and estimate subtrends per location (like census tracts) when estimating local price indexes. Francke and van de Minne (2017) show how a structural time series repeat sales framework can contain both a common trend as well as locational subtrends. The estimated subtrends are (log) deviations from the common trend. However, there are two issues with this setup that we aim to improve on in this paper: computational efficiency and spatial correlation in price dynamics. The computational power needed to estimate many trends can become infeasible. For example, in our present application we are interested in computing 218 census tract trends. Assuming 80 quarters (20 years) that would result in 80*218 = 17,440 parameters to be estimated. In such cases it is not uncommon to have less observations compared to the parameters to estimate.

In order to ameliorate the computational burden, we specify the census tract trends as linear combinations of lower dimensional latent dynamic factors, a non-spatial dynamic factor model (NSDFM). The NSDFM repeat sales model is as follows:

$$\begin{array}{c}\mathrm{ln}{P}_{itm}-\mathrm{ln}{P}_{ism}={\upmu }_{t} -{\upmu }_{s}+{\sum }_{k=1}^{K}{\Gamma }_{mk}\left({F}_{tk}-{F}_{sk}\right)+{\upepsilon }_{itm} - {\upepsilon }_{ism}\\ {\upmu }_{t}\sim \mathcal{N}\left({\upmu }_{t-1},{\upsigma }_{\upmu }^{2}\right), t= 2,\dots ,T, {\mu }_{1}=0\\ {\mathrm{F}}_{\mathrm{t},\mathrm{k}}\sim \mathcal{N} \left({\mathrm{F}}_{\mathrm{t}-1,\mathrm{k}},{\upsigma }_{\mathrm{F},\mathrm{k}}^{2}\right),\mathrm{t} =2,\dots ,\mathrm{T},{\mathrm{F}}_{1,\mathrm{k}} =0\end{array}$$

(5)

where m = 1,…,M are the submarkets (census tracts in our application), whereas F (T × K) contain the dynamic factors k = 1,…,K, where K <  < M. The selection of the number of latent trends K is typically done with an information criterion (Zuur et al., 2003), in our case the Leave-One-Out Information Criterion (LOO-IC, see Vehtari et al., 2017). The LOO-IC is a method for estimating pointwise out-of-sample prediction accuracy from a fitted Bayesian model. Recent literature in the field of Bayesian modeling has adapted the LOO-IC as the method of choice to measure fit (see for example Dainese et al., 2019; Dehning et al., 2020; Theobald et al., 2020, among many others).⁶

This application produces unique census tract indexes as the loadings Γ (M × K) on the factors are unique per market m. In other words, every census tract λ_m (T × 1) is a linear combination of latent trends F and loadings Γ, λ_m = F Γ^′_m,., where Γ_m,. denotes row m of Γ. Like for the common trend µ, we assume the factors F to follow a random walk. For identification purposes, the loading matrix Γ has the following structure:

$$\Gamma =\left[\begin{array}{ccccc}{\upgamma }_{11}^{+}& 0& \cdots & \cdots & 0\\ {\gamma }_{21}& {\gamma }_{22}^{+}& \ddots & & \vdots \\ \vdots & \vdots & \ddots & 0& \vdots \\ {\gamma }_{K-\mathrm{1,1}}& {\gamma }_{K-\mathrm{1,2}}& \cdots & {\gamma }_{K-1,K-1}^{+}& 0\\ {\gamma }_{K,1}& {\gamma }_{K,2}& \cdots & {\gamma }_{K,K-1}& {\gamma }_{K,K}^{+}\\ \vdots & \vdots & \cdots & \vdots & \vdots \\ {\gamma }_{M,1}& {\gamma }_{M,2}& \cdots & {\gamma }_{M,K-1}& {\gamma }_{M,K}\end{array}\right]$$

(6)

Thus, Γ is upper triangular, where the elements on the diagonal are necessarily positive. This is sufficient to identify parameter matrix Γ (see Geweke & Zhou, 1996; Stock & Watson, 2002, 2005; Bernanke et al., 2005, among others). In order to estimate Γ for markets with a few or no observations, the parameters in Γ will receive a largely uninformative prior (Gelman, 2006). More specifically, we assume γ_m,k ∼ N(0,1).

A second restriction we put on the parameters for identification purposes is that on the variance hyperparameter for the latent trends, σ_F,k². We will assume that this variance is shared among all latent trends, effectively dropping subscript k. As a result, we can simply use σ_F,k² = 1 for all latent trends F. Finally, all latent trends F start at zero (similar to the common trend). Thus, F_t=1,k = 0 for all latent trends in K. Together, these restrictions allow for a unique solution, taking away issues caused by multi-modality (Yao et al., 2018).

We further add to the indexing literature by allowing for a spatial structure on the loadings Γ, following Strickland et al. (2011), Lopes et al. (2011), and Gamerman et al. (2008), among others. More specifically, we assume that parameters of adjacent census tracts are related per column of Γ. For example, if census tract m = 1 and census tract m = 100 are neighbors in space, we would expect the loadings γ_1,k and γ_100,k on latent trend F_t,k to be relatively similar. This further improves computational efficiency as we put more structure (although flexible) on the loadings. Note that we do not assume such a relationship over the rows of Γ.

Extant literature provides multiple ways to model spatial relationships between two points (Gelfand et al., 2010). Two early examples are the two-step Kriging procedure (Matheron, 1963), or the Spatial Gaussian Markov Fields from Besag (1974) and Besag and Kooperberg (1995). In this paper we opt to use the Spatial Random Walk (SRW), introduced by Francke and Van de Minne (2021). The SRW involves two steps. First, we estimate a Traveling Sales Person algorithm (Lawler et al., 1985) through the coordinates of interest, in our case census tract centroids. This collapses a 2D space into a 1D line. The 1D line goes through all the coordinates once using the shortest possible route (the starting point is arbitrary). Next, we assume a structure on the ordered census tracts’ parameters over this 1D line, for example a random walk:

$${\upgamma }_{\left(m\right),k}\sim \mathcal{N}\left({\upgamma }_{\left(m-1\right),k},{\upsigma }_{\upgamma }^{2}\right)$$

(7)

where subscripts (m) denote census tracts ordered by the TSP-route. We assume that each SRW, column k = 1,…,K, has the same variance ${\upsigma }_{\upgamma }^{2}$, although this can be generalized. Equations (5) – (7) give the spatial dynamic factor repeat sales (SDFM) model. We use the SRW model mostly because of its speed to estimate, and the fact that previous literature has shown it provides similar estimates to the Besag (1974)-type models (Francke & Van de Minne, 2021). We leave it to future research to test out alternative spatial structures, like Gaussian (Markov) Random Fields (Gamerman et al., 2008; Lopes et al., 2011; Strickland et al., 2011), which might improve the indexes.

The estimation is performed using the No-U-Turn-Sampler (NUTS), introduced by Hoffman and Gelman (2014). For full transparency we provide our full spatial dynamic factor repeat sales model code (which we estimate in RStan) in Appendix A. We sample 2,500 times over 4 parallel chains, while using half of the samples as a warm-up. This is consistent with previous literature in our field (van de Minne et al., 2020; van Dijk et al., 2022). Moreover, the scale reduction factor of Gelman and Rubin (1992) indicated convergence of all chains for both models. These results are available upon request.

Note that our setup differs from the ‘standard’ DFM literature in a few important ways. First, to the best of our knowledge, this is the first application of such dynamic factor models on micro-level housing data—in our case, a repeat sales model for housing.⁷ Second, DFMs are normally used to summarize a large number of time series into just a few (van de Minne et al., 2022). In other words, the output of such models are the latent trends F. However, in our case we are interested in the resulting M tract indexes. This is an important differentiation as a large bulk of the DFM literature is concerned with the rotation of Γ, via for example Varimax or Oblimin. The reason being is that the estimates of Γ— and the corresponding latent trends—will depend on the ordering of the markets. For example, if the first market is a particularly ‘hot’ market, the first latent trend will look differently compared to when the first market is a ‘cold’ one. Ex-post rotation solves these issues, meaning you will get the same results independent of the ordering of the markets. But again, given that we are not specifically interested in the latent trends and loadings per se, but just in the linear combination of the two (which do not change due to the rotation), we keep all estimates as is.

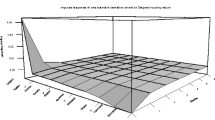
Figure 1 summarizes the degrees of freedom saved from using our approach compared to an interactive setup. Specifically, we map the gain as a function of submarkets and latent trends where the gain is a fraction of the amount of parameters in a dynamic factor setup as compared to an interactive setup. In an interactive setup a time series (T) per market (M) is estimated, meaning there are I_c = T × M parameters—ignoring a possible common trend here. In the dynamic factor setup, there are K latent trends for which you have to estimate time series (and again K <  < M), plus a loading for every market M. This results in I_d = T × K + K × M parameters. Figure 1 provides the share of the dynamic factor parameters compared to the amount of parameters in an interactive setup, or I_d/I_c, assuming 80 quarters (20 years). Subsequently, we simulate the amount of latent trends K (k = 1,…,15), and amount of markets M (m = 50,…,500). If I_d/I_c < 1, one requires less parameters to estimate the dynamic factor model and vice versa. On average, we estimate 9% of the parameters in a dynamic factor setup as compared to a ‘classical’ interactive setup according, see Fig. 1. With a low amount of markets M, and high number of latent trends K, the difference naturally becomes negligible in the extremes, but overall the preservation of degrees of freedom is considerable. Note that the gain-profile only changes marginally after 200 markets. Our measure of gain is between 1.5% (K = 1) and 23% (K = 15) after 200 markets on average.

Fig. 1

Increasing Degrees of Freedom Using the Dynamic Factor Approach. M is amount of submarkets, and K is amount of latent trends. The gain is a fraction of the amount of parameters in a dynamic factor setup, compared to an interactive setup. We use 20 years of data, or T = 80 quarters. The gain is calculated as: $\frac{\left(T\times M\right)}{\left(T\times K\right)+\left(K\times M\right)}$

Data

Our data consists of condominium transactions in Manhattan, New York between 2006 and 2019. We use the address and the apartment number to construct repeat sales. In addition to the transaction price and address, we observe the date of sale.⁸ These data are provided to us by Rezitrade, a company that uses proprietary vision based techniques to scan and categorize deed documents which are publicly available. Property addresses are used to determine the census tract the property is located in. In total, we observe 14,726 repeat transactions throughout Manhattan in 218 different census tracts.⁹ A map with the location of our transactions is provided in Panel (a) of Fig. 2. Place Fig. 2 about here.

Fig. 2

Building location and Traveling Sales Person route through tracts

Descriptive statistics of the data can be found in Table 1. On average, properties are $1.5 M when bought (price at “time of buy”) and $1.8 M when subsequently sold (price at “time of sale”), with an average (log) return of 20%. The holding period is 6 years on average, implying an average annualized return of 3.6%. Note that only the time of buy, time of sale, and the return over the holding period is needed in the repeat sales model. On average we have less than 70 repeat sales per tract, which can be considered a limited amount of observations. However, the variation is quite large. For example, there are 38 tracts with less than 10 observations, and there are almost 20 tracts with more than 200 observations. It is a challenge to estimate the K loadings for the non-spatial dynamic factor repeat sales model for the tracts with few observations.

Table 1 Repeat sales data summary statistics

Panel (b) of Fig. 2 depicts the estimated Traveling Sales Person’s (TSP) route given a random starting point.¹⁰ Following the points (which represent the centroids of the 218 census tracts), the connecting line gives the shortest route through all the dots, while only going through the dots once (Hahsler & Hornik, 2007; Lawler et al., 1985). We use this route to construct the Spatial Random Walk, similar to Francke and Van de Minne (2021).

Results.

Summary of All the Models

Table 2 provides summary statistics for all estimated models with different numbers of dynamic factors, K = 1,…,10, for both the spatial (Panel A) and non-spatial (Panel B) dynamic factor repeat sales models. Model-fit deteriorates rapidly after higher K; thus, we include up to 10 trends.

Table 2 Summary Statistics of Dynamic Factor Models with K = 1,…, 10 latent trends

First we observe that, on average, the estimates of all the loadings in Γ are positive. This result makes intuitive sense since some co-movement between all indexes is expected (Guo et al., 2014; van de Minne et al., 2020). Given that we do not rotate the loadings, the direct interpretation is difficult, and comparison between the two specifications is incomplete without comparing the latent trends as well. We therefore provide a subset of tract indexes (λ_m) in Fig. 3 which can be compared directly between all the models.

Fig. 3

Example of tract indexes for a selection of three markets. The low count market has 19 observations, the medium count market has 176 observations, and the high-count market has 427 observations. Horizontal axis is the time of sale with format YYYYQ, and vertical axis is the log price level. The lines themselves are the estimated (log) indexes using a different number of K latent trends

Next in Table 2, the LOO-IC (the Leave-One-Out Information Criterium, Vehtari et al., 2017) provides a measure of fit. A lower value indicates better fit, and a difference of 5 is seen as considerable. For reading ease we highlight the lowest values per model. On average we find that the spatial model has a superior fit, by quite a margin. More specifically, the average LOO-IC for the spatial model is 3,928, as compared to an average LOO-IC of its nonspatial counterpart of 4,049—approximately a 120-point difference. Within each model, we find that 6 latent trends provide the best fit for the spatial model (LOO-IC = 3,788), and 4 latent trends give the best fit (LOO-IC = 3,921) for the non-spatial model.

The RMSE (σ_ϵ) is lowest for the spatial models at 6 through 8 latent trends, whereas the RMSE keeps decreasing even at 10 latent trends for the non-spatial model. For completeness, we provide the variance parameter on the common trend for both models (σ_µ), and the variance parameter for the spatial random walk (σ_γ). However, as before, the interpretation of these parameters is cumbersome. Note that the spatial model (Panel A) also includes a spatial hyperparameter (σ_γ), which the non-spatial model lacks (Panel B).

In total we have 218 tract indexes. For the sake of brevity, we focus on three for illustrative purposes.¹¹ We present one low count census tract with only 19 repeat sales observations, a medium count census tract with 176 repeat sales, and a high-count census tract with 427 repeat sales.¹² The volatility of the index returns is displayed in Table 3.

Table 3 Standard deviation of the log price index returns for low, medium, and high count tracts

Figure 3 presents the (log) index level for the corresponding market using different latent trends K for both the spatial and non-spatial dynamic factor repeat sales models. The black line represents the K = 1 index, the orange dashed line is the K = 2 index. The remaining lines indicate the K ≥ 3 indexes. There are a few things we focus on when analyzing the indexes. First is erratic or excessive volatility of the indexes, which could indicate noise affecting our estimates (Guo et al., 2014). Table 3 gives the standard deviation of the log returns.¹³ Second is how much the indexes change after introducing an extra latent trend. Such ‘revisions’ are a great cause for concern since it decreases the trustworthiness of the individual indexes (Francke & van de Minne, 2017). We can evaluate the overall model-fit using the LOO-IC; however, a small LOO-IC does not imply we have found the best fit for an individual index / census tract. Therefore, if the results are relatively similar for all K latent trend specifications, misspecification concerns on a census tract level are removed. In Table 4 we first compute the range of all K indexes per time period then take the average.

Table 4 Average range of (log) index values

Starting at the low count market (GEOID: 36,061,013,000, 19 observations) we find the largest standard deviations, revisions, and differences between the two proposed models. With respect to differences, the non-spatial method results in a (log) end value of 0.6 on average, as compared to an average end value of 0.3 for the spatial model. The average standard deviation of the returns of the non-spatial model is almost three times that of the spatial model (rightmost column in Table 3). However, it is especially the range of possible indexes that makes the non-spatial model seemingly unrealistic. On average the range over time is 0.33 log points for said model. In contrast, it is only 0.09 for the spatial model, see Table 4. It is unsurprising that estimating the loadings (10 maximum) is challenging with only 19 observations. The spatial structure of the SDFM, greatly reduces some extreme estimates in Γ.

For the medium count market (GEOID: 36,061,013,700, 176 observations) the indexes of the two models start to coalesce. More specifically, on average the non-spatial model ends on 0.31, and the spatial model on 0.26. The average volatility is the same between the two models. However, the non-spatial model still has the largest range between the K indexes (Table 4). The average range is 0.05 for the spatial model, and 0.07 for the non-spatial model. This larger range for the non-spatial model is also easy to spot in Fig. 3. It is especially apparent in the time period closely preceding the GFC (2008) and when the Manhattan market started to cool down around 2015–2016. In other words, there is some evidence that the estimates of the non-spatial model change considerably whenever there is a turning point in the market.

The end-point differences between the two models is negligible for the high count market (GEOID: 36,061,015,102, 427 observations). Both end around 0.19. The volatility and range is still lower for the spatial model as compared to its non-spatial counterpart (Tables 3 and 4 respectively). However, in both cases the non-spatial results do not look ‘excessive.’ As noted in Guo et al. (2014), high volatile indexes are evidently noise driven.

Comparison with Other Index Methodologies

To further elaborate on the strength of our proposed methodology, we compare our indexes with indexes created using alternative methodologies. The first of these benchmarks is the ‘standard’ Bailey et al. (1963) method (Eq. (3)), which is estimated by Ordinary Least Squares. The second benchmark model is a locally weighted repeat sales model (McMillen, 2003). This model is similar to the Bailey et al. (1963) method, but it also allows for the consideration of transactions from neighboring census tracts. This will naturally increase the amount of observations. However, observations that are further away will receive less weight. More specifically, we first take the centroid of every census tract and calculate the distance of this centroid to every transaction in the data (designated d_i) and only keep b nearest neighbors.¹⁴ Denoting the maximum distance found in the (sub)data as D, we calculate the weights as follows:

$${w}_{i}={\left[1-{\left(\frac{{d}_{i}}{D}\right)}^{3}\right]}^{3}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}I\left({d}_{i}\le D\right)$$

(8)

After calculating the weights, we re-estimate the repeat sales model using Generalized Least Squares. The tri-cube weighting scheme is based on earlier research by McMillen (2003). Note that even though we estimate the model census tract by census tract, the actual sample sizes will be equal, as we take b closest neighbors for every census tract.

For our third and fourth benchmark models, we replace the time fixed effects of the Bailey et al. (1963) model with a random walk (Eqs. (3) – (4)), and a local linear trend (LLT, see Francke, 2010). The local linear trend closely relates to the random walk (RW) model, but adds a time varying drift to the state equation.¹⁵ Both models are estimated using the No-U-Turn Sampler, similar to our dynamic factor repeat sales models. As a result, any differences between the structural time series models (including our newly proposed DFM repeat sales models) cannot be explained by differences in estimation techniques. Finally, note that all benchmark models are repeat sales specifications, and are estimated census tract by census tract. (Although the locally weighted regression does include observations from outside the target census tract, one must still re-sample the data for every individual census tract.)

In the previous subsection, we find that the best fit for the spatial model employs six latent trends. Both RMSE and LOO-IC are superior as compared to different numbers of latent trends. For the sake of brevity, we therefore only compare the benchmark models with the DFMs with K = 6 latent trends.¹⁶The resulting indexes for the same markets (low, medium, and high count) used before are provided in Fig. 4. We additionally provide some index return statistics in Table 5. It should also be noted here that it would be more fair to compare our estimates with that of a hierarchical (repeat sales) model, as in Francke and van de Minne (2017). Indeed, both hierarchical and DFM models use the entire dataset, not just data of one census tract. However, we found that estimating such models in our setup is computational impossible on standard machines due to the large number of parameters needing to be estimated. In fact, as noted in Sect. 2.2, that is one of the strengths of our proposed methodology.¹⁷

Fig. 4

Comparison of the dynamic factor repeat sales models (with K = 6) with other index methodologies (a) low count. (b) medium count. (c) high count. Notes: Counts for the low, medium, and high market are 19, 176, and 427 respectively. The horizontal axis is the time of sale with format YYYYQ; the vertical axis is the log price level. For the standard Bailey et al. (1963) repeat sales model the dots are connected only when there are estimates for two periods in a row

Table 5 Summary statistics of returns of the different indexes for three census tracts

The results for the low count market (GEOID: 36,061,013,000, 19 observations) are as expected. With only 19 repeat sales the standard Bailey et al. (1963) model ‘breaks’—the model cannot provide an estimate of the index for all time periods due to a lack of observations. By comparison, the locally weighted and structural time series models do not break in a similar fashion. A second observation is that the standard Bailey et al. (1963) model is very volatile when estimates are available. For example, the difference between the index in 2006q1 and 2008q1 is 400%, which is unreasonable, and is evidently driven by noise (Guo et al., 2014). The random walk and local linear trend models look very comparable (the biggest divergence happens in the first year or so), and both fit an essentially flat line between 2013 and 2019 where we have no observations. This is obviously caused by a lack of observations. Also note that it is hard to observe price declines during the Great Financial Crisis using these models which also brings to question the relevancy of using such models in an extreme low observation environment. The locally weighted model and spatial DFM model follow a very similar path with the crisis clearly visible in both. The big difference between the two is that the former produces a considerable negative first-order autocorrelation (Table 5, panel A). More specifically, the first-order autocorrelation for the SDFM model (column VI) is 0.222, as opposed to -0.464 for the locally weighted model (column II). The locally weighted model also has twice the volatility. The negative first-order autocorrelation and high volatility of the series is an indication that noise is impacting the estimates (Guo et al., 2014). All other structural time series models do produce a positive first-order autocorrelation, except for the NSDFM (column V). Note that we cannot provide a meaningful standard deviation or first-order autocorrelation for the standard Bailey et al. (1963) model due to the large number of missing periods.

Moving to the medium count market (GEOID: 36,061,013,700, 176 observations) we find that the Bailey et al. (1963) model is now able to estimate an index for most periods of time.¹⁸ Unfortunately, the volatility remains excessive, and we observe a large negative first-order autocorrelation. To be more precise, the standard deviation of the quarterly (log) returns is 0.25, and the first-order autocorrelation is -0.356 (Panel B of Table 5). It is also apparent from Fig. 4-b that the random walk and the local linear trend models both follow the general path of the Bailey et al. (1963) model, albeit with less volatility (the standard deviation of the quarterly log returns is approximately 0.0165 for both). Given that these three models work with the same data, it is not surprising to find such an outcome. Our newly proposed models and the locally weighted model display a slightly different index. For example, the boom-bust cycle is more pronounced during the GFC years of 2006–2010. Also, these models estimate no price decrease after 2016, but rather a flatlining. The reason why the dynamic factor and locally weighted repeat sales models are different from the other models lies mostly in the fact that the latter can only use data from the census tract itself. Even though we designate this census tract ‘medium count’ it still only contains 3 observations per quarter on average, which results in noisy data. The dynamic factor models use all data, and the locally weighted model uses (b =) 20% of all data in our specific setting. Not only is the general path of the indexes quite different, the volatility and first-order autocorrelation are distinct as well. (Panel B, Table 5.) The random walk and local linear trend models smooth the indexes to a great extent due to the lack of data, with high first-order autocorrelation (+ 0.76 on average) and little volatility (0.016), only being partially able to detect the signal from the noisy data. The spatial and non-spatial dynamic factor repeat sales models, using data from all census tracts, allow for twice the volatility (0.034), and show zero to very little first-order autocorrelation. The volatility of the locally weighted repeat sales is still high, and comparable to the finding of the low count market (0.064 and 0.068 respectively). This was to be expected as the sample sizes are equal sized for this model. Furthermore, the first-order autocorrelation is still negative. The correlation between the index returns across all models is already quite high at 0.803.

For the high-count census tract (GEOID: 36,061,015,102, 427 observations) we find that all indexes coalesce to a large degree. The average correlation between the returns across all models is 0.938, and all indexes have an endpoint between 0.17 and 0.18 (rounded), except for the locally weighted model. We also observe similar boom-bust cycles. The quarterly volatility of the Bailey et al. (1963) model is still large (0.12), but less extreme than in the medium and low-count examples. The first-order autocorrelation remains large and negative. (Panel C of Table 5.) The standard deviation of the returns are relatively similar in magnitude between all four structural time series models. The first-order autocorrelation reduced for the random walk and local linear trend model (compared to Panel B), although the latter is still relatively high (0.495). In principle all indexes should be similar, as there is enough data within the census tract to produce a reliable index. We are therefore confident that our proposed methodology is not mis-specified in any way. Finally, note that the estimates of the locally weighted model take a different path after 2015 or so (Fig. 4-c), and therefore end at a much high (log) level of 0.30. This result is likely due to the fact that neighboring census tract experienced greater price appreciation than the target census tract during this period. Our dynamic factor model ‘ignores’ the information from nearby census tracts (through the imposed spatial and temporal structure) if sufficient data is available in the census tract.

In summary, we find that traditional repeat sales methodologies and our newly proposed models provide similar indexes given enough observations in a census tract. However, most census tracts have (very) little observations, especially on a quarterly basis. In those instances, traditional OLS models ‘break’ and/or show unrealistic levels of volatility. Our benchmark structural time series repeat sales models do not suffer from breaking or excessive volatility, but evidently have difficulty extracting a signal from noisy data, resulting in very ‘flat’ indexes. Our proposed spatial dynamic factor repeat sales model does not suffer from such caveats.

Latent Trends and Loadings

In this Section we will focus on the latent trends and loadings in more detail. This is a useful exercise given the opaque nature of the construction of trends and loadings. To be consistent with the previous Section, we will specifically look at the SDFM with K = 6 latent trends. First, we provide the common trend µ for the spatial model in Fig. 5.

Fig. 5

Estimates of the common trend µ_t of the SDFM

The common trend displays a predictable path. Prices increased before the Great Financial Crisis (GFC) with a subsequent large downturn, followed by an upswing around 2010. Prices in Manhattan have struggled since 2015, with prices dropping after 2018. The estimated latent trends (F) and corresponding loadings (not-rotated) are given in Fig. 6a.

Fig. 6

Latent trends and loadings per trend for the SDFM. The spatial dynamic factor repeat sales model includes 6 latent trends. The x-axis for the loadings represents the TSP route

Figure 6a displays the six latent trends from the spatial dynamic factor repeat sales model. All trends start at zero for identification purposes, but magnitudes diverge substantially over the sample period. The difference between the largest and smallest values at the end of the sample period is approximately 8 in log levels. The correlation between the returns is also low as shown in Table 6. There is only one occurrence of a correlation larger than + 0.5 with many correlations being negative. The loadings (plotted over the TSP line) displayed in Fig. 6b also differ considerably for every location on the TSP route. Further, even though the average loading is positive (as established in Table 2 as well), many times we estimate a negative loading.

Table 6 Correlation between returns of latent trends for our spatial dynamic factor model, with K = 6

To get a better understanding of the differences between the spatial and non-spatial dynamic factor repeat sales models, we plot and compare the loadings on the first latent trend in Fig. 7. We also use the 6 latent trend model for the non-spatial model, even though this did not provide the best fit (Table 2) this makes the comparison between model outcomes more straightforward. The dotted line (representing the non-spatial model) gives a more ‘porcupine’ appearance, whereas the estimates of the spatial model look less random.¹⁹ Statistically, we find an AR(1) estimate of 0.95 for the SDFM loadings over the TSP route, whereas it is only 0.18 for the NSDFM model. In some instances the models also are in clear agreement. For example, the loadings are (large) negative around location 92 and 155. In other cases the loadings gravitate towards zero for the non-spatial model, mostly due to data shortages.

Fig. 7

Loadings of the first latent trend for both spatial and non-spatial models. The spatial dynamic factor repeat sales model includes 6 latent trends. The x-axis represents the TSP route

In Fig. 8 we provide choropleths of the cumulative log index return (λ_m) for each tract between 2006 and 2019 both for the spatial and nonspatial models. The resulting spatial pattern in Fig. 8a depicts some clear patterns. The south and north end of Manhattan display the highest returns between 2006 and 2019. In the north and southeast, we capture the well documented gentrification of Harlem, the Lower East Side and Chinatown. In the southwest—White Hall, Tribeca, Soho neighborhoods—the high returns may reflect the large-scale development projects like Battery Park and subsequent ‘super-gentrification’ experienced in that area (Lees, 2003).²⁰ The pattern is slightly less clear in the non-spatial model provided in Fig. 8b as a number of significant outliers are present.

Fig. 8

Cumulative log index returns for all census tracts. Cut points based on deciles of the non-spatial dynamic factor model log index. Grey tracts indicate tracts with no observations

As before in Sect. 4.2, both the spatial and non-spatial indexes will converge whenever there are a sufficient number of observations. To further drive home this point, we provide a choropleth with the mean absolute difference (MAD) between the spatial and non-spatial indexes in Fig. 9 (right panel), together with the number of observations (left panel). A clear pattern emerges. For example, the MAD is relatively large anywhere north of central park, while the number of observations are also low in that same area. We see a similar pattern in the southeast of Manhattan as well. Unsurprisingly, the correlation between the two series is -0.272, indicating that higher number of observations will result in a lower MAD. Finally, we provide the MAD by transaction count in Fig. 10. More specifically, we create bins based on the number of transactions in a tract and calculate the MAD between the indexes. The difference substantially declines as the number of transactions in a tract increases, i.e. the indexes are more similar when sample size in a tract is large.

Fig. 9

Transaction count and mean absolute difference for spatial vs. nonspatial indexes. Cut points based on deciles of counts and mean absolute difference. To highlight the (somewhat weak) negative correlation between transaction count and mean absolute difference, we reverse the color scale between the two panels. Grey tracts indicate tracts with no observations

Fig. 10

Mean absolute difference between spatial and non-spatial index by count deciles. We count the number of transactions per census tract then calculate the mean absolute difference between the spatial and non-spatial index for tracts within each count decile bin

Conclusion

We contribute to a growing literature that provides new methods for constructing (house) price indexes over fine geographies and high frequencies. Sparse data is an inherent issue at such geographies and temporal frames. We overcome sparse data issues with the application of a new methodology to construct census tract level indexes on a quarterly basis. Specifically, we augment a traditional repeat sales model with a dynamic factor model. Within this framework, we estimate a limited number of latent trends running through all census tracts where we allow separate loadings for each census tract on said latent trends. This structure greatly reduces the number of parameters needed to be estimated. We further allow the loadings on the latent trends to follow a spatial random walk which captures important information from similar neighboring markets. In an application of the model using Manhattan condominium sales, we demonstrate the construction of 218 quarterly indexes using only 15 thousand observations in total—approximately 70 observations per census tract. Our methodology can be readily applied to single-family residential and commercial real estate as well. Future research might benefit from employing different spatial structures on the loadings.

The main benefit of the spatial specification is the production of a less noisy index as compared to a non-spatial specification. This opens up an opportunity to construct granular, high frequency price indexes for geographies and frequencies not supported by traditional repeat sales models. Access to such data can improve decision making for policymakers, homeowners, banks, and investors.

Appendix 1 Stan Code of the Spatial Dynamic Factor Repeat Sales Model