“If molecules could talk, would physicists refuse to listen?”

Alan Blinder Footnote 1

Introduction

Wealth and housing surveys usually elicit a current market value of owner-occupied dwellings by simply asking the owner for an estimate. This yields owner-estimated values (OEVs). These surveys may serve for constructing representative price indices in the absence or insufficiency of market transaction data and they have several valuable features. One is the coverage: country-representative surveys potentially provide an exhaustive picture of the existing residential housing stock and are not limited to only those dwellings currently on the market. Usually, surveys also come with ample information about the property (including sometimes even its location) and its owner enabling micro-links to other economic dimensions. Surveys regularly also ask homeowners for the original acquisition price which – together with the OEV – yields price pairs potentially usable for repeat-sales type of statistics. Thus, OEVs are regularly used as if they were true market prices.Footnote 2

Despite these advantages, OEVs need to be treated with care: OEVs might not be equivalent to market data as they may just reflect owners’ beliefs – and maybe wishes. Specifically, in a survey, the owner is asked to anticipate the outcome of a bargaining process given current market conditions: she is not asked to estimate some type of “fundamental value” but really what she thinks she could earn when the dwelling was put on sale at the day of the survey interview. This is anything but an easy task – in particular for non-experts.Footnote 3

Beyond a lack of knowledge and skills, responses may very well be affected by psychological biases too. Previous studies have documented a general tendency of homeowners to over- estimate the value of their home (Kish & Lansing, 1954; Goodman Jr & Ittner, 1992; Kiel & Zabel, 1999; Agarwal, 2007; Benítez-Silva et al., 2015; Gallin et al., 2018; Molloy & Nielsen, 2018). This may hint towards an endowment effect (Kahneman et al., 1991): owners may assign a higher value to their home than could realistically be achieved on the market – simply because they own it. However, owners in very tight markets may also lag behind developments in the real estate market. Davis and Quintin (2017) provide evidence that OEVs show less extreme trends over the US boom-bust housing cycle between 2000 and 2011: OEVs did not increase as rapidly as transaction prices during the boom and did not decline as severely during the bust. Similarly, Naidin et al. (2022) establish a micro-match between survey data and real estate advertisements, and detect over-reporting by home-owners for the very tight Luxembourg housing market.

Systematic overestimation would be consistent with an endowment effect as often argued, yet causal proofs are rare. In general, only few studies explicitly examine the effects of psycho- logical biases in the context of housing markets. Scott and Lizieri (2012) show (in a stylized lab experiment with students who did not own a house) that anchoring strongly influences judgments about house prices. There is also evidence that loss aversion has a significant im- pact on prices (Anenberg, 2011; Chan et al., 2016; Einiö et al., 2008; Genesove & Mayer, 2001): home-owners whose dwellings lost value demand significantly higher prices. Stephens and Tyran (2012) use Danish panel data to show that nominal loss aversion has a severe impact on the evaluation of the advantageousness of transactions, whereas real losses do not play an important role. Van der Cruijsen et al. (2014) relate the accuracy of OEVs reported in a Dutch survey to the duration of ownership – which they argue tests an endowment effect – and the loan-to-value ratio to test for loss aversion. They report strong effects. The importance of psychological effects for the build-up of housing bubbles has been popularized in Shiller (2015).

All these documented effects and potential problems question the appropriateness of taking OEVs as if they were true market prices to study housing market dynamics or measuring housing wealth stocks. Understanding in which contexts their use is justified is hence an important prerequisite for every empirical analysis relying on OEVs. How to delineate these cases and providing suitable measurement vehicles are thus the research questions we address here.

To do so, we first develop suitable techniques to construct hedonic and repeat-sales style house price indices from (partly repetitively reported) OEVs, dwelling characteristics and acquisition prices. The techniques are inspired by standard house price index construction but adapted to fit survey data. Thanks to three datasets (the American Housing Survey, the Italian Survey of Household Income and Wealth and the European Household Finance and Consumption Survey), we derive multiple series of subjective residential property price indices for 20 countries spanning several decades. We first test for internal validity of our methods to elicit subjective indices and show that the indices based on different construction techniques generally elicit very similar house price dynamics. Subsequently, we perform convergent validity tests using traditional objective residential property price indices (in other words, transaction-based indices) as benchmarks.Footnote 4 This suggests that indices constructed from survey data are quite consistent regardless of the method used as well as the phase of the housing cycle. We thus conclude that the “wisdom of the home-owner crowd” is sufficient to study objective house price dynamics. Unlike other studies, we do not find systematic deviations between indices constructed from objective market data and those from OEVs which likely hints towards shortcomings in previously applied index construction techniques when relying on OEVs. Yet, we use our data also to test for the accuracy of reported house price levels. This test fails, which has far-reaching consequences whenever treating OEVs as accurate price measures.

With these methods and findings we contribute to several strands of the literature. We first develop tools to construct subjective house price indices, which are firmly rooted in state-of- the-art price index methodology and adapted to fit the specifities of survey data. Since for some countries the resulting indices are even longer than currently existing objective counterparts, we additionally provide new information on long-term trends for these housing markets. Third, we carefully design and execute convergent validity tests to understand how and when OEVs are useful to study house price levels and dynamics, and for which kinds of questions using OEVs is doomed to fail.

The remainder of this article is organized as follows. The “Strategy and Methodology” section presents the principles of our convergent validity tests as well as the techniques to compile subjective house price indices. In the “Data and Methodological Details” section, we describe the different datasets used in our empirical application, which is carried out in the “Convergent Validity Test Results” section. Finally, “Conclusions” section summarizes results. The appendix provides supplemental details and data tables containing all compiled subjective indices.

Strategy and Methodology

Testing Strategy

In this section, we explain how to construct residential property price indices (RPPI) tailored to the set of information typically available in surveys. Just like in the case of an objective residential property price index (O-RPPI), for gaining solid subjective indices (S-RPPIs) some kind of quality-adjustment needs to be performed. This guarantees that like is compared with like as a large fraction of cross-sectional and temporal variations of house prices is due to differences in the mix of dwellings’ locational and physical characteristics.

Generally, wealth and housing surveys do not use a standardized questionnaire. In most cases, however, these surveys ask for an OEV by motivating the owner to put herself hypothetically in the shoes of a seller or buyer. Some surveys also have a longitudinal component, yielding OEVs for the same property elicited several times over a rather short period of time. Additionally, surveys sometimes collect the original acquisition price, the year of purchase, the location of the property as well as some dwelling characteristics.

We propose three main index construction techniques and a hybrid one making use of some of the above listed pieces of information provided in surveys. All methods and quality-adjustment procedures are inspired by either hedonic or repeat-sales indices. By doing so, we set the stage for a reasonable comparison between the capacity of objective- and subjective-based RPPIs for filtering price dynamics. This is the basis of our convergent validity tests: whenever a S-RPPI matches an O-RPPI, we can arguably conclude that the data used to construct the S-RPPI contains internally coherent information on housing market dynamics. In other words, our testing strategy follows a wisdom of the crowd principle: we aim to test whether the collective knowledge and joint perceptions of many individuals reproduce objectively observable market trends.

Subjective Residential Property Price Indices

This section describes how to adapt index construction methodologies to suit survey data. We develop four approaches, one relying on hedonics and three on repeated observations over time. The latter comprises a repeat-observations-panel (ROP), repeat-observations-acquisitions (ROA) and a hybrid repeat-observation approach (RO hybrid). Depending on the information available in a survey, one or more techniques may be applicable. Below we provide method- ological details as well as a discussion of the pros and cons of each approach.

A Hedonic Approach

Hedonic valuation assumes that differentiated products are completely described by a vector of objectively measured characteristics and that observed prices of these goods are composed of implicit or “shadow” prices associated with these characteristics (Rosen, 1974). As dwellings are highly heterogeneous goods, hedonic valuation approaches are widely used in this context. Thereby, the relevant characteristics describe both the major features of the structure and the attractiveness of the dwelling’s location.

In general, all types of hedonic techniques can be applied to subjective data just as to transaction data (see Hill, 2013; de Haan & Diewert, 2013, for a survey on techniques). We suggest a chained hedonic adjacent-period time-dummy index as it is ideally suited for standard survey designs.

We estimate hedonic models that regress the logged price of the dwelling on a matrix of physical (X) and locational (L) characteristics with associated shadow prices stored in the vectors β and λ, respectively. We pool data from two adjacent survey waves, and hence time dummies Ds and Ds−1 enter the model. In the classical approach, time dummies refer to the period of sale. In the subjective version, the time dummies indicate the period of valuation – the survey year. The associated scalar parameters δs and δs−1 filter pure price changes over time net of differences in dwelling characteristics X and L:

$$\mathrm{log}\left(P\right)={\delta }_{s}{D}_{s}+{\delta }_{s-1}{D}_{s-1}+X\beta +L\lambda +\varepsilon ,$$
(1)

thereby ε denotes a vector of independent and normally distributed error terms. From each model, we extract the price changeFootnote 5 from period s − 1 to period s via the estimated scalar time-dummy parameters

$$\mathrm{exp}\left({\widehat{\delta }}_{s}-{\widehat{\delta }}_{s-1}\right).$$

An index number stating the price change between the base period t∗ = 1 and any other period t > 1 is obtained by chaining all period-to-period changes up to period t, i.e., 

$$I_{hedonic}(t)=\prod \limits_{s=1} \limits^t \mathrm{exp} (\widehat{\delta}_{s}- \widehat{\delta}_{s-1}).$$

In the case of bi- or triennial surveys, index numbers for years between survey waves need to be reconstructed. Here, we do so by linear interpolation.

This chained time-dummy approach has two distinct advantages when dealing with survey data. First, the list of variables collected in surveys regularly changes. It is often the case that a variable is collected in some waves, and at some point dropped or replaced by a similar yet not identical question. The chained approach requires only that the same characteristics are available in two adjacent periods but not throughout the entire time span. Thus, the flexibility of the chained approach allows us to exploit (almost) all available characteristics. Second, shadow prices associated with structural and – even more importantly – locational characteristics may change over time due to changes in tastes or attractiveness of a certain areas compared as to other locations. This is particularly relevant when dealing with long time periods spanning several decades. The chained approach automatically allows shadow prices to adapt over time as each hedonic model uses data from two consecutive survey years only.

Future researchers planning to use such an approach should bear in mind that hedonic equations are not without limitations. First, a sufficiently comprehensive list of physical and locational characteristics needs to be available to filter out price changes over time net of differences in characteristics among dwellings. While surveys usually collect the most important physical characteristic (such as the age of the structure and the living surface), their public files often lack information on location.

The subjective version inherits other points of critique from its objective counterpart: the high data demand in terms of dwelling characteristics and the discretion of the researcher in the choice of the specification of the hedonic equation (see Shiller, 2008). One could also argue that it is impossible to identify all the important characteristics and that many of them are even simply not measurable in an objective and processable way. Although they are not perfect, hedonic techniques remain widely applied for constructing house price indices.

Repeat-Observations Approaches

A standard repeat-sales index (see Bailey et al., 1963; Case & Shiller, 1987, 1989) exploits paired price information from repeatedly sold dwellings. Only price changes of the same dwelling are considered and these changes are then aggregated to an overall index. By that, an almost perfect quality-adjustment is obtained.

We propose two main versions of subjective indices inspired by the repeat-sales methodology: the repeat-observations-panel (ROP) and the repeat-observations-acquisitions (ROA) index. We also compile a hybrid version of the two labelled the RO hybrid approach.

The standard repeat-sales index is criticized for ignoring changes in the age (and hence often the quality) of the structure, measurement errors from unobserved renovations, the exclusion of first sales, and a potential lemons’ bias, as low-quality homes tend to sell more frequently (see Wallace & Meese, 1997). As detailed below, all these commonly discussed drawbacks are irrelevant in the case of survey data.

Additionally, heteroskedacity sourcing from variability of the duration between consecutive sales has been argued to be a serious issue that may demand additional adjustments (Shiller, 1991). This concern also applies to the ROA index, yet is irrelevant for our preferred version – the ROP index.

The ROP Approach

For surveys including a panel component, repeatedly reported OEVs referring to the same dwelling can be linked and used to compile a repeat-sales-type index. To construct this index, the logged ratio of prices related to subsequent sales is regressed on dummy variables indicating the period of first and second sale. When using survey data, we take the ratio of OEVs obtained from two consecutive survey waves and apply the standard repeat-sales regression:

$$\log\left(\frac{P_{i,t}}{P_{i,s}}\right)=\sum \limits_{m=1} \limits^{T_{S}} \tau^{m}_{ROP}D^{m}_{i}+ \varepsilon_{i},$$
(2)

where Pi,t and Pi,s denote dwelling i’s OEV at times t and s with 1 ≤ s < t ≤ TS, and TS the number of survey waves. In a standard repeat-sales framework, the dummy variables Dm are Dm=s =  − 1 for the period of the first sale, Dm=t = 1 for the period of re-sale and 0 otherwise.

For survey data, the periods of sale and re-sale are identified with subsequent survey waves. Finally, εi denotes an independent and normally distributed error term.

The estimated coefficients \({\widehat{\tau }}^{t}\) are used to construct the price index: the change in prices between the base period t∗  = 1 and any later period t > 1 is given by

$${{\varvec{I}}}_{ROP}\left(t\right)=\mathrm{exp}({\widehat{\tau }}_{ROP}^{t}).$$

In the common case of bi- or triennial surveys, index numbers for years between survey waves – just as in the case of hedonic indices – are obtained by linear interpolation.

A ROP index does not inherit the commonly cited shortcomings of repeat-sales indices yet benefits from its merits. Specifically, we identify four major points of critique that do not apply to survey panel data. First, there is no reason to believe that surveys over-represent owners of low-quality homes and hence a lemons’ bias is ruled out.Footnote 6 Second, homes that were just bought are excluded like for objective repeat-sales indices. The prices of these dwellings will only be included into the index as soon as the household was contacted again in the subsequent survey wave. This is, however, much less of a concern compared to transaction data, since surveys take place much more frequently than re-sells. This drawback of standard repeat-sales indices is thus also not particularly relevant for survey data. Third, due to short time periods between survey waves (usually wealth or housing surveys take place every two to three years), the aging of the dwelling between price observations is negligible. Additionally, some surveys contain information on major renovations, which thus can be controlled for by adding this information as an additional predictor to the repeat-sales regression (2). Such kind of information is usually not available for market data. Forth, the short and for all dwellings equal time elapsed between survey waves, per construction, rules out heteroskedasticity concerns naturally arising when using sales data merging consecutive transactions all spanning periods of different lengths.

The ROA Approach

The ROA approach differs from the ROP approach in the way price pairs are constructed. In the absence of a panel structure, the original acquisition price can be matched to an OEV to identify price pairs for the same dwelling.

Let tS(i) for i ∈ {1,..., TS} denote survey years. The acquisition year is set as base period 1, and T is the number of years elapsed between the earliest observed acquisition in the sample and the latest available survey year. The function S: {1,..., TS} → {1,..., T} maps survey years to the period of observation. We denote the year of acquisition by s, the acquisition price by Pi,s and the OEV provided in a survey year \(t \in \{t_{S(i)}\}_{i=1}^{T_S}\) by Pi,t. Consequently, Dm=t = 1, Dm=s =  − 1 and Dm = 0 for m \(\not \in\){s, t}. Per construction, 1 ≤ s < t ≤ T and TS ≤ T. Then, model (2) turns into

$$\left[\log \left(\frac{P_{i,t}}{P_{i,s}}\right)=\sum \limits_{m=1} \limits^{T} \tau_{ROA}^{m}D_{i}^{m}+\varepsilon_{i}\right]$$

and the estimated parameters τROA are used to construct the index

$${{\varvec{I}}}_{ROA}\left(t\right)=\mathrm{exp}({\widehat{\tau }}_{ROA}^{t}).$$

The method only needs an OEV together with the original acquisition price and year. Asking for this information is a very common feature of both wealth and housing surveys. Thus, this method is applicable to most of those surveys, which largely increases the number of countries for which such an index can be constructed. As long as some homes were acquired in years between survey waves, the ROA approach yields index numbers also for these intermediate years making wave-to-wave interpolation obsolete. This is a clear advantage of the ROA method as compared to the before discussed hedonic and ROP approaches.

Additionally, the start of the index is not restricted to the first survey year but, at least in theory, the year of the earliest acquisition reported by survey participants. In other words, the index spans the period between the earliest acquisition year and the last survey year, and provides index numbers not just for the (usually much smaller) subset of survey years \(\{S(1), . . . , S(T_{S})\}\subset \{1, . . . , T \}\). In practice, one would disregard years with only very few observed acquisitions and let the index start once there are sufficient observations to guarantee a stable index. Still, the ROA approach may produce index numbers for several decades and may even lead to substantially longer time series than currently available objective indices. This is indeed the case for several countries in our sample.

The length of the index comes at the cost of potentially long time spans between the two observed prices for the same dwelling. In the meantime, the dwelling may have been refurbished, renovated and/or depreciated, which makes the dwelling at time of acquisition less comparable to the dwelling at the time of the survey interview. Additionally, heteroskedasticity likely is an issue. These arguments mean that the index is in general not expected to be very precise and less reliable for years very distant in time from the survey year as only few observations inform these index numbers. However, precision increases when approaching the survey years. Additionally, the general quality of the index increases with every additional survey wave as new price pairs becomes available. This also means a more fine-grained net of acquisition prices and thus the reliability of the index for years distant in time increases with this additional data.

However, we show in “OEVs and Acquisition Prices” that the resulting index numbers tend to not be reliable for the survey years themselves due to systematic deviations between transaction prices and OEVs. Reasons therefore are simulated in the Appendix. However, in the case of bi- or triennial surveys, the ROA index numbers before the first survey wave and between subsequent survey years tend to be reliable. Hence, the adjusted ROA index leaves out index numbers referring to survey years and reconstructs the missing index numbers again via linear interpolation. This means for, e.g., a biennial survey, the following adjustment:

$$I_{ROA_{adj}}(t)=\left\{\begin{array}{cc}I_{ROA}(t)&\mathrm{if}\; t \not\in \left\{t_{S(i)}\right\}^{T_{S}}_{i=1}, \\ \frac{ I_{ROA} (t+1)-I_{ROA}(t-1)}{2}&\mathrm{if}\; t \in \left\{t_{s(i)}\right\}^{T_{S}}_{i=1}. \end{array}\right.$$

Whenever applying a ROA-type approach, we definitely recommend to not combine acquisition prices with OEVs without such an adjustment.

The RO Hybrid Approach

Both the ROA and ROP approach link prices for the same dwelling available at different points in time. They differ in the type of prices used: The ROP approach links repeatedly reported OEVs, while the ROA approach links an OEV to the original acquisition price. While the ROP is expected to precisely measure price dynamics between the first and last survey years, i.e., for \(\{S(1), . . . , S(T_{S})\}\), the ROA approach is very attractive due to the length of the resulting series. However, the ROA index is expected to be affected by systematic over-reporting among home-owners in the period overlapping survey years (as simulated in the Appendix).

To benefit from the advantages of either method, a hybrid approach splices the ROP and ROA indices together: prior to the year of the first survey wave, an ROA index yields reliable results, whereas thereafter a ROP index should be preferred. This is achieved as folows: First, the ROA index IROA as well as the ROP index IROP are normalized to the first survey year tS(1), i.e.,

$${\widetilde{I}}_{ROA}\left(t\right)=\frac{{I}_{ROA}\left(t\right)}{{I}_{ROA}\left({t}_{S\left(1\right)}\right)}\quad \mathrm{and \ }\quad{\widetilde{I}}_{ROP}\left(t\right)=\frac{{I}_{ROP}\left(t\right)}{{I}_{ROP}\left({t}_{S\left(1\right)}\right)}.$$

Then, the hybrid index is obtained via

$$I_{RO_{hybrid}}(t)=\left\{\begin{array}{cc}\tilde{I}_{ROA}(t)& \mbox{if } t \leq t_{S(1)}, \\ \tilde{I}_{ROP}(t) &\mbox{if } t > t_{S(1)}.\end{array}\right.$$

Per construction,  \(I_{RO_{hybrid}}(t_{S(1)}) = 1\), but it can be normalized to any preferred base period after splicing the two series. In the absence of a panel structure, the ROP index can, of course, also be substituted by a hedonic index. Yet, we recommend using an ROP index if possible as this means splicing two conceptually more similar approaches.

Data and Methodological Details

To implement our convergent validity tests, two types of information are necessary. First, we need at least one country-representative residential property price index based on transaction data. Although transaction-based indices are not free of problems, they are the most commonly used objective indices in the literature and are probably the best objective benchmark.Footnote 7 These O-RPPIs come from statistical agencies, central banks as well as the existing academic literature and we will describe our sources at the end of this section.

Second, we need survey data to compile our subjective counterparts. For this matter, we make use of two exceptionally comprehensive population-representative surveys, which allow us to compile the three main types of subjective indices described above (hedonic, ROP and ROA). Specifically, we use the American Housing Survey (AHS) and the Italian Survey on Household Income and Wealth (SHIW). Both surveys ask for an OEV and an acquisition price necessary for compiling an ROA index, have a panel component enabling us to compile ROPs and provide sufficient information on dwelling characteristics and location to estimate hedonic models. Additionally, we introduce the pan-European Household Finance and Consumption Survey (HFCS) that comes with a rather limited set of information on dwelling characteristics yet allows us to highlight pitfalls of using OEVs as well as extending results to the entire euro area. The appendix provides all resulting S-RPPIs we compile from these surveys.

The remainder of this section describes how each survey elicits OEVs and provides methodological details on how to use the pieces of information available in each particular survey for constructing S-RPPIs.

American Housing Survey

Description of the Data

The American Housing Survey (AHS), sponsored by the US Department of Housing and Urban Development and carried out by the US Census Bureau, is a national housing survey collecting various housing and demographic characteristics. The sample unit is the dwelling. There are two samples drawn from: a national and a metropolitan one. The national sample is longitudinal and conducted in odd-numbered years. The metropolitan sample is cross-sectional and usually conducted in even-numbered years. The survey documentation provides further details.Footnote 8

We only use data for regular owner-occupied dwellings excluding rented units, mobile homes and land lots. The necessary identifiers are available from 1999 onward. Hence, we use 1999 as start year. Upon writing this article, the latest available wave was from 2013. Table B.2 in the appendix reports summary statistics for the national sample.

For eliciting an OEV, the survey participant is asked the following question for each property listed: How much do you think your […] would sell for on today’s market? The placeholder […] specifies for which item mentioned earlier in the survey, the price should be estimated. This could be either a house, a lot, an apartment, a mobile home or just any other unspecified property.

Methodological Notes on the S-RPPI

The Hedonic Index

Next to year dummies, we include the number of bedrooms (five categories: 1, 2, 3, 4, more than 4), the number of bathrooms including half-bathrooms (ten categories: 0, 1, 1.5, …,4, 4.5, more than 4.5), the age of the dwelling (with an unspecified functional form f (age)), the living surface (in log), as well as dummies indicating the existence of a complete kitchen, central air conditioning and the type of dwelling (detached house, attached house or multi-units structure). Additionally, we include the location of the dwelling via region dummies and location dummies (that we also interact). As described in “Subjective Residential Property Price Indices”, hedonic models are estimated by pooling two consecutive survey waves. Table 1 reports regression results when pooling all waves and including time dummies.

Table 1 Hedonic regression: US
Full size table

The ROP Index

The index links OEVs reported for the same dwelling over time. There are 202,136 observations that appear at least twice in the sample. These observations refer to 39,794 unique dwellings. We construct 162,342 price pairs, which enter the repeat-observations model.

The ROA Index

The index links a dwelling’s acquisition price to the OEV. The earliest acquisition price is reported for 1919, however, due to low numbers of observations at the beginning of the century, we only consider acquisition prices from 1932 onward. We disregard observations with a missing acquisition price or a reported acquisition price of less than USD 100.

We end up with 174,641 price pairs to estimate the ROA index. We also estimate a ROA index from the metropolitan sample, which yields 157,381 price pairs.

Italian Survey on Household Income and Wealth

Description of the Data

The Survey on Household Income and Wealth (SHIW), sponsored and carried out by the Banca d’Italia, is a population-representative survey collecting data on households’ income, wealth and savings as well as demographic characteristics (see Baffigi et al., 2016, for more details on the evolution of the dataset). The sample unit is the household. A part of the survey is longitudinal. Table B.1 in the appendix provides descriptive statistics and the survey documentation is again to be found online.Footnote 9

The OEV is elicited using the following question: In your opinion, how much is your house/flat worth (unoccupied)? In other words, what price could you ask for it today (including any cellar, garage or attic)?

Methodological Notes on the S-RPPI

The Hedonic Index

From 1986 onward, the survey contains a sufficient scope of dwelling characteristics for estimating hedonic models. Due to the quite frequent changes in variables and definitions, the hedonic equation is not fixed but allowed to flexibly change over time. Thus, we cannot provide an overall hedonic model as reported for the US data (Table 1). Instead, we make use of six specifications that comprehensively exploit the information collected in each pair of consecutive survey waves. Table 2 reports some general results for pairwise hedonic models. When assessing individual regressions, coefficients are as expected: the OEV increases with increasing living surface, when there are more bathrooms, and the rating of the property is higher. The functional form of age is roughly quadratic. The locational characteristics including the interactions are highly significant.

Table 2 Hedonic specification – IT
Full size table

The ROP Index

The index links OEVs reported for the same dwelling over time. There are 49,389 observations that appear at least twice in the sample. These observations refer to 13,844 unique dwellings. We construct 35,545 price pairs, which enter the repeat-observations model.

The ROA Index

The index links a dwelling’s acquisition price to the OEV. The earliest acquisition price is reported for 1900, however, due to low numbers of observations, we only consider acquisition prices from 1960 onward. We disregard observations with missing acquisition prices, an acquisition price of less than EUR 1,000, and observations where the ratio between OEV and acquisition price is less than 0.5. This selection criteria yield 23,898 usable price pairs to estimate the ROA index.

Household Finance and Consumption Survey

Description of the Data

The HFCS is a pan-European, ex-ante harmonized survey on households’ finances and consumption carried out by national central bank or national statistical office of all participating countries. The survey is coordinated by the European Central Bank that also publishes the harmonized survey data we rely on.

We use the first two waves, which were released respectively in April 2013 and December 2016. Since the fieldwork periods differ from country to country, the country data refer to different years (see Table 3). Due to the heterogeneity of the data, we refrain from reporting classical summary statistics but refer the interested reader to the survey’s ample online documentation.Footnote 10 In most countries, where a household wealth survey had already existed before launching the HFCS (e.g., Italy), the national surveys were usually extended to fit into the HFCS. For other countries, the HFCS constitutes the first wealth survey. In both cases, national surveys are usually extended to accommodate local demands and are thus more comprehensive than the harmonized HFCS version. Yet, for compiling cross-European indices, we purely rely here on the harmonized questionnaire.

Table 3 Summary of HFCS data used to construct a ROA
Full size table

In the HFCS, owner-occupiers are asked to estimate the current market value of their home which yields OEVs. The following question (translated to the respective languages used in each country) is asked: What is the value of this property, i.e. if you could sell it now how much do you think would be the price of it?

Methodological Notes on the S-RPPI

Country-specific ROA Indices

The harmonized HFCS data lacks sufficient hedonic characteristics for compiling such an index. In particular, there is no information on the location of the dwelling and only very limited information on other physical characteristics. Also, the harmonized questionnaire does not foresee a panel component. Thus, constructing subjective hedonic and ROP indices is not possible. However, there is information on the original acqui- sition price and an OEV is elicited, thus we can construct an adjusted ROA index.

Table 3 reports the number of waves that are available for each country as well as the respective fieldwork periods. Additionally, the numbers of observations used for constructing the index are reported. These numbers differ strongly across countries, which is due to three reasons: there is substantial variation in the size of European countries, the share of owner-occupiers as compared to renter in the population varies a lot, and also the relative size of the survey sample differs substantially across countries. Hence, the number of observations is related to the number of households as well as the number of owner-occupiers. These shares are exceptionally small for Germany and Poland. Thus, one would expect least reliable indices for these two countries, which is indeed what we find (see Fig. 4).

We also construct adjusted ROA indices. Hence, index numbers referring to survey years are left out and substituted by linearly interpolated values. As some of the survey fieldwork coincide with the peak of a housing boom (particularly in Spain), the indices are per construction unable to properly detect the spike. The more survey waves become available, the more acquisition prices will be available for neighbouring year, which will ultimately increase precision.

The Euro Area ROA Index

To create an aggregate subjective RPPI for the euro area (EA), we use the weighted average over all ROA indices belonging to the EA-17, i.e., the euro area as composed in 2011 including 17 countries. The weights are held constant over the period and refer to the 2013 GDP at market prices. Using a country’s GDP for weighting in this context mimics the methodology applied by the ECB for constructing aggregate RPPIs as outlined below.

As the HFCS lacks data to compile a ROA for Finland (no original acquisition price is available), this country is excluded. Finland’s share of euro area GDP amounts to roughly 2% only, which is why the impact of this exclusion is expected to be minor.

Benchmark O-RPPIs

For bench-marking subjective indices we rely on all readily available and country-representative O-RPPIs matching our survey data in geographic and temporal terms. We prefer indices covering the longest period possible, performing some kind of quality adjustment, and covering the whole country and all types of residential dwellings (apartments and houses). In terms of frequency, the survey data produces annual series that can easily be matched to higher- frequency indices. We thus consider both annual and more frequent series.

For some countries, more than one index fulfills these criteria and thus we use all of them for our comparisons. Overall, we identify 36 suitable indices taken from the Bank for International Settlements (BIS) data warehouse (see also Scatigna et al., 2014) and the academic literature. The latter yields some extended time widows. Table B.5 in the appendix summarizes all objective RPPIs used in this article.

Next to country indices, we make use of an euro area RPPI compiled by the European Central Bank. In line with its subjective counterparts, we use the index that reports changes in house prices for EA-17. The EA-RPPI is a weighted average of individual, country-specific RPPIs. Weights are determined by the contribution of a country’s GDP to the overall EA-17 GDP.

When comparing the earliest start years of our long S-RPPIs, namely the (adjusted) ROAs, our method actually extends these series back in time for several European countries (i.e., Austria, Cyprus, Estonia, Latvia, Malta, Netherlands, Poland, Portugal, Slovenia, Slovakia) as well as the euro area as a whole.

Convergent Validity Test Results

Hedonic Indices and Repeated OEVs

We start assessing the general quality and internal validity of our S-RPPIs by checking whether different index construction techniques yield similar results. We first focus on subjective hedonic and ROP indices and compute pairwise Pearson correlation coefficients for annualized changes in these S-RPPIs. Table 4 and Fig. 1 report the results: ROP and hedonic indices show strikingly high correlations. For the US we find ρUS = 0.998 and for Italy ρIT = 0.925.

Table 4 Correlations: changes in S-RPPIs
Full size table
Fig. 1
figure 1

S-RPPIs. Notes: The figures compare several types of S-RPPIs. All indices are normalized to 2000

Full size image

Reassuringly, that finding indicates that both methods elicit essentially the same house price dynamics. This suggests that indices constructed from survey data are quite consistent regardless of the method used. Thus, dynamics seem to be driven by measurable changes in the data rather than changes in the methodology applied.

After establishing this fact, we next compare these S-RPPIs with their respective objective counterparts. For the US, we use three suitable O-RPPIs covering the entire country: the Case & Shiller, the FHFE and the Zillow index. For Italy, two suitable indices are available: one index compiled by the Banca d’Italia and one by Cannari and Faiella (2008). Details are reported in Table B.5 in the appendix.

We find again strikingly high correlations ranging between 0.81 and 0.96 as reported in Table 5Footnote 11, with the correlations being somewhat larger for the US. Figure 2 provides a visual support of our conclusions. This is a remarkable result as the various O-RPPIs we use differ in terms of geographical coverage, data used (sales prices, appraised prices, imputed prices) and index construction methodology applied.

Table 5 Correlations: changes in S-RPPIs vs. changes in O-RPPIs
Full size table
Fig. 2
figure 2

S-RPPIs versus O-RPPIs. Notes: The figures compare the subjective RO hybrid index to O-RPPIs. Details about the O-RPPIs used are documented in Table B.5 in the appendix. All indices are normalized to 2000

Full size image

To validate this result, we compute 95% bootstrap confidence intervals for the correlation coefficients for all indices used. The lower bound ranges between 0.86 and 0.94 for the US and between 0.74 and 0.78 for Italy indicating that even when accounting for measurement insecurity in full, correlations remain strikingly high.

We hence firmly conclude that subjective hedonic and ROP indices survive our convergent validity tests. This means that the relationship between dwelling characteristics and OEVs, and repeated OEVs provided by the same owner for the same property are internally and externally consistent: the market dynamics inherent in these data are coherent regardless of index construction method used and also closely follow objectively measured market trends.

OEVs and Acquisition Prices

Next, we assess different types of ROA indices. In contrast to the results above, ROA indices are only weakly related to other subjective indices. Table 4 reports correlation coefficients for the ROA index and the ROP / hedonic index of 0.128 / 0.084 (Italy) and 0.498 / 0.498 (US) only. This means that we cannot confirm any internal validity of these indices. Still, we compare the subjective indices again to the same objective indices used before. Table 5 reports correlation results: for both countries the coefficients are low. For Italy, the Pearson correlation coefficients are not even statistical significantly different from zero. In other words, there is no co-movement detectable.

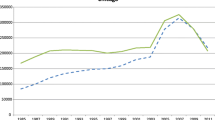
Why are unadjusted ROA indices so poorly correlated with their subjective and objective counterparts? The source of these weak correlations becomes evident from Fig. 3, which plots the ROA indices: in survey years, there are spikes in the index, while in non-survey years the index returns to its original price path. In the US, the spikes are less pronounced than in Italy. Still, in every single survey year, the index jumps up. Such a pattern – clearly not a realistic feature of the housing market – emerges when the prices reported for survey years, i.e., the OEVs, are systematically higher than acquisition prices that dominate the remaining, non-survey years.

Fig. 3
figure 3

ROA Indices: Combining Objective and Subjective Prices. Notes: The figure compares a raw ROA index to a ROA index, where index numbers for survey years are discarded and replaces by interpolated values. Survey years in Italy (left panel): 2002, 2004, 2006, 2008, 2010, 2012, 2014 and 2016; survey years in the US (right panel): 1999, 2001, 2003, 2005, 2007, 2009, 2011 and 2013. Indices are normalized to the year 2000. Dwellings that were acquired in survey years are discarded

Full size image

To confirm that systematically inflated OEVs are indeed consistent with our empirical results, we carry out a simulation study exemplarily calibrated to the US housing market. Details are provided in the Appendix. Indeed, a systematic bias – which we artificially induce in our simulation study – does create exactly the same patter we document here.

This finding is consistent with previous studies that document a tendency of owners to provide overly optimistic price estimates when referring to their own home. While our data does not allow us to explicitly test for the cause of such a bias – e.g., if it was indeed an endowment effect, we would need a measure of loss aversion, which is not available in survey data – our findings are consistent with an endowment effect: owners’ may put extra value on their home (not necessarily shared by buyers) simply because they own it.

Another potential explanation would be that owners collectively believe that their homes appreciated more than dwellings on the market or, put differently, their assets outperformed the market. This belief is different as compared to a belief that the intrinsic value of their home is higher. We can rule out this explanation: if it was a belief about higher appreciation rates, these would also be reflected in ROP indices. ROP indices, however, match objective indices almost perfectly. Also, we simulate this intuition and find that this explanation – in contrast to a one-time premium consistent with an endowment effect – does not reproduce the observed pattern (see again the Appendix).

A third explanation focuses on differences in tastes of owners and “the market” or an average buyer. Heston and Nakamura (2009) report that owners tend to provide significantly higher estimates of the hypothetical market rent their home could achieve as compared to observed market rents. One explanation they provide is that owners may place greater value than the market on certain features of their home, i.e., that owners’ subjective hedonic shadow prices associated with certain amenities are higher than the average “market shadow price” and that the taste of owners is different than the taste of renters. If that was indeed the prime explanation, this must already be reflected in the acquisition price. Some owners certainly remodel their dwelling after purchase to make it fit their taste. However, if that happened systematically, we would again need to see this in ROP indices, which we do not.

Regardless of the reason, we can conclude that OEVs are systematically higher in levels than objective market prices. Hence, our third convergent validity test fails. Thus, we recommend to refrain from using acquisition prices paired with OEVs to measure price developments and, importantly, using OEVs as reliable sources for measuring housing wealth.

The latter has far reaching implications: As OEVs tend to be the major vehicle to measure housing wealth – arguably one of the most important wealth components for large parts of the population – strong evidence for systematically inflated values means that any statistics relying on these values are expected to be biased. These include total and distributional wealth measures as well as studies focusing on housing assets and indebtedness directly.

Combining surveys with more market-driven prices (see, e.g., Molloy & Nielsen, 2018; Naidin et al., 2022) may thus be a viable way forward to benefit from both, the wide extra information on the micro-level provided by surveys and, at the same time, realistic price estimates for real estates.

A hybrid RO index

In the absence of (trustworthy) O-RPPIs or whenever O-RPPIs are only available for short periods of time, S-RPPIs may be a valuable source of information describing housing market trends.Footnote 12

Table 6 Starting year of the adjusted ROA and the matched O-RPPIs
Full size table

While the spikes observed in ROA indices certainly do not reflect market trends, leaving out these years and interpolating between survey years leads to a less frequent and precise index, but the result is still well capable to reproduce overall long-term trends. This partly interpolated index is called the “ROA adjusted” index and shown in Figs. 1 and 3. The correlations with other indices is not as high as for the cleaner ROP and hedonic indices, but still over 0.6 for Italy and even around 0.9 in the US (see Tables 4 and 5).

A “best-off” index hence exploits the ROA index’ advantage of being long as well as the ROP (or hedonic) index’ advantage of being more precise in survey years. This hybrid RO index equals the ROP index whenever it exists and extends it to the past using the ROA index. Methodological details are again explained in “Subjective Residential Property Price Indices”. Such an index also directly overcomes the issue of spikes resulting from systematic mis-evaluation and thus solves one aspect of shortcomings related to OEVs.

Validation of Results by Extending the Geographic Scope

To rule out that our results may only be valid for Italy and the US, we extend our analysis here to several European countries using the HFCS survey. As we have shown that an adjusted ROA-index correlates with the other subjective indices, we compute such indices for all countries participating in the HFCS and benchmark them against O-RPPIs (see Fig. 4).

Fig. 4
figure 4figure 4

ROA Indices for European Countries – HFCS data

Full size image

Although the adjusted ROA methodology is not our preferred one, the information available in the HFCS only allows us to construct such indices. On top, the HFCS is a “young survey” with only two waves available upon writing this article. These are probably the worst circumstances to estimate a subjective index and, therefore, this setting provides a very strong sensitivity analysis. Again, we find that S-RPPIs – even those relying on very small numbers of observations – reproduce overall market trends strikingly well.

Figure 5 shows an aggregated S-RPPI for the euro area. We aggregate country-specific S- RPPIs by weighting them with the country’s share of euro area GDP. This aggregation method mimics the procedure applied by the European Central Bank to obtain their euro area O-RPPI. Even on this supra-aggregated level, S-RPPIs and O-RPPIs match strikingly well. As revealed by Fig. 5, our techniques can be used to produce trends that go beyond the time span covered by currently existing objective indices and thus extends our knowledge of past housing market dynamics.

Fig. 5
figure 5

A S-RPPI for the Euro Area. Notes: The official O-RPPI for the euro area is a weighted index of country-specific O-RPPIs and compiled by the ECB. Weights are determined by a country’s share of euro area GDP. We replicate a S-RPPI for the euro area and use the 2013 GDP in current prices, which is composed as shown in the right panel. For Finland, no acquisition prices are collected and hence no S-RPPI is computed and the euro area S-RPPI misses Finland’s contribution. Since S-RPPIs are of different lengths, only between 1995 and 2010 the index is representative for the EA-17 (except Finland). The coverage in terms of euro area GDP is indicated by the bars at the bottom of the left panel

Full size image

Hence, we conclude that our findings are not particular to Italy or the US, but generalize to a large set of countries. These countries experienced quite different price dynamics in the past, which further increases confidence in the persistence and general nature of our results.

Conclusions

We argue that subjective data – specifically, owners’ estimated current market value of their main residence (OEVs) – is a valuable source to study housing market dynamics over time. To support our arguments, we design and apply three convergent validity tests that assess the internal and external validity of OEVs. These tests rely on price indices compiled from survey data together with existing objective counterparts. For the first, we develop several index construction techniques suitable for distinct pieces of information regularly collected in housing or wealth surveys. We apply our tests to data from three surveys (the American Housing Survey, the Italian SHIW and the European HFCS) and demonstrate that subjective indices are a credible alternative to describe housing market dynamics.

The subjective indices yield substantial information on house price developments over ex- tended periods of time and, in fact, for some countries even extend the coverage of currently existing official information on house price developments back in time. This is indeed the case for eleven countries we study here.

Further, we document that OEVs combined with house characteristics as well as repeatedly provided OEVs over time for the same dwelling reproduce the evolution of objectively observed transaction data strikingly well. This supports the use of OEVs for measuring relative price changes over time based on survey data.

Yet, we document that levels are systematically inflated. This questions the reliability of owner-estimated levels of current housing prices as well as thereof derived statistics (see also Naidin et al., 2022, for simulations of potential consequences).

The convergent validity tests are carried out for a large set of countries, several years and several methodological approaches. Hence, we are confident that our conclusions apply to a wide variety of contexts.