Coming of Age: Renovation Premiums in Housing Markets

Abstract

We rely on novel textual analysis of real estate listings and identify renovated dwellings in a dataset of Norwegian transactions to estimate the renovation premium in an urban housing market. The renovation premium is estimated in a hedonic framework by classical regression approaches and a random forest algorithm. The strength of the latter is that it allows for a more complex interplay between the renovation premium and explanatory variables. We estimate a significant positive renovation premium of 5–7 percent for renovated dwellings and a negative premium of 9–10 percent for unmaintained/neglected dwellings. These averages mask significant variations in these premiums over time, particularly, a counter-cyclical effect. Omitting renovation information also has implications for estimated short-term house price growth. Unmaintained dwellings tend to transact more in the fourth quarter, indicating that parts of the seasonal price variation reported in the literature are due to compositional variation with respect to renovation. This composition effect bias price movement estimates downward, if uncontrolled for, as unmaintained dwellings transact at significantly lower prices.

Introduction

The housing market is of keen interest to households and policymakers alike. Real estate constitutes the major wealth component for most households. The last financial crisis made us painfully aware that the housing market is not a passive receiver of shocks; it can be the originator of an economic downturn with dire consequences (e.g., Leamer, 2015). However, houses transact infrequently and are highly differentiated with respect to their characteristics. An important dimension of this heterogeneity is related to variations in the quality of the structure. Quality heterogeneity can arise in markets for durable goods, such as real estate, where consumers have a choice of new or used goods that have deteriorated to a lower quality (Sweeney, 1974). Owing to this, monitoring the housing market is far from easy, a recurrent issue within macroprudential policy.

Economic models of house prices have various strategies to control for heterogeneity. Hedonic models, where house prices are explained by a wide array of house characteristics, such as location, size, number of bedrooms, etc., date back to Rosen (1974). Models of repeated sales tackle the issue of heterogeneity by considering same-house sales (e.g., Case & Shiller, 1989). The fundamental assumption of both workhorse house price models is the ability to control for quality variation, either directly (hedonic) or indirectly by assuming the house quality does not change between sales (repeated sales). Failure of these assumptions will likely lead to biased inference if the omitted information is essential. For instance, the dwelling size and location are typically found to be more important for the transaction price than a fireplace and an extra bathroom (see Xiao, 2017). In this hierarchy of price determinants, renovation is likely to be high on the list but seldom included due to data limitations. The listing of dwellings for sale online may change this.

Online listings often state that a dwelling is newly renovated as this information is likely to attract interested parties. A wide range of positive words is used to describe newly renovated units (gorgeous, flawless, exclusive, lavish) along with information on the extent of renovation. Online listings also include photos, and poorly maintained dwellings are easy to spot. The wording, in this case, tends to focus on a unit’s potential and attract interested parties that are comfortable with a major renovation. Hence, these listing texts shed information about the renovation and the maintenance level of the dwelling for sale.

We study the renovation premium in a hedonic framework for an urban housing market over five years (2014–2019). The period contains a boom followed by a bust and thus allows us to address the potential time variation of the renovation premium, particularly whether it is pro- or countercyclical. The analysis relies on two novel datasets, mainly a listing dataset and in addition a detailed prospectus dataset of transacted dwellings in Oslo, Norway.¹ We pair transaction data with their listings text and, through text analysis, classify dwellings into four groups, unmaintained, partially renovated, fully renovated, and none of the first three.

It is important to stress that the incentive to renovate is higher in attractive areas since the expected gain from renovations exceeds the cost by a greater margin (Gyourko & Saiz, 2004). In other words, one may expect a spatially clustered vintage effect (Randolph, 1988b) that creates challenges for estimations of the renovation premium. We address this concern by applying flexible random forest techniques as well as classical hedonic- based regression approaches. The major takeaway from our analysis is the importance of renovation as a price determinant. Failure to control for renovation leads to significant biases of housing price levels and indices. Unfortunately, these are not only considerable but also tend to vary over time and across space.

We find a premium for the fully renovated (in the 5 to 7 percent range) and a negative premium for the unmaintained (in the 9 to 10 percent range). Our estimates can be interpreted as a lower bound of the renovation premium. These average effects gloss over interesting temporal variation. In particular, heated housing markets diminish both the positive premium of the fully renovated dwellings and the negative premium of the unmaintained. The counter-cyclical effect is especially strong for the fully renovated. In a heated market, buyers, on average, do not distinguish renovated from non-renovated dwellings in terms of pricing.

These results could be explained by changes in the composition of buyers over the housing cycle, in line with the predictions of Chernobai and Chernobai (2013), leading to variations in the bargaining process between buyers and sellers on certain characteristics (Bourassa et al., 2009). A second candidate explanation is the income-mortgage effect. The market heat is like a tide that lifts all boats, but the attractive and expensive in several market segments to a lesser extent due to income and mortgage financing limitations. This may result in less competition for expensive dwellings, which include the fully renovated for otherwise constant characteristics. In contrast, unmaintained dwellings allow for a future renovation and, as such, involve a potential investment smoothing.

Another notable finding is a systematic quarter-to-quarter variation, where the 4th quarter sees more unmaintained dwellings changing hands. This composition effect has implications for the seasonal variation observed in house price indices and tends to bias price movement estimates downward, if uncontrolled for, as unmaintained dwellings transact at significantly lower prices. Finally, our results show that the renovation bias tends to be higher in less central areas, driven by a higher frequency of unmaintained dwellings transacted.

The literature on renovation and renovation premiums in the housing market is sparse. The lion’s share of academic contributions concerns neighborhood effects. These may be related to externalities or positive spillover effects (e.g., Wilson & Kashem, 2017). One form of externality regards sustainability, that renovation may have a negative impact on the environment, at least in the short run (Liu et al., 2020). In the case of the Taiwanese market, Lee et al. (2017) estimate the renovation premium per area unit (ping²) to 10.0 percent (14,880 NTD), but the focus is spillover effects of urban regeneration. Another branch of literature concerns the renovation premium through energy-efficiency-related renovations. McLean et al. (2013) estimate a renovation premium of 9.4 percent from increased energy efficiency for the Hungarian housing market. Therefore, little is known about the isolated impacts of general renovations. Our paper, in contrast, considers small-scale, household-initiated renovation or lack thereof. Spillover effects are likely to play a minor role in our case.³ The direct impact of a renovation that involves improved energy efficiency is likely to be part of the renovation premium.

The literature on renovation and repeat sales indices is more extensive and points to a significant difference in estimated house price growth with and without renovation information. McMillen and Thorsnes (2006) estimate a repeat sales index (median quantile) for Chicago for the period 1993–2002 and find that the index overestimates price growth by 9 percent without renovation information. Bourassa et al. (2013) arrive at an even larger overestimate (14 percent) for Louisville, Kentucky (1988–2010) for their repeat sales index. Furthermore, Bogin and Doerner (2019) asserts that overestimation tends to be severe in central areas due to an uneven concentration of renovation activity. Our paper contrasts this literature by the renovation information used⁴ and by studying the renovation premium and renovation bias in a hedonic framework. The two main reasons for the choice of the hedonic methodology are, firstly, the ability to estimate implicit prices. Secondly, we do not observe the renovation status of the dwellings at previous sales. For the broader role of housing quality, early contributions appeared at the same time as the seminal work on attribute prices of bundled goods. Two of these are Sweeney (1974) and Cubbin (1974).

The remainder of the paper is organized as follows. Data Description and Renovation Classification describes the data and classification details. Methodology for Assessing the Impact of Renovation discuss measurement and outline empirical strategies. Results Empirical Analysis reports results for the renovation premium. Temporal Variation in the Renovation Premium consider temporal heterogeneity in the renovation premium, and Renovation Bias in House Price Growth estimates the "renovation bias" in short term house price growth. Additional Tests and Robustness Analysis perform additional tests. Conclusion and Discussion concludes.

Data Description and Renovation Classification

Institutional Detail and Data Description

Most real estate transactions in Norway are arm’s length brokered sales. The seller contacts a broker who puts the house on the market. The broker is also responsible for preparing the sales prospectus and listing, and when the house is placed on the market, the listing and sales prospectus are available online. Moreover, the broker organizes an open house and manages the ascending-bid auction, which usually takes place on the first business day after the open house. Bids are submitted by telephone or electronically, and each bid is legally binding.

The listing data contains the main text of the listing and a wide range of characteristics for 10,350 transacted dwellings in Oslo, Norway. The dataset is acquired from Eiendomsverdi ASA, a private company that collects all transactions in the Norwegian housing market and provides price valuations based on the automated valuation method (AVM) for banks and brokers, considered the best valuation by market agents and the government. In addition, the listing data includes zip codes, geographic coordinates, and both the transaction price and the AVM price valuation. It covers the period from primo 2014 to medio 2019. Table 1 provides summary statistics for the main variables. The dwellings have a mean age of 54.6 years, mean size of 79.7 square meters, and the majority of transactions are apartments (85.5 percent).

Table 1 Summary Statistics for prices and key housing characteristics for listing data. Prices in million NOK. N = 10,350

Renovation Classification

The main focus of this paper is quality-enhancing renovations in the context of real estate sales. In contrast to most previous work, information on renovations within the structure, such as a new kitchen and bathroom, is also extracted.⁵

One challenge in creating a renovation classification is that it is essentially a continuous variable. A new house is "renovated" and begins its journey toward “unmaintained”. As a dwelling age, its quality deteriorates in two ways. First, everything from plumbing fixtures to window frames is subject to natural tear and wear. Second, after a certain amount of time, the materials and construction become outdated and no longer reflect the current zeitgeist. To offset or dampen these effects, owners may decide to do a partial or full renovation. To distinguish these cases, a renovation variable with two positive values for partial renovation (1) and full renovation (2) and one negative value for unmaintained (-1) or neglected units in need of renovation is constructed. Dwellings that are neither renovated nor unmaintained but somewhere in between are labeled neutral (0). Since we are unable to estimate renovation more precisely for the entire dataset, a scale is used as a proxy.

A combination of machine search and a careful reading of all listings was undertaken to assign one of the values 2, 1, 0, or -1 to the renovation variable. About half of the units classified as renovated (48 percent) had "renovated" in their list text.⁶ Whether the renovation is interpreted as full or partial depends on whether it includes the most expensive rooms to renovate, as well as the timing of the renovation, and the overall impression of the extent of the renovations. For instance, units with a new kitchen, floors, and bathroom or that is described as "fully renovated" receive a score of 2. In contrast, units with new paint and a kitchen installed seven years ago or described to have "some renovations" receive a score of 1. Only new paint and no further renovation signaling information receive the score 0. As much as 89 percent of dwellings classified as unmaintained had "unmaintained" in their list text. These and similar wordings are assigned the score -1. Thus, incomplete information in the listings may result in many dwellings being classified with a renovation score of zero. To address this concern, a second dataset of prospectuses with extensive detail is used to see if the distribution of renovation scores differs greatly from the distribution based on the listing dataset.⁷

Classification Results

In total, we find a share of 12.4 percent renovated (7.0 percent fully renovated) and 8.7 percent unmaintained transactions, based on information in the listings. Our results for the share renovated are roughly comparable to those of McMillen and Thorsnes (2006), who estimates a renovation share of transactions associated with issued building permits in Chicago of 10.7 percent over 1993–2002. However, these results are significantly larger than those of Bogin and Doerner (2019).⁸

In addition, we can shed some light on the development of renovated transactions over time. Figure 1 shows the quarterly distribution of sales by renovation class. The highest combined renovation share of sales for a single quarter is 26 percent in 2016-Q4 (neutral non-renovated units, denoted R0, account for 74 percent), and the lowest is 13 percent in 2018-Q3. There is evidence of systematic quarter-to-quarter variation, where the 4th quarter (Q4) sees more unmaintained dwellings changing hands, with an average of 11 percent of sales compared to 7–8.5 percent in Q1-Q3.⁹

Fig. 1

The Renovation Class of House transactions by share of sales between 2014-Q1 and 2019-Q2. N = 10,350. The figure shows the quarterly results of a classification of sales by renovation level based on real estate listings in Oslo, Norway. Notes: R-1 $\sim$ unmaintained, R0 $\sim$ neutral, R1 $\sim$ partially renovated, R2 $\sim$ fully renovated

Finally, there are notable differences in dwelling age and price per square meter by renovation class. For instance, older dwellings are increasingly likely to be renovated (Table 2).¹⁰ This accords with the result in Lee et al. (2005) that the renovation (redevelopment) propensity increases with the age of the dwelling. Since older dwellings tend to be located in more attractive parts of this urban area, one might expect a spatially clustered vintage effect (Randolph, 1988b) that creates challenges for estimation of the renovation premium. This age-renovation patterning may partly be driven by a pure age effect caused by the extent of depreciation. Partly by an investment effect caused by higher incentives to renovate in attractive areas since the expected gain from renovation exceeds the cost by a greater margin (Gyourko & Saiz, 2004).

Table 2 Classification Results. The number of House transactions in each Renovation class (frequency in percent) in the listing dataset (top) and the Age distribution by Renovation class (bottom). N = 10,350

Methodology for Assessing the Impact of Renovation

The observed renovation premium is defined as the expected increase in the equilibrium house price for an average renovation, derived from the well-known hedonic equilibrium price function $P=f\left(X, \varepsilon \right).$ The price function maps the relationship between the observed and unobserved to the economist attributes, respectively $\left(X, \varepsilon \right)$, and the house price $P$. The implicit price reflects the marginal willingness to pay for renovation (Rosen, 1974).

We build on Randolph (1988a) and Randolph (1988b) in our understanding of how renovation combines with closely related attributes such as residential depreciation and overall quality of a unit in the price function. In this view, residential depreciation can be defined as the value of the portion of unmeasured quality change caused by aging alone. A renovation is a discrete upward shift in the aging/quality depreciation curve. The interpretation for the hedonic relationship is that any measurements of age depreciation are expected to capture renovations that are unobserved to the economist in addition to age-only depreciation. This is consistent with Diewert et al. (2015) who defines the net depreciation rate as the "true" gross depreciation rate of the house less an average renovation appreciation rate.

The following sections presents empirical strategies for identifying and examining the renovation premium. Because the fraction of measured age depreciation that is attributable to renovation or quality of materials is unobserved, and for simplicity, our analysis focus on the observed renovation premium (according to our classification), which is referred to below as the renovation premium. However, it should be inferred from this discussion that there are potentially important interactions, correlated characteristics, and nonlinear effects in the hedonic relationship, especially when considering the isolated impact of renovation/neglect on the house price. We address these concerns by applying flexible random forest techniques as well as classical hedonic-based regression approaches. As a measure of the gain in house valuation performance from our renovation information, the loss in predictive performance with and without renovation information included as characteristics is compared.

A classical Linear Regression Model

As a benchmark specification, a classical log-linear regression that has become standard in the hedonic house price literature (see Xiao, 2017, for a recent review) is estimated. The house price model includes dummies for renovation class, along with a set of characteristics. Subsequently, the benchmark specification is extended to include interaction terms between characteristics such as renovation and location and location and age of the unit. These regressions with interactions highlight spatial variation in the renovation premium and the age distribution of dwellings. Our regression specification is, $\forall i \in \left(1, {N}_{T}\right):$

$$\mathrm{log}{P}_{i}= {\beta }_{0}+ {\beta }_{1}\mathrm{log}\left({Size}_{i}\right)+ \sum_{\forall s\in S}{\beta }_{S}{D}_{is}+ \sum_{\forall l\in L}{\beta }_{l}{L}_{il}+\sum_{\forall k\in K}{\delta }_{k}{R}_{ik}+ {\varepsilon }_{i}.$$

(1)

where ${P}_{i}$ is the house price, ${Size}_{i}$ is the area (in sqm.), ${D}_{is}$ are either dummy variables or dummy interaction variables, $s\in$(dwelling type, ownership type, dwelling age cohort, sales quarter, administrative area dummies and/or price zone dummies), ${L}_{il}$ are administrative level fixed effects, $l\in$(income level, education level), and ${R}_{ik}$ are renovation classes $k\in$(-1, 1, 2). The delineation of the age cohorts and log-form of house size is proposed in a preliminary analysis by a random forest estimation.¹¹${\varepsilon }_{i}$ is an error term. The coefficients of primary interest are estimates of the renovation premium, ${\delta }_{k}.$ The dataset¹² is split into an estimation set ${S}_{T}$ containing 70 percent of the data and an out-of-sample set ${S}_{O}$ containing 30 percent.

A Random Forest Algorithm

The hedonic theory provides little guidance about the functional form of the relationship between the house price and various characteristics. This is especially relevant when there are likely to be non-linear effects or complex interactions among characteristics. To address this concern, a growing body of literature uses more flexible methods to value real estate; among these, non-parametric random forest algorithms.¹³ Many studies conclude that a random forest improves predictive performance relative to more standard approaches to house price modelling (e.g., Bogin & Shui, 2020; Čeh et al., 2018; Yoo et al., 2012) or when dealing with other challenging prediction problems (Auret & Aldrich, 2012), although several caveats remain when interest concerns consistent and stable coefficient estimates (Mullainathan & Spiess, 2017).

The random forest algorithm is a particularly interactive class of models that builds a random ensemble of decision trees by bootstrapping. Specifically, we use the methodology described in (Breiman, 2001) with cross-validation to select an optimal complexity level that maximizes prediction accuracy without overfitting. Candidate variables for each decision tree split are drawn randomly from the complete set of variables, making each tree distinct.¹⁴ The random forest and classical regression models use the same set of independent variables to ensure comparability of inferences.

Predictive performance is compared out-of-sample (O). The squared correlation coefficient (R² and adjusted R²) and root mean square error (RMSE) are among the most commonly used measures of accuracy, where $RMSE =$ $\sqrt{\frac{1}{{N}_{O}}{\sum }_{i}{(\mathrm{log}\left({P}_{i}\right)-\mathrm{log}\left({\widehat{P}}_{i}\right))}^{2},}$ and weights larger errors more heavily than smaller errors.

Spatial Aggregation

A well-documented challenge in regression methods such as hedonic house price estimation arises from spatial dependence and spatial heterogeneity when models do not adequately capture spatial structure or omits essential variables (Anselin, 1990; LeSage & Pace, 2009). To obtain robust estimates of the spatial price premium, both standard administrative area districts from zip codes and noncontiguous price zone dummies are constructed. The price zones are estimated with the methodology described by Sommervoll and Sommervoll (2019).¹⁵ This flexible aggregation method allows us to find spatially distant areas with similar location premiums.

The prize-zone algorithm can be summarized as follows:

• 1. Estimate an auxiliary hedonic house price regression.

• 2. Use a grid to partition Oslo into rectangular cells.

• 3. Restrict the number of submarkets to be fixed at 12.

• 4. Search for maxima for the auxiliary hedonic regression (here R²) by varying the spatial aggregation of the cells using a genetic algorithm, a variant of gradient ascent.

• 5. The final result is an aggregation of 370 zip codes to 12 submarkets, represented by a 370-dimensional vector $(7, 2, 7, \mathrm{1,12},\dots )$ with cells estimated to have the highest location premium in price zone nr. 12 and the lowest in price zone nr. 1.

The administrative areas and price zones should be interpreted differently. For instance, while administrative areas capture the aggregated value of neighborhood amenities such as the quality of schools and area reputation, the price zones capture the aggregated value of amenities across space such as the extent of view, hours of sun and transportation access.¹⁶ Any aforementioned unexplained spatial clustering of dwelling vintages (different construction vintages may imply variations in the quality of materials etc.) is also expected to be captured to some extent in the price zones.

To evaluate the spatial implementation and compare regression models, spatial autocorrelation is tested for by estimating the global Moran’s I statistic on model residuals (LeSage & Pace, 2009; Moran, 1948). It uses the location of dwellings, where location is a pair of latitude and longitude coordinates $\{{lat}_{i}, {lon}_{i}\},$ and is defined:

$$MI= \frac{{N}_{T}}{S}\frac{{\sum }_{i}{\sum }_{j}{w}_{ij}{z}_{i}{z}_{j}}{{\sum }_{i}{z}_{i}^{2}} .$$

where ${N}_{T}$ is the number of units in the estimation data, ${z}_{i}= {\widehat{\varepsilon }}_{i}-{\overline{\varepsilon }}_{i}$ is the deviation from mean of residual $i$, ${w}_{ij}$ is the spatial weight that defines the spatial relationship between pairs of observations $i$ and $j$ and $S$ is the sum of all weights. The definition of ${w}_{ij}$ is crucial for measuring spatial autocorrelation, as it implies a conjecture of how observations are related in space. We assume that local autocorrelation is the main potential issue and construct a set of ${N}_{T}\times {N}_{T}$ spatial weight matrices ${W}_{r}$ of different ranges within 0.1–1.5 km as contiguity matrices¹⁷ using the great circle distance around each dwelling as calculated by the Haversine formula. Dwellings within each cutoff distance receive an equal weight in the final row-standardized ${W}_{r }, \forall \mathrm{r}\in (0.1, 0.5, 1.0, 1.5)$.

Results Empirical Analysis

The Renovation Premium in the Classical Model

Table 3 reports results for the effects of three levels of renovation on price. Included is a comparison for the classic regression model with area dummies and area fixed effects (column 1) and one that also includes the price zone dummies (column 2).¹⁸ Column 3 shows the results for the model in column 2 without the renovation variable. Column 4 shows the results with interaction terms between dwelling age and area, and column 5 also adds interactions between renovation class and area.¹⁹

Table 3 Regression Results: Classical linear model

Across the different specifications in columns (1)-(5), these results suggest a significant positive average renovation premium²⁰ in the range of 5.4–6.1 percent for fully renovated (R2) dwellings, and a negative premium in the range of 9.1–9.5 percent for unmaintained (R-1) dwellings. The following adjustment is used to interpret the coefficients as the percent change in price: $\left[\mathrm{exp}\left({\widehat{\delta }}_{k}\right)-1\right]\times 100.$ The coefficient for partial renovation (R1) is slightly positive but close to zero in most cases. This could be due to the difficulty distinguishing "somewhat" renovated from neutral (R0).

To interpret the economic magnitude of the average renovation premium, we focus on the results in column 2. Expressed in market prices, a renovation premium of 5.7 percent implies a premium of NOK 255,800 (USD 28,100) for the average-priced dwelling sold in the middle of the period. A negative premium of 9.2 percent for unmaintained units implies a discount of NOK 414,100 (USD 45,600). These are substantial sums for the average working person, who earned an average of NOK 522,700 per year before taxes in the middle of the period.²¹

When excluding the renovation variable in column 3, this is seen to scale the other model coefficients, in particular the age coefficients. This is consistent with age-renovation correlations. A similar effect is seen for the age coefficients when including the price zones in column 2, suggesting spatial clustering of dwelling vintages is captured to some extent in the price zones. Including dwelling age and area interactions in column 4, the average marginal effect (AME) renovation premium for fully renovated is estimated to 5.9 percent. The AME estimate for unmaintained units is similar to the previous. Column 5 displays area-specific renovation premiums, suggesting spatial variation.²² In addition to the possibility of heterogeneous "treatment effects" of renovations, such patterns may be due to systematic geographically heterogeneous "treatments," i.e., the size and monetary value of the renovation. It is likely that investments are larger in high-end areas due to more expensive tastes and higher expected resale values, so fully renovated does not mean the same on average for different locations.

Improvements in Prediction Performance. Comparison of the Random Forest and the Classical Model

The random forest algorithm achieves moderately higher overall performance than the classical regression model out-of-sample, such as a decrease in RMSE from 0.128 to 0.115 in Table 4 Panel B, columns 1 and 7. R squared increases from 0.898 to 0.918. However, the random forest is also found to reduce spatial dependence in the residuals for all sets of spatial variables, indicating its superiority in capturing spatial structure and heterogeneous effects. This is in accordance with McMillen (2010), who argues that problems with functional form may lie behind any observed spatial autocorrelation and suggests the use of flexible methods. The random forest achieves slightly higher out-of-sample performance than in-sample,²³ consistent with that the predictor is not overfitting to the estimation data (Hastie et al., 2009).

Table 4 Moran’s I (in-sample) and Model performance (out-of-sample)

The inclusion of the price zone dummies is found to reduce spatial dependence, as evidenced by lower spatial autocorrelation of the residuals (see the results of the Moran’s I test in Panel A).²⁴ The spatial autocorrelation is estimated to be positive and strongest at a radius of 100 m around each dwelling. Although significantly different from its theoretical mean (close to zero) under the null hypothesis of no spatial autocorrelation, Moran’s I test statistics between 0.026–0.162 (first column) and 0.012–0.117 (fourth column) are considered low.²⁵

When excluding the renovation variable in the linear model, there is a modest decrease in adjusted R squared overall, from 0.902 to 0.896 (columns 1 and 4). RMSE increases from 0.128 to 0.131. Model performance for the random forest changes to a similar extent. Because of well-known issues with the interpretation of "coefficients" or derived partial effects as consistent estimates for the random forest algorithm (e.g., Mullainathan & Spiess, 2017), we restrict attention to the magnitude of the estimated parameters in the classical models.

The marginal improvement in adjusted R squared by including the renovation variable is larger in the upper and lower quartiles (P75 and P25, respectively) of the house price distribution, as seen for the linear model when comparing the second and fifth columns of Table 4 where it increases from 0.604 to 0.629. This larger tail effect bears resemblance to McMillen and Thorsnes (2006) who also points to larger effects from omitting renovation information in the upper and lower quartiles.²⁶

Overall, Table 4 shows that spatial dependence is not expected to be a major concern for our preferred model specifications in columns 1 (classical) and 4 (random forest). This supports our results for the renovation premium obtained previously. Second, the gains in model performance from including the renovation variable is similar for the classical model and the more flexible random forest, with larger gains in the tails of the house price distribution.

A Model with Professional AVMs

A challenge to hedonic valuation is that unobserved factors may be correlated with the house price and characteristics of interest. This is relevant for the probability of renovating a house and could lead to inconsistent estimates of the renovation premiums (see a discussion in Bajari et al., 2012). To illustrate, omitting unit-specific characteristics such as a fireplace and balcony may be correlated with expected resale value and thus, the decision to renovate or not renovate prior to sale. To address this issue, we collect external price valuations used by market participants and produced at the time of sale. The AVMs are based on all transactions in the Norwegian housing market (including those outside Oslo) and a more comprehensive set of hedonic characteristics. The following strategy is used, $\forall i\in \left(1,\dots , {N}_{V}\right):$

• 1. Regress the valuation price ${logP}_{AVM,i}$ on our set of hedonic characteristics. Variable interpretations are the same as for model (1):

  $$\mathrm{log}{P}_{AVM,i}= {\overline{\beta }}_{0}+ {\overline{\beta }}_{1}\mathrm{log}\left({Size}_{i}\right)+ \sum_{\forall s\in S}{\overline{\beta }}_{S}{D}_{is}+ \sum_{\forall l\in L}{\overline{\beta }}_{l}{L}_{il}+\sum_{\forall k\in K}{\overline{\delta }}_{k}{R}_{ik}+ {\overline{\varepsilon }}_{AVM,i}.$$

  (2)

• 2. Calculate the vector of residuals, ${\widehat{\overline{\varepsilon }}}_{AVM,i}.$

• 3. Estimate the hedonic classical model including the orthogonalized residuals, ${\widehat{\overline{\varepsilon }}}_{AVM,i}$, our estimate of unobserved price-determining factors:

  $$\mathrm{log}{P}_{i}= {\overline{\overline{\beta }}}_{0}+ {\overline{\overline{\beta }}}_{1}\mathrm{log}\left({Size}_{i}\right)+ \sum_{\forall s\in S}{{\overline{\overline{\beta }}}_{s}D}_{is}+ \sum_{\forall l\in L}{{\overline{\overline{\beta }}}_{l}L}_{il}+\sum_{\forall k\in K}{{\overline{\overline{\delta }}}_{k}R}_{ik}+ {\widehat{\overline{\varepsilon }}}_{AVM,i}+ {\epsilon }_{i}.$$

  (3)

Table 5 display results with the AVM instrument for omitted characteristics. Due to dataset variations²⁷ the classical model is re-estimated in column (1), resulting in a lower premium for full renovation estimated at 4.4 percent. Results for the other premiums are similar. Column 2 contains the results of model (3) estimated with OLS. These results strengthen our previous findings for the renovation premiums. The coefficients are identical up to two decimal places and more stable, suggesting that our estimates are robust when the extensive price-determining characteristics in the AVM valuation is controlled for. The quality of the AVM valuation is also reflected in the large increase in adjusted R squared from 0.909 to 0.945 (0.935 without our hedonic characteristics in column 3).

Table 5 Regression Results: A model with professional AVMs

Temporal Variation in the Renovation Premium

The period for which we have access to renovation information contains a boom followed by a bust. This section examines the temporal variation in the renovation premium and compare the trajectory of the premium with the housing market cycle. In addition to the benchmark linear hedonic model and the nonparametric random forest considered earlier, a rolling-window version of model (1) is estimated. For this purpose, the estimation sample is split into three adjacent parts. Each estimator is used to predict the identical time window out-of-sample.²⁸ The adjacent window approach is useful for studying parameter variation. The random forest index results are used to determine breakpoints for the rolling window model.

To study temporal variations in the renovation premium, our procedure is to trace out the renovation premium over time by estimating the HPI by renovation class and computing their ratios. Since interest lies in level movements for a bundle of characteristics, it is convenient to consider a Laspeyres price index.²⁹ Each price index, defined as ${I}_{{x}_{i}\in {S}_{B}}^{0-t}$ for any period $t$ relative to period 0, is obtained by predicting the classical linear, rolling-window, and random forest models on a fixed set of house transactions at the beginning of the period, ${S}_{B} \left({N}_{B}=954\right),$ named the base period. The characteristics of the base period, ${x}_{i}\in {S}_{B}$ where $B=$ 2014–2015,  are held constant and reassessed subsequent periods. It is essential that the composition of the characteristics is reasonably evenly distributed and that the base period set is sufficiently large. Fortunately, both the renovation classes and the other characteristics appear to be largely balanced in ${S}_{B}$ and later periods, with some small variations.³⁰

Figure 2 shows separate house price indexes by renovation class (right) and the corresponding renovation premium (left). One notable result is that the premiums vary considerably in this volatile market period when considering the random forest model (a), allowing for such variability. Panel (e) and Table 6 columns (1)-(3) gives results for the rolling window model that support the time variation trend in the renovation premium found by the random forest model. During the boom-bust period, the premium on full renovation is not significantly different from zero. As a result, when excluding the boom- bust periods in the rolling window model, the average premium on fully renovated units increases to 6.7–7.0 percent. The discount on unmaintained units is also reduced during the boom-bust period, although the reduction is smaller in magnitude. Panel (d) shows the equivalent index for the classical linear model, where the price development by renovation class are multiplicative shifts from each other, a consequence of the log-linear form of the model.

Fig. 2

Renovation Premiums in a housing market (left). Separate hedonic House price Indexes by Renovation class (right) (a) Random Forest Renovation premium (b) Random Forest Index (c) Linear Renovation premium (d) Linear model Index (e) Linear Rolling window Renovation premium (f) Linear Rolling window Index. The figure displays results for the temporal variation in the renovation premiums. Notes: The renovation premium in period $t$ (figures on the left) is defined as the difference between the estimates of the HPI level of fully renovated (R2) and neutral (R0) units at $t$, for out-of-sample HPI predictions (right-hand side). Similarly for R-1. The confidence interval for the renovation premium is twice the standard error of the differences in the average predictions. The random forest uses the jackknife median standard errors of the predictions

Table 6 Regression Results: Rolling window model^a

Figure 3 show the renovation premium predictions of the random forest model (Fig. 2a) along with macro-variables providing information on the housing cycle, as measured by house price growth and housing investment growth.³¹ These results suggest the renovation premium is counter-cyclical during the boom and bust. This finding is consistent with Zabel (2015) who estimates a counter-cyclical variation in hedonic implicit prices for other housing quality characteristics for Boston, US. The result of a counter-cyclical premium for unmaintained houses also resembles the findings of Bourassa et al. (2009) who asserts that the values of atypical homes rise at higher-than-average rates in strong markets, whereas the reverse holds in weak markets.

Fig. 3

Renovation premium, House price growth and Housing investment growth. The figures display results for the renovation premiums compared to the housing market cycle. Notes: House price and residential investment growth are official estimates from Eiendomsverdi ASA and Statistics Norway, respectively. The premium for unmaintained dwellings is shifted up by 0.07 percentage points for ease of interpretation

Renovation Bias in House Price Growth

This section examines the impact of omitting renovation information on the HPI. The previous sections document evidence of differences in the composition of renovated dwellings over time. Moreover, that the renovation premium is significant. This may have implications for estimated house price growth.

The difference in the house price growth estimates for the classical linear model is calculated. The quarterly house price growth for the Laspeyres HPI described earlier is computed, including, and excluding the renovation variable. The results in columns 2–3 in Table 3 is used. The absolute deviation in the house price growth estimate is defined as the renovation bias:

$$\left|\Delta log{I}_{R}^{t-(t+1)}- \Delta log{I}_{None}^{t-(t+1)}\right| , \forall t\in \left(1,\dots ,T\right).$$

(4)

The average absolute deviation in estimated house growth for the city total and smaller strata is displayed in Fig. 4 Quarterly House Price Growth, with and without Renovation informationand summarized in Table 7. Evident in the figures is a systematic fourth quarter effect. Since the frequency of unmaintained dwellings is considerably higher in the fourth quarter, this tends to bias the fourth quarter price movement estimates downward, if uncontrolled for, as unmaintained dwellings transact at a significantly lower price. For the City total the renovation bias is estimated to 0.32 percentage points per quarter, which is 8.08 percent of the average absolute quarterly growth over this period. The results for the Central region are similar. In the less affluent East, omitting renovation information leads to a larger deviation in estimated price growth, 0.70 pp. on average, equivalent in absolute terms to 14.83 percent of average quarterly growth.³² This finding contrasts with Bogin and Doerner (2019) who proposes the bias in the HPI is greatest in downtown areas of large cities. Most, but not all, quarterly differences are statistically significant (Fig. 4).³³

Fig. 4

Quarterly House Price Growth, with and without Renovation information (a) City total (b) Central (c) East. The figure displays results for the quarterly absolute renovation omission bias (%) of the linear classical hedonic model for the City total, the Central strata, and the East strata. Notes: HPG omitted omit renovation and HPG renovation includes renovation in the hedonic regression

Table 7 Renovation bias in quarterly house price growth

Additional Tests and Robustness Analysis

This section addresses a shortcoming of the renovation classification and tests if a change in demand for centrality could confound the results. The main takeaway from these analyses is that our results for the renovation premium and counter-cyclical variation largely hold. However, as there are likely to be renovations not reflected in the online-listings texts, this is expected to create a downward bias in the estimates of the renovation premium. As such, our estimates can be interpreted as a lower bound of the renovation premium.

Adjustments for Shortcomings of the Renovation Classification

Comparing the classification based on listings with a classification based on complete prospectuses, we expect that too few units are classified with renovation class R1 and R2.³⁴ The discrepancy is estimated to be 8 points of transactions for the fully renovated. In the repeat-sales framework, researchers often aim to address unobserved factors such as renovations and remodeling by approximate methods such as truncating the tails in the error or price change distribution. For instance, Bajari et al. (2012) and Harding et al. (2007) removes observations in the top appreciation rate percentiles. In the hedonic framework, it is common to remove units based on outlier prices and characteristics, such as very large or very expensive dwellings (e.g., Xiao, 2017).

Similarly, two observations based on our renovation classification are exploited to roughly target undetected renovated units. First, one can observe that a larger share of the detected renovated units would end up in the top right tail of the error distribution. Table 8 reports results for each renovation class by residual percentile based on the classical linear hedonic model without renovation information. While 11.5 percent of the detected fully renovated units appear in the upper P80-P100 percentile residual distribution, only 2.1 percent appear in the bottom P0-P20 percentile. Second, renovated dwellings tend to be dated. As many as 24–25 percent of dwellings above 90 years are detected renovated, while this is the case for less than 1 percent of dwellings aged 10 years or younger.³⁵ Specifically, we restrict candidate dwellings to units initially assigned renovation class R0 in the right tail of the price error distribution based on the linear hedonic model specification that includes the renovation information from the listings.³⁶ Sales from the boom year 2016 are excluded since any large unexplained price may be related to, among others, market tightness rather than renovations.

Table 8 Renovation class (share) by Price Residual percentile

Four different dataset truncations are tested, and the linear models are re-estimated on each corresponding adjusted dataset (Table 9). Columns 1–2 adjust the samples solely on upper price residual criteria. When truncating the upper six percentile (P94) and four percentile (P96) error distribution, the coefficient on partial renovation increases to 2.0–2.4 percent and is highly significant. The coefficient on full renovation increases to 6.7–7.1 percent and the discount on unmaintained units reduces to 7.5–7.9 percent. Noting that the detected renovated units are not as right skewed in the error distribution as in the dwelling age distribution, columns 3–4 consider a broader part of the error distribution and add age criteria. Column 3 excludes units in the top 30 error percentile (P70) if they are more than 70 years. In column 4, this reasoning is taken even further, where units in the top 50 percentile (P50) error distribution are excluded if they are more than 90 years. Results for the renovation premiums are similar, although the increase in the premium estimates for partial and full renovation is even more substantial. Columns 5–7 displays the results of the rolling window model for scenario P70 Age I. The pattern of temporal variation in the renovation premium is still evident, with R1-R2 premiums declining sharply in the boom-bust years.

Table 9 Adjusted sample Regression Results: Classical and Rolling window model

Overall, the reductions in the right tail of the price error and age distributions have resulted in larger implicit price estimates for renovation. However, this approach probably involves removal of dwellings that are old but not renovated or receive an unexplained high price (by our model) for reasons unrelated to renovation. Although we suspect that our renovation premium estimates are somewhat biased downward, it is plausible to expect that these rough adjusted sample-estimates are biased upward. Thus, our results can be interpreted as a lower bound of the renovation premium. Moreover, we gain support for the finding of counter-cyclical temporal variation.

Testing if Variations in the Renovation Premium are Driven by Variations in the Implicit Price for Centrality

Based on hedonic theory, it could be argued that all implicit prices may exhibit a similar pattern to the renovation premium in times of disequilibrium. More importantly, movements in one implicit price may be confounded by movements in another if not accounted for. Using the random forest, HPIs segmented by other hedonic characteristics (such as size and type) are examined for similar patterns of temporal variation. Potential heterogeneity in implicit prices for apartments vs. single-family units has received some attention among practitioners. We find that the temporal variation in size- and dwelling type coefficients are considerably more modest.³⁷ However, the average HPI by geographical strata follows a similar, but less pronounced, pattern where the centrality premium reduces temporarily during the boom.

From this finding, there is the possibility that our results for the variations of the renovation premiums may in part be driven by shifts in the centrality premium. To test this contingency, the temporal variation of the renovation premium for more homogeneous urban strata is examined. The most central urban area around the CBD (Central), an affluent western suburb (West), and a less affluent eastern suburb (East),³⁸ although this distinction is not exact. Figure 5 displays the renovation premium for the Central and East regions. The renovation premium shows similar patterns with considerable cyclic variation over the period, implying that our results are robust to lower geographical segmentation.

Fig. 5

Strata: Random Forest Renovation premiums (a) Central (b) East. The figure displays our results for the temporal variation in the renovation premiums in two urban strata, the most central urban area around the CBD (Central) and a less affluent eastern suburb (East). Note: The methodology is identical to Fig. 2. The out-of-sample dataset for 2014–2015 for the Central region is of size ${N}_{central,O\in (Q114,Q415)}=493$, whereas the estimation dataset is of size ${N}_{central, T}=\mathrm{3,212}$. Similarly for the East, ${N}_{east,O\in (Q114,Q415)}=172$ and ${N}_{east,T}=\mathrm{1,098}$

Conclusion and Discussion

The housing market involves transactions of dwellings that differ with respect to hedonic characteristics. A fundamental assumption of workhorse house price models is the ability to control for quality variation. Failure of this assumption is likely to lead to biased inference if the omitted information is essential. This paper addresses the price determinant renovation, which is of unknown importance, being seldom included in house price estimation due to data limitations.

Texts of online listings of houses transacted in the Oslo market for the period 2014 to 2019 are used to sort dwellings according to four renovation classes.³⁹ We find that the renovation premium (fully renovated) is in the 5 to 7 percent range. The negative premium for unmaintained dwellings is somewhat higher, estimated at 9 to 10 percent. Our results for fully renovated dwellings are lower than the estimates in McLean et al. (2013) of 9.4 percent for Hungary. However, when comparing our point estimates with other studies, the differences in the renovation data should be kept in mind.⁴⁰

Nevertheless, one limitation of this study is that it relies on less than perfect identification of renovation class for the dwellings in question. This creates a downward bias, and as such, our estimates can be interpreted as a lower bound of the renovation premium. However, the importance of renovation as a price determinant is an undeniable takeaway from our analysis. Failure to control for renovation leads to significant biases of housing price levels and indices. Moreover, these are unfortunately not only considerable, but they also tend to vary over time and across space.

The time dimension is important for two reasons. First, it appears to be a variation with the business cycle, where the renovation premium is considerably lower in a more heated housing market. This effect is the opposite for unmaintained dwellings, where the negative premium is reduced in a heated housing market. These results could be explained by changes in the composition of buyers over the housing cycle, in line with the predictions of Chernobai and Chernobai (2013), leading to variations in the bargaining process between buyers and sellers on certain characteristics (Bourassa et al., 2009). A related explanation is shifts in investment motives and levels of exuberance. Depken et al. (2011) estimates that in a boom phase, a large percentage of transactions are speculative or “flips” in Las Vegas, US, while this share is highly reduced in a bust.

Another candidate driving factor is the income-mortgage effect. The market heat is like a tide that lifts all boats, but the attractive and expensive in several market segments to a lesser extent due to income and mortgage financing limitations. This may result in less competition for expensive dwellings, including fully renovated for otherwise constant characteristics. Unmaintained dwellings allow for a future renovation and, as such, involve a potential investment smoothing. Future research extends this analysis by incorporating micro data on housing search and the holding times of each renovation class to study if variations in renovation premiums are matched by variations in search and the extent of flipping.

Second, our analysis indicates that part of the well-known seasonality in house price indices is partly due to composition effects. The frequency of unmaintained dwellings is considerably higher in the fourth quarter. This composition effect has implications for the seasonal variation observed in house price indices and tends to bias price movement estimates downward, if uncontrolled for, as unmaintained dwellings transact at a significantly lower price. Adding to this, the systematic temporal variation in renovation premiums may also bias estimates for price indices and house price growth.

Finally, this study observes significant spatial variation in renovation classes. Existing evidence (e.g., Bogin & Doerner, 2019) concludes that a higher renovation activity in central areas is the primary explanation for biased HPI estimates. In contrast, our results show that the renovation bias tends to be higher in less central areas, driven by a higher frequency of unmaintained dwellings transacted. We ascribe the differing results mainly to variations in the information sets used, mainly that our study also includes the unmaintained characteristic. There are reasons to believe that both higher renovation frequency in central areas and higher propensity to not undertake necessary maintenance in more distant areas from the city center apply to most cities. As both effects lead to a smaller price difference between central and non-central areas when adjusting for renovation (or lack thereof), this finding has implications for the literature regarding beta and sigma convergence in metropolitan areas (see e.g., Wood et al., 2016).

At a higher level, our analysis of online listings points to a way to control for renovation. Other ways, for example, using computer vision (Yencha, 2019), may prove an even more powerful way to measure the degree of renovation and get closer to quality-adjusted price levels and price indices for the housing market. In this sense, our analysis is an early contribution that shows controlling for renovation is feasible and involves significant rewards.

Appendices

Appendix 1

Table 10

Table 10 Data Preparation prospectus data and Summary Counts listings and prospectus data. Averages and totals

Table 11

Table 11 Frequent Words in listing texts and Summary Statistics by Renovation class $N=\mathrm{10,350}$

Table 12

Table 12 Validation: Renovation Classification Results between 2017-Q2 and 2019-Q2. Shares and volumes. Prospectuses (P) and Listings (L)

Table 13

Table 13 Administrative areas in Oslo by Strata

Figure 6

Fig. 6

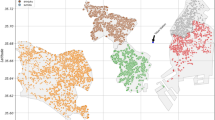
The share of Renovated transacted dwellings by administrative area between 2014-Q1 and 2019-Q2. Left: Renovated (R1-R2). Right: Unmaintained (R-1). The figure maps the spatial distribution of the share of renovated transacted dwellings for the five-year period. According to these findings, renovation shares R1-R2 are positively associated with urban location (left graph), with the highest shares in central, high-end suburbs. Unmaintained sales are more common in low-income southern and eastern suburbs (right panel). For instance, renovated dwellings are more frequent in area 3 which includes the city center. Unmaintained units are more frequent in area 12, the cheapest housing areas in the city. The numbering corresponds to Table 13. Notes: Oslo’s large most Northern administrative area, including mainly recreational zoning areas, is excluded from the map (Marka)

Figure 7

Fig. 7

Transactions in Administrative areas (by color) and non-contiguous Price zones (by color). $N=\mathrm{8,203}$ Notes: The administrative areas in (a) are described above. The price zones in (b) are constructed based on the methodology described in Sommervoll and Sommervoll (2019)

Table 14

Table 14 Data Preparation listing data

Table 15

Table 15 Checks for Balances: Summary Statistics estimation data, out-of-sample data, and data with AVMs. Prices and Key housing characteristics. Prices in million NOK

Appendix 2

Random forest details

Random forest algorithms require hyperparameters that control how many decision trees are grown, how many variables are included in each split (mtry), and how small each terminal node of the tree can be (node size). The chosen performance measure minimizes the predictions’ root mean squared error (RMSE). To find the optimal set of hyperparameters, we run a loop of hyperparameter combinations using fivefold cross-validation.

Although regression tree models often use categorical data in their natural form, it is worth considering whether alternative coding can improve performance. In this case, including all variables in numerical form produces the best predictive results. The best performing models, in the sense of no significant gains in model performance (R squared or RMSE) from altering the hyperparameters, is found around the parameter set where the number of trees is about 1,000, as this is demonstrated to be sufficient to achieve a stable error rate in our case (see the discussion in Breiman, 2001), $mtry$ is 5–6, and the final $node size$ is 5. With a node size beyond 6, performance is reduced. The final hyperparameters used are $mtry=$ 5, $node size=5$, $trees=\mathrm{1,000}$. The infinitesimal jackknife for bagging is used to estimate the standard errors. The $Ranger$, $Caret$ and $RandomForest$ packages in $R$ are used to estimate the models. Reported estimation results are based on the Ranger package (see Wright & Ziegler, 2015).