Commonalities in Private Commercial Real Estate Market Liquidity and Price Index Returns

Abstract

We examine co-movements in private commercial real estate index returns and market liquidity in the US (apartment, office, retail) and for eighteen global cities, using data from Real Capital Analytics over the period 2005–2018. Our measure of market liquidity is based on the difference between supply and demand price indexes. We document for all analyzed markets much stronger commonalities in changes in market liquidity compared to commonalities in real price index returns. We further provide empirical evidence that space markets are less integrated than capital markets by analyzing co-movements in net-operating-income and cap rate spreads (over similar maturity bond yields). In a theoretical simulation model, we show that the strong integration of capital markets compared to space markets, is in fact the reason why market liquidity co-moves so strongly compared to returns. Our results are of interest for large private real estate investors such as pension funds and other institutional investors who are interested in spreading risk. Our findings imply that fully diversified price return benefits may be difficult to obtain, because market liquidity may dry up in all markets simultaneously, which makes portfolio re-balancing more difficult and costly.

Motivation and Research Questions

Investors in private commercial real estate (CRE) properties do not only face price risk, but also the risk of illiquidity, the uncertain time it takes to sell properties (Cheng et al., 2010; 2013). Commonalities in private CRE market liquidity – the ease of trading a property – are in particular relevant for investors directly investing in CRE properties, such as pension funds and other institutional investors. Large investors tend to have multiple holdings across many regions, most likely because of diversification benefits in terms of price and income returns. Price return diversification benefits are only feasible if properties can be traded on a “normal” liquid basis. If, for example, liquidity dries up in all markets simultaneously, it may not be possible to reap the full diversified price return benefits. Depending on the degree of commonality in segments (for example apartments, offices, retail, and industrial) and regions within national and international markets it might be possible to diversify liquidity risk in their portfolio.

To the best of our knowledge this is the first paper systematically documenting and analyzing commonalities in (changes in) market liquidity for several private commercial real estate markets: 25 large US markets, the 6 largest US markets subdivided by sector (office, retail, and apartment), and 18 Global Gateway markets, using transaction data from Real Capital Analytics in the period from 2005Q1 to 2018Q4.

Commonality in liquidity has been studied for other, more liquid, assets, mostly being stocks and bonds. Chordia et al. (2000) analyze common determinants in the liquidity of stocks, providing suggestive evidence that inventory risk and asymmetric information affect liquidity over time. Hasbrouck and Seppi (2001) study price discovery and liquidity in equity markets and find that both returns and order flows have common factors. Moreover, they find that commonality in order flows explains about two-third of return commonalities. Korajczyk and Sadka (2008) analyze various liquidity measures using 18 years of intraday stock data and find that across-measure systematic liquidity is priced, while within-measure systematic liquidity is not. Lee (2011) finds that liquidity risk in stock markets is priced independently of market risk, but vary over countries, having implications for international portfolio diversification. Karolyi et al. (2012) relate variation in stock market liquidity to supply-side (funding liquidity) and demand-side determinants (such as correlated trading behaviour and investor sentiment). They find that differences in commonality in liquidity between countries can be attributed to volatility, the presence of international investors, and correlated trading activity. Chordia et al. (2005) explore cross-market liquidity dynamics in the stock and Treasury bond market. Their results show that common factors drive liquidity in both markets. The commonality between returns and stock market liquidity risk for listed real estate has been examined by Hoesli et al. (2017). The authors find that commonalities in stock market liquidity result in risk factors for REIT returns, but that this only holds in bad times.

The nature of private real estate markets makes it hard to observe large quantities of transactions. Real estate assets are traded in private deals, mostly between a single buyer and seller, resulting in a relatively long time to sell a property. Moreover, unique assets are traded infrequently and irregularly through time (Geltner, 2015). This makes liquidity in private real estate markets very different from liquidity in public securities markets, where, unlike for private assets, inventories, order flows and market makers play a role in market liquidity.

This paper uses as a measure for market liquidity the difference between supply and demand price indexes relative to a standard price index, following Fisher et al. (2003) and Fisher et al. (2007) and Clayton et al. (2008). We use the method of Van Dijk et al. (2020), who derive supply and demand indexes in a repeat sales model framework. This approach has the advantage of effectively dealing with heterogeneity in commercial real estate assets, without the need for many property characteristics or assessed values. Moreover, by using Bayesian techniques the supply and demand indexes can be robustly estimated in small samples. Several other market liquidity metrics exist, relating to different dimensions of liquidity, such as transaction volume, Amihud measure (2002), turnover ratio, time-on-the-market, and trading frequency. For an extensive overview and discussion of liquidity measures in real estate markets we refer to Ametefe et al. (2016).

It is well known that market liquidity and asset prices in real estate markets co-move; changes in market liquidity tend to be pro-cyclical to changes in asset prices. This holds for CRE markets (Fisher et al., 2003; Clayton et al., 2008) as well as for residential real estate markets (Goetzmann and Peng, 2006; De Wit et al., 2013). Most of the studies on the interaction of liquidity and return dynamics focus on a single CRE market (Fisher et al., 2003; Fisher et al., 2007; Clayton et al., 2008; Wiley, 2017). There are a few exceptions. Ling et al. (2009) study price dynamics and transaction activity for ten segments in private commercial real estate in the UK over the period 1987–2007. They find a statistically significant positive relationship between lagged turnover and contemporaneous capital returns. Devaney et al. (2017) study determinants of variations in transaction activity for a set of 49 US MSA office markets in the period 2002–2015. Van Dijk et al. (2020) note that for the US market, liquidity movements tend to be stronger correlated across markets than price movements. Brounen et al. (2019) study the relation between liquidity and price returns in international listed real estate markets. They find wide variations across ten markets using four different liquidity measures (trading volume, stock turnover, Amihud measure and the number of zero return days). Moreover, they document evidence for international trend-chasing behavior.

Commonalities in private real estate market returns have been extensively researched. For example, Srivatsa and Lee (2012) examine the convergence of yields and rents in European offices markets, MacGregor and Schwann (2003) find common cycles in UK CRE returns, and Van de Minne et al. (2018) find two common factors that summarize the variation in price index returns for 80 US CRE markets. Clark and Coggin (2009) provide evidence of commonalities in US housing returns and Holly et al. (2011) look at the relationship between London, other UK, and New York housing returns.

Because market liquidity and prices in private real estate markets move together, we compare commonalities in market liquidity changes to commonalities in real price index returns. Furthermore, by comparing commonalities in market liquidity and prices, we are able to provide a better interpretation of how big those commonalities are. Most investors will have a rough idea on how big commonalities in returns are, therefore this serves as a natural benchmark to economically interpret the magnitude of the market liquidity commonalities. For example, we are able to make statements that the commonalities in changes in market liquidity are larger, smaller, or similar to return commonalities for the same group of markets.

We add to the real estate literature by documenting that co-movements in market liquidity changes are much stronger than co-movements in price index real returns. In fact, for the 25 largest US MSAs we find that commonalities in changes in market liquidity are almost twice as big as return commonalities. Significantly larger commonalities for market liquidity compared to returns are also found for US markets subdivided by industry and for Global Gateway markets. We use the method of Roll (1988) and Karolyi et al. (2012), a R²-based method, to measure the degree of commonality.

We further analyze drivers of the difference in the degree of commonality between market liquidity and price. We present simulation results from a theoretical “cap rate” model, in which the different components – net-operating income, risk-free rate, risk premium and growth expectations – co-move to a different degree across markets, and buyers and sellers have different views on these components. We show under which assumptions we have stronger co-movements in market liquidity changes compared to price index returns. First, the cross-market co-movement in the risk premium component (determined by capital markets) needs to be stronger than the cross-market co-movement in rents (determined by space markets). We provide empirical evidence for this assumption by showing that space markets are less integrated than capital markets by analyzing co-movements in net-operating-income and cap rate spreads (over similar maturity bond yields). Second, sellers need to lag buyers “sufficiently” in their perception of risk premium compared to net-operating-income. The second assumption relates to “loss aversion” or anchoring (Bokhari and Geltner, 2011). The seller bought the property some time ago against the financing conditions that prevailed at that time. Hence, it is reasonable to assume that the current perception about financing conditions is a function of past financing conditions that applied to the property in question. Also, information asymmetries might play a role here, where sellers are not able to “digest” all possible market information instantaneously (Carrillo et al., 2015; Van Dijk & Francke, 2018).

In summary, we pose three questions related to private CRE markets:

• (i) “How strong is the co-movement in changes in market liquidity?”

• (ii) “How strong is the co-movement in real price index returns?”

• (iii) “Which factors drive the difference in commonality between market liquidity changes and real price index returns?”

The paper proceeds as follows. Section “Methodology” provides details on the construction of market liquidity and commonality measures. Section “Data” describes the data, documenting per market summary statistics on price index returns and changes in market liquidity. Section “4 4” shows the degree of empirical commonality in both market liquidity changes and price index returns. In addition, this section shows degrees of integration for net-operating-income and risk premia. Section “Robustness Checks” provides results from three different robustness checks: (i) an alternative commonality measure by principal components, (ii) two alternative market liquidity measures: transaction volume and the Amihud measure (Amihud, 2002), (iii) the findings when excluding the effect of the Global Financial Crisis. Section “Theoretical Simulation Framework” provides simulation results to justify the use of our empirical commonality measure and to understand the factors that drive the difference in commonality between liquidity and price. Section “Conclusion and Possible Extensions” concludes.

Methodology

Price Index Returns in Real Estate

Fundamentally, space market as well as capital market characteristics should be reflected in the price of real estate. We can express the prices in the celebrated “cap rate” model as follows¹:

$$ P_{i,j,t} = \frac{NOI_{i,j,t}}{RF_{i,t}+RSP_{i,j,t}-G_{i,j,t}}, $$

(1)

where subscripts i,j and t denote a market, property and time-period, respectively. NOI is the net operating income of the property, G the prospective growth rate of the NOI, RF the risk-free rate, and RSP the risk premium. Rewriting Eq. 1 in logs yields:

$$ p_{i,j,t} = noi_{i,j,t}-\log(RF_{i,t}+RSP_{i,j,t}-G_{i,j,t}), $$

(2)

where the lowercase variables are the log-transformed uppercase variables. Property level price (capital) returns can be obtained by rewriting the log-model in first differences:

$$ {\varDelta} p_{i,j,t} = {\varDelta} noi_{i,j,t}-{\varDelta}\log(RF_{i,t}+RSP_{i,j,t}-G_{i,j,t}). $$

(3)

This equation implies that price returns in market i for period t are dependent on changes in both capital market variables (RF, RSP) and space market variables (noi, G). Price indexes could be derived from a model that includes both local market conditions and property characteristics (time-invariant property characteristics cancel out in a repeat-sales setting²):

$$ \begin{array}{@{}rcl@{}} p_{i,j,t}&=&\beta_{i,t}+x_{i,j}^{\prime}\alpha+\varepsilon_{i,j,t}, \end{array} $$

(4)

$$ \begin{array}{@{}rcl@{}} {\varDelta} p_{i,j,t}&=&{\varDelta} \beta_{i,t}+{\varDelta} \varepsilon_{i,j,t}, \end{array} $$

(5)

where x_i,j is a K-dimensional vector of time-invariant property characteristics with corresponding coefficient vector α, and ε is an independent normally distributed error term with mean zero. β_i,t (Δβ_i,t) is the common log price index (return) for market i at time t. These common trends are the market-wide developments in prices. Relating this to the fundamental price (3), these trends reflect market-wide trends in risk-free rates, risk premia, and NOI growth rates. The property characteristics usually capture property-specific variables, such as location, size, maintenance, parking facilities etc.

Returning to our research questions on commonalities, it is straightforward to see that commonalities in index returns across different markets (i.e. the co-movement in Δβ_i,t across different i) are determined by the commonalities in changes of the separate components of Eq. 3. The NOI and growth rate (G) are more likely to be determined by space markets, whereas the risk-free rate (RF) and the risk-premium (RSP) tend to be determined more by capital markets. Space markets are determined by local characteristics and capital markets tend to be nationally or even internationally integrated. Even though space markets may co-move across markets as well, it is reasonable to assume that this holds to a larger extent for capital markets. This is something we examine in our empirical setup and assume in our theoretical simulation later on.

Market Liquidity in Real Estate Markets

In order to introduce our concept of market liquidity, we begin by disentangling the pricing (4) into buyer and seller components.³ Doing so, we get something commonly referred to in the literature as reservation prices of buyers and sellers (Fisher et al., 2003):

$$ \begin{array}{@{}rcl@{}} rp^{b}_{i,t} &=&noi^{b}_{i,t}-\log(RF^{b}_{i,t}+RSP^{b}_{i,t}-G^{b}_{i,t}), \end{array} $$

(6)

$$ \begin{array}{@{}rcl@{}} rp^{s}_{i,t} &=&noi^{s}_{i,t}-\log(RF^{s}_{i,t}+RSP^{s}_{i,t}-G^{s}_{i,t}), \end{array} $$

(7)

where rp denote (log) reservation prices. Superscripts b and s denote buyers and sellers, respectively. The other symbols are equivalent as discussed in the previous section. Note that buyers and sellers might have different perspectives on income, prospective growth rate, risk premium, and the risk-free rate.⁴ Again, we can reformulate Eqs. 6–7 in a linear model:

$$ \begin{array}{@{}rcl@{}} rp_{i,t}^{b}&=&\beta_{i,t}^{b}+x_{i}^{\prime}\alpha^{b}+\varepsilon_{i,t}^{b}, \end{array} $$

(8)

$$ \begin{array}{@{}rcl@{}} rp_{i,t}^{s}&=&\beta_{i,t}^{s}+x_{i}^{\prime}\alpha^{s}+\varepsilon_{i,t}^{s}. \end{array} $$

(9)

In this case, ${\beta _{t}^{b}}$ and ${\beta _{t}^{s}}$ are common trends across the reservation prices of all buyers and sellers, respectively. These common trends are the market-wide developments of the central tendencies of buyers’ and sellers’ reservation prices.

Reservation prices, however, are latent unobserved variables that are not readily available. Fisher et al. (2003, 2007) develop a method to disentangle buyers’ and sellers’ reservation prices from transactions data. Van Dijk et al. (2020) extend this method in a repeat sales and structural time-series framework such that the method can be applied on most transaction data-sets on a regional scale. Van Dijk et al. (2020) further propose a metric for market liquidity based on the difference of buyers’ and sellers’ reservation prices scaled by the prevailing transactions price. To answer our question on commonalities, we use this method to construct demand and supply reservation price indexes as well as liquidity indexes on a regional scale. The model assumes that heterogeneous properties trade in a double-sided search market. Buyers and sellers base their valuation of a given property (reservation prices) on observable property characteristics. In this model, we observe a transaction if $rp_{i,t}^{b}>rp_{i,t}^{s}$.

Assuming equal bargaining power for the buyer and seller side, the average asset price valuation β_t that we measure in general in price indexes per Eq. 4 is halfway in-between buyers’ and sellers’ reservation price:

$$ \begin{array}{@{}rcl@{}} \beta_{i,t} = \frac{\beta_{i,t}^{b}+\beta_{i,t}^{s}}{2}. \end{array} $$

(10)

Following Fisher et al. (2003), the indexes are transformed such that the mean of the buyers’, sellers’, and midpoint price indexes is equal. We start the log price index at an arbitrary value of zero.⁵ By looking at the difference between buyers’ and sellers’ reservation price indexes, we are able to construct a liquidity metric. The liquidity metric can be interpreted as the sum of the buyers’ and and sellers’ reservation prices as a percent of the current prevailing consummated transaction price that would bring the market to long-run average liquidity. In that case the liquidity metric would be equal to 0. The metric for a given market i at time t is defined as:

$$ \begin{array}{@{}rcl@{}} Liq_{i,t} &= (\beta_{i,t}^{b} - \beta_{i,t}^{s}) - \beta_{i,t}. \end{array} $$

(11)

The term $\beta _{i,t}^{b}-\beta _{i,t}^{s}$ denotes the time trend of the probability of sale per period, keeping constant the included property characteristics. The components of the liquidity metric can be estimated by a two-step approach (Heckman, 1979) using a probit model to estimate $\beta _{i,t}^{b}-\beta _{i,t}^{s}$, and an adjusted linear regression model to estimate β_i,t. For a more elaborate description of the variables, the model, and estimation procedure we refer to Van Dijk et al. (2020). The liquidity metric is theoretically and empirically closely related to other liquidity metrics based on for example the time-on-market in housing or the turnover rate (Van Dijk, 2018). The main difference is that this liquidity metric is quantified in the price dimension, relative to the currently prevailing price level. This makes the used measure in this paper particularly suitable to compare market liquidity dynamics to price dynamics.

Because the price and liquidity metrics are estimated for regional markets for which sometimes few transactions are available (the markets are said to have thin data), we estimate the price and liquidity indexes in a structural time-series repeat sales framework to efficiently distinguish between signal and noise. The price index returns are assumed to follow a first-order autoregressive process. For more information on the smoothing procedures, see Van Dijk et al. (2020).⁶ Please note that the time trend of the probability of sale $\beta _{i,t}^{b}-\beta _{i,t}^{s}$ is estimated using all sales, including one-only sales as well. We further recognize that the literature sometimes uses different market liquidity metrics. Therefore, we have devoted a robustness check that uses two alternative measures of market liquidity: Transaction volume and the Amihud measure, see subsection “Two Alternative Market Liquidity Measures”.

The individual components of our fundamental pricing equations of buyers’ and sellers’ reservation prices (6–7) are reflected in the price index (β_i,t) and in the liquidity metric (Liq_i,t). Price index returns essentially reflect the average of buyers’ and sellers’ changes in valuations. The market liquidity metric, however, is the difference between the valuations of buyers and sellers. As a consequence, common valuation of characteristics common to both buyers and sellers cancels out. The remaining liquidity metric should thus reflect the characteristics that are valued differently by buyers and sellers. It is not straightforward to answer whether space or capital market characteristics cancel out in this case. We will show in a simulation framework in Section “Theoretical Simulation Framework” that, with minimal assumptions, it is mostly the space market components that are cancelled out. Hence, changes in the liquidity metric mostly reflect changes in the capital market components.

Measuring Commonality

We employ two different measures for the commonality in market liquidity and returns. First, we use measures frequently applied in stock market research. More specifically, we model regional market returns on national (aggregate) market returns. See Roll (1988) and Morck et al. (2000) for stock return applications and Karolyi et al. (2012) for a stock market liquidity application. The regional real market index return r_i,t for regional market i in period t can be expressed as:

$$ \begin{array}{@{}rcl@{}} r_{i,t} &= \alpha_{i}^{Ret} + r_{m,t}^{-i} \beta_{i}^{Ret} + \varepsilon_{i,t}^{Ret}, \end{array} $$

(12)

where $r_{m,t}^{-i}$ is the aggregate real market capital return for each country-asset class combination m (e.g. US commercial real estate, global gateway commercial real estate, US office etc.) in period t, excluding regional market i to prevent a simultaneity bias. We calculate the aggregate market capital return by taking the weighted (by the total number of transactions, apart from regional market i, over the whole sample) average return for each country-asset class combination. The commonality measure is the R² of Eq. 12. The degree of integration for each country-asset class combination is calculated by the average R² of all regional markets within this combination. Note that we use real returns in order to prevent that common movements in inflation are captured by the R²-measure.

In order to determine the commonality in market liquidity we adapt the approach by Karolyi et al. (2012). We first filter liquidity per regional market i by the following time series model:

$$ \begin{array}{@{}rcl@{}} Liq_{i,t} &= a_{i}^{Liq}Liq_{i,t-1} + D_{\tau} + \omega_{i,t}^{Liq}. \end{array} $$

(13)

Here, Liq is the estimated liquidity metric from Eq. 11, D_τ are seasonal dummy variables. Following Karolyi et al. (2012) we include lagged liquidity in these filtering equations, such that we essentially take (cleaned) periodic innovations in liquidity. We use the residuals $\hat {\omega }^{Liq}_{i,t}$ to obtain measures of commonality in real estate market liquidity for each regional market i by calculating the R² from the following model:

$$ \hat{\omega}^{Liq}_{i,t} = \alpha_{i}^{Liq} + \sum\limits_{j=-1}^{1} \hat{\omega}^{Liq,-i}_{m,t+j} \beta_{i,j}^{Liq} + \varepsilon_{i,t}^{Liq}. $$

(14)

Here, $\hat {\omega }^{Liq,-i}_{m,t}$ denotes the weighted (again by the total number of transactions, apart from regional market i, over the whole sample) aggregate market residual from Eq. 13 for country-asset class combination m, again excluding regional market i in calculating the aggregate market residual. Following Chordia et al. (2000) and Karolyi et al. (2012) we include one lead and lag of aggregate market liquidity in order to capture any lagged adjustment in commonality.⁷ Note that we use $\hat {\omega }^{Liq,-i}_{m,t}$ to determine the degree of integration in liquidity. Because this residual is “cleaned” for lagged liquidity, this essentially captures the change in liquidity between periods. Estimating the integration models in levels could result in serious econometric issues because of non-stationarity (Chordia et al., 2000). In fact, our liquidity metric in levels also proves to be non-stationary, as opposed to $\hat {\omega }^{Liq,-i}_{m,t}$ or regular first-differences.⁸

To test whether the means (of all markets within a country-asset class combination) of the R²s of the innovations in the liquidity metric and returns are statistically different from each other, we run Two-Sample t-tests. Because the distribution of the R²s are unknown, there may be issues in computing the standard errors to carry out regular t-tests. Therefore, we opt to bootstrap the t-test with 10,000 replications.

In order to explain the underlying factors driving our results, we also run a similar integration analysis on NOI and cap rates. We determine the degree of integration of NOI and risk premia (cap rate spreads) by the return (12). Hence, in this case we have: r_i,t ∈{Δnoi,ΔRSP}. We recognize that risk premia and cap rate spreads are not the same, because cap rate spreads also include the growth component. However, for our purposes it is sufficient if the level of the risk premium is larger than the level of the growth rate. This is generally the case, because we observe positive cap rate spreads, even in environments with very low risk-free interest rates. See also Section “Theoretical Simulation Framework”.

Because the above regressions from Eq. 12 are essentially CAPM regressions, concerns may arise regarding the applicability of the CAPM to private real estate assets. For example, real estate is not solely an investment good and we already take regional market returns as “individual” returns. Additionally, the regional market indexes for prices and liquidity are already aggregated indexes from individual transactions. However, since we are interested in the R² from these regressions, and not in the “market β”, we expect that this should not pose a big problem.⁹ It is merely a statistical technique in order to determine the degree of co-movement. Nevertheless, in order to provide extra robustness to our analysis, we apply a different statistical technique in order to determine the degree of market integration. More specifically, we perform a robustness check where we run several principal component analyses (PCA). Here, we determine the degree of integration by looking at how much information the first common factor contains in explaining individual market variation (see Section “Alternative Integration Measure: PCA”).

Data

An overview of the markets for which the consummated quarterly price and liquidity indexes are estimated is included in Table 1. We use individual transactions data from Real Capital Analytics (RCA) from the period 2005Q1–2018Q4. We follow Van Dijk et al. (2020) and use MSAs as regional market segmentation as defined by RCA. In the US, we focus on the largest 25 MSAs, and additionally estimate indexes for other sub-asset classes within commercial real estate (i.e. apartment, office, retail). We additionally estimate indexes for 18 global markets. We use the same international markets that RCA identifies as “Global Commercial Real Estate Gateway” markets.

Table 1 Overview of markets and summary statistics

An important assumption of the methodology is that the whole population of properties should be included in the data. Because the data include transactions (and not individual properties that are not transacted), this assumption is met if all properties in the property universe are transacted at least once during the sample period. In general, this is not the case in our data sources. However, the high capture rate of the data sets combined with the length of the sample, provides comfort that we observe a sufficiently large part of the property universe. The coverage of the transactions for the US commercial real estate from RCA is larger than 90% for properties over $2.5 million.¹⁰ Also, for commercial real estate, properties that are not in the data after 18 years might never become part of the investment universe that investors are interested in (i.e. properties that trade on a regular basis). For commercial real estate in other countries the capture rates are somewhat lower (these capture rates are not disclosed). Also, the price floors are higher internationally (€ 5 million for Europe and $10 million for Asia-Pacific). This explains why there are relatively few transactions in some non-US markets (Table 1). Additionally, the capture rates are lower internationally before 2007Q1 compared to the period thereafter. Therefore, we will focus a major part of the analysis on US markets only, where this should not be a problem. We also run a robustness check on a post-crisis sample in which the capture rates should be more constant.

Table 1 reveals that the volatilities of the first difference of the liquidity metric are much higher than the return volatilities. This could have implications for our integration results as more noise will obscure commonalities. However, because changes in market liquidity are more noisy than returns, this will favor commonalities in returns. This implies that our results could be on the conservative side on this regard, see also footnote 6.

We obtain CPI inflation for each country from the St. Louis Fed in order to calculate real returns. We additionally use quarterly MSA-data on NOI per square foot and risk premia in the form of cap rate spreads.¹¹ For the US markets, we have access to NOI per square foot (ft²) per MSA per quarter. For international markets, we do not have this data available. Therefore, in the analysis that concerns international markets, we opt to use the imputed rent instead. The imputed rent is defined as: caprate × price/ft². Quarterly regional data on cap rates and risk premia (i.e. cap rate spreads), NOI of institutional properties per market, and price per ft² are also provided by RCA. The summary statistics of the percentage changes in NOI (log-changes) and changes in risk premia in basis-points are shown in Table 3. Here, we observe that the imputed rent changes do not always coincide with the changes in NOI for the US Global Gateway markets that are also included in the US-analysis. The high standard deviations of the imputed rent changes also indicate these are rather noisy.¹² We distinguish between local asset markets and national/global capital markets. This implies that we should not see a strong within-market correlation between NOI growth and changes in cap rate spreads. A simple correlation analysis shows that this is indeed the case: there is only a small correlation of -0.1.

Co-movements in Market Liquidity, Returns, Net Operating Income and Risk Premium

To examine the extent of integration of market liquidity across markets, we first visually examine the degree to which the market liquidity metrics and price indexes co-move. As a second step, we run more formal tests on the commonality in changes in market liquidity and real price index returns. In order to put our findings in price and liquidity commonalities in the context of the cap rate models from subsections “Price Index Returns in Real Estate” and “Market Liquidity in Real Estate Markets”, we also show degrees of integration for NOI and risk premia. This also aids to make assumptions later in our theoretical simulation framework (Section “Theoretical Simulation Framework”). We present the results for three different types of market type combinations: (i) US commercial real estate, (ii) US commercial real estate divided into separate asset classes (apartment, office, and retail), and (iii) international commercial real estate.

US Commercial Real Estate

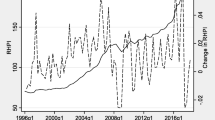
Market liquidity metrics for 25 different regional markets of US commercial real estate are plotted in the panel (a) of Fig. 1. Visually, it is clear that market liquidity shows a strong commonality across regions. The Global Financial Crisis (GFC) of 2008–2009 is clearly visible in the decreasing liquidity metrics in all markets. Also the recovery in market liquidity to pre-crisis levels (2010–2014) is remarkably similar across different markets. Price indexes for the 25 US markets are shown in panel (b) Fig. 1. It is clear that there is substantial co-movement in prices across the different metropolitan areas, but also that the co-movement is much smaller than that of the liquidity indexes.

Fig. 1

Commercial real estate market liquidity (a) and log price indexes (b) for 25 US MSAs

More formally, Fig. 2a shows the degree of integration based on the R² for both liquidity and returns. Additionally, Table 2 includes the R²s and related p-values of the main analyses and robustness checks. In general, market liquidity seems to be strongly integrated across markets and the integration of liquidity is much stronger than the integration of real returns. The $R^{2}_{liq}$ for US commercial real estate is about 0.55 on average, whereas the average $R^{2}_{ret}$ lies around 0.30.¹³ To put these numbers in perspective, Karolyi et al. (2012) document $R^{2}_{liq}$ for US stock markets of about 0.23 on average. In other words, the integration in private real estate market liquidity seems to be much stronger.¹⁴

Fig. 2

Panel (a) shows the empirical R² measures of integration of real returns and quarterly innovations in market liquidity for the studied market combinations. Panel (b) shows the measures of integration for changes in risk premia and changes in NOI. Means as displayed in the charts, standard deviations, and p-values for test of equality in means can be found in Table 2

Table 2 Means, standard deviations, and p-values of R²-measures of integration for different types of market type combinations

Table 3 Summary statistics changes in net operating income and risk premia per market

Note that the R²-bars from Fig. 2 concern the average R² over all MSAs. We run a bootstrapped t-test to test for the equality of means between the liquidity and return integration metrics. This yields a p-value of 0.000, which indicates that the means are indeed statistically different from each other (Table 2).¹⁵ This table further shows that the mean adjustedR² is significantly higher for the liquidity metric than that of the returns. This implies that the extra covariates in the liquidity equations are not the cause of the extra commonality in the changes in liquidity.

Additionally, we can inspect the individual R²s for each market, i.e. the R²s from the regressions based on Eq. 11. The $R^{2}_{liq}$ ranges from 0.25 to 0.78 and the $R^{2}_{ret}$ from 0.06 to 0.72. The correlation between the $R^{2}_{liq}$ and $R^{2}_{ret}$ of individual markets is about 0.27, which suggests that markets that co-move more with market liquidity also tend to co-move somewhat more with national aggregate returns. The market that shows the strongest co-movement with the national market, both is terms of market liquidity and real returns, is Los Angeles. The market that co-moves the least with national market in terms of liquidity is Detroit. In terms of returns, this is Washington D.C.

As suggested, the relatively large regional co-movement in risk premia (cap rate spreads) compared to income might be the reason of the relative strong commonality in market liquidity compared to prices. Figure 2b provides empirical evidence for this claim for the 25 examined US MSAs. Here, we show the results of the R² analyses for changes in risk premia ($R^{2}_{{\varDelta } rsp}$) and NOI ($R^{2}_{{\varDelta } noi}$) of the regional markets. The mean of $R^{2}_{{\varDelta } rsp}$ is about 0.87 compared to only 0.24 for $R^{2}_{{\varDelta } noi}$. A bootstrapped t-test confirms that these means are significantly different from each other (Table 2).

US Commercial Real Estate Within Asset Class

To answer the question how strong the co-movement in real estate market liquidity within the same asset class is, we estimate price and liquidity indexes for separate asset classes. We consider three different asset classes: (i) apartments, (ii) office, and (iii) retail. The liquidity and log price indexes for these three asset classes for the six largest markets in the US, “The Big 6”, are shown in Fig. 3.¹⁶ Visually, the co-movement in market liquidity seems to be very strong within each different asset class. Again, the co-movement in liquidity is much stronger than the co-movement in price indexes (compare the left and right panels in Fig. 3).

The R² metrics for both liquidity and returns for the three separate asset classes are shown in Fig. 2a. The figure also contains the integration analysis for all three asset classes of all six markets lumped together as a reference point “US CRE Big 6 Subtypes”. Overall, the co-movement is stronger for market liquidity than for returns. The average R²s of the asset classes combined for market liquidity and real returns are 0.42 and 0.22, respectively. These results are slightly lower than those found for the 25 MSAs in subsection “US Commercial Real Estate”, but similar in terms of difference between the degree of integration of liquidity and returns. The difference is again significant at the 1%-level (see column “USA6 ST” in Table 2). The integration of market liquidity is the strongest within the retail market, where the average R² is 0.45. The difference between the R² of market liquidity and returns is also the largest for the retail markets. For returns, the co-movement in the office market prices is stronger than for the two other asset classes. The average R² over office market returns is 0.29. The co-movement in market liquidity is still stronger (0.38), but the p-value of 0.11 only indicates a marginally statistically significant difference (Table 2).

Figure 2b shows the degrees of integration for NOI and risk premia for the examined six markets for the different asset classes. Overall, the integration in risk premia is much stronger across the markets for the different asset classes than the integration in operating income and the difference is significant at the 1%-level in all cases (Table 2). Interestingly, the integration of risk premia and the difference between the integration of risk premia and NOI is the largest for retail markets. The retail markets also showed the strongest integration in market liquidity compared to returns (Fig. 2a). Overall, these results strongly corroborate the claim that the relatively strong integration of cap rate spreads compared to NOI lies at the root of strong co-movements in market liquidity compared to returns.

Fig. 3

Commercial real estate market liquidity and log price indexes for 6 big US MSAs for different asset classes: US apartments liquidity (a), US apartments log price (b), US office liquidity (c), US office log price (d), US retail liquidity (e), and US retail log price (f)

Global Commercial Real Estate

This section looks at the integration of liquidity and real returns of global commercial real estate markets. We consider 18 large international global gateway markets in the analysis. Figure 4 panel (a) includes the market liquidity indexes for the global gateway markets. It is clear that co-movement in liquidity is less strong than for the US commercial real estate markets only. Nevertheless, the run-up to the GFC is visible in most markets, as is the GFC itself. The recovery after the GFC also occurs in all markets, mostly at the same pace. The co-movement of the price indexes of the 18 global markets is shown in panel (b) of Fig. 4. It can clearly be observed that the co-movement in the price indexes is less than in the liquidity indexes.

Fig. 4

Commercial real estate market liquidity (a) and log price indexes (b) for 18 Global Gateway markets

More formally, the degree of integration for market liquidity and real returns per the R² measures are shown in Fig. 2a. Again, the degree of integration in market liquidity is much stronger than the integration of real returns. The average R²s for market liquidity innovations and real returns are 0.30 and 0.14, respectively. Note that the global integration measures are lower than those for US commercial real estate alone. Nevertheless, there is still evidence that market liquidity co-moves strongly internationally and the finding that liquidity co-moves stronger than returns also holds internationally. A bootstrapped t-test also indicates this difference is significant at the 1%-level.

Additionally, the co-movement in risk premia in the international case is also much stronger than that in income (Fig. 2b). The mean of $R^{2}_{{\varDelta } rsp}$ is about 0.84 compared to a mean $R^{2}_{{\varDelta } noi}$ of only about 0.05, which is significant at the 1%-level.¹⁷

To summarize, the R² analyses with bootstrapped t-tests suggest that market liquidity co-moves significantly stronger than returns. This holds for US commercial real estate, for different real estate asset classes, as well as for international commercial real estate. Empirically, there is strong evidence that the relatively strong co-movement in cap rates compared to that in net operating income lies at the root of the relatively strong co-movement in market liquidity compared to returns. Section “Theoretical Simulation Framework” will provide a simulation exercise to show that this is indeed reasonable to assume from a theoretical perspective.

Robustness Checks

In this section, we present three different robustness checks:

• (i) an alternative integration measure (PCA),

• (ii) two alternative market liquidity measures (transaction volume and the Amihud measure), and

• (iii) the post-crisis sample to examine the effect of the GFC.

Alternative Integration Measure: PCA

As a first robustness check, we run a principal component analysis (PCA) to determine the degree of integration of returns and market liquidity. We look at the information in the first component with respect to individual market variations to determine this degree of integration. Intuitively, this measure is higher when the first component explains more of the variation in returns or market liquidity innovations. This implies that the markets are stronger integrated because their common factor is relatively more important for the variation in individual markets. We run the PCAs on real returns and cleaned liquidity innovations $\hat {\omega }^{Liq}_{i,t}$ from Eq. 13. This is to ensure our variables are stationary and to compare to our main analysis. An important downside of the PCA compared to the R²-method is that regional market i is included in the calculation of the principal component, which introduces a simultaneity bias. This should be mitigated if many regional markets are compared in one setup, but could be a problem if the analysis does not include many markets.

In general, the PCA results confirm the main finding that market liquidity innovations are stronger integrated than returns. For the USA 25 MSAs, the first component seems to explain about 35% of the returns, compared to about 54% in changes in the liquidity metric (Fig. 5a). For the separate asset classes the PCA gives somewhat different results than the R² measure. The reason is that there are only six markets compared simultaneously (or five in the case of apartments due to the lack of observations in Washington D.C., see Section “Data”). This makes the PCA somewhat unreliable because a single market is for a large part responsible for the variation in the common factor (i.e. the simultaneity bias is larger when the number of markets is small). Note that, contrary to the PCA-measure, the R²-measure excludes market i in calculating aggregate market returns or liquidity (see Eqs. 12–14). Hence, in the R²-measure this should not be a problem.

Fig. 5

Figures for three robustness checks. Panel (a) shows the results of robustness check (i): PCA measures of integration. Panel (b) shows the results of robustness check (ii): R² measures for two alternative market liquidity measures; transaction volume ($R^2_{Delta vol}$) and Amihud measure ($R^2_{Amh}$). Panel (c) shows the results of robustness check (iii): R² measures for the post-GFC sample period (2010Q1-2018Q4). Means of the R² as displayed in the charts, standard deviations, and p-values for test of equality in means can be found in Table 2

If we lump together the sub-asset categories in “US CRE Big 6 Subtypes” and perform the PCA on this set of markets, we do find stronger evidence that the co-movement in liquidity changes is stronger than that of returns.

In the international case, the percentages of variance explained by the first factor of market liquidity changes and returns are 0.34 and 0.26, respectively. Hence, there is a difference in terms of the degree of integration, but it is small. Also note that the simultaneity bias might be a bit larger than in the US case, because the international comparison includes only 18 markets.

Two Alternative Market Liquidity Measures

The second robustness check employs two different measures for market liquidity. The measure for market liquidity that we use to obtain our main results, allows specifically for the construction of regional indexes expressed in the price dimension. This allows for a more straightforward comparison to prices (or returns). Other proxies for different concepts of market liquidity used in the literature include the number of transactions, transaction volume, and the Amihud measure (Amihud, 2002; Ametefe et al., 2016). The downside of many other measures it that they can be too noisy for regional markets because of the lack of the number of transactions. In this robustness check, we will consider two alternative measures that relate to at least several dimensions of market liquidity.¹⁸ Transaction volume is total transaction volume in a given quarter for a given market and is provided by RCA. The Amihud measure is defined as:

$$ Amh_{i,t} = \frac{|Ret_{i,t}|}{Vol_{i,t}}. $$

(15)

Here, Amh is the Amihud measure for market i in quarter t, |Ret| is the absolute price index return, and V ol is total transaction volume.¹⁹ Due to data availability, we are only able to run this robustness check for the USA 25 MSA markets.²⁰

Figure 5b shows the R² integration measures for changes in log total volume (Δvol) and the Amihud measure (Amh). The figure additionally includes the degrees of integration for returns (ret) and the market liquidity measure (liq) as used in the main results as reference points. Of the three liquidity measures, the Amh and liq measures show the strongest degree of integration, remarkably similar at around 0.55. The Δvol measure is less integrated at around 0.45, but still much stronger than the degree of integration of real returns (0.30). Overall, the results that market liquidity is stronger integrated than returns are robust to the usage of different market liquidity measures.

Effect of Global Financial Crisis

The third robustness check aims at examining the effect of the GFC. The GFC is an interesting period in terms of commonalities. Many different asset classes went down in terms of returns and market liquidity. This implies that commonalities increase. It is also at this time when market liquidity might be important for investors that need to sell assets, because they are in distress or for investors that need to re-balance portfolios. Because the calculation of the integration measure requires a “large enough” time sample, we are not able to run the measures for the GFC only.²¹ Instead, we opt to estimate the degrees of integration for the post-GFC (2010–2018), and compare those to the estimates for the full sample (2005–2018). Differences between those degrees of integration are likely to be attributed to the GFC. Visually, it is clear that the GFC might be a large driver in the large commonality of both market liquidity and returns. See, for example, Fig. 1 for the 25 US MSAs.

Figure 5c shows the degrees of integration for the post-GFC sample period. This figure should be compared to Fig. 2a, which shows the degrees of integration for the whole sample. Alternatively, all R²-numbers are included in Table 2. Overall, the degrees of integration are smaller than those based on the whole sample, but the finding that market liquidity is stronger integrated than returns remains robust. For market liquidity for the US 25 MSAs, the mean $R^{2}_{Liq}$ for the shortened sample is about 0.32, compared to about 0.54 for the whole sample. This difference is significant at the 1%-level according to a bootstrapped t-test (Table 2). Note, however, that the degree of integration of returns is also much smaller: 0.10 in the post-GFC sample versus 0.30 for the whole sample (which is also significant). In other words, integration of both market liquidity and returns is significantly less strong (stronger) after (during) the GFC. This makes sense intuitively as everything (such as market liquidity and returns) goes down in every market during a crisis and cross-market correlations move to 1. In fact, a back-of-the-envelope calculation suggests that the $R^{2}_{liq}$ should be roughly 0.94 in the period 2005–2009, which largely includes the GFC.²² The fact that market liquidity is stronger integrated in crisis times is also consistent with findings for the US stock market (Karolyi et al., 2012). Here it is shown that the $R^{2}_{liq}$ during the GFC was about twice as large as during normal times (0.2 compared to 0.4). This finding is important to note for investors as it is likely that especially during these times investors might be in need for market liquidity. The lack of liquidity in all markets during these times, implies that full price return diversification benefits might be difficult to obtain.

The pattern of less integration in both returns and market liquidity, but stronger integration in market liquidity than in returns, can clearly be seen in most considered market combinations (and is also significant for most combinations as shown in Table 2). The only notable exception is the US office market, where returns and market liquidity are similarly integrated (note that the difference was also smaller over the whole sample). We do not have a clear explanation for this, but we note that returns in the office market are relatively strongly integrated compared to other asset classes, both in the post-GFC and full sample. We leave a more thorough investigation for future research.

Theoretical Simulation Framework

This section presents simulated price and liquidity indexes and sheds additional light on our empirical findings that we discuss in this paper. Additionally, it provides extra comfort to the empirical integration measure from subsection “Measuring Commonality”. In this simulation exercise, we simulate buyers’ and sellers’ price indexes and calculate quarterly price indexes and the corresponding liquidity metric for 25 hypothetical markets for 56 periods. This is similar to our empirical setup which runs from 2005Q1–2018Q4.

Simulation Model

We start off by simulating the individual components from the buyers’ reservation price equation (6). We simulate all components as correlated auto-regressive processes with noise. The signal of the components are allowed to correlate across the markets according to correlation coefficient ϕ. To mimic our empirical setup for the US situation, we simulate 56 quarters from 2005Q1 to 2018Q4 for 25 markets. The auto-regressive process with noise is defined as:

$$ \begin{array}{@{}rcl@{}} x_{i,t} &=& \kappa_{i,t} + \eta_{i,t}, \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} \kappa_{i,t} &=& \mu (1-\rho) + \rho \kappa_{i,t-1} + \varepsilon_{i,t}. \end{array} $$

(17)

Here x is the simulated variable (e.g. NOI, risk-free rate, risk premium, or growth expectations) for regional market i at quarter t. Next, κ is the state variable, μ is the mean of the process and ρ is the auto-regressive term. For |ρ| < 1 the process is stationary, and for ρ = 1 the process is a non-stationary random walk. The innovations ε_i,t over time are sampled from a multivariate normal distribution. We specify different variance-covariance matrices that contain the cross-market correlation structures of the signal for each variable x. That is, $\varepsilon \sim \mathcal {N}(\mathbf {0},\mathbf {{\Sigma }_{\varepsilon }})$. Further, we assume normal i.i.d. noise for each series: $\eta \sim \mathcal {N}(\mathbf {0},\mathbf {{\Sigma }_{\eta }})$. To introduce information asymmetries between buyers and sellers, we assume that sellers observe changes in (some of the) individual components with a lag relatively to buyers. Buyers observe the true process: $x^{b}_{i,t} = x_{i,t}$.²³ More specifically, we assume that sellers gradually adjust their perception about the component in their market according to the following equation:

$$ x^{s}_{i,t} = \alpha_{x} x^{s}_{i,t-1}+(1-\alpha_{x}) x^{b}_{i,t}. $$

(18)

Here, α_x ∈ [0, 1] denotes the “lag-factor”. Note that for α_x = 0, the buyers’ and sellers’ perception about the component is equivalent. If this is the case for all components, there will be no difference between the buyers’ and sellers’ reservation prices and the liquidity metric would be 0 at all times. Empirically, this is an unlikely situation as liquidity tends to move over the cycle as well.

Next, we calculate the normal “midpoint” price indexes and our liquidity metric according to Eqs. 10 and 11, respectively. Similar to our empirical setup, we transform the indexes such that the mean of the buyers’, sellers’, and midpoint price indexes is equal.

Baseline Calibration

We have calibrated some parameters in the baseline setup based on empirical facts as much as possible. The other parameters are calibrated such that the integration metrics are similar in size as the empirical results. This additionally provides some insights in how the parameter assumptions should be in order to replicate reality in a cap rate model.

Because there is only one risk-free rate for all market participants across all markets, we will assume a correlation of 1 between all markets and no seller lag.²⁴ We assume a rather high mean for the risk-free rate of 0.15 in order to prevent a negative log in Eqs. 6–7 in some simulations in highly persistent processes (i.e. |α| or |ρ| is close to 1). This does not influence the results in terms of differences in correlations between prices and liquidity. Likewise, we fix the level of NOI across specifications, which also does not influence the results in terms of correlations in returns or market liquidity changes. Next, because the relative correlations and sizes of both log terms in the cap rate models from Eqs. 6 and 7 will matter, we will fix the growth expectations across the setups for tractability reasons.²⁵ We will assume some correlation in growth expectations between the markets: 0.3. We assume no seller lag factor on the growth expectations. Additionally, we will assume similar starting values and variances ($\sigma ^{2}_{\varepsilon }$ and $\sigma ^{2}_{\eta }$) across the different simulations.²⁶ We assume an AR-parameter ρ of 0.9 on both the risk premium and NOI as the levels of these variables. For the difference in correlation between liquidity changes and returns, the size of ρ does not matter. This leaves four free simulation parameters: (i) the correlation of the risk premium across markets, (ii) the correlation of NOI across markets, (iii) the seller lag factor of the risk premium, and (iv) the seller lag factor of NOI.

Table 4 in the Appendix shows the used variances, correlations, and starting values to autoregressive processes of the baseline setup. We have some empirical evidence of how high these correlations should be. The baseline assumes a 0.9 correlation of the risk premium across markets, which is similar to the empirical correlation over 2005–2018 in cap rate spreads (see also Section “4 4”). We note that cap rate spreads are not the same as risk premia as cap rate spreads also include a growth component. However, because risk premia are the dominant component in cap rates spreads, it seems reasonable to assume a similar correlation for the baseline (see also footnote 25). Next, we assume a correlation of 0.3 in NOI changes across markets, which is about the same as the correlation that we empirically observe in the US market over 2005–2018. The other parameters are calibrated in order to obtain similar empirically found integration measures: a 0.8 seller smoothing factor on the risk premium and a 0.1 seller lag factor on NOI. This implies that sellers need to smooth about 8 times more in terms of the risk premium compared to NOI in order to generate empirically consistent results (see also Section “Other Setups and Two Main Assumptions”).

The simulated liquidity and price indexes according to the baseline setup are shown in Fig. 7 (in the Appendix). With these indexes, we can calculate our “empirical” commonality measures. Figure 6 shows the estimated average R² for the 25 simulated markets. The average R² for the changes in the liquidity metric (0.52) is much higher than that of the returns (0.26), indicating that the integration of liquidity is higher. A bootstrapped t-test reveals that this difference is also significant at the 1%-level.²⁷ Figure 6 additionally shows the degree of integration according to the PCA-method. The PCA-results also indicate that the integration of liquidity is stronger than that of returns among the simulated markets. This provides additional comfort that the integration measures that we propose are able to capture the variation of interest.

Fig. 6

Simulated R² and PCA measures of integration of real returns and quarterly innovations in market liquidity the simulated markets

Other Setups and Two Main Assumptions

So far, we have calibrated our simulation setup to reflect the empirically observed situation as closely as possible. In order determine how much these parameters may deviate from the baseline assumptions, we will provide additional simulation results based on different assumptions of the four free parameters. To do so, we let these parameters range between 0 and 1 with increments of 0.01 in four setups additional to our baseline. We keep the other parameters equivalent to the assumed values in the baseline, hence we can interpret these findings ceteris paribus. Figure 8 (see Appendix) shows the average correlations between changes in (log) prices and changes in the liquidity metric across the 25 markets for different free parameter values.

As we will show next, we are able to provide two main assumptions for market liquidity to be stronger correlated than returns across regions: The cross-market correlation in the risk premium component needs to be stronger than the cross-market correlation in NOI and the seller smooth lag factor in the risk premium needs to be sufficiently large compared to the seller smooth factor in NOI.

The first assumption is very much in line with the perception that capital markets tend to be stronger integrated across markets than space markets. Empirically, this assumption also holds as the correlation in cap rates tends to be much higher than the correlation in NOI. See also subsections “US Commercial Real Estate” and “Baseline Calibration”. Panels (a) and (b) of Fig. 8 provide additional insights regarding this assumption in the simulation framework.

In Fig. 8 panel (a) we allow for different values in the cross-market correlation in the risk premium and in panel (b) we allow for different values of cross-market correlation in NOI. The baseline values of the parameters are indicated by the dotted vertical lines. The plot in panel (a) shows that correlation in market liquidity increases more than the correlation in returns when the correlation in the risk premium increases. As such, when the cross-market correlation in risk premium is higher than the cross-market correlation in NOI, the correlation in changes in the liquidity metric will be higher than the correlation in returns. Panel (a) shows that, in our simulation setup, the correlation in the risk premium can be as low as 0.3 (the same as the correlation in NOI changes) in order for market liquidity to be stronger integrated than returns. Admittedly, it would be empirically difficult to observe differences in correlation for values lower than 0.6. Panel (b) shows a mirror image of that of panel (a): the correlation in returns increases stronger than the correlation in market liquidity when the correlation in the NOI increases. In other words, if the cross-correlation in NOI is smaller than the cross-correlation in risk premium, the correlation in the liquidity metric changes will be higher than the correlation in returns. In our setup, this implies than the correlation in NOI changes can be as high as 0.9.

The second assumption can be seen as a “loss aversion” or anchoring argument because of the relatively large degree of uncertainty in the risk premium compared to the NOI. The latter is a largely objective value. There is less scope for investors to use their judgment about what the NOI is. Hence, there is less scope for smoothing or lagging. The risk premium, in contrast, is not observable directly, because it is an ex ante, expected risk premium, dependent on perceptions of how much risk is there and what is the market’s current price of risk. Thus, the risk premium is much more subjective than is the NOI. This subjectivity allows for lagging and smoothing. Additionally, the seller bought the property some time ago against the financing conditions that prevailed at that time. Hence, it is reasonable to assume that the current perception about financing conditions is a function of past financing conditions that applied to the property in question. See Bokhari and Geltner (2011) for evidence of anchoring in commercial real estate markets.

We examine the implications of the above mentioned second assumption in panels (c) and (d) of Fig. 8. Panel (c) shows different average correlations for multiple values in the sellers smoothing factor of the risk premium. Panel (d) shows the effect on average market correlations of different seller smoothing values for NOI. The results implicate that in case the seller smoothing factor in NOI is sufficiently small, changes in liquidity will be stronger correlated than returns. Sufficiently small in this case depends on the level of the cross-market correlations and the seller smooth factors of the NOI and risk premia. In general, if the seller smooth factor of the risk premium is relatively large compared to the seller smooth factor of the NOI, this will favor the correlation in liquidity changes. How much larger or smaller also depends on the levels of the correlations of NOI and risk premia. If the difference between these levels is smaller, the differential in the seller smooth factor in the risk premium and NOI also needs to be larger to generate stronger market liquidity integration. In our setup, with baseline assumption of correlations of the risk premium and NOI of 0.9 and 0.3, respectively, this implies that the seller smooth factor on the risk premium can be as low as 0.3. For higher values, liquidity will be stronger integrated (see panel c). Similarly, as shown in panel (d), for lower values of the seller smooth factor on NOI, liquidity changes will be stronger integrated. The seller smooth factor on NOI changes can be as high as 0.5 to observe higher correlation in liquidity changes in our simulation (see panel d).

Conclusion and Possible Extensions

In this paper we have examined commonalities in both price index real returns and liquidity changes for private commercial real estate markets. To return to our three main questions: (i) “How strong is the co-movement in changes in market liquidity?”, (ii) “How strong is the co-movement in real price index returns?”, and (iii) “Which factors drive the difference in commonality between market liquidity changes and real price index returns?”, we find the following.

Using data from Real Capital Analytics spanning the period 2005Q1–2018Q4, we document substantial co-movement in market liquidity dynamics. By calculating the commonality measure of Roll (1988) and Karolyi et al. (2012), we find document commonalities in changes in market liquidity for the 25 examined MSAs in the US. We use the market liquidity metric based on differences in buyer and seller reservation prices (Fisher et al., 2003; Fisher et al., 2007; Van Dijk et al., 2020). For the largest six MSAs, we are also able to confirm significant commonalities for thee different asset classes (apartment, office, and retail). Even for global commercial real estate (18 MSAs), we find substantial co-movement in market liquidity changes. For all these market combinations, we additionally find some co-movement in price index real returns. However, the co-movement in returns is found to be much smaller than the co-movement in liquidity changes in all studied market combinations.

We additionally find that our commonality findings are robust to the use of a different measure of integration (principal component analysis). Second, percentage changes in volume and the Amihud measure (two alternative market liquidity measures) also show stronger integration than price index returns. Third, by leaving out the Global Financial Crisis (GFC), we find that the degree of commonalities decreases. The increase in commonalities in market liquidity and returns during the GFC implies that market liquidity can dry up simultaneously across all markets in times of crisis. The finding that market liquidity changes are stronger integrated than returns remains robust. The US office market is the only notable exception, where returns co-move relatively strong compared to other asset classes and compared to market liquidity. We leave a further investigation to future research, but note that the relatively strong co-movement in US office returns was also visible in the sample that includes the GFC.

In order to examine the underlying factors of this relatively strong co-movement in market liquidity, we present a theoretical simulation framework. Using this framework, we show that two main assumptions are required to simulate these results: (i) the cross-market co-movements in the risk premium need to be stronger than the co-movements in NOI and (ii) the seller lag in risk premium needs to be sufficiently large compared to the seller lag in NOI. Consistent with these assumptions, we hypothesize that the strong integration in market liquidity is driven by the fact that capital markets are stronger integrated than space markets. We confirm this argument empirically by showing that risk premia co-move much stronger than changes in NOI across markets.

We recognize at least two limitations to our research. First, we examine intertemporal changes in market liquidity across markets and not cross-sectional level differences between markets. It might still be the case that some markets are more liquid than others in levels. The same holds for individual properties, some properties might be more liquid than others. We only document findings related to market liquidity dynamics, because we do not have a reliable measure for level differences between markets or for individual property liquidity. Also, diversification usually refers to the time-series component of the variables that an investor would like to diversify on. Hence, we feel that price and liquidity dynamics capture the major part of this question. Second, because of data constraints, we are only able to include larger markets. Large markets may be inherently different than small markets, also in terms of co-movements with other markets. Most (international) capital will tend to flow to these large cities as opposed to the smaller cities. Hence, a large chunk of private real estate investment, happens in these large markets. This makes our sample – to some extent – maybe even more relevant for large investors.

The results are of interest for large private real estate investors such as pension funds, and other institutional investors who are interested in spreading risk. Our results indicate that it may be very difficult to spread market liquidity risk. This implies that it may also be difficult to reap the full return diversification benefits, because portfolio re-balancing may be more difficult and costly. One of the robustness checks in fact shows that market liquidity commonalities were even stronger during the GFC, which implies that market liquidity can dry up simultaneously across all markets. This would make risk diversification even more difficult in times when it is needed most. We argue that market liquidity is to a large extent driven by capital market movements, which cannot be diversified easily in terms of geographical diversification or asset class diversification. Internationally, we do find less co-movement in both returns and market liquidity, which should make diversification easier. However, international diversification in market liquidity still remains difficult, because market liquidity also co-moves stronger than returns in the international case. Future research could address the question how investors could diversify (internationally) the best way in terms of liquid and illiquid assets. A related interesting question would be how do liquidity and price shocks propagate through time and space. The results are also important to understand for policymakers, as they are – at least partly – capable of direly influencing capital market movements by changing the lending rate or indirectly through asset purchase programs, affecting risk premia. The results suggest that capital markets will strongly affect market liquidity, effects that possibly need to be taken into account when implementing measures that affect capital markets.

Appendix: Additional Figures and Tables

Table 4 Parameters used to simulate the different components in the simulation exercises

Fig. 7

Market liquidity (a) and log price indexes (b) for 25 simulated markets

Fig. 8

Average correlations between 25 simulated markets of changes in (log) prices and changes in the liquidity metric for different parameter sets. Each subplot shows results for a different free parameter: correlation RSP (a), correlation noi (b), seller smooth factor RSP (c), seller smooth factor noi (d)