Cornish-Fisher Expansion for Commercial Real Estate Value at Risk

Abstract

The computation of Value at Risk has traditionally been a troublesome issue in commercial real estate. Difficulties mainly arise from the lack of appropriate data, the non-normality of returns, and the inapplicability of many of the traditional methodologies. As a result, calculation of this risk measure has rarely been done in the real estate field. However, following a spate of new regulations such as Basel II, Basel III, NAIC and Solvency II, financial institutions have increasingly been required to estimate and control their exposure to market risk. As a result, financial institutions now commonly use “internal” Value at Risk (V a R) models in order to assess their market risk exposure. The purpose of this paper is to estimate distribution functions of real estate V a R while taking into account non-normality in the distribution of returns. This is accomplished by the combination of the Cornish-Fisher expansion with a certain rearrangement procedure. We demonstrate that this combination allows superior estimation, and thus a better V a R estimate, than has previously been obtainable. We also show how the use of a rearrangement procedure solves well-known issues arising from the monotonicity assumption required for the Cornish-Fisher expansion to be applicable, a difficulty which has previously limited the useful of this expansion technique. Thus, practitioners can find a methodology here to quickly assess Value at Risk without suffering loss of relevancy due to any non-normality in their actual return distribution. The originality of this paper lies in our particular combination of Cornish-Fisher expansions and the rearrangement procedure.

Appendices

Appendix A: Quantile Functions

The quantile function (or inverse cumulative distribution function) of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will fall below with that specified probability. In fact it is an alternative to the probability density function (pdf).

Let X be a random variable with a distribution function F, and let α∈(0,1). A value of x such that F(x)=P(X≤x)=α is called a quantile of order α for the distribution. Then we can define the quantile function by:

$$q_{\alpha}(X)\equiv F^{-1}(\alpha)=inf \left\lbrace x \in \mathbb{R} : F(x)\geq \alpha\right\rbrace ,\alpha\in(0,1). $$

The quantile function q _α (X) thus yields the value which the random variable of the given distribution will fail to exceed with probability α.

Appendix B: Skewness and Kurtosis

Given a probability distribution f(x) of the random variable X and a real-valued function g(x), one defines the expectation $E[g(X)]=\int g(x)f(x)dx$, in which case the first moment is μ=E[X], whereas the higher central moments are then defined as μ _k =E[(X−μ)^k]. The first task in almost all statistical analyses is to characterize the location and variability of a data set. This is captured by the moments of order one and two, usually called the mean μ and the variance σ ²=μ ₂, respectively. A further characterization of the data often includes the standardized moments of order three and four, called the skewness S=μ ₃/σ ³ and kurtosis K=μ ₄/σ ⁴, respectively. These last two measurements further describe the shape of a probability distribution. We briefly recall the significance of these two last parameters.

Skewness is a measure of symmetry, or more precisely, the lack of symmetry. A distribution, or data set, is symmetric if it looks the same to the right and left of its center (which is then the mean μ). The skewness of any symmetric distribution, such as a Gaussian one, is necessarily zero. Negative values for the skewness coefficient indicate data that are skewed to the left whereas positive values indicate that the data that are right skewed (see Fig. 15), with left-skewness meaning that the left tail of the distribution is long relative to the right one.

Fig. 15

Example of a right skewed distribution (S=1.75)

Kurtosis refers to whether the data are peaked or flat relative to a normal distribution. That is, data sets with high kurtosis tend to have a distinct peak near the mean, then decline rather rapidly, but still have heavy tails (see Fig. 16). Data sets with low kurtosis tend to have a flat top near the mean rather than a sharp peak. The kurtosis formula measures the degree of this peakedness, where the kurtosis of a Gaussian distribution turns out to be 3.

Fig. 16

Example of a fat tailed distribution (K=9)

Appendix C: The Cornish-Fisher Procedure

The Cornish-Fisher expansion is a useful tool for quantile estimation. For any α∈(0,1), the αth-quantile of F _n is defined by q _n (α)=s u p{x:F _n (x)≤α}, where F _n denotes the cdf of $\xi _{n}=(\sqrt {n}/\sigma )(\bar {X}-\mu )$ and $\bar {X}$ is the sample mean of i.i.d. observations X ₁,…,X _n . If z _α denotes the upper αth-quantile of N(0,1), then, the fourth order Cornish-Fisher expansion can be expressed as:

$$q_{n}(\alpha)= z_{\alpha}+\frac{1}{6\sqrt{n}}(z_{\alpha}^{2}-1)S+\frac{1}{24n}(z_{\alpha}^{3}-3z_{\alpha})(K-3)-\frac{1}{36n}(2z_{\alpha}^{3}-5z_{\alpha})S^{2}+o(n^{3/2}), $$

where S and K are the skewness and kurtosis of the observations X _i .

The Cornish-Fisher expansion is useful because it allows one to obtain more accurate results than using the central limit theorem (CLT) approximation, which would be just the z _α defined in the body. A demonstration and example of the greater accuracy that the Cornish-Fisher expansion brings compared to the CLT approximation is reported in Barndorff-Nielsen and Cox (1989), p. 119.

Appendix D: The Rearrangement Procedure

This paper applies a procedure called rearrangement, or more precisely, increasing rearrangement. We use this procedure to restore the monotonicity of the Cornish-Fisher expansions. The procedure is briefly described here.¹⁵

A convenient way to think of the rearrangement is as a sorting operation: given values of a data set, we simply sort the values in an increasing order. The function created is the rearranged function.

Following Chernozhukov et al. (2010), we define the procedure more precisely as follows. “Let χ be a compact interval. Without loss of generality, it is convenient to take this interval to be X=[0,1]. Let f(x) be a measurable function mapping χ to K, a bounded subset of $\mathbb {R}$. Let $F_{f}(x)={\int }_{\chi }1 \left \lbrace f(u)\leq y\right \rbrace du$ denote the distribution of f(x) when X follows the uniform distribution on [0,1]. Let

$$f^{*}(x)=Q_{f}(x)=inf \left\lbrace y \in \mathbb{R} : F_{f}(y)\geq x \right\rbrace $$

be the quantile function of F _f (y). Thus,

$$f^{*}(x)=inf \left\lbrace y \in \mathbb{R} : \left[ {\int}_{\chi}1\left\lbrace f(u)\leq y \right\rbrace du\right]\geq x \right\rbrace. $$

This function f ^∗ is called the increasing rearrangement of the function f.”

In our approach, this allows us to respect one of the basic conditions of the probability distribution function: monotonicity. As a result, Value at Risk becomes inversely proportional to the threshold, and so, as expected, one has V a R _{0.5 %} ≥V a R _{5 %} .

The rearrangement procedure also has the practical implication, demonstrated by Chernozhukov et al. (2010), that the resulting rearranged estimate has a smaller estimation error (in the Lebesgue norm) than does the original estimate whenever the latter is not monotone. This property is independent of the sample size and of the way the original approximation is obtained. Thus, the benefits of using a rearrangement procedure in our paper are both to obtain estimates of the distribution satisfying the logically necessary monotonicity restriction and also to obtain better approximation properties.

Appendix E: Comparison of Cornish-Fisher VaR for Various Window Lengths

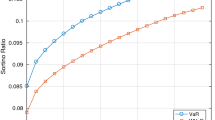
Here, we revisit the length of window choice. In Figs. 17 and 18, V a R of the 10, 11, 12.5, 14 and 15-year periods are represented simultaneously. Before the middle of 2008, the longer the window, the higher is the V a R. After that date, we observe the opposite effect. Modifications created by the window length are qualitatively the same for the Gaussian and Cornish-Fisher V a Rs. The difference between these two approaches to V a R is stable whatever the choice of windows (the order of the curves appears in the same order). This illustrates that effects of window length is not relative to the Cornish-Fisher expansion but to the V a R computation, and more generally to distribution estimation. As mentioned previously, regulators often fix the length exogenously, with a 10-year window being chosen in much financial analysis.

Fig. 17

Gaussian VaR for various window lengths

Fig. 18

Cornish-Fisher corrected VaR for various window lengths