The Predictive Power of Anisotropic Spatial Correlation Modeling in Housing Prices

Abstract

This paper develops a method to capture anisotropic spatial autocorrelation in the context of the simultaneous autoregressive model. Standard isotropic models assume that spatial correlation is a homogeneous function of distance. This assumption, however, is oversimplified if spatial dependence changes with direction. We thus propose a local anisotropic approach based on non-linear scale-space image processing. We illustrate the methodology by using data on single-family house transactions in Lucas County, Ohio. The empirical results suggest that the anisotropic modeling technique can reduce both in-sample and out-of-sample forecast errors. Moreover, it can easily be applied to other spatial econometric functional and kernel forms.

Appendix 1 Numerical example of anisotropic neighborhood definition

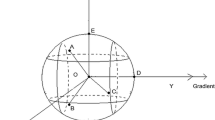
Using the properties in Fig. 8 as examples, we illustrate here how to construct an anisotropic neighborhood. The center property A has latitude and longitude of (49.665556, −83.5686870).

Table 5 shows the latitude, longitude, and spatial trends $\hat \varepsilon \left( {{s_i}} \right)$ of property A and the nearest twenty properties. When defining an isotropic neighborhood, we must first use latitudes and longitudes to calculate the straight line distances under the geodetic coordinate system from each of the twenty properties to property A (Table 7, column 3). These properties are then sorted by ascending distance (Table 7, column 2) and we construct the isotropic neighborhood by using the ten nearest properties within a range of 0.027 (c.a. 2500 m), i.e., properties 1 to 10 (identified in Fig. 8a). The following steps show how to construct an anisotropic neighborhood.

Table 5 Property descriptions

Table 6 Gradient estimation

Table 7 Distances under the geodetic and local coordinate systems

Gradient Estimation

We first calculate the two-dimensional gradient from the nearest twenty properties to property A using Eq. 5. Table 2a shows spatial changes Δε _Aj , distance vectors $\Delta {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{D}}_{Aj}}$, and the estimated gradients. For example, the gradient from property A to property A1 can be calculated as follows:

$$ \nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\rho }}({s_{A1}},{s_A}) = \frac{{\Delta {\varepsilon_{A1}}}}{{\Delta {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{D}}}_{A1}}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{{\hat \varepsilon }_{A1}} - {{\hat \varepsilon }_A}}}{{{u_{A1}} - {u_A}}}} \\ {\frac{{{{\hat \varepsilon }_{A1}} - {{\hat \varepsilon }_A}}}{{{v_{A1}} - {v_A}}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{ - 1.191223 + 1.170891}}{{41.669310 - 41.665556}}} \\ {\frac{{ - 1.191223 + 1.170891}}{{ - 83.569028 + 83.568687}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{ - 0.020332}}{{0.003754}}} \\ {\frac{{ - 0.020332}}{{ - 0.000341}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}{c}} { - 5.419533} \\ {59.624633} \\ \end{array} } \right]. $$

The difference between the two longitudes is 0.000341 (about 20 m). Because of the small distance the gradient is unusually large while the spatial condition is unlikely to exhibit large changes. If the difference in latitude or longitude is less than 0.0015 (about 135 m) we set the gradient equal to zero; hence, $\nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\rho }}\left( {{s_{A1}}} \right) = \left[ {\begin{array}{*{20}{c}} { - 5.419533} \\ 0 \\ \end{array} } \right].$ The 20 estimated gradient vectors are in Table 6.

Using Eq. 6, the gradient at location S _A is calculated as the average gradient of the nearest neighbor properties:

$$ \nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\rho }}({s_A}) = \frac{1}{{20}}{\text{(}}\nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\rho }}({s_{A1}}) + \nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\rho }}({s_{A2}}) + \ldots + \nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftharpoonup}$}}{\rho }}({s_{A20}})) = \left[ {\begin{array}{*{20}{c}} { - 26.8191} \\ {53.0670} \\ \end{array} } \right], $$

as in Fig. 8b. The strength of $\nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\rho }}({s_A})$ is $\left| {\nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\rho }}({s_A})} \right| = \sqrt {{{( - 26.8191)}^2} + {{53.0670}^2}} = 65.373$. We can represent the direction of $\nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\rho }}({s_A})$ as a unit vector ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\tau }}_u} = \frac{{\nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\rho }}}}{{\left| {\nabla {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\rho }}\left( {{s_A}} \right)} \right|}} = \left[ {\begin{array}{*{20}{c}} {\frac{{ - 26.8191}}{{65.373}}} \\ {\frac{{53.0670}}{{65.373}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}{c}} { - 0.43184} \\ {0.90195} \\ \end{array} } \right]$, and the perpendicular direction as ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\tau }}_v} = \left[ {\begin{array}{*{20}{c}} { - 0.90195} \\ { - 0.43184} \\ \end{array} } \right]$.

Coordinate Transformation

We can define the shrinkage rate φ as a function of the gradient strength using Eq. 9. For b = 2.5, the shrinkage rate φ for property A is given as $\varphi = {1 \mathord{\left/{\vphantom {1 {\sqrt {{{1 + 65.373} \mathord{\left/{\vphantom {{1 + 65.373} {2.5}}} \right.} {2.5}}} = 0.192}}} \right.} {\sqrt {{{1 + 65.373} \mathord{\left/{\vphantom {{1 + 65.373} {2.5}}} \right.} {2.5}}} = 0.192}}$. When ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\tau }}_u}$, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\tau }}_v}$, and φ are known, the distances in the local transformed coordinate system can be calculated using Eq. 8. For example, the new distance between properties A and A1 can be calculated as:

$$ \begin{array}{*{20}{c}} {d\prime \left( {{s_A},{s_{A1}}} \right) = \sqrt {{{\left( {\Delta {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{D}}}_{A1}}^\prime \cdot{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\tau }}}_u}} \right)}^2} + {{\left( {\varphi \Delta {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{D}}}_{A1}}^\prime \cdot{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\tau }}}_v}} \right)}^2}} } \\ { = \sqrt {{{\left( {{{\left[ {\begin{array}{*{20}{c}} {0.003754} \\ { - 0.000341} \\ \end{array} } \right]}^\prime } \times \left[ {\begin{array}{*{20}{c}} { - 0.43184} \\ {0.90195} \\ \end{array} } \right]} \right)}^2} + {{\left( {0.192 \times {{\left[ {\begin{array}{*{20}{c}} {0.003754} \\ { - 0.000341} \\ \end{array} } \right]}^\prime } \times \left[ {\begin{array}{*{20}{c}} { - 0.90195} \\ { - 0.43184} \\ \end{array} } \right]} \right)}^2}} } \\ { = 0.002020} \\ \end{array} . $$

Similarly, the distance between properties A and A2 can be recalculated as:

$$ \begin{array}{*{20}{c}} {d\prime \left( {{s_A},{s_{A2}}} \right) = \sqrt {{{\left( {\Delta {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{D}}}_{A2}}^\prime \cdot{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\tau }}}_u}} \right)}^2} + {{\left( {\varphi \Delta {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{D}}}_{A2}}^\prime \cdot{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\tau }}}_v}} \right)}^2}} } \\ { = \sqrt {{{\left( {{{\left[ {\begin{array}{*{20}{c}} {0.003442} \\ {0.002355} \\ \end{array} } \right]}^\prime } \times \left[ {\begin{array}{*{20}{c}} { - 0.43184} \\ {0.90195} \\ \end{array} } \right]} \right)}^2} + {{\left( {0.107 \times {{\left[ {\begin{array}{*{20}{c}} {0.003442} \\ {0.002355} \\ \end{array} } \right]}^\prime } \times \left[ {\begin{array}{*{20}{c}} { - 0.90195} \\ { - 0.43184} \\ \end{array} } \right]} \right)}^2}} } \\ { = 0.001024} \\ \end{array} . $$

The new distances between the twenty properties and property A under the local coordinate system are given in Table 7, column 5. Comparing the distances under both the geodetic and the local coordinate system, we can observe ordering changes. For example, property 17 is the seventeenth nearest property to property A under the geodetic coordinate system, but it ranks sixth under the local coordinate system.

For the local coordinate system, we can calculate range R′, to determine which properties make up the revised neighborhood, as follows: $R\prime = R\varphi = 0.027 \times 0.192 = 0.005184$. In this case, the nearest ten properties under both the geodetic coordinate system and transformed local coordinate system are with their own range (0.027 and 0.005184, respectively). So ten properties are chosen by both isotropic and anisotropic approach, but they are different ten properties.